Basins of coexisting multi-dimensional tori in a vibro-impact system

Abstract

Based on the method of Poincaré mapping under cell reference, we describe basins of attraction for coexisting multi-dimensional tori attractors in a three-degree-of-freedom vibro-impact system. Because the multi-dimensional tori attractors are very rare in the low-dimensional systems, we find that these coexisting tori attractors have positive measure basins in the sense of Milnor. The coexisting multi-dimensional tori attractors can be distinguished by the exactly Poincaré mapping and Lyapunov dimension. The basin of attraction can be estimated by the limit cycle in the Poincaré section from the viewpoint of engineering.

1 Introduction

It is well known that there may be multiple final stable motions, called attractors, in a nonlinear dynamical system [1]. The final state of a multi-stable system depends crucially on the initial conditions and the set of initial conditions that give rise to a set of trajectories converging toward to the attractor, are called basin of attraction for this attractor. An equilibrium is said to be a simple attractor if it is stable, and it will be a point attractor of the system which attracts all nearby orbits. Besides the zero-dimensional point attractors, there are also one-dimensional periodic attractors, called limit cycles. A quasiperiodic attractor (QA) with $N$ incommensurate frequencies is also denoted as torus ${T}^{N}$ [2]. Two types of strange attractors are referred to as chaotic attractors (CA) [3] and strange nonchaotic attractors (SNAs) [4], which usually chaotic attractors are characterize by sensitive dependence on initial conditions. Attractors for dynamical systems are traditionally viewed as being stable invariant sets which have a neighborhood that absorbs all sufficiently close initial conditions. However, in the absence of smoothness or invertibility, it is clear that more exotic attractors have no basins or only zero measure basins [5]. Partly in response to this problem, Milnor [6] introduced a concept of measure attractor (now usually called Milnor attractor), which is compact invariant set whose basin of attraction has positive measure in phase space. This gave a theoretical framework for understanding attractors (stable motions) with normal basins that are attracting for a large-measure set of initial conditions (ignoring initial conditions on a set of zero measure). As regard as the coexisting attractors in vibro-impact systems, earlier studies have shown excellent correlation between the coexisting attractors (a ${T}^{2}$ torus exhibiting a Hopf circle and a ${T}^{1}$ torus exhibiting a fixed point in a Poincaré section) and a degenerate Hopf bifurcation of Poincaré map in a two-degree-of-freedom impact oscillator [7]. A particular feature of multi-degree-of-freedom vibro-impact systems is the occurrence of so-called Hopf–Hopf bifurcations [8–10], which provides a fascinating feature in nonlinear dynamics, exhibiting multi-dimensional tori ${T}^{N}$ attractors. The motivation for the current work is the following: On the theoretical side, coexisting multi-dimensional tori ${T}^{N}$ is interesting in itself. In previous studies, two antisymmetric tori ${T}^{3}$ can coexist in a vibro-impact system with symmetric two-sided rigid constraints [11] and an unstable ${T}^{2}$ attractor embedded in ${T}^{3}$ attractor can be observed [12]. However, it is still not clear whether these coexisting attractors are Milnor attractors (with positive measure basin). Thus, it is necessary to investigate their basins of attraction. From the viewpoint of applications, this multi-stable phenomenon often can create inconvenience in the design of an impact device (e.g., a shaker) with specific characteristics, where multi-stability needs to be avoided or the desired state. To assess the significance of a specific attractor in vibro-impact system, it is necessary to know its basin of attraction. The main purpose of this paper is to describe the basins of attraction for the coexisting multi-dimensional tori attractors (coexisting tori ${T}^{3}$ and tori ${T}^{2}$, coexisting one-tori ${T}^{2}$and multi-tori ${T}^{2})$.

The attractors and their basins of attraction in the region of interest must be delineated to characterize the global behavior of the system [12]. No analytical method can accomplish such a global analysis effectively. There are a number of techniques for determining the basins of attraction for periodic solutions. Two kinds of cell mapping methods used for computing basins of attraction provide a useful insight into computational efficiency [13–15]. Virgin et al. [16] had used the interpolated cell mapping method to an impact-friction oscillator. Since interpolated cell mapping (ICM) method cannot distinguish multiple strange attractors or limit cycles, ICM cannot use for global analysis of presented multi-dimensional tori attractors. Thus, some modified or developed method based on cell mapping had been used for different types of systems, see, for example [17–19] and references therein. For three-degree-of-freedom vibro-impact system (higher-dimensional systems), the motion of this system is a combination of smooth motions governed by linear differential equation interrupted by a series of nonsmooth impacts and the flow of the solutions may experience a disjointed evolution. The multi-degrees-of-freedom cell mapping (MDCM) method overcomes the scaling limitations of other cell mapping methods, allowing efficiency benefits to be realized for higher-dimensional systems [20, 21]. These methods can improve computational efficiency for locating periodic attractors, which is still not precise to locate the tori ${T}^{3}$ and multi-tori ${T}^{2}$. For attractors with special properties, some analytical tools must be used to distinguish the types of attractors, e.g., the phase sensitivity exponent and the maximal Lyapunov exponent is used to detect the basins of SNAs [22]. Though these methods on global analysis are not straightforward to apply to the vibro-impact systems under the consideration of above elements, the good news is that the exact Poincaré map can be obtained in the vibro-impact system [23]. Furthermore, there are some studies on calculation of Lyapunov exponents and Lyapunov dimension in the vibro-impact systems [23–25], which these methods can distinguish tori ${T}^{N}$. We combine these techniques to locate tori attractors and consider the method of Poincaré mapping under cell reference [26–28]. We show that the coexisting tori attractors have positive measure basins in the sense of Milnor. Under suitable system parameter conditions, the system can exhibit different quasiperiodic behaviors. From the viewpoint of engineering, the basin of attraction for special ${T}^{2}$ tori motions can be estimated by the limit cycle in the Poincaré section.

2 Mechanical model and method on identifying multi-dimensional tori

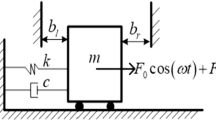
We consider a three-degree-of-freedom vibro-impact system, which is shown schematically in Fig. 1. The masses $M_1$ and $M_2$ are connected to linear springs with stiffness $K_1$ and $K_2$, and linear viscous dashpots with damping constants $C_1$ and $C_2$. The excitation on mass $M_1$ is harmonic with amplitudes $P$, the excitation frequency $\Omega$ and the phase $\tau$. The mass $M_3$ impacts against $M_1$ when $M_3$sinks from the upward side of $M_1$ due to gravitation. The displacements of $M_1$, $M_2$ and $M_3$, are represented by $X_1,X_2$ and $X_3$, respectively. The impact is described by a coefficient of restitution $R$, and it is assumed that the duration of impact is negligible compared to the period of the force. Damping in the mechanical model is assumed as proportional damping of the Rayleigh type.

Fig. 1

Schematics of the vibro-impact system

The system can be considered in a non-dimensional form, and all parameters and variables are assumed to be non-dimensional. The governing equations for the system away from impact can be expressed as

$$\begin{aligned} \mathbf{M}{\ddot{\mathbf X}}+ \mathbf{C}\dot{\mathbf {X}}+ \mathbf{KX}&= \bar{{\mathbf f}}\sin (\omega t+\tau ) \end{aligned}$$

(1)

$$\begin{aligned} \ddot{x}_3&= -\delta \end{aligned}$$

(2)

where $\mathbf{M} = \left[ {\begin{array}{cc} 1&{}0 \\ 0&{}\alpha \\ \end{array}} \right]$, $\mathbf{C}=\left[ {{\begin{array}{cc} {2\zeta (1+\beta )}&{} {-2\zeta \beta } \\ {-2\zeta \beta }&{} {2\zeta \beta } \\ \end{array} }} \right]$ and $\mathbf{K}=\left[ {{\begin{array}{cc} {1+\gamma }&{} {-\gamma } \\ {-\gamma }&{} \gamma \\ \end{array} }} \right]$ represents non-dimensional mass, damping and stiffness matrixes, respectively, $\mathbf{X}=(x_1,x_2 )^{T},{\bar{\mathbf{f}}}=(1,0)$, a dot $(\cdot )$ denotes differentiation with respect to the non-dimensional time $t$, and the non-dimensional quantities are given by

$$\begin{aligned} \alpha&= \frac{M_2}{M_1},\;\quad \beta =\frac{K_2}{K_1},\;\quad \gamma =\frac{C_2}{C_1},\;\;\mu =\frac{M_3}{M_1},\nonumber \\ \omega&= \Omega \sqrt{\frac{M_1}{K_1}},\quad t=T\sqrt{\frac{K_1}{M_1}},\quad \zeta =\frac{C_1 }{2\sqrt{K_1 M_1}},\nonumber \\ \delta&= \frac{M_3 g}{P}\;\quad x_i =\frac{X_i K_1 }{P}\quad (i=1,2,3) \end{aligned}$$

(3)

The impact equation of mass $M_1$ and $M_3$ may be modeled using an instantaneous coefficient of restitution rule such that $\dot{x}_{1-} +\mu \dot{x}_{3-} =\dot{x}_{1+} +\mu \dot{x}_{3+}$ and $\dot{x}_{1+} -\dot{x}_{3+} =-R(\dot{x}_{1-} -\dot{x}_{3-})$, where, $\dot{x}_{1-}$ and $\dot{x}_{3-}$ represent respectively velocities of mass $M_1$ and $M_3$ immediately before impact. And where, $\dot{x}_{1+}$ and $\dot{x}_{3+}$ represent respectively velocities of mass $M_1$ and $M_3$ immediately after impact.

Since the method using exact mappings can be used to locate exact attractors, we first give the exact Poincaré map of the system. Periodic-impact motions of the vibro-impact system can be characterized by the symbol $n-p$, where $p$ is the number of impacts and $n$ is the number of the forcing cycles. We found the analytical expressions for $n-1$ motion and its disturbed map of the system by choosing a Poincaré section $\sum =\{(x_1,\dot{x}_1 ,x_2,\dot{x}_2,x_3,\dot{x}_3,\theta )\in R^{6}\times S^{1}|x_1 =x_3,\dot{x}_1 =\dot{x}_{1+},\dot{x}_3 =\dot{x}_{3+} \}$ in [23]. Suppose that a periodic motion starts at the fixed point $\mathbf{X}^{\mathbf{*}}=(x_{10},\dot{x}_{10},x_{20},\dot{x}_{20},\dot{x}_{30},\tau )^{{T}}$ on $\sum$, we establish the Poincaré map associated with the periodic motion

$$\begin{aligned} \mathbf{\Delta }\mathbf{X}^{\prime }=\mathbf{f}(\varvec{\sigma },\varvec{\Delta } \mathbf{X}) \end{aligned}$$

(4)

where $\theta =\omega t$, $\varvec{\Delta } {\mathbf{X}}'\in R^{6}$ and ${\varvec{\Delta } \mathbf{X}}\in R^{6}$ are the perturbed vector of $\mathbf{X}^{*}$, $\varvec{\Delta } \mathbf{X}=(\Delta x_{10},\Delta \dot{x}_{1+},\Delta x_{20},\Delta \dot{x}_{20} ,\Delta \dot{x}_{30},\Delta \tau )^{{T}}$, ${\varvec{\Delta } \mathbf{X}'}\!=\!(\Delta {x}'_{10},\Delta {\dot{x}}'_{1+},\Delta {x}'_{20},\Delta {\dot{x}}'_{20},\Delta {\dot{x}}'_{30},\Delta {\tau }')^{{T}}$, ${\varvec{\sigma }}$ is the parameter vector.

In some vibro-impact systems, it is easy to visualize from an intuitive viewpoint when some coexisting attractors are shown in the Poincaré sections. A torus ${T}^{2}$ can easily be observed by a torus ${T}^{1}$ in a Poincaré section (Fig. 2). Similarly, a torus ${T}^{3}$ can easily be observed by a torus ${T}^{2}$ in a Poincaré section. If a torus ${T}^{1}$ becomes folded, we will denote the torus as multi-torus ${T}^{1}$. The Poincaré map technique can be used to identify the type of attractors qualitatively, such periodic attractors, quasi-periodic attractors, chaotic attractors. To verify the multi-dimensional tori attractors (the quasi-periodic attractors with different dimensions) in the vibro-impact system, we give the method to compute the Lyaponov dimension. The spectrum of Lyaponov exponents has been calculated for many smooth, continuous systems described by differential equation of motion and for discrete maps described by difference equations. But, if a system is nonsmooth, the calculation of Lyaponov exponents is not straightforward because of the discontinuity. We use a transcendental map that describes the solutions of the differential equations between impacts. In our previous work, we have obtained the transcendental map and the Jacobian matrix $J_n$ of the transcendental map by the analytical solution [23]. Suppose the variables just after the $n$-th impact is $\mathbf{X}_\mathbf{n}$, then the transcendental map can be obtained

$$\begin{aligned} \mathbf{X}_{\mathbf{n+1}} = \mathbf{F}(\mathbf{X}_\mathbf{n}) \end{aligned}$$

(5)

and its variational equation

$$\begin{aligned} \mathbf{Y}_{\mathbf{n+1}} = \mathbf{J}_\mathbf{n} \mathbf{Y}_\mathbf{n} \end{aligned}$$

(6)

For the considered systems, the transcendental maps are six-dimensional. In this case, the Lyapunov exponents are expressed by the following case

$$\begin{aligned} \lambda _j = {{\mathop {\lim }\limits _{{N\rightarrow \infty }}}} \frac{1}{N}\ln \left| {\Lambda _{j}{}^{N}} \right| \end{aligned}$$

(7)

where $\left| {\Lambda _{j}^{N}} \right|$ are eigenvalues of the matrix $\mathbf{M}={{\mathop {\Pi }\limits _{{n=1}}^{N}}}\mathbf{J}_\mathbf{n}$ and $\mathbf{J}_\mathbf{n}$ is the Jacobian matrix of the $n\hbox {th}$ iteration of the transcendental map. The Lyapunov exponents are ranked from large to small as $\lambda _1 \ge \lambda _2 \ge \cdots \ge \lambda _6$. The Eq. (7) cannot be used to calculate the Lyapunov exponents directly. The reason for this is that the components of matrix $\mathbf{M}$ become very large for chaotic attractors and null for the periodic attractors when the number of iteration of the transcendental map increases. To avoid the overflow trouble, we must convert the matrix $\mathbf{M}$ into a product of the orthogonal matrices and the upper right triangular matrices. In this way, the matrix $\mathbf{M}$ is transformed in product of the upper right triangular matrices, whose eigenvalues are the numbers along the diagonal and Lyapunov exponents can be expressed by

$$\begin{aligned} \lambda _j ={{\mathop {\lim }\limits _{N\rightarrow \infty }}} \frac{1}{N}\ln \left| {a_j ^{N}} \right| \end{aligned}$$

(8)

where $a_j ^{N}$ are diagonal components of $n\hbox {th}$ iteration of the product of the upper right triangular matrices. Thus, the convergence of the Lyapunov exponents occurs with good precision after just a few thousand iterations. Let $K$ be the largest integer such that $\lambda _1 +\lambda _2 +\cdots +\lambda _K \ge 0$, the Lyapunov dimension as defined by Kaplan and Yorke [29] is

$$\begin{aligned} D_L =K+\frac{\sum \nolimits _{i=1}^K {\lambda _i }}{\left| {\lambda _{K+1}} \right| } \end{aligned}$$

(9)

where $\sum \nolimits _{i=1}^K {\lambda _i} \ge 0$, $\sum \nolimits _{i=1}^{K+1} {\lambda _i}<0$. If no such $K$ exists, as is the case for a fixed point, $D_L$ is defined to be 0.

Fig. 2

Schematics of Poincaré section on a two-dimensional torus

Therefore, different multi-dimensional tori attractors are distinguished by the Lyapunov dimension.

3 Method of PMUCR and basins of coexisting multi-dimensional tori

The cell reference used in the vibro-impact system (1)–(2) is composed of a cell coordinate system. The cell coordinate system is the same as the one developed by Jiang and Xu, which is used to construct a cell space and the characteristic functions defined in the cell space [28]. A cell is no longer regarded as a mathematical element, and no map is defined in the cell space, namely, the cell references plays only a role as an inspector or a recorder and does not make any change on the results of the Poincaré mapping method in the initial step.

Let $x_i, i=1,2,\ldots ,N$ be the state variables of the state space. To construct a cell coordinate, divide the coordinate axis of a state variable $x_i$ into a countable infinite number of intervals of uniform size $h_i$. The interval $z_i$ along the $x_i$ -axis is defined to be one which contains all $x_i$ satisfying

$$\begin{aligned} (z_{i}-1/2)h_{i} <x_{i} \le (z_{i} +1/2)h_i \quad {i=1,\ldots ,N},\nonumber \\ \end{aligned}$$

(10)

where $z_i$ is an integer. A $N$ -tuple $z_i$ is then called a cell vector of the state space and denoted by $\mathbf{z}$. In this way, a cell coordinate system $\mathbf{Z}^{n}$ is created. For clarity, we give the brief notion, adding some important details (more details are shown in reference [30]). For any two cell vectors $\mathbf{z}$ and $\mathbf{{z}'}$, the distance between them denoted by $d(\mathbf{z},\mathbf{z}')=\max \left| {\mathbf{z}'_{i} -\mathbf{z}_{i} } \right| \quad (1<i<N)$. Two cells $\mathbf{z}$ and $\mathbf{{z}'}$ are adjoining if and only if $d(\mathbf{z},\mathbf{{z}'})=1$. The cells in the corresponding part of the cell coordinate are finite, say $N_{c}$ called the studied cells. Usually, a point $x$ in the state space is related to a cell represented by a positive integer $c$ and $c\in S=\{1,2,\ldots ,N_c \}$. We use two preliminary characteristic functions called the character identification function $Id(c)$ and the determinacy measurement function $Ib(c)$ by the cell reference. The values of $Id(c)$ and $Ib(c)$ can be stored by two one-dimensional integer arrays of length $N_c$. The value of $Id(c)$ is used to characterize the studied cell and the value of $Ib(c)$ of a cell reflects the number of processed points that this cell contains. A cell is called a virgin cell characterized by $Id(c)=0$ if the cell has not captured any processed pints, or no trajectory has started from or passed by the cell. A boundary cell characterized by $Id(c)=N_c$ refer to the processed points within the cell tend to different attractors. A basin cell (for the $n\hbox {th}$ attractor) is characterized by $Id(c)=n$ if all the processed points contained in the cell belong to the same basin of attraction of an attractor. An attracting cell of the $n\hbox {th}$ attractor is denoted by $Id(c)=-n$, which is defined as follows. The boundary cell is easily detected by the value of $Ib(c)$ when two processed points (belong to different basins of attraction) are detected within the cell. Since the value of $Ib(c)$ for the basin cell can be varies from a small number to a large number, an updating basin cell (UBC) is always used in the process of a computation. Given a large positive integer $I_p$ as an analyzer, if the processed points in UBC contain the points of a steady-state response and the number of processed points in this cell have no less than $I_p$, or if the number of the processed points in UBC exceeds a positive integer $I_{P*} (I_{P*} <I_p )$ and there are no three types of cells (virgin cells, boundary cells and UBC to other attractors to be the adjoining cells of basin cell), then this basin cell is called an attracting cell. All the attracting cells to a same attractor are denoted as an attracting set of the attractor.

Below, we introduce a computational method of PMUCR using the Poincaré map (4) and add the additional analyzer to previous method in order to detect the tori attractors. It is noted that each trajectory from an initial point is terminated when it settles on an attractor. More generally, a small number of initial points are used to detect all attractors in the chosen region as well as the corresponding initial attracting sets. For a given initial point $x_0$, first determine in which cell it is located, say $c_0$, then apply mapping (4) to get the image point $\mathbf{f}^{1}\mathbf{(x}_\mathbf{0} )$ and determine in which cell $\mathbf{f}^{1}\mathbf{(x}_\mathbf{0} )$ lies, say $c_1$. Repeat this process continuously and a sequence of points and a set of cells are obtained, which record the cells passed by this trajectory. In each step of generating trajectory, some criterions on detecting different attractors are used to check. For different periodic attractor, the method in the references [26–28] describes the process of implementation in more details. For different quasi-periodic attractor, the additional analyzer (e.g., Lyapunov dimensions) is used to distinguish different attractors. For the process $A : x_0 \rightarrow \mathbf{f}^{1}\mathbf{(x}_\mathbf{0} \mathbf{)} \rightarrow \mathbf{f}^{2}\mathbf{(x}_\mathbf{0})\rightarrow \cdots \rightarrow \mathbf{f}^{m}\mathbf{(x}_\mathbf{0})\rightarrow$, is companied by the process $B:c_0 \rightarrow c_1 \rightarrow c_2 \rightarrow \cdots \rightarrow c_{m} \rightarrow$. Assume the sequential number of $A$ is ${n}'$and all points in trajectory $A$ are marked to be the processed point of ${n}'\hbox {th}$ attractor. This process works in the following way. For a virgin cell $c_i$, the process $B$ is marked by $Id(c_i )$=0, assign $Id(c_i )={n}'$. For a cell $c_i$, in the process $B$ with $abs(Id(c_i ))={n}'$, keep $Id(c_i )$unchanged. For a cell $c_i$, in the process $B$ with $abs(Id(c_i ))\ne {n}'$, change $Id(c_i )$ to $N_c$. To update the value of$Ib(c_i )$, do $Ib(c_i )=Ib(c_i )$+1 for all the cells in the process $B$. After all the initial points have been processes in this manner, attractors can be accurately determined. Simultaneously, the cells studied have been classified into the virgin cells, the basin cells to different attractors and the boundary cells. Of course, a trajectory will be terminated when it is mapped into an attracting cell characterized by $Id(c_i )<0$ if we obtain the attracting sets. Namely, if the newly generated point $\mathbf{f}^{m}\mathbf{(x}_\mathbf{0} )$ is in a cell $c_{m}$ with $Id(c_m )\ge 0$, the generation is continued forward to the next point $\mathbf{f}^{m+1}\mathbf{(x}_\mathbf{0} )$ in the trajectory. If the newly generated point $\mathbf{f}^{m}\mathbf{(x}_\mathbf{0} \mathbf{)}$ is in a cell with $Id(c_m )<0$, the trajectory is terminated and all the points in this trajectory will be considered to be the processed points of attractor ${n}'$ with $Id(c_m )={n}'$. In order to construct a basin portrait of the region describe by

$$\begin{aligned}&\Omega =\{x\in R^{N}\left| {x_i ^{(l)}} \right. \le x_i \le x_i ^{(u)}, \nonumber \\&\qquad i=1,2\cap x_i =x_i ^{*},i=3,4,\ldots ,N\} \end{aligned}$$

(11)

where $x_i ^{\mathbf{*}}$ is the $i-\hbox {th}$ component element of fixed point $\mathbf{X}^{*}$ in the Poincaré map.

In the first example, the vibro-impact system with parameters (1): $\alpha =0.25, \beta =\gamma =0.35, R=0.07,\zeta =0.01, \mu =0.4, \delta =0.25, \omega =3.91$ have been chosen for analyses. The project region of the state space to be examined is defined by $-0.135\le x_2 \le -0.085$ and $-0.060\le x_2 \le 0.010$. For these parameters two coexisting multi-dimensional tori attractors exist. The coexistence of a torus ${T}^{3 }$ (red) and a torus ${T}^{2}$ (blue) attractor is presented (Fig. 3a, b) where a torus ${T}^{3}$ is presented by a torus ${T}^{2}$ in a Poincaré section in Fig. 3a and a torus ${T}^{2}$ attractor is presented by a torus ${T}^{1}$ in a Poincaré section in Fig. 3b. We calculate their Lyapunov exponents and Lyapunov dimensions (shown in Table 1). The Lyapunov dimension of Fig. 3a is 3 and the Lyapunov dimension of Fig. 3b is 2. In the second example, the vibro-impact system with parameters (2): $\alpha =0.25,\beta =\gamma =0.35,R=0.07,\zeta =0.01, \mu =0.4, \delta =0.25, \omega =3.92$ have been chosen for analyses. A multi-torus ${T}^{2}$ (red) and one-torus ${T}^{2}$ (blue) can also coexist, where a multi-torus ${T}^{2}$ is presented by a multi-torus ${T}^{1}$ in a Poincaré section in Fig. 3c and a one-torus ${T}^{2}$ attractor is presented by a one-torus ${T}^{1}$ in a Poincaré section in Fig. 3d. Table 1 shows that their Lyapunov dimensions are 2. We will show that these coexisting multi-dimensional tori attractors have positive measure basins in the sense of Milnor. To get a fine resolution of basins of attraction of an $800\times 800$ plot, a cell coordinate system is built in the state space, which overlays a cell array of dimension $800\times 800$ in the chose region. The sets of cells studied consist of 640,000 cells. Two integer arrays, $Id(640{,}000)$ and $Ib(640{,}000)$ are used to store the updating values of the character identification function and the character certainty function. Still, it must be noted that the coexisting attractors present an illusion of overlap in the project section. A grid of $60\times 60$ initial points is used to determine attractors and the initial attracting set. For example, Fig. 4a, b shows the initial attracting set to two tori attractors for parameters (2). The attracting cells are selected from the basin cells whose $Ib(c)$ values are larger than 1,000. Figure 5a describes their basins of attraction, where the basin of the torus ${T}^{1}$ is shown in light gray and the basin of the torus ${T}^{2}$ is shown in white for parameters (1). Figure 5b describes the basins of multi-torus ${T}^{2}$ and one-torus ${T}^{2}$, where the basin of the one-dimensional multi-torus is shown in gray and the basin of the one-torus ${T}^{1}$ is shown in white for parameters (2). Obviously, their basins have positive measures so that these tori attractors are common in the sense of Milnor. From the viewpoint of engineering, we can estimate the basin of attraction for this type of coexisting attractors. It is very easy to find the limit cycle attractors when we find the fixed point of the Poincaré map for the vibro-impact systems. For the vibro-impact systems with linear ODEs coupled to an impact map at collisions between the two primary components, it is not a difficult task. Figure 5c, d gives two examples to estimate the basins (gray) of limit cycles.

Fig. 3

Coexisting multi-dimensional tori ${T}^{N}$ attractors in a Poincaré section. a Torus ${T}^{2}$ (in red) for $\omega =3.91$; b torus ${T}^{1}$ (in blue) for $\omega =3.91$; c one-dimensional multi-torus for $\omega =3.92$; d one-dimensional one-torus ${T}^{1}$ (in blue) for $\omega =3.92$. (Color figure online)

Fig. 4

Attracting sets correspond two attractors for $\omega =3.92$: a multi-torus ${T}^{2}$; b one-torus ${T}^{2}$

Fig. 5

Basin of attraction. a The basin of the torus ${T}^{1}$ is shown in light gray and the basin of the torus ${T}^{2}$ is shown in white for $\omega =3.91$; b the basin of the one-dimensional multi-torus is shown in gray and the basin of the one-torus ${T}^{1}$ is shown in white for $\omega =3.92$; c estimate the basin of attraction for the torus ${T}^{1}$ for $\omega =3.91$; d estimate the basin of attraction for the torus ${T}^{1}$ for $\omega =3.92$

Table 1 The Lyapunov exponents, Lyapunov dimension, and the type of attractors

4 Conclusions

Precious results show that the vibro-impact systems have coexisting periodic attractors and chaotic attractors. It is interesting and striking to see that this vibro-impact system reported here has coexisting multi-dimensional tori attractors. We investigated their basins and answer the question about the existence of these attractors in the sense of Milnor. We combine Poincaré map mapping and Lyapunov dimension techniques to describe tori attractors. We described their basins of attraction by the method of PMUCR. In the precious work on the PMUCR, it is used to detect the periodic attractors in two-dimensional systems. Here, we have tried to expend this method to the nonsmooth systems with high dimensions. We combined the idea of multi-degrees-of-freedom cell mapping and construct a basin portrait of the studied regions by a two-dimensional subset [20]. In this two-dimensional section, we introduce the cell reference method and the method has reduced the computational cost. The vibro-impact systems shown in Fig. 1 (or others [7, 11]) are piecewise linear hybrid dynamical systems with linear ODEs coupled to an impact map at collisions between the two primary components. It is not hard to obtain the exact Poincaré map which provides an accurately global analysis method for this type of vibro-impact systems. Thus, we can verify that coexisting tori attractors have positive measure basins in the sense of Milnor.

We have done a large number of numerical experiments and found that these coexisting tori attractors can occur in other parameters. In the implementation of PMUCR for some vibro-impact systems or different parameters, a factor (the number of processed points may be very large) will affect the accuracy and efficiency of the computation except for the choice the discretization of the state or the cell size of the cell reference. In order to keep the accuracy, it is of importance to choose the number of processed points. An important application where the model studied here may be of use is in the dynamics of vibration hammers, impact dampers, inertial shakers, pile drivers, offshore structures, and machinery. The basin dynamics play an important role in assessing the significance of a specific attractor (motion). Statistically speaking, the more important attractors may have large basins of attraction. The larger the relative size of a basin of attraction, the higher the probability that an initial condition picked at random will converge to this attractor. Thus, the results and methods may help engineers to design system parameters or select expected motions. We believe that the arguments of this paper concerning the basin for special tori attractors can also be applied to other vibro-impact systems.