Coexistence of strange nonchaotic attractors and a special mixed attractor caused by a new intermittency in a periodically driven vibro-impact system

Abstract

We focus on the coexistence of strange nonchaotic attractors (SNAs) and a novel mixed attractor in a periodically driven three-degree-of-freedom vibro-impact system with symmetry. SNAs are characterized by the local largest Lyapunov exponent and the phase sensitivity property. The Poincaré map P is the twofold composition of a six-dimensional implicit map Q, implying the symmetry of the vibro-impact system. Since the map Q can capture two conjugate attractors, it is used to investigate the dynamics of the system. With a suitable parameter combination, the Poincaré map P of the vibro-impact system exhibits Neimark–Sacker–pitchfork (NS-P) bifurcation. It is shown that dense phase-locking regions exist in a small parameter interval near this NS-P bifurcation point. Three types of attractors alternate in this small interval: two conjugate phase-locked periodic attractors, two conjugate SNAs and a special type of mixed attractor. As the force frequency $\omega$ is increased gradually, many phase-locking regions disappear, and the coexistence of two conjugate SNAs takes place instead, which is accompanied by a quick decrease in the width of phase-locking. If two conjugate strange nonchaotic limit sets are suddenly embedded in a chaotic one, a special mixed attractor is caused by a new intermittency accompanied by symmetry restoring bifurcation. This symmetry restoring bifurcation is the result of the collision between two conjugate strange nonchaotic limit sets and a symmetric limit set.

1 Introduction

Grebogi et al. [1] first reported an interesting and unusual attractor named strange nonchaotic attractors (SNAs) that exist typically in quasiperiodically forced systems. SNAs are strange in the geometrical sense, but are nonchaotic in the dynamical sense. Corresponding to regular motion, they do not show sensitivity with respect to changes in the initial conditions, i.e., all their Lyapunov exponents are negative. However, typical trajectories experience arbitrarily long time intervals of expansion similar to those for chaotic attractors. There are various mechanisms which have been proposed for the birth of SNA in quasiperiodically forced systems, including blowout bifurcation [2], symmetry breaking and tori-collision [3, 4], fractalization of a torus [5–8], intermittency routes [9–12], boundary crisis [13, 14], interior crisis [15, 16], band-merging transitions [17], bubbling route [18, 19]. Feudel et al. [20] show that for the quasiperiodically forced circle map at sufficiently large forcing, a positive Lebesgue measure set in parameter space corresponding to SNA is interspersed with regions of two-frequency quasiperiodic phase-locking. The study of the width of the largest phase-locking region with zero rotation number suggests that the phase-locking regions in parameter space are connected with the appearance of the SNA. Furthermore, the influence of the quasiperiodic force on the shape of the phase-locking regions in parameter space was studied in Ref. [21]. It is shown that on the boundary of the phase-locking regions a collision of stable and unstable invariant curve takes place. This collision leads to the birth of SNAs or three-frequency torus motion. SNAs may be created as the shape of the phase-locking regions turns from tongue-like to leaf-like with the increasing of the forcing. Since SNAs studied in [1–21] all exist in quasiperiodically forced systems, we are facing an interesting and unavoidable question: is the external quasiperiodic force the necessary condition for the birth of SNAs? That is, can SNAs be observed in other systems that are not driven by quasiperiodically force? Grebogi et al. [1] proposed a conjecture that, in general, continuous time systems which are not externally driven at two incommensurate frequencies should not be expected to have SNAs except possibly on a set of measure zero in the parameter space. An apparent SNA in an autonomous four-dimensional mapping was reported in [22]. However, the accurate calculation of the largest Lyapunov exponents shows that this claim on the observation of a SNA in the autonomous system is not confirmed [23]. Recently, it is shown that SNA can be observed near a codimension three bifurcation point in a periodically driven nonlinear vibro-impact system [24]. The author argues that the creation of SNA is the result of the collision of doubled torus with some unstable periodic orbits. In this paper, we observe the coexistence of SNAs near a NS-P bifurcation point in a periodically driven vibro-impact system with symmetry. It is shown that the appearance of SNAs is closely related to a quick decrease in the width of phase-locking regions, which coincides well with the mechanism suggested in Ref. [20, 21]. The SNA is characterized by the local largest Lyapunov exponent and the phase sensitivity property.

There are symmetry-increasing bifurcations in the discrete dynamics of symmetric mappings [25], in which two (or more) chaotic attractors merge to form a single chaotic attractor with symmetry. As the control parameter crosses a crisis, two attractors may both simultaneously touch the basin boundary separating their two basins [26]. This also means that two attractors collide with saddle unstable orbits on the basin boundary [27, 28]. After the crisis, the characteristic behavior is an intermittent switching between behaviors characteristic of attractors before merging. The term crisis-induced intermittency is used to describe the characteristic temporal behavior which occurs for this crisis. It is shown that bifurcations might otherwise be called symmetry breaking; symmetry creation via collision and symmetry creation via explosion are all the result of a collision between conjugate attractors (i.e., attractors that related to each other by the symmetry) and a symmetry limit set [29]. In this paper, we reveal a special mixed attractor which is caused by a new intermittency accompanied by symmetry restoring bifurcation in a periodically driven vibro-impact system. This mixed attractor contains three components: two conjugate strange nonchaotic limit sets and a chaotic one.

Study on the dynamics of the vibro-impact system has important significance for the optimization design and noise control in the mechanical system. Because of the existence of the impact, vibro-impact systems are strongly nonlinear. Vibro-impact systems can exhibit abundant dynamical behaviors and offer a good platform for nonlinear dynamics and nonsmooth dynamics. References [30–33] considered the single-degree-of-freedom vibro-impact system and investigated the existence of periodic motion and its stability, bifurcation and chaotic behavior. For multi-degree-of-freedom vibro-impact system, two or more bifurcation types may coexist at the bifurcation point, which leads to various codimension two bifurcations. These bifurcation types interact with each other, which has important effects on the local dynamics of the vibro-impact system. Using the center manifold-normal form theory and numerical simulations, Refs. [34–37] studied many codimension two bifurcations systematically, including Hopf-flip bifurcation, Hopf–Hopf bifurcation, Hopf bifurcation in various strong resonance cases, and Neimark–Sacker–pitchfork (NS-P) bifurcation. When the control parameter varies to some critical point, the oscillator of the vibro-impact system will impact with the impact side by zero velocity. This phenomenon in vibro-impact systems is known as “grazing.” At the grazing point, the Poincaré map of the system is discontinuous, and some nontypical bifurcations can be induced by such nonsmooth factor [38–47]. For some other studies on the dynamics of vibro-impact systems in recent years, see [48–62]. In this paper, we considered the periodically driven vibro-impact system with symmetry discussed in [37, 60, 61]. In this paper, we show that dense phase-locking regions exist in a small parameter interval near a Neimark–Sacker–pitchfork (NS-P) bifurcation point. Three types of attractors alternate in this small interval: two conjugate phase-locked periodic attractors, two conjugate SNAs and a special type of mixed attractor. The relationship of these three types of attractors is also discussed.

The paper is organized as follows: Sect. 2 represents the mechanical model, the expressions of the virtual implicit Poincaré map Q and the computation of the Jacobi matrix. In Sect. 3, for six-dimensional map Q, phase sensitivity property and local Lyapunov exponent are introduced to characterize SNA. In Sect. 4, symmetric fixed point and symmetric limit set are defined, and symmetry restoring bifurcation of limit set is discussed. In Sect. 5, by numerical simulations, we study the coexistence of SNAs and a special type of mixed attractor caused by a new intermittency near the NS-P bifurcation point. Conclusions are given in Sect. 6.

2 Mechanical model, virtual implicit Poincaré map Q and Jacobi matrix

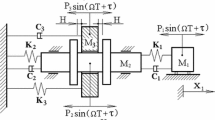
A three-degree-of-freedom system with symmetric two-sided rigid constraints is shown in Fig. 1 [37, 60, 61]. The system has three masses $M_1$, $M_2$, $M_3$. $M_2$ is a horizontal shaft with two stops and is connected to rigid plane via linear spring $K_2$ and linear viscous dashpot $C_2$. $M_1$ and $M_3$ are connected to $M_2$ via linear springs $K_1$ and $K_3$, and linear viscous dashpots $C_1$ and $C_3$, respectively. The excitation on mass $M_i$ ($i=1,2,3)$ is harmonic with amplitude $P_i$. For small forcing amplitudes, the system undergoes simple oscillations and behaves as a linear system. However, as the amplitudes increased, $M_3$ begins to collide with two stops of $M_2$, and the system becomes strongly nonlinear. The impact is described by a coefficient of restitution r. $C_1$, $C_2$ and $C_3$ are assumed as proportional damping.

Fig. 1

Three-degree-of-freedom vibro-impact system with symmetry

According to Newton’s second law, between any two consecutive impacts, the control equation of motions is

$$\begin{aligned} \left. \begin{array}{l} {M_1 \ddot{X}_1 =P_1 \sin (\Omega T+\tau )-C{ }_1(\dot{X}_1 -\dot{X}_2 )-K_1 (X_1 -X_2 )} \\ {\begin{array}{c} M_2 \ddot{X}_2 =P_2 \sin (\Omega T+\tau )+C_1 (\dot{X}_1 -\dot{X}_2 )+K_1 (X_1 -X_2 ) \\ \quad -C_2 \dot{X}_2 -K_2 X_2 +C_3 (\dot{X}_3 -\dot{X}_2 )+K_3 (X_3 -X_2 ) \\ \end{array}} \\ {M_3 \ddot{X}_3 =P_3 \sin (\Omega T+\tau )-C{ }_3(\dot{X}_3 -\dot{X}_2 )-K_3 (X_3 -X_2 )} \\ \end{array}\right\} , \end{aligned}$$

(1)

and the nondimensional differential equation of motion is given by

$$\begin{aligned} \mathbf{M}{\ddot{\mathbf{Y}}}+2\zeta \mathbf{C} {\dot{\mathbf{Y}}}+\mathbf{KY}=\mathbf{P}f\sin (\omega t+\tau ), \end{aligned}$$

(2)

where $\mathbf{Y}\,{=}\,[x_1 ,x_2 ,x_3 ]^{\mathbf{T}}$, $\mathbf{M}\,{=}\,\hbox {diag}[u_{m_1 } ,u_{m_2 } ,u_{m_3 } ]$, $\mathbf{P}=[u_{f_1 } ,u_{f_2 } ,u_{f_3 }]^{\mathbf{T}}$, $\mathbf{C}=\left[ {{\begin{array}{lll} {u_{c_1 } }&{} {-u_{c_1 } }&{} 0 \\ {-u_{c_1 } }&{} {u_{c_1 } +u_{c_2 } +u_{c_3 } }&{} {-u_{c_3 } } \\ 0&{} {-u_{c_3 } }&{} {u_{c_3 } } \\ \end{array}}} \right] ,\quad \mathbf{K}=\left[ {{\begin{array}{lll} {u_{k_1 } }&{} {-u_{k_1 } }&{} 0 \\ {-u_{k_1 } }&{} {u_{k_1 } +u_{k_2 } +u_{k_3 } }&{} {-u_{k_3 } } \\ 0&{} {-u_{k_3 } }&{} {u_{k_3 } } \\ \end{array} }} \right] .$ The nondimensional variables and parameters are: $t=T\sqrt{\frac{K_3 }{M_3 }}$, $\zeta =\frac{C_3 }{2\sqrt{K_3 M_3 }}$, $\omega =\Omega \sqrt{\frac{M_3 }{K_3 }}$, $f=\frac{P_3 }{P_0 }$, $u_{m_i } =\frac{M_i }{M_3 }$, $u_{k_i } =\frac{K_i }{K_3 }$, $u_{c_i } =\frac{C_i }{C_3 }$, $u_{f_i } =\frac{P_i }{P_3 }$, $x_i =\frac{X_i K_3 }{P_0 }$, where $P_0 =\sum \nolimits _{i=1}^3 {\left| {P_i } \right| }$, $i=1, 2, 3$.

As $M_3$ collides with the left and the right stops of $M_2$, the nondimensional displacements of two masses satisfy $\left| {x_2 -x_3 } \right| \equiv h$, where $h=\frac{K_1 H}{P_0 }$. Newton’s impact model is used for the process of impact. The velocity of $M_i$ at time t is denoted by $y_i (t)=\dot{x}_i (t)$. Let $y_{i-} =\dot{x}_{i-}$, $y_{i+} =\dot{x}_{i+}$ be the nondimensional velocities of $M_i$ before and after impact, respectively. After each impact, the velocities of $M_2$ and $M_3$ change as follows according to the impact law and the momentum conservation rule:

$$\begin{aligned} y_{2+}= & {} \delta _{11} y_{2-} +\delta _{12} y_{3-},\nonumber \\ y_{3+}= & {} \delta _{21} y_{2-} +\delta _{22} y_{3-}, \end{aligned}$$

(3)

where $\delta _{11} =\mu (u_{m2} -r)$, $\delta _{12} =\mu (1+r)$, $\delta _{21} =\mu u_{m2} (1+r)$, $\delta _{22} =\mu (1-u_{m2} r)$, and $\mu =\frac{1}{1+u_{m2} }$.

The three differential equations in Eq. (2) are coupling, and $\mathbf{M}$, $\mathbf{K}$ and $\mathbf{C}$ are all symmetric matrixes. The three undamped natural frequencies are the positive roots of the following frequency equation [63]:

$$\begin{aligned} u_d= & {} u_{m1} u_{m2} u_{m3} \omega ^{6}-(u_{k1} u_{m2} u_{m3} \nonumber \\&+\,u_{m1} u_k u_{m3} +u_{m1} u_{m2} u_{k3} )\omega ^{4} \nonumber \\&+\,(u_{k1} u_k u_{m3} +u_{k1} u_{m2} u_{k3} +u_{m1} u_k u_{k3}\nonumber \\&-\,u_{m1} u_{k3}^2 -u_{k1}^2 u_{m3} )\omega ^{2}-u_{k1} u_2 u_{k3} =0 \end{aligned}$$

(4)

where $u_k =u_{k1} +u_{k2} +u_{k3}$. Equation (4) is a cubic equation about $\omega ^{2}$. Then $\omega _i^2 \quad (i=1,2,3)$ can be solved firstly, and the three positive roots $\omega _i$ are obtained subsequently.

The dominant mode matrix can be obtained as [63]

$$\begin{aligned} {\varvec{{\upvarphi }}}=\left[ {{\varvec{{\upvarphi }}}{ }_1,{\varvec{{\upvarphi }}}_2 ,{\varvec{{\upvarphi }}}_3 } \right] , \end{aligned}$$

(5)

where ${\varvec{{\upvarphi }}}_i =\left[ {{\begin{array}{lll} {\frac{u_{k1} (-u_{m3} \omega _i^2 +u_{k3} )}{u_{k3} (u_{k1} -u_{m1} \omega _i^2 )}}&{} {\frac{-u_{m3} \omega _i^2 +u_{k3} }{u_{k3} }}&{} 1 \\ \end{array} }} \right] ^{\mathbf{T}}$, $(i=1,2,3)$. Let the dominant mass matrix be $\mathbf{M}_P ={\varvec{{\upvarphi }}}^{T}{} \mathbf{M{\upvarphi }}=\hbox {diag}\left[ {{\begin{array}{lll} {M_{P1} }&{} {M_{P2} }&{} {M_{P3} } \\ \end{array} }} \right]$, and the dominant stiffness matrix be $\mathbf{K}_P ={\varvec{{\upvarphi }}}^{T}{} \mathbf{K{\upvarphi }}$. Then the normal mode matrix is expressed as

$$\begin{aligned} {\varvec{\uppsi }}=\left[ {{\begin{array}{lll} {\frac{{\varvec{{\upvarphi }}}_1 }{\sqrt{M_{P1} }}}&{} {\frac{{\varvec{{\upvarphi }}}_2 }{\sqrt{M_{P2} }}}&{} {\frac{{\varvec{{\upvarphi }}}_3 }{\sqrt{M_{P3} }}} \\ \end{array} }} \right] . \end{aligned}$$

(6)

As shown in Ref. [63], because $\mathbf{M}$ and $\mathbf{C}$ are both symmetric matrixes, the property of orthogonality of any two modes exists. Making the change of variable $\mathbf{Y}={\varvec{\uppsi }} \mathbf{Z}$, based on the relations of orthonormality, the corresponding mass matrix is ${\varvec{\uppsi }}^{T}{} \mathbf{M}\varvec{\psi }=\mathbf{I}$ (i.e., identity matrix), and the stiffness matrix is ${\varvec{\uppsi }}^{T}\mathbf{K\psi }={\varvec{\Lambda }}=\hbox {diag}\left[ {{\begin{array}{lll} {\omega _1^2 }&{} {\omega _2^2 }&{} {\omega _3^2 } \\ \end{array} }} \right]$. Since $C_1$, $C_2$ and $C_3$ are assumed to be mass-proportional and stiffness-proportional, Eq. (2) can be decoupled as

$$\begin{aligned} \mathbf{I}{\ddot{\mathbf{Z}}}+\mathbf{C}{\dot{\mathbf{Z}}}+{\varvec{\Lambda }}{} \mathbf{Z}={\bar{\mathbf{P}}}\sin (\omega t+\tau ), \end{aligned}$$

(7)

where $\mathbf{C}=2\zeta {\varvec{\Lambda }}$, ${\bar{\mathbf{P}}}={\varvec{\uppsi }}^{\mathbf{T}}{} \mathbf{P}f$.

Let $\psi _{ij}$ denote the element of ${\varvec{\uppsi }}$, based on the solutions of Eq. (7), the general solution of Eq. (2) is given by [63]

$$\begin{aligned} x_i (t)= & {} \sum _{j=1}^3 {\psi _{ij} } \{e^{-\eta _j t}[a_j \cos (\omega _{dj} t)+b_j \sin (\omega _{dj} t)]\nonumber \\&+\,A_j \sin (\omega t+\tau )+B_j\cos (\omega t+\tau )\}, \end{aligned}$$

(8a)

$$\begin{aligned} y_i (t)= & {} \dot{x}_i (t)=\sum _{j=1}^3 {\psi _{ij} } \{e^{-\eta _j t}\nonumber \\&\times \left[ (-\eta _j a_j +\omega _{dj} b_j )\cos (\omega _{dj} t)\right. \nonumber \\&\left. +\,(-\eta _j b_j -\omega _{dj} a_j )\sin (\omega _{dj} t)\right] \nonumber \\&+\,A_j \omega \cos (\omega t+\tau )-B_j \omega \sin (\omega t+\tau )\} \end{aligned}$$

(8b)

where $\eta _j =\zeta \omega _j^2$, $\omega _{dj} =\sqrt{\omega _j^2 -\eta _j^2 }$, $j=1,2,3$. And $a_j$ and $b_j$ are integration constants determined by the initial conditions, $A_j$ and $B_j$ are amplitude constants: $A_j =\delta (\omega _j^2 -\omega ^{2})\bar{{P}}_j$, $B_j =-2\delta \eta _j \omega \bar{{P}}_j$, where $\delta =\frac{1}{(2\eta _j \omega )^{2}+(\omega _j^2 -\omega ^{2})^{2}}$ and ${\bar{{P}}}_j$ is the element of ${\bar{\mathbf{P}}}$.

The Poincaré section ${\varvec{\Pi }}_0$ is chosen at the moment after impacting at the left stop, where $x_2 -x_3 \equiv h$. The Poincaré map $\mathbf{P}$ is a composition of following four submaps: (1) $\mathbf{P}_1$: the map from the instant after impacting at the left stop to the instant before impacting at the right stop; (2) $\mathbf{P}_2$: the map of impacting at the right stop; (3) $\mathbf{P}_3$: the map from the instant after impacting at the right stop to the instant before impacting at the left stop; (4) $\mathbf{P}_4$: the map of impacting at the left stop. Hence, the Poincaré map can be expressed as: $\mathbf{P}=\mathbf{P}_4 \circ \mathbf{P}_3 \circ \mathbf{P}_2 \circ \mathbf{P}_1$, where the symbol “$\circ$” denotes the composition of two maps.

Let $\mathbf{Q}_u$ denote the map from the instant after impacting at the left stop to that after impacting at the right stop (i.e., $\mathbf{Q}_u =\mathbf{P}_2 \circ \mathbf{P}_1 )$ and $\mathbf{Q}_v$ denote the map from the instant after impacting at the right stop to that after impacting at the left stop (i.e., $\mathbf{Q}_v =\mathbf{P}_4 \circ \mathbf{P}_3 )$, then $\mathbf{P}=\mathbf{Q}_v \circ \mathbf{Q}_u$. Let the coordinates of map point be $(x_1 ,x_2 ,x_3 ,y_1 ,y_2 ,y_3 )$, where $y_i =\dot{x}_i$ is the velocity of $M_i$; Eq. (2) can be rewritten as ${\dot{\mathbf{X}}}=\mathbf{F}(\mathbf{X},t)$. Based on the expressions of $\mathbf{F}(\mathbf{X},t)$, two relations $\mathbf{F}(\mathbf{X},t+\frac{2\pi }{\omega })=\mathbf{F}(\mathbf{X},t)$ and $\mathbf{F}(-\mathbf{X},t+\frac{\pi }{\omega })=-\mathbf{F}(\mathbf{X},t)$ exist. Defining a transformation: $\mathbf{R}:(\mathbf{X},t)\mapsto (-\mathbf{X},t+\frac{n\pi }{\omega })$, where n is an odd integer, we have

$$\begin{aligned} \mathbf{RF}(\mathbf{X})=\mathbf{F}(\mathbf{RX}). \end{aligned}$$

(9)

Introducing a map $\mathbf{Q}=\mathbf{R}^{-1}\circ \mathbf{Q}_u$, it has been proved in [37] that

$$\begin{aligned} \mathbf{Q}_v =\mathbf{R}\circ \mathbf{Q}_u \circ \mathbf{R}^{-1}, \end{aligned}$$

(10)

then the Poincaré map can be expressed as :

$$\begin{aligned} \mathbf{P}= & {} \mathbf{Q}_v \circ \mathbf{Q}_u =\mathbf{R}\circ \mathbf{Q}_u \circ \mathbf{R}^{-1}\circ \mathbf{Q}_u\nonumber \\= & {} \mathbf{R}^{2}\circ (\mathbf{R}^{-1}\circ \mathbf{Q}_u )^{2}=\mathbf{Q}^{2}. \end{aligned}$$

(11)

Now we give the expressions of map Q. Since $\mathbf{Q}=\mathbf{R}^{-1}\circ \mathbf{Q}_u$ and $\mathbf{Q}_u =\mathbf{P}_2 \circ \mathbf{P}_1$, according to Eqs. (3) and (8), the map Q can be expressed as

$$\begin{aligned}&{} \mathbf{Q}:R^{6}\rightarrow R^{6}:\nonumber \\&x_1 (n+1)=f_1 (x_1 (n),x_2 (n),y_1 (n),y_2 (n),y_3 (n),\tau (n))\nonumber \\&\quad =-\sum _{j=1}^3 {\psi _{1j} } \{e^{-\eta _j t}[a_j \cos (\omega _{dj} t)+b_j \sin (\omega _{dj} t)]\nonumber \\&\qquad +\,A_j \sin (\omega t+\tau (n))+B_j \cos (\omega t+\tau (n))\}, \end{aligned}$$

(12a)

$$\begin{aligned}&x_2 (n+1)=f_2 (x_1 (n),x_2 (n),y_1 (n),y_2 (n),y_3 (n),\tau (n)) \nonumber \\&\quad =-\sum _{j=1}^3 {\psi _{2j} } \{e^{-\eta _j t}[a_j \cos (\omega _{dj} t)+b_j \sin (\omega _{dj} t)]\nonumber \\&\qquad +\,A_j \sin (\omega t+\tau (n))+B_j \cos (\omega t+\tau (n))\}, \end{aligned}$$

(12b)

$$\begin{aligned}&y_1 (n+1)=f_3 (x_1 (n),x_2 (n),y_1 (n),y_2 (n),y_3 (n),\tau (n)) \nonumber \\&\quad =-\sum _{j=1}^3 {\psi _{ij} } \{e^{-\eta _j t}[(-\eta _j a_j +\omega _{dj} b_j )\cos (\omega _{dj} t)\nonumber \\&\qquad +\,(-\eta _j b_j -\omega _{dj} a_j )\sin (\omega _{dj} t)] \nonumber \\&\qquad +\,A_j \omega \cos (\omega t+\tau (n))-B_j \omega \sin (\omega t+\tau (n))\},\nonumber \\ \end{aligned}$$

(12c)

$$\begin{aligned}&y_2 (n+1)=f_4 (x_1 (n),x_2 (n),y_1 (n),y_2 (n),y_3 (n),\tau (n))\nonumber \\&\quad =-\delta _{11} \sum _{j=1}^3 {\psi _{2j} } \{e^{-\eta _j t}[(-\eta _j a_j +\omega _{dj} b_j )\cos (\omega _{dj} t)\nonumber \\&\qquad +\,(-\eta _j b_j -\omega _{dj} a_j )\sin (\omega _{dj} t)] \nonumber \\&\qquad +\,A_j \omega \cos (\omega t+\tau (n))\nonumber \\&\qquad -\,B_j \omega \sin (\omega t+\tau (n))\}\nonumber \\&\qquad -\,\delta _{12} \sum _{j=1}^3 {\psi _{3j} } \{e^{-\eta _j t}[(-\eta _j a_j +\omega _{dj} b_j )\cos (\omega _{dj} t)\nonumber \\&\qquad +\,(-\eta _j b_j -\omega _{dj} a_j )\sin (\omega _{dj} t)]\nonumber \\&\qquad +\,A_j \omega \cos (\omega t+\tau (n))-B_j \omega \sin (\omega t+\tau (n))\},\nonumber \\ \end{aligned}$$

(12d)

$$\begin{aligned}&y_3 (n+1)=f_5 (x_1 (n),x_2 (n),y_1 (n),y_2 (n),y_3 (n),\tau (n)) \nonumber \\&\quad =-\delta _{21} \sum _{j=1}^3 {\psi _{2j} } \{e^{-\eta _j t}[(-\eta _j a_j +\omega _{dj} b_j )\cos (\omega _{dj} t)\nonumber \\&\qquad +\,(-\eta _j b_j -\omega _{dj} a_j )\sin (\omega _{dj} t)] \nonumber \\&\qquad +\,A_j \omega \cos (\omega t+\tau (n))-B_j \omega \sin (\omega t+\tau (n))\}\nonumber \\&\qquad -\,\delta _{22} \sum _{j=1}^3 {\psi _{3j} } \{e^{-\eta _j t}[(-\eta _j a_j +\omega _{dj} b_j ) \cos (\omega _{dj} t)\nonumber \\&\qquad +\,(-\eta _j b_j -\omega _{dj} a_j )\sin (\omega _{dj} t)]+A_j \omega \cos (\omega t+\tau (n))\nonumber \\&\qquad -\,B_j \omega \sin (\omega t+\tau (n))\}, \end{aligned}$$

(12e)

$$\begin{aligned}&\tau (n+1)=f_6 (x_1 (n),x_2 (n),y_1 (n),y_2 (n),y_3 (n),\tau (n)) \nonumber \\&\quad =\omega t+\tau (n)-n \pi \end{aligned}$$

(12f)

where the integration constants $a_i$ and $b_i (i=1,2,3)$ can be expressed as the function of the initial conditions (see “Appendix 1”):

$$\begin{aligned}&a_i (x_1 (n),x_2 (n),\tau (n))=\alpha _{1i} x_1 (n)\nonumber \\&\quad +\,\alpha _{2i} x_2 (n)+\alpha _{3i} \sin \tau (n)\nonumber \\&\quad +\,\alpha _{4i} \cos \tau (n)+\alpha _{5i} , \end{aligned}$$

(13a)

$$\begin{aligned}&b_i (x_1 (n),y_1 (n),x_2 (n),y_2 (n),y_3 (n),\tau (n))=\beta _{1i} x_1 (n)\nonumber \\&\quad +\,\beta _{2i} x_2 (n)+\beta _{3i} y_1 (n)+\beta _{4i} y_2 (n)\nonumber \\&\quad +\,\beta _{5i} y_3 (n)+\beta _{6i} \sin \tau (n)+\beta _{7i} \cos \tau (n)+\beta _{8i},\nonumber \\ \end{aligned}$$

(13b)

where $\alpha _{ji} (j=1,\ldots ,5)$ and $\beta _{ki} (k=1,\ldots ,8)$ are constants determined by system parameters. It should be noted that the map $\mathbf{Q}_u =\mathbf{P}_2 \circ \mathbf{P}_1$ ends at the instant after impacting at the right stop. Since relation $x_2 -x_3 \equiv -h$ holds after impacting at the right stop, $x_3 (n+1)$ can be determined by $x_2 (n+1)$. Hence, $x_3 (n+1)$ does not appear in Eqs. (12). However, as shown in Eq. (12f), $\tau (n+1)$ is added to express the phase angle after every iteration (i.e., after impacting at the right stop). Therefore, once the Poincaré map is established, the coordinates of map point $\mathbf{X}$ in the Poincaré section are transformed from $(x_1 ,x_2 ,x_3 ,y_1 ,y_2 ,y_3 )$ to $(x_1 ,x_2 ,y_1 ,y_2 ,y_3 ,\tau )$.

The time t in Eq. (12) is the time interval from the instant after impacting at the left stop to that after impacting at the right stop. The initial time is always set to zero after impacting at the left stop. Because the relation $x_2 -x_3 +h=0$ always holds after impacting at the right stop, t is the solution of the following equation:

$$\begin{aligned} G= & {} x_2 (n+1)-x_3 (n+1)+h \nonumber \\= & {} \sum _{j=1}^3 {\psi _{2j} } \{e^{-\eta _j t}[a_j \cos (\omega _{dj} t)+b_j \sin (\omega _{dj} t)]\nonumber \\&+\,A_j \sin (\omega t+\tau (n))+B_j \cos (\omega t+\tau (n))\} \nonumber \\&-\,\sum _{j=1}^3 {\psi _{3j} } \{e^{-\eta _j t}[a_j \cos (\omega _{dj} t)+b_j \sin (\omega _{dj} t)]\nonumber \\&+\,A_j \sin (\omega t+\tau (n))+B_j \cos (\omega t+\tau (n))\}\nonumber \\&+\,h=0. \end{aligned}$$

(14)

The value of t has not the analytic expression, implying that Q $_{u},$ Q, P are all implicit maps. Since the map Q can capture two conjugate attractors [60], it is used to investigate the dynamics of vibro-impact system and is called virtual Poincaré map.

Let the coordinates of the initial map point $\mathbf{X}_0$ be $(x_{10} ,x_{20} ,y_{10} ,y_{20} ,y_{30} ,\tau _0 )$. According to Eq. (14), we obtain $\frac{\partial t}{\partial x_{10} }$, $\frac{\partial t}{\partial x_{20} }$, $\frac{\partial t}{\partial y_{10} }$, $\frac{\partial t}{\partial y_{20} }$, $\frac{\partial t}{\partial y_{30} }$, $\frac{\partial t}{\partial \tau _0 }$ by the implicit function theorem. Let $\mathbf{J}_\mathbf{Q} (\mathbf{X}_0 )$ denote the Jacobi matrix of the virtual Poincaré map Q at the initial map point $\mathbf{X}_0$. By the computation of partial derivatives of Eq. (12), the Jacobi matrix of map Q can be obtained, see “Appendix 2.”

3 Phase sensitivity property and local Lyapunov exponent

SNA, which has negative Lyapunov exponents, was defined as attractors which is not a finite set of points and is not piecewise differentiable in Ref. [1, 64]. Therefore, one can identify SNAs by (1) checking that the attractor is not differentiable and (2) calculating the largest Lyapunov exponent.

Phase sensitivity was introduced originally by Pikovsky and Feudel [64] to capture the nondifferentiability of attractors and is an effective tool to characterize SNAs [5, 15]. This method is based on the sensitivity of the attractor to the phase of the external force. As shown in Ref. [64], for SNAs, there are some special tangent bifurcation points where the derivate of one branch of attracting sets with respect to phase $\tau$ is infinite, i.e., the tangent of this branch is orthogonal to the $\tau$ axis, implying the nonsmoothness of the attracting set. Now let the attractor be given by

$$\begin{aligned} \mathbf{X}=\mathbf{F}(\tau ), \end{aligned}$$

(15)

where $\mathbf{X}=\left[ {x_1 ,x_2 ,x_3 ,y_1 ,y_2 ,y_3 } \right] ^{\mathbf{T}}$ and $\mathbf{F}=\left[ F_1 (\tau ),F_2 (\tau ),F_3 (\tau ),F_4 (\tau ),F_5 (\tau ),F_6 (\tau ) \right] ^{\mathbf{T}}$, then the derivate with respect to the external phase

$$\begin{aligned} S_i^N =\frac{\partial F_i }{\partial \tau } \end{aligned}$$

(16)

provides a suitable tool to distinguish between strange and nonstrange attractors, where N is the iteration number. If one of the maxima of $S_i^N \quad (i=1,2,3,4,5,6)$ does not exist (i.e., infinite), the attractor is nonsmooth and absent from differentiability, which means that the attractor is strange.

The phase sensitivity can be estimated from the time series of the attractor [64]. Now take a time series $\{\mathbf{X}_N \}$. For each given small $\varepsilon$, one can find such a $n_0$ that the phase difference $\varepsilon _0 =\left| {\tau _{n_0 } -\tau _0 } \right| <\varepsilon$, then

$$\begin{aligned} S_i^N =\frac{\partial F_i }{\partial \tau }\approx \left| {\frac{F_i (k+n_0 )-F_i (k)}{\tau (k+n_0 )-\tau (k)}} \right| , \end{aligned}$$

(17)

where $k+n_0 \le N$ and $F_i (n)$ denotes the $n\hbox {th}$ iteration of $F_i$. The maximum of $S_i^N$ with $N\hbox {th}$ iteration is denoted by

$$\begin{aligned} \gamma _i^N (\mathbf{X}_0 ,\tau _0 )=\max \{S_i^N \}. \end{aligned}$$

(18)

If the value of $\gamma _N$ grows with N, which means the arbitrarily large values of $S_i^N$ appear, then the attractor cannot have finite derivate with respect to the external phase, i.e., the attractor is nonsmooth. And the maximum difference of the ith coordinates is

$$\begin{aligned} \max \{d_i^N \}=\max \left| {z_i (k+n_0 )-z_i (k)} \right| , \end{aligned}$$

(19)

where $z_i$ denotes the ith coordinate. If the attractor is nonsmooth, then $\max \{d_i^N \}$ is expected for large N to be of the order of the size of the attractor. As shown in Ref. [64], for a “true” SNA this behavior does not depend on $\varepsilon _0$, but the time to obtain this maximum increases. However, if the attractor is a smooth one, then the distance of neighboring points on the attractor gets smaller and tends to zero with decreasing phase difference $\varepsilon _0$.

Now we compute the Lyapunov exponents based on the Jacobi matrix. For the initial map point $\mathbf{X}_0$, after Nth iteration of map Q, let the product of all the Jacobi matrix along the whole orbit be

$$\begin{aligned} \mathbf{J}_\mathbf{Q}^N (\mathbf{X}_0 )=\mathbf{J}_\mathbf{Q} (\mathbf{Q}^{N-1}\mathbf{X}_0 )\cdots \mathbf{J}_\mathbf{Q} (\mathbf{QX}_0 )\mathbf{J}_\mathbf{Q} (\mathbf{X}_0 ), \end{aligned}$$

(20)

where $\mathbf{Q}^{k}{} \mathbf{X}_0$ represents the kth iteration of Q at the map point $\mathbf{X}_0$. Let $\Lambda _j^N$ be eigenvalues of the matrix $\mathbf{J}_\mathbf{Q}^N (\mathbf{X}_0 )$, and the Lyapunov exponents can be computed as [65]

$$\begin{aligned} \lambda _i =\mathop {\lim }\limits _{N\rightarrow \infty } \frac{1}{N}\ln \left| {\Lambda _i^N } \right| , \quad i=1, 2, 3, 4, 5, 6 \end{aligned}$$

(21)

where the Lyapunov exponents are ranked from large to small as $\lambda _1 \ge \lambda _2 \ge \cdots \ge \lambda _6$.

When N is a finite iteration number, the local Lyapunov exponent (i.e., the finite-time Lyapunov exponents) [66–68] is obtained via Eq. (21). For example, for a finite iteration number K, the local Lyapunov exponent is

$$\begin{aligned} \overline{\lambda }_i^K =\frac{1}{K}\ln \left| {\Lambda _i^K } \right| . \end{aligned}$$

(22)

the local largest Lyapunov exponent $\overline{\lambda }_1^K$ can be taken as another effective measure for characterizing SNAs [9, 12, 15, 18, 26, 64, 69]. As shown in Ref. [64], high burst of the finite sum $S_i^N$ corresponds to such parts of the trajectory possessing a positive $\overline{\lambda }_1^K$. In the case that $\overline{\lambda }_1^K$ can be positive with nonzero probability, the local largest multiplier can be arbitrarily large, implying nonexistence of the derivate with respect to the external phase. Hence, the existence of a positive $\overline{\lambda }_1^K$ means that the attractor is strange. The probability distribution of $\overline{\lambda }_1^K$ takes on negative values for periodic attractor and positive value for Chaos. However, for SNAs, it takes both positive and negative values with tail extending predominantly into the negative region [70]. This means that for SNAs, $\overline{\lambda }_1^K$ will fluctuate in the vicinity of zero for some time and converge to a negative value finally. In Ref. [71], a method of generating SNA, based on taking piece of trajectories with positive and negative Lyapunov exponents, was discussed, which implies the importance of local Lyapunov exponents.

However, Eq. (21) or (22) cannot be used to calculate the Lyapunov exponents directly. The reason for this is that, when the number of iteration of the map Q increases, the components of matrix $\mathbf{J}_\mathbf{Q}^N (\mathbf{X})$ may become infinite for chaotic attractors and null for periodic attractors. To avoid the overflow trouble, the QR method, as a tool of continuous orthogonalization, is applied repeatedly to the computation [61, 65, 67, 68].

Singular continuous power spectrum analysis is also used to characterize SNAs [5, 12, 72–74]. There is a discrete spectrum for periodic attractors and quasiperiodic attractors, but a continuous spectrum for chaotic attractors. However, for SNAs, there is a singular continuous spectrum, which is intermediate between discrete and continuous. However, it is not clear how strictly to separate these discrete and singular continuous components. Dimensions of SNA were also discussed in Ref. [74]. However, it is very difficult to verify the result numerically because of huge computational time required.

4 Symmetric fixed point, symmetric limit set and symmetry restoring bifurcation

Here the singularity induced by the discontinuity of the Poincaré map is not considered. Hence, it is assumed that $\mathbf{Q}_u$, $\mathbf{Q}$, $\mathbf{P}$ are all continuous and invertible.

Definition 1

(Symmetric fixed point). The fixed point $\mathbf{X}^{*}$ of map Q, i.e., the solution of

$$\begin{aligned} \mathbf{X}=\mathbf{Q}(\mathbf{X}) \end{aligned}$$

(23)

is called the symmetric fixed point of the Poincaré map P of the vibro-impact system.

The symmetry of the vibro-impact system allows that symmetric period n-2 motions (i.e., symmetric double impacts at right and left stops in n force periods) exist in the suitable parameter combinations [37, 60, 61]. As shown in Ref. [37], the fixed point of map P (i.e., the solution of $\mathbf{X}=\mathbf{P}(\mathbf{X}))$ corresponds to the associated periodic motion, and the fixed point of map Q (i.e., the solution of $\mathbf{X}=\mathbf{Q}(\mathbf{X}))$ corresponds to the associated symmetric period n-2 motion. Since $\mathbf{Q}=\mathbf{R}^{-1}\circ \mathbf{Q}_u$, $\mathbf{X}=\mathbf{Q}(\mathbf{X})$ means $\mathbf{RX}=\mathbf{Q}_u (\mathbf{X})$, which implies that after $M_3$ impacts the right and the left stops, the associated state coordinates of map point are equal in absolute value and opposite in direction (i.e., symmetric). For both stable and unstable cases, the coordinates of the symmetric fixed point X $^{*}$ can be determined analytically by $\mathbf{X}=\mathbf{Q}(\mathbf{X})$, see “Appendix 3” for detail.

The $\omega$-limit sets of $\mathbf{X}$ generated by the iterations of the $\mathbf{P}$ map and the $\mathbf{Q}$ map are denoted by $\omega _\mathbf{P} (\mathbf{X})$ and $\omega _\mathbf{Q} (\mathbf{X})$, respectively. A limit set can be attracting or nonattracting. Here we define an attractor to be an asymptotically stable $\omega$-limit set.

Definition 2

(Conjugate fixed points and conjugate $\omega$-limit sets) If $\mathbf{Q}(\mathbf{X})\ne \mathbf{X}$, $\mathbf{X}$ and $\mathbf{Q}(\mathbf{X})$ are called a pair of conjugate map points, two $\omega$-limits sets $\omega _\mathbf{P} (\mathbf{X})$ and $\omega _\mathbf{P} (\mathbf{Q}(\mathbf{X}))$ (i.e., $\mathbf{Q}(\omega _\mathbf{P} (\mathbf{X}))$ generated by $\mathbf{X}$ and $\mathbf{Q}(\mathbf{X})$ (i.e., $\omega _{\mathbf{Q}^{2k}} (\mathbf{X})$ and $\omega _{\mathbf{Q}^{2k+1}} (\mathbf{X}))$ are called a pair of conjugate $\omega$-limit sets.

The positive orbit of the map point $\mathbf{X}$ under the $\mathbf{Q}$ map is $\mathbf{X}$, $\mathbf{Q}(\mathbf{X})$, $\mathbf{Q}^{2}(\mathbf{X})$, $\mathbf{Q}^{3}(\mathbf{X})$, ..., $\mathbf{Q}^{2k} (\mathbf{X})$, $\mathbf{Q}^{2k+1} (\mathbf{X})$, .... Since the $\mathbf{P}$ map is the second iteration of the $\mathbf{Q}$ map, then we have $\mathbf{Q}^{2k} (\mathbf{X})=\mathbf{P}^{k}(\mathbf{X})$, and $\mathbf{Q}^{2k+1} (\mathbf{X})=\mathbf{P}^{k}(\mathbf{Q}(\mathbf{X}))$. That is, the orbit of the map point $\mathbf{X}$ under the map $\mathbf{P}$ comes from the even number iterating of the map $\mathbf{Q}$, and the orbit of the map point $\mathbf{Q}(\mathbf{X})$ under the map $\mathbf{P}$ comes from the odd number iterating of the map $\mathbf{Q}$. Therefore, we have $\omega _{\mathbf{Q}^{2k}} (\mathbf{X})=\omega _\mathbf{P} (\mathbf{X})$ and $\omega _{\mathbf{Q}^{2k+1}} (\mathbf{X})=\omega _\mathbf{P} (\mathbf{Q}(\mathbf{X}))$. Since $\omega _\mathbf{Q} (\mathbf{X})=\omega _{\mathbf{Q}^{2k}} (\mathbf{X})\cup \omega _{\mathbf{Q}^{2k+1}} (\mathbf{Q}(\mathbf{X}))$, then

$$\begin{aligned} \omega _\mathbf{Q} (\mathbf{X})=\omega _\mathbf{P} (\mathbf{X})\cup \omega _\mathbf{P} (\mathbf{Q}(\mathbf{X})). \end{aligned}$$

(24)

In addition, since

$$\begin{aligned} \mathbf{Q}(\mathbf{P}^{k}(\mathbf{X}))=\mathbf{Q}^{2k+1} (\mathbf{X})=\mathbf{P}^{k}(\mathbf{Q}(\mathbf{X})), \end{aligned}$$

(25)

then

$$\begin{aligned} \mathop {\lim }\limits _{k\rightarrow \infty } \mathbf{Q}(\mathbf{P}^{k}(\mathbf{X}))=\mathop {\lim }\limits _{k\rightarrow \infty } \mathbf{P}^{k}(\mathbf{Q}(\mathbf{X})), \end{aligned}$$

(26)

that is

$$\begin{aligned} \mathbf{Q}(\omega _\mathbf{P} (\mathbf{X}))=\omega _\mathbf{P} (\mathbf{Q}(\mathbf{X})). \end{aligned}$$

(27)

Definition 3

(Symmetric $\omega$-limit sets). If the $\omega$-limit sets of $\mathbf{Q}^{2k}$ and that of $\mathbf{Q}^{2k+1}$ satisfy

$$\begin{aligned} \omega _{\mathbf{Q}^{2k}} (\mathbf{X})=\omega _{\mathbf{Q}^{2k+1}} (\mathbf{X}), \end{aligned}$$

(28)

then $\omega _{\mathbf{Q}^{2k}} (\mathbf{X})=\omega _{\mathbf{Q}^{2k+1}} (\mathbf{X})=\omega _\mathbf{Q} (\mathbf{X})$, and $\omega _{\mathbf{Q}^{2k}} (\mathbf{X})$, $\omega _{\mathbf{Q}^{2k+1}} (\mathbf{X})$ and $\omega _\mathbf{Q} (\mathbf{X})$ are all symmetric limit sets.

Equation (28) is equivalent to $\omega _\mathbf{P} (\mathbf{X})=\omega _\mathbf{P} (\mathbf{Q}(\mathbf{X}))$. Hence, this definition is the same as the definition 7 in Ref. [29]. That is, if the $\omega$-limit sets of $\mathbf{X}$ are equal to its conjugate limit set, $\omega _\mathbf{P} (\mathbf{X})$ is a symmetric limit set. Moreover, an $\omega$-limit set is symmetric if $\mathbf{P}$ and $\mathbf{Q}$ have the same limit set (i.e., $\omega _\mathbf{P} (\mathbf{X})=\omega _\mathbf{Q} (\mathbf{X}))$. Besides, $\omega _\mathbf{P} (\mathbf{X})$ is symmetric if it is mapped onto itself under the $\mathbf{Q}$ map (i.e., $\mathbf{Q}(\omega _\mathbf{P} (\mathbf{X}))=\omega _\mathbf{P} (\mathbf{X}))$. According to this definition, the map Q can capture two conjugate attractors of the Poincaré map P (i.e., two conjugate motions in the phase space).

Proposition 4

If $\omega _\mathbf{P} (\mathbf{X})$ is an attractor, and

$$\begin{aligned} \omega _{\mathbf{Q}^{2k}} (\mathbf{X})\cap \omega _{\mathbf{Q}^{2k+1}} (\mathbf{X})\ne {\varnothing }, \end{aligned}$$

(29)

then  $\omega _{\mathbf{Q}^{2k}} (\mathbf{X})$, $\omega _{\mathbf{Q}^{2k+1}} (\mathbf{X})$ and $\omega _\mathbf{Q} (\mathbf{X})$ are all symmetric limit sets.

Since $\omega _{\mathbf{Q}^{2k}} (\mathbf{X})=\omega _\mathbf{P} (\mathbf{X})$ and $\omega _{\mathbf{Q}^{2k+1}} (\mathbf{X})=\omega _\mathbf{P} (\mathbf{X})$, the proof is the same as that of proposition 10 in [29]. That is, as a parameter changes, once two conjugate limit sets intersect each other, symmetry restoring bifurcation takes place. It was proved firstly in [25] that if $h:\mathbf{R}^{n}\rightarrow \mathbf{R}^{n}$ is continuous and commutes with a matrix $\rho$, $A\in \mathbf{R}^{n}$ is an attractor and if $A\cap \rho (A)\ne {\varnothing }$, then $A=\rho (A)$. However, in our case, $\omega _{\mathbf{Q}^{2k}}$ (i.e., $\omega _\mathbf{P} (\mathbf{X}))$ is dependent on time. Since there is not a single $\rho$ which can take elements in $\omega _\mathbf{P} (\mathbf{X})$ to its conjugate, the matrix $\rho$ is replaced by the map Q, and the condition $A\cap \rho (A)\ne {\varnothing }$ is replaced by $\omega _\mathbf{P} (\mathbf{X})\cap \mathbf{Q}(\omega _\mathbf{P} (\mathbf{X}))\ne {\varnothing }$, equivalently.

According to Proposition 4, it is certain that symmetry restoring bifurcation takes place if two conjugate chaotic attractors contact each other directly (i.e., $\omega _{\mathbf{Q}^{2k}} (\mathbf{X})\cap \omega _{\mathbf{Q}^{2k+1}} (\mathbf{X})\ne {\varnothing })$. In this case, chaos–chaos intermittency is induced by the chaotic attractor-merging crisis. It is known that the collisions of two conjugate chaotic attractors also mean that they collide with saddle unstable orbit (i.e., the unstable symmetric fixed point) on the basin boundary. To detect the critical point of symmetry restoring bifurcation (i.e., attractor-merging crisis in this case), we define a distance sequence between two conjugate chaotic limit sets and the unstable symmetric fixed point X $^{*}$:

$$\begin{aligned} D(N)=\sqrt{(x_1^*-x_{1N} )^{2}+(y_1^*-y_{1N} )^{2}+(x_2^*-x_{2N} )^{2}+(y_2^*-y_{2N} )^{2}+(x_3^*-x_{3N} )^{2}+(y_3^*-y_{3N} )^{2}}, \end{aligned}$$

(30)

where $(x_1^*,y_1^*,x_2^*,y_2^*,x_3^*,y_3^*)$ are the coordinates of X $^{*}$ and $(x_{1N} ,y_{1N} ,x_{2N} ,y_{2N} ,x_{3N} ,y_{3N} )$ are the coordinates of map point X at the Nth iteration. As the iteration number N is increased, there is a distance sequence $\{D(N)\}$. Since $\min \{D(N)\}=0$ indicates the direct collision between $\omega _{\mathbf{Q}^{2k}} (\mathbf{X})$ and $\omega _{\mathbf{Q}^{2k+1}} (\mathbf{X})$, it can be used to detect the critical point of attractor-merging crisis.

However, in this paper we reveal another special type of symmetry restoring bifurcation which generates a mixed limit set. This symmetry restoring bifurcation occurs as two conjugate strange nonchaotic limit sets are suddenly embedded in another chaotic one. In this case, two conjugate strange nonchaotic limit sets do not contact directly each other (i.e., $\min \{D(N)\}\ne 0)$, but the condition $\omega _{\mathbf{Q}^{2k}} (\mathbf{X})\cap \omega _{\mathbf{Q}^{2k+1}} (\mathbf{X})\ne {\varnothing }$ is also satisfied. Here the intersection of $\omega _{\mathbf{Q}^{2k}} (\mathbf{X})$ and $\omega _{\mathbf{Q}^{2k+1}} (\mathbf{X})$ is exactly the two conjugate strange nonchaotic limit sets. As suggested in Ref. [29], this symmetry restoring bifurcation is still the result of the collision between conjugate limit sets and a symmetric limit set. However, since $\min \{D(N)\}\ne 0$, here the symmetric limit set is not the unstable symmetric fixed point X $^{*}$, but may be an unstable symmetric multi-periodic point, an unstable quasiperiodic limit set or an unstable chaotic limit set.

For the two conjugate strange nonchaotic sets, map point cannot enter directly from one into another because they have not intersection. However, the appearance of the chaotic set makes the transition possible. Therefore, the iteration interval of the chaotic set is always between that of two conjugate strange nonchaotic sets. Now for map $\mathbf{Q}^{2k}$, pick three iteration intervals $I_1 \in [s,s+s_1 ]$, $I_2 \in (s+s_1 ,s+s_1 +s_2 ]$, and $I_3 \in (s+s_1 +s_2 ,s+s_1 +s_2 +s_3 ]$, where $s,s_1$, $s_2$, $s_3$ are positive integers, and $s_1 =s_3$. As $s\rightarrow +\infty$, let $\omega _{\mathbf{Q}^{2k}}^{I_1 } (\mathbf{X})$, $\omega _{\mathbf{Q}^{2k}}^{I_2 } (\mathbf{X})$ and $\omega _{\mathbf{Q}^{2k}}^{I_3 } (\mathbf{X})$ be three components of the $\omega$-limit sets of map $\mathbf{Q}^{2k}$ corresponding to the iteration interval $I_1$, $I_2$ and $I_3$, respectively. That is, $\omega _{\mathbf{Q}^{2k}}^{I_1 } (\mathbf{X})$ and $\omega _{\mathbf{Q}^{2k}}^{I_3 } (\mathbf{X})$ are two conjugate sets, and $\omega _{\mathbf{Q}^{2k}}^{I_2 } (\mathbf{X})$ is the chaotic set. The following proposition proves strictly that the appearance of a mixed limit set always means that symmetry restoring bifurcation takes place at the same time.

Proposition 5

If $\omega _{\mathbf{Q}^{2k}} (\mathbf{X})$ (or $\omega _{\mathbf{Q}^{2k+1}} (\mathbf{X}))$ contains two conjugate sets $\omega _{\mathbf{Q}^{2k}}^{I_1 } (\mathbf{X})$ and $\omega _{\mathbf{Q}^{2k}}^{I_3 } (\mathbf{X})$ which do not necessarily intersect and a chaotic set $\omega _{\mathbf{Q}^{2k}}^{I_2 } (\mathbf{X})$, then $\omega _\mathbf{Q} (\mathbf{X})$, $\omega _{\mathbf{Q}^{2k}} (\mathbf{X})$ and $\omega _{\mathbf{Q}^{2k+1}} (\mathbf{X})$ are all symmetric, and

$$\begin{aligned} \omega _{\mathbf{Q}^{2k}} (\mathbf{X})\cap \omega _{\mathbf{Q}^{2k+1}} (\mathbf{X})\supset \omega _{\mathbf{Q}^{2k}}^{I_1 } (\mathbf{X})\cup \omega _{\mathbf{Q}^{2k}}^{I_3 } (\mathbf{X})\ne {\varnothing }.\nonumber \\ \end{aligned}$$

(31)

Proof

Since $\omega _{\mathbf{Q}^{2k}} (\mathbf{X})$ is a mixed set containing three components, then

$$\begin{aligned} \omega _{\mathbf{Q}^{2k}} (\mathbf{X})=\omega _{\mathbf{Q}^{2k}}^{I_1 } (\mathbf{X})\cup \omega _{\mathbf{Q}^{2k}}^{I_2 } (\mathbf{X})\cup \omega _{\mathbf{Q}^{2k}}^{I_3 } (\mathbf{X}). \end{aligned}$$

(32)

Because $\omega _{\mathbf{Q}^{2k}}^{I_1 } (\mathbf{X})$ and $\omega _{\mathbf{Q}^{2k}}^{I_3 } (\mathbf{X})$ are two conjugate sets, then

$$\begin{aligned} \mathbf{Q}(\omega _{\mathbf{Q}^{2k}}^{I_1 } (\mathbf{X}))=\omega _{\mathbf{Q}^{2k}}^{I_3 } (\mathbf{X}). \end{aligned}$$

(33)

Equation (32) implies

$$\begin{aligned} \omega _{\mathbf{Q}^{2k}} (\mathbf{X})\supset \omega _{\mathbf{Q}^{2k}}^{I_1 } (\mathbf{X}), \end{aligned}$$

(34)

hence

$$\begin{aligned} \mathbf{Q}(\omega _{\mathbf{Q}^{2k}} (\mathbf{X}))\supset \mathbf{Q}(\omega _{\mathbf{Q}^{2k}}^{I_1 } (\mathbf{X})). \end{aligned}$$

(35)

According Eqs. (33), (35) can be rewritten as

$$\begin{aligned} \omega _{\mathbf{Q}^{2k+1}} (\mathbf{X})\supset \omega _{\mathbf{Q}^{2k}}^{I_3 } (\mathbf{X}). \end{aligned}$$

(36)

Similarly, because

$$\begin{aligned} \omega _{\mathbf{Q}^{2k}} (\mathbf{X})\supset \omega _{\mathbf{Q}^{2k}}^{I_3 } (\mathbf{X}), \end{aligned}$$

(37)

and

$$\begin{aligned} \omega _{\mathbf{Q}^{2k}}^{I_1 } (\mathbf{X})=\mathbf{Q}(\omega _{\mathbf{Q}^{2k}}^{I_3 } (\mathbf{X})), \end{aligned}$$

(38)

we obtain

$$\begin{aligned} \omega _{\mathbf{Q}^{2k+1}} (\mathbf{X})\supset \omega _{\mathbf{Q}^{2k}}^{I_1 } (\mathbf{X}). \end{aligned}$$

(39)

According to Eqs. (34), (36), (37) and (39), we prove Eq. (31). Then, based on Proposition 4, $\omega _\mathbf{Q} (\mathbf{X})$, $\omega _{\mathbf{Q}^{2k}} (\mathbf{X})$, $\omega _{\mathbf{Q}^{2k+1}} (\mathbf{X})$ are all symmetric limit sets since $\omega _{\mathbf{Q}^{2k}} (\mathbf{X})\cap \omega _{\mathbf{Q}^{2k+1}} (\mathbf{X})\ne {\varnothing }$. $\square$

If $\omega _{\mathbf{Q}^{2k+1}} (\mathbf{X})$ is a mixed set containing two conjugate sets and a chaotic set, the proof is similar to the above. Proposition 9 in Ref. [29] is suitable for the case that two conjugate sets have different initial conditions. However, here Proposition 5 is suitable for the case that a mixed set contains two conjugate components which have the same initial conditions.

5 Coexistence of SNAs and a special type of mixed attractor caused by a new intermittency near a NS-P bifurcation point

5.1 NS-P bifurcation

Consider the vibro-impact system with system parameters [37]: $n=1$, $\zeta =0.008$, $R=0.85$, $h=0.08$, $u_{m1}=5$, $u_{m2}=2$, $u_{m3}=1$, $u_{k1}=0.8$, $u_{k2}=1$, $u_{k3}=1$, $u_{f1} =0.49$, $u_{f2}=0.3787240036$, $u_{f3}=1$, $\omega =1.14388$. The six eigenvalues and of the Jacobian matrix of the Poincaré map $\mathbf{P}$ can be computed as: $\lambda _{1,2} =0.343288\pm 0.748114i$, $\left| {\lambda _{1,2} } \right| =0.823117;\lambda _{3,4} =0.906843\pm 0.421469i, \left| {\lambda _{3,4} } \right| =1.000000;\lambda _5 =0.536714; \lambda _6 =1.000000$. They satisfy the following conditions of NS-P bifurcation:

(H1) :

DP has three eigenvalues on the unit circle: a pair of complex conjugate eigenvalues $\lambda _{1,2} =e^{\pm i\theta _0 }$, and a real eigenvalue $\lambda _6 =+1$. The other eigenvalues of DP are inside the unit circle;

(H2) :

$\lambda _{1,2} =e^{\pm i\theta _0 }$ satisfies nonresonant conditions: $\lambda _{1,2}^n \ne 1$, $n=1, 2, 3, 4, 5, 6$, and $\lambda _{1,2}^n \ne -1$, $n=4, 5$.

Thus, this combination of parameters is NS-P bifurcation point.

The two-parameter dynamical behavior in the vicinity of this NS-P bifurcation point is shown in Fig. 2, taking ${\varvec{\upmu =}}[\omega ,u_{f2} ]^{\mathrm{T}}$ as the control parameter vector. If there are different two-parameter perturbations, various dynamical behaviors take place. The map point of the even iteration (i.e., $\omega _{\mathbf{Q}^{2k}} (\mathbf{X}))$ is denoted by red, and that of the odd iteration (i.e., $\omega _{\mathbf{Q}^{2k+1}} (\mathbf{X}))$ is denoted by blue. The virtual Poincaré map Q may exhibit two conjugate fixed points $\mathbf{X}_\alpha$ and $\mathbf{X}_\beta$ (Fig. 2a), one symmetric quasiperiodic attractor (Fig. 2b), two conjugate quasiperiodic attractors (Fig. 2c). As shown in Fig. 2d, as a result of interaction of Neimark–Sacker bifurcation and pitchfork bifurcation, the map point bifurcates into two unstable conjugate fixed points firstly and settles into one symmetric quasiperiodic attractor at last.

Fig. 2

Phase portraits in the projected Poincaré section $(y_1 ,x_2 )$: a $\Delta {\varvec{\upmu }}=[0.006618,0.02]^{\mathrm{T}}$: two conjugate fixed points, b $\Delta {\varvec{\upmu }}=[0.006616,0.02]^{\mathrm{T}}$: one symmetric quasiperiodic attractor, c $\Delta {\varvec{\upmu }}=[-0.000118,-0.0008]^{\mathrm{T}}$: two conjugate quasiperiodic attractors, d $\Delta {\varvec{\upmu }}=[0.00661725,0.02]^{\mathrm{T}}$: from two unstable conjugate fixed points to one symmetric quasiperiodic attractor

Fig. 3

Bifurcation diagrams. a $\omega \in [1.14386,1.14408]$, b $\omega \in [1.14403,1.14408]$

5.2 Coexistence of two conjugate SNAs and a special mixed attractor induced by a novel intermittency

Choose the external force frequency $\omega$ as the control parameter; bifurcation diagrams are shown in Fig. 3. As $\omega$ varies in the interval $\omega \in [1.14386,1.14408]$, the bifurcation diagram is represented in Fig. 3a. Because $\omega _A =1.14388$ is the NS-P bifurcation point, a symmetric orbit bifurcates into two conjugate periodic orbits as $\omega$ is increased and passes through $\omega _A$. Subsequently, at $\omega _B$ the two conjugate periodic orbits evolve into two conjugate quasiperiodic orbits, which will lead to two conjugate chaotic orbits at some point. However, these two conjugate chaotic orbits merge to form a single symmetric chaotic orbit via symmetry restoring bifurcation at $\omega _C =1.1440405$. Because $\min \{D(N)\}=0$ at $\omega _C$, this symmetry restoring bifurcation belongs to the so-called attractor-merging crisis, which brings about chaos–chaos intermittency. While $\omega$ is increased to $\omega _D$, phase-locking regime appears, and SNAs will take place in some small parameter intervals as $\omega$ changes continuously. The amplification of the bifurcation diagram in the interval $\omega \in [1.14403,1.14408]$ is represented in Fig. 3b. It seems that phase-locking exists in the parameter interval $[\omega _D ,\omega _E ]$ and $[\omega _F ,\omega _G ]$. However, the following analysis shows that phase-locking regime exists in the whole interval $[\omega _D ,\omega _G ]$, including interval $[\omega _E ,\omega _F ]$.

Now the bifurcation diagram of a small interval $\omega \in [1.14405780,1.14405784]\subset [\omega _E ,\omega _F ]$ is discussed firstly. As shown in Fig. 4a, this small interval is not full of SNAs. The following analysis shows that there are three states in this small interval: two conjugate SNAs, phase-locking and a type of mixed attractor. These three states intertwine in the whole parameter interval $[\omega _E ,\omega _F ]$. However, because these three types of attractor have different sizes, they can be distinguished by the vertical coordinate $x_2$ in the bifurcation diagram. Mixed attractors own the largest size. For the two conjugate SNAs, the smaller one is denoted by SNA$_{1}$ (red point) and the larger one is denoted by SNA$_{2}$ (blue point). It should be noted that the bifurcation diagram of an arbitrary small parameter interval in $[\omega _E ,\omega _F ]$ is always similar to that shown in Fig. 4a. This means that the phase-locking regions are dense in the parameter interval $[\omega _E ,\omega _F ]$ (i.e., the width of phase-locking is smaller than the accuracy of the computation and cannot be detected). Second, as shown in Fig. 4b, while $\omega$ is decreased to some value near $\omega _E$, the chance of the appearance of the phase-locking and the mixed attractor degenerates, and the coexistence of SNAs dominates gradually the parameter interval. However, as $\omega$ is decreased gradually and pass through $\omega _E$, phase-locking regime dominates abruptly the whole parameter interval, accompanying with a small amount of mixed attractors. Third, as shown in Fig. 4c, while $\omega$ is increased to some value near $\omega _F$, the coexistence of SNAs dominates gradually the parameter interval. However, as $\omega$ is increased gradually and pass through $\omega _F$, phase-locking state dominates again the whole parameter interval, accompanying with a small amount of coexistence of SNAs.

Fig. 4

Bifurcation diagrams. a $\omega \in [1.14405780,1.14405784]$, b $\omega \in [1.1440556,1.1440557]$, c $\omega \in [1.1440625,1.1440635]$

The three types of attractors are analyzed in detail as below. Figure 5 represents two states: phase-locked periodic attractor and SNAs. The even number iterations of map Q (i.e., $\omega _{\mathbf{Q}^{2k}} (\mathbf{X}))$ are denoted by red points, and the odd number iterations of map Q (i.e., $\omega _{\mathbf{Q}^{2k+1}} (\mathbf{X}))$ are denoted by blue points. For example, while $\omega =1.14405566$ and $\omega =1.144063$, two conjugate SNAs coexist, see Fig. 5a, c, respectively. As $\omega =1.144058$, two conjugate phase-locked periodic attractors coexist, see Fig. 5b.

Fig. 5

Phase portraits in the projected Poincaré section $(x_2 ,y_2 )$: a $\omega =1.14405566$: two conjugate SNAs, b $\omega =1.144058$: two conjugate phase-locked periodic attractors, c $\omega =1.144063$: two conjugate SNAs

SNAs shown in Fig. 5a, c can be characterized by local Lyapunov exponents and phase sensitivity. Fig. 6a, b represents the convergence of the largest Lyapunov exponent with the change of iteration number in the case of $\omega =1.14405566$ and $\omega =1.144063$, respectively. It is shown that $\lambda _1$ begins with a positive value and waves between the positive region and the negative region in some iteration regions. After that, $\lambda _1$ enters into negative region forever and converge to a negative number as iteration number is increased infinitely. The existence of a positive local Lyapunov exponent $\overline{\lambda }_1^N$ implies the strange of the attractor. However, the negative value of $\lambda _1$ as $N\rightarrow \infty$ guarantees the fact that the attractor is nonchaotic

Fig. 6

Convergence of the largest Lyapunov exponent with the change of iteration number. a $\omega =1.14405566$, b $\omega =1.144063$

Nonsmoothness (i.e., strange) of the attractor can also be determined by discussing the phase sensitivity property. As an example, the case of $\omega =1.144063$ is considered. If we choose $n_0 =40$, then $\varepsilon _0 =3.3768\times 10^{-6}$. If the iteration number N is 1800, the value of $S_1^N$ seems very intermittent and reaches the maximum 18.626 at $N=1183$, see Fig. 7a. It seems that $\gamma _1^N$ (i.e., the maximum of $S_1^N )$ grows infinitely with increasing N, see Fig. 7b. However, because the value of $S_i^N$ is estimated from time series, there is a saturated value $S_i^N$ with some N. The iteration number which is necessary to achieve the saturated $S_1^N$ can be estimated as $N\sim \frac{1}{\varepsilon _0 }=3\times 10^{5}$. Here as N is increased to 336816, $S_1^N$ reaches the maximum $4.7\times 10^{4}$ and can be regarded as $\max \{S_1^\infty \}$, see Fig 7c. The corresponding $\gamma _1^N$ with change of N is shown as Fig. 7d. The huge $\max \{S_1^\infty \}$ means that there are some special points where the derivate of one branch of attracting sets with respected to phase $\tau$ is nearly infinite, implying the nonsmooth of the attractor shown in Fig. 5c.

Fig. 7

$\omega =1.144063$: phase sensitivity from time series. a 1800 iterations: $S_1^N$, b 1800 iterations: maximum $\gamma _1^N$, c $10^{5}$ iterations: $S_1^N$, d $10^{5}$ iterations: maximum $\gamma _1^N$

If different $\varepsilon _0$ are chosen, the saturated values $\max \{d_i^\infty \}(i=1, 2, 6$) and $\gamma _1^\infty$ are shown as Table 1. It is shown that while $n_0$ is decreased gradually, the initial phase difference $\varepsilon _0$ deceases significantly. As $n_0 =40$, $\varepsilon _0$ decreases to 3.37710$^{-6}$, which is very close to zero. If the attractor is smooth, then $\max \{d_i^\infty \}$ must get smaller and tends to zero with the decreasing phase difference $\varepsilon _0$. However, as shown in Table 1, although the saturated value $\max \{d_i^\infty \}$ has a small fluctuation, but does not depend on $\varepsilon _0$, implying the strange of the attractor.

Table 1 Saturated value $\max \{d_i^\infty \}(i=1, 2, 6)$ and $\gamma _1^\infty$ in the case of $\omega =1.144063$

The third type of attractor is a mixed attractor, which is the combination of two conjugate strange nonchaotic limit sets and a chaotic limit set. For example, as $\omega =1.144059$, a mixed attractor is shown in Fig. 8a. The size of the two conjugate strange nonchaotic components is smaller than that of the chaotic one. That is, the two conjugate strange nonchaotic limit sets are embedded into the chaotic one. Convergence of the largest Lyapunov exponent with the change of iteration number is represented in Fig. 8b. While $N<6\times 10^{3}$, $\lambda _1$ changes from positive region to negative region and has a remarkable fluctuation between positive and negative as $1\times 10^{4}<N<4\times 10^{4}$. After that, $\lambda _1$ stays in the negative region for some time. This indicates that the map point settles into two conjugate strange nonchaotic limit sets first. Consequently, the map point enters into the chaotic component and alternates always between conjugate strange nonchaotic limit sets and chaotic one since then. Therefore, $\lambda _1$ enters into positive region again and has an obvious fluctuation forever.

Fig. 8

$\omega =1.144059$: Mixed attractor. a Phase portraits, b convergence of the largest Lyapunov exponent with the change of iteration number

It is necessary to analyze the structure of the mixed attractor shown in Fig. 8a. There are three components of the attractor. Since the two conjugate strange nonchaotic components are embedded in the chaotic one, the chaotic component owns the largest size and is denoted by CA. For the two conjugate strange nonchaotic components, the small one is denoted by SNA$_{1}$ and the bigger one is denoted by SNA$_{2}$. Now the diagram of coordinate $x_2$ versus iteration number N is given in Fig. 9. Figure 9a, b represents the iteration of $\mathbf{Q}^{2k}$ and $\mathbf{Q}^{2k+1}$, respectively. Figure 9c gives the iteration of $\mathbf{Q}$, which is the combination of the above two cases. As shown in Fig. 9a, for $\mathbf{Q}^{2k}$, the map point first enters into SNA$_{2}$ before 60000 iteration or so. Subsequently, between 60000 and 200000 iterations, it wanders on the CA. Then, between 200000 and 240000 iterations, it enters into $\hbox {SNA}_{1}$ before settling into CA again. This process is repeated forever, and the iteration sequence is: $\hbox {SNA}_{2}\rightarrow \hbox { CA }\rightarrow \hbox {SNA}_{1}\rightarrow \hbox { CA }\rightarrow \hbox {SNA}_{2}\rightarrow \hbox { CA }\rightarrow {\ldots }$. For $\mathbf{Q}^{2k+1}$, the iteration sequence is: $\hbox {SNA}_{1}\rightarrow \hbox { CA }\rightarrow \hbox {SNA}_{2}\rightarrow \hbox {CA}\rightarrow \hbox {SNA}_{1}\rightarrow \hbox {CA}\rightarrow {\ldots }$, see Fig. 9b. For $\mathbf{Q}$, the iteration sequence is: $\hbox {TCSNAs}\rightarrow \hbox {CA}\rightarrow \hbox {TCSNAs}\rightarrow \hbox {CA}\rightarrow {\ldots }$, where TCSNAs denotes the two conjugate strange nonchaotic components, see Fig. 9c. For $\mathbf{Q}^{2k}$ and $\mathbf{Q}^{2k+1}$, the map point in one conjugate strange nonchaotic component cannot jump directly into another; hence, the chaotic component is the necessary transition between them. Thus, this mixed attractor is induced by the intermittency between three components: two conjugate strange nonchaotic limit sets and a chaotic one.

Fig. 9

$\omega =1.144059$: Intermittency between two conjugate limit sets and a chaotic one. a $\mathbf{Q}^{2k}$, b $\mathbf{Q}^{2k+1}$, c $\mathbf{Q}$

The relationship of the three types of attractors is analyzed as follows. Each phase-locked regime corresponds to a region (i.e., Arnol’d tongue) in the two parameters plane. Between these tongues, the rotational number is irrational. The bifurcation diagram in an arbitrary small interval in $[\omega _E ,\omega _F ]$ is always similar to that shown in Fig. 4a, implying the dense of the phase-locking regions. If the stable and unstable periodic orbits collide at some parameter value, tangent bifurcation of two conjugate phase-locked periodic orbits occurs. The possible subsequence of this collision may be two-frequency quasiperiodic attractor, chaotic attractor or SNA [20, 21]. As shown in Fig. 4b, while the external force frequency $\omega$ is increased and passes through $\omega _E$, there is a quick decrease in the width of phase-locking. At the same time, the width of phase-locking becomes smaller than the accuracy of the computation and cannot be detected, which results in the fact that the shape of the phase-locking regions changes from tongue-like to leaf-like [21]. This transition leads to the appearance of two conjugate SNAs. The result coincides well with the mechanism of the birth of SNAs suggested in Ref. [20, 21]. However, here the vibro-impact system is excited by periodic force, but not quasiperiodic force. Hence, the only difference is that two-frequency torus and three-frequency torus in [20, 21] should be replaced by the phase-locked periodic orbit and two-frequency torus in our case.

If two conjugate strange nonchaotic limit sets are suddenly embedded in a chaotic one, a special mixed attractor is induced by a new intermittency accompanying with symmetry restoring bifurcation. In this case, two conjugate limit sets do not contact each other directly (i.e., $\min \{D(N)\}\ne 0)$, but the condition $\omega _{\mathbf{Q}^{2k}} (\mathbf{X})\cap \omega _{\mathbf{Q}^{2k+1}} (\mathbf{X})\ne {\varnothing }$ is also satisfied. Here the intersection of $\omega _{\mathbf{Q}^{2k}} (\mathbf{X})$ and $\omega _{\mathbf{Q}^{2k+1}} (\mathbf{X})$ is exactly the two strange nonchaotic limit sets. According to Proposition 5, symmetry restoring bifurcation takes place at this critical point. As suggested in Ref. [29], this symmetry restoring bifurcation is the result of the collision between two strange nonchaotic conjugate limit sets and a symmetric limit set. However, here the symmetric limit set is not the unstable symmetric fixed point X $^{*}$, but may be an unstable symmetric multi-periodic points, an unstable quasiperiodic limit set or an unstable chaotic limit set.

6 Conclusions

For the periodically forced three-degree-of-freedom vibro-impact system with symmetry, the Poincaré map P is the twofold composition of a six-dimensional implicit map Q. Since map Q can capture two conjugate attractors, it is used to investigate the dynamics of the system. With a suitable parameter combination, the Poincaré map P of the vibro-impact system exhibits NS-P bifurcation. It is shown that near this NS-P bifurcation point, phase-locking regime appears after attractor-merging crisis. Consequently, as the external force frequency $\omega$ is increased and passes through some critical value, there is a quick decrease in the width of phase-locking. As $\omega$ is increased gradually, many of these phase-locking regions disappear, and the coexistence of SNA appears instead. The SNA is characterized by the local largest Lyapunov exponent and the phase sensitivity property. It is shown that the phase-locking regions are dense in a small parameter interval. Three types of attractor alternate in this small region: two conjugate long periodic attractors, two conjugate SNAs and a special type of mixed attractor.

If two conjugate strange nonchaotic limit sets are suddenly embedded in a chaotic one, a special mixed attractor is induced by a new intermittency accompanied by symmetry restoring bifurcation. In this case, although two conjugate limit sets do not contact each other directly, the two strange nonchaotic components are the intersection of $\omega _{\mathbf{Q}^{2k}} (\mathbf{X})$ and $\omega _{\mathbf{Q}^{2k+1}} (\mathbf{X})$. Hence, the appearance of the mixed attractor always accompanies with symmetry restoring bifurcation and is the result of the collision between two conjugate strange nonchaotic limit sets and a symmetric limit set. With the changing of the iteration number, the map point enters into two conjugate strange nonchaotic components and the chaotic one in turn, indicating the intermittency between these three limit sets. For the map P (i.e., $\mathbf{Q}^{2k}$ or $\mathbf{Q}^{2k+1})$, the map point cannot jump from one strange nonchaotic component to another. However, the appearance of the chaotic component makes it possible and plays a key role for this intermittency. Chaos–chaos intermittency has been studied extensively [75–78]. For our knowledge, this intermittency, which occurs between two conjugate strange nonchaotic limit sets and a chaotic one, has not been reported in the literature till now. We believe that the results in this paper have some positive significance for both the optimization design of vibro-impact systems and the study on the intermittency of nonlinear dynamical system.

Appendices

Appendix 1: Expressions of the integration constants $a_i$ and $b_i$ as the function of the initial conditions

Let the coordinates of the initial map point $\mathbf{X}_0 \in {\varvec{\Pi }} _1$ be $(x_{10} ,x_{20} ,y_{10} ,y_{20} ,y_{30} ,\tau _0 )$. Substituting $t=0$ into the general solutions shown in Eq. (8), we obtain

$$\begin{aligned} x_{i0}= & {} \psi _{i1} (a_1 +A_1 \sin \tau _0 +B_1 \cos \tau _0 )\nonumber \\&+\,\psi _{i2} (a_2 +A_2 \sin \tau _0 +B_2 \cos \tau _0 ) \nonumber \\&+\,\psi _{i3} (a_3 +A_3 \sin \tau _0 +B_3 \cos \tau _0 ),\nonumber \\ i= & {} 1,\, 2; \end{aligned}$$

(40)

and

$$\begin{aligned} y_{i0}= & {} \psi _{i1} (-\eta _1 a_1 +\omega _{d1} b_1 +A_1 \omega \cos \tau _0 -B_1 \omega \sin \tau _0 )\nonumber \\&+\,\psi _{i2} (-\eta _2 a_2 +\omega _{d2} b_2 \nonumber \\&+\,A_2 \omega \cos \tau _0 -B_2 \omega \sin \tau _0 )\nonumber \\&+\,\psi _{i3} (-\eta _3 a_3 +\omega _{d3} b_3 \nonumber \\&+\,A_3 \omega \cos \tau _0 -B_3 \omega \sin \tau _0 )\nonumber \\ i= & {} 1, 2, 3; \end{aligned}$$

(41)

Besides, since $x_2^*-x_3^*=h$ with $t=0$, the following relation holds:

$$\begin{aligned} x_{20} -x_{30}= & {} \psi _{21} a_1 +\psi _{22} a_2 +\psi _{23} a_3 \nonumber \\&+\,(\psi _{21} A_1 +\psi _{22} A_2 +\psi _{23} A_3 )\sin \tau _0 \nonumber \\&+\,(\psi _{21} B_1 +\psi _{22} B_2 +\psi _{23} B_3 )\cos \tau _0 \nonumber \\&-\,[\psi _{11} a_1 +\psi _{12} a_2 +\psi _{13} a_3 \nonumber \\&+\,(\psi _{11} A_1 +\psi _{12} A_2 +\psi _{13} A_3 )\sin \tau _0 \nonumber \\&+\,(\psi _{11} B_1 +\psi _{12} B_2 +\psi _{13} B_3 )\cos \tau _0 ] \nonumber \\= & {} h. \end{aligned}$$

(42)

(44), (45) and (46) generate six equations about six unknowns $a_i$ and $b_i$ ($i=1, 2, 3$). Then the integration constants $a_i$ and $b_i$ can be expressed as the following functions depending on the initial conditions $(x_{10} ,x_{20} ,y_{10} ,y_{20} ,y_{30} ,\tau _0 )$:

$$\begin{aligned}&a_i (x_{10} ,x_{20} ,\tau _0 )=\alpha _{1i} x_{10} +\alpha _{2i} x_{20} \nonumber \\&\quad +\,\alpha _{3i} \sin \tau _0 +\alpha _{4i} \cos \tau _0 +\alpha _{5i}, \end{aligned}$$

(43a)

$$\begin{aligned}&b_i (x_{10} ,y_{10} ,x_{20} ,y_{20} ,y_{30} ,\tau _0 )=\beta _{1i} x_{10}\nonumber \\&\quad +\,\beta _{2i} x_{20} +\beta _{3i} y_{10} +\beta _{4i} y_{20} \nonumber \\&\quad +\,\beta _{5i} y_{30} +\beta _{6i} \sin \tau _0 +\beta _{7i} \cos \tau _0 +\beta _{8i}, \end{aligned}$$

(43b)

where $\alpha _{ji} (j=1,\ldots ,5)$ and $\beta _{ki} (k=1,\ldots ,8)$ are constants determined by system parameters.

If the initial conditions $(x_{10} ,x_{20} ,y_{10} ,y_{20} ,y_{30} ,\tau _0 )$ are replaced by $(x_1 (n),x_2 (n),y_1 (n),y_2 (n),y_3 (n),\tau (n))$, Eq. (13) is obtained.

Then we obtain the partial derivatives of the integration constants about the initial conditions $(x_{10},x_{20},y_{10},y_{20},y_{30},\tau _0)$:

$$\begin{aligned} \frac{\partial a_i }{\partial x_{10} }= & {} \alpha _{1i} ,\quad \frac{\partial a_i }{\partial x_{20} }=\alpha _{2i} ,\nonumber \\ \frac{\partial a_i }{\partial y_{10} }= & {} 0,\quad \frac{\partial a_i }{\partial y_{20} }=0,\quad \frac{\partial a_i }{y_{30} }=0,\nonumber \\ \frac{\partial a_i }{\tau _0 }= & {} \alpha _{3i} \cos \tau _0 -\alpha _{4i} \sin \tau _0 , \end{aligned}$$

(44a)

$$\begin{aligned} \frac{\partial b_i }{\partial x_{10} }= & {} \beta _{1i} ,\quad \frac{\partial b_i }{\partial x_{20} }=\beta _{2i} ,\quad \frac{\partial b_i }{\partial y_{10} }=\beta _{3i},\nonumber \\ \frac{\partial b_i }{\partial y_{20} }= & {} \beta _{4i} , \quad \frac{\partial b_i }{\partial y_{30} }=\beta _{5i} ,\nonumber \\ \frac{\partial b_i }{\tau _0 }= & {} \beta _{6i} \cos \tau _0 -\beta _{7i} \sin \tau _0 . \end{aligned}$$

(44b)

Appendix 2: Expressions of Jacobi matrix

We replace the initial conditions $(x_1 (n),x_2 (n),y_1 (n),y_2 (n),y_3 (n),\tau (n))$ by $(x_{10} ,x_{20} ,y_{10} ,y_{20} ,y_{30} ,\tau _0 )$, Eq. (14) is rewritten as:

$$\begin{aligned} G= & {} x_2 (n+1)-x_3 (n+1)+h \nonumber \\= & {} \sum _{j=1}^3 {\psi _{2j} } \{e^{-\eta _j t}[a_j \cos (\omega _{dj} t)+b_j \sin (\omega _{dj} t)]\nonumber \\&+\,A_j \sin (\omega t+\tau _0 )+B_j \cos (\omega t+\tau _0 )\} \nonumber \\&-\sum _{j=1}^3 {\psi _{3j} } \{e^{-\eta _j t}[a_j \cos (\omega _{dj} t)\nonumber \\&+\,b_j \sin (\omega _{dj} t)]+A_j \sin (\omega t+\tau _0 )\nonumber \\&+\,B_j \cos (\omega t+\tau _0 )\}+h =0 \end{aligned}$$

(45)

According to the implicit function theorem, we obtain

$$\begin{aligned} \frac{\partial t}{\partial x_{10} }= & {} {-\frac{\partial G}{\partial x_{10} }}\Big /{\frac{\partial G}{\partial t}},\quad \frac{\partial t}{\partial x_{20} }={-\frac{\partial G}{\partial x_{20} }}\Big /{\frac{\partial G}{\partial t}},\nonumber \\ \frac{\partial t}{\partial y_{10} }= & {} {-\frac{\partial G}{\partial y_{10} }}\Big /{\frac{\partial G}{\partial t}},\nonumber \\ \frac{\partial t}{\partial y_{20} }= & {} {-\frac{\partial G}{\partial y_{20} }}\Big /{\frac{\partial G}{\partial t}},\quad \frac{\partial t}{\partial y_{30} }={-\frac{\partial G}{\partial y_{30} }}\Big /{\frac{\partial G}{\partial t}},\nonumber \\ \frac{\partial t}{\partial \tau _0 }= & {} {-\frac{\partial G}{\partial \tau _0 }}\Big /{\frac{\partial G}{\partial t}}. \end{aligned}$$

(46)

Let the Jacobi matrix $\mathbf{J}_\mathbf{Q} (\mathbf{X}_0 )=[J_{ij} ]_{6\times 6}$. According to the expression shown in Eq. (12), $a_{ij}$ can be computed as follows by the chain rule:

$$\begin{aligned} J_{i1}= & {} \frac{\partial f_i }{\partial a_1 }\frac{\partial a_1 }{\partial x_{10} }+\frac{\partial f_i }{\partial b_1 }\frac{\partial b_1 }{\partial x_{10} }+\frac{\partial f_i }{\partial a_2 }\frac{\partial a_2 }{\partial x_{10} }+\frac{\partial f_i }{\partial b_2 }\frac{\partial b_2 }{\partial x_{10} }\nonumber \\&+\,\frac{\partial f_i }{\partial a_3 }\frac{\partial a_3 }{\partial x_{10} }+\frac{\partial f_i }{\partial b_3 }\frac{\partial b_3 }{\partial x_{10} }+\frac{\partial f_i }{\partial t}\frac{\partial t}{\partial x_{10} }, \end{aligned}$$

(47a)

$$\begin{aligned} J_{i2}= & {} \frac{\partial f_i }{\partial a_1 }\frac{\partial a_1 }{\partial x_{20} }+\frac{\partial f_i }{\partial b_1 }\frac{\partial b_1 }{\partial x_{20} }+\frac{\partial f_i }{\partial a_2 }\frac{\partial a_2 }{\partial x_{20} }\nonumber \\&+\,\frac{\partial f_i }{\partial b_2 }\frac{\partial b_2 }{\partial x_{20} }+\frac{\partial f_i }{\partial a_3 }\frac{\partial a_3 }{\partial x_{20} }+\frac{\partial f_i }{\partial b_3 }\frac{\partial b_3 }{\partial x_{20} }+\frac{\partial f_i }{\partial t}\frac{\partial t}{\partial x_{20} },\nonumber \\ \end{aligned}$$

(47b)

$$\begin{aligned} J_{i3}= & {} \frac{\partial f_i }{\partial a_1 }\frac{\partial a_1 }{\partial y_{10} }+\frac{\partial f_i }{\partial b_1 }\frac{\partial b_1 }{\partial y_{10} } +\frac{\partial f_i }{\partial a_2 }\frac{\partial a_2 }{\partial y_{10} }\nonumber \\&+\,\frac{\partial f_i }{\partial b_2 }\frac{\partial b_2 }{\partial y_{10} }+\frac{\partial f_i }{\partial a_3 }\frac{\partial a_3 }{\partial y_{10} }+\frac{\partial f_i }{\partial b_3 }\frac{\partial b_3 }{\partial y_{10} }+\frac{\partial f_i }{\partial t}\frac{\partial t}{\partial y_{10} },\nonumber \\ \end{aligned}$$

(47c)

$$\begin{aligned} J_{i4}= & {} \frac{\partial f_i }{\partial a_1 }\frac{\partial a_1 }{\partial y_{20} }+\frac{\partial f_i }{\partial b_1 }\frac{\partial b_1 }{\partial y_{20} }+\frac{\partial f_i }{\partial a_2 }\frac{\partial a_2 }{\partial y_{20} }\nonumber \\&+\,\frac{\partial f_i }{\partial b_2 }\frac{\partial b_2 }{\partial y_{20} }+\frac{\partial f_i }{\partial a_3 }\frac{\partial a_3 }{\partial y_{20} }+\frac{\partial f_i }{\partial b_3 }\frac{\partial b_3 }{\partial y_{20} }+\frac{\partial f_i }{\partial t}\frac{\partial t}{\partial y_{20} },\nonumber \\ \end{aligned}$$

(47d)

$$\begin{aligned} J_{i5}= & {} \frac{\partial f_i }{\partial a_1 }\frac{\partial a_1 }{\partial y_{30} }+\frac{\partial f_i }{\partial b_1 }\frac{\partial b_1 }{\partial y_{30} }+\frac{\partial f_i }{\partial a_2 }\frac{\partial a_2 }{\partial y_{30} }+\frac{\partial f_i }{\partial b_2 }\frac{\partial b_2 }{\partial y_{30} }\nonumber \\&+\,\frac{\partial f_i }{\partial a_3 }\frac{\partial a_3 }{\partial y_{30} }+\frac{\partial f_i }{\partial b_3 }\frac{\partial b_3 }{\partial y_{30} }+\frac{\partial f_i }{\partial t}\frac{\partial t}{\partial y_{30} }, \end{aligned}$$

(47e)

$$\begin{aligned} J_{i6}= & {} \frac{\partial f_i }{\partial a_1 }\frac{\partial a_1 }{\partial \tau _0 }+\frac{\partial f_i }{\partial b_1 }\frac{\partial b_1 }{\partial \tau _0 }+\frac{\partial f_i }{\partial a_2 }\frac{\partial a_2 }{\partial \tau _0 }+\frac{\partial f_i }{\partial b_2 }\frac{\partial b_2 }{\partial \tau _0 }\nonumber \\&+\,\frac{\partial f_i }{\partial a_3 }\frac{\partial a_3 }{\partial \tau _0 }+\frac{\partial f_i }{\partial b_3 }\frac{\partial b_3 }{\partial \tau _0 }+\frac{\partial f_i }{\partial t}\frac{\partial t}{\partial \tau _0 }+\frac{\partial f_i }{\partial \tau _0 }. \end{aligned}$$

(47f)

where $\frac{\partial a_i }{\partial x_{10} }$, $\frac{\partial a_i }{\partial x_{20} }$, $\frac{\partial a_i }{\partial y_{10} }$, $\frac{\partial a_i }{\partial y_{20} }$, $\frac{\partial a_i }{y_{30} }$, $\frac{\partial a_i }{\tau _0 }$,$\frac{\partial b_i }{\partial x_{10} }$, $\frac{\partial b_i }{\partial x_{20} }$, $\frac{\partial b_i }{\partial y_{10} }$, $\frac{\partial b_i }{\partial y_{20} }$, $\frac{\partial b_i }{\partial y_{30} }$, $\frac{\partial b_i }{\tau _0 }$ are shown as Eq. (44).

Appendix 3: Analytic solutions of symmetric fixed point

Let the coordinates of the symmetric fixed point X $^{*}$ be $(x_1^*,x_2^*,y_1^*,y_2^*,y_3^*,\tau ^{*})$. For both stable and unstable cases, the coordinates of the symmetric fixed point X $^{*}$ can be determined analytically by $\mathbf{X}^{*}=\mathbf{Q}(\mathbf{X}^{*})$. Since $\mathbf{Q}=\mathbf{R}^{-1}\circ \mathbf{Q}_u$, $\mathbf{X}^{*}=\mathbf{Q}(\mathbf{X}^{*})$ means $\mathbf{RX}^{*}=\mathbf{Q}_u (\mathbf{X}^{*})$, which implies that after $M_3$ impacts the right and the left stops, the associated state coordinates of map point are equal in absolute value and opposite in direction.

Let the initial time be $t_0 =0$ after impacting at the left stop, and inserting it to Eq. (8), we obtain the coordinates $x_i (t_0 )$ and $y_i (t_0 )=\dot{x}_i (t_0 )(i=1,2,3)$ after impacting at the left stop. Then let the time be $t_1 =\frac{n\pi }{\omega }$ (i.e., half of n excitation periods) where n is an odd integer, and inserting it into Eq. (8), we obtain the coordinates $x_i (t_1 )$ and $y_i (t_1 )=\dot{x}_i (t_1 )(i=1,2,3)$ after impacting at the right stop.

Based on $\mathbf{RX}^{*}=\mathbf{Q}_u (\mathbf{X}^{*})$, we have

$$\begin{aligned} x_i (t_0 )= & {} -x_i (t_1 ),\nonumber \\ y_i (t_0 )= & {} -y_i (t_1 ) (i=1,2,3);\quad x_2 (t_0 )\nonumber \\&-x_3 (t_0 )=-h. \end{aligned}$$

(48)

Then we obtain the following seven equations about $\tau =\tau ^{*}$, $a_i$ and $b_i (i=1,2,3)$:

$$\begin{aligned}&\sum _{j=1}^3 {\psi _{1j} } (e^{-\eta _j t}a_j +A_j \sin \tau ^{*}+B_j \cos \tau ^{*}) \nonumber \\&\quad =-\sum _{j=1}^3 {\psi _{1j} } \{e^{-\eta _j t_1 }[a_j \cos (\omega _{dj} t_1 )+b_j \sin (\omega _{dj} t_1 )]\nonumber \\&\qquad -A_j \sin \tau ^{*}-B_j \cos \tau ^{*}\} \end{aligned}$$

(49a)

$$\begin{aligned}&\sum _{j=1}^3 {\psi _{2j} } (e^{-\eta _j t}a_j +A_j \sin \tau ^{*}+B_j \cos \tau ^{*}) \nonumber \\&\quad =-\sum _{j=1}^3 {\psi _{2j} } \{e^{-\eta _j t_1 }[a_j \cos (\omega _{dj} t_1 )+b_j \sin (\omega _{dj} t_1 )]\nonumber \\&\qquad -A_j \sin \tau ^{*}-B_j \cos \tau ^{*}\} \end{aligned}$$

(49b)

$$\begin{aligned}&\sum _{j=1}^3 {\psi _{3j} } (e^{-\eta _j t}a_j +A_j \sin \tau ^{*}+B_j \cos \tau ^{*})\nonumber \\&\quad =-\sum _{j=1}^3 {\psi _{3j} } \{e^{-\eta _j t_1 }[a_j \cos (\omega _{dj} t_1 )+b_j \sin (\omega _{dj} t_1 )]\nonumber \\&\qquad -A_j \sin \tau ^{*}-B_j \cos \tau ^{*}\} \end{aligned}$$

(49c)

$$\begin{aligned}&\sum _{j=1}^3 {\psi _{1j} } (-\eta _j a_j +\omega _{dj} b_j +A_j \omega \cos \tau ^{*}-B_j \omega \sin \tau ^{*}) \nonumber \\&\quad =\sum _{j=1}^3 {\psi _{1j} } \{e^{-\eta _j t_1 }[(-\eta _j a_j \nonumber \\&+\omega _{dj} b_j )\cos (\omega _{dj} t_1 )+(-\eta _j b_j -\omega _{dj} a_j )\sin (\omega _{dj} t_1 )]\nonumber \\&\qquad -A_j \omega \cos \tau ^{*}+B_j \omega \sin \tau ^{*}\} \end{aligned}$$

(49d)

$$\begin{aligned}&\sum _{j=1}^3 {\psi _{2j} } (-\eta _j a_j +\omega _{dj} b_j +A_j \omega \cos \tau ^{*}-B_j \omega \sin \tau ^{*}) \nonumber \\&\quad =\sum _{j=1}^3 {\psi _{2j} } \{e^{-\eta _j t_1 }[(-\eta _j a_j \nonumber \\&\quad +\,\omega _{dj} b_j )\cos (\omega _{dj} t_1 )+(-\eta _j b_j -\omega _{dj} a_j )\sin (\omega _{dj} t_1 )]\nonumber \\&\qquad -A_j \omega \cos \tau ^{*}+B_j \omega \sin \tau ^{*}\} \end{aligned}$$

(49e)

$$\begin{aligned}&\sum _{j=1}^3 {\psi _{3j} } (-\eta _j a_j +\omega _{dj} b_j +A_j \omega \cos \tau ^{*}-B_j \omega \sin \tau ^{*}) \nonumber \\&\quad =\sum _{j=1}^3 {\psi _{3j} } \{e^{-\eta _j t_1 }[(-\eta _j a_j +\omega _{dj} b_j )\cos (\omega _{dj} t_1 )\nonumber \\&\qquad +\,(-\eta _j b_j -\omega _{dj} a_j )\sin (\omega _{dj} t_1 )]\nonumber \\&\qquad -A_j \omega \cos \tau ^{*}+B_j \omega \sin \tau ^{*}\} \end{aligned}$$

(49f)

$$\begin{aligned}&\sum _{j=1}^3 {\psi _{2j} } (e^{-\eta _j t}a_j +A_j \sin \tau ^{*}+B_j \cos \tau { }^*)\nonumber \\&\quad -\sum _{j=1}^3 {\psi _{3j} } (e^{-\eta _j t}a_j +A_j \sin \tau ^{*}+B_j \cos \tau ^{*})=-h.\nonumber \\ \end{aligned}$$

(49g)

By elimination and simplification, we obtain the following equation about $\tau ^{*}$:

$$\begin{aligned} u\cos \tau ^{*}+v\sin \tau ^{*}=h \end{aligned}$$

(50)

where u and v are constants determined by the system parameters. Then $\tau ^{*}$ can be solved as

$$\begin{aligned} \tau ^{*}=\left\{ {{\begin{array}{ll} 2\tan ^{-1}\left( {\frac{v\pm \sqrt{u^{2}+v^{2}-h^{2}}}{u+h}} \right) ,&{}\quad u+h\ne 0 \\ 2\tan ^{-1}\left( {\frac{h-u}{2v}} \right) ,&{}\quad u+h=0 \\ \end{array} }} \right. . \end{aligned}$$

(51)

Subsequently, inserting the expression of $\tau ^{*}$ into Eq. (49), we obtain expressions of integration constants $a_i$ and $b_i \quad (i=1,2,3)$. Inserting the value of $a_i$, $b_i$ and $\tau ^{*}$ into Eq. (8), and letting the time $t=0$, we obtain the coordinates $(x_1^*,x_2^*,y_1^*,y_2^*,y_3^*,\tau ^{*})$ of the symmetric fixed point X $^{*}$.