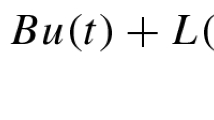Unknown input observer design for one-sided Lipschitz nonlinear systems

Abstract

This paper considers the observer design problem for one-sided Lipschitz nonlinear systems with unknown inputs. The systems under consideration are a larger class of nonlinearities than the well-studied Lipschitz systems and have inherent advantages with respect to conservativeness. For such systems, we first propose a full-order nonlinear unknown input observer (UIO) by using the linear matrix inequality (LMI) approach. Following a similar design procedure and using state transformation, the reduced-order nonlinear UIO is also constructed. Sufficient conditions to guarantee existence of full-order and reduced-order UIOs are established by carefully considering the one-sided Lipschitz condition together with the quadratic inner-bounded condition. Based on the matrix generalized inverse technique, the UIO conditions are formulated in terms of LMIs. Moreover, the proposed observers are applied to a single-link flexible joint robotic system with unknown inputs. Simulation results are finally given to illustrate the effectiveness of the proposed design.

1 Introduction

The problem of observing the state of dynamical systems in the presence of unknown inputs has received considerable attention in the past decades (see [1–17] and the references therein). This problem is of great importance in both theory and practice, since there are many situations where disturbances and partial inputs are inaccessible [3]. For instance, in machine tool applications the cutting force exerted by the tool is often unavailable or very expensive to be measured [9]. In the field of fault detection and isolation, the effect of incipient failure of actuators or plant components can be regarded as a kind of unknown inputs [4, 5, 8]. Moreover, in the chaos synchronization-based secure communication system, the transmitted message at the receiver end is actually a kind of unknown information [13, 14]. In the existing literature, the design of state observer for systems with unknown inputs is also referred to as the unknown input observer (UIO) design problem [3, 4].

The early work of the UIO design can be dated back to 1970s [1, 2]. Up to now, for linear systems the problem has been extensively investigated and many useful design approaches have been developed in the literature [1–8]. However, the design of UIOs for nonlinear systems is more complicated. Most of the existing results are focused on some special classes of nonlinear systems [9–19]. The Lipschitz nonlinearities are commonly used due to the fact that most physical models satisfy a Lipschitz condition, at least locally. For systems without unknown input, the Lipschitz observer has been extensively studied (see, e.g., [20, 21]). For the Lipschitz system with unknown inputs, several design methods are available in recent references. For example, Ha and Trinh [9] studied the problem of estimating simultaneously the states and inputs of Lipschitz nonlinear systems. An LMI approach was presented by Chen and Saif [22] to solve the full-order Lipschitz UIO design. Recently, Pertew et al. [23] introduced a new dynamic framework to design a linear UIO for Lipschitz systems. The UIO design for uncertain Lischitz nonlinear systems was developed by Yang et al. [17], Xiong and Saif [24], and Kalsi et al. [25] by using the sliding-mode observer approach.

The traditional Lipschitz condition is frequently used in existing studies of nonlinear observer design. However, a major limitation in the existing results is that they usually work only for the small Lipschitz constant [26]. When the Lipschitz constant becomes large, most of the existing results may fail to provide a solution. To overcome this drawback, the so-called one-sided Lipschitz condition was introduced to nonlinear observer design by Hu [27]. Following Hu’s work, further results can be found in [28–30]. More recently, Abbaszadeh and Marquez [26] extended the concept of one-sided Lipschitz and proposed a systematic approach to design one-sided Lipschitz nonlinear observer. Less conservative observer design approaches for one-sided Lipschitz nonlinear systems based on Riccati equations or the LMI technique were proposed by Zhang et al. [31, 32]. The discrete-time case observer design of one-sided Lipschitz system was addressed by Benallouch et al. [34] and Zhang et al. [33], respectively. Very recently, Barbata et al. in [35] have investigated the exponential observer design for a class of one-sided Lipschitz stochastic nonlinear systems.

Generally speaking, there are twofold advantages on the one-sided Lipschitz condition [26]. The first is the condition covers a broad family of nonlinearities, which includes its well-known Lipschitz counterpart as a special case. Another inherent advantage is it can reduce conservativeness in existing observer design [26, 27, 31–33]. It should be noted that most of the above-mentioned references on the one-sided Lipschitz observer design are assumed that the system input is available. However, from the previous discussion, there are many situations where disturbances and partial inputs are inaccessible. Therefore, it is important to study the UIO design problem for one-sided Lipschitz nonlinear systems. However, to the best of our knowledge, until now, few results have been given on the study of UIOs design for one-sided Lipschitz systems. This motivates our present research.

In this paper, we deal with the UIO design problem for one-sided Lipschitz nonlinear systems with unknown inputs (disturbance). The main contributions of this paper are three folds. First, the classical Lipschitz assumption employed in the design of UIOs is replaced by the one-sided Lipschitz condition, which is an extension of its known Lipschitz condition and possesses inherent advantages with respect to conservativeness. Second, a novel LMI-based approach is developed to design the full-order UIO for such a system. Sufficient conditions that guarantee the existence of UIOs are obtained. Also, for design purpose, we transform these conditions into the tractable LMI format through using the matrix generalized inverse technique. Third, the reduced-order nonlinear UIO for the system is also constructed by using a state transformation approach. We derive the existence LMI condition of the proposed reduced-order nonlinear UIO by following a similar design procedure of the full-order one. Moreover, as applications of the proposed observers, a single-link flexible joint robot subject to unknown disturbance is given as an example.

This paper is organized as follows. In Sect. 2, we formulate the problem to be investigated. A full-order nonlinear UIO for one-sided Lipschitz nonlinear systems is proposed in Sect. 3. In Sect. 4, we address the reduced-order nonlinear UIO design problem. In Sect. 5, simulation results on two examples are provided to illustrate the effectiveness of the proposed design. Finally, some conclusions are drawn in Sect. 6.

Notations $\mathbb {R}^n$ denotes the $n$-dimensional real Euclidean space. $\mathbb {R}^{m \times n}$ represents the set of all $m\times n$ real matrices. $\langle \cdot , \cdot \rangle$ is the inner product in $\mathbb {R}^n$, i.e., given $x,y \in \mathbb {R}^n$, then $\langle x,y\rangle = x^Ty$, where $x^T$ denotes the transpose of the column vector $x$. $\left\| { \cdot } \right\|$ represents the Euclidean norm. For a square real matrix $P$, $P > 0$ ($P < 0)$ means that the matrix is symmetric and positive definite (negative definite). In symmetric block matrices, we use an ‘$*$’ to represent a term that is induced by symmetry. $I$ denotes an identity matrix with appropriate dimension.

2 Problem statement

Consider the following nonlinear dynamical system described by

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}(t) = Ax(t) + Bu(t) + D_F f(F_L x,u) + Dv(t) \\ y(t) = Cx(t) \\ \end{array}} \right. \end{aligned}$$

(1)

where $x(t) \in \mathbb {R}^n$ is the state vector, $y(t) \in \mathbb {R}^p$ is output vector, $u(t) \in \mathbb {R}^m$ is the known input, and $v(t) \in \mathbb {R}^s$ is the unknown input (or disturbance) vector, respectively. $A$, $B$, $C$, $D_F$, $F_L$, and $D$ are known matrices with appropriate dimensions. $D$ is called the unknown input distribution matrix [4]. The term $Dd(t)$ can be used to describe additive disturbances as well as many kinds of modeling uncertainties such as noise, nonlinear or time-varying terms, model reduction errors, and parameter variations. It can also represent system inputs which are inaccessible (or unmeasurable) [23]. Without loss of generality, we assume that $C$ is of full row rank and $D$ is of full column rank, i.e., $rank(C) = p$ and $rank(D) = q$. The vector function $f(F_L x,u): \mathbb {R}^r \times \mathbb {R}^m \rightarrow \mathbb {R}^r$ represents the nonlinear part of the system. Throughout the paper, we assume that $f(F_L x,u)$ satisfies the following two assumptions [26].

Assumption 1

$f(F_L x,u)$ verifies the one-sided Lipschitz condition, i.e.,

$$\begin{aligned} \left\langle f(F_L \hat{x},u) - f(F_L x,u),F_L \left( {\hat{x} - x} \right) \right\rangle \le \rho \left\| {F_L \left( {\hat{x} - x} \right) } \right\| ^2,\nonumber \\ \end{aligned}$$

(2)

where $\rho \in \mathbb {R}$ is the so-called one-sided Lipschitz constant.

Assumption 2

$f(F_L x,u)$ verifies the quadratic inner-bounded condition, i.e.,

$$\begin{aligned}&\left\| {f(F_L \hat{x},u) - f(F_L x,u)} \right\| ^2 \le \beta \left\| {F_L \left( {\hat{x} - x} \right) } \right\| ^2 \nonumber \\&\quad + \gamma \left\langle f(F_L \hat{x},u) - f(F_L x,u),F_L \left( {\hat{x} - x} \right) \right\rangle , \end{aligned}$$

(3)

where $\beta \in \mathbb {R}$ and $\gamma \in \mathbb {R}$ are known constants.

Remark 1

Every vector function that is locally Lipschitz satisfies the one-sided Lipschitz condition, but the converse is not true [36]. For example, the function $f: \mathbb {R} \rightarrow \mathbb {R}$ defined by $f(0)=0$ and $f(x)=x \log (|x|)$ for $x \ne 0$ is one-sided Lipschitz on a neighborhood of zero, but is not locally Lipschitz at zero. As shown in [27], usually the one-sided Lipschitz constant can be found to be much smaller than the Lipschitz constant. Moreover, the Lipschitz condition implies quadratic inner-boundedness, but the converse is not true [26]. Thus, the class of nonlinear systems being considered in this paper is fairly general. It includes many well-known systems, such as the Lorenz system, recurrent neural networks, Chua’s circuit, and so on [37]. It is worth noting that the one-sided Lipschitz condition has been frequently employed in the study of synchronization of complex networks [38].

In this paper, our main goal was to design a full-order nonlinear UIO or a reduced-order nonlinear UIO for system (1) under Assumptions 1 and 2. More specially, we attempt to design a full-order state observer or a reduce-order one such that it can estimate asymptotically the state of system (1) without any knowledge of the time-varying input $v(t)$.

3 Full-order nonlinear UIO design

This section considers the full-order nonlinear UIO design for system (1). To begin with, let us consider the following full-order observer

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{\xi }(t) = N\xi (t) + Gy(t) + TBu(t) + TD_F f(F_L \hat{x},u) \\ \hat{x}(t) = \xi (t) - Ey(t) \\ \end{array}} \right. \end{aligned}$$

(4)

where $\xi (t) \in \mathbb {R}^n$ represents the state vector of the observer and $\hat{x}(t) \in \mathbb {R}^n$ is the estimate of $x(t)$. $N$, $G$, and $T$ are real matrices of appropriate dimensions and are defined as

$$\begin{aligned} N&= TA - KC,\end{aligned}$$

(5)

$$\begin{aligned} G&= K(I + CE) - TAE,\end{aligned}$$

(6)

$$\begin{aligned} T&= I + EC, \end{aligned}$$

(7)

where $E$ and $K$ are two matrices to be designed later.

Define the state estimation error as

$$\begin{aligned} e(t) =\hat{x}(t) - x(t) = \xi - x - Ey = \xi - Tx. \end{aligned}$$

Then, we can obtain the following error dynamics

$$\begin{aligned}&\dot{e} = \dot{\xi } - T\dot{x} = Ne + (NT + GC - TA)x \nonumber \\&\quad + TD_F \Delta f - TDv \end{aligned}$$

(8)

where

$$\begin{aligned} \Delta f = f(F_L \hat{x},u) - f(F_L x,u) \end{aligned}$$

(9)

It follows from (5–7) that $NT + GC - TA = 0$. Thus, we can rewritten (8) as

$$\begin{aligned} \dot{e} = Ne + TD_F \Delta f - TDv. \end{aligned}$$

(10)

Now, we present a sufficient condition that guarantees the full-order observer (4) is indeed an asymptotic nonlinear UIO for system (1) under Assumptions 1 and 2.

Theorem 1

Under Assumptions 1 and 2, the error dynamics (10) is asymptotically stable, if there exist matrices $P > 0$, $E$ , and $K$ with appropriate dimensions, and two positive scalars $\tau _1 > 0$, $\tau _2 > 0$ such that

$$\begin{aligned}&\left[ \begin{matrix} {N^TP + PN + 2 \eta F_L^T F_L } &{}\quad {PTD_F + \sigma F_L^T } \\ * &{}\quad {-2 \tau _2 I} \end{matrix} \right] < 0,\nonumber \\ \end{aligned}$$

(11)

$$\begin{aligned}&ECD = - D, \end{aligned}$$

(12)

where $\eta = \tau _1 \rho + \tau _2 \beta$ and $\sigma = \tau _2 \gamma - \tau _1$.

Proof

From the Eqs. (7) and (12), we have $TD = 0$, then the observer error dynamics become

$$\begin{aligned} \dot{e} = Ne + TD_F \Delta f. \end{aligned}$$

(13)

Now, let the Lyapunov candidate function be $V(t) = e^T(t)Pe(t)$, where $P>0$ is to be determined later. The time derivative of $V(t)$ along the solution of error dynamics (13) is then given by

$$\begin{aligned}&\dot{V}(t) = 2e^T(t)P\left( {Ne + TD_F \Delta f} \right) \nonumber \\&\quad = e^T(N^TP + PN)e + \Delta f^T(TD_F )^TPe\nonumber \\&\qquad +\,\, e^TPTD_F \Delta f. \end{aligned}$$

(14)

It follows from Assumption 1 that for any positive scalar $\tau _1$,

$$\begin{aligned} 2\tau _1 (\rho e^TF_L^T F_L e - e^TF_L^T \Delta f) \ge 0. \end{aligned}$$

(15)

Similarly, from Assumption 2, we have

$$\begin{aligned} 2\tau _2 (\beta e^TF_L^T F_L e + \gamma e^TF_L^T \Delta f - \Delta f^T\Delta f) \ge 0, \end{aligned}$$

(16)

where $\tau _2$ is a positive scalar. Then, adding the left-hand side terms of (15) and (16) to the right-hand side term of (14) yields

$$\begin{aligned}&\dot{V}(t) \le e^T(N^TP + PN + 2\eta F_L^T F_L )e \nonumber \\&\qquad +\,\, \Delta f^T \left[ {(TD_F )^TP + \sigma F_L } \right] e \nonumber \\&\qquad + \,\,e^T\left( {PTD_F + \sigma F_L^T } \right) \Delta f - 2\tau _2 \Delta f^T\Delta f \nonumber \\&\quad \le \left[ \begin{matrix} e \\ {\Delta f} \end{matrix} \right] ^T\left[ \begin{matrix} {N^TP + PN + 2\eta F_L^T F_L } &{} {PTD_F + \sigma F_L^T } \\ * &{} { - 2\tau _2 I} \\ \end{matrix} \right] \nonumber \\&\qquad \times \left[ \begin{matrix} e \\ {\Delta f} \end{matrix} \right] \end{aligned}$$

(17)

Then, $\dot{V}(t) < 0$ if the condition (11) is satisfied, which implies that $e(t)$ tends to zero asymptotically for any initial value $e(0)$. This ends the proof. $\square$

Theorem 1 provides a sufficient condition that ensures the existence of the nonlinear UIO (4). In order to design the full-order UIO (4), we must find some suitable matrices $P > 0$, $E$ , and $K$ such that the conditions (11) and (12) are satisfied. Since $D$ is of full column rank, one necessary condition for $ECD = - D$ is that $CD$ is of full column rank, i.e.,

$$\begin{aligned} rank(CD) = rank(D) = q. \end{aligned}$$

(18)

If (18) is satisfied, the general solution of the Eq. (12) is then given by

$$\begin{aligned} E = - D(CD)^\dag + Y(I - (CD)(CD)^\dag ) \end{aligned}$$

(19)

where $(CD)^\dag$ is the generalized inverse of $CD$ that satisfying $CD(CD)^\dag CD = CD$ and $Y$ is an arbitrary real matrix with appropriate dimension. For convenience, we denote

$$\begin{aligned} U = - D(CD)^\dag , \quad V = I - (CD)(CD)^\dag . \end{aligned}$$

(20)

Then, we have

$$\begin{aligned} E = U + YV. \end{aligned}$$

(21)

And then

$$\begin{aligned}&N = (I + UC + YVC)A - KC = \Delta _N + Y\Delta _1 - KC,\nonumber \\ \end{aligned}$$

(22)

$$\begin{aligned}&TD_F = (I + UC + YVC)D_F = \Delta _T + Y\Delta _2 , \end{aligned}$$

(23)

where

$$\begin{aligned}&\Delta _N = A + UCA, \quad \Delta _T = (I + UC)D_F, \quad \Delta _1 = VCA, \quad \nonumber \\&\Delta _2 = VCD_F . \end{aligned}$$

(24)

Substituting (21–23) into the matrix inequality (11) yields

$$\begin{aligned} \left[ \begin{matrix} (1,1) &{}\quad {P\Delta _T + X_1 \Delta _2 + \sigma F_L^T }\\ * &{}\quad { - 2\tau _2 I} \end{matrix} \right] < 0, \end{aligned}$$

(25)

where

$$\begin{aligned} (1,1)&= \Delta _N^T P + P\Delta _N + X_1 \Delta _1 + \Delta _1^T X_1^T - X_2 C \nonumber \\&-\,\, C^TX_2^T + 2\eta F_L^T F_L ,\nonumber \\ X_1&= PY, \quad X_2 = PK. \end{aligned}$$

(26)

Now, we can formulate the sufficient condition in Theorem 1 as an LMI. Actually, based on the above discussion, we can easily derive the following conclusion.

Theorem 2

Assume that $CD$ is of full column rank and Assumptions 1 and 2 are satisfied. Then, (4) is a full-order nonlinear UIO for system (1) if there exist matrices $P > 0$, $X_1$ , $X_2$, and scalars $\tau _1 > 0$, $\tau _2 > 0$, such that the LMI (25) has a feasible solution.

Remark 2

Based on Theorem 2, it is easy to give a full-order UIO algorithm for system (1). In fact, if the LMI (25) has a feasible solution $P > 0$, $X_1$ , and $X_2$, then by (26)

$$\begin{aligned} Y = P^{-1}X_1, \quad K = P^{-1}X_2. \end{aligned}$$

(27)

Consequently, we can compute $E$, $N$, $T$, and $G$ by using (21) and (4–6). Thus, we can use (4) to design a full-order nonlinear UIO for system (1).

Remark 3

It should be noted that most of the available UIOs in the existing literature are designed for Lipschitz systems (see, e.g., Ha and Trinh [9], Yang et al. [17], Chen and Saif [22], Pertew et al. [23], Xiong and Saif [24], and Kalsi et al. [25]). The existence conditions of the Lipschitz UIOs are usually dependent on the Lipschitz constant. When this constant becomes large, most of the existing results may fail to provide a solution. As an extension, Theorem 2 develops an one-sided Lipschitz UIO and may result in a less conservative design (see Example 2). Moreover, compared with the one-sided Lipschitz observers developed in [26, 31, 32], Theorem 2 can be applied to deal with the nonlinear systems with unknown inputs (or disturbance).

4 Reduced-order nonlinear UIO design

This section presents a reduced-order nonlinear UIO for system (1). In order to simplify our discussion, in this section we assume that $C= [I_p \ \ 0]$. In fact, since $C$ is of full row rank, there always exists a suitable coordinate transformation on the states such that $C$ holds this form. In such a coordinate system, the state vector is of the form $\left[ \begin{array}{l} y \\ w \end{array} \right]$, where $w \in \mathbb {R}^{n - p}$ is the unmeasurable part of the state vector, and system (1) can be rewritten as the following form:

$$\begin{aligned} \left[ \begin{matrix} {\dot{y}} \\ {\dot{w}} \end{matrix} \right]&= \left[ \begin{matrix} {A_{11} } &{} {A_{12} } \\ {A_{21} } &{} {A_{22} } \end{matrix} \right] \left[ \begin{matrix} {y} \\ {w} \end{matrix} \right] + \left[ \begin{matrix} {B_1 } \\ {B_2 } \end{matrix} \right] u \nonumber \\&+ \left[ \begin{matrix} {D_{F1} } \\ {D_{F2} } \end{matrix} \right] f(F_{L1} y + F_{L2} w,u) + \left[ \begin{matrix} {D_1 } \\ {D_2 } \\ \end{matrix} \right] v,\nonumber \\ \end{aligned}$$

(28)

where $A_{11} \in \mathbb {R}^{p\times p}$, $B_1 \in \mathbb {R}^{p\times m}$, $D_{F1} \in \mathbb {R}^{p\times r}$, $F_{L1} \in \mathbb {R}^{r\times p}$, and $D_1 \in \mathbb {R}^{p\times q}$. Then, a reduced-order UIO for system (1) can be designed as follows:

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{\hat{z}}_2 = (A_{22} + LA_{12} )\hat{z}_2 + My + (LB_1 + B_2 )u + D_L f\left( {\hat{\omega },u} \right) \\ \hat{\omega } = F_{L1} y + F_{L2} (\hat{z}_2 - Ly) \\ \hat{x} = \left( {{\begin{array}{*{20}c} y \\ {\hat{z}_2 - Ly} \\ \end{array} }} \right) \\ \end{array}} \right. \end{aligned}$$

(29)

where $L$ is a gain matrix to be determined later, and

$$\begin{aligned} M&= L(A_{11} - A_{12} L) + A_{21} - A_{22} L,\end{aligned}$$

(30)

$$\begin{aligned} D_L&= LD_{F1} + D_{F2}. \end{aligned}$$

(31)

Now, we state the following conclusion.

Theorem 3

Let $C= [I_p \ \ 0]$. Then, under Assumptions 1 and 2, the reduced-order nonlinear UIO (29) is an asymptotic observer for system (1) if there exist matrices $Q > 0$ and $L$ with appropriate dimensions and scalars $\tau _1 > 0$ and $\tau _2 > 0$ such that

$$\begin{aligned}&\left[ \begin{matrix} {(A_{22} \!+\! LA_{12} )^TQ \!+\! Q(A_{22} \!+\! LA_{12} ) \!+\! 2\eta F_{L2}^T F_{L2} } &{}\quad {QD_L + \sigma F_{L2}^T } \\ * &{}\quad { - 2\tau _2 I_r } \\ \end{matrix} \right] \nonumber \\&\quad \quad < 0, \end{aligned}$$

(32)

$$\begin{aligned} LD_1 + D_2 = 0. \end{aligned}$$

(33)

where $\eta = \tau _1 \rho + \tau _2 \beta$ and $\sigma = \tau _2 \gamma - \tau _1$.

Proof

Take a coordinate transformation of $z = T_s x$, where $T_s = \left[ \begin{array}{l@{\quad }l} {I_p } &{} 0 \\ L &{} {I_{n - p} } \\ \end{array} \right]$. Let $z = \left( \begin{array}{l} {z_1 } \\ {z_2 } \end{array} \right)$ where $z_1 = y \in \mathbb {R}^p$ and $z_2 \in \mathbb {R}^{n - p}$. Then, from (28), $z_2$ satisfies the following equation:

$$\begin{aligned} \dot{z}_2&= (A_{22} + LA_{12} )z_2 + My + (LB_1 + B_2 )u \nonumber \\&+ \,\,D_L f\left( {\omega ,u} \right) + (LD_1 + D_2 )v, \end{aligned}$$

(34)

where

$$\begin{aligned} \omega = F_{L1} y + F_{L2} (z_2 - Ly). \end{aligned}$$

Note that $LD_1 + D_2 = 0$. Subtracting the first equation of (29) from (34), the error $\tilde{z}_2 = \hat{z}_2 - z_2$ is then governed by

$$\begin{aligned} \dot{\tilde{z}}_2 = (A_{22} + LA_{12} )\tilde{z}_2 + D_L \Delta f_\omega \end{aligned}$$

(35)

where

$$\begin{aligned} \Delta f_\omega = f\left( {\hat{w},u} \right) - f\left( {w,u} \right) . \end{aligned}$$

Consider the Lyapunov function candidate

$$\begin{aligned} V_2 (t) = \tilde{z}_2^T (t)Q\tilde{z}_2 (t). \end{aligned}$$

(36)

Its time derivative along the trajectories of error dynamics (35) is

$$\begin{aligned}&\dot{V}_2 = \tilde{z}_2^T \left[ {(A_{22} + LA_{12} )^TQ + Q(A_{22} + LA_{12} )} \right] \tilde{z}_2 \nonumber \\&\qquad +\,\, 2\tilde{z}_2^T QD_L \Delta f_\omega \nonumber \\&\quad = \left[ \begin{matrix} {\tilde{z}_2 } \\ {\Delta f_\omega } \end{matrix} \right] ^T\left[ \begin{matrix} {(A_{22} + LA_{12} )^TQ + Q(A_{22} + LA_{12} )} &{}\quad {QD_L } \\ {D_L^T Q} &{}\quad 0 \end{matrix} \right] \nonumber \\&\qquad \times \left[ \begin{matrix} {\tilde{z}_2 } \\ {\Delta f_\omega } \end{matrix} \right] \end{aligned}$$

(37)

Using the one-sided Lipschitz condition (2), we have

$$\begin{aligned} \left\langle \Delta f_\omega ,F_L \left( \begin{matrix} 0 \\ {\tilde{z}_2 } \\ \end{matrix} \right) \right\rangle \le \rho \left\| {F_L \left( \begin{matrix} 0 \\ {\tilde{z}_2 } \\ \end{matrix} \right) } \right\| ^2, \end{aligned}$$

The above inequality implies that $\tilde{z}_2^T F_{L2}^T \Delta f_\omega \le \rho \tilde{z}_2^T F_{L2}^T F_{L2} \tilde{z}_2$. Therefore, for any positive scalar $\tau _1$, we have

$$\begin{aligned} \tau _1 \left[ \begin{matrix} {\tilde{z}_2 } \\ {\Delta f_\omega } \end{matrix} \right] ^T\left[ \begin{matrix} {2\rho F_{L2}^T F_{L2} } &{} { - F_{L2}^T } \\ { - F_{L2} } &{} 0 \\ \end{matrix} \right] \left[ \begin{matrix} {\tilde{z}_2 } \\ {\Delta f_\omega } \end{matrix} \right] \ge 0. \end{aligned}$$

(38)

On the other hand, from the condition (3) of quadratic inner-boundedness, we get

$$\begin{aligned} \Delta f_\omega ^T \Delta f_\omega \le \beta \left\| {F_L \left( {{\begin{array}{*{20}c} 0 \\ {\tilde{z}_2 } \\ \end{array} }} \right) } \right\| ^2 + \gamma \left\langle \Delta f_\omega ,F_L \left( {{\begin{array}{*{20}c} 0 \\ {\tilde{z}_2 } \\ \end{array} }} \right) \right\rangle ,\nonumber \\ \end{aligned}$$

(39)

which implies that

$$\begin{aligned} \Delta f_\omega ^T\Delta f_\omega \le \beta \tilde{z}_2^T F_{L2}^T F_{L2} \tilde{z}_2 + \gamma \tilde{z}_2^T F_{L2}^T \Delta f_\omega , \end{aligned}$$

Thus, for any positive scalar $\tau _2$, we have

$$\begin{aligned} \tau _2 \left[ \begin{matrix} {\tilde{z}_2 } \\ {\Delta f_\omega } \end{matrix} \right] ^T\left[ \begin{matrix} {2\beta F_{L2}^T F_{L2} } &{}\quad {\gamma F_{L2}^T } \\ {\gamma F_{L2} } &{}\quad { - 2I_r } \\ \end{matrix} \right] \left[ \begin{matrix} {\tilde{z}_2 } \\ {\Delta f_\omega } \\ \end{matrix}\right] \ge 0. \end{aligned}$$

(40)

Then, adding the left-hand side terms of (38) and (40) to the right-hand side term of (37) yields

$$\begin{aligned} \dot{V}_2 \le \left[ \begin{matrix} {\tilde{z}_2 } \\ {\Delta f_\omega } \end{matrix} \right] ^T\Pi \left[ \begin{matrix} {\tilde{z}_2 } \\ {\Delta f_\omega } \end{matrix} \right] , \end{aligned}$$

(41)

where

$$\begin{aligned} \Pi = \left[ \begin{matrix} (A_{22} + LA_{12} )^TQ + Q(A_{22} + LA_{12} ) + 2\eta F_{L2}^T F_{L2} &{} {QD_L + \sigma F_{L2}^T } \\ * &{} { - 2\tau _2 I_r } \\ \end{matrix}\right] . \end{aligned}$$

The condition (32) is equivalent to $\Pi < 0$. Thus, we have $\dot{V}_2 < 0$, which implies that $\tilde{z}_2 (t)$ tends to zero asymptotically. This completes the proof.$\square$

The design of the reduced-order UIO (29) for system (1) can be achieved by following a similar procedure of the full-order UIO. In fact, it is possible to choose a matrix $L$ satisfies (33) if

$$\begin{aligned} rank(D_1 ) = rank\left[ \begin{matrix} {D_1 } \\ {D_2 } \end{matrix} \right] = q. \end{aligned}$$

(42)

Since $LD_1 + D_2 = 0$, the general solution of this equation is

$$\begin{aligned} L = - D_2 D_1 ^\dag + Z(I_p - D_1 D_1 ^\dag ), \end{aligned}$$

(43)

where $D_1^\dag$ is the generalized inverse of $D_1$ that satisfying $D_1 D_1^\dag D_1 = D_1$ and $Z$ is an arbitrary real matrix with appropriate dimension. For convenience, we denote

$$\begin{aligned} U_D = - D_2 D_1 ^\dag , \quad V_D = I_p - D_1 D_1 ^\dag . \end{aligned}$$

(44)

Then, we have

$$\begin{aligned} L = U_D + ZV_D . \end{aligned}$$

(45)

And then

$$\begin{aligned} D_L = U_D D_{F1} + D_{F2} + ZV_D D_{F1} = \Delta _D + Z\Delta _F , \end{aligned}$$

where

$$\begin{aligned} \Delta _D = U_D D_{F1} + D_{F2}, \quad \Delta _F = V_D D_{F1}. \end{aligned}$$

(46)

Substituting $L$ given by (45) into the matrix inequality in (32) yields

$$\begin{aligned} \left[ \begin{matrix} {(1,1)} &{}\quad {Q\Delta _D + S\Delta _F + \sigma F_{L2}^T } \\ * &{}\quad { - 2\tau _2 I_r } \\ \end{matrix} \right] < 0, \end{aligned}$$

(47)

where

$$\begin{aligned} (1,1)&= \Delta _U^T Q + Q\Delta _U + A_{12}^T V_D^T S^T + SV_D A_{12} \nonumber \\&+\,\, 2\eta F_{L2}^T F_{L2}, \end{aligned}$$

(48)

$$\begin{aligned} \Delta _U = A_{22} + U_D A_{12}, \quad S = QZ. \end{aligned}$$

(49)

From the above discussion and using Theorem 3, we now can easily derive the following conclusion.

Theorem 4

Assume that $C= [I_p \ \ 0]$ and $rank(D_1) = q$. Then under Assumptions 1 and 2, the reduced-order nonlinear UIO (29) is an asymptotic observer for system (1) if there exist matrices $Q > 0$ and $S$ with appropriate dimensions, and scalars $\tau _1 >0$ and $\tau _2 > 0$ such that the LMI (47) is satisfied.

Remark 4

Based on Theorem 4, it is not difficult to give an algorithm to design the reduced-order UIO (29). In fact, if the LMI (47) has a feasible solution $Q > 0$ and $S$, then $Z = Q^{- 1}S$. Consequently, we can compute $L$ and then $M$ and $D_L$ by using (45) and (30–31). Thus, we can use (29) to design a reduced-order nonlinear UIO for system (1).

Remark 5

Compared with the full-order UIO (4), the reduced-order UIO (29) takes the measurable output into account and then has a lower dimension, which implies that it can be constructed with fewer integrators and the whole control system will be simpler. Moreover, the proposed reduced-order UIO can be viewed as an extension of the reduced-order observer developed in [32].

5 Simulation study

In this section, the proposed full-order and reduced-order nonlinear UIOs in this paper will be illustrated by two examples.

Example 1

Consider a single-link flexible joint robotic system in the presence of unknown disturbance. The dynamics of this system without disturbance can be described as follows (see, e.g., [20]):

$$\begin{aligned} \dot{\theta }_m&= \omega _m , \\ \dot{\omega }_m&= \frac{k}{J_m }(\theta _{\ell } - \theta _m ) - \frac{B_{vf}}{J_m}\omega _m + \frac{K_\tau }{J_m }u, \\ \dot{\theta }_{\ell }&= \omega _{\ell }, \\ \dot{\omega }_{\ell }&= - \frac{k}{J_{\ell }}(\theta _{\ell } - \theta _m ) - \frac{mgh}{J_m }\sin (\theta _{\ell }) \end{aligned}$$

where $J_m$ represents the inertia of the actuator (d.c. motor), and $J_{\ell }$ stands for the inertia of the link. $\theta _m$ and $\theta _{\ell }$ are the angles of rotations of the motor and the link, respectively. $\dot{\theta }_m$ and $\dot{\theta }_{\ell }$ are their angular velocities. $k$, $K_\tau$, $m$, $g$, and $h$ are positive constants, see Table 1.

Table 1 Robot parameters

Physically, one can measure the motor position and velocity, but the measurement of the other sates is nontrivial. Note that $u$ is the known control input of the system. Suppose that this system also exists an unknown time-varying input (or disturbance) $v(t)$ and the unknown input distribution matrix is chosen as $D = \left[ 5 \ 5 \ 2 \ 1 \right] ^T$. Then, for the parameters given in Table 1, we can rewrite the system in the form of (1) with:

$$\begin{aligned}&A = \left[ \begin{matrix} 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ {-48.6} &{}\quad { -1.25} &{}\quad {48.6} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ {19.5} &{}\quad 0 &{}\quad { - 19.5} &{}\quad 0 \\ \end{matrix} \right] , \quad B = \left[ \begin{matrix} 0 \\ {21.6} \\ 0 \\ 0 \end{matrix} \right] ,\\&D_F = \left[ \begin{matrix} 0 \\ 0 \\ 0 \\ {-1} \end{matrix} \right] , \quad C =\left[ \begin{matrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ \end{matrix} \right] , \quad F_L = \left[ \begin{matrix} 0 &{} 0 &{} 1 &{} 0 \\ \end{matrix} \right] ,\\&f(F_L x,u) = 3.33 \sin (x_3). \end{aligned}$$

For this example, one can verify that Assumptions 1 and 2 are satisfied with $\rho = 3.33$, $\beta = 11.2$, and $\gamma =0$. In fact, we have

$$\begin{aligned}&\left\langle 3.33(sin\hat{x}_3 - sin{x_3}), (\hat{x}_3-x_3) \right\rangle \le 3.33 \left\| \hat{x}_3-x_3 \right\| ^2,\\&\left\| 3.33(sin\hat{x}_3 - sin{x_3}) \right\| ^2 \le 3.33^2 \left\| \hat{x}_3-x_3 \right\| ^2\\&\quad < 11.2 \left\| \hat{x}_3-x_3\right\| ^2. \end{aligned}$$

Moreover, we have $rank(CD) = rank(D) = 1$ and $rank(D_1) = 1$. Consequently, we can apply Theorems 2 and 4 to design the full-order and reduced-order nonlinear UIOs, respectively. To design the full-order nonlinear UIO (4), we need solve the LMI (25). Using the Matlab LMI tools, we get

$$\begin{aligned}&N = \left[ \begin{matrix} -0.5000 &{}\quad -1.9347 &{}\quad 66.6267 &{} 0 \\ 1.9347 &{}\quad -0.5000 &{}\quad -6.9800 &{}\quad 0 \\ -128.1283 &{}\quad 13.4230 &{}\quad -17.8808 &{}\quad 1 \\ -153.7540 &{}\quad 16.1076 &{}\quad -24.4569 &{}\quad 0 \end{matrix} \right] ,\\&G = \left[ \begin{matrix} -64.8967 &{}\quad 21.8361 \\ 9.4801 &{}\quad -4.9690 \\ -160.1764 &{}\quad 171.5327 \\ -189.4256 &{}\quad 204.1292 \end{matrix}\right] ,\\&E = \left[ \begin{matrix} -2.3709 &{}\quad 1.3709 \\ 0.1436 &{}\quad -1.1436 \\ -0.0321 &{}\quad -0.3679 \\ -0.0980 &{}\quad -0.1020 \end{matrix} \right] ,\\&T = \left[ \begin{matrix} -1.3709 &{}\quad 1.3709 &{} 0 &{} 0 \\ 0.1436 &{}\quad -0.1436 &{} 0 &{} 0 \\ -0.0321 &{}\quad -0.3679 &{} 1 &{} 0 \\ -0.0980 &{}\quad -0.1020 &{} 0 &{} 1 \end{matrix} \right] . \end{aligned}$$

Thus, we can design a full-order UIO in the form of (4) for the system. One the other hand, we can use Theorem 4 to design a reduced-order UIO for this system. Solving the LMI (47) yields

$$\begin{aligned}&Q = \left[ \begin{matrix} 1.3738 &{}\quad -0.5495 \\ -0.5495 &{}\quad 0.4579 \end{matrix} \right] , \\&S = \left[ \begin{matrix} 0.3175 &{}\quad -0.1417 \\ 0.7894 &{}\quad 0.9721 \end{matrix} \right] . \end{aligned}$$

Consequently, from (30, 31, 45) and $Z = Q^{- 1}S$, we have

$$\begin{aligned}&L = \left[ \begin{matrix} -0.0321 &{}\quad -0.3679 \\ -0.0980 &{}\quad -0.1020 \end{matrix} \right] , \quad D_L = \left[ \begin{matrix} 0 \\ -1 \end{matrix} \right] , \\&M = \left[ \begin{matrix} 17.4051 &{}\quad -6.0488 \\ 23.6723 &{}\quad -8.9686 \end{matrix} \right] . \end{aligned}$$

For simulation, we assume that the known input in this example is $u=sin(t)$ and the unknown disturbance is $v=2sin(5t)$. Figures 1 and 2 show the trajectories of state $x(t)$ along with its estimate via the full-order UIO (4) under the initial conditions $x(0)=({-1} \; 3 \; {-2} \; 2)^T$ and $\hat{x}(0)=(3\; {-2} \; 1 \; {-1})^T$. On the contrast, Fig. 3 shows the trajectories of $x_3(t)$ and $x_4(t)$ along with their estimates via the reduced-order UIO (29) under the initial conditions $x(0)=({-2} \; 1 \; {-1} \; 1)^T$ and $\hat{z}_2(0)=({1} \; {-2})^T$. From Figs. 1, 2, and 3, it can be seen that both the full-order and the reduced-order UIOs perform as expected and the system state is very well estimated.

Fig. 1

Simulation of $x_1$ and $x_2$ via full-order UIO in example 1

Fig. 2

Simulation of $x_3$ and $x_4$ via full-order UIO in example 1

Fig. 3

Simulation of $x_3$ and $x_4$ via reduced-order UIO in example 1

Example 2

Consider the following system described by (1) with

$$\begin{aligned}&A = \left[ \begin{matrix} -3 &{} 1 \\ 1 &{} -6 \\ \end{matrix} \right] , \quad B = \left[ \begin{matrix} 0 \\ 1 \end{matrix} \right] ,\\&f(F_Lx,u) = \left[ \begin{matrix} { - x_1 (x_1^2 + x_2^2 )} \\ { - x_2 (x_1^2 + x_2^2 )} \\ \end{matrix} \right] .\\&C = \left[ \begin{matrix} 1&0 \end{matrix} \right] , \quad D = \left[ \begin{matrix} 1 \\ 0 \end{matrix} \right] , \quad D_F=F_L=I_2. \end{aligned}$$

From [26], we know that $f(F_Lx,u)$ is globally one-sided Lipschitz with respect to $x$ and the one-sided Lipschitz constant is $\rho = 0$. However, the system is only locally Lipschitz [26]. Hence, the results developed for globally Lipschitz in [9, 17, 22, 23] cannot be directly applied to this case.

Consider the set $\Omega = \left\{ {x \in {\mathbb {R}}^2:\left\| x \right\| \le r } \right\}$. Let

$$\begin{aligned} r \!=\! \min \left( {\sqrt{ - \frac{\gamma }{4}} , \root 4 \of {\beta + \frac{\gamma ^2}{4}}} \right) , \quad \gamma \!<\! 0, \quad \beta + \frac{\gamma ^2}{4} > 0. \end{aligned}$$

Then, one can verify the quadratically inner-bounded property of $f(F_Lx,u)$ in $\Omega$ with respect to $x$ [26]. Note also that the region $\Omega$ can be made arbitrarily large by choosing appropriate values for $\gamma$ and $\beta$.

Now, we are ready to design UIOs for this system. Letting $\beta =-200$ and $\gamma =-300$ and following a similar procedure as in Example 1 yield

$$\begin{aligned} E&= \left[ \begin{matrix} -1 \\ 0 \\ \end{matrix}\right] , \quad T = \left[ \begin{matrix} 0 &{}\quad 0 \\ 0 &{}\quad 1 \\ \end{matrix}\right] ,\\ \quad N&= \left[ \begin{matrix} -2.5033 &{}\quad 0 \\ 0 &{}\quad -6 \\ \end{matrix}\right] , \quad G =\left[ \begin{matrix} 0 \\ 1 \end{matrix}\right] . \end{aligned}$$

The one can use (4) to design a full-order UIO. For simulation, we assume the known input of the system is $u=sin(t)$ and the unknown disturbance is $v=sin(3t)$. Figure 4 shows the trajectories of $x_1(t)$ and $x_2(t)$ and their estimates under the initial conditions $x(0)=({-2} \; \;3)^T$ and $\hat{x}(0)=(1 \; {-2})^T$.

Fig. 4

Simulation of $x_1$ and $x_2$ via full-order UIO in example 2

The reduced-order UIO for this system can also be designed by applying Theorem 4. According to Remark 4, we have $L=0$, $D_L=[0 \; \; 1]$ and $M=1$. Then, we can use (29) to estimate the unmeasurable state $x_2(t)$. The simulation for $x_2(t)$ via the reduce-order UIO (29) is displayed in Fig. 5, where the initial conditions are $x(0)=(-2 \; \; {3})^T$ and $\hat{z}_2(0)=-3$. As shown in Figs. 4 and 5, the state is very well estimated.

Fig. 5

Simulation of $x_2$ via reduced-order UIO in example 2

6 Conclusion

We have studied the full-order and the reduced-order nonlinear UIO design problems for a class of one-sided Lipschitz nonlinear systems, which include its well-known Lipschitz counterpart as a special case. The nonlinear UIO design problem has been solved by using a direct design procedure and the LMI technique. We established the observer existence conditions that guarantee the asymptotic observers for both full-order and the reduced-order UIOs. For the design purpose, these conditions also formulated in terms of LMIs, so that they are numerically tractable via standard software algorithms. We also have applied the proposed full-order and reduced-order UIOs to a single-link flexible joint robotic system subject to unknown disturbance. The effectiveness of the proposed UIO design has been illustrated using numerical simulation.