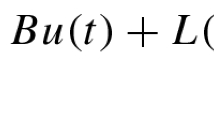1 Introduction

It is known that state estimation plays a key role not only in the control synthesis of dynamical systems, but also in many engineering applications such as energy systems, fault detection and isolation, and chaos-based secure communication [3, 8, 16, 20, 21, 30]. However, as we know, it is often difficult or even impossible to design a state observer for a general nonlinear system. Therefore, many recent efforts have been undertaken to design observers for some particular classes of nonlinear systems. A popular class of nonlinear systems is the Lipschitz system, owing to the fact that most physical system models satisfy a Lipschitz condition, at least locally [13]. Thau [19] first considered the state observer for Lipschitz nonlinear systems. Following Thau’s work, many others researchers studied the Lipschitz observer design problem using various approaches. For instance, the existence conditions of full-order as well as reduced-order observers were established in Rajamani [17] and Zhu and Han [31], respectively. A nonlinear adaptive resilient observer was proposed in Pourgholi and Majd [15]. Observer syntheses for discrete-time Lipschitz systems and Lipschitz descriptor systems were studied in Zemouche and Boutayeb [22] and Lu and Ho [11], respectively. Robust H ∞ observers for uncertain Lipschitz nonlinear systems were investigated in Abbaszadeh and Marquez [1] using a linear matrix inequality (LMI) optimization approach.

In general, Lipschitz nonlinear observers can be carried out by using pseudolinear design techniques [2, 22]. However, this kind of technique may lead to more conservative results. In the recent literature, many efforts have been made to reduce the conservativeness of the existing results for Lipschitz nonlinear systems [2, 10, 22]. There are broadly two approaches to do this. One approach attempts to extend the classical Lipschitz condition to the “one-sided Lipschitz condition” [2], which includes its well-known Lipschitz counterpart as a special case. For example, Zhang et al. in [26] and [27] considered full-order and reduced-order observers for one-sided Lipschitz nonlinear systems. Another approach is to develop new design techniques and less conservative conditions that ensure the asymptotic stability of the observer error dynamics for Lipschitz nonlinear systems. For instance, Phanomchoeng and Rajamani [14] studied the Lipschitz nonlinear observer by using Riccati equations [29]. The circle criterion approach was developed in [3, 7, 10]. By using an LMI approach, less conservative observer synthesis conditions were established in [22, 28] for discrete-time Lipschitz nonlinear systems.

On the other hand, one important application of the nonlinear observer design approach is that it can be applied to chaos synchronization [5, 23, 25, 30]. Indeed, chaos synchronization or chaos-based secure communication can be regarded as a special case of an observer design problem, in which only the input and output information of a drive system is used to construct the state information of the drive system. Consequently, many useful results have been developed based on the nonlinear observer design technique. In Boutayeb [5], an observer-based method was used to achieve synchronization and input recovery for a class of digital nonlinear systems. The related estimation can also be considered as a state and input simultaneous estimation problem [9]. More recently, Zemouche and Boutayeb [23] provided a unified observer design method for discrete-time Lipschitz systems and extended it to H ∞ synchronization and unknown input recovery. They used a particular Lyapunov function and obtained some observer existence conditions. However, it seems that this particular Lyapunov function cannot reduce the conservativeness [28]. Therefore, how to obtain a less conservative observer synthesis condition is still a challenging problem, and this motivates our present research.

In this paper, motivated by the recent work of Zemouche and Boutayeb [23], we revisit the observer design problem for a class of discrete-time Lipschitz nonlinear systems and consider its application to H ∞ synchronization and unknown input estimation. The main contribution of this work is twofold. First, we derive a new observer synthesis condition, due to a generalized observer structure. Unlike [23], we only employ the usual quadratic Lyapunov function to analyze the asymptotical stability of the observer error dynamics. The obtained synthesis condition is simpler, but it can show that the proposed condition is less conservative than that in [23]. Second, under the framework of H ∞ filtering, we extend the proposed observer design method to the H ∞ synchronization and unknown input recovery problem for discrete-time Lipschitz systems in the presence of disturbances in both the state and output equations. New observer-based H ∞ synthesis conditions are established and formulated in terms of LMIs. A numerical example on the discrete-time Rössler chaotic system is provided to illustrate the effectiveness of the proposed design.

Notation

\(\mathbb{R}^{n}\) represents the n-dimensional real Euclidean space. The symbol ∥⋅∥ denotes the Euclidean norm. For a symmetric matrix A, A>0 (A<0) means that this matrix is positive definite (negative definite). In symmetric block matrices, we use an asterisk “∗” to represent a term that is induced by symmetry. I is an identity matrix with appropriate dimension. The notation

$$\|x\|_{\ell^{r}_2}= \Biggl(\sum^{\infty}_{k=0} \big\|x(k)\big\|^2 \Biggr)^{\frac{1}{2}} $$

is the \(\ell^{r}_{2}\) norm of the vector \(x\in \mathbb{R}^{r}\), where the set \(\ell^{r}_{2}\) is defined by

$$\ell^{r}_2= \bigl\{ x\in \mathbb{R}^r: \|x \|_{\ell^{r}_2} < + \infty \bigr\}. $$

2 Problem Statement and Observer Synthesis Conditions

This section considers the observer design problem for a class of digital nonlinear systems, i.e., the discrete-time Lipschitz nonlinear systems. Unlike the approach developed in Zemouche and Boutayeb [23], here we do not employ the particular Lyapunov function to deduce the stability conditions for observer error systems. A simpler but less conservative condition is provided to ensure the existence of a state observer with a generalized observer structure.

2.1 Problem Statement

Consider the following class of discrete-time nonlinear systems described by

$$ \left \{\begin{array}{l} x(k + 1) = Ax(k) + Bf(Hx(k),y(k)) + c, \\ y(k) = Cx(k) \\ \end{array} \right . $$
(1)

where \(x(k) \in \mathbb{R}^{n}\) is the state and \(y(k) \in \mathbb{R}^{p}\) is the measured output. The matrices \(A \in \mathbb{R}^{n\times n}\), \(C \in \mathbb{R}^{p \times n}\), \(B \in \mathbb{R}^{n\times q}\), and \(H \in \mathbb{R}^{s\times n}\) are known constant matrices, \(c \in \mathbb{R}^{n}\) is a constant vector, and \(f: \mathbb{R}^{s}\times \mathbb{R}^{p} \to \mathbb{R}^{q}\) is the nonlinear function of system (1). The nonlinear map f is assumed to be global Lipschitz, i.e., the inequality

$$ \bigl \Vert {f(v,y) - f(w,y)} \bigr \Vert \le \gamma \Vert {v - w} \Vert $$
(2)

holds for all \(v,w \in \mathbb{R}^{s}\), where γ>0 is independent of y.

As proposed in Zemouche and Boutayeb [23], we consider the following observer:

$$ \left \{ \begin{array}{l} \hat {x}(k + 1) = A\hat {x}(k) + Bf(w(k),y(k))+ L(y(k) - C\hat {x}(k)) + c ,\\ w(k) = H\hat {x}(k) + K(y(k) - C\hat {x}(k)). \\ \end{array} \right . $$
(3)

Notice that it holds a generalized structure due to the gain K introduced in the nonlinear part of the observer [23]. The design goal is to find the gains K and L such that the estimation error

$$ e(k) = x(k) - \hat {x}(k) $$
(4)

converges asymptotically toward zero. The error dynamics is governed by

$$ e(k + 1) = (A - LC)e(k) + B\Delta f_k, $$
(5)

where

$$ \Delta f_k = f\bigl(v(k),y(k)\bigr) - f\bigl(w(k),y(k)\bigr), \quad v(k) = Hx(k). $$
(6)

In the following, we will propose a new observer synthesis condition for system (1) under the Lipschitz condition (2). The comparison of conservativeness between our condition and that given in Zemouche and Boutayeb [23] is also provided.

2.2 Observer Synthesis Conditions

Theorem 1

The observer error dynamics (5) is asymptotically stable if there exist a scalar ε>0 and some matrices P>0, R, and K of appropriate dimensions such that the following matrix inequality is feasible:

(7)

If the matrix inequality (7) is feasible, then the gain matrix L is given by L=P −1 R T, and the gain matrix K is a solution of (7).

Proof

Consider the following candidate Lyapunov function:

$$ V(k) = e^\mathrm{T}(k)Pe(k). $$
(8)

Denote ΔV k =V(k+1)−V(k). Then

$$\Delta V_k = e^\mathrm{T}(k + 1)Pe(k + 1) - e^\mathrm{T}(k)Pe(k) $$
(9)

where \(\bar {A} = A - LC\) and

(10)

From the Lipschitz condition (2), we have

$$ \Vert {\Delta f_k } \Vert \le \gamma \bigl \Vert {(H - KC)e(k)} \bigr \Vert . $$
(11)

Denote H K =H−KC. Then, from (11) we have

$$ \varepsilon \gamma ^2 e^\mathrm{T}(k) H_K^\mathrm{T} H_K e(k)- \varepsilon \Delta f_k^\mathrm{T} \Delta f_k \ge 0, $$
(12)

or

(13)

Adding the left-hand side term of (13) to the right-hand side term of (9) yields

$$ \Delta V_k \le \xi _k^\mathrm{T} \varPi \xi _k , $$
(14)

where

By applying the Schur complement (see, e.g., Boyd et al. [6]), Π<0 is equivalent to

(15)

Using the notation R=L T P, inequality (15) leads to (7). Therefore, if condition (7) is satisfied, we have Π<0, and then it follows from (14) that ΔV k <0 for all e(k)≠0. Consequently, the error dynamics (5) is asymptotically stable according to the standard Lyapunov stability theory. Moreover, if matrix inequality (7) has a feasible solution (P s ,R s ,K s ), we can obtain the observer gain \(L = P_{s}^{-1}R_{s}^{\mathrm{T}}\). This completes the proof. □

Remark 1

Note that the proposed condition (7) is not a strict LMI. However, one can use the LMI solver to find a feasible solution of (7) through fixing, a priori, the scalar variable ε.

Remark 2

Let us consider a special case, i.e., H=I and K=0. Under this situation, the observer (3) will be reduced to the usual Luenberger-like observer as studied in [4], [22], and [28]. In this case, by using the Schur complement, the observer synthesis condition (7) will be reduced to the following LMI condition:

(16)

which is the main result of Bara et al. [4]. In this sense, our result is an extension of [4].

In a recent work by Zemouche and Boutayeb [23], the authors also provided a synthesis condition by using a particular Lyapunov function, i.e., \(V(k) = e^{\mathrm{T}}(k)Pe(k)+ \Delta f_{k}^{\mathrm{T}} Q \Delta f_{k} \), where P>0 and Q>0, to analyze the asymptotic stability of the error dynamics. However, it seems that this treatment cannot reduce the conservativeness [28]. On the contrary, we will show that their results are not less conservative than Theorem 1. For the purpose of comparison, here we list one of the main results of [23] (i.e., Theorem 2.2 in [23]) as follows.

Proposition 1

(Theorem 2.2 in [23])

The estimation error converges asymptotically toward zero if there exist scalars α>0, β>0, and matrices P>0, Q>0, R, and K of appropriate dimensions such that the following matrix inequalities are feasible:

(17)
(18)

where η=1+γ 2. If these inequalities have a feasible solution, the gain matrix L is then given by L=P −1 R T, and the gain matrix K is a solution of (17) and (18).

Compared to those in Proposition 1, the sufficient condition (7) in Theorem 1 is simpler and involves fewer matrix variables. However, in the following we will show that the proposed condition (7) in Theorem 1 is less conservative than those in Proposition 1.

Theorem 2

If there exist scalars α>0, β>0, and matrices P>0, Q>0, R, and K of appropriate dimensions such that the matrix inequalities (17) and (18) are satisfied, then the matrices P, R, K and \(\varepsilon = \textstyle{{\alpha + \beta } \over \eta }\) satisfy condition (7), where η=1+γ 2.

Proof

Assume that there exist some scalars α>0, β>0, and matrices P>0, Q>0, R, and K of appropriate dimensions satisfying the conditions (17) and (18). It then follows from (18) that Q−αI q <0 and

(19)

Denote L=P −1 R T. Using the Schur complement, (19) is equivalent to

(20)

where

$$ \varXi_{11} = \eta (A - LC)^\mathrm{T}P(A - LC) - P + \beta \gamma ^2H_K^\mathrm{T} H_K. $$

On the other hand, condition (7) is equivalent to

(21)

Let \(\varepsilon = \frac{\alpha + \beta }{\eta }\). Then

(22)

Therefore, we have ϒ<0, i.e., condition (7) is satisfied, which completes the proof. □

3 H ∞ Synchronization and Unknown Input Recovery

In this section, we will extend the observer design method in the previous section to a nonlinear system with unknown inputs. In general, the simultaneous state and input estimation for a class of nonlinear systems is still a challenging problem [9]. We revisit this problem in the background of H ∞ synchronization and unknown input recovery for chaotic communication systems. Further details on this topic can be found in [5, 23].

As studied in [23], in this section we consider the nonlinear model described by

$$ \left \{ {\begin{array}{l} x(k + 1) = Ax(k) + A_s s(k) + E_\omega \omega (k)+ Bf(H_x x(k),H_s s(k)), \\ y(k) = Cx(k) + Ds(k) + D_\omega \omega (k) \\ \end{array}} \right . $$
(23)

where \(x(k) \in \mathbb{R}^{n}\) is the state vector, \(s(k) \in \mathbb{R}^{m}\) denotes the information to be estimated, \(y(k) \in \mathbb{R}^{p}\) is the received signal, and \(w(k) \in \ell_{2}^{r} \) is the vector of bounded disturbances. A, A s , B, C, D, H x , H s , E ω , and D ω are constant matrices of appropriate dimensions.

The nonlinear function \(f: \mathbb{R}^{d_{1} }\times \mathbb{R}^{d_{2} } \to \mathbb{R}^{q}\) is assumed to be Lipschitz, i.e.,

(24)

where κ f >0 is the Lipschitz constant. The matrix D is assumed to be of full column rank. To simplify the presentation, we use the following notation:

(25)
(26)

Since D is of full column rank, the following matrix:

(27)

is nonsingular. Thus, if we define

(28)

where S and T are two real matrices of (n+m)×n and (n+m)×p, respectively, from (28) we have

$$ SE + TH = I_{n + m}. $$
(29)

For system (23) with the unknown input s(k), we can design a state observer as follows:

$$ \left \{ {\begin{array}{l} z(k + 1) = Nz(k) + Ly(k) + SBf(v(k)), \\ v(k) = H_{x,s} \hat {\varsigma }(k) + K(y(k) - H\hat {\varsigma }(k)), \\ \hat {\varsigma }(k) = z(k) + Ty(k) \\ \end{array}} \right . $$
(30)

where

(31)

Note that the above observer holds the same form as that proposed in Zemouche and Boutayeb [23]. Now, let us consider the estimation error

$$ \varepsilon (k) = \hat {\varsigma }(k) - \varsigma (k). $$
(32)

Then, we have

$$ \varepsilon (k) = z(k) - SE\varsigma (k) + TD_\omega \omega (k). $$
(33)

The dynamics of the estimation error is then given by

(34)

where

$$ \delta f_k = f\bigl(v(k)\bigr) - f\bigl(H_{x,s} \varsigma (k)\bigr), \qquad F = L - NT. $$
(35)

By setting

$$ N = SM - FH, $$
(36)

the error dynamics can be rewritten as follows:

$$ \varepsilon (k + 1) = (SM - FH)\varepsilon (k) + SB\delta f_k + (\bar {E}_\omega + F\bar {D}_\omega )\bar { \omega }(k), $$
(37)

where

(38)
(39)

Thus, our design goal is to find some appropriate matrices L, N, and K such that the estimation error converges H ∞ asymptotically to zero, i.e.,

$$ \Vert \varepsilon \Vert _{\ell_2^{n + m} } \le \lambda \Vert \omega \Vert _{\ell_2^r } , $$
(40)

where λ>0 is the prescribed disturbance attenuation level. Without loss of generality, we assume that the disturbances ω(0)=0 [23]. Then the above inequality is equivalent to

$$ \Vert \varepsilon \Vert _{\ell_2^{n + m} } \le \frac{\lambda }{\sqrt{2} } \Vert \bar {\omega } \Vert _{\ell_2^{2r} }. $$
(41)

Consequently, the above observer design problem is equivalent to the following H ∞ filtering design problem: Given the system (23) and the observer (30), the H ∞ filtering design problem is to determine the matrices N, L, and K so that lim k→∞ ε(k)=0 for ω(k)=0, and

$$ \Vert \varepsilon \Vert _{\ell_2^{n + m} } \le \frac{\lambda }{\sqrt{2} } \Vert \bar {\omega } \Vert _{\ell_2^{2r} } \quad \forall \omega (k) \ne 0; \ \varepsilon (0) = 0. $$
(42)

According to [23], the H ∞ filtering design problem is reduced to finding a Lyapunov function V k such that

$$ W_k = \Delta V_k + \varepsilon ^\mathrm{T}(k)\varepsilon (k) - \frac{\lambda ^2}{2} \bar {\omega }^\mathrm{T}(k)\bar {\omega }(k) < 0, $$
(43)

where

$$ \Delta V_k = V_{k + 1} - V_k . $$
(44)

Theorem 3

For a prescribed λ>0, the H ∞ filtering design problem corresponding to the systems (23) and the observer (30) is solvable, with the H ∞ performances less than λ, if there exist a scalar α>0 and matrices P>0, R, and K of appropriate dimensions such that the following matrix inequality is feasible:

(45)

where \(\tilde {B} = SB\), H K =H x,s −KH, \(K_{\omega}= K\bar {D}_{\omega}\), and

(46)
(47)

If (45) admits a solution, then the matrix F is given by F=P −1 R T. The matrices N and L can be deduced from (35) and (36), and the gain K is a direct solution of (45).

Proof

Let the Lyapunov function candidate be given as V k =ε T(k)Pε(k). Then, from (37) we obtain

$$ W_k = \chi ^\mathrm{T} \varOmega_1 \chi $$
(48)

where

(49)

with \(\tilde {M} = SM - FH\), \(\tilde {F} = \bar {E}_{\omega}+ F\bar {D}_{\omega}\), \(\tilde {B} = SB\), and

(50)

Now, let us consider the Lipschitz condition (24). For arbitrary scalar α>0, the following inequality holds:

$$ \alpha \kappa_f^2 (v_k - H_{x,s} \xi _k )^\mathrm{T}(v_k - H_{x,s} \xi _k ) - \alpha \delta f_k^\mathrm{T} \delta f_k \ge 0, $$
(51)

where

Note that the inequality (51) is equivalent to

$$ \alpha \chi ^\mathrm{T}\varOmega _2 \chi \ge 0 $$
(52)

where

(53)

By adding the left-hand side term of (52) to the right-hand side term of (48), we get

$$ W_k \le \chi ^\mathrm{T} \varOmega \chi , $$
(54)

where

$$ \varOmega = \varOmega _1 + \varOmega _2 . $$
(55)

Applying the Schur complement and using the notation R=F T P, we can show the equivalence between Ω<0 and (45). Consequently, the estimation error vector converges H ∞ asymptotically toward zero with disturbance attenuation level less than λ, i.e.,

$$ \Vert \varepsilon \Vert _{\ell_2^{n + m} } \le \frac{\lambda }{\sqrt{2} } \Vert \bar {\omega } \Vert _{\ell_2^{2r} }. $$
(56)

From the equivalence between (41) and (40), we have

$$ \Vert \varepsilon \Vert _{\ell_2^{n + m} } \le \lambda \Vert \omega \Vert _{\ell_2^r}, $$
(57)

which completes the proof. □

Remark 3

Comparing the above Theorem 3 with the corresponding results in Zemouche and Boutayeb [23], we easily find that the condition (45) involves fewer matrix variables. In this sense, our result is simpler than that in [23]. On the other hand, the simulation example below illustrates that Theorem 3 may be less conservative than Zemouche and Boutayeb’s result.

4 Simulation Example

In this section, we use an example to illustrate the effectiveness of our results. For convenience, we borrow the example given in [23]. Let us consider the discrete-time version of Rössler’s chaotic system (see Fig. 1), obtained from the Euler discretization method with a sampling time h=0.01. The parameters of the system, after adding an information signal s(k) as in (23), are given by

(58)
(59)
$$ f(H_x x,H_s s) = h(x_1 x_3 + x_1 s + b), $$
(60)

where a=0.1, b=0.1, and c=22, for which the system exhibits a chaotic behavior. Notice that here the parameter values are different from those in [23]. Assume that only the transmitted signal is corrupted by noise, i.e., E ω =0. Moreover, we set D ω =1. Note that, from the definition (28), matrices S and T can be deduced as follows:

(61)
Fig. 1
figure 1

The Rössler attractor with a=b=0.1 and c=22

Full size image

From [23], we know the Lipschitz constant κ f =0.045 by extending the nonlinear term f to a globally Lipschitz function on \(\mathbb{R}^{3}\). If we set the value of α with α=100, the condition (45) will become an LMI. By solving this LMI, one can obtain the following solutions:

(62)
(63)

and the optimal value of the disturbance attenuation level is λ=40.9125.

For simulation, the information to be encrypted and recovered is assumed to be of the form s(k)=sin(100hk). Assume that the disturbance ω(⋅) is a Gaussian distributed random signal with mean zero and standard deviation σ=0.01. Figures 2 and 3 show the synchronization error and decryption error with respect to k, respectively. The simulation results verify the effectiveness of the proposed design.

Fig. 2
figure 2

Simulation results for synchronization error \(x(k)-\hat{x}(k)\) with σ=0.01

Full size image
Fig. 3
figure 3

Simulation results for decryption error \(s(k)-\hat{s}(k)\) with σ=0.01

Full size image

Similarly, the proposed design technique can be applied to image transmission by using a picture as the unknown input information. Moreover, the observer design approach in this article may have some potential applications in H ∞ filtering for discrete-time singular systems (see, e.g., Lu et al. [12]), observer-based control of time-delay systems [24], and the H ∞ control of active suspension systems (see, e.g., Sun et al. [18]).

5 Conclusions

We have addressed the synchronization and input recovery problem for a class of discrete-time Lipschitz systems by using a nonlinear observer design approach. First, sufficient conditions for the existence of observers with a generalized structure have been provided and formulated in terms of LMIs. The proposed conditions are simpler but less conservative than those in Zemouche and Boutayeb [23], which can be established theoretically. Moreover, the observer design method is applied to deal with H ∞ chaos synchronization and unknown input recovery for discrete-time Lipschitz nonlinear systems. Finally, the effectiveness and advantages of the proposed design are illustrated via a numerical example.