1 Introduction

Since more than three centuries, a great number of researchers focussed their attention on the mathematical topics of fractional calculus, dealing with derivatives and integrations of non-integer order. Compared to the classical theory, fractional differential equations can more accurately describe many systems in interdisciplinary fields, such as viscoelastic systems, dielectric polarization, electrode–electrolyte polarization, the nonlinear oscillation of earthquakes, mechanics and electromagnetic wave systems [1].

Fractional-order systems have shown very attractive performances and properties, and therefore many applications of such systems have been performed in different domains such as automatic control [2, 3], robotics [4], signal processing [5], image processing [6] and renewable energy [7].

In the last decade, considerable research efforts have been dedicated to fractional systems that display chaotic behaviour like: Duffing model [8], Chua system [9], Chen dynamic circuit [10], Jerk model [11], Rössler model [12], characterization [13] and Newton–Leipnik formulation [14]. The synchronization or control of these systems is a difficult task because the main characteristic of chaotic systems is their high sensitivity to initial conditions [15]. However, it is gathering more and more research effort due to several potential applications especially in cryptography [16,17,18].

For the particular case of fractional-order systems with chaotic dynamics, many methods have been introduced to realize chaos synchronization, such as PC control [19], fractional-order PI\(^{\lambda }\)D\(^{\mu }\) control [20, 21], nonlinear state observer method [22], fuzzy adaptive control [23], adaptive back-stepping control [24], sliding mode control [25, 26] etc.

In the present work, we are interested by the problem of fractional-order chaotic system synchronization by means of sliding mode control [27, 28]. Sliding mode control is a very suitable method for handling such nonlinear systems because of its robustness against disturbances and plant parameter uncertainties and its order reduction property [29, 30].

The main objective is to design an appropriate control law such that the sliding mode is reached in a finite time. The system trajectory moves toward the sliding surface and stays on it. The conventional SMC uses a control law with large control gains yielding undesired chattering while the control system is in the sliding mode [31]. Based on the Lyapunov stability theorem, an efficient control algorithm is proposed that guarantees feedback control system stability via the sliding mode robust tracking design technique.

The manuscript is organized as follows. Section 2 presents an introduction to fractional calculus with some numerical approximation methods. The problem of fractional-order chaotic system synchronization is given in §3. Section 4 presents the proposed sliding mode synchronization technique and the control law design. The stability analysis is performed in §5. In §6, applications of the proposed control scheme on Genesio–Tesi fractional-order systems and the modified Jerk systems are investigated. Finally, conclusion remarks with future works are pointed out in §7.

2 Basics of fractional-order systems

Fractional calculus is an old mathematical research topic, but it is retrieving popularity nowadays. Fractional calculus theory appeared and grows up mainly since three centuries. A recent reference presented by Miller and Boss [32] provides a good source of documentation on fractional systems and operators. However, topics about the application of fractional-order operator theory to dynamic system control are just a recent focus of interest [6, 33].

2.1 Basic definitions

There are many mathematical definitions of fractional integration and derivation. We shall here, present two currently used definitions.

2.1.1 Riemann–Liouville (R–L) definition

It is one of the most popular definitions of the fractional-order integrals and derivative [32]. The R–L integral of fractional-order \(\lambda >0\) is given as

$$\begin{aligned} I^{\lambda }_{\mathrm {RL}}g(t)= & {} D^{-\lambda }_{\mathrm {RL}}g(t) \nonumber \\= & {} \frac{1}{\Gamma (\lambda )}\int ^{t}_{0}(t-\zeta )^{\lambda -1}g(\zeta )\mathrm {d}\zeta \end{aligned}$$
(1)

and the R–L derivative of fractional-order \(\mu \) is

$$\begin{aligned} D^{\mu }_{\mathrm {RL}}g(t)=\frac{1}{\Gamma (n-\mu )}\frac{\mathrm {d}^{n}}{\mathrm {d}t^{n}}\int ^{t}_{0}(t-\zeta )^{n-\mu -1}g(\zeta )\mathrm {d}\zeta ,\quad \end{aligned}$$
(2)

where the integer n verifies: \((n-1)< \mu < n\). The fractional-order derivative (2) may also be expressed from eq. (1) as

$$\begin{aligned} D^{\mu }_{\mathrm {RL}}g(t)=\frac{\mathrm {d}^{n}}{\mathrm {d}t^{n}}\{I^{(n-\mu )}_{\mathrm {RL}}g(t)\}. \end{aligned}$$
(3)

2.1.2 Grünwald–Leitnikov (G–L) definition

The G–L fractional-order integral with order \(\lambda > 0\) is

$$\begin{aligned} I^{\lambda }_{\mathrm {GL}}g(t)= & {} D^{-\lambda }_{\mathrm {GL}}g(t)\nonumber \\= & {} \lim _{h\rightarrow 0}h^{\lambda }\sum ^{k}_{j=0}(-1)^{j}\begin{pmatrix}-\lambda \\ j \end{pmatrix} g(kh-jh). \end{aligned}$$
(4)

Here, h is the sampling period with the coefficients \(\omega ^{(-\lambda )}_{j}\) verifying

$$\begin{aligned} \omega ^{(-\lambda )}_{0}=\left( \begin{array}{c}-\lambda \\ 0 \end{array}\right) =1 \end{aligned}$$

which belong to the following polynomial:

$$\begin{aligned} (1-z)^{-\lambda }=\sum ^{\infty }_{j=0}(-1)^{j}\begin{pmatrix}-\lambda \\ j \end{pmatrix} z^{j}=\sum ^{\infty }_{j=0}\omega ^{(-\lambda )}_{j} z^{j}. \end{aligned}$$
(5)

The G–L definition for fractional-order derivative with order \(\mu > 0 \) is

$$\begin{aligned} D^{\mu }_{\mathrm {GL}}g(t)= & {} \frac{\mathrm {d}^{\mu }}{\mathrm {d}t^{\mu }}g(t) \nonumber \\= & {} \lim _{h\rightarrow 0} h^{-\mu }\sum ^{k}_{j=0}(-1)^{j}\begin{pmatrix}\mu \\ j \end{pmatrix} g(kh-jh), \end{aligned}$$
(6)

where the coefficients

$$\begin{aligned} \omega ^{(\mu )}_{j}=\begin{pmatrix}\mu \\ j \end{pmatrix}=\frac{\Gamma (\mu +1)}{\Gamma (j+1)\Gamma (\mu -j+1)} \end{aligned}$$

with \(\omega _{(\mu )}^{0}={(\begin{array}{c}\mu \\ 0 \end{array})}=1\), are those of the polynomial:

$$\begin{aligned} (1-z)^{\mu }=\sum ^{\infty }_{j=0}(-1)^{j}\begin{pmatrix}\mu \\ j \end{pmatrix} z^{j}=\sum ^{\infty }_{j=0}\omega ^{(\mu )}_{j} z^{j}. \end{aligned}$$
(7)
Fig. 1
figure 1

Chaos in the fractional-order Genesio–Tesi system: (a) States behaviour and (b) phase portrait in the (x, y) plane.

Full size image
Fig. 2
figure 2

SMC synchronization of the fractional-order Genesio–Tesi systems: (a) Trajectories of the master and the slave state variables and (b) the corresponding errors \(e_{x}\) , \(e_{y}\) and \(e_{z}\).

Full size image
Fig. 3
figure 3

SMC synchronization fractional-order Genesio–Tesi systems: (a) Sliding-surface function and (b) the control signal.

Full size image
Fig. 4
figure 4

SMC synchronization of the fractional-order Genesio–Tesi systems in the presence of disturbances: (a) Trajectories of the master and slave state variables and (b) the corresponding errors \(e_{x}\) , \(e_{y}\) and \(e_{z}\).

Full size image
Fig. 5
figure 5

SMC synchronization of the ‘disturbed’ fractional-order Genesio–Tesi systems: (a) Sliding-surface function and (b) the control signal.

Full size image

2.2 Implementation of fractional operator

Generally, industrial control processes are sampled, and so a numerical approximation of the fractional operator is necessary. There exist several approximation approach classes depending on temporal or frequency domain. In the literature, the currently used approaches in frequency domain are those of Charef [33, 34] and Oustaloup [6]. In temporal domain, there is a lot of work about the numerical solution of the fractional differential equations. Diethelm has proposed an efficient method based on the predictor–corrector Adams algorithm [35]. The definitions cited above have numerical approximations also (see refs [32] and [33]).

2.3 Fractional-order system stability

Let us recall the stability definition in the sense of Mittag–Leffler functions [36].

DEFINITION 1

The Mittag–Leffler function is frequently used in the solutions of fractional-order systems. It is defined as

$$\begin{aligned} E_{\alpha }(z)= \sum ^{\infty }_{k=0} \frac{z^{k}}{\Gamma (k\alpha + 1)}, \end{aligned}$$
(8)

where \(\alpha > 0\). The Mittag–Leffler function with two parameters has the following form:

$$\begin{aligned} E_{\alpha ,\beta }(z)= \sum ^{\infty }_{k=0} \frac{z^{k}}{\Gamma (k\alpha + \beta )}, \end{aligned}$$
(9)

where \(\alpha > 0\) and \(\beta > 0\). For \(\beta = 1\), we have \(E_{\alpha }(z) = E_{\alpha ,1}(z)\).

DEFINITION 2

Consider the Riemann–Liouville fractional non-autonomous system

$$\begin{aligned} D^{\alpha }_{\mathrm {RL}}x(t) = f (x,t), \end{aligned}$$
(10)

where f(x, t) is Lipschitz with a Lipschitz constant \(l > 0\) and \( \alpha \in (0, 1)\).

The solution of (10) is said to be Mittag–Leffler stable if

$$\begin{aligned} \left\| x(t)\right\| \le \left[ m\left( x(t_{0})\right) E_{\alpha }(-\lambda (t-t_{0})\alpha )\right] ^{b}, \end{aligned}$$
(11)

where \(t_{0}\) is the initial time, \(\alpha \in (0, 1)\), \(\lambda > 0\), \(b > 0\), \(m(0) = 0\), \(m(x)\ge 0\) and m(x) is locally Lipschitz on \(x \in B \subset R^{n}\) with Lipschitz constant \(m_{0}\).

An important stability result is given below [36].

Lemma 1

Let \(x = 0\) be a point of equilibrium for the fractional-order system (10). Suppose there exist a Lyapunov function V(t, x(t)) such that

$$\begin{aligned}&\epsilon _{1} \left\| x\right\| ^{\eta } \le V(t, x) \le \epsilon _{2} \left\| x\right\| , \end{aligned}$$
(12)
$$\begin{aligned}&\dot{V}(t, x) \le -\epsilon _{3} \left\| x\right\| , \end{aligned}$$
(13)

where \(\epsilon _{1}\), \(\epsilon _{2}\), \(\epsilon _{3}\) and \(\eta \) are positive constants. Then the equilibrium point of system (10) is Mittag–Leffler (asymptotically) stable.

3 Definition of synchronization problem

The following class of n-dimensional non-autonomous fractional-order chaotic system is considered [37]:

$$\begin{aligned} \left\{ \begin{array}{l} D^{q}x_{1} = x_{2}, \\ \vdots \\ D^{q}x_{n-1} = x_{n},\\ D^{q}x_{n} = f(\mathbf x ,t), \end{array} \right. \end{aligned}$$
(14)

where \(\mathbf x =[x_1, x_2, ... , x_n ]^T = [x, x^{(q)}, x^{(2q)}, ...,x^{((n-1)q)} ]^T \in \mathfrak {R}^{n}\), \(f(\mathbf x ,t)\) is a nonlinear function of \(\mathbf x \) and \(0< q < 1\).

Taking (14) as the drive system, the response system with a control input \(u(t)\in \mathfrak {R}\) becomes

$$\begin{aligned} \left\{ \begin{array}{l} D^{q}y_{1} = y_{2}, \\ \vdots \\ D^{q}y_{n-1} = y_{n},\\ D^{q}y_{n} = g(\mathbf y ,t) + u, \end{array} \right. \end{aligned}$$
(15)

where \(\mathbf y =[y_1, y_2, ... , y_n ]^T \in \mathfrak {R}^{n}\), \(g(\mathbf y ,t)\) is the nonlinear function of \(\mathbf y \).

Defining the error vector \(\mathbf e(t) = \mathbf y(t) - \mathbf x(t) \), and from eqs (14) and (15), the error equation is as follows:

$$\begin{aligned} \left\{ \begin{array}{l} D^{q}e_{1} = e_{2}, \\ \vdots \\ D^{q}e_{n-1} = e_{n},\\ D^{q}e_{n} = g(\mathbf y ,t) - f(\mathbf x ,t) + u. \end{array} \right. \end{aligned}$$
(16)

Thus, the problem of synchronizing two fractional-order nonlinear systems is equivalent to the problem of finding a control u(t) ensuring that the error \(\mathbf e \) in (16) converges to zero. A sliding mode controller is designed to achieve this objective in the next section.

4 Design of the sliding mode controller

The main reason for the growing popularity of sliding mode control (SMC) is its robustness against disturbances under certain conditions [29, 38].

In our contribution, the proposed fractional-order sliding surface is

$$\begin{aligned} s(t) = k_{1} D^{q-1}e_{n} + k_{2} \int ^{t}_{0}\sum ^{n}_{i=1} c_{i}e_{i}(\xi )\mathrm {d}\xi , \end{aligned}$$
(17)

where \(k_{1},\, k_{2}\) are positive coefficients and \(c_{i}\), \(i = 1, 2,..., n\) are sliding surface parameters to be determined.

The equivalent sliding mode control is obtained by taking the derivative of eq. (17) as follows:

$$\begin{aligned} \dot{s}(t)&= k_{1} D^{q}e_{n} + k_{2} \sum ^{n}_{i=1} c_{i}e_{i} = 0\nonumber \\&\Rightarrow D^{q}e_{n}= -\frac{k_{2}}{k_{1}}\sum ^{n}_{i=1} c_{i}e_{i}. \end{aligned}$$
(18)

Hence, using eqs (16) and (17) we obtain the equivalent sliding mode control

$$\begin{aligned} u_{\mathrm{eq}}(t) = -g(\mathbf y ,t) + f(\mathbf x ,t) - k \sum ^{n}_{i=1} c_{i}e_{i}, \end{aligned}$$
(19)

where \(k = {k_{2}}/{k_{1}}\) is a positive real number. Choosing the following switch control law

$$\begin{aligned} u_{\mathrm{sw}}(t) = - k \ \mathrm {sign}(s) \end{aligned}$$
(20)

the sliding mode control can be obtained as

$$\begin{aligned} u(t)=&\,u_{\mathrm{eq}}(t) + u_{\mathrm{sw}}(t) \nonumber \\ =&-g(\mathbf y ,t) + f(\mathbf x ,t) - k \sum ^{n}_{i=1} c_{i}e_{i} - k \ \mathrm {sign}(s). \end{aligned}$$
(21)

The objective is that the state trajectories of the system described by eq. (15) converge towards the sliding surface. Thus, by defining

$$\begin{aligned} c^{\star }_{i} = -\frac{k_{2}}{k_{1}}c_{i} \end{aligned}$$
(22)

the sliding mode dynamics are given by the following equations:

$$\begin{aligned} \left\{ \begin{array}{l} D^{q}e_{1} = e_{2}, \\ \vdots \\ D^{q}e_{n-1} = e_{n},\\ D^{q}e_{n} = \sum ^{n}_{i=1} c^{\star }_{i}e_{i}, \end{array} \right. \end{aligned}$$
(23)

or in a matrix equation form as

$$\begin{aligned} D^{q}{} \mathbf e = A \mathbf e , \end{aligned}$$
(24)

where

$$\begin{aligned} \mathbf e =[e_1, e_2, ... , e_n ]^T \end{aligned}$$

and

$$\begin{aligned}A = \left[ \begin{array}{cccc} 0 &{} 1 &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} 1 \\ c^{\star }_{1} &{} c^{\star }_{2} &{} \cdots &{} c^{\star }_{n} \end{array} \right] .\end{aligned}$$

The selection of the fractional-order sliding surface parameters \(c^{\star }_{i} \,( i = 1, 2,..., n )\) obeys the stability theorem of Matignon [39] which imposes for the sliding surface of eq. (17) to be asymptotically stable that the stability condition \(\left| \mathrm {arg}(\mathrm {eig}(A))\right| > q\pi /2\) is verified.

5 Stability analysis

The principal result of this work is expressed by the following theorem:

Theorem 1

Synchronization of systems (14) and (15) is perfectly achieved by the sliding mode control law (21) with \(k = {k_{2}}/{k_{1}}\).

Proof

We shall prove that the systems given by eqs (14) and (15) are completely synchronized which means that the error dynamical system (16) is asymptotically stable.

Let us choose a positive definite Lyapunov candidate function such that

$$\begin{aligned} V = \left| s\right| . \end{aligned}$$
(25)

(It is obvious that the Lyapunov function V(t, e(t)) satisfies the conditions in Lemma 1 for \(\eta =1\) and some positive constants \(\epsilon _{1}\) and \(\epsilon _{2}\).)

We get by simple derivative,

$$\begin{aligned} \dot{V}= & {} \mathrm {sign}(s)\dot{s} \\= & {} \mathrm {sign}(s)\left( k_{1} D^{q}e_{n} + k_{2} \sum ^{n}_{i=1} c_{i}e_{i}\right) \\= & {} \mathrm {sign}(s)\left( k_{1} (g(\mathbf y ,t) - f(\mathbf x ,t) + u ) + k_{2} \sum ^{n}_{i=1} c_{i}e_{i}\right) \\= & {} \mathrm {sign}(s)\left( k_{1} \left( -k \sum ^{n}_{i=1} c_{i}e_{i} -k \ \mathrm {sign}(s)\right) \right. \\&\left. +\, k_{2} \sum ^{n}_{i=1} c_{i}e_{i}\right) . \end{aligned}$$

We set

$$\begin{aligned} k = \frac{k_{2}}{k_{1}}. \end{aligned}$$
(26)

Then we have

$$\begin{aligned} \dot{V}= & {} \mathrm {sign}(s)\left( k_{1} \left( -\frac{k_{2}}{k_{1}} \sum ^{n}_{i=1} c_{i}e_{i} -\frac{k_{2}}{k_{1}} \ \mathrm {sign}(s)\right) \right. \nonumber \\&\left. +\,\, k_{2} \sum ^{n}_{i=1} c_{i}e_{i}\right) \nonumber \\= & {} \mathrm {sign}(s)\left( -k_{2} \sum ^{n}_{i=1} c_{i}e_{i} -k_{2} \ \mathrm {sign}(s) + k_{2} \sum ^{n}_{i=1} c_{i}e_{i}\right) \nonumber \\= & {} \mathrm {sign}(s)\left( -k_{2} \ \mathrm {sign}(s) \right) \nonumber \\= & {} -k_{2}. \end{aligned}$$
(27)

Then, it is always possible to find the positive constant \(\epsilon _{3}\) such that

$$\begin{aligned} \dot{V} = -k_{2} \le -\epsilon _{3} \left\| \mathbf e \right\| \end{aligned}$$

and following Lemma 1, system (16) is Mittag–Leffler stable and the error asymptotically converges to zero, which completes the proof.

6 Simulation results

In order to illustrate the effectiveness of the proposed synchronization scheme, two numerical simulation examples of application to the fractional-order Genesio–Tesi chaotic systems and the fractional-order modified Jerk systems are proposed, in ideal and disturbed conditions.

6.1 Synchronization of fractional-order Genesio–Tesi systems

The fractional-order Genesio–Tesi system is defined as [20]

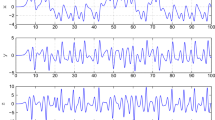
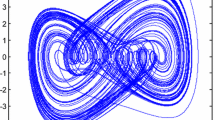
$$\begin{aligned} \left\{ \begin{array}{l} D^{q}x = y, \\ D^{q}y = z,\\ D^{q}z = -c x -b y -a z + x^{2}. \end{array} \right. \end{aligned}$$
(28)

For the system parameters’ values \((a,b,c) = (1.2,2.992,6)\) and taking \(q = 0.99\), the Genesio–Tesi system presents a chaotic behaviour as shown in figure 1.

Initial conditions are [40]: \(x(0) = -1.0032\), \(y(0) = 2.3445\) and \(z(0) = -0.087\).

Table 1 Response time and quadratic error criteria vs. control parameter k.
Full size table
Fig. 6
figure 6

Chaotic behaviours of modified fractional-order Jerk system: (a) (x, y) plane, (b) (x, z) plane, (c) (y, z) plane, (d) (x, y, z) space.

Full size image

Figure 1a shows the chaotic behaviour of the fractional-order Genesio–Tesi system, whereas figure 1b presents the numerical simulation of its attractor.

Fig. 7
figure 7

SMC synchronization of the modified fractional-order Jerk systems: (a) Trajectories of the master and the slave state variables and (b) the corresponding errors \(e_{x}\) , \(e_{y}\) and \(e_{z}\).

Full size image
Fig. 8
figure 8

SMC synchronization of the modified fractional-order Jerk system: (a) Sliding-surface function and (b) the control signal.

Full size image

6.1.1 Synchronization in the ideal case (without disturbances)

Taking the sliding surface parameters as [37]: \((c_{1}, c_{2}, c_{3})= (6, 1, 5)\), we apply the sliding mode control law (21) when the parameters \(k_{1} = 1\) and \(k_{2} = 0.13\).

The obtained simulation results when applying the synchronizing control action at \(t=40\) s with the initial condition values \((-1.0032, 2.3545, -0.87)\) and \((-2, 1, -0.5)\) for the master and the slave systems respectively are presented in figures 2 and 3.

As shown in figure 2, there are three stages of the controlled system [41]. In the first 40 s, without the controller, the system is chaotic as we can see in figure 1. In the second phase (known as reaching phase), after \(t = 40\) s, the fractional-order chaotic system is forced towards the sliding manifold by the sliding mode controller. When the trajectory touches the sliding surface, the system enters the third phase, which is called sliding mode operation. The results presented here show the good performance exhibited by the proposed synchronization schemes.

6.1.2 Synchronization of disturbed fractional Genesio–Tesi systems

It is well known that uncertain disturbance and random factors exist everywhere in real-world [42, 43]. Sliding mode control has proved to be an efficient solution for control and synchronization of disturbed chaotic systems [38].

Let us apply a random disturbance signal \(\zeta (t)\) on the fractional Genesio–Tesi slave system to investigate the performance of the proposed SMC control law in bad operating conditions. The corresponding mathematical model is given by eq. (29).

$$\begin{aligned} \left\{ \begin{array}{l} D^{q}x = y, \\ D^{q}y = z,\\ D^{q}z = -cx -by -az +x^{2} + \zeta , \end{array} \right. \end{aligned}$$
(29)

where \(\zeta (t)\) is a random signal of amplitude \(A=0.1\).

Figures 4 and 5 present the synchronization results using the proposed SMC law (21) with \(k = {k_{2}}/{k_{1}} = 0.1\).

As shown by the simulation results, although the slave system contains an additive disturbance, the tracking is achieved. When the proposed SMC is applied, the control input is much smooth, and the switching control part is small once the sliding layer is entered as shown in figure 5b.

In order to point out the performance of the control system vs. the control parameter k, let us define the quadratic error criterion \(J_{k}\) as

$$\begin{aligned} J_{k} =\sqrt{\int ^{t_{f}}_{t_{c}} (e^{2}_{x} + e^{2}_{y} + e^{2}_{z})\mathrm {d}t}, \end{aligned}$$
(30)

where \(t_{c}\) is the time of control application and \(t_{f}\) is the simulation time duration.

Table 1 illustrates the effect of the control parameter k on the performance of control system (response time \(\tau _{r}\) and quadratic error criterion \(J_{k}\)).

The simulation results demonstrate the efficiency of the proposed SMC control method to achieve the synchronization of the two Genesio–Tesi systems with disturbance rejection.

6.2 Synchronization of fractional-order Jerk systems

The modified fractional-order Jerk system is given as follows [44]:

$$\begin{aligned} \left\{ \begin{array}{l} D^{q}x = y, \\ D^{q}y = z,\\ D^{q}z = -\epsilon _{1}x -y -\epsilon _{2}z -f(x(t)), \end{array} \right. \end{aligned}$$
(31)

where the parameters are given by \(\epsilon _{1} = 1.5\), \(\epsilon _{2} = 0.35\) and f(x(t)) is a piecewise-linear function defined by

$$\begin{aligned} f(x(t)) = \frac{1}{2}(\theta _{0}-\theta _{1})\left( \left| x(t) + 1\right| - \left| x(t) - 1\right| \right) + \theta _{1} x(t), \end{aligned}$$
(32)

where \(\theta _{0}< -1< \theta _{1} < 0\) and \(\theta _{0} = -2.5\), \(\theta _{1} = -0.5\).

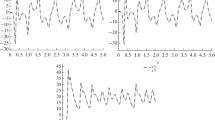
When the initial values are chosen as \((1, 1, 1)^{T}\) and the fractional-order \(q = 0.98\) [44], the modified fractional-order Jerk system shows chaotic behaviours as illustrated in figure 6.

6.2.1 Synchronization in the ideal case (without disturbances)

Taking the sliding surface parameters as [37]: \((c_{1}, c_{2}, c_{3})= (6, 1, 5)\), we apply the sliding mode control law (21) with the parameters \(k_{1} = 1\) and \(k_{2} = 0.13\).

The simulation results obtained when applying the synchronizing control action at \(t=20\) s with a simulation sampling period \(h=0.01\) s and the initial condition values \((-1.0032, 2.3545, -0.87)\) and \((-2, 1, -0.5)\) for the master and the slave systems respectively are presented in figures 7 and 8.

Table 2 Dynamical performance of the modified Jerk systems vs. control parameter k.
Full size table
Fig. 9
figure 9

Quadratic error criterion \(J_{k}\) vs. the controller parameters \(k_1\) and \(k_2\).

Full size image
Fig. 10
figure 10

SMC synchronization of the modified fractional-order Jerk system with delay disturbance: (a) Trajectories of the master and the slave state variables and (b) the corresponding errors \(e_{x}\) , \(e_{y}\) and \(e_{z}\).

Full size image
Fig. 11
figure 11

SMC synchronization of the modified fractional-order Jerk system with delay disturbance: (a) Sliding-surface function and (b) the control signal.

Full size image

As shown in figure 7, there are three stages of the controlled system [41]. In the first 20 s, without controller, the system is chaotic as we can see in figure 6. In the second phase (known as the reaching phase), after \(t = 20\) s, the fractional-order chaotic system is forced towards the sliding manifold by the sliding mode controller. When the trajectory touches the sliding surface, the system enters the third phase, which is called sliding mode operation. The results presented here show the good performance exhibited by the proposed synchronization schemes.

6.2.2 Synchronization of delayed fractional-order modified Jerk system

Here, we try to synchronize two fractional-order modified Jerk systems (31) with different initial conditions and a delay disturbance on the slave system as represented in (33)

$$\begin{aligned} \left\{ \begin{array}{l} D^{q}x(t) = y(t - \tau ), \\ D^{q}y(t) = z(t - \tau ),\\ D^{q}z(t) = -\epsilon _{1}x(t - \tau ) -y(t - \tau ) -\epsilon _{2}z(t - \tau )\\ \qquad \qquad \quad -f(x(t - \tau )). \end{array} \right. \end{aligned}$$
(33)

The proposed control law (21) is applied with the parameters \(k_{1} = 1\) and \(k_{2} = 0.001\), where the delay on the slave system is \(\tau = 5\; \mathrm{h}\). The results obtained for different values of the control parameter k are presented in table 2, where \(\tau _{r}\) is the response time and \(J_{k}\) is the quadratic error criterion defined by (30).

The variation of quadratic error criterion \(J_{k}\) vs. the controller parameters \(k_1\) and \(k_2\) is illustrated in figure 9.

Choosing \(k = 0.0001\), we obtain the simulation results presented in figures 10 and 11.

Simulation results in figure 10 show that, even though the value of delay is not used in the proposed controller (21), the time responses of the closed-loop system with the proposed controller are as effective as in the ideal case (without delay disturbances) [45]. This confirms the acceptable performance of the proposed controller. In fact, the control gain ratio k allows adapting the SMC control to counteract disturbances and delays introduced in the response system, which renders the control system more robust in practical operating conditions [46].

7 Conclusion

A new efficient fractional sliding mode control scheme design has been studied to enable the synchronization of a class of fractional-order chaotic systems. The considered design approach provides a set of fractional-order laws that guarantee asymptotic stability of the fractional-order chaotic systems in the sense of the Lyapunov stability theorem.

The illustrative simulation results are given for the synchronization of two fractional-order Genesio–Tesi chaotic systems and two fractional-order modified Jerk systems. The systems show good performance and excellent effectiveness even in the presence of disturbances and delays affecting the slave system.

Future work will concern the problem of control and synchronization of fractional-order uncertain chaotic systems using adaptive sliding mode control laws.