Static bifurcation and primary resonance analysis of a MEMS resonator actuated by two symmetrical electrodes

Abstract

This paper investigates the static and dynamic characteristics of a doubly clamped micro-beam-based resonator driven by two electrodes. The governing equation of motion is introduced here, which is essentially nonlinear due to its cubic stiffness and electrostatic force. In order to have a deep insight into the system, static bifurcation analysis of the Hamiltonian system is first carried out to obtain the bifurcation sets and phase portraits. Static and dynamic pull-in phenomena are distinguished from the viewpoint of energy. What follows the method of multiple scales is applied to determine the response and stability of the system for small vibration amplitude and AC voltage. Two important working conditions, where the origin of the system is a stable center or an unstable saddle point, are considered, respectively, for nonlinear dynamic analysis. Results show that the resonator can exhibit hardening-type or softening-type behavior in the neighborhood of different equilibrium positions. Besides, an attractive linear-like state may also exist under certain system parameters if the resonator vibrates around its stable origin. Whereafter, the corresponding parameter relationships are deduced and then numerically verified. Moreover, the variation of the equivalent natural frequency is analyzed as well. It is found that the later working condition may increase the equivalent natural frequency of the resonator. Finally, numerical simulations are provided to illustrate the effectiveness of the theoretical results.

1 Introduction

Electrostatically actuated microbeams, due to their geometric simplicity, broad applicability, and easy-to-implement characteristic, have become major components in many micro-electro-mechanical systems (MEMSs) devices [1], such as switches [2, 3], sensors [4], and resonators [5]. However, these structures are small in size and may exhibit relatively large deformations [6]. Moreover, as the existence of structure nonlinearity and nonlinear electrostatic force, they can exhibit rich static and dynamic behaviors [1, 7]. These behaviors have attracted many attentions and have been studied by many MEMS communities. In this paper, a doubly clamped microbeam-based resonator actuated by two symmetrical electrodes [8] is considered to study its static bifurcation and small vibration characteristics in the neighborhood of stable equilibrium positions.

Pull-in instability is always a key issue in the design of MEMS [9]. When the DC voltage is increased beyond a critical value, stable equilibrium positions of the microbeam cease to exist [10], and pull-in is triggered. Early studies mainly focus on the static pull-in analyses which only take care of the static deflection of the microbeam. For instance, Abdel-Rahman et al. [11] investigated an electrically actuated microbeam accounting for mid-plain stretching and finally derived its static pull-in position. Pamidighantam et al. [12] derived a closed-form expression for the pull-in voltage of two types of microbeams and validated its effectiveness through finite-element simulation. Younis et al. [13] presented an analytical approach and accurately predicted the pull-in voltage of microbeam-based MEMS. Hu et al. [14] used a distributed model to more accurately predict the static pull-in position.

However, many studies have indicated that the motion of the system induced by inertial effects, DC voltage loading and AC voltage excitation is also important and cannot be neglected [7, 10]. Actually, the dynamic pull-in voltage is lower than the static pull-in voltage [14]. Therefore, dynamic pull-in analysis seems to be necessary as well in the design of MEMS. This instability is usually undesirable in dynamic MEMS devices. It can lead to collapse of the microbeam and hence the failure of the devices. Studies have indicated that bifurcation, transient process and perturbations can lead to dynamic pull-in [7]. A capacitive accelerometer simplified as a micro-cantilever resonator was theoretically and experimentally investigated to grasp its nonlinear characteristics, including dynamic pull-in [15, 16]. Krylov [17] proposed a largest Lyapunov exponent criterion and well evaluated the dynamic pull-in instability of a doubly clamped microbeam. A series of AC voltages was applied into the electrode and successfully controlled the dynamic pull-in phenomenon of a microbeam [18]. Based on a high-frequency AC tension, dynamic pull-in of a MEMS resonator was successfully suppressed [19]. Fang and Li [10] derived a new approach and model to accurately determine the dynamic pull-in voltage and position of a cantilever and a clamped–clamped beam.

During working process, nonlinear dynamic analysis of these microbeams is also crucial in MEMS devices. For example, nonlinear model analysis was applied to study the dynamics of a doubly clamped microswitch in the presence of geometric nonlinearity and nonlinear energy coupling [20]. Luo and Wang [21, 22] investigated the resonant conditions and chaotic motion of a simplified time-varying capacitor. Subjected to random disturbance, the chaotic behaviors of a doubly clamped MEMS resonator were analytically and numerically studied in [23]. Nonlinear dynamics of a simplified comb-drive actuator, including a fractional order situation, were numerically studied in [24]. What is more, parametrically excited vibration of microbeams was also investigated in [25–31]. Recently, nonlinear dynamics of imperfect microbeams or MEMS arches were investigated in [32–36]. Results showed some interesting nonlinear phenomena, such as hysteresis, softening behavior, snap through, and dynamic pull-in. These analyses are helpful to further grasp the dynamic instability of this type of micro-components. Besides, nonlinear dynamics of microbeams made from some special materials, such as functionally graded materials [37] and piezoelectric materials [38], have also attracted many attentions.

Nonlinearities may lead to chaotic behaviors of MEMS components [24], which are also undesirable in MEMS devices. Therefore, some chaotic control methods are used to suppress this unexpected behavior. Voltage control [39, 40], optimal linear feedback control [24], and time-delayed feedback control [41] were applied to successfully suppress the chaotic motion while enlarging the stable operation range of the system. Moreover, some modern control theories, such as fuzzy control [42], fractional order control [43], and sliding mode control [44] also showed their advantages in control strategy.

It can be concluded from the above analysis that static or dynamic pull-in instabilities and nonlinear characteristics are both important in the design of MEMS and should be taken into account [11, 45]. Studies show that under different parameter combinations, the equilibrium positions of a doubly clamped microbeam actuated by two symmetrical electrodes are variable [27, 46, 47]. Besides zero equilibrium position, there may be other stable centers at either side of the origin [8, 27, 48]. Meanwhile, under small perturbations, this type of MEMS resonator may exhibit nonlinear characteristics such as softening-type or hardening-type behavior [49, 50]. This implies nonlinear stiffness may affect the vibration state of the system. However, to the best of our knowledge: (1) There are fewer quantitative results about a general analysis of equilibrium position variations of this type of microresonator, especially from the viewpoint of static bifurcation; (2) the nonlinear characteristics of the resonator in the neighborhood of different equilibrium positions are still unclear, which motivates our present work. Here, a relatively simplified one degree-of-freedom (1-DOF) model of a doubly clamped microresonator with two symmetrically actuated electrodes [8] is used to try to quantitatively make a complete description of the static bifurcation and transition mechanism of nonlinear jumping phenomena. Some detail characteristics are investigated based on doubly clamped beam’s first vibration mode assumption [51].

The structure of this paper is as follows. In Sect. 2, an analytical model is described [8] and the potential energy of the system is given. In Sect. 3, static bifurcation analysis is carried out. Static and dynamic pull-in concepts are considered to define the stable regions under nondimensional parameters. In Sect. 4, the method of multiple scales is applied to determine the response and stability of the system under small vibration amplitude and AC voltage. In Sect. 5, based on the frequency response equation, hardening-type or softening-type behavior is investigated. A neutral state, linear-like state is also discussed. Moreover, the equivalent natural frequency is analyzed as well. In Sect. 6, case studies are carried out to investigate the effect of physical parameters on system behaviors discussed in former sections. Finally, summary and conclusions are presented in the last section.

2 System description

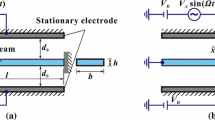
The electrostatically actuated microresonator is shown in Fig. 1, in which $\hat{{x}}$ is the flexural displacement of the beam and $d_0$ is the initial gap width. Deflected by a DC voltage and actuated by an AC voltage, the governing equation of motion of this system can be expressed as [8]

$$\begin{aligned}&m{\hat{{x}}}''+c{\hat{{x}}}'+k_1 \hat{{x}}+k_3 \hat{{x}}^{3}=\frac{1}{2}\frac{C_0 d_0 }{(d_0 -\hat{{x}})^{2}}\nonumber \\&\quad \times \,[V_\mathrm{dc} +V_\mathrm{ac} \sin (\Omega t)]^{2}-\frac{1}{2}\frac{C_0 d_0 }{(d_0 +\hat{{x}})^{2}}V_\mathrm{dc}^2 \end{aligned}$$

(1)

where ($'$) represents the derivative with respect to time $t,\,m,\,c,\,k_1$ and $k_3$ are the effective lumped mass, damping, linear and cubic stiffness of the system, respectively. $C_0 ={\varepsilon _{d} A_{s}}/{d_{0}}$ is the capacitance over the gap when $\hat{{x}}=0,\,\varepsilon _{d}$ is the permittivity of the gap medium, $A_{s}$ is the overlapped area between the microbeam and the stationary electrode, $V_\mathrm{dc}$ is the DC voltage, $V_\mathrm{ac}$ and $\Omega \,(\Omega =2\pi f_\mathrm{e})$ are the amplitude and angular frequency of AC harmonic voltage, in which, $f_\mathrm{e}$ is the frequency of AC voltage.

Fig. 1

Schematic diagram of an electrostatically actuated microresonator

Introduce the following nondimensional variables

$$\begin{aligned}&\tau =\omega _0 t, x=\frac{\hat{{x}}}{d_0 }, \mu =\frac{c}{\sqrt{k_1 m}}, \alpha =\frac{k_3 d_0^2 }{k_1 },\nonumber \\&\quad \gamma =\frac{C_0 V_\mathrm{dc}^2 }{2k_1 d_0^2 }, \rho =\frac{V_\mathrm{ac} }{V_\mathrm{dc} }, \omega =\frac{\Omega }{\omega _0 } \end{aligned}$$

(2)

where $\omega _0 =\sqrt{{k_1 }/m}$ is the natural angular frequency of the microbeam; then, the nondimensional form of Eq. (1) can be written as

$$\begin{aligned}&\ddot{x}+\mu \dot{x}+x+\alpha x^{3}=\gamma \left[ {\frac{1}{(1-x)^{2}}-\frac{1}{(1+x)^{2}}} \right] \nonumber \\&\quad \,+\,\frac{2\gamma \rho }{(1\!-\!x)^{2}}\sin (\omega \tau )\!+\!\frac{\gamma \rho ^{2}}{2(1\!-\!x)^{2}}[1\!-\!\cos (2\omega \tau )]\qquad \end{aligned}$$

(3)

where ($\cdot$) represents the derivative with respect to nondimensional time $\tau$.

Essentially, electrostatically actuated MEMS components are parametrically excited systems and may exhibit rich dynamics [25–31]. Parametric vibration investigations are meaningful to grasp the complicated vibration properties of MEMS devices, which are very useful for MEMS designer. However, our present investigations assume the resonator to be deflected by a DC voltage and actuated by a relatively small AC voltage ($V_\mathrm{ac} \ll V_\mathrm{dc}$ yields $\rho \ll 1$), which is one main working condition for such microresonators [41, 49]. Besides, damping coefficient is relatively small in practice [7]. Therefore, system (3) can be reduced to a forced vibration system under some certain conditions as mentioned in [41], and the dissipation and excitation terms can be regarded as perturbations to the corresponding Hamiltonian system.

The potential energy of the corresponding Hamiltonian system [8] can be described as below if the potential energy is set to be zero at $x=0$

$$\begin{aligned} V(x)=\frac{1}{2}x^{2}+\frac{\alpha }{4}x^{4}-\gamma \left( {\frac{1}{1-x}+\frac{1}{1+x}} \right) +2\gamma \nonumber \\ \end{aligned}$$

(4)

The variation of equilibrium positions versus nondimensional parameter $\gamma$ was described in reference [8]. Melnikov analysis was applied to investigate the homoclinic bifurcation when the origin of the perturbed system was unstable and two new centers emerged at either side of it. What follows, a robust adaptive fuzzy control method was applied to stabilize the chaotic motion into a high-amplitude oscillation state. These analyses are useful in the design of dynamic MEMS resonators. However, it must be pointed out that static bifurcation analysis is also significant in grasping the dynamic characteristic of this type of MEMS. It can provide a comprehensive understanding of the parameter space where the number of equilibrium positions of the system varies as the variation of system parameters. Elata and Abu-Salih [46] pointed out that the stability of zero equilibrium position can be used as a criterion to judge whether side pull-in instability happens. Besides, Mobki et al. [47] also discussed this type of instability through a distributed beam model. However, some studies show that when the origin is unstable, there may be another two new centers emerge at either side of the origin [8, 27, 48]. Krylov [27] built a reduced order model using the Galerkin decomposition, found the first and secondary pull-in voltages by analyzing the fundamental frequency of the system and discussed the phase portraits under each case as well. However, he only took two specific simulation cases with different initial gap widths to describe these phenomena. Approximate physical parameter relationships when the first and secondary pull-in voltages coexist were not obtained in this research. Haghighi and Markazi [8] only discussed a relatively large amplitude vibration case through Taylor expansion of the electrostatic force and did not analyze the phase portraits of the system. Miandoab et al. [48] used the simplified model by Haghighi and Markazi [8] to approximately obtain different shapes for potential function and discussed the chaos prediction of the large amplitude vibration case. Here, one must be noticed that when static bifurcation analysis is carried out, some particular phenomena may be overlooked by Taylor expansion of the electrostatic force. Therefore, the corresponding Hamiltonian system of Eq. (3) without any approximation seems to be more appropriate to investigate the whole equilibrium position property. Besides, mathematical derivation and proof are necessary as well. These are the main work in following section.

3 Static bifurcation analysis

In this section, static bifurcation analysis is carried out to investigate the variation of equilibrium positions versus nondimensional parameters. The dissipation and AC excitation terms can be treated as perturbations to the corresponding Hamiltonian system (5) for a microresonator with high quality factor and AC driving voltage much smaller than DC voltage [8]

$$\begin{aligned} \!\left\{ \begin{array}{l} \dot{x}=y \\ \dot{y}=-x-\alpha x^{3}+\gamma \left[ {\frac{1}{(1-x)^{2}}-\frac{1}{(1+x)^{2}}} \right] \\ \end{array} \right. \end{aligned}$$

(5)

Setting $\dot{x}=\dot{y}=0$ in Eq. (5) gives the equilibrium position $(x_\mathrm{e}, 0)$, where the abscissa $x_\mathrm{e}$ can be determined by

$$\begin{aligned} x_\mathrm{e} +\alpha x_\mathrm{e}^3 -\gamma \left[ {\frac{1}{(1-x_\mathrm{e} )^{2}}-\frac{1}{(1+x_\mathrm{e} )^{2}}} \right] =0 \end{aligned}$$

(6)

It is clear from Eq. (6) that only $\alpha$ and $\gamma$ can affect the number of equilibrium positions. According to the expressions in Eq. (2), one can notice that $\alpha >0$ and $\gamma >0$. With the existence of DC voltage ($\gamma >0$), Eq. (6) can be rewritten in the following equivalent form

$$\begin{aligned} x_\mathrm{e} [\alpha x_\mathrm{e}^6 +(1-2\alpha )x_\mathrm{e}^4 +(\alpha -2)x_\mathrm{e}^2 +(1-4\gamma )]=0\nonumber \\ \end{aligned}$$

(7)

Besides $x_\mathrm{e} =0$, the other roots of Eq. (7) can be indirectly derived by solving Eq. (8)

$$\begin{aligned} \alpha X^{3}+(1-2\alpha )X^{2}+(\alpha -2)X+(1-4\gamma )=0 \end{aligned}$$

(8)

where $X=x_\mathrm{e}^2$.

The roots of Eq. (8) can be written as follows

$$\begin{aligned} X_1&= \varpi \cdot \root 3 \of {-\frac{q}{2}+\sqrt{\left( {\frac{q}{2}} \right) ^{2}+\left( {\frac{p}{3}} \right) ^{3}}}\nonumber \\&\quad +\,\varpi ^{2}\cdot \root 3 \of {-\frac{q}{2}-\sqrt{\left( {\frac{q}{2}} \right) ^{2}+\left( {\frac{p}{3}} \right) ^{3}}}-\frac{1-2\alpha }{3\alpha } \nonumber \\ X_2&= \varpi ^{2}\cdot \root 3 \of {-\frac{q}{2}+\sqrt{\left( {\frac{q}{2}} \right) ^{2}+\left( {\frac{p}{3}} \right) ^{3}}}\nonumber \\&\quad +\,\varpi \cdot \root 3 \of {-\frac{q}{2}-\sqrt{\left( {\frac{q}{2}} \right) ^{2}+\left( {\frac{p}{3}} \right) ^{3}}}-\frac{1-2\alpha }{3\alpha } \nonumber \\ X_3&= \root 3 \of {-\frac{q}{2}+\sqrt{\left( {\frac{q}{2}} \right) ^{2}+\left( {\frac{p}{3}} \right) ^{3}}}\nonumber \\&\quad +\,\root 3 \of {-\frac{q}{2}-\sqrt{\left( {\frac{q}{2}} \right) ^{2}+\left( {\frac{p}{3}} \right) ^{3}}}-\frac{1-2\alpha }{3\alpha } \end{aligned}$$

(9)

where $p=-\frac{(1+\alpha )^{2}}{3\alpha ^{2}}, q=\frac{2[(1+\alpha )^{3}-54\alpha ^{2}\gamma ]}{27\alpha ^{3}}, \varpi =\frac{-1+\sqrt{3}i}{2}, i=\sqrt{-1}$.

The discriminant and the relationship between roots and coefficients of Eq. (8) can be, respectively, written as

$$\begin{aligned} \Delta&= \left( {\frac{q}{2}} \right) ^{2}+\left( {\frac{p}{3}} \right) ^{3}=\frac{4\gamma [27\alpha ^{2}\gamma -(1+\alpha )^{3}]}{27\alpha ^{4}}\end{aligned}$$

(10)

$$\begin{aligned} \kappa _1&= X_1 +X_2 +X_3 =\frac{2\alpha -1}{\alpha },\nonumber \\ {\kappa _2}&= \frac{1}{{{X_1}}} + \frac{1}{{{X_2}}} + \frac{1}{{{X_3}}} = \frac{{2 - \alpha }}{{1 - 4\gamma }},\nonumber \\ {\kappa _3}&= {X_1}{X_2}{X_3} = \frac{{4\gamma - 1}}{\alpha } \end{aligned}$$

(11)

Several possible cases of Eq. (8) can be distinguished by using the discriminant:

• 1. If $\Delta >0$, then the equation has one real root and two conjugate complex roots;

• 2. If $\Delta =0$, then the equation has three real roots, two of which are equal (notice: $p\ne 0)$;

• 3. If $\Delta <0$, then the equation has three distinct real roots.

The above possible cases will be analyzed below, respectively. Before our analysis, introduce the following variable

$$\begin{aligned} M=\frac{(1+\alpha )^{3}}{27\alpha ^{2}} \end{aligned}$$

(12)

It is easy to prove that $\alpha =2$ is the only extreme and minimum point, and the minimum is $\min (M)=0.25$. This property is very important in our following study.

Case 1 $\Delta >0$, i.e., $\gamma >M$

It is easy to know that $X_3$ is real, while $X_1$ and $X_2$ are conjugate complex roots with $X_1 \cdot X_2 >0$. In light of $\gamma >M\ge 0.25$, the expression of $\kappa _3$ in Eq. (11) is positive, which yields $X_3 >0$. Actually, $X_3$ is greater than 1. The complete proof is given in Appendix.

Case 2 $\Delta =0$, i.e., $\gamma =M$

The expressions of $X_1 ,\,X_2$, and $X_3$ in Eq. (9) can be simplified as $X_1 =X_2 =\frac{\alpha -2}{3\alpha }$, and $X_3 =\frac{1+4\alpha }{3\alpha }$. Obviously, $X_3 >X_{1,2}$. If $0<\alpha <2,\,X_{1,2} <0$ and $X_3 >1$. If $\alpha \ge 2,\,X_{1,2} \ge 0$ and $X_3 >1$.

Case 3 $\Delta <0$, i.e., $\gamma <M$

As $p<0$, three real roots can be rewritten in the following convenient forms

$$\begin{aligned} X_1&= 2\root 3 \of {r}\cos \left( \theta -\frac{4\pi }{3}\right) -\frac{1-2\alpha }{3\alpha }\nonumber \\ X_2&= 2\root 3 \of {r}\cos \left( \theta -\frac{2\pi }{3}\right) -\frac{1-2\alpha }{3\alpha } \nonumber \\ X_3&= 2\root 3 \of {r}\cos (\theta )-\frac{1-2\alpha }{3\alpha } \end{aligned}$$

(13)

where $r=\sqrt{-\left( {\frac{p}{3}} \right) ^{3}}=\frac{\left( {1+\alpha } \right) ^{3}}{27\alpha ^{3}}$, and $\theta =\frac{1}{3}\arccos \left( {-\frac{q}{2r}} \right) ,\,\,(0<\theta <\frac{\pi }{3})$.

Based on the expression of $r$ and the range of $\theta$, the relationships between $X_1,\,X_2$ and $X_3$ can be derived as

$$\begin{aligned}&-\frac{1}{\alpha }<X_1 <\frac{\alpha -2}{3\alpha }, \frac{\alpha -2}{3\alpha }<X_2 <1,\nonumber \\&\quad 1<X_3 <\frac{1+4\alpha }{3\alpha }\end{aligned}$$

(14)

$$\begin{aligned}&X_2 -X_1 =2\sqrt{3}\root 3 \of {r}\cdot \sin (\theta )>0,\nonumber \\&X_3 -X_2 =2\sqrt{3}\root 3 \of {r}\cdot \sin \left( \frac{\pi }{3}-\theta \right) >0 \end{aligned}$$

(15)

Obviously, $X_3 >1$. Here, one situation with $\gamma =0.25$ must be mentioned because of the meaningless definition of $\kappa _2$ in Eq. (11). This corresponds to $X_1 <0$ and $X_2 =0$ if $0<\alpha <2;\,X_1 =0$ and $X_2 >0$ if $\alpha >2$. Notice that $\alpha \ne 2$ as $\gamma <M$. Next, we assume $\gamma \ne 0.25$. Then, the signs of $X_1$ and $X_2$ are related to the values of $\gamma$ and $\alpha$ [see $\kappa _2$ and $\kappa _3$ in Eq. (11)]. When $0<\gamma <0.25,\,\kappa _3 <0$, that is to say $X_1 \cdot X_2 <0$. As $X_2 -X_1 >0$, it is clear that $X_1 <0$ and $X_2 >0$. When $0.25<\gamma <M,\,X_1 \cdot X_2 >0$. At this point, the signs of $X_1$ and $X_2$ are decided by the value of $\alpha$. When $0<\alpha <2,\,\kappa _2 <0$, which means $X_1 <0$ and $X_2 <0$. When $\alpha >2,\,\kappa _1 >0$ and $\kappa _2 >0$, which corresponds to $X_1 >0$ and $X_2 >0$.

According to the relationship $X=x_\mathrm{e}^2$ and the above analysis, the number of equilibrium positions of the Hamiltonian system (5) and their expressions can be summarized in Table 1.

Table 1 Equilibrium positions of the Hamiltonian system

In view of the displacement constraint $\left| {x_\mathrm{e} } \right| <1$, static bifurcation sets and phase portraits of the Hamiltonian system (5) can be shown in Fig. 2. Boundary curves separate the nondimensional parameter space $\alpha -\gamma$ into four regions. Each region has its own phase property.

Fig. 2

Bifurcation sets and phase portraits of the Hamiltonian system in different $\alpha$–$\gamma$ domains (solid line physically possible; dashed line physically impossible)

There is one attractive feature of the phase portraits that needs to pay attention to. Although the number of equilibrium positions is invariable in region II, the phase portraits may have a distinct difference. Through analysis, we find that this difference can be distinguished from the viewpoint of potential energy. As is shown in Fig. 3, the ball at the origin can exhibit three different states of motion: stable (green one), critical (red one), and pull-in (gray one). An ideal situation is considered here, in which the moving surface is assumed to be perfectly smooth. The ball at the origin starts to move under small perturbations. When system parameters satisfy $V(\pm x_\mathrm{e,2} )<0$, corresponding to the last state of motion, the ball will overpass the left or right potential barrier and then falls into an infinite potential well. Then, pull-in instability is triggered. Generally speaking, static pull-in analysis only takes care of the variation of stable equilibrium positions and the critical pull-in voltage. At this point, the former pull-in state is stable as there are two table centers at either side of the origin. However, static pull-in analysis neglects the inertial effects [10] induced by DC voltage changing instantaneously from zero to the specified design value. For this type of microresonator, the microbeam is subjected to two symmetrical DC loadings. Assume the origin is unstable, only when the microbeam suffers small perturbations will it move to a new stable center, just like the motion of the ball in Fig. 3. Many studies [7] have shown that dynamic pull-in is important as well in the design of MEMS. Then, the transient process due to inertial effects needs to be taken into account. Therefore, in our point of view, the pull-in condition of this dynamic MEMS component in region II should be defined by

$$\begin{aligned} V(\pm x_\mathrm{e,2} )=0 \end{aligned}$$

(16)

where $x_\mathrm{e,2} =\sqrt{X_2 }$.

Fig. 3

Potential energy of the Hamiltonian system in region II ($x_\mathrm{e,2} =\sqrt{X_2 }$). (Color figure online)

When the system parameters are in region II, what is needed is to let $V(\pm x_\mathrm{e,2} )>0$ in order to keep the system beyond dynamic pull-in. Take $\alpha =10$ as an example, the value of $M$ is approximately equal to 0.493, while the critical value of $\gamma$ satisfying Eq. (16) is equal to 0.45. In Fig. 4, the red solid lines represent the phase diagrams of system (3), the blue dotted-dashed lines and black dashed lines represent the contour lines of which the Hamiltonian energies are equal to zero and $V(\pm x_\mathrm{e,2} )$, respectively. It can be observed from Fig. 4 that when $\gamma$ is smaller than 0.45, the system is stable (Fig. 4a); otherwise, it is triggered to pull-in (Fig. 4b). Therefore, the value of $M$ overestimates the dynamic pull-in value of $\gamma$.

Fig. 4

Phase portraits of the microresonator with initial conditions (0, 0): $\alpha =10,\,\mu =0.005,\,\rho =0.003,\,\omega =0.5$ (dashed line Hamiltonian energy is equal to $V(\pm x_\mathrm{e,2} )$; dotted-dashed line Hamiltonian energy is equal to zero). a $\gamma =0.448$, b $\gamma =0.452$. (Color figure online)

As is shown in Fig. 4a, the phase portraits of the system are restricted within the Hamiltonian energy $V(\pm x_\mathrm{e,2} )$. This implies that the maximal energy of the system cannot overpass this energy value. In the presence of perturbations due to dissipation and AC excitation, this system may be away from dynamic pull-in only if the maximal energy is smaller than $V(\pm x_\mathrm{e,2} )$, in other words, the potential barrier $V(\pm x_\mathrm{e,2} )$ is big enough.

As is known to us, the variation of $\gamma$ is directly related to DC voltage $V_\mathrm{dc}$. During working process, it seems that the nondimensional parameter $\gamma$ is more important for MEMS designers. Therefore, the effect of parameter $\gamma$ to the static bifurcation of the system is investigated in our following research. For convenience, introduce the following variables: $x_{\mathrm{e},0} =0,\,x_{\mathrm{e},1} =\sqrt{X_1},\,x_\mathrm{e,2} =\sqrt{X_2 },x_{\mathrm{e},3} =\sqrt{X_3}$. The stability of $(\pm x_{\mathrm{e},i} ,0),\,(i=0,1,2,3)$ can be determined through the Jacobi matrix $\mathbf{J}$ of the system (5), which can be written as

$$\begin{aligned} \mathbf{J}=\left[ \begin{array}{cc} 0&{} 1 \\ {-1-3\alpha x_{\mathrm{e},i}^2 +\frac{2\gamma }{(1\mp x_{\mathrm{e},i} )^{3}}+\frac{2\gamma }{(1\pm x_{\mathrm{e},i} )^{3}}}&{} 0 \\ \end{array} \right] \end{aligned}$$

(17)

As is shown in Fig. 5, the number of abscissa coefficients varies as the variation of $\gamma$. When: (1) $\alpha >0$ and $0<\gamma <0.25$, the system has one stable center point $(0,0)$ and two unstable saddle points $(\pm x_\mathrm{e,2} ,0)$; (2) $\alpha <2$ and $\gamma >0.25$, or $\alpha >2$ and $\gamma >M$, the system only has one unstable saddle point $(0,0)$; (3) $\alpha >2$ and $0.25<\gamma <M$, three unstable saddle points $(0,0),\,(\pm x_\mathrm{e,2} ,0)$, and two center points $(\pm x_\mathrm{e,1} ,0)$. Here, one must be noticed that $x_\mathrm{e,3}$ always exists, but it is meaningless for this system. Maybe the relative size of $x_\mathrm{e,3}$ can explain some behaviors such as the speed of transient time to pull-in [13]. However, this is beyond the scope of our research.

Fig. 5

Static bifurcation of the Hamiltonian system versus $\gamma$ under different $\alpha$ (solid line stable; dashed line unstable)

The above analysis indicates that if $\alpha$ and $\gamma$ satisfy some certain conditions, the system may vibrate in the neighborhood of $(0,0)$ or $(\pm x_\mathrm{e,1} ,0)$. In our study, the perturbations are assumed to be small enough, which yield a small vibration state of the microresonator around either one of the stable equilibrium positions. As the existences of cubic stiffness and electrostatic actuation, the vibration is essentially nonlinear. For better understanding of the small vibration of the system, perturbation methods should be utilized to derive approximate expressions for the dynamic behavior. That is the work in our following section.

4 Perturbation analysis

In this section, the method of multiple scales [52] is used to investigate the response of the microresonator with small vibration amplitude around three stable equilibrium positions, respectively.

Introduce $x=x_\mathrm{e} +u$, where $u=O(\varepsilon )$ is the dynamic amplitude of motion and $\varepsilon$ is regarded as a small nondimensional bookkeeping parameter only [41]. Considering the terms $V_\mathrm{dc} =O(1),\,V_\mathrm{ac} =O(\varepsilon ^{3})$, scaling the damping and expanding the electro-dynamic term of Eq. (3) up to third order of $\varepsilon$, one can obtain

$$\begin{aligned} \ddot{u}+\varepsilon ^{2}\mu \dot{u}+\omega _n^2 u+a_q u^{2}+a_c u^{3}=\varepsilon ^{3}f\sin (\omega \tau ) \end{aligned}$$

(18)

where

$$\begin{aligned}&a_q =3\alpha x_\mathrm{e} -\frac{3\gamma }{(1-x_\mathrm{e} )^{4}}+\frac{3\gamma }{(1+x_\mathrm{e} )^{4}} \nonumber \\&a_c =\alpha -\frac{4\gamma }{(1-x_\mathrm{e} )^{5}}-\frac{4\gamma }{(1+x_\mathrm{e} )^{5}} \nonumber \\&\omega _n^2 =1+3\alpha x_\mathrm{e}^2 -\frac{2\gamma }{(1-x_\mathrm{e} )^{3}}-\frac{2\gamma }{(1+x_\mathrm{e} )^{3}} \nonumber \\&f=\frac{2\gamma \rho }{(1-x_\mathrm{e} )^{2}} \end{aligned}$$

(19)

One can see that $\omega _n$ is the equivalent natural angular frequency of the resonator in nondimensional form.

In a microbeam-based resonator, the beam is deflected by a DC voltage and then driven to vibrate around its natural frequency by an AC loading [7]. Therefore, the primary resonance is investigated here. To describe the nearness of the primary resonance, a detuning parameter $\sigma$ is introduced and defined by

$$\begin{aligned} \omega =\omega _n +\varepsilon ^{2}\sigma \end{aligned}$$

(20)

One seeks the approximate solution of Eq. (18) in the form

$$\begin{aligned} u(\tau ;\varepsilon )&= \varepsilon u_1 (T_0 ,T_1 ,T_2 )+\varepsilon ^{2}u_2 (T_0 ,T_1 ,T_2)\nonumber \\&\quad +\,\varepsilon ^{3}u_3 (T_0 ,T_1 ,T_2 )+\cdots \end{aligned}$$

(21)

where $T_n =\varepsilon ^{n}\tau ,\,(n=0,1,2)$.

Substituting Eqs. (20) and (21) into Eq. (18) and equating coefficients of like powers of $\varepsilon$, yield

$$\begin{aligned}&O(\varepsilon ^{1}): D_0^2 u_1 +\omega _n^2 u_1 =0\end{aligned}$$

(22)

$$\begin{aligned}&O(\varepsilon ^{2}): D_0^2 u_2 +\omega _n^2 u_2 =-2D_0 D_1 u_1 -a_q u_1^2\end{aligned}$$

(23)

$$\begin{aligned}&O(\varepsilon ^{3}): D_0^2 u_3 +\omega _n^2 u_3 =-2D_0 D_1 u_2\nonumber \\&\quad -\,2D_0 D_2 u_1 -D_1^2 u_1 -\mu D_0 u_1 \nonumber \\&\quad -\,2a_q u_1 u_2 -a_c u_1^3 +f\sin (\omega _n T_0 +\sigma T_2 ) \end{aligned}$$

(24)

where $D_n =\frac{\partial }{\partial T_n },\,(n=0,1,2)$.

The general solution of Eq. (22) can be written as

$$\begin{aligned} u_1 (T_0 ,T_1 ,T_2 ){=}A(T_1 ,T_2 )\text {e}^{i\omega _n T_0 }+\bar{{A}}(T_1 ,T_2 )\text {e}^{-i\omega _n T_0 }\nonumber \\ \end{aligned}$$

(25)

Substituting Eq. (25) into Eq. (23), yields

$$\begin{aligned} D_0^2 u_2 +\omega _n^2 u_2&= -2i\omega _n \frac{\partial A}{\partial T_1 }\text {e}^{i\omega _n T_0}\nonumber \\&-\,a_q (A^{2}\text {e}^{2i\omega _n T_0 }+A\bar{{A}})+\hbox {cc} \end{aligned}$$

(26)

where cc represents the complex conjugate terms.

To eliminate the secular term, one needs

$$\begin{aligned} -2i\omega _n \frac{\partial A}{\partial T_1 }=0 \end{aligned}$$

(27)

which indicates that $A$ is only the function of $T_2$.

Thus, Eq. (26) becomes

$$\begin{aligned} D_0^2 u_2 +\omega _n^2 u_2 =-a_q (A^{2}\text {e}^{2i\omega _n T_0 }+A\bar{{A}})+\hbox {cc} \end{aligned}$$

(28)

The solution of $u_2$ can be given as

$$\begin{aligned} u_2 (T_0 ,T_2 )=\frac{a_q A^{2}}{3\omega _n^2 }\text {e}^{i2\omega _n T_0 }-\frac{a_q A\bar{{A}}}{\omega _n^2 }+\hbox {cc} \end{aligned}$$

(29)

Substituting Eqs. (25) and (29) to Eq. (24) yields the secular terms

$$\begin{aligned}&2i\omega _n \frac{\hbox {d}A}{\hbox {d}T_2 }+\mu i\omega _n A-\frac{10a_q^2 A^{2}\bar{{A}}}{3\omega _n^2}\nonumber \\&\quad +\,3a_c A^{2}\bar{{A}}+i\frac{f}{2}\text {e}^{i\sigma T_2 }=0 \end{aligned}$$

(30)

At this point, it is convenient to express $A$ in the polar form

$$\begin{aligned} A=\frac{1}{2}a(T_2 )\text {e}^{i\beta (T_2 )} \end{aligned}$$

(31)

Substituting Eq. (31) into Eq. (30), and separating the imaginary and real parts, yield

$$\begin{aligned}&\frac{\hbox {d}a}{\hbox {d}T_2}=-\frac{\mu }{2}a-\frac{f}{2\omega _n }\cos \varphi \end{aligned}$$

(32)

$$\begin{aligned}&a\frac{\hbox {d}\varphi }{\hbox {d}T_2}=a\sigma +\left( \frac{5q_q^2 }{12\omega _n^3 }-\frac{3a_c }{8\omega _n }\right) a^{3}+\frac{f}{2\omega _n }\sin \varphi \end{aligned}$$

(33)

where $\varphi =\sigma T_2 -\beta$.

Steady-state response can be obtained by imposing the condition $\frac{\hbox {d}a}{\hbox {d}T_2 }=\frac{\hbox {d}\varphi }{\hbox {d}T_2 }=0$. Finally, the frequency response equation can be derived as

$$\begin{aligned} a^{2}\left[ {\left( {\sigma +\kappa a^{2}} \right) ^{2}+\left( {\frac{\mu }{2}} \right) ^{2}} \right] =\left( {\frac{f}{2\omega _n }} \right) ^{2} \end{aligned}$$

(34)

where $\kappa =\frac{5a_q^2 }{12\omega _n^3}-\frac{3a_c}{8\omega _n}$.

The vibration peak value and backbone curve can be decided by $a_{\max } =f/{(\mu \omega _n )}$ and $\omega =\omega _n -\kappa a_{\max }^2$, respectively. And the stability of the periodic solution can be determined by the method in Ref. [41].

5 Small vibration around equilibrium positions

Frequency response Eq. (34) is similar to that of Duffing oscillator. It is obvious that the softening-type or hardening-type behavior of the system depends on the sign of $\kappa$. Positive $\kappa$ can lead to softening-type behavior, while negative one can lead to hardening-type behavior.

When the resonator vibrates in the neighborhood of $(0,0)$, Eq. (19) can be simplified as $a_q =0,\,a_c =\alpha -8\gamma ,\,\omega _n^2 =1-4\gamma ,\,f=2\gamma \rho$. At this point, $\kappa ={3(8\gamma -\alpha )}/{(8\sqrt{1-4\gamma })}$. If $\alpha >8\gamma$, the system exhibits hardening-type behavior. If $\alpha <8\gamma$, the system exhibits softening-type behavior. A special case with $\alpha =8\gamma$ needs to be mentioned here. At this point, the system exhibits linear-like behavior. That may be an ideal state for MEMS designers. Besides, the equivalent natural angular frequency $\omega _n$ is also an important factor in design process. As is known to us, $\omega _n$ is only the function of $\gamma$. The increase of $\gamma$ can reduce the value of $\omega _n$. Notice that $\gamma$ must satisfy $\gamma <0.25$ in order to keep $\omega _n >0$. When the system has no stable equilibrium position, $\omega _n$ drops to zero and pull-in is triggered. This result coincides with the former static bifurcation analysis.

Next, the vibration properties in the neighborhood of two nonzero stable equilibrium positions $(\pm x_\mathrm{e,1} ,0)$ are investigated. According to the expressions of Eq. (19), one can notice that: $a_q (x_\mathrm{e,1} )=-a_q (-x_\mathrm{e,1} ),\,a_c (x_\mathrm{e,1} )=a_c (-x_\mathrm{e,1} ),\,\omega _n^2 (x_\mathrm{e,1} )=\omega _n^2 (-x_\mathrm{e,1} ),\,f(x_\mathrm{e,1} )>f(-x_\mathrm{e,1} )$, and $\kappa (x_\mathrm{e,1} )\!=\!\kappa (-x_\mathrm{e,1} )$. From these expressions, it is obvious that around any equilibrium position: (1) The equivalent natural angular frequencies are the same; (2) the values of $\kappa$ are the same; and (3) the vibration amplitude around left equilibrium position is smaller than that around right one.

Based on the analysis in Sect. 3, the value of $\kappa$ can be qualitatively classified into two cases. As is shown in Fig. 6a, when $0<\alpha <2$ and $0<\gamma <0.25$, the system has only one stable equilibrium position $(0,0)$. $\kappa$ may be negative, zero or positive. If $\alpha >2$ and $0<\gamma <M$, as is shown in Fig. 6b, the value of $\kappa$ holds to be negative when $0<\gamma <0.25$ (hardening-type behavior) and positive when $0.25<\gamma <M$ (softening-type behavior).

Fig. 6

The value of $\kappa$ versus $\gamma$ under different $(\alpha , \gamma )$ combinations. a $0<\alpha <2$, $0 < \gamma < 0.25$, b $\alpha >2,0<\gamma <M,$

In order to validate the above analysis, long-time integration (LTI) of Eq. (3) is used to obtain some numerical solutions (discrete points), compared with the analytical solution derived from the method of multiple scales (MMS). Figure 7 corresponds to the situation in Fig. 6a, while Fig. 8 corresponds to situation in Fig. 6b. One can see that they have good agreements.

Fig. 7

Frequency response curves obtained using LTI and MMS for $0<\alpha <2:\,\alpha =0.8,\,\mu =0.005$ (solid line stable; dashed line unstable; dotted-dashed line backbone curve)

Fig. 8

Frequency response curves obtained using LTI and MMS for $\alpha >2:\,\alpha =3,\,\mu =0.005$ (solid line stable; dashed line unstable; dotted-dashed line backbone curve). a $\gamma =0.08,\rho =0.0026$, b $\gamma =0.26,\rho =0.00013$

Next, the effect of the $\gamma$ on the equivalent natural angular frequency $\omega _n$ under different $\alpha$ is shown in Fig. 9. When $\alpha <2,\,\omega _n =\sqrt{1-4\gamma }$. The maximum of $\omega _n$ is equal to 1, which corresponds to no-DC-voltage situation. As the increase of $\gamma ,\,\omega _n$ gradually decreases. When $\alpha >2$ and $0<\gamma <0.25$, the variation of $\omega _n$ is the same as former case. When $\alpha >2$ and $\gamma >0.25,\,\omega _n$ first increases and then dramatically decreases as the increase of $\gamma$. If inertial effects of this type of resonator are neglected, the system will undergo pull-in when $\gamma =M$, and the equivalent natural angular frequency $\omega _n$ sudden drops to zero. If transients due to inertial effects are taken into account, then pull-in $\gamma$ will be smaller than $M$. Different parameter combinations can lead to different frequency ranges. In Fig. 9, $\omega _n$ is not more than 1 if $\alpha <2$ and may be greater than 1 if $\alpha >2$. This characteristic may be useful for MEMS designers if they want to enlarge the working frequency of the resonator.

Fig. 9

Variation of the equivalent natural angular frequency $\omega _n$ versus $\gamma$ under different $\alpha$ (dotted-dashed line the value of $\gamma$ when $V(\pm x_\mathrm{e,2} )=0)$

6 Numerical results

In this section, case studies of a microbeam [53] are done to investigate the effect of some physical parameters on the vibration of the system. The main geometric and material parameters of a microbeam are given in Table 2. The equivalent principle between a one degree-of-freedom microbeam model and a distributed mass model can be realized based on first mode assumption [51]: $m=0.396\rho _m \textit{whl},\,k_1 ={125.1\textit{EI}}/{l^{3}},\,k_3 ={0.767k_1 }/{h^{2}}$, where $I={\textit{wh}^{3}}/{12}$ is the moment of inertia. Through the analysis, one can obtain $\alpha ={0.767d_0^2 }/{h^{2}}$. According to $\alpha =2$, the critical value of initial gap width $d_0$ can be derived as $d_0 \approx 1.615$ $h$. When $d_0 >1.615$ $h$, the microbeam may exhibit the case as mentioned in region II.

Table 2 Geometric and material parameters of a microbeam [53]

Table 3 shows four cases with different initial gap widths and DC voltages. Based on the analysis in former section, the softening-type behavior (ST) or hardening-type behavior (HT) can be predicted. Numerical results are obtained through LTI of Eq. (1). As is shown in Fig. 10, the analytical solutions agree well with the numerical results.

Table 3 Simulation cases

Fig. 10

Frequency response curves obtained using LTI and MMS under different simulation cases (solid line stable; dashed line unstable; dotted-dashed line backbone curve). a Case 1, b Case 2, c Case 3, d Case 4

The situation with $\alpha <2$ is one interesting case that needs to be investigated. As is known to us, the nonlinearity due to cubic stiffness and electrostatic force can lead to nonlinear vibration of the microresonator. However, if $\alpha$ satisfies $\alpha =8\gamma$, the system approximately exhibit linear-like behavior. Given that the microbeam is predesigned and the dimension and material are fixed, the effects of the initial gap width and DC voltage on linear-like behavior are studied as shown in Fig. 11. Blue lines are some contour lines of the equivalent natural angular frequency, while red line represents $\kappa =0$. Obviously, the intersections of these two types of lines correspond to a linear-like state with certain $\omega _n$. According to MEMS design requirement, a linear-like state can be realized by analyzing Fig. 11. For example, an initial gap width $d_0 =2{\upmu }\hbox {m}$ is designed and the DC voltage is approximately calculated as $V_\mathrm{dc} =9.653\hbox {V}$ (red point in Fig. 11). Then, the equivalent angular natural frequency is approximately equal to 0.785, which corresponds to 67.45 kHz. The frequency response curves under different AC voltage are shown in Fig. 12, which verifies the correctness of our theoretical analysis.

Fig. 11

The effects of the initial gap width and DC voltage on linear-like behavior of the microresonator. (Color figure online)

Fig. 12

Frequency response curves obtained using LTI and MMS under different AC voltages (dotted-dashed line backbone curve)

Next, the effect of the DC voltage $V_\mathrm{dc}$ on equivalent natural frequency $f_n (f_n ={\omega _0 \omega _n }/{2\pi })$ under different initial gap widths $d_0$ is investigated (Fig. 13). When $d_0$ is small enough, the operating stroke of $V_\mathrm{dc}$ is relatively small. Tiny change of $V_\mathrm{dc}$ will lead to dramatic change of $f_n$, but $f_n$ is always smaller than $f_0$. As the increase of $d_0$, the operating stroke of DC voltage becomes larger and larger. When $d_0 >1.615h$, as the increase of $V_\mathrm{dc} ,\,f_n$ becomes smaller and smaller until it is equal to zero. Continue to increase DC voltage, $f_n$ first increases and then dramatically decreases to zero. Here, one attractive characteristic is that the upper limit of $f_n$ may be greater than $f_0$. This reflects that the MEMS working frequency can be enlarged. However, one should be noticed that it needs more DC voltage output and the vibration of the resonator will deviate from the origin.

Fig. 13

Variation of the equivalent natural frequency $f_n$ versus DC voltage $V_\mathrm{dc}$ under different initial gap widths $d_0$ (dotted-dashed lines the value of $V_\mathrm{dc}$ when $V(\pm x_\mathrm{e,2})=0)$

7 Summary and conclusions

This paper presented the static and dynamic investigations of a doubly clamped microresonator actuated by two symmetrical electrodes. Static bifurcation analysis was carried out to investigate the variation of equilibrium positions when system parameters changed. Through analysis, bifurcation sets and phase portraits of the Hamiltonian system were obtained and static pull-in positions and parameter relationships were theoretically derived. Due to the distinct nonlinearity of electrostatic force, the phase portraits might have obvious difference in region II (Fig. 2), although the number of equilibrium positions was the same. Whereafter, this attractive feature was explained from the viewpoint of potential energy, and dynamic pull-in condition of this type of microresonator was identified.

Under small perturbations, the resonator might vibrate in the neighborhood of the origin or new center at either side of the origin. In order to grasp the nonlinear vibration characteristic of the system, the method of multiple scales was applied to obtain approximate frequency response equation. Results show that beyond static or dynamic pull-in instability, different parameter combinations may lead to hardening-type or softening-type behavior. An interesting feature is that, if $\alpha <2$, the system may vibrate in a linear-like state around the origin. This property may be useful for MEMS designers. When $\alpha >2$, the vibration around the origin exhibits hardening-type behavior and that around the new center at either side of the origin exhibits softening-type behavior. Under the same AC loading, the vibration amplitude around left center is smaller than that around the right one. Moreover, the equivalent natural frequency of the system was discussed as well. The nondimensional natural frequency may be greater than 1, which means the working frequency can be enlarged. Finally, simulation results of case studies based on original dimensional equation were used to verify the correctness of the present theoretical results.

Appendix

The proof of $X_3 >1$ when $\Delta >0$ can be summarized as follows.

The derivative of $X_3$ with respect to $\gamma$ can be written as

$$\begin{aligned} \frac{\hbox {d}X_3 }{\hbox {d}\gamma }=\frac{\root 3 \of {\eta _1 +6\sqrt{3}\alpha \eta _2 }-\root 3 \of {\eta _1 -6\sqrt{3}\alpha \eta _2 }}{\sqrt{3}\eta _2 } \end{aligned}$$

(35)

where $\eta _1 =-(1+\alpha )^{3}+54\alpha ^{2}\gamma$ and $\eta _2 =\sqrt{-[(1+\alpha )^{3}-27\alpha ^{2}\gamma )]\gamma }$.

As $\gamma >{(1+\alpha )^{3}}/{(27\alpha ^{2})}\ge 0.25$, it is clear that $\eta _1 >(1+\alpha )^{3}>0$ and $\eta _2 >0$, leading to $\frac{\hbox {d}X_3 }{\hbox {d}\gamma }>0$. According to the continuity of $X_3$ to $\gamma$ as $\gamma \ge {(1+\alpha )^{3}}/{(27\alpha ^{2})}$, it is clear that $X_3 >\left. {X_3 } \right| _{\gamma =0.25}$, where the expression of $\left. {X_3 } \right| _{\gamma =0.25}$ can be given by

$$\begin{aligned}&\left. {X_3 } \right| _{\gamma =0.25}\nonumber \\&\quad {=}\frac{\alpha \left[ {4+2^{2/3}\left( {B_1 {+}iB_2 } \right) ^{1/3}+2^{2/3}\left( {B_1 {-}iB_2 } \right) ^{1/3}} \right] {-}2}{6\alpha }\nonumber \\ \end{aligned}$$

(36)

where $B_1 =\frac{21\alpha ^{2}-6\alpha -2\alpha ^{3}-2}{\alpha ^{3}}$ and $B_2 =3\sqrt{3}\sqrt{\frac{(\alpha -2)^{2}(1+4\alpha )}{\alpha ^{4}}}$.

If $\alpha =2,\,B_2 =0$ and $\left. {X_3 } \right| _{\gamma =0.25} =\frac{3}{2}$, else $\alpha \ne 2,\,\left. {X_3 } \right| _{\gamma =0.25}$ can be rewritten as

$$\begin{aligned} \left. {X_3 } \right| _{\gamma =0.25} =\frac{4\alpha +4(1+\alpha )\cos (\varphi )-2}{6\alpha } \end{aligned}$$

(37)

where $\varphi =\frac{1}{3}\arccos (\frac{B_1 }{\sqrt{B_1^2 +B_2^2 }}),\,\,0\le \varphi <\frac{\pi }{3}$.

The property $\frac{1}{2}<\cos (\varphi )\le 1$ leads to $1<\left. {X_3 } \right| _{\gamma =0.25} \le \frac{4\alpha +1}{3\alpha }$. It is obvious that $X_3 >1$.$\square$