Experimental analysis of the influence of damping on the resonance behavior of a spherical pendulum

Abstract

This study describes the experimental and numerical dynamic analysis of a kinematically excited spherical pendulum. The stability of the response in the vertical plane was analyzed in the theoretically predicted auto-parametric resonance domain. Three different types of the resonance domain were investigated the properties of which depended significantly on the dynamic parameters of the pendulum and the excitation amplitude. A mathematical model was used to represent the nonlinear characteristics of the pendulum, which includes the asymmetrical damping. A special frame was developed to carry out the experiments, which contained the pendulum supported by the Cardan joint and two magnetic units attached to the supporting axes of rotation, and this was able to reproduce linear viscous damping for both of the principal response components. The stability analysis of the system was compared with the numerical solution of the governing equations and experimental observation. The most significant practical outcomes for designers are also summarized.

1 Introduction

Many systems used in civil engineering such as towers, masts, chimneys, buildings, power piping systems, the massive foundations of rotating machines, and other general purpose systems have to be equipped with devices that reduce the dynamic response to external excitation with deterministic or random characteristics. In their simplest form, passive tuned mass dampers (TMDs) are such devices. When designed and positioned correctly on a structure, they draw the vibrational energy away from the structure and dissipate it internally, thereby reducing undesired responses. Several studies have addressed the topic of vibration absorbers, such as the seminal work by Hartog [1] and later work by Korenev [2]. Theoretical aspects of TMDs are still attracting the attention of researchers throughout the world. Many studies have considered various aspects of this subject. For example, an optimal design theory for structures implemented with TMD was proposed [3]. This method facilitates more extensive applications and removes the limitations based on simplifying assumptions. The design parameters are determined by minimizing a performance index. In another study [4], a control system was introduced for multiple dampers, and a remarkable decrease in the amplitudes of a steel TV tower was reported. In [5], the efficiency of a TMD in controlling the self-excited motion of a bridge due to wind-structure interaction forces was described. In the paper [6], the use of a nonlinear element was introduced to describe the nonlinear behavior of the cross-tie reducing the vibration of stay-cables.

Another interesting type of absorber, i.e., tuned liquid column dampers (TLCDs), was presented in [7]. TLCDs belong to the class of liquid dampers that damp out the oscillations of a system via the oscillations in a U-shaped liquid column. The optimum values for damping have been investigated using multiple TLCDs under wind excitation. Another case with multiple dampers in the structure was analyzed in [8], and their performance was optimized. A random loading was applied in [9], where a collection of several mass dampers with distributed natural frequencies were investigated under random loading. A ball type of absorber was studied theoretically in [10, 11]. The authors discussed the function and efficiency of its practical implementation.

A TMD is frequently a pendulum in the aforementioned disciplines. This low cost passive device (and its variants) is used on tall masts and towers, and it is very popular because of its reliability and simple maintenance, e.g., see a theoretical outline of pendulum dampers in engineering practice in [12]. However, their dynamic behavior is significantly more complex than is assumed by the widely used linear single degree-of-freedom (SDOF) models, which work in one vertical plane. This linear model is only satisfactory if the amplitude of the kinematic excitation at the suspension point is very low, and if its frequency remains outside a resonance frequency domain. However, this is possible but at the cost of a damper with lower efficiency.

In experimental and numerical treatments, unidirectional harmonic excitation is generally assumed, which may bring complexity. If the excitation frequency is in the resonance domain, post-critical states can emerge. These states are characterized either by a highly increased longitudinal response, or by more or less complicated space trajectories of various types on a spherical surface. From a practical point of view, this type of the response destroys the effectiveness of the TMD. As the frequency increases, the shape of the motion stabilizes in an elliptic trajectory. After the frequency exceeds a certain limit, the spatial movement (solution) disappears, and the stable solution in the principal plane is restored.

The existence and stability level of individual solutions or response types depend on the pendulum geometry and the excitation characteristics. To facilitate more efficient designs, the absorber should be treated as a two degree-of-freedom system with at least weak nonlinear behavior. However, this treatment increases the difficulty of the mathematics inherent in nonlinear systems and the auto-parametric systems that represent a special class of them. A typical feature is represented by the existence of a semi-trivial solution, which means that part of the system vibrates whereas the rest of the system remains idle. In certain conditions, the semi-trivial solution becomes unstable and auto-parametric resonance is induced. Typical properties such as saturation effects and the occurrence of non-periodic and quasi-periodic vibration have been illustrated, for example, in [13] or [14].

The auto-parametric systems and related topics have been discussed in recent decades by Tondl and co-authors, e.g., [13, 15] and many others such as the authors of [16, 17] and [18]. Several monographs, e.g., [19], have presented comprehensive overviews of results and methods. The application of these techniques includes stability analysis see e.g., [20] and vibration suppression published in [21] and recently in [22], or only theoretical analyses of dynamical systems as in [23].

The motivations of these studies come from various areas of mechanical and civil engineering. The evaluation of a pendulum vibration absorber for a Duffing system was reported in [24], which used the multiple scales method to ascertain the auto-parametric resonance conditions and to compare the results of a nonlinear analysis with a similar application of a pendulum absorber in a linear primary system. The influence of the primary Duffing members on the absorber frequency response has also been presented in a numerical manner. In [25], for example, experimental and numerical investigations are carried out using an auto-parametric system, which comprised a composite pendulum attached to a harmonically base-excited mass-spring subsystem. An interesting analysis of a structure-pendulum interaction was presented in [26], where a planar pendulum was assumed. However, the frequencies of the structure and the pendulum are comparable when dealing with TMD, which violated the first assumption of the study.

The horizontally excited spherical pendulum was first studied by Miles [27] who considered the problem of the stability of planar oscillations to non-planar perturbations with small amplitude forcing in the neighborhood of resonance using truncated equations. He found that planar solutions become unstable to non-planar perturbations in particular parameter ranges and that nonplanar oscillations also emerged. Later, a more detailed study by Miles [28] analyzed a set of bifurcation diagrams for planar and non-planar motions, as well as chaotic motion. The experiments carried out by Tritton [29] confirmed the theoretical model and showed good agreement. An investigation of the nonlinear damping mechanisms governing the dynamics of a chaotic spherical pendulum was presented in [30]. The authors commented on the discrepancies between the theoretical predictions and the experiments when neglecting the real nonlinear nature of the damping.

In the present study, we focused on the analysis of the behavior of a spherical pendulum under the influence of damping on the overall stability. This study is an extension of a recently published article [31] in which the analysis of the pendulum was carried out with respect to the variation of both principal damping coefficients.

The movement of the pendulum is described analytically using a published purely analytical and numerical approach [14], which uses the coordinates $\theta ,\varphi$ on a spherical surface to represent the nonlinear interaction of both components, or in two Cartesian coordinates $\xi ,\zeta$, which represent the projection of the pendulum’s bob on the $x,y$ plane. The pendulum response is described by a system of two simultaneous second-order nonlinear ordinary differential equations. The interaction between both components derives from the nonlinear coupling terms. Depending on its parameters, various types of stability loss can occur so the critical amplitude and frequency of the excitation can be detected. A semi-trivial solution may occur, where one component is non-trivial, while the second remains at zero. In certain conditions, which are also analyzed, the semi-trivial solution can lose its stability, and various specific types of response can occur.

Experimentally, the pendulum was examined using a specially developed experimental rig, where the kinematically driven pendulum was suspended from a Cardan joint. The response components were measured by rotation sensors. They are working on the principle of an encoder comprising a magnetic actuator and separate encoder body. Frictionless rotation of the actuator is sensed by a custom encoder chip within the body and processed to the required output. The angular resolution is up to 8,192 positions per one revolution. The key parameter (damping) could be adjusted for each response component via two independent magnetic units attached to the frame and to the supporting axes of rotation. These units were used to reproduce the linear viscous damping. The stability of the system was analyzed experimentally and numerically based on several damping values. This analytical, numerical, and experimental study produced several recommendations for designers.

2 Mathematical model

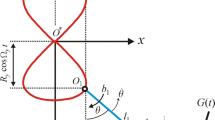
The spherical pendulum is modeled as a strongly nonlinear dynamic system with kinematic external excitation in the suspension point, as shown in Fig. 1.

Fig. 1

Mechanical model of the idealized spherical pendulum

To describe the motion in the $xz$ plane, where the semi-trivial solution can be analyzed, the problem needs to be formulated using the components $\xi , \zeta$, which correspond to the $x, y$ coordinates. In this case, it would be inconvenient to analyze the dynamics of the pendulum in more natural spherical coordinates, because the angle $\varphi (t)$ changes very quickly when $\theta$ is close to $0$, and it cannot be defined as a function with an arbitrary small norm, as shown in Fig. 1. Moreover, the excitation $a(t)$ acts in the $x$ direction only so the basic type of motion occurs in the vertical ($xz$) plane if the time history starts with homogeneous initial conditions.

The mathematical model is based on the principle of the balance between kinetic and potential energies $T, V$ ($m$ is mass of the pendulum).

$$\begin{aligned} T&= {\frac{m}{2}(\dot{\xi }^2+\dot{\zeta }^2+\dot{\eta }^2+2\dot{a}\dot{\xi }+\dot{a}^2)} \end{aligned}$$

(1a)

$$\begin{aligned} V&= mg\eta \end{aligned}$$

(1b)

The relationship between the basic Cartesian system $(\xi =\xi (t), \zeta =\zeta (t), \eta =\eta (t))$ and the coordinates $\varphi , \theta , r$ can be expressed by the spherical transformation:

$$\begin{aligned} \xi \!=\!r\sin \theta \cos \varphi ; \!\quad \! \zeta \!=\!r\sin \theta \sin \varphi ;\! \quad \! \eta \!=\!r(1\!-\!\cos \theta )\nonumber \\ \end{aligned}$$

(2)

Parameter $g$ is the gravitational acceleration, and the pendulum has the suspension length $r$. The geometry of the model illustrated in Fig. 1 also gives the following kinematic constraint:

$$\begin{aligned} r^2 = \xi ^2+\zeta ^2+(r-\eta )^2 \end{aligned}$$

(3)

The vertical coordinate $\eta$ starts at the lower pole of the sphere. The equations for the potential and kinetic energy can be modified using the Taylor expansions for $\theta$:

$$\begin{aligned} \theta =\arcsin \!\left( \!\frac{\sqrt{\xi ^2\!+\!\zeta ^2}}{r}\!\right) \!\approx \!\frac{\sqrt{\xi ^2+\zeta ^2}}{r}+\frac{1}{6}\!\left( \!\frac{\sqrt{\xi ^2\!+\!\zeta ^2}}{r}\!\right) ^3\nonumber \\ \end{aligned}$$

(4)

and for $1-\cos \theta$, respectively:

$$\begin{aligned} 1-\cos \theta \approx \frac{1}{2}\theta ^2-\frac{1}{24}\theta ^4 \end{aligned}$$

(5)

Using algebra, the following equations are obtained for the kinetic and potential energy:

$$\begin{aligned} T&= \frac{m}{2} \Biggl [\dot{\xi }^2+\dot{\zeta }^2+\frac{1}{4r^2} \left( \frac{\mathrm {d}}{\mathrm {d}t}\left( \xi ^2+\zeta ^2\right) \right) ^2 \nonumber \\&\cdot \left( 1+\frac{\xi ^2+\zeta ^2}{2r^2}\right) ^2 + 2\dot{a}\dot{\xi } + \dot{a}^2\Biggr ] \end{aligned}$$

(6a)

$$\begin{aligned} V&= mg\left[ \frac{1}{2r}(\xi ^2+\zeta ^2)+\frac{1}{8r^3}(\xi ^2+\zeta ^2)^2 \right] \end{aligned}$$

(6b)

The linear viscous damping with the coefficients $\beta _{\xi }, \beta _{\zeta }$ should be included to facilitate an analysis of the true stationary response. The damping is incorporated into the Langrange’s equations using the quadratic Rayleigh dissipative function, see, e.g., [32]. By combining the previous equations, this function can be written as

$$\begin{aligned}&F=\frac{1}{2}mr^2\left[ \beta _{\xi }\dot{\xi }^2+\beta _{\zeta }\dot{\zeta }^2+\beta _{\eta }\dot{\eta }^2\right] , \nonumber \\&\text{ where: }\; \dot{\eta }^2=\frac{({\xi }\dot{\xi }+{\zeta }\dot{\zeta })^2}{r^2}\left( \!\!1\!+\!\frac{\xi ^2\!+\zeta ^2}{2r^2}\right) ^{2} \end{aligned}$$

(7)

The damping in the vertical direction $z$ will be neglected, because we consider it to be linear; the vertical velocity ($\dot{\eta }$) is small at a higher order. Finally, using Eq. (6a, b), an approximate Lagrangian system based on the $x,y$ coordinates of the components $\xi , \zeta$ on the level $O(\varepsilon ^6);\;\varepsilon ^2=(\xi ^2+\zeta ^2)/r^2$ can be obtained after applying Hamilton’s principle. The final form of the differential system is (see [14] for the full derivation):

$$\begin{aligned}&\begin{aligned}&\ddot{\xi }+\frac{1}{2r^2}\xi \frac{\mathrm {d}^2}{\mathrm {d}t^2}(\xi ^2+\zeta ^2) +2\beta _{\xi }\dot{\xi } \\&\quad +\omega _0^2\xi \left( 1+\frac{1}{2r^2}(\xi ^2+\zeta ^2)\right) =-\ddot{a} \end{aligned} \end{aligned}$$

(8a)

$$\begin{aligned}&\begin{aligned}&\ddot{\zeta }+\frac{1}{2r^2}\zeta \frac{\mathrm {d}^2}{\mathrm {d}t^2}(\xi ^2+\zeta ^2) + 2\beta _{\zeta }\dot{\zeta }\\&\quad + \omega _0^2\zeta \left( 1+\frac{1}{2r^2}(\xi ^2+\zeta ^2)\right) = 0 \end{aligned} \end{aligned}$$

(8b)

The natural frequency of the corresponding linear pendulum is $\omega _0^2=g/r$. The above equations are mutually independent if only the linear terms are considered; their interaction is given by the nonlinear terms only. Each of the response components $\xi ,\zeta$ can be separately considered as arbitrarily small in the norm, and independently and continuously limited to zero, whereas the other one remains non-trivial. Therefore, the system is auto-parametric, and appropriate procedures can be applied.

3 Solution strategies

3.1 Properties of the pendulum and descriptions of the experiments

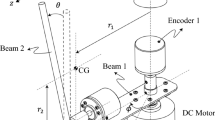
In general, stability problems are very sensitive to the boundary and initial conditions. Therefore, any simulation device and its mechanical parts need to be well prepared and manufactured to avoid the generation of parasitic effects. This applies to a complex kinematic mechanism and a relatively simple spherical pendulum. The specific experimental setup was designed to comply with the assumptions of the theoretical and numerical model. The pendulum shown in Fig. 2a was suspended at a Cardan joint, which was attached to a trolley that could move on two parallel miniature rails. The length of the pendulum was $0.41\,$m.

Fig. 2

Experimental setup and the details of the damping unit used to measure the auto-parametric vibration of the kinematically excited spherical pendulum. a Spherical pendulum attached to moving support on the rails with a Cardan joint and the damping units. b Damping unit with aluminum disk (light gray), disks with magnets (dark gray), counter and rotational sensors. (Color figure online)

Two specially designed magneto-dynamic units based on the practical application of the electromagnetic induction and the Lorentz force exploited the effect of eddy currents induced in the aluminum circular disk moving between two disks with circumferentially uniformly distributed magnets. Thus, the moving disk acted as a proportional viscous damper. This assembly is shown in Fig. 2b. The crank spindle mechanism allowed the adjustment of damping in the practically full range from zero to the critical level by adjusting the axial distance between magnets (neodymium) attached to the gear wheels with slightly different numbers of gear teeth (see [31] for further details). The damping was calibrated a posteriori, from the free vibration decay.

The construction of the pendulum differed slightly from the ideal. Therefore, an equivalent mathematical pendulum with the properties based on the measurement was used in the numerical solution. The main parameters of the pendulum are summarized in Table 1. The sinusoidal kinematic excitation (movement) of the trolley was provided by an electrodynamic shaker, which was controlled by a wave generator. Measurements of this horizontal excitation amplitude $a_0$ were obtained using a linear variable differential transformer (LVDT). Differences between prescribed and measured amplitudes were negligible.

Table 1 Properties of the pendulum

The response of the pendulum was measured in the specific range of the excitation frequencies, as shown in Table 1. To include the full resonance interval, each sweep started at an excitation frequency that was slightly higher than the natural frequency of the pendulum $\omega _0^2$, and a small initial disturbance was applied (manually or occasionally by a random ambient excitation) to the pendulum. The excitation frequency was changed gradually in small up or down increments to cover the whole frequency range. Each frequency was kept constant for 3 min, and the pendulum angles were recorded with a pair of identical high-speed rotary magnetic encoders, which were attached to the axes of rotation. To eliminate the transitory effects, only the last minute of each recording was used for post-processing.

3.2 Analytical solution

In this section, the system (8) is analyzed from a stability perspective. With an increase in the excitation $a(t)$ amplitude in the Eq. (8a), auto-parametric stability loss can occur, and the post-critical state of the auto-parametric resonance emerges. We assessed the stability of the semi-trivial solution previously (see [14, 31]). Similar procedure can be used also for the asymmetrical damping, where the stability limits depend on the individual damping coefficients. In the present work, a different procedure from [14] and [31] is used, however. The part related to the semi-trivial stability is omitted here, and the focus is put on the more general form of the solution.

Hence, the response of the pendulum to the harmonic excitation $a(t) =a_0 \cos (\omega t)$, where $a_0$ and $\omega$ are the amplitude and frequency of excitation, respectively, is expected in the harmonic form:

$$\begin{aligned} \begin{array}{llll} \displaystyle \xi (t) &{}=&{} a_c(t)\cos \omega t + a_s(t)\sin \omega t \\ \displaystyle \zeta (t) &{}=&{} b_c(t)\cos \omega t + b_s(t)\sin \omega t \end{array} \end{aligned}$$

(9)

The partial amplitudes $a_c(t), a_s(t), b_c(t)$, and $b_s(t)$ are assumed to be functions of “slow time” where the system response is at least nearly stationary. This has the advantage that it allows the use of the harmonic balance method.

Let us now substitute the expressions (9) into the differential system (8) and apply the harmonic balance operation. This procedure leads to the nonlinear differential system, which can be written in the form:

$$\begin{aligned} \mathbf {H}(\mathbf {X})\;\dot{\mathbf {X}} = \mathbf {K}(\mathbf {X})\mathbf {X}+\mathbf {F}; \; \end{aligned}$$

(10)

The detailed structures of the right-hand side vector $\mathbf {F}$ and the vector of the amplitudes $\mathbf {X}$ are as follows:

$$\begin{aligned}&\!\!\!\mathbf {X}(t) = [a_c(t),a_s(t),b_c(t),b_s(t)]^T, \end{aligned}$$

(11)

$$\begin{aligned}&\!\!\!\mathbf {F}= \left[ 0,4 r^2 \omega ^2 a_0, 0, 0\right] ^T \end{aligned}$$

(12)

The system matrix $\mathbf {H}(\mathbf {X})\in \mathbb {R}^{4\times 4}$ is

$$\begin{aligned} \mathbf {H}(\mathbf {X})=\omega \begin{bmatrix} \mathbf {Z}_a,&\mathbf {Z}_{ab} \\ \mathbf {Z}_{ab},&\mathbf {Z}_b \end{bmatrix} \end{aligned}$$

(13)

where

$$\begin{aligned}&\mathbf {Z}_x=\begin{bmatrix} -2 x_c x_s,&\!\! \!\! 4 r^2+3 x_c^2+x_s^2\\ -4 r^2-x_c^2-3 x_s^2,\!\!\!\!&2 x_c x_s \end{bmatrix},\\&\qquad \mathrm {for}\ x\in \{a,b\}\\&\mathbf {Z}_{ab}=\begin{bmatrix} -a_s b_c-a_c b_s ,&3 a_c b_c+a_s b_s \\ -a_c b_c-3 a_s b_s,&a_s b_c+a_c b_s \end{bmatrix} \end{aligned}$$

The system matrix $\mathbf {H}$ is always regular because its determinant is positive, which follows from this expression:

$$\begin{aligned} \det \mathbf {H}(\mathbf {X})\!=\!16 r^2 \omega \left( 4 r^2\!+\!R^2\right) \left( 4 r^4\!+\!3 r^2 R^2\!+\!2 S^4\right) \nonumber \\ \end{aligned}$$

(14)

where

$$\begin{aligned} R^2\!=\! \mathbf {X}^T\cdot \mathbf {X}\!=\! a_c^2\!+\!a_s^2\!+\!b_c^2\!+\!b_s^2,\ S^2\!=\!a_sb_c-a_cb_s\nonumber \\ \end{aligned}$$

(15)

It can be shown that the following holds for the matrix $\mathbf {K}(\mathbf {X})$:

$$\begin{aligned} \mathbf {K}(\mathbf {X})\!=\! -( 4 \Omega _2 r^2\!+\frac{1}{2} R^2 \Omega _1\! )\, \mathbf {I}+ \begin{bmatrix} 8r^2\omega \beta _{\xi }\,\mathbf {J} ,&\! - S^2 \Omega _4\, \mathbf {J}\\ S^2\Omega _4\,\mathbf {J},&8r^2\omega \beta _{\zeta }\, \mathbf {J} \end{bmatrix}\nonumber \\ \end{aligned}$$

(16)

where $\mathbf {I}$ represents the $4\times 4$ identity matrix and the following notation is used:

$$\begin{aligned}&\!\!\!\!\begin{array}{ll} \Omega _1=3\omega _0^2-4\omega ^2,&{}\ \Omega _2=\omega _0^2-\omega ^2 ,\\ \Omega _3=\omega _0^2+4\omega ^2, &{}\ \Omega _4=\omega _0^2-4\omega ^2, \end{array} \end{aligned}$$

(17)

$$\begin{aligned}&\!\!\!\!\mathbf {J}=\begin{bmatrix} 0,&\; 1\\ -1,&\; 0 \end{bmatrix} \end{aligned}$$

(18)

It should be remembered that the validity of Eq. (10) is limited to conditions where the harmonic balance operation is meaningful. In principle, the variability in time of the above amplitudes should be small to accept that their increments are negligible within one period.

At this point, the normal form of the differential system can be formulated using the inverse of $\mathbf {H}$. However, the determinant (14) is always positive, so the qualitative analysis of the overall system behavior can be determined equivalently simply by using the original right-hand side.

Let us consider the steady state response of the system. In this case, the derivatives $\dot{\mathbf {X}}$ vanish, and the differential system (10) reduces to an algebraic equation

$$\begin{aligned} \mathbf {K}(\mathbf {X})\mathbf {X}=-\mathbf {F}\end{aligned}$$

(19)

The general properties of the amplitudes $a_c,a_s,b_c$, and $b_s$ can be described using $R^2$ and $S^2$. We sum up the squares in all the rows of (19) and subtract the product of the 2nd and 3rd rows from the product of the 1st and 4th rows, and two relationships for generalized amplitudes emerge after some adaptation:

$$\begin{aligned}&\begin{aligned}&R^2 \left( \!\frac{R^2 \Omega _1}{8 r^2}+\Omega _2\!\right) ^{\!2} + 4\omega ^2 \left( R_1^2 \beta _{\zeta }^2+R_0^2 \beta _{\xi }^2\right) \\&\quad + S^2\! \left( \!\! P^2 \omega \left( \beta _{\zeta }-\beta _{\xi }\right) -S^2 \!\left( \!\left( \!\frac{R^2 \Omega _1}{8 r^2}+\Omega _2\!\right) \right. \right. \\&\quad \left. \left. -\,\frac{R^2\Omega _4}{16r^2}\!\right) \!\right) \!\frac{\Omega _4}{r^2} =a_0^2 \omega ^4 \end{aligned} \end{aligned}$$

(20)

$$\begin{aligned}&\begin{aligned} S^2 \Biggl (4 \omega ^2 \beta _{\zeta }\beta _{\xi }+\Omega _2^2+ \frac{R^2}{4 r^2} \Biggl (\frac{R^2}{16 r^2} \Omega _1\Omega _3 +2\omega _0^2\Omega _2 \Biggr ) \\ + \,\frac{S^4\Omega _4^2}{16 r^4}\Biggr ) +2P^2 \omega \left( \beta _{\xi }-\beta _{\zeta }\right) \left( \!\frac{R^2 \Omega _1}{8 r^2}+\Omega _2\!\right) =0 \end{aligned} \end{aligned}$$

(21)

where $R$ and $S$ were introduced in (15),

$$\begin{aligned} R_0^2 = \left( a_c^2+a_s^2\right) ,\ R_1^2=\left( b_c^2+b_s^2\right) ,\ R^2=R_0^2+R_1^2 \end{aligned}$$

and $S^2 =a_sb_c-a_cb_s,\ P^2=a_cb_c+a_sb_s.$

The parameter $R^2$ represents the total amplitude of the response, and $S^2$ and $P^2$ represent the vector and scalar product of the individual response components, respectively.

Both of the Eqs. (20–21) introduce a new parameter $P^2$ into the expressions, which makes both conditions less transparent and usable. Let us analyze these equations in detail. First, we analyze the stability of the movement in the planar $\xi$ condition. If we assume that motion occurs in this direction only, we can see that $S$, $P$, and $R_1$ vanish. Thus, $R=R_0$ and this holds for the reduced Eq. (20) as follows:

$$\begin{aligned} \fancyscript{R}_0(\omega ,R_0^2)&= R_0^2\left( \!4 \omega ^2 \beta _\xi ^2 +\left( \!\Omega _2+\frac{1}{8 r^2}\Omega _1 R_0^2 \right) ^{\!\!2}\right) \nonumber \\&-\,\omega ^4 a_0^2 =0 \end{aligned}$$

(22)

This equation is the relationship for the resonance curve of the semi-trivial (planar $\xi$) solution, which was derived earlier in detail in a previous study [14]. It describes the theoretical steady state response of the pendulum moving in the vertical plane only. Eq. (22) is a cubic equation for $R^2$. By varying the excitation amplitude $a_0$ or damping $\beta _\xi$, a set of resonance curves can be obtained as functions of the excitation frequency $\omega$. It is well known that these functions can lose their uniqueness in some intervals of $\omega$, which are related to the existence of one or three real roots of Eq. (22) for particular values of the parameters $a_0,\beta _{\xi }$, see Fig. 3a.

Fig. 3

Stable and unstable parts of the individual branches of the resonance curve $\fancyscript{R}_0(\omega ,R_0^2)=0$ (blue solid and red dashed) and the stability limits $\fancyscript{X}_0,\fancyscript{X}_1$ (black, long-dashed and dotted, respectively) and $\fancyscript{D}$ (magenta, dot-dashed). The hatched areas indicate the instability intervals $(c_1,c_2)$ and $(c_3,c_4)$. a In the general case, the resonance is affected detrimentally by both types of instability. b Detail of Fig. a showing the stable and unstable resonance curves (solid blue and dashed red respectively). c Critical case, $c_1=c_2$, according to (31). d Critical case, $c_3=c_4$, according to (33). (Color figure online)

Provided that the resonance curve remains single-valued, the nonlinear behavior of the pendulum is negligible. However, the presence of multiple branches of the resonance curve indicates possible problems with the efficiency of the damper. The positions of both ends of this interval (see $c_1$ and $c_2$ in Fig. 3a) are determined by solving the nonlinear system:

$$\begin{aligned} \fancyscript{R}_0(\omega ,R_0^2)=0;\quad \frac{\mathrm {d}\fancyscript{R}_0(\omega ,R_0^2)}{\mathrm {d}(R_0^2)}=0 \end{aligned}$$

(23)

where

$$\begin{aligned} \begin{aligned} \frac{\mathrm {d}\fancyscript{R}_0(\omega ,R_0^2)}{\mathrm {d}(R_0^2)}&=4 \omega ^2 \beta _{\xi }^2+ \left( \!\frac{ R_0^2}{8r^2} \Omega _1+\Omega _2\!\right) \\&\qquad \left( \!\frac{3R_0^2}{8r^2} \Omega _1+\Omega _2\!\right) =\fancyscript{X}_0(\omega ,R_0^2) \end{aligned} \end{aligned}$$

(24)

The curve $\fancyscript{X}_0=0$ defined by Eq. (24) defines the stability limit of the domain of the linear response type of the pendulum, which depends on $\beta _\xi$, and it only affects the longitudinal component $\xi$ of the response. The intersections $c_1$ and $c_2$ of (22) and (24) indicate the unstable parts of the resonance curve (22), and the interval of the ambiguous values of the response amplitude, respectively.

Next, we can analyze the case with the non-planar motion of the pendulum bob, i.e., $\xi \ne 0; \; \zeta \ne 0$. In this case, the analytic solution is much more difficult to obtain, if not impossible, because the terms $S$ and $P$ are non-zero, and the structure of Eqs. (20–21) is rather complex. However, we can make their qualitative analysis more transparent by neglecting the difference between both dampings. Thus, by setting $\beta _\xi =\beta _\zeta$ in these equations, they are simplified, because the terms involving $P$ become zero, and we can compare the results with the solution given in [14] by observing the restored structure of the original equations.

Therefore, assuming $\beta =\beta _\xi =\beta _\zeta$, Eq. (21) for the unknown $S^2$ has another two real roots in addition to one zero root (solved in the paragraph above):

$$\begin{aligned} S_{2,3}^2=&\pm 4r^2\frac{\sqrt{-\fancyscript{D}(\omega ,R^2)}}{\Omega _4} \end{aligned}$$

(25)

where the discriminant is as follows:

$$\begin{aligned} \fancyscript{D}(\omega ,R^2)&= 4\omega ^2 \beta ^2 + \left( \!\Omega _2+\frac{R^2}{8 r^2} \Omega _1\!\!\right) \nonumber \\&\left( \!\Omega _2+\frac{R^2}{8 r^2} \left( \Omega _1-2 \Omega _4\right) \!\!\right) \end{aligned}$$

(26)

Given $S^2\ne 0$, the necessary condition required for a positive value of $S^2$ (for $\Omega _4=\omega _0^2-4\omega ^2<0$) is the negative discriminant value $\fancyscript{D}(\omega ,R^2)$ in (25). Thus, the curve magenta

$$\begin{aligned} \fancyscript{D}(\omega ,R^2)=0 \end{aligned}$$

(27)

represents a limit of such part of the $(\omega ,R^2)$ plane, where the value of $S^2$ attains real values. This curve cuts out an another unstable part of the resonance curve (see $c_3$ and $c_4$ in Fig. 3, curve (27) itself is shown in magenta, dot-dashed line). This corresponds to the range of excitation frequencies where a pure planar movement is unstable, and a spatial movement is stable. An explicit form of the resonance curve in this case can be obtained by substituting the positive root $S_2^2$ defined in (25) into Eq. (20). The resulting generalized resonance curve comprises the amplitudes of both components $\xi$ and $\zeta$:

$$\begin{aligned} \begin{aligned}&\fancyscript{R}_1(\omega ,R^2)=R^6 \frac{1}{8 r^4}\frac{\Omega _1}{\Omega _4} \omega _0^4 \\&\quad + R^4 \frac{1}{4 r^2}\frac{\Omega _2}{\Omega _4} \left( \left( \Omega _4-2 \Omega _1\right) ^2-\Omega _1^2\right) \\&\quad +R^2 \left( 2 \frac{\Omega _1}{\Omega _4} \left( 4\beta ^2 \omega ^2+3 \Omega _2^2\right) -4\Omega _2^2\right) \\&\quad + 16 r^2 \frac{\Omega _2}{\Omega _4} \left( 4 \beta ^2 \omega ^2+\Omega _2^2\right) -a_0^2 \omega ^4=0 \end{aligned} \end{aligned}$$

(28)

A plot of both branches of the generalized resonance curve is shown in Fig. 3a, c, where the stable resonance curve is plotted as solid blue curves, and the unstable parts are shown as dashed red curves.

The unstable part of the spatial branch is delimited by a stability limit $\fancyscript{X}_1$ (black-dotted line in Fig. 3):

$$\begin{aligned} \fancyscript{X}_1=\frac{\mathrm {d}\fancyscript{R}_1(\omega ,R^2)}{\mathrm {d}(R^2)}=0 \end{aligned}$$

(29)

Point $c_5$ in Fig. 3a, c shows intersection of the resonance curve $\fancyscript{R}_1$ and the stability limit $\fancyscript{X}_1$, defined by Eqs. (28) and (29), respectively.

The determination of the limit values of the damping and the excitation amplitude is of importance from a practical viewpoint. These critical values correspond to the case where $c_1=c_2$ or $c_3=c_4$ and the resonance curve touches the corresponding limit (see Fig. 3c and d). The first case is characterized by the system:

$$\begin{aligned} \frac{\mathrm {d}\fancyscript{R}_0(\omega ,R_0^2)}{\mathrm {d}(R_0^2)}=0;\quad \frac{\mathrm {d}^2 \fancyscript{R}_0(\omega ,R_0^2)}{\mathrm {d}(R_0^2)^2}=0 \end{aligned}$$

(30)

The solution of (30) leads to the relationship between the system parameters $a_0$ and $\beta _\xi$ with the following form:

$$\begin{aligned}&512 r^2 \beta _{\xi }^3= 3 a_0^2 \nonumber \\&\cdot \left( \sqrt{9 \beta _{\xi }^2+3\omega _0^2} \left( 48 \beta _{\xi }^2+\omega _0^2\right) -9 \beta _{\xi } \left( 16 \beta _{\xi }^2+3 \omega _0^2\right) \right) \nonumber \\ \end{aligned}$$

(31)

where $a_0$ can be approximately expressed as a series in $\beta _\xi$:

$$\begin{aligned} a_0\approx r \root 4 \of {3}\left( \frac{16 \sqrt{2} }{3 \omega _0^{3/2}} \beta _{\xi }^{3/2}+ \frac{24 \sqrt{6} }{\omega _0^{5/2}} \beta _{\xi }^{5/2}\right) +O\left( \beta _{\xi }^{7/2}\right) \nonumber \\ \end{aligned}$$

(32)

According to condition (27), the critical values of the damping and excitation coefficients follow from the relationship:

$$\begin{aligned} \mathbf {G}=\begin{pmatrix} \fancyscript{R}_0(\omega ,R^2)\\ \fancyscript{D}(\omega ,R^2) \end{pmatrix}=\mathbf {0};\qquad \det \, \mathrm {d}\mathbf {G}=0 \end{aligned}$$

(33)

where $\mathrm {d}\mathbf {G}$ is the Jacobi matrix of the system $\mathbf {G}$. Unfortunately, there is no closed-form solution, and the system (33) has to be solved numerically.

It is worth noting that whereas condition (31) or its approximate version (32) depends on $\beta _\xi$ only, the stability limit (27) and the corresponding critical value (33) depend on both $\beta _\xi ,\beta _\zeta$. Indeed, the symbol $\beta ^2$ in Eqs. (26)–(28) represents the product $\beta _\xi \beta _\zeta$ if symbols $\beta _\xi ,\beta _\zeta$ are kept formally distinct during the derivation.

Figure 3 summarizes the possible mutual positions of the resonance curve and the stability limit for three different excitation amplitudes. We note that neither of the stability limits (24), (27) and (29), which are represented as black long-dashed curve, magenta dot-dashed and black-dotted curves, respectively, do not depend on the excitation amplitude. Figure  3a shows the case when both intervals $(c_1,c_2)$ and $(c_3,c_4)$ are non-empty, where the intervals are indicated by forward and backward hatching, respectively. In $(c_1,c_2)$ and $(c_4,c_5)$, the amplitude of the response can attain two distinct (stable) values. The length of the unstable part of the resonance curve between $c_1$ and $c_2$ or $c_4$ and $c_5$ is positive. A magnified detail of the resonance peak is shown in Fig. 3b. In $(c_3,c_4)$, the resonance curve has two individual branches, where the planar branch becomes unstable. Case (c) corresponds to a critical case where the planar resonance curve loses its uniqueness with the increasing excitation amplitude, $c_1=c_2$, cf. Eq. (30). Finally, Fig. 3d shows the second critical case: the excitation amplitude computed based on the relationship (33) leads to contact between the resonance curve and the stability limit, $c_3=c_4$.

Figure 4 shows the mutual dependence of the critical values of the individual damping coefficients, $\beta =\beta _\xi =\beta _\zeta$, and the corresponding amplitude of harmonic excitation $a_0$. The area below the curve corresponds to the safe configuration. It is clear that while increasing the excitation amplitude and keeping the damping constant, the transverse stability limit (33) is exceeded first, i.e., the green-dashed line. The figure also shows that the approximation (32) is always on the safe side of the critical limit defined by (31).

Fig. 4

Dependency of the critical excitation amplitude $a_0$ on the damping coefficient $(\beta =\beta _\xi =\beta _\zeta )$ values, leading to the crossing of the resonance curve and the respective stability limit. Solid line: exact value according to (31); dotted: approximate expression (32), where both are related to the stability limit $\fancyscript{X}$, $c_1=c_2$. Dashed: expression (33) related to the stability limit $\fancyscript{D}$, $c_3=c_4$. (Color figure online)

In general, the mutual position of the resonance curve and both stability limits depend on the structural ($r,\omega _0, \beta _{\xi }, \beta _{\zeta }$) and excitation ($a_0$) parameters. With a low excitation amplitude $a_0$ or sufficiently large damping $\beta$, the curves do not intersect, and the instability interval can disappear completely. By contrast, with a large excitation amplitude and/or small damping, the instability interval can occupy a wide frequency domain. This suggests that in the design recommendation, the damping should not drop below a certain limit to avoid instability, which indicated reduced pendulum efficiency, especially with broad band excitation.

3.3 Analytical-numerical solution

As mentioned in 3.1, reflecting the asymmetry of the individual damping coefficients causes difficulties in the analytical treatment of the stability assessment. In this case, the stationary solutions of Eq. (10) must be searched to find solutions to the nonlinear algebraic Eq. (19). The positions of the numerical roots, which depend on the excitation frequency, can be enumerated using various continuation techniques. Selected resonance curves are shown in Fig. 5. This figure is organized as follows: the plots in the rows have common values of $\beta _\xi$ and a common scale, but they differ with respect to the increasing value of the transverse damping coefficient $\beta _\zeta$. The graphs in the columns correspond to increasing $\beta _\xi$, and they differ in scale. The peak value on the right-hand spike is cut off in cases (d), (g), and (h) to ensure that the plot range is consistent. Its position in case (d) is $\omega =5.45,R^2=0.18$, in case (g) it is $\omega =11.85,R^2=3.4$, and in case (h) it is $\omega =5.46,R^2=0.18$.

Fig. 5

Resonance curves with a fixed excitation amplitude $a_0=0.0022$ and various damping coefficients $\beta _\xi , \beta _\zeta \in \{0.005,0.0015,0.0025\}$. The stable branches are shown as solid blue lines and the unstable branches as dashed red curves. (Color figure online)

With respect to the planar resonance curve, it should be noted that the relationship (22) is valid even in the case of asymmetrical damping. In this case, both $S^2$ and $P^2$ vanish, and Eq. (21) becomes trivial, while (20) reduces to (22). Thus, the planar resonance curve depends only on $\beta _\xi$ and $a_0$, and it does not change within the rows in Fig. 5. By contrast, the spatial branch of the resonance curve ($S^2 \ne 0$ and $P^2\ne 0$) depends on both $\beta _\xi$, $\beta _\zeta$, and it changes within each row.

The spatial response is characterized by the side branch of the resonance curve, which begins close to the highest peak of the planar resonance and ends at the right foot of the resonance area. This is analogous to the spatial branch defined by (28), which is indicated by points $c_3$ and $c_4$ in Fig. 3. The right-hand part of the spatial response increasing from the local minima corresponds to the spatial movement of the pendulum in the form of a spatial curve, which resembles an ellipse (see [14]). Both the numerical and experimental verifications confirm the stability of the upper spatial and the lower planar branch of the resonance curve, although the spatial stable response is generally not easy to reach.

The most significant difference from the symmetrical case occurs in the first column of Fig. 5, in cases (a) and (d) where $\beta _\zeta$ is kept low at 0.005, and $\beta _\xi$ is significantly higher. The stable part of the resonance curve of the spatial motion exceeds the peak value of the planar resonance curve even with decreasing values of $\omega$, and it returns to $\fancyscript{R}_0$ as an unstable solution (see the details in Fig. 5 cases (a) and (d)). However, the interpretation of this theoretical result is problematic, because numerical and experimental models exhibit chaotic behavior in the lower part of the resonance interval. The response of the system is not static so the first assumption of the preceding theoretical analysis is violated. Thus, the interval of the frequencies $\omega$ with an unstable response should be subjected to detailed analysis. The resonance curve only provides very rough or no information about the response in this interval. The non-stationary response of the damping device can have very negative effects on the structure, and this behavior has to be avoided in practical designs of a TMD.

4 Discussion of the results

4.1 Comments on the numerical results

To obtain an overview of the system behavior in the resonance frequency intervals, several numerical analyses of the governing differential system (8) were performed. In the numerical simulation, the implicit Backward Difference Method as implemented in NDSolve from Mathematica [33] for variable difference order 2–5 or the $M=2$ variant of the implicit Gear method (routine gear2) from the GNU Scientific Software Library [34] was the most stable and efficient.

Figure 6 shows the maximum and minimum amplitudes depending on the excitation frequency ($\omega , \text{ rad }\,\text{ s }^{-1}$). The responses computed for several of damping coefficient $(\beta \in \{0.04,\ldots 1.2\})$ values are shown in the individual rows. The longitudinal $\xi$ and transverse $\zeta$ components are shown in the left and right columns, respectively. To reach the steady state, only the last 25 % of the integration interval $t\in (0,900)$ was considered. Three curves are present in each plot, which represent the maximum, minimum, and mean values of the amplitudes. In the case where all three curves coincide, the response of the pendulum is harmonic. If the minimum and maximum curves form a stripe, a multi-harmonic or chaotic type of response occurs. However, this very simple criterion cannot be used to distinguish chaotic, quasi-periodic, and multi-harmonic responses.

Fig. 6

Numerical integration: computed amplitudes (m) of the response depending on the excitation frequencies $\omega =4.6\ldots 6.1 \, \mathrm{rad}\, \mathrm{s}^{-1}$ for several values of damping coefficients, which are the same in both directions. Longitudinal movement ($\xi$) is shown on the left-hand side and the transverse response ($\zeta$) on the right-hand side. For each plot, the maximum, minimum, and mean amplitudes are shown. The parameters of the model were selected to satisfy the geometrical properties of the experimental setup. Base excitation is $a_0=0.01\;\text{ m }$. (Color figure online)

4.2 Comments on the experimental results

The resonance curves were investigated via semi-continuous sweep procedure described in Sect. 3.1. In some cases with low damping, the pendulum entered an auto-parametric oscillation without any external impulse, but in other cases a random initial disturbance was given to the pendulum manually. Nevertheless, amplitude of this initial $\varphi$ and $\dot{\varphi }$ was not important for a pendulum bob to reach the stable trajectory, because just above the natural frequency of the pendulum is the periodic spatial trajectory the only stable solution, see [14]. There were several cases of the asymptotic stability of semi-trivial solution, as well as cyclic oscillations with regular and quasi-harmonic patterns. The forcing frequency was in the interval $\omega _{l} = 3.58$ to $\omega _{u}=4.02\,$ rad${}^{-1}$. The frequency increment was selected as $\Delta \omega =0.0126\,$ rad${}^{-1}$. The natural frequency in both directions was 3.877  rad${}^{-1}$. The base excitation was kept constant during the whole experiment at the value $a_0=0.01\;\text{ m }$.

Figure 7 shows the measured amplitudes, depending on the excitation frequency $\omega$ and damping coefficients values $\beta \in \{0.04,\ldots ,1.2\}$. The longitudinal $\xi$ and transverse $\zeta$ components are shown in the left and right columns, respectively, analogously to the numerical case.

Fig. 7

Experimental pendulum: measured amplitudes (m) of the response depending on the excitation frequency $\omega =4.6\ldots 6.1 \,\hbox {rad}\,\hbox {s}^{-1}$ for several damping coefficient values, which were the same in both directions. Longitudinal movement ($\xi$) is shown on the left-hand side and the transverse response ($\zeta$) is on the right-hand side. In each plot, the maximum, minimum, and mean amplitudes are shown. Base excitation is $a_0=0.01\;\text{ m }$. (Color figure online)

To assess the agreement between the numerical simulations and experimental results, let us compare Figs. 6 and 7. These graphs show the resonance curves obtained from the computed and measured data, respectively. The qualitative behavior is comparable at the lower end of the resonance interval, whereas there is a fairly significant difference in the upper part of the studied frequency interval, specifically with low damping coefficients $\beta _\xi =\beta _\zeta \in \{0.04,$ $0.05\}$. It appears that the experimental pendulum was able to follow the (less stable) upper branch of the solution during the sweep-up simulation better than it did in the numerical model in Eqs. (8). It is because this model does not comprise the significant dependence of the instantaneous frequency of the response on its instant amplitude. For a given excitation frequency and large amplitude of the response, the frequency of the response of the experimental pendulum is lower than it is determined by the numerical solution; thus it remains in the resonance interval. This effect became more apparent than it was in [31], for other pendulums.

4.3 Influence of damping on the amplitude

Let us consider the influence of the individual damping coefficients on the overall response of the system (8) in both directions. Figure 8 shows selected results obtained during the extensive parametric study. For the interval of excitation frequencies $\omega \in (4.6,6.1)$ and the values of damping coefficients $\beta _\xi ,\beta _\zeta \in (0.005,0.12)$, the system (8) was integrated repeatedly, and the maximum amplitudes were recorded in both directions. In this case, the integration of each excitation frequency started from non-zero but low initial conditions. Thus, only the lower stable response branches were covered by this study in the areas where multiple stable branches coexist.

Fig. 8

Maximum amplitude of the response depending on the damping coefficients values in both directions $\beta _\xi ,\beta _\zeta \in (0.005,0.12)$ for excitation frequencies $\omega =\in \{4.7, 4.72,\ldots , 4.88\}$. For each frequency, the left plot shows the response in the longitudinal direction ($\xi$), and the right plot corresponds to the transverse direction

Ten pairs of grayscale plots are shown in Fig. 8, where each pair of plots corresponds to a single excitation frequency $\omega \in \{4.7,\ldots ,4.88\}$, i.e., the areas close to the natural frequency of the pendulum. In each pair, the left plot shows the response in the longitudinal direction ($\xi$), and the right plot corresponds to the transverse direction. The values on the horizontal axis of each plot represent the damping coefficients $\beta _\xi$, whereas the vertical axis represented the values of the damping coefficients $\beta _\zeta$. Finally, the grayscale map shows the distribution of the maximum amplitudes of $\xi$ and $\zeta$ in the left and right plots, respectively. The black dots in each plot represent the discrete values of $\beta$ used in the simulation.

Several points can be highlighted based on observations of Fig. 8.

• 1. It appears that the presence of the spatial characteristics of the system response did not depend significantly on the value of the damping coefficient $\beta _\zeta$ (transverse motion). Similarly, the overall amplitude of the response appears to have been influenced mostly by $\beta _\xi$ (longitudinal motion) and far less by $\beta _\zeta$.

• 2. The spatial response in the lower part of the resonance interval had higher amplitudes, but it could be suppressed by lower damping values, $\beta _\xi$. The lower amplitudes that appear in the upper part of the resonance interval require higher damping $\beta _\xi$ for their removal.

• 3. It is not always the case that higher damping (in transverse direction) automatically leads to a lower response (cf. $\xi$ plots for $\omega >4.78$ in Fig. 8).

For comparison with the numerical study, Fig. 9 summarizes the maximum amplitudes of the measured response in directions $\xi$ and $\zeta$ using individual configurations of the damping coefficients $\beta _\xi$ and $\beta _\zeta$. The left figure shows clearly that the maximum longitudinal response $\xi$ depended mainly on the value of $\beta _\xi$, and the influence of $\beta _\zeta$ was negligible.

Fig. 9

The maximum amplitude of the measured response in the $\xi$ (left) and $\zeta$ (right) direction with various values of $\beta _\xi$ and $\beta _\zeta$

4.4 Influence of damping on resonance

Experiments were also conducted to test the damping influence on the resonance curves. The results are summarized in Figs. 10–12. Each figure shows the experimental and numerical resonance curves for selected values of the damping coefficients. The experimental results are shown by plain thick lines (blue and purple), which represent the maximum and minimum amplitudes of the measured time histories, as shown in the previous figures. The grayish area between these curves indicates the non-stationarity of the response. Thus, both curves coincided if the response was stationary. The brown curve with bullets in the figures for the $\xi$ component (left) and the green line with triangles in figures for $\zeta$ (right) show the numerically computed maxima. The numerical results were obtained by following the procedure used to generate Fig. 8, i.e., by performing a semi-continuous sweep that resembled the experiment.

Fig. 10

Experimental and numerical resonance plots for $\beta _\xi =0.018$ with increasing $\beta _\zeta$. Longitudinal component ($\xi$) and total amplitude are shown on the left, with transverse movement ($\zeta$) and the total amplitude on the right. In Figs. 10–12: solid lines—experimental data; solid lines with signs—numerical data; dotted and dashed lines—theoretical results; cf. Fig. 5. Blue, magenta, brown, & green—component amplitudes ($\xi$ and $\zeta$). (Color figure online)

Fig. 11

Experimental and numerical resonance plots for $\beta _\xi =0.038$ with increasing $\beta _\zeta$. The longitudinal component ($\xi$) and total amplitude are shown on the left, with the transverse movement ($\zeta$) on the right. (Color figure online)

Fig. 12

Experimental and numerical resonance plots for $\beta _\xi =0.073$ with increasing $\beta _\zeta$. The longitudinal component ($\xi$) and the total amplitude are shown on the left, with transverse movement ($\zeta$) on the right. (Color figure online)

Finally, each figure is supplemented with the theoretical resonance curve of the corresponding semi-trivial solution (thin dotted) and two ($\xi$-,$\zeta$-) stability limits (thin dot-dashed and dashed, respectively). In this case, the resonance curve (22) and $\xi$ stability limit (24) were computed using the longitudinal damping value $\beta _\xi$ and the curve corresponding to $\zeta$ stability limit (27) using the value of transverse damping $\beta _\zeta$.

The resonance interval, which was also analyzed by [28] and [14], is characterized by a stationary or non-stationary spatial response, which is indicated by the presence/absence of the grayish area in the resonance plots. The non-stationary response has the form of a quasi-periodic or chaotic movement. The stationary spatial response is characterized by movement on an elliptic trajectory. This movement was very stable in the case of the experimental pendulum. The total amplitude $R$ of the stationary response followed the $S\ne 0$ branch of the resonance curve (20) (see the solid curves in Fig. 5 and their increasing parts).

The difference between the numerical and experimental amplitude responses in the stationary part of the resonance interval was not highly significant. This agrees with the formulation of the approximate mathematical model, where the instantaneous frequency does not depend on the amplitude of the pendulum. However, the good agreement between the numerical and experimental resonance curves in the non-stationary part of the resonance interval is surprising.

In Fig. 10, the longitudinal damping is set to a low value $\beta _\xi =0.018$. The correspondence between the numerical and experimental resonance curve is rather good, but the main difference is in the upper stable branch of the theoretical resonance curve. Despite this, the frequency increment in the experimental case was larger than that in the numerical computation ($0.063$ vs. $0.01$ rad s${}^{-1}$, i.e., $0.01$ vs. $0.0016$ Hz), where the experimental pendulum followed the stable spatial branch significantly longer (i.e., up to higher frequencies) than the numerical procedure, see Sect. 4.2.

Increasing $\beta _\zeta$ from $0.023$ to $0.094$ while maintaining $\beta _\xi =0.018$ reduced the upper end of the resonance interval significantly, i.e., from 6.0 to 5.1 rad s${}^{-1}$. The lower end depended on the value of $\beta _\xi$. However, maintaining $\beta _\zeta$ at a constant value $0.023$ and increasing $\beta _\xi$ to $0.073$ almost completely eliminated the non-stationary response, and it moved the upper end of the resonance interval even lower, i.e., to 5.05  rad s${}^{-1}$ (see the first lines of Figs. 10–12). Similar conclusions can be drawn based on the results shown in the individual Figs. 10–12 compared with the results in the first, second, or third rows of these graphs. Increasing $\beta _\xi$ while maintaining $\beta _\zeta$ at a constant value caused the non-stationary response region to fade away and the interval of the stationary spatial response declined in size. Increasing $\beta _\zeta$ and maintaining $\beta _\xi$ had only a marginal effect on the non-stationary response, but it significantly reduced the interval of stationary spatial response.

5 Conclusions

Using analytical, experimental, and numerical approaches, the widely used linear model of a damping pendulum was shown to be acceptable only for a very limited set of parameters related to the pendulum characteristics and excitation properties. Thus, a more complex nonlinear model must be introduced for general analysis.

The results of the experimental and numerical investigations exhibited good agreement. The descriptions of the influence of the individual damping coefficients $\beta _\xi$ and $\beta _\zeta$ were improved compared with previous studies. It was shown that the initiation of the spatial response is more sensitive to damping in the longitudinal direction ($\beta _\xi$). The maximum amplitude of the longitudinal response had almost no sensitivity to the value of the transverse damping ($\beta _\zeta$). Increasing both components, $\beta _\xi$ and $\beta _\zeta$, shortened the resonance interval and reduced the maximal amplitude of the transverse component of the response.

It was also shown that the stable branch of the resonance curve that corresponded to spatial movement of the pendulum could coexist with a much milder stable planar branch, and both branches could be reached numerically and experimentally. However, the spatial movement was much more sensitive to the initial conditions in both the numerical and experimental approaches. Surprisingly, the experimental pendulum could follow the spatial branch of the resonance curve for significantly longer that the numerical procedure with an increasing excitation frequency.

From a practical viewpoint, it is highly recommended that in a case of advanced design, damping pendulum absorber is projected to avoid any intersections of the stability limits with the resonance curve. In particular, intersections with the longitudinal stability limit should be prevented; otherwise the negative influence of the pendulum in the resonance domain is to be expected in both the along-wind and cross-wind directions.