Dynamics of a mass–spring–pendulum system with vastly different frequencies

Abstract

We investigate the dynamics of a simple pendulum coupled to a horizontal mass–spring system. The spring is assumed to have a very large stiffness value such that the natural frequency of the mass–spring oscillator, when uncoupled from the pendulum, is an order of magnitude larger than that of the oscillations of the pendulum. The leading order dynamics of the autonomous coupled system is studied using the method of Direct Partition of Motion (DPM), in conjunction with a rescaling of fast time in a manner that is inspired by the WKB method. We particularly study the motions in which the amplitude of the motion of the harmonic oscillator is an order of magnitude smaller than that of the pendulum. In this regime, a pitchfork bifurcation of periodic orbits is found to occur for energy values larger that a critical value. The bifurcation gives rise to nonlocal periodic and quasi-periodic orbits in which the pendulum oscillates about an angle between zero and π/2 from the down right position. The bifurcating periodic orbits are nonlinear normal modes of the coupled system and correspond to fixed points of a Poincare map. An approximate expression for the value of the new fixed points of the map is obtained. These formal analytic results are confirmed by comparison with numerical integration.

1 Introduction

The nontrivial effect of fast excitation has been elaborately studied in recent years [2–4, 6, 7, 12–14]. It is known that mechanical systems, under high frequency parametric excitation, can undergo apparent changes in system properties such as the number of equilibrium points, stability of equilibrium points, natural frequencies, stiffness, and bifurcation paths [14]. The method of direct partition of motion (DPM), formalized by Blekhman [2], serves to facilitate the study of such problems. DPM is most suitable to study motions which can be represented as the sum of a leading order slow component and an overlaid fast component. The fast component of motion is often only interesting in the extent that it affects the main slow dynamics. Unlike the averaging method or the method of multiple timescales, DPM offers no systematic way to obtain higher order terms in an asymptotic expansion of the solution, and instead is limited to the leading order dynamics of the system. In return for this limitation, one gains efficiency in terms of the required mathematical manipulations.

In most problems addressed in the literature, the fast excitation is due to an external source, that is, the system considered is non-autonomous. However, similar nontrivial effects could occur even if the fast excitation is internal to the system, instead of coming from an external source. An example of such a case would be a nonlinear oscillator coupled to a much faster oscillator [1, 9, 11, 15–17]. In these latter autonomous systems with widely separated frequencies, the leading order dynamics, particularly the frequency, of the fast oscillator is unaffected by the slow oscillator. This latter condition allows the use of the standard method of averaging, that is, the fast oscillation is assumed to be, to leading order, a harmonic oscillation with a constant frequency. Then the equations of motion are averaged with respect to the fast timescale over a period of 2π [15]. This is not the case for the system we study in this paper, as the amplitude and frequency of the fast oscillation, to leading order, are found to be a function of the amplitude of the slow oscillation. This is established by observing that the equation of the fast degree of freedom can be treated as a fast oscillator with a slowly varying frequency, for which the WKB method is particularly suited, and thus using a transformation of fast time analogous to that proposed by the WKB method [19]. We present this work as an academic example that serves to shed light on the nontrivial dynamics that can arise in more general systems of this type, that is, systems with vastly different frequencies and nonlinear coupling that allows the slow variable to modulate the frequency of oscillation of the fast variable. Moreover, we use this example to illustrate how the strategy used here, which combines DPM with the WKB method, can be useful for the study of systems of this type. For simplicity, we restrict our attention here to the conservative case, ignoring dissipation and external forcing. We see this as a first basic step towards the understanding of the full dynamics that such systems are able to exhibit.

A well known variation of the mass–spring–pendulum system at hand is that in which the spring is constrained to move vertically instead of horizontally. It is known in the literature as a typical example in which autoparametric resonance can occur [18], that is, the system exhibits interesting dynamics if the ratio of the frequencies of the two degrees of freedom is 2:1 or 1:1; in such studies, the case in which the frequencies are widely separated is not given any attention. Another system similar to the one we study here is a mathematical model of two coupled Huygen’s clocks; the system represents two pendula hanging from a rigid beam support that is connected on one side to a wall through a linear spring [5]. Again in the latter system, the frequency of the linear support is considered to be of the same order of magnitude as that of the pendula. When such systems are addressed in the literature, the focus is often on the dynamics arising due to resonances, being internal, external or autoparametric resonances [8]. We emphasize that the dynamics addressed in this work is not due to any of the known types of resonance, that is, the frequencies of the two modes need not be commensurate. The prerequisite condition for the interaction addressed here is that the frequencies be of different orders of magnitude. Also, the direct modulation of the frequency and amplitude of the fast oscillation by the slow one is another feature of this interaction that is not present in the case of ordinary resonance.

In Sect. 2, we present the system of equations representing the mass–spring–pendulum that we consider, and the scaled equations that correspond to the relevant regime of small motions of the mass–spring oscillator; we also illustrate the nontrivial solutions that the system exhibits. Appendix A explains the motivation for the proposed form of solution while Sect. 3 presents the end result of the DPM procedure in the form of an autonomous equation governing the leading order slow oscillation; we also present the approximate expression of the leading order fast oscillation. The details of obtaining the latter are presented in Appendix C, while the DPM implementation is detailed in Appendix B. In Sect. 4, we discuss the bifurcation that occurs in the slow dynamics and it’s relation to the bifurcation in a Poincare map of the full system (1). The details of the analysis of the slow dynamics and the predictions based on it are presented in Appendices D and E. Section 5 briefly summarizes the main results. Then, in Sect. 6, we compare the approximate solution to that from numerical integration of the full system (1) and try to check the validity of the predictions we make based on the approximate solution.

2 The mass–spring–pendulum system

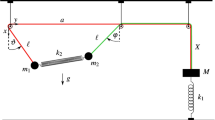
We consider a simple pendulum whose point of suspension is connected to a mass on a spring that is restricted to move horizontally, as shown in Fig. 1. Ignoring dissipation, the system is governed by the following equations of motion:

where primes denote differentiation with respect to time τ. We introduce the following change of variables:

$$x = \frac{{\tilde{x}}}{l},\qquad t = \sqrt{\frac{g}{l}} \tau . $$

The nondimensionalized equations, which we refer to as the full system, become:

$$ \everymath{\displaystyle }\begin{array}{@{}l} \ddot{\theta}+ \sin\theta= - \ddot{x}\cos\theta, \\ \noalign {\vspace {5pt}} \ddot{x} + \tilde{\varOmega}^2 x = - \mu\bigl( {\ddot{\theta}\cos\theta- \dot{\theta}^2 \sin\theta} \bigr), \end{array} $$

(1)

where $\mu =\frac{m}{{M + m}}$, $\tilde{\varOmega}^{2} =\frac{{kl}}{{g ( {M + m} )}}$, and dots represent differentiation with respect to time t.

Fig. 1

Schematic for the mass–spring–pendulum system

2.1 Assumptions

We are interested in the case where the linear oscillator has a natural frequency that is an order of magnitude larger than the linearized frequency of the pendulum, and its motion has an amplitude that is an order of magnitude smaller than that of the pendulum. This is implemented through the following rescaling:

$$x=\varepsilon\chi,\qquad \tilde{\varOmega}^2 =\frac{{\varOmega^2}}{{\varepsilon^2 }}. $$

Here, Ω and χ are O(1) quantities while ε≪1. Without loss of generality, we take Ω=1. The rescaled equations become:

$$ \everymath{\displaystyle }\begin{array}{@{}l} \ddot{\theta}+ \sin\theta= - \varepsilon\ddot{\chi}\cos\theta, \\ \noalign {\vspace {5pt}} \ddot{\chi}+ \frac{1}{{\varepsilon^2 }} \chi= - \frac{\mu }{\varepsilon} \bigl( { \ddot{\theta}\cos\theta- \dot{\theta}^2 \sin\theta} \bigr). \end{array} $$

(2)

This system has a conserved quantity that can be expressed as:

2.2 Typical solutions

We numerically integrate the full system in Eq. (1) for typical parameter values and initial conditions (ICs), in order to illustrate the type of nontrivial solutions that it exhibits. As an example, we take μ=0.4 and $\tilde{\varOmega}=50$ (ε=0.02). Since the system is conservative, we will look at how the dynamics change as the energy is increased.

For h=0.5, we choose the following set of initial conditions:

$$ \begin{array}{@{}l} \left \{\begin{array}{l} \dot{\theta}( 0 ) = 0, \\ \noalign {\vspace {3pt}} \theta ( 0 ) = \pi/9 \approx0.349, \\ \end{array} \right .\\ \noalign {\vspace {6pt}} \left \{\begin{array}{l} \dot{x} ( 0 ) = 0, \\ \noalign {\vspace {3pt}} x ( 0 ) = \varepsilon ( {{0.9756}} ) \approx0.0195. \\ \end{array} \right . \end{array} $$

(3)

For the ICs in Eq. (3), the pendulum oscillates about the downright position θ=0, it’s motion consists of a slow oscillation overlaid with a small fast oscillation, as shown in Fig. 2(a); Fig. 2(b) shows the mass–spring fast oscillation while Fig. 3 shows how its amplitude is modulated over the slow timescale.

Fig. 2

Plot of time series for the initial conditions in Eq. (3)

Fig. 3

Variation of the amplitude of the x oscillation over the slow timescale

Figure 6(a) shows the Poincare map $(x=0,\,\dot{x}>0 )$ for the energy level h=0.5, and the arrow points at the orbit corresponding to the ICs in Eq. (3). The shown fixed point (center) of the map corresponds to a periodic orbit in which θ≈−x. This periodic orbit is a nonlinear normal mode [10] of the coupled system that appears as a nearly straight line through the origin if viewed in the configuration plane θ vs. x. Now we look at the dynamics for h=0.7, and choose the following set of initial conditions:

$$ \begin{array}{@{}l} \left \{\begin{array}{l} \dot{\theta}( 0 ) = 0, \\ \noalign {\vspace {3pt}} \theta ( 0 ) = \pi/9 \approx0.349, \\ \end{array} \right . \\ \noalign {\vspace {5pt}} \left \{\begin{array}{l} \dot{x} ( 0 ) = 0, \\ \noalign {\vspace {3pt}} x ( 0 ) = \varepsilon ( {{1.1626}} ) \approx0.0233. \\ \end{array} \right . \end{array} $$

(4)

Figure 4(a) shows how the slow oscillation, overlaid by a small fast oscillation, is now no longer about the origin. Instead, the pendulum oscillates about an angle ≈0.33. The amplitude of the fast mass–spring oscillation is still slowly modulated, as shown in Fig. 3.

Fig. 4

Plot of time series for the initial conditions in Eq. (4)

Keeping the energy fixed at h=0.7, we choose a different set of ICs:

$$ \begin{array}{@{}l} \left \{ \begin{array}{l} \dot{\theta}( 0 ) = 0, \\ \noalign {\vspace {3pt}} \theta ( 0 ) = \pi/6 \approx{0.5236,} \\ \end{array} \right . \\ \noalign {\vspace {5pt}} \left \{\begin{array}{l} \dot{x} ( 0 ) = 0, \\ \noalign {\vspace {3pt}} x ( 0 ) = \varepsilon ( {{1.1370}} ) \approx{0.0227.} \\ \end{array} \right . \end{array} $$

(5)

As shown in Fig. 5(a), the pendulum is back to oscillating about the downright position and the modulation of the amplitude of x (Fig. 3) is still visible.

Fig. 5

Plot of time series for the initial conditions in Eq. (5)

Figure 6(b) shows the Poincare map for h=0.7. The arrows point to the orbits corresponding to the solutions in Fig. 4(a) (pointed arrow) and Fig. 5(a) (square head arrow). We can see from the Poincare map that the fixed point corresponding to the nonlinear normal mode with θ≈−x has lost stability and is now a saddle point of the map. Consequently, we can predict that two new fixed points (centers) were born in the process, and that the oscillations of the pendulum about a nonzero angle correspond to closed orbits of the map about the new centers.

Fig. 6

Poincare map (x=0, $\dot{x} >0$) for (a) h=0.5, (b) h=0.7

The aim of this paper is to shed light on these latter nontrivial solutions, in which the pendulum oscillates about a nonzero angle, and describe their dependence on initial conditions and the parameter μ.

3 The approximate solution

We look for a solution in which the oscillation of the slow degree of freedom (the pendulum) is partitioned according to the method of direct partition of motion [2]:

$$ \left \{\begin{array}{l} \chi=\chi ( {t,T} ),\\ \noalign {\vspace {3pt}} \theta ( {t,T} ) = \theta_0 ( t ) + \varepsilon\theta_1 ( {t,T} ), \\ \end{array} \right . $$

(6)

where

$$ \frac{{dT}}{{dt}} = \frac{{\omega ( t )}}{\varepsilon}, \quad \mathrm{or}\quad T = \int_0^t {\frac{{\omega ( {t'} )}}{\varepsilon}dt'}, $$

(7)

and

$$ \omega( t ) = \frac{1 }{{\sqrt{1 - \mu\cos^2 \theta_0 } }}. $$

(8)

Here, we have introduced a new fast timescale, T, in a way similar to the WKB method [19]; the choice of ω(t) is justified in Appendix C. We note that we do not apply DPM to the fast degree of freedom since it is under the influence of a slower oscillator, while DPM is only applicable to a slow oscillator that is influenced by a much faster oscillation (as in the case of the pendulum in this system). Thus, as detailed in Appendix C, the WKB method is instead needed for the analysis of the fast degree of freedom.

After applying the standard DPM procedure [2] to the θ equation of motion, we find that, to leading order, θ ₀ is governed by the following equation (see Appendix B for the details):

(9)

θ ₁ is found to depend on θ ₀ and χ as follows:

$$ \theta_1 = - \chi\cos\theta_0. $$

(10)

To leading order, χ is given by (see Appendix C for the details):

$$ \chi\approx C\sqrt{\omega( t )} \cos T, $$

(11)

where C is an arbitrary constant that depends on initial conditions.

Consequently, the motion of the pendulum, in the rescaled system described by Eq. (2), can be expressed as:

$$\theta\approx\theta_0 - \varepsilon\chi\cos \theta_0, $$

where θ ₀ is governed by Eq. (9) and χ is given by Eq. (11).

Recall that Eq. (2) are a rescaled version of the original system of interest given by Eq. (1), where χ is related to the motion of the mass–spring oscillator as follows:

$$x = \varepsilon\chi. $$

Hence, the solution to Eq. (1), for the assumed regime of motion, can be expressed in terms of the variables of Eq. (1) as follows:

$$ \theta\approx\theta_0 - x \cos\theta_0, $$

(12)

$$ x \approx\varepsilon C\sqrt{\omega( t )} \cos T. $$

(13)

4 The slow dynamics

At the end of the procedure that is described in Appendices B and C, the solution to the two degree of freedom mass–spring–pendulum system is expressed in Eq. (12)–(13) in terms of θ ₀, the leading order slow motion of the pendulum, which is governed by the following equation:

The arbitrary constant C that appears in the equation can be expressed in terms of the initial conditions. For initial zero velocities, the initial conditions take the form:

with

(14)

Now, we rewrite the equation governing θ ₀ as a system of two first order equations:

$$ \everymath{\displaystyle }\begin{array}{@{}l} {\dot{\theta}_0 = \phi,}\\ \noalign {\vspace {8pt}} \dot{\phi}= - \sin\theta_0 + \frac{{1}}{2}C^2 \frac{\sin\theta_0 \cos\theta_0}{ (1-\mu\cos^2\theta_0 )\sqrt{1- \mu\cos^2\theta_0}}. \end{array} $$

(15)

For small enough values of C, the above system has a neutrally stable equilibrium point (center) at the origin (ϕ=0,θ ₀=0) and two saddle points at (ϕ=0, θ ₀=±π), so that the phase portrait resembles that of the simple pendulum. As C increases in value, a pitchfork bifurcation takes place, in which the origin becomes a saddle point and two new centers are born. The critical value of C is related to the parameter μ as follows (see Appendix D for the details):

$$ C_{cr}^2 = 2 ( {1 - \mu} )^{\frac{3}{2}} . $$

(16)

In Appendix D, it is explained how this condition on C translates into the following condition on the energy value h:

$$h_{cr}=1-\mu. $$

For the example presented in Sect. 2.2, the critical values of C and h are as follows:

So a qualitative change in the solution is expected as h increases past h=0.6, which explains the difference in solution between h=0.5 and h=0.7, cf. Figs. 6(a)–6(b).

To illustrate the relation of the solution of the full system (1) to the θ ₀ dynamics, we find the value of C for the ICs presented in Sect. 2.2.

For the ICs in Eq. (3) corresponding to Fig. 2, we have:

Figure 7(a) shows the corresponding phase portrait for the system in Eq. (15) with this value of C. The slow oscillation of the pendulum in Fig. 2(a) corresponds to the closed orbit surrounding the origin in this phase portrait.

Fig. 7

Phase portrait for the θ ₀ equation for (a) ICs in Eq. (3) corresponding C=0.8749, (b) ICs in Eq. (4) corresponding C=1.0427, (c) ICs in Eq. (5), corresponding to C=1.0400

For the ICs in Eq. (4) corresponding to Fig. 4, we have:

For this value of C, Fig. 7(b) shows that the origin is a saddle point and the system in Eq. (15) has two nontrivial neutrally stable equilibrium points (centers). The slow oscillation of the pendulum in Fig. 4(a) corresponds to the small closed orbit surrounding one of the nontrivial equilibrium points in this phase portrait.

For the same energy levels, different ICs result in different values of C and different orbits in the resulting phase plane. For the ICs in Eq. (5), we get:

The resulting slow oscillation in Fig. 5(a) corresponds to the closed orbit enclosing the homoclinic orbit in the phase portrait shown in Fig. 7(c). This illustrates how, despite the presence of the two nontrivial equilibrium points, oscillations about the origin are still possible and correspond to large amplitude orbits that are outside the homoclinic orbit.

4.1 The predicted nonlinear normal modes

Note that each value of C leads to a phase portrait filled with closed orbits, however, out of those orbits, the only one which corresponds to a solution of the full system (1) is that associated with the specific ICs that led to that value of C.

An interesting case occurs when the choice of ICs results in a phase portrait that has a nontrivial equilibrium point which coincides in value with the initial θ ₀ amplitude, A. That is, we start with ICs of the form:

$$\left \{\begin{array}{l} \dot{\theta}( 0 ) = 0, \\ \noalign {\vspace {3pt}} \theta ( 0 ) = \theta_0 ( 0 ) = A, \\ \end{array} \right . \qquad \left \{\begin{array}{l} \dot{x} ( 0 ) = 0, \\ \noalign {\vspace {3pt}} x ( 0 ) = \varepsilon B, \\ \end{array} \right . $$

and the corresponding value of C results in nontrivial equilibrium points (centers) for the θ ₀ equation at:

$$\theta_0 = \pm E,\qquad \phi=0. $$

Then, if E=A, θ ₀ will remain equal to E for all time. It would mean that we are starting at a neutrally stable equilibrium point of the θ ₀ equation, so the solution will remain at that point for all time.

Appendix D shows that these special values of initial θ amplitude can be expressed in terms of h and μ as:

(17)

The corresponding value of x is expressed as:

$$ x ( 0 ) = \varepsilon B^* = \varepsilon\sqrt{2 \bigl( {h - \mu \bigl( {1 - \cos A^*} \bigr)} \bigr) }. $$

(18)

Hence, we predict that these special initial amplitudes, with zero initial velocities, will lead to a solution in which:

$$ \theta\approx A^* -x\cos A^*. $$

(19)

Such a solution would be a nonlinear normal mode of the coupled mass–spring–pendulum system.

4.2 Relation of θ ₀ to the Poincare map

For a given energy level, the phase portrait of the θ ₀ equation is filled with closed orbits and the picture is topologically similar to that of the Poincare map. That is, for a given initial condition, the resulting orbit in the θ ₀ phase plane corresponds to a closed orbit in the Poincare map, however, the orbits are not identical. This is due to the fact that, while θ≈θ ₀, $\dot{\theta}$ differs from $\dot{\theta}_{0}$ by an O(1) quantity; as shown in Appendix E, for the points of the Poincare map, $\dot{\theta}$ can be expressed in terms of $\dot{\theta}_{0}$ as follows:

$$ \dot{\theta}_{Pm} \approx\dot{\theta}_0 - C \bigl( {1 - \mu\cos^2 \theta_0 } \bigr)^{ - \frac{3}{4}} \cos\theta_0. $$

(20)

So for a given ICs, we can obtain the corresponding orbit in the Poincare map, by first numerically integrating the θ ₀ equation to obtain θ ₀ and $\dot{\theta}_{0}$ and then generating the orbit in the Poincare map by plotting the corresponding values of $\dot{\theta}_{Pm}$ vs. θ ₀. This means that we can generate an approximate picture of the Poincare map of the full system (1) by numerically integrating the slow dynamics equation governing θ ₀ instead of integrating the full system (1) which contains the fast dynamics and thus requires a much smaller step size of integration.

Also, by comparing this procedure with the results of numerical integration, we can obtain a check on the accuracy of the various approximations made in this work.

5 Summary of results

We restate here the original equations governing the considered mass–spring–pendulum system:

We have shown that θ≈θ ₀+O(ε) where θ ₀ is governed by the following equation:

where C is a constant that depends on the ICs. x is assumed to be O(ε) and is found to be expressed as:

$$x \approx\varepsilon C\sqrt{\omega( t )} \cos T $$

with

$$\omega( t ) = \frac{1}{{\sqrt{1 - \mu\cos^2 \theta_0 } }} \quad \mathrm{and}\quad T = \int _0^{2\pi} {\frac{{\omega ( {t'} )}}{\varepsilon}dt'}. $$

Our analysis gives that a pitchfork bifurcation occurs in the Poincare map as energy increases past the following critical value:

$$h_{cr}=1-\mu. $$

This bifurcation corresponds to a bifurcation in periodic orbits of the full system (1) in which the nonlinear normal mode corresponding to θ≈−x loses stability and two new stable nonlinear normal modes are born in which θ≈A ^∗−xcosA ^∗, where A ^∗ is expressed in terms of h and μ as:

$$A^* = \pm\cos^{ - 1} \biggl( {\frac{{\mu - h \pm\sqrt{ ( {h - \mu} )^2 + 8\mu} }}{{4\mu}}} \biggr). $$

These new nonlinear normal modes correspond to the nontrivial fixed points of the Poincare map.

6 Comparison to numerics

We compare the solution resulting from the numerical integration of the original equations with that from the integration of the θ ₀ equation. Figure 8 displays the Poincare map orbits for h=1. Near each of the orbits, a small arrow points to the orbit which is predicted from the θ ₀ equation for corresponding initial conditions. Figures 9, 10 and 11 display comparison plots for several initial conditions. Unless otherwise mentioned, we have set μ=0.4 and $\tilde{\varOmega}=50$ (ε=0.02). In the plots of θ vs. time, the thick line correspond to the solution of the numerical integration of the full system (1), and the apparent thickness is due to the fast component present in the oscillation of the pendulum; the thin line corresponds to the approximate solution, that is, from the numerical integration of the θ ₀ equation, and captures only the leading order slow component of the pendulum oscillation. In the plots of x vs. time, the arrow points at the approximate solution.

Fig. 8

Comparison of the predicted Poincare map orbits (arrows) with those from the integration of the full system (1)

Fig. 9

Comparison plot of time series for ICs in Eq. (3)

Fig. 10

Comparison plots of time series for ICs in Eq. (4)

Fig. 11

Comparison plots of time series for ICs in Eq. (5)

We can see that the approximate solution compares well with that from numerical integration of the full system (1).

7 Conclusion

We have used the method of direct partition of motion to study the dynamics of a mass–spring–pendulum system in which the harmonic oscillator is restricted to move horizontally. We have considered the case where the stiffness of the spring is very large, so that the frequency of the oscillation of the uncoupled harmonic oscillator is an order of magnitude larger than that of the uncoupled pendulum. We have also limited our attention to the regime of motion where the amplitude of motion of the harmonic oscillator is an order of magnitude smaller than that of the pendulum. Under these assumptions, an approximate expression for the solution of the two degree of freedom system is found in terms of θ ₀, the leading order slow oscillation of the pendulum. An equation governing θ ₀ is presented and found to undergo a pitchfork bifurcation for a critical value of C which is a parameter related to the initial amplitudes of θ and x. It is shown that the pitchfork bifurcation in the slow dynamics equation corresponds to a pitchfork bifurcation of periodic orbits of the full system (1) that occurs as the energy is increased past a critical value which is expressed in terms of the parameter μ. This bifurcation can be seen to occur in the Poincare map of the full system (1), where the fixed point corresponding to the nonlinear normal mode θ≈−x loses stability and two new centers are born in the map. The new centers correspond to new periodic motions, which are nonlinear normal modes with θ≈A ^∗−xcosA ^∗, where the expression for A ^∗ is found in terms of μ and h. For these modes, the motion of the pendulum is predicted to be a small fast oscillation about the nonzero value θ=A ^∗. Along with these special motions, quasi-periodic motions exist in which the pendulum undergoes slow oscillation about a nonzero angle, with overlaid fast oscillation. These latter orbits correspond to closed orbits about the new centers in the Poincare map. A relation between $\dot{\theta}$ and $\dot{\theta}_{0}$ is given for points of the Poincare map such that the orbits of the map can be generated approximately by numerically integrating the slow dynamics equation. Finally, the approximate solution, as well as the predications made based on it, is checked against numerical integration of the full system (1) and found to agree well.

Although this paper dealt with a specific system, we suggest that the strategy used to study this system, that is, DPM in combination with the WKB method, could be applicable to a general class of systems that posses two degrees of freedom with vastly different frequencies and nonlinear coupling that allows the modulation of the fast oscillation by the slow one.

As a final note, we emphasize that the nontrivial dynamics observed in this example system was primarily due to the nonlinear interaction between oscillations of vastly different frequencies. Particularly, these oscillations represented the natural response of the system to initial conditions in the absence of any dissipation or external forcing. However, preliminary numerical integration of the corresponding system with linear damping and external harmonic forcing clearly shows solutions that are qualitatively similar to those exhibited by the conservative system. These latter solutions consist of slow oscillation of the pendulum about a nonzero angle accompanied by fast oscillation of the mass on the spring with an amplitude that is modulated on the slow timescale. Such solutions are also observed in the free response of the corresponding system in which the fast degree of freedom is subject to nonlinear damping (such as a van der Pol type nonlinearity) that allows it to undergo sustained fast oscillations. Detailed analysis of such non-conservative versions of the example studied here is beyond the scope of this work and is left for future investigations.

Appendices

Appendix A: Motivation for the assumed form of solution

The considered mass–spring–pendulum system is governed by the following system of equations:

$$\ddot{\theta}+ \sin\theta= - \varepsilon\ddot{\chi}\cos\theta, $$

$$\ddot{\chi}+ \frac{1}{{\varepsilon^2 }} \chi= - \frac{\mu }{\varepsilon} \bigl( {\ddot{\theta}\cos\theta- \dot{\theta}^2 \sin\theta} \bigr). $$

In its present form, each of the equations contains the second derivative of both χ and θ. We can rewrite the system of equations so that each second derivative appears in only one of the equations, as follows:

In this latter form, the θ equation appears as that of a nonlinear oscillator parametrically forced by χ, which we expect to be a fast oscillation. Hence this suggests the partitioning of the θ motion into a slow component overlaid by a fast component, as in the DPM ansatz. Also, we can see that the χ equation appears as that of a fast oscillator with a frequency whose magnitude is modulated by θ which we expect to be a slow oscillation, that is, it appears as an equation of a fast oscillator with a slowly changing frequency, similar to that which the WKB method is well suited for. This suggests rescaling fast time in the following manner:

$$\frac{{dT}}{{dt}} = \frac{{\omega ( t )}}{\varepsilon} \quad \mathrm{or}\quad T = \int_0^t {\frac{{\omega ( {t'} )}}{\varepsilon}dt'}, $$

and the assumed solution becomes:

$$\left \{\begin{array}{l} \chi=\chi ( {t,T} ),\\ \noalign {\vspace {3pt}} \theta ( {t,T} ) = \theta_0 ( t ) + \varepsilon\theta_1 ( {t,T} ). \\ \end{array} \right . $$

Here, ω(t) is to be chosen such that the fast oscillation is a perturbation of a harmonic oscillation on the new timescale T. That is, we will choose ω(t) so as the χ equation has the form:

$$\frac{{\partial^2 \chi}}{{\partial T^2 }} + \chi+ O ( \varepsilon) = 0, $$

then, an approximate expression for χ can be found using regular perturbations.

Appendix B: Details of the method of direct partition of motion

The method of direct partition of motion is based on the following three main assumptions:

• The motion of the slow oscillator, which is subject to fast parametric forcing, is partitioned as a sum of a leading order purely slow motion and an overlaid fast component.

• All functions of fast time are periodic with a zero average over a period of fast oscillation.

• Purely slow motions are treated as constants when averaging over a period of fast oscillation.

We start by substituting the form of solution presented in Appendix A into the following equations of motion:

$$ \everymath{\displaystyle }\begin{array}{@{}l} \ddot{\theta}+ \sin\theta= - \varepsilon\ddot{\chi}\cos\theta, \\ \noalign {\vspace {6pt}} \ddot{\chi}+ \frac{1}{{\varepsilon^2 }} \chi= - \frac{\mu }{\varepsilon} \bigl( {\ddot{\theta}\cos\theta- \dot{\theta}^2 \sin\theta} \bigr). \end{array} $$

(21)

The θ equation becomes:

(22)

We proceed to apply the standard DPM procedure [2] to this equation:

• 1. We average Eq. (22) over a period of fast timescale, while making use of the second and third assumption of DPM. The resulting averaged equation is:

  $$ \frac{{d^2 \theta_0 }}{{dt^2 }} + \sin\theta_0 - \omega^2 \sin\theta_0 \biggl\langle{\frac{{\partial^2 \chi}}{{\partial T^2 }}\theta_1 } \biggr\rangle_T = 0, $$

  (23)

  where 〈•〉 _T denotes averaging with respect to the fast timescale, T, over a period of fast oscillation which is equal to 2π:

  $$\langle\bullet\rangle_T = \frac{1}{{2\pi}} \int_0^{2\pi} ( \bullet)\,dT. $$

• 2. We subtract Eq. (23) from Eq. (22), then retaining the leading order terms only gives:

  $$ \frac{{\partial^2 \theta_1 }}{{\partial T^2 }} + \frac {{\partial^2 \chi}}{{\partial T^2 }}\cos\theta_0 =0. $$

  (24)

• 3. We integrate the latter equation twice with respect to T:

  $$\theta_1 = - \chi\cos\theta_0 + c_1 T +c_2. $$

• 4. In order to satisfy the second assumption of DPM, we set c ₁=c ₂=0, and obtain the following expression for θ ₁:

  $$ \theta_1 = - \chi\cos\theta_0. $$

  (25)

Substituting the latter into Eq. (23), we get:

$$ \frac{{d^2 \theta_0 }}{{dt^2 }} + \sin\theta_0 +\omega^2 \biggl\langle{\frac{{\partial^2 \chi}}{{\partial T^2 }}\chi} \biggr\rangle_T \cos \theta_0 \sin\theta_0 = 0. $$

(26)

From Appendix C, we have:

$$\chi\approx C\sqrt{\omega( t )} \cos T $$

with

$$\omega( t ) = \frac{1}{{\sqrt{1 - \mu\cos^2 \theta_0 } }}. $$

So the averaged term in Eq. (26) becomes:

We substitute this into Eq. (26) along with the expression for ω(t). Then the equation governing θ ₀, to leading order, reduces to:

Appendix C: Solving for χ

For convenience, we restate here the assumed form of solution:

$$\left \{\begin{array}{l} \chi=\chi ( t,T ), \\ \noalign {\vspace {3pt}} \theta ( t,T ) = \theta_0 ( t ) + \varepsilon\theta_1 ( t,T ), \\ \end{array} \right . $$

where

$$\frac{{dT}}{{dt}} = \frac{\omega ( t)}{\varepsilon} \quad \mathrm{or}\quad T = \int_0^t {\frac{{\omega ( {t'} )}}{\varepsilon}dt'} . $$

We substitute this into the following equations of motion:

$$\ddot{\theta}+ \sin\theta= - \varepsilon\ddot{\chi}\cos\theta, $$

$$\ddot{\chi}+ \frac{1}{{\varepsilon^2 }} \chi= -\frac{\mu }{\varepsilon} \bigl( {\ddot{\theta}\cos\theta- \dot{\theta}^2 \sin\theta} \bigr). $$

The χ equation becomes:

(27)

In order to eliminate the second derivative of θ ₀ from the above equation, we substitute the expression for θ ₁ from Eq. (25) into Eq. (22) in Appendix B. Then, the θ equation becomes:

We substitute this expression into Eq. (27), along with the expression for θ ₁ from Eq. (25). Then, multiplying by ε ², the χ equation becomes:

(28)

For the above equation to be of the form:

$$\frac{\partial^2 \chi}{\partial T^2 } + \chi+ O ( \varepsilon ) = 0, $$

we choose

$$ \omega( t ) = \frac{1}{{\sqrt{1 - \mu \cos^2 \theta_0 } }}. $$

(29)

The χ equation becomes:

(30)

Now, we are ready to expand χ in an asymptotic series:

$$\chi( {t,T} ) = \chi_0 ( {t,T} ) + \varepsilon \chi_1 ( {t,T} ) + \cdots. $$

Substituting this into Eq. (30), and collecting terms of the same order, we get:

O(1): 

$$\frac{{\partial^2 \chi_0 }}{{\partial T^2 }} +\chi_0 =0, $$

O(ε): 

The first equation gives:

$$\chi_0 = X ( t )\cos T. $$

Then, killing secular terms from the χ ₁ equation results in the following equation relating the amplitude X and θ ₀:

$$\frac{1}{{\omega^2 }}\frac{{d\omega}}{{dt}}X + \frac{2}{\omega}\frac {{dX}}{{dt}} + 2 \omega\mu\sin\theta_0 \cos\theta_0 \frac{{d\theta_0 }}{{dt}}X = 0, $$

which we rearrange into

$$\frac{1}{\omega}\frac{{d\omega}}{{dt}} + \frac{2}{X}\frac{{dX}}{{dt}} + 2 \omega^2 \mu\sin\theta_0 \cos\theta_0 \frac{{d\theta_0 }}{{dt}} = 0. $$

Integrating with respect to t, we get

$$ \everymath{\displaystyle }\begin{array}[b]{@{}l} \int{\frac{1}{\omega}d\omega} + \int{\frac{2}{X}dX} + \int{2 \omega^2 \mu\sin\theta_0 \cos\theta_0 \,d\theta_0 } = 0 \\ \noalign {\vspace {6pt}} \quad \Rightarrow\quad \ln\omega+ 2\ln X + \int 2\omega^2\mu\sin\theta_0 \cos\theta_0 \,d\theta_0 = k, \\ \noalign {\vspace {6pt}} \end{array} $$

(31)

where k is an arbitrary constant.

But

So Eq. (31) becomes

(32)

As a result, to leading order, χ is given by

$$ \chi\approx C\sqrt{\omega( t )} \cos T $$

(33)

with

$$\omega( t ) = \frac{1}{{\sqrt{1 - \mu\cos^2 \theta_0 } }}, $$

where C is an arbitrary constant that depends on initial conditions.

Appendix D: The bifurcation in the slow dynamics

θ ₀ is governed by the following equation:

(34)

We rewrite this as a system of two first order equations:

$$ \everymath{\displaystyle }\begin{array}{@{}l} \dot{\theta}_0 = \phi,\\ \noalign {\vspace {6pt}} \dot{\phi}= - \sin\theta_0 + \frac{{C^2 }}{2} \frac{{ \sin\theta_0 \cos\theta_0 }}{{ (1-\mu\cos^2\theta_0 )\sqrt {1 - \mu\cos^2 \theta_0 } }}. \end{array} $$

(35)

Looking for the value of θ ₀ that corresponds to equilibrium points of this equation (with ϕ=0):

$$\everymath{\displaystyle }\begin{array}{@{}l} \sin\theta_0 = 0, \quad \mathrm{or} \\ \noalign {\vspace {5pt}} 1 - \frac{{C^2 }}{2}\frac{\cos\theta_0}{ (1-\mu\cos^2\theta_0 ) \sqrt{1 - \mu\cos^2 \theta_0 } } = 0. \end{array} $$

So the first condition gives θ ₀=0,π,−π, while the second condition allows two additional equilibrium points θ ₀=E such that

(36)

To know when a root to this equation actually exists,

$$\mathrm{let} \alpha= \cos^2 E, \quad \mathrm{so} \ 0 \le\alpha\le1. $$

Consider the two functions f and g, illustrated in Fig. 12:

$$f ( \alpha) = ( {1 - \mu\alpha} )^3,\qquad g ( \alpha) = \frac{{C^4 }}{4}\alpha. $$

f is a decreasing function of α with

$$f ( 0 ) = 1 \quad \mathrm{and} \quad f ( 1 ) = ( {1 - \mu} )^3. $$

The function g is the line through the origin, with a slope of C ⁴/4. So, the two functions will intersect for some α∈[0,1] when the following condition is met:

$$ \frac{{C^4 }}{4} \ge( {1 - \mu} )^3. $$

(37)

Hence, when C satisfies this above condition, two new equilibrium points will exist at θ ₀=±E , ϕ=0, such that cosE satisfies Eq. (36).

Fig. 12

Schematic of the two functions f(α)&g(α)

The Jacobian for the system in Eq. (35) has a zero trace while the determinant is given by the following expression:

looking at the value of this determinant for θ ₀=0:

$$\Delta_{\theta_0 = 0} = 1 - \frac{{C^2}}{2}\frac{1}{ ( {1 - \mu})^{3/2}} $$

$$\Delta_{\theta_0 = 0} > 0 \quad \Rightarrow\quad \frac{{C^4 }}{4} \le( {1 - \mu})^3. $$

So the origin goes from being a center to a saddle as the two new equilibrium points are born, hence, a pitchfork bifurcation takes place. To check the determinant for θ ₀=±E, we solve for C ² from Eq. (36):

$$ C^2 =\frac{2 ( {1 - \mu\cos^2 E} )^{3/2}}{\cos E}; $$

(38)

substituting this into the expression for the determinant, we get:

$$\Delta_{\theta_0 = E} = \frac{{\mu\sin^2 ( {2E} ) + 2\sin^2 ( E )}}{{2\cos E ( {1 - \mu\cos^2 E} )}} > 0, $$

where we have used Eq. (38) to judge that cosE>0. This confirms that the two new equilibrium points are centers.

To summarize, when the following condition is met:

$$ C^2 > 4 ( {1 - \mu} )^{\frac{3}{2}}, $$

(39)

the approximate equation governing θ ₀ undergoes a pitchfork bifurcation where two new equilibrium points are born (θ ₀=±E, ϕ=0) such that

$$\bigl( {1 - \mu\cos^2 E} \bigr)^3 = \frac{{C^4}}{4} \cos^2 E. $$

The arbitrary constant C that appears in the equation can be expressed in terms of the initial conditions. As mentioned in Sect. 4, for initial zero velocities, the initial conditions take the form:

with

$$\omega( 0 ) = \frac{1}{\sqrt{1 - \mu\cos^2 A} }. $$

Then C can be expressed as follows:

$$\quad \Rightarrow \quad C = B \bigl( {1 - \mu\cos^2 A} \bigr)^{\frac{1}{4}} . $$

The bifurcation condition in Eq. (39) becomes

$$ B^4 \bigl(1 - \mu\cos^2 A \bigr) > 4 ( {1 - \mu} )^3. $$

(40)

Also, for such initial conditions, the energy function h that corresponds to the full system (1) is

$$h = \frac{1}{2}B^2 + \mu( {1 - \cos A} ); $$

solving for B ² in terms of h and substituting the resulting expression into Eq. (40), we can derive a minimum required value of h so that the bifurcation occurs:

which leads to the following condition on h:

$$h \ge\mu( {1 - \cos A} ) + \sqrt{\frac{{ ( {1 - \mu} )^3 }}{{1 - \mu\cos^2 A}}} . $$

The expression on the right hand side of the equality increases as A increases. For A=0, it takes the value 1−μ. This leads to the following minimum requirement for the pitchfork bifurcation to happen:

$$h > 1 - \mu. $$

Now, going back to the full system (1), we recall from Eq. (12) that the approximate θ motion took the form:

$$\theta\approx\theta_0 -x \cos\theta_0, $$

where θ ₀ is governed by Eq. (34).

So, when the condition for the existence of the two new equilibrium points is met, we expect certain solutions that obey approximately the following relation:

$$\theta\approx E - x \cos E. $$

That is, if we start with an initial condition $\theta (0 )=\theta_{0} (0 )=E, \dot{\theta}= \phi=0$, then the approximate equation for θ ₀ predicts that θ ₀ will remain equal to E for all time, since θ ₀=E,ϕ=0 is a neutrally stable fixed point (center) of Eq. (35).

Now we look for the initial amplitude of θ that corresponds to such solutions. That is, for each constant value of h that allows the mentioned bifurcation to occur, we look for θ ₀(0)=A, such that E=A. From Eq. (38), we have:

$$ C^2 = \frac{{2 ( {1 - \mu\cos^2 E} ) ^{3/2} }}{{\cos E}}, $$

(41)

but the expression for C in terms of the initial conditions is:

(42)

We substitute Eq. (41) into Eq. (42), and require

$$ E=A=\theta_0 (0). $$

(43)

We get

$$B^2 = \frac{{2 ( {1 - \mu\cos^2 A} )}}{{\cos A}}. $$

Now, we can substitute this relation into the expression for h, in order to solve for A:

We rewrite this as

(44)

For such a solution to exist, we need

which coincides with the condition for the existence of the pitchfork bifurcation.

To summarize, for a fixed value of μ, we expect to see a fixed point in the map (x=0 and $\dot{x}>0$) if we choose a value for h that meets h>1−μ, and integrate the system in Eq. (1), with the following initial conditions:

$$\everymath{\displaystyle }\left \{\begin{array}{@{}l} \theta ( 0 ) = \pm A^* \\ \noalign {\vspace {5pt}} \qquad = \pm\cos^{ - 1} \biggl( {\frac{{\mu - h \pm\sqrt{ ( {h - \mu} )^2 + 8\mu} }}{{4\mu}}} \biggr), \\ \noalign {\vspace {5pt}} \dot{\theta}( 0 ) = 0, \\ \noalign {\vspace {5pt}} x ( 0 ) = \varepsilon B^* = \varepsilon \sqrt{2 \bigl( h - \mu ( {1 - \cos A} ) \bigr) }, \\ \noalign {\vspace {5pt}} \dot{x} ( 0 ) = 0. \end{array} \right . $$

Figure 13 shows the pendulum oscillation for the special ICs for which θ is predicted to be θ≈A ^∗−xcosA ^∗, that is, θ is predicted to undergo no slow oscillation and instead the motion of the pendulum will consist of a fast oscillation about the θ=A ^∗. Due to the error in the approximate solution and numerical integration, θ undergoes a small amplitude slow oscillation instead of no slow oscillation. Figure 14 shows that this slow oscillation gets smaller in amplitude as energy is increased farther from the bifurcation value. This can be explained by the fact that the value of A ^∗ increases as energy increases and thus the relative error decreases. The solution also gets closer to the predicted one as ε is decreased, as illustrated in Fig. 15.

Fig. 13

θ vs. time for the initial condition corresponding to θ(0)=A ^∗ for h=0.7, ε=0.02

Fig. 14

θ vs. time for the initial condition corresponding to θ(0)=A ^∗ for h=2 with ε=0.02

Fig. 15

θ vs. time for the initial condition corresponding to θ(0)=A ^∗ for h=2 with ε=0.01

Appendix E: Relating the curves of the Poincare map to θ ₀

The Poincare map considered in the body of this paper corresponds to a plot of $\dot{\theta}$ vs. θ with x=0 and $\dot{x}>0$. If we could relate $\dot{\theta}$ to $\dot{\theta}_{0}$, and θ to θ ₀, then we can approximately generate the Poincare map of the full system (1) from the solution to the θ ₀ equation.

θ was found to be expressed as

$$\theta\approx\theta_0 -x \cos\theta_0. $$

With x assumed to be O(ε), we can say

$$\theta\approx\theta_0 +O (\varepsilon). $$

To find an expression for $\dot{\theta}$ in terms of $\dot{\theta}_{0}$, we differentiate both sides of the expression for θ with respect to time:

(45)

Note that since x is O(ε), we ignore the term multiplied by x, however, we retain the term containing the derivative of x since x oscillates with a frequency of O(1/ε) and so $\dot{x}$ is of O(1).

In order to eliminate $\dot{x}$ from the expression for $\dot{\theta}$, we observe that

where we have used the fact that

$$\frac{{dT}}{{dt}} = \frac{{\omega ( t )}}{\varepsilon}. $$

Now, for the Poincare map, we have

$$\left \{\begin{array}{l} \noalign {\vspace {-1pt}} x = 0 \quad \Rightarrow \quad\cos T = 0 \\ \noalign {\vspace {3pt}} \dot{x} > 0 \quad \Rightarrow \quad\sin T < 0 \\ \noalign {\vspace {-1pt}} \end{array} \right . \quad \Rightarrow \quad \sin T = - 1, $$

then

$$\frac{{dx}}{{dt}} \approx C\omega\sqrt{\omega}+ O ( \varepsilon). $$

Substituting this into Eq. (45), we get

$$\frac{{d\theta}}{{dt}} = \frac{{d\theta_0 }}{{dt}} - C\omega\sqrt{\omega}\cos \theta_0 + O ( \varepsilon). $$

Substituting the following expression for ω(t) yields

$$\omega( t ) = \frac{1}{{\sqrt{1 - \mu\cos^2 \theta_0 } }} = \bigl( {1 - \mu\cos^2 \theta_0 } \bigr)^{ - \frac{1}{2}} . $$

We obtain the following expression for the $\dot{\theta}$ values, corresponding to points in the Poincare map, in terms of $\dot{\theta}_{0}$ and θ ₀:

$$\frac{{d\theta}}{{dt}} \approx\frac{{d\theta_0 }}{{dt}} - C \bigl( {1 - \mu \cos^2 \theta_0 } \bigr)^{ - \frac{3}{4}} \cos \theta_0. $$