1 Introduction

Optical solitons have the potential to become carriers in the telecommunication systems because of the capability of propagating long distances with high intensity and without attenuation [1–12]. Dynamics of light pulses are described by the nonlinear Schrödinger (NLS)-typed equations with cubic nonlinear terms [8, 13], and the non-Kerr nonlinearity effect comes into play [9] when the intensity of the incident light field becomes stronger, which is described by the NLS-typed equations with higher-order nonlinear terms [10]. The NLS equation is a vital model to describe certain phenomena from Physics and Engineering to Biochemistry [14]. Certain interest has been focused on the NLS-typed equations since the experimental observation ofthe multi-stability of solitons in non-Kerr fibers [1, 9, 15–27].

In this paper, the coupled cubic–quintic nonlinear NLS equations with variable coefficients [2, 22] describing the effects of quintic nonlinearity on the ultrashort optical pulse propagation in the non-Kerr media are investigated [28],

$$\begin{aligned}&i q_{1z}+r(z)\,q_{1tt}+m(z)\, \left( |q_1|^2+|q_2|^2\right) q_1\nonumber \\&\quad +n(z)\, \left( |q_1|^2+|q_2|^2\right) ^2 q_1\nonumber \\&\quad -i\,p(z)\,\left[ \left( |q_1|^2+|q_2|^2\right) q_1\right] _t \nonumber \\&\quad +i\,s(z)\,\left( q_1^{*} q_{1t}+q_2^{*} q_{2t}\right) q_1=0 ,\nonumber \\&i q_{2z}+y(z)\,q_{2tt}+k(z)\,\left( |q_1|^2+|q_2|^2\right) q_2\nonumber \\&\quad +w(z)\,\left( |q_1|^2+|q_2|^2\right) ^2 q_2\nonumber \\&\quad -i\,a(z)\left[ (|q_1|^2+|q_2|^2) q_2\right] _t\nonumber \\&\quad +i\,b(z)\left( q_1^{*} q_{1t}+q_2^{*} q_{2t}\right) q_2=0 , \end{aligned}$$
(1)

where the components \(q_1\) and \(q_2\) of the electromagnetic fields propagate along the coordinate \(z\) in the two cores of an optical waveguide, \(t\) is the local time [28, 29], \(r(z)\) and \(y(z)\) represent the group velocity dispersions, \(m(z)\) and \(k(z)\) are the nonlinearity parameters, \(n(z)\) and \(w(z)\) are the saturation of the nonlinear refractive indexes, \(p(z)\) and \(a(z)\) are the self-steepening, and \(s(z)\) and \(b(z)\) are the delayed nonlinear response effects [30]. With a reduction of \(q_1=q\) and \(q_2=0\) (or \(q_1=0\) and \(q_2=q\)), Eq. (1) turns to the integrable Kundu–Eckhaus equation [1, 22] with variable coefficients, which possesses the applications in the nonlinear optics [27], quantum field theory [25], and weakly nonlinear dispersive matter waves [26]. Equation (1) with constant coefficients has been investigated in several respects [1]. But as far as we know, the Lax pair, Darboux transformation (DT), and conservation laws of Eq. (1) have not been presented as yet.

The outline of this paper is organized as follows: In Sect. 2, a Lax pair of Eq. (1) is presented and the corresponding DT constructed. In Sect. 3, one-soliton solutions of Eq. (1) is obtained and some physical quantities such as the amplitude, velocity, width, initial phases, and energy are, respectively, analyzed. In Sect. 4, an infinite number of conservation laws of Eq. (1) are derived by symbolic computation [2, 31–37]. Section 5 contains our conclusions.

2 Lax pair and DT of Eq. (1)

In this section, we present a Lax pair of Eq. (1) [38]. Linear eigenvalue problem for Eq. (1) can be given as [1]

$$\begin{aligned} {\varPsi _t}=U{\varPsi },\quad {\varPsi _z}=V{\varPsi }, \end{aligned}$$
(2)

where \(\varPsi ={[ \psi _1(z,t), \psi _2(z,t),\psi _3(z,t)]}^T,\,T\) denotes the transpose of the vector, while \(U\) and \(V\) are respectively given by

$$\begin{aligned}&U=\nonumber \\&\quad \left( \begin{array}{ccc} i L \theta _t(z,t)\!-\!i \lambda &{} q_1 \rho _1(z) &{} q_2\rho _2(z) \\ -q_1^* \rho _1^*(z) &{} i \lambda \!-\!i L\theta _t(z,t) &{} 0 \\ -q_2^* \rho _2^*(z) &{} 0 &{} i \lambda \!-\!i L \theta _t(z,t) \end{array} \right) ,\nonumber \\&V=\nonumber \\&\left( \! \begin{array}{ccc} a_1(z) \lambda ^2\!+\!a_2(z,t) &{} \lambda b_1(z,t)\!+\!b_2(z,t) &{} \lambda f_1(z,t)\!+\!f_2(z,t) \\ \lambda c_1(z,t)\!+\!c_2(z,t) &{} d_1(z) \lambda ^2\!+\!d_2(z,t) &{} k_1(z,t) \\ \lambda g_1(z,t)\!+\!g_2(z,t) &{} k_2(z,t) &{} d_1(z) \lambda (t)^2\!+\!h_2(z,t) \end{array} \!\right) ,\nonumber \\ \end{aligned}$$
(3)

where \(L\) is a constant and

$$\begin{aligned}&a(z)\!=\!b(z)\!=\!s(z)\!=\!p(z),\ \ \ \ w(z)\!=\!n(z)\!=\!L\,b(z), \\&r(z)\!=\!y(z)\!=\!\frac{b(z)}{4L},\ \ \ \theta (z,t)\!=\! \int \left( |q_1|^2\!+\!|q_2|^2\right) \, \mathrm{d}t, \\&m(z)=\frac{b(z)|\rho _2(z)|^2}{2L}, \ \ \ \ \ k(z)=\frac{b(z)|\rho _1(z)|^2}{2L}, \\&b_1(z,t)=\frac{1}{2} i \left[ a_1(z) q_1 \rho _1(z)-d_1(z) q_1 \rho _1(z)\right] , \\&d_1(z)=4 i r(z)+a_1(z), \\&f_1(z,t)=\frac{1}{2} i \left[ a_1(z) q_2 \rho _2(z)-h_1(z) q_2 \rho _2(z)\right] ,\\&c_1(z,t)=\frac{1}{2} i \left[ d_1(z) q_1^* \rho _1^*(z)-a_1(z) q_1^* \rho _1^*(z)\right] , \\&g_1(z,t)=\frac{1}{2} i \left[ h_1(z) q_2^* \rho _2^*(z)-a_1(z) q_2^* \rho _2^*(z)\right] , \\&k_1(z,t)=\frac{1}{4} q_2 q_1^* \rho _1^*(z) \left[ a_1(z)-d_1(z)\right] \rho _2(z), \\&k_2(z,t)=\frac{1}{4} q_1 q_2^* \rho _2^*(z) \left[ a_1(z)-d_1(z)\right] \rho _1(z), \\&b_2(z,t)=\frac{ i \left[ a_1(z)-d_1(z)\right] }{4}\\&\qquad \qquad \qquad \!\!\times \left\{ 2 L \rho _1(z) |q_1|^2 q_1+\Delta _1+i \rho _1(z) q_{1t}\right\} , \\&f_2(z,t)=\frac{i \left[ a_1(z)-h_1(z)\right] }{4}\\&\qquad \qquad \qquad \!\!\times \left[ \Delta _2+i \rho _{2t}(z,t) q_2+i \rho _2(z) q_{2t}\right] , \\&c_2(z,t)=\frac{i \left[ d_1(z)-a_1(z)\right] }{4}\\&\qquad \qquad \qquad \!\!\times \left( 2 L |q_1|^2 q_1^*+2 L |q_2|^2 q_1^*-i q_{1t}^*\right) \rho _1^*(z), \\&g_2(z,t)=\frac{i \left[ d_1(z)-a_1(z)\right] }{4}\\&\qquad \qquad \qquad \!\!\times \left( 2 L |q_2|^2+2 L |q_1|^2 q_2^*-i q_{2t}^*\right) \rho _2^*(z), \\&a_2(z,t)=\frac{1}{4} \left[ d_1(z)-a_1(z)\right] \\&\qquad \qquad \qquad \!\!\times \left[ |q_1|^2 |\rho _1(z)|^2 +|q_2|^2|\rho _2(z)|^2\right] \\&\qquad \qquad \qquad +a_{22}(z)+i L \theta _z(z,t), \\&h_2(z,t)=h_{22}(z)+\frac{1}{4} |q_2|^2 \rho _2^*(z) \\&\qquad \qquad \qquad \!\!\times \left[ a_1(z)-d_1(z)\right] \rho _2(z)-i L \theta _z(z,t), \\&d_2(z,t)=d_2(z)+\frac{1}{4} |q_1|^2 \rho _1^*(z) \\&\qquad \qquad \qquad \!\!\times \left[ a_1(z)-d_1(z)\right] \rho _1(z)-i L \theta _z(z,t), \\&\Delta _1=\left[ 2 L |q_2|^2 \rho _1(z) +i \rho _{1t}(z,t)\right] q_1, \\&\Delta _2=2 L \rho _2(z) |q_2|^2 q_2+2 L |q_1|^2 \rho _2(z) q_2, \end{aligned}$$

the asterisk is the complex conjugate and \(\lambda \) denotes the spectral parameter. Equation (1) can be achieved from the compatibility condition

$$\begin{aligned} U_z-V_t+[\,U,\,V\,]=0, \end{aligned}$$
(4)

where \([\,U,\,V\,]=U\,V-V\,U\). Thus, the Lax pair of Eq. (1) has been derived.

As DT is composed of the eigenfunction and potential transformation, it can be used to construct a series of explicit solutions for the nonlinear evolution equations (NLEEs) from the initial ones in a recursive manner [39, 40], and the procedure of the DT can be achieved by symbolic computation [41, 42]. DT has been used to investigate many NLEEs [39, 40] as a straightforward algorithm. Eigenfunction transformation for Lax Pair (2) can be taken as

$$\begin{aligned} \hat{\varPsi }\!=\!D \varPsi \!=\!\left( \begin{array}{ccc} A_n(z,t) &{} 0 &{} 0 \\ 0 &{} B_n(z,t) &{} 0 \\ 0 &{} 0 &{} C_n(z,t) \end{array} \right) (\lambda I\!-\!S)\varPsi , \nonumber \\ \end{aligned}$$
(5)

where \(n=1,2,3\), and \(A_n(z,t),\,B_n(z,t)\), and \(C_n(z,t)\) are the functions of \(z\) and \(t\) to be determined, \(I\) is the \(3\times 3\) identity matrix, \(S\) is a \(3\times 3\) matrix to be determined, and \(\hat{\varPsi }\) is required to satisfy

$$\begin{aligned} \hat{\varPsi }_t=\hat{U} \hat{\varPsi },\ \ \ \ \hat{\varPsi }_z=\hat{V} \hat{\varPsi }, \end{aligned}$$
(6)

that is,

$$\begin{aligned}&D_t+D U-\hat{U} D=0,\end{aligned}$$
(7)
$$\begin{aligned}&D_z+D V-\hat{V} D=0, \end{aligned}$$
(8)

with

$$\begin{aligned}&\hat{U}=\nonumber \\&\left( \begin{array}{ccc} i L \hat{\theta } _t(z,t)-i \lambda &{} \hat{q}_1 \rho _1(z) &{} \hat{q}_2\rho _2(z) \\ -\hat{q}_1^* \rho _1^*(z) &{} i \lambda (t)-i L\hat{\theta }_t(z,t) &{} 0 \\ -\hat{q}_2^* \rho _2^*(z) &{} 0 &{} i \lambda -i L \hat{\theta } _t(z,t) \end{array} \right) ,\nonumber \\&\hat{V}=\nonumber \\&\left( \begin{array}{ccc} a_1(z) \lambda ^2\!+\!\hat{a}_2(z,t) &{} \lambda \hat{b}_1(z,t)\!+\!\hat{b}_2(z,t) &{} \lambda \hat{f}_1(z,t)\!+\!\hat{f}_2(z,t) \\ \lambda \hat{c}_1(z,t)\!+\!\hat{c}_2(z,t) &{} d_1(z) \lambda ^2\!+\!\hat{d}_2(z,t) &{} \hat{k}_1(z,t) \\ \lambda \hat{g}_1(z,t)\!+\!\hat{g}_2(z,t) &{} \hat{k}_2(z,t) &{} d_1(z) \lambda (t)^2\!+\!\hat{h}_2(z,t) \end{array} \right) ,\nonumber \\ \end{aligned}$$
(9)

and

$$\begin{aligned}&\hat{\theta }(z,t)= \int \left( |\hat{q_1}|^2+|\hat{q_2}|^2\right) \, \mathrm{d}t, \\&\hat{b}_1(z,t)=\frac{1}{2} i \big [a_1(z) \hat{q_1} \rho _1(z)-d_1(z) \hat{q_1} \rho _1(z)\big ],\\&\hat{f}_1(z,t)=\frac{1}{2} i \big [a_1(z) \hat{q_2} \rho _2(z)-h_1(z) \hat{q_2} \rho _2(z)\big ], \\&\hat{c}_1(z,t)=\frac{1}{2} i \big [d_1(z) \hat{q_1}^* \rho _1^*(z)-a_1(z) \hat{q_1}^* \rho _1^*(z)\big ],\\&\hat{g}_1(z,t)=\frac{1}{2} i \big [h_1(z) \hat{q_2}^* \rho _2^*(z)-a_1(z) \hat{q_2}^* \rho _2^*(z)\big ],\\&\hat{b}_2(z,t)=\frac{1}{4} i \big [a_1(z)-d_1(z)\big ]\\&\qquad \qquad \quad \times \Big \{2 L \rho _1(z) |\hat{q_1}|^2 \hat{q_1}+\hat{\Delta _1}+i \rho _1(z) \hat{q}_{1t}\Big \},\\&\hat{f}_2(z,t)=\frac{1}{4} i \big [a_1(z)-h_1(z)\big ]\\&\qquad \qquad \quad \times \big [\hat{\Delta _2}+i \rho _{2t}(z,t) \hat{q_2}+i \rho _2(z) \hat{q}_{2t}\big ],\\&\hat{c}_2(z,t)= \frac{1}{4}i \big [d_1(z)-a_1(z)\big ]\\&\qquad \qquad \qquad \times \!\left( 2 L |\hat{q_1}|^2 \hat{q_1}^*\!+\!2 L |\hat{q_2}|^2 \hat{q_1}^*\!-\!i \hat{q}_{1t}^*\right) \rho _1^*(z),\\&\hat{g}_2(z,t)= \frac{1}{4} i \big [d_1(z)-a_1(z)\big ]\\&\qquad \qquad \qquad \times \!\left( 2 L |\hat{q_2}|^2\!+\!2 L |\hat{q_1}|^2 \hat{q_2}^*-i \hat{q}_{2t}^*\right) \rho _2^*(z),\\&\hat{k}_1(z,t)=\frac{1}{4} \hat{q_2} \hat{q_1}^* \rho _1^*(z) \big [a_1(z)-d_1(z)\big ] \rho _2(z), \\&\hat{k}_2(z,t)=\frac{1}{4} \hat{q_1} \hat{q_2}^* \rho _2^*(z) \big [a_1(z)-d_1(z)\big ] \rho _1(z),\\&\hat{a}_2(z,t)=\frac{1}{4} \big [d_1(z)\!-\!a_1(z)\big ]\\&\qquad \qquad \qquad \times \big [|\hat{q_1}|^2 |\rho _1(z)|^2 +|\hat{q_2}|^2|\rho _2(z)|^2\big ]\\&\qquad \qquad \qquad +\,a_{22}(z)+i L \hat{\theta } _z(z,t),\\&\hat{h}_2(z,t)=\frac{1}{4}|\hat{q_2}|^2 \rho _2^*(z) \big [a_1(z)-d_1(z)\big ] \rho _2(z) _z(z,t)\\&+h_{22}(z)-i L \hat{\theta },\\&\hat{d}_2(z,t)=\frac{1}{4}|\hat{q_1}|^2 \rho _1^*(z) \big [a_1(z)-d_1(z)\big ] \rho _1(z)\\&\qquad \qquad \qquad -i L \hat{\theta } _z(z,t)+d_2(z),\\&\hat{\Delta _1}=\big [2 L |\hat{q_2}|^2 \rho _1(z) +i \rho _{1t}(z,t)\big ] \hat{q_1}, \\&\hat{\Delta _2}=2 L \rho _2(z) |\hat{q_2}|^2 \hat{q_2}+2 L |\hat{q_1}|^2 \rho _2(z) \hat{q_2}, \end{aligned}$$

Then, the matrix \(S\) can be constructed as

$$\begin{aligned} S= H\, \varLambda \, H^{-1}, \end{aligned}$$
(10)

with

$$\begin{aligned}&H=\left( \begin{array}{ccc} \psi _1\,\left( \lambda _1\right) &{} \psi _2^*\,\left( \lambda _1\right) &{} \psi _3^*\,\left( \lambda _1\right) \\ \psi _2\,\left( \lambda _1\right) &{} -\psi _1^*\,\left( \lambda _1\right) &{} 0 \\ \psi _3\,\left( \lambda _1\right) &{} 0 &{} -\psi _1^*\,\left( \lambda _1\right) \end{array} \right) , \nonumber \\&\varLambda =\left( \begin{array}{ccc} \lambda _1 &{} 0 &{} 0 \\ 0 &{} \lambda _1^* &{} 0 \\ 0 &{} 0 &{} \lambda _1^* \end{array} \right) , \end{aligned}$$
(11)

and

$$\begin{aligned}&A(z,t)=\alpha _1(z)\, \exp \Big [-{\int \Delta _3\,\mathrm{d}t}\Big ],\nonumber \\&B(z,t)=\alpha _2(z)\, \exp \Big [{\int \Delta _3\,\mathrm{d}t}\Big ],\nonumber \\&C(z,t)=\alpha _3(z)\, \exp \Big [{\int \Delta _3\,\mathrm{d}t}\Big ] ,\nonumber \\&\Delta _3=\nonumber \\&\quad \frac{4iL\left( \lambda _1-\lambda _1^*\right) ^2|\psi _1|^2\left( |\rho _2(z)|^2|\psi _2|^2\!+\!|\rho _1(z)|^2|\psi _3|^2\right) }{|\rho _1(z)|^2|\rho _2(z)|^2\left( |\psi _1|^2\!+\!|\psi _2|^2\!+\!|\psi _3|^2\right) ^{2}},\nonumber \\ \end{aligned}$$
(12)

where \({[ \psi _1(\lambda _1), \psi _2(\lambda _1), \psi _3(\lambda _1)]}^T\) is the solution of Lax Pair (2) with \(\lambda =\lambda _1,\,\alpha _1(z)\,\alpha _2(z)\) and \(\alpha _3(z)\) are functions of \(z\). Transformations between the new potentials \(\hat{q_1},\,\hat{q_2}\) and the old ones \(q_1,\,q_2\) can be presented as

$$\begin{aligned} \hat{q}_1&= A(z,t) B(z,t)^{-1}\rho _1(z)^{-1} \nonumber \\&\times \left( q_1\rho _1(z)+\frac{4\,\text {Im}\left( \lambda _1\right) \, \psi _1 \psi _2^*}{|\psi _1|^2+|\psi _2|^2+|\psi _3|^2}\right) ,\nonumber \\ \hat{q}_2&= A(z,t)C(z,t)^{-1}\rho _2(z)^{-1} \nonumber \\&\times \left( q_2\rho _2(z)+\frac{4\,\text {Im}\left( \lambda _1\right) \, \psi _1 \psi _3^*}{|\psi _1|^2+|\psi _2|^2+|\psi _3|^2}\right) . \end{aligned}$$
(13)

3 One-soliton solutions of Eq. (1)

In this section, we will construct the one-soliton solutions of Eq. (1). Taking \(q_1=q_2=0\) as the seed solutions of Eq. (1), Lax Pair (2) with \(\lambda =\lambda _1\) can be solved as

$$\begin{aligned}&\psi _1\left( \lambda \right) =c_1 e^{\xi },\ \ \psi _2\left( \lambda \right) =c_2 e^{-\xi },\ \ \ \ \ \psi _3\left( \lambda \right) =c_3 e^{-\xi },\nonumber \\ \end{aligned}$$
(14)

where \(c_1,\,c_2\) and \(c_3\) are arbitrary constants and \(\xi =\int \big [a_1(z) \lambda _1^2+a_{22}(z)\big ] \, \mathrm{d}z-i t \lambda _1 \).

Substituting Eq. (14) into Eq. (13), we can get one-soliton solutions of Eq. (1) as follows:

$$\begin{aligned}&|q_1|=\frac{4 |\text {Im} \left( \lambda _1\right) c_2|}{|\rho _1(z)|\sqrt{|c_2|^2+|c_3|^2}}\, \text {sech} \Bigg [\xi +\xi ^* +\mathrm {ln}\Delta _4\Bigg ],\nonumber \\\end{aligned}$$
(15)
$$\begin{aligned}&|q_2|=\frac{4 |\text {Im} \left( \lambda _1\right) c_3|}{|\rho _2(z)|\sqrt{|c_2|^2+|c_3|^2}}\, \text {sech} \Bigg [\xi +\xi ^* +\mathrm {ln}\Delta _4\Bigg ],\nonumber \\\\&\Delta _4=\frac{|c_1|}{\sqrt{|c_2|^2+|c_3|^2}}.\nonumber \end{aligned}$$
(16)

Some physical quantities such as the amplitude \(A\), velocity \(v\), width \(W\), initial phases \(I_p\), and energy \(E\) are given to characterize the features of propagating solitons:

$$\begin{aligned}&A_1\!=\!\frac{4\, |\text {Im} \left( \lambda _1\right) c_2|}{|\rho _1(z)|\sqrt{|c_2|^2\!+\!|c_3|^2}},\ A_2\!=\!\frac{4\, |\text {Im} \left( \lambda _1\right) c_3|}{|\rho _2(z)|\sqrt{|c_2|^2\!+\!|c_3|^2}}, \nonumber \\&W_1=W_2=\frac{1}{2\, \text {Im}\left( \lambda _1\right) }, \quad I_{p1}=I_{p2}=\frac{1}{2\, \text {Im}\left( \lambda _1\right) } \mathrm {ln}\varDelta _4, \\&v_1=v_2=\frac{\text {Re}\big [a_1(z) \lambda _1^2+a_{22}(z)\big ]}{-\text {Im} \left( \lambda _1\right) },\nonumber \\&E=\frac{32\, |\text {Im}\left( \lambda _1\right) |^2}{|\rho _1(z)|^2}. \end{aligned}$$

From above, we can see that the width and initial phases are both dependent on the imaginary part of \(\lambda _1\), while the amplitude, velocity, and energy are determined by the imaginary part of \(\lambda _1\) and variable coefficients.

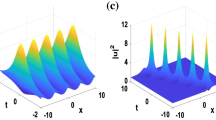
Multi-soliton solutions can be achieved by the iterative algorithm. The dynamic features of the obtained soliton solutions are depicted in Fig. 1 using Eqs. (15)\(-\)(16).

Fig. 1
figure 1

The stable propagation of one-soliton solutions (15)–(16). Parameters are given as follows: \(a_1(z)=z,\,a_{22}(z)=1+i,\,c_1=c_2=1,\,c_3=1+i,\,\rho _1(z)=3+2i,\,\rho _2(z)=2-3i\) and \(\lambda _1=1+2 i\)

Full size image

4 An infinite number of conservation laws

In this section, according to Refs. [43, 44] we present infinitely many independent conservation laws as a further support of the integrability for Eq. (1).

We will introduce two new variables,

$$\begin{aligned} \varGamma _{1}=\frac{\psi _{2}}{\psi _{1}}, \ \ \ \varGamma _{2}=\frac{\psi _{3}}{\psi _{1}}, \end{aligned}$$
(17)

and take derivative of \( \varGamma _{j} \) (\( j=1,2 \)) with respect to \(t\) by the use of Eq. (2) to obtain the following two Riccati-type equations:

$$\begin{aligned}&\varGamma _{1,t} \!=\! -\,q_1^* \rho _1^*(z)\!+\!2\big [i \lambda _1 \!-\! i L\theta _t(z,t) \big ] \varGamma _1- \varGamma _1^2q_1 \rho _1(z)\nonumber \\&\qquad \qquad \!-\,q_2\rho _2(z)\varGamma _1\varGamma _2, \end{aligned}$$
(18)
$$\begin{aligned}&\varGamma _{2,t}\!=\! -\,q_2^* \rho _2^*(z)\!+\!2\big [i \lambda _1 \!-\!i L\theta _t(z,t) \big ] \varGamma _2- \varGamma _1\varGamma _2q_1 \rho _1(z)\nonumber \\&\qquad \qquad -\,q_2\rho _2(z)\varGamma _2^2, \end{aligned}$$
(19)

then multiply Eqs. (18) and (19), respectively, by \( q_1 \) and \(q_2\), and expand \( q_1 \varGamma _1 \) and \( q_2 \varGamma _2 \) in power series of \(1/\lambda \),

$$\begin{aligned} q_1 \varGamma _1 \!=\! \sum _{m=1}^{\infty } {\lambda }^{-m} {\varGamma _{1}}_{m}(z, t), \ \ \ q_2 \varGamma _2 \!=\! \sum _{m=1}^{\infty } {\lambda }^{-m}{\varGamma _{2}}_{m}(z, t), \nonumber \\ \end{aligned}$$
(20)

\( {\varGamma _{1}}_{m} \) and \( {\varGamma _{2}}_{m} \) (\( m= 1, 2, \ldots \)) are determined by

$$\begin{aligned}&{\varGamma _{1}}_{1} = -\frac{i}{2}|q_1|^{2}\left( \rho _1\right) ^*(z), \ \ \ {\varGamma _{2}}_{1} = - \frac{i}{2}|q_2|^{2}\left( \rho _2\right) ^*(z), \\&\varGamma _{12} = -\frac{1}{4}\,q_1\,q_{1t}^* \left( \rho _1\right) ^*(z)- \frac{i}{2}\,|q_1|^2\,\left( \rho _1\right) ^*(z)L\theta _t(z,t), \\&{\varGamma _{2}}_{2} = -\frac{1}{4}\,q_2\,q_{2t}^* \left( \rho _2\right) ^*(z)- \frac{i}{2}\,|q_2|^2\,\left( \rho _2\right) ^*(z)L\theta _t(z,t), \\&{\varGamma _{1}}_{m+1} =-\frac{i}{2}\Big [\rho _1(z)\sum _{k=1}^{m-1} {\varGamma _{1}}_{m-1-k}{\varGamma _{1}}_{k} +\rho _2(z) \sum _{k=1}^{m-1}\\&\quad {\varGamma _{1}}_{m-k}{\varGamma _{2}}_{k}\!+\! \left( \frac{\varGamma _{1m}}{q_1}\right) _t\,q_1 \!+\!2i\,L\theta _t(z,t)\,{\varGamma _{1}}_{m} \Big ] \ (m \!>\! 2), \\&{\varGamma _{2}}_{m+1} =-\frac{i}{2}\Bigg [\rho _2(z)\sum _{k=1}^{m-1} {\varGamma _{2}}_{m-1-k}{\varGamma _{2}}_{k} +\rho _1(z) \sum _{k=1}^{m-1}\\&{\varGamma _{1}}_{m-k}{\varGamma _{2}}_{k}\!+|! \left( \frac{\varGamma _{2m}}{q_2}\right) _t\,q_2 \!+\!2i\,L\theta _t(z,t)\,{\varGamma _{2}}_{m} \Bigg ] \ (m \!>\! 2). \end{aligned}$$

By the compatibility condition \( \left( {\log \psi _{1}}\right) _{zt} = \left( {\log \psi _{1}}\right) _{tz} \) yields the following equation in the form of conservation law:

$$\begin{aligned}&\Big \{ \big [\!-\!i \lambda _1 +i L\theta _t(z,t) \big ]\!+\!q_1\,\varGamma _{1}\rho _1(z)\!+\!q_2\,\varGamma _{2}\rho _2(z)\Big \}_{t}\! \!\nonumber \\&\quad =\Big \{a_1(z) \lambda ^2+a_2(z,t) + \big [\lambda b_1(z,t)+b_2(z,t)\big ] \varGamma _1 \nonumber \\&\quad \quad +\big [\lambda f_1(z,t)+f_2(z,t)\Big \}_{z}. \end{aligned}$$
(21)

By substituting Eq. (20) into Eq. (21) and equating the terms with the same power of \( 1/\lambda \), we can obtain a sufficiently large number of conservation laws: \( i\,\frac{\partial \rho _{k}}{\partial t} = \frac{\partial J_{k}}{\partial z} \,(k=1,2,\ldots )\), where \( \rho _{k} \) and \( J_{k}\) (\(k=1,2,\ldots \)) are the conserved densities and associated fluxes, respectively.

5 Conclusions

Twin-core nonlinear fibers and waveguides, i.e., couplers, have become a current interest in nonlinear optics [28]. In this paper, by virtue of DT (5) and symbolic computation, Eq. (1) describing the effects of quintic nonlinearity on the ultrashort optical pulse propagation in non-Kerr media has been investigated. Lax Pair (2) of Eq. (1) has been presented, and the corresponding DT (5) has been constructed. Moreover, one-soliton solutions, i.e., Solutions (15)–(16), have been obtained and an infinite number of conservation laws, i.e., Expressions (20)–(21), have also been derived. Using Solutions (15)–(16), the dynamic features of the soliton solutions have been displayed in Figure 1. Some physical quantities such as the amplitude, velocity, width, initial, phases, and energy are also, respectively, analyzed. These results might be of some value for the ultrashort optical pulse propagation in the non-Kerr media.