1 Introduction

Mathematical modeling in theoretical ecology has gained a lot of importance during the last few decades. It improves understanding of the natural world by revealing how the dynamics of species populations are often based on fundamental biological conditions and processes. Mathematical modeling also provides understanding of the mechanisms that influence the growth of populations and their existence and stability. The first theoretical treatment of population dynamics was presented by Malthus [29]. Verhulst [47] formed a mathematical model based on logistic equation. The most major advancement in population dynamics was presented by Lotka [27] and Volterra [48], they first proposed the mathematical model of predator–prey system. Many ecologists put greater interest on competition in population dynamics. There is a classical model of competition due to Lotka and Volterra. The classical theory of ecological competition between two or more species attributed to Lotka-Volterra is an extension of the basic logistic model of single species growth that came from Verhulst. The Lotka-Volterra competition model is an interference competition model: two species are assumed to diminish each other’s per capita growth rate by direct interference. Prey–predator models are also discussed by Erbe [9], Freedman [10–12], Maiti et al. [30–32], Ruan and Xiao [42], Kuznetsov [19]. There are many other kind of predator–prey population models with different kinds of functional responses [13, 17, 18, 22, 23, 26, 35, 44–46].

Harvesting policy and bio-economic modeling of multi-species fisheries and wildlife management is becoming a very important field in population dynamics. These bio-economic models assist natural resource managers in controling appropriate level of stocks and catches. Most of the existing literatures of multi-species fisheries derive from the work of Clark [6, 7] who introduced economic and biological aspects of renewable resource management. He assumed that each species would follow a logistic growth law in the absence of harvesting, and the harvesting rate for each species is proportional to both its stock level and harvesting effort. His work was extended by Mesterton-Gibbons [33], who discussed the optimal approach to equilibrium. There are many other researchers such as Ragozin and Brown [40], Wilen and Brown [49], etc. who had investigated the optimal policy for harvesting of predator–prey model. Chaudhuri [3] had formulated an optimal control problem for combined harvesting of two competing species. Later it was extended by Mesterton-Gibbons [34]. Predator–prey model with combined harvesting has been also discussed by Hannesson [16], Chaudhuri and Roy [4], Samanta et al. [43], Chen and Hsui [5], Palma and Olivares [37], Rebaza [41], Bhattacharya and Begum [2]. Das et al. [8] presented a predator–prey model in presence of toxicity and discussed optimal harvesting policy using Pontryagin’s maximal principle [39]. Li and Wang [24], Li et al. [25] presented a stochastic logistic population model with optimal harvesting policy. Recently Zhang et al. [51] have studied Hopf bifurcation of a predator–prey system with predator harvesting and two delays using local parameterization method of the differential-algebraic systems. Lv et al. [28] have analysed two Holling type II predator–prey models with continuous threshold harvesting, which represents situations when the harvesting policy needs to be applied only when the harvest population is above the threshold \(T\).

Most of the researchers in theoretical ecology have developed their models based on the assumption that the biological parameters are precisely known. But in reality the scenario is different. Always the values of all parameters can not be known precisely for the lack of information, lack of data, mistakes in the measurement process and determining the initial conditions. From this point of view models with imprecise parameters are more realistic and helpful to overcome the limitations. There are different approaches to handle such models with imprecise parameters such as stochastic approach, fuzzy approach, fuzzy-stochastic approach, etc. In stochastic approach the imprecise parameters are replaced by random variables with known probability distributions. In fuzzy approach the imprecise parameters are replaced by fuzzy sets with known membership functions. In fuzzy-stochastic approach some parameters are as fuzzy in nature, and rest of the parameters are taken as random variables. However, it is very difficult to construct a suitable membership function or a suitable probability distribution for each of the imprecise biological parameters. Some researchers have introduced fuzzy models in predator–prey population biology such as Bassanezi et al. [1], Peixoto et al. [38], Guo et al. [15], etc. Pal et al. [36] presented an optimal harvesting predator–prey system with imprecise biological parameters and discussed bio-economic equilibrium and optimal harvesting policy.

In this paper, we have considered a two species competition model with combined harvesting. To make the model more realistic we have considered imprecise biological parameters and have tried to develop a method to discuss the dynamical behaviour of the model. Some important definitions are discussed in Sect. 2. The construction of our model system is sketched in Sects. 3 and 4. Section 5 deals with the equilibrium points of the system, their existence and stability analysis. We have also analysed the bionomic equilibrium of the harvesting model in Sect. 6. Next we have derived the equilibrium solution of the control problem, and dynamical optimization of the harvest policy is then carried out taking combined harvesting effort as a dynamic variable by invoking Pontryagin’s Maximum Principle in Sect. 7. Our important analytic results are numerically verified in the Sect. 8. Finally, Sect. 9 contains the general discussions of the paper and ecological implications of our mathematical findings.

2 Basic definitions

We give some basic definitions of the interval number and interval-valued function which have been used further in this paper.

Definition 1

(Interval number). An interval number \(A\) is presented by closed interval \([a_l,a_u]\) and defined as \(A=[a_l,a_u]=\{x: a_l\le x\le a_u, x\in {\mathbb {R}}\},\) where \({\mathbb {R}}\) is the set of real numbers, and \(a_l, a_u\) are the lower and upper limits of the interval number, respectively. We can represent every real number in the terms of interval number as \([a,a]\) for all \(a\in {\mathbb {R}}.\)

Some arithmetic operations for any two interval numbers \(A=[a_l,a_u]\) and \(B=[b_l,b_u]\) are defined as follows:

$$\begin{aligned}&\!\!\!Addition: A\!+B=[a_l,a_u]+[b_l,b_u]=[a_{l}+b_{l},a_{u}+b_{u}].\\&\!\!\!Subtraction: A-B=[a_l,a_u]-[b_l,b_u]=[a_{l}-b_{l},a_{u}-b_{u}].\\&\!\!\!Scalar multiplication:\alpha A=\alpha [a_l,a_u]=[\alpha a_{l},\alpha a_{u}]. \end{aligned}$$

Definition 2

(Interval-valued function). Let \(a\!>\!0, b\!>\!0\) and consider the interval \([a,b].\) The interval \([a,b]\) can be represented by a function \(g(p)=a^{(1-p)}b^p\) for \(p\in [0,1].\) This function is called interval-valued function.

3 Mathematical model

Let us consider the following competition model between two interacting species:

$$\begin{aligned} \frac{dx(t)}{dt}&= x(t)[r_{1}-b_{11}x(t)-b_{12}y(t)]\nonumber \\ \frac{dy(t)}{dt}&= y(t)[r_{2}-b_{22}y(t)-b_{21}x(t)]. \end{aligned}$$
(1)

Here \(x(t)\) and \(y(t)\) denote the population density of the first species and the second species, respectively.

Here \(r_{i}, b_{ij} (i,j=1,2)\) are all positive constants, and \(r_{i}\) are the linear birth rates, \(b_{ii}\) are the co-efficients of intraspecific competition, \(b_{ij} (i\ne j)\) measure the degree to which the presence of species \(j\) affects the growth of species \(i.\)

Assuming that there is demand for all the species in the market so the harvesting of both the species are carried out. Let both the species are subjected to combined harvesting effort \(E\). Then the previous model becomes

$$\begin{aligned} \frac{dx(t)}{dt}&= x(t)[r_{1}\,-\,b_{11}x(t)\,-\,b_{12}y(t)]\,-\,q_1Ex(t)\nonumber \\ \frac{dy(t)}{dt}&\!=y(t)[r_{2}\!-\!b_{22}y(t)\!-\!b_{21}x(t)]\!-\!q_2Ey(t), \end{aligned}$$
(2)

where \(q_1\) and \(q_2\) are the catchability coefficients of two species, respectively.

4 Imprecise competition model with two species

Now, if any of the parameters \(r_{i}, b_{ij}\ (i,j=1,2)\) are imprecise, i.e. if any parameter is interval number rather than a single value, then it is not so easy to convert the equations to the standard form and analyse the dynamical behaviour of the system. For imprecise coefficients, we represent the system with interval coefficients as described below.

4.1 Two species competition model with interval coefficients

Let \(\hat{r}_{i}, \hat{b}_{ij}\ (i,j=1,2)\) be the interval counterparts of \(r_{i}, b_{ij}\ (i,j=1,2)\), respectively. Then the two species competition model with combined harvesting effort \(E\) becomes:

$$\begin{aligned} \frac{dx}{dt}&= x(t)[\hat{r}_{1}-\hat{b}_{11}x(t)-\hat{b}_{12}y(t)]-q_1Ex(t)\nonumber \\ \frac{dy}{dt}&= y(t)[\hat{r}_{2}-\hat{b}_{22}y(t)-\hat{b}_{21}x(t)]-q_2Ey(t), \end{aligned}$$
(3)

where \(\hat{r}_{i}=[r_{il},r_{iu}], \hat{b}_{ij}=[b_{ijl},b_{iju}]\) and \(r_{il}>0, b_{ijl}>0 \ \ \ (i,j=1,2)\).

4.2 Two species competition model with parametric interval coefficients

For fixed \(m,\) let us consider the interval-valued function \(g_m(p)=a_m^{(1-p)}b_m^p\) for \(p \in [0,1]\) for an interval \([a_m,b_m].\) Since \(g_m(p)\) is a strictly increasing and continuous function, the system (3) can be written in the parametric form as follows:

$$\begin{aligned} \frac{dx(t;p)}{dt}&= x(t)[(r_{1l})^{(1-p)}(r_{1u})^{p}-(b_{11l})^{(1-p)}(b_{11u})^{p}x(t)\nonumber \\&-\,(b_{12l})^{(1-p)}(b_{12u})^{p}y(t)]-q_1Ex(t)\nonumber \\ \frac{dy(t;p)}{dt}&= y(t)[(r_{2l})^{(1-p)}(r_{2u})^{p}-(b_{22l})^{(1-p)}(b_{22u})^{p}y(t)\nonumber \\&-\,(b_{21l})^{(1-p)}(b_{21u})^{p}x(t)]-q_2Ey(t), \end{aligned}$$
(4)

where \(p \in [0,1].\)

The reason behind this is as follows: In a fine-grained environment, heterogeneity appears as an average, in a coarse-grained environment as alternatives and hence uncertainty. Here selection maximizes \(a_m^{(1-p)}b_m^p\) for \(p \in [0,1],\) the value of \(p\) depends on the underlying environment [21].

5 Equilibrium points: their existence and stability

In this section we will study the existence and stability behaviour of the system (4) at equilibrium points. The equilibrium points of the model system (4) are given below.

  • 1. Trivial Equilibrium : \(E_{0}(0,0).\)

  • 2. Axial Equilibrium : (a) \(E_{1}(\bar{x},0),\) where \(\bar{x}=\frac{(r_{1l})^{(1-p)}(r_{1u})^{p}-q_1 E}{(b_{11l})^{(1-p)}(b_{11u})^{p}},\) (b) \(E_{2}(0,\tilde{y}),\) where \(\tilde{y}=\frac{(r_{2l})^{(1-p)}(r_{2u})^{p}-q_2 E}{(b_{22l})^{(1-p)}(b_{22u})^{p}}.\)

  • 3. Interior Equilibrium : \(E^{*}(x^{*},y^{*}),\) where

$$\begin{aligned} x^{*}&= \frac{1}{[(b_{11l})^{(1-p)}(b_{11u})^{p}(b_{22l})^{(1-p)}(b_{22u})^{p}-(b_{12l})^{(1-p)}(b_{12u})^{p}(b_{21l})^{(1-p)}(b_{21u})^{p}]}[\{(b_{22l})^{(1-p)}(b_{22u})^{p}\\&(r_{1l})^{(1-p)}(r_{1u})^{p}-(b_{12l})^{(1-p)}(b_{12u})^{p}(r_{2l})^{(1-p)}(r_{2u})^{p}\}\\&+\,E\{(b_{12l})^{(1-p)}(b_{12u})^{p}q_2-(b_{22l})^{(1-p)}(b_{22u})^{p}q_1\}],\\ y^{*}&= \frac{1}{[(b_{11l})^{(1-p)}(b_{11u})^{p}(b_{22l})^{(1-p)}(b_{22u})^{p}-(b_{12l})^{(1-p)}(b_{12u})^{p}(b_{21l})^{(1-p)}(b_{21u})^{p}]}[\{(b_{11l})^{(1-p)}(b_{11u})^{p}\\&(r_{2l})^{(1-p)}(r_{2u})^{p}-(b_{21l})^{(1-p)}(b_{21u})^{p}(r_{1l})^{(1-p)}(r_{1u})^{p}\}\\&+\,E\{(b_{21l})^{(1-p)}(b_{21u})^{p}q_1-(b_{11l})^{(1-p)}(b_{11u})^{p}q_2\}]. \end{aligned}$$

5.1 Trivial equilibrium

Now, the variational matrix of system (4) at \(E_0(0,0)\) is given by

$$\begin{aligned}&\!\!\!V\left( E_0\right) \\&=\left( \begin{array}{ll} (r_{1l})^{(1-p)}(r_{1u})^{p}-q_1 E &{} 0 \\ 0 &{} (r_{2l})^{(1-p)}(r_{2u})^{p}-q_2 E \end{array}\right) \!. \end{aligned}$$

Therefore, eigenvalues of the characteristic equation of \(V(E_0)\) are \(\lambda _1=(r_{1l})^{(1-p)}(r_{1u})^{p}-q_1 E, \lambda _2=(r_{2l})^{(1-p)}(r_{2u})^{p}-q_2 E.\) Now, \(E_0\) is stable if \(\lambda _1<0\) and \(\lambda _2<0\), i.e. \((r_{1l})^{(1-p)}(r_{1u})^{p}-q_1 E<0\) and \((r_{2l})^{(1-p)}(r_{2u})^{p}-q_2 E<0\) which implies that \(E>\frac{1}{q_1}(r_{1l})^{(1-p)}(r_{1u})^{p}\) and \(E>\frac{1}{q_2}(r_{2l})^{(1-p)}(r_{2u})^{p}.\) So, we come to the following theorem:

Theorem 1

The trivial equilibrium \(E_0(0,0)\) of the system (4) is locally asymptotically stable if \(E>\max \left\{ \frac{1}{q_1}(r_{1l})^{(1-p)}(r_{1u})^{p}, \frac{1}{q_2}(r_{2l})^{(1-p)}(r_{2u})^{p}\right\} .\)

5.2 Axial equilibrium

(a) \(E_1(\bar{x},0)\) exists only when \((r_{1l})^{(1-p)}(r_{1u})^{p}-q_1 E>0,\), i.e. \(E<\frac{1}{q_1}(r_{1l})^{(1-p)}(r_{1u})^{p}.\) Now, the variational matrix of system (4) at \(E_1(\bar{x},0)\) is given by

$$\begin{aligned} V\left( E_1\right) = \left( \begin{matrix} -(b_{11l})^{(1-p)}(b_{11u})^{p}\bar{x} &{} -(b_{12l})^{(1-p)}(b_{12u})^{p}\bar{x} \\ 0 &{} (r_{2l})^{(1-p)}(r_{2u})^{p}-(b_{21l})^{(1-p)}(b_{21u})^{p}\bar{x}-q_2 E\end{matrix}\right) \end{aligned}$$

Therefore, eigenvalues of the characteristic equation of \(V(E_1)\) are \(\lambda _1=-(b_{11l})^{(1-p)}(b_{11u})^{p}\bar{x}<0, \lambda _2=(r_{2l})^{(1-p)}(r_{2u})^{p}-(b_{21l})^{(1-p)}(b_{21u})^{p}\bar{x}-q_2 E.\) It is clear that \(\lambda _1\) is negative. Now, \(E_1\) is stable if \(\lambda _2<0,\) i.e. \((r_{2l})^{(1-p)}(r_{2u})^{p}-(b_{21l})^{(1-p)}(b_{21u})^{p}\bar{x}-q_2 E<0\) which implies that \(E>\frac{1}{q_2}[(r_{2l})^{(1-p)}(r_{2u})^{p}-(b_{21l})^{(1-p)}(b_{21u})^{p}\bar{x}].\) So, we come to the following theorem:

Theorem 2

The axial equilibrium \(E_1(\bar{x},0)\) of the system (4) exists and is locally asymptotically stable if \(\frac{1}{q_2}[(r_{2l})^{(1-p)}(r_{2u})^{p}-(b_{21l})^{(1-p)}(b_{21u})^{p}\bar{x}]<E<\frac{1}{q_1}(r_{1l})^{(1-p)}(r_{1u})^{p}.\) Then the trivial equilibrium \(E_0(0,0)\) becomes unstable.

(b) \(E_2(0,\tilde{y})\) exists only when \((r_{2l})^{(1-p)}(r_{2u})^{p}-q_2 E>0,\) i.e. \(E<\frac{1}{q_2}(r_{2l})^{(1-p)}(r_{2u})^{p}.\) Now, the variational matrix of system (4) at \(E_2(0,\tilde{y})\) is given by

$$\begin{aligned} V\left( E_2\right) =\left( \begin{matrix} (r_{1l})^{(1-p)}(r_{1u})^{p}-(b_{12l})^{(1-p)}(b_{12u})^{p}\tilde{y}-q_1 E &{} 0 \\ -(b_{21l})^{(1-p)}(b_{21u})^{p}\tilde{y} &{} -(b_{22l})^{(1-p)}(b_{22u})^{p}\tilde{y} \end{matrix}\right) \end{aligned}$$

Therefore, eigenvalues of the characteristic equation of \(V(E_2)\) are \(\lambda _1=(r_{1l})^{(1-p)}(r_{1u})^{p}-(b_{12l})^{(1-p)}(b_{12u})^{p} \tilde{y}-q_1 E, \lambda _2=-(b_{22l})^{(1-p)}(b_{22u})^{p}\tilde{y}<0.\) It is clear that \(\lambda _2\) is negative. Now, \(E_2\) is stable if \(\lambda _1<0,\) i.e. \((r_{1l})^{(1-p)}(r_{1u})^{p}-(b_{12l})^{(1-p)}(b_{12u})^{p}\tilde{y}-q_1 E<0\) which implies that \(E>\frac{1}{q_1}[(r_{1l})^{(1-p)}(r_{1u})^{p}-(b_{12l})^{(1-p)}(b_{12u})^{p}\tilde{y}].\) So, we come to the following theorem:

Theorem 3

The axial equilibrium \(E_2(0,\tilde{y})\) of the system (4) exists and is locally asymptotically stable if \(\frac{1}{q_1}[(r_{1l})^{(1-p)}(r_{1u})^{p}-(b_{12l})^{(1-p)}(b_{12u})^{p}\tilde{y}]<E<\frac{1}{q_2}(r_{2l})^{(1-p)}(r_{2u})^{p}.\) Then the trivial equilibrium \(E_0(0,0)\) becomes unstable.

5.3 Interior equilibrium

\(E^*(x^*,y^*)\) exists only when

$$\begin{aligned}&(i)(b_{11l})^{(1-p)}(b_{11u})^{p}(b_{22l})^{(1-p)}(b_{22u})^{p}\\&>(b_{12l})^{(1-p)}(b_{12u})^{p}(b_{21l})^{(1-p)}(b_{21u})^{p},\\&(ii)\{(b_{22l})^{(1-p)}(b_{22u})^{p}(r_{1l})^{(1-p)}(r_{1u})^{p}\\&-\,(b_{12l})^{(1-p)}(b_{12u})^{p}(r_{2l})^{(1-p)}(r_{2u})^{p}\}\\&+\,E\{(b_{12l})^{(1-p)}(b_{12u})^{p}q_2-(b_{22l})^{(1-p)}(b_{22u})^{p}q_1\}>0,\\&(iii)\{(b_{11l})^{(1-p)}(b_{11u})^{p}(r_{2l})^{(1-p)}(r_{2u})^{p}\\&-\,(b_{21l})^{(1-p)}(b_{21u})^{p}(r_{1l})^{(1-p)}(r_{1u})^{p}\}\\&+\,E\{(b_{21l})^{(1-p)}(b_{21u})^{p}q_1-(b_{11l})^{(1-p)}(b_{11u})^{p}q_2\}>0, \end{aligned}$$

or

$$\begin{aligned}&(iv)(b_{11l})^{(1-p)}(b_{11u})^{p}(b_{22l})^{(1-p)}(b_{22u})^{p}\\&<(b_{12l})^{(1-p)}(b_{12u})^{p}(b_{21l})^{(1-p)}(b_{21u})^{p},\\&(v)\{(b_{22l})^{(1-p)}(b_{22u})^{p}(r_{1l})^{(1-p)}(r_{1u})^{p}\\&-\,(b_{12l})^{(1-p)}(b_{12u})^{p}(r_{2l})^{(1-p)}(r_{2u})^{p}\}\\&+\,E\{(b_{12l})^{(1-p)}(b_{12u})^{p}q_2-(b_{22l})^{(1-p)}(b_{22u})^{p}q_1\}<0,\\&(vi)\{(b_{11l})^{(1-p)}(b_{11u})^{p}(r_{2l})^{(1-p)}(r_{2u})^{p}\\&-\,(b_{21l})^{(1-p)}(b_{21u})^{p}(r_{1l})^{(1-p)}(r_{1u})^{p}\}\\&+\,E\{(b_{21l})^{(1-p)}(b_{21u})^{p}q_1-(b_{11l})^{(1-p)}(b_{11u})^{p}q_2\}<0. \end{aligned}$$

Now, the variational matrix of system (4) at \(E^*(x^*,y^*)\) is given by

$$\begin{aligned}&\!\!\!V\left( E^*\right) \\&~=\left( \begin{matrix} -(b_{11l})^{(1-p)}(b_{11u})^{p}x^* &{} -(b_{12l})^{(1-p)}(b_{12u})^{p}x^* \\ -(b_{21l})^{(1-p)}(b_{21u})^{p}y^* &{} -(b_{22l})^{(1-p)}(b_{22u})^{p}y^* \end{matrix}\right) \!. \end{aligned}$$

Therefore, the characteristic equation of \(V(E^*)\) is given by

$$\begin{aligned} \lambda ^{2}+ A_1\lambda +A_2=0, \end{aligned}$$
(5)

where

$$\begin{aligned} A_1=(b_{11l})^{(1-p)}(b_{11u})^{p}x^*+(b_{22l})^{(1-p)}(b_{22u})^{p}y^* \end{aligned}$$

and

$$\begin{aligned} A_2&= [(b_{11l})^{(1-p)}(b_{11u})^{p}(b_{22l})^{(1-p)}(b_{22u})^{p}\\&-\, (b_{12l})^{(1-p)}(b_{12u})^{p}(b_{21l})^{(1-p)}(b_{21u})^{p}]x^*y^*. \end{aligned}$$

It is clear that \(A_1>0.\) Now, \(E^*\) is locally asymptotically stable if \(A_2>0,\) i.e. \((b_{11l})^{(1-p)}(b_{11u})^{p}(b_{22l})^{(1-p)} (b_{22u})^{p}>(b_{12l})^{(1-p)}(b_{12u})^{p}(b_{21l})^{(1-p)}(b_{21u})^{p}.\)

So, we come to the following theorem:

Theorem 4

The interior equilibrium \(E^*(x^*,y^*)\) of the system (4) exists and is locally asymptotically stable if

$$\begin{aligned}&(i)(b_{11l})^{(1-p)}(b_{11u})^{p}(b_{22l})^{(1-p)}(b_{22u})^{p}\\&>(b_{12l})^{(1-p)}(b_{12u})^{p}(b_{21l})^{(1-p)}(b_{21u})^{p}\\&(ii)\{(b_{22l})^{(1-p)}(b_{22u})^{p}(r_{1l})^{(1-p)}(r_{1u})^{p}\\&-\,(b_{12l})^{(1-p)}(b_{12u})^{p}(r_{2l})^{(1-p)}(r_{2u})^{p}\}\\&+\,E\{(b_{12l})^{(1-p)}(b_{12u})^{p}q_2-(b_{22l})^{(1-p)}(b_{22u})^{p}q_1\}>0\\&(iii)\{(b_{11l})^{(1-p)}(b_{11u})^{p}(r_{2l})^{(1-p)}(r_{2u})^{p}\\&-\,(b_{21l})^{(1-p)}(b_{21u})^{p}(r_{1l})^{(1-p)}(r_{1u})^{p}\}\\&+\,E\{(b_{21l})^{(1-p)}(b_{21u})^{p}q_1-(b_{11l})^{(1-p)}(b_{11u})^{p}q_2\}>0. \end{aligned}$$

Observations: Yedavalli and Devarakondathe [50] have used ‘qualitative stability’ concept in the standard uncertain matrix theory as a means of achieving ‘robust stability’ for a complex community composed of many species, numerous interactions take place. They have studied it as a ‘sufficient condition’ for checking the robust stability of a class of interval matrices (with the elements being uncertain varying in some given intervals). Here we have studied ‘robust stability’ for a two species competition model with combined harvesting using imprecise biological parameter values \(\hat{r}_i = (r_{il})^{(1-p)}(r_{iu})^{p},\) \(\hat{b}_{ij} = (b_{ijl})^{(1-p)}(b_{iju})^{p}\) \((i,j=1,2)\) and \(p \in [0,1]\) defined in (4). For a particular value of \(p \in [0,1]\) we get the ‘non-robust stability (classical stability)’ behaviour.

6 Bionomic equilibrium

To discuss the bionomic equilibrium of the imprecise two species competition model (4), we consider the following parameters.

  • \(c :\) fishing cost per unit effort,

  • \(p_1 :\) price per unit biomass of the first species \((x),\)

  • \(p_2 :\) price per unit biomass of the second species \((y).\)

The economic rent ( net revenue ) at any time is given by

$$\begin{aligned} R=(p_1q_1x+p_2q_2y-c)E. \end{aligned}$$
(6)

The interior equilibrium solution of the system (4) occurs at a point on the line given by

$$\begin{aligned}&x[q_1(b_{21l})^{(1-p)}(b_{21u})^{p}-q_2(b_{11l})^{(1-p)}(b_{11u})^{p}]\nonumber \\&+\,y[q_1(b_{11l})^{(1-p)}(b_{11u})^{p}\nonumber \\&-\,q_2(b_{12l})^{(1-p)}(b_{12u})^{p}]=q_1(r_{2l})^{(1-p)}(r_{2u})^{p}\nonumber \\&-\,q_2(r_{1l})^{(1-p)}(r_{1u})^{p} \end{aligned}$$
(7)

in the first quadrant of the phase plane.

The biological equilibrium line (7) meets the x-axis and the y-axis at \((\hat{x},0)\) and \((0,\hat{y}),\) respectively, where

$$\begin{aligned} \hat{x}&= \frac{q_1(r_{2l})^{(1-p)}(r_{2u})^{p}-q_2(r_{1l})^{(1-p)}(r_{1u})^{p}}{q_1(b_{21l})^{(1-p)}(b_{21u})^{p}-q_2(b_{11l})^{(1-p)}(b_{11u})^{p}},\nonumber \\ \hat{y}&= \frac{q_1(r_{2l})^{(1-p)}(r_{2u})^{p}-q_2(r_{1l})^{(1-p)}(r_{1u})^{p}}{q_1(b_{11l})^{(1-p)}(b_{11u})^{p}-q_2(b_{12l})^{(1-p)}(b_{12u})^{p}}.\nonumber \\ \end{aligned}$$
(8)

Now, \(\hat{x}>0\) and \(\hat{y}>0\) if

$$\begin{aligned}&q_1(r_{2l})^{(1-p)}(r_{2u})^{p}>q_2(r_{1l})^{(1-p)}(r_{1u})^{p},\\&q_1(b_{21l})^{(1-p)}(b_{21u})^{p}>q_2(b_{11l})^{(1-p)}(b_{11u})^{p},\\&q_1(b_{11l})^{(1-p)}(b_{11u})^{p}>q_2(b_{12l})^{(1-p)}(b_{12u})^{p}, \end{aligned}$$

or

$$\begin{aligned}&q_1(r_{2l})^{(1-p)}(r_{2u})^{p}<q_2(r_{1l})^{(1-p)}(r_{1u})^{p},\\&q_1(b_{21l})^{(1-p)}(b_{21u})^{p}<q_2(b_{11l})^{(1-p)}(b_{11u})^{p},\\&q_1(b_{11l})^{(1-p)}(b_{11u})^{p}<q_2(b_{12l})^{(1-p)}(b_{12u})^{p}. \end{aligned}$$

The bionomic equilibrium of the imprecise two species harvesting is given by (7) together with the condition

$$\begin{aligned} R=(p_1q_1x+p_2q_2y-c)E=0, \end{aligned}$$
(9)

which is referred to as the ‘zero-profit line’.

As long as \((p_1q_1x+p_2q_2y-c)<0\) for all points on the equilibrium line (7), the fishery remains unexploited because it fails to produce any positive economic revenue.

To find the bionomic equilibrium, there may arise three cases:

  • Case I : When the bionomic equilibrium is established at a point \((x_\infty ,0)\) leading to the complete extinction of second species. As a result, the fishing of the second species is not practicable, and only the fishing of first prey is possible (Fig. 1). Here,

    $$\begin{aligned} x_\infty =\frac{c}{p_1q_1} \end{aligned}$$

    provided that

    $$\begin{aligned} c=\frac{p_1q_1[q_1(r_{2l})^{(1-p)}(r_{2u})^{p}\!-\!q_2(r_{1l})^{(1-p)}(r_{1u})^{p}]}{q_1(b_{21l})^{(1-p)}(b_{21u})^{p}-q_2(b_{11l})^{(1-p)}(b_{11u})^{p}}\!,\\ \end{aligned}$$

    with either

    $$\begin{aligned}&q_1(r_{2l})^{(1-p)}(r_{2u})^{p}>q_2(r_{1l})^{(1-p)}(r_{1u})^{p},\nonumber \\&q_1(b_{21l})^{(1-p)}(b_{21u})^{p}>q_2(b_{11l})^{(1-p)}(b_{11u})^{p},\nonumber \\&\qquad \qquad \qquad \qquad \qquad \quad \hbox {or}\nonumber \\&q_1(r_{2l})^{(1-p)}(r_{2u})^{p}<q_2(r_{1l})^{(1-p)}(r_{1u})^{p},\nonumber \\&q_1(b_{21l})^{(1-p)}(b_{21u})^{p}<q_2(b_{11l})^{(1-p)}(b_{11u})^{p}. \end{aligned}$$
    (10)

  • Case II : When the bionomic equilibrium occurs at a point \((0,y_\infty )\) resulting in the complete extinction of first species. As a result, the fishing of the first species is not practicable, and only the fishing of first prey is possible (Fig. 2). Here,

    $$\begin{aligned} y_\infty =\frac{c}{p_2q_2} \end{aligned}$$

    provided that,

    $$\begin{aligned} c\!=\!\frac{p_2q_2[q_1(r_{2l})^{(1-p)}(r_{2u})^{p}-q_2(r_{1l})^{(1-p)}(r_{1u})^{p}]}{q_1(b_{11l})^{(1-p)}(b_{11u})^{p}\!-\!q_2(b_{12l})^{(1-p)}(b_{12u})^{p}}\!,\\ \end{aligned}$$

    with either

    $$\begin{aligned}&q_1(r_{2l})^{(1-p)}(r_{2u})^{p}>q_2(r_{1l})^{(1-p)}(r_{1u})^{p},\\&q_1(b_{11l})^{(1-p)}(b_{11u})^{p}>q_2(b_{12l})^{(1-p)}(b_{12u})^{p},\nonumber \\&\qquad \qquad \qquad \qquad \qquad \quad \hbox {or}\nonumber \\&q_1(r_{2l})^{(1-p)}(r_{2u})^{p}<q_2(r_{1l})^{(1-p)}(r_{1u})^{p},\nonumber \\&q_1(b_{11l})^{(1-p)}(b_{11u})^{p}<q_2(b_{12l})^{(1-p)}(b_{12u})^{p}. \end{aligned}$$
    (11)

  • Case III : When the bionomic equilibrium is established at a point \((x_\infty ,y_\infty )\) where \(x_\infty >0\) and \(y_\infty >0.\) As a result, the fishing of the both species (first and second) is possible (Fig. 3). Here

Fig. 1
figure 1

The ‘biological equilibrium line’ and the ‘zero-profit line’ for Case I

Full size image
Fig. 2
figure 2

The ‘biological equilibrium line’ and the ‘zero-profit line’ for Case II

Full size image
Fig. 3
figure 3

The ‘biological equilibrium line’ and the ‘zero-profit line’ for Case III

Full size image
$$\begin{aligned} x_\infty =\frac{[p_2q_2\{q_1(r_{2l})^{(1-p)}(r_{2u})^{p}-q_2(r_{1l})^{(1-p)}(r_{1u})^{p}\}-c\{q_1(b_{22l})^{(1-p)}(b_{22u})^{p}-q_2(b_{12l})^{(1-p)}(b_{12u})^{p}\}]}{[p_1q_1\{q_1(b_{21l})^{(1-p)}(b_{21u})^{p}-q_2(b_{11l})^{(1-p)}(b_{11u})^{p}\}-p_1q_1\{q_1(b_{22l})^{(1-p)}(b_{22u})^{p}-q_2(b_{12l})^{(1-p)}(b_{12u})^{p}\}]} \end{aligned}$$

provided either

$$\begin{aligned}&(i)c<\frac{p_2^2q_2^2\{q_1(b_{21l})^{(1-p)}(b_{21u})^{p}-q_2(b_{11l})^{(1-p)}(b_{11u})^{p}\}\{q_1(r_{2l})^{(1-p)}(r_{2u})^{p}-q_2(r_{1l})^{(1-p)}(r_{1u})^{p}\}}{p_1q_1\{q_1(b_{22l})^{(1-p)}(b_{22u})^{p}-q_2(b_{12l})^{(1-p)}(b_{12u})^{p}\}^{2}}\!\!\!\nonumber \\&\hbox {or}\!\!\!\! \nonumber \\&(ii)c>\frac{p_2^2q_2^2\{q_1(b_{21l})^{(1-p)}(b_{21u})^{p}-q_2(b_{11l})^{(1-p)}(b_{11u})^{p}\}\{q_1(r_{2l})^{(1-p)}(r_{2u})^{p}-q_2(r_{1l})^{(1-p)}(r_{1u})^{p}\}}{p_1q_1\{q_1(b_{22l})^{(1-p)}(b_{22u})^{p}-q_2(b_{12l})^{(1-p)}(b_{12u})^{p}\}^{2}}\!\!\!\!\! \end{aligned}$$
(12)

and

$$\begin{aligned} y_\infty =\frac{[p_1q_1\{q_1(r_{2l})^{(1-p)}(r_{2u})^{p}-q_2(r_{1l})^{(1-p)}(r_{1u})^{p}\}-c\{q_1(b_{21l})^{(1-p)}(b_{21u})^{p}-q_2(b_{11l})^{(1-p)}(b_{11u})^{p}\}]}{[p_1q_1\{q_1(b_{22l})^{(1-p)}(b_{22u})^{p}-q_2(b_{12l})^{(1-p)}(b_{12u})^{p}\}-p_2q_2\{q_1(b_{21l})^{(1-p)}(b_{21u})^{p}-q_2(b_{11l})^{(1-p)}(b_{11u})^{p}\}]} \end{aligned}$$

provided either

$$\begin{aligned}&(iii)c<\frac{p_1^2q_1^2\{q_1(b_{22l})^{(1-p)}(b_{22u})^{p}-q_2(b_{12l})^{(1-p)}(b_{12u})^{p}\}\{q_1(r_{2l})^{(1-p)}(r_{2u})^{p}-q_2(r_{1l})^{(1-p)}(r_{1u})^{p}\}}{p_2q_2\{q_1(b_{21l})^{(1-p)}(b_{21u})^{p}-q_2(b_{11l})^{(1-p)}(b_{11u})^{p}\}^{2}}\nonumber \\&\hbox {or}\nonumber \\&(iv)c>\frac{p_1^2q_1^2\{q_1(b_{22l})^{(1-p)}(b_{22u})^{p}-q_2(b_{12l})^{(1-p)}(b_{12u})^{p}\}\{q_1(r_{2l})^{(1-p)}(r_{2u})^{p}- q_2(r_{1l})^{(1-p)}(r_{1u})^{p}\}}{p_2q_2\{q_1(b_{21l})^{(1-p)}(b_{21u})^{p}-q_2(b_{11l})^{(1-p)}(b_{11u})^{p}\}^{2}} \end{aligned}$$
(13)

Thus, we come to the following theorem:

Theorem 5

The bionomic equilibrium point

  1. (i)

    \((x_\infty ,0)\) exists when conditions \((10)\) hold,

  2. (ii)

    \((0,y_\infty )\) exists when conditions \((11)\) hold and (iii) \((x_\infty ,y_\infty )\) exists when conditions \((12)\) and \((13)\) hold simultaneously.

7 Optimal harvesting policy: equilibrium solution and the dynamic optimization

In this section, our objective is to maximise the objective functional \(J\) of the harvesting model (4) given by

$$\begin{aligned} J=\int _{0}^{\infty }e^{-\delta t}[p_1q_1x+p_2q_2y-c]E(t)dt \end{aligned}$$
(14)

where \(\delta \) denotes the instantaneous annual rate of discount, subject to the state equations (7) by invoking Pontryagin’s Maximum Principle [39] and the control constraints

$$\begin{aligned} 0\le E(t) \le E_{\max }. \end{aligned}$$

At the optimal level of \(R\) the optimal steady state solution \((x_{\delta },y_{\delta })\) can be computed from \(\displaystyle \frac{\partial R}{\partial x}=\frac{\partial R}{\partial y}=0\) as

$$\begin{aligned} x_{\delta }&= \frac{1}{[\{(b_{12l})^{(1-p)}(b_{12u})^{p}p_1+(b_{21l})^{(1-p)}(b_{21u})^{p}p_2\}^2-4p_1p_2(b_{11l})^{(1-p)}(b_{11u})^{p}(b_{22l})^{(1-p)}(b_{12u})^{p}]}\\&\times {[\{(b_{12l})^{(1-p)}(b_{12u})^{p}p_1+(b_{21l})^{(1-p)}(b_{21u})^{p}p_2\}\{(r_{2l})^{(1-p)}(r_{2u})^{p}p_2}\\&+\,(b_{12l})^{(1-p)}(b_{12u})^{p}c_1\\&+\,(b_{22l})^{(1-p)}(b_{22u})^{p}c_2\}-2(b_{22l})^{(1-p)}(b_{22u})^{p}p_2\{(r_{1l})^{(1-p)}(r_{1u})^{p}p_1\\&+\,(b_{11l})^{(1-p)}(b_{11u})^{p}c_1\\&+\,(b_{21l})^{(1-p)}(b_{21u})^{p}c_2\}] \end{aligned}$$

and

$$\begin{aligned} y_{\delta }&= \frac{1}{[\{(b_{12l})^{(1-p)}(b_{12u})^{p}p_1+(b_{21l})^{(1-p)}(b_{21u})^{p}p_2\}^2-4p_1p_2(b_{11l})^{(1-p)}(b_{11u})^{p}(b_{22l})^{(1-p)}(b_{12u})^{p}]}\\&\times {[\{(b_{12l})^{(1-p)}(b_{12u})^{p}p_1+(b_{21l})^{(1-p)}(b_{21u})^{p}p_2\}\{(r_{1l})^{(1-p)}(r_{1u})^{p}p_1+(b_{11l})^{(1-p)}(b_{11u})^{p}c_1}\\&+\,(b_{21l})^{(1-p)}(b_{21u})^{p}c_2\}-2(b_{11l})^{(1-p)}(b_{11u})^{p}p_1\{(r_{2l})^{(1-p)}(r_{2u})^{p}p_2+(b_{12l})^{(1-p)}(b_{12u})^{p}c_1\\&+\,(b_{22l})^{(1-p)}(b_{22u})^{p}c_2\}]. \end{aligned}$$

Here, we have taken \(c=c_1q_1+c_2q_2\) so that

\(c_1q_1xE =\) cost of harvesting the x-species at a rate \(q_1xE\) and

\(c_2q_2yE =\) cost of harvesting the y-species at a rate \(q_2yE.\)

Now, \((x_{\delta },y_{\delta })\) lies in the first quadrant of the phase plane iff

$$\begin{aligned}&\!\!\! \{(b_{12l})^{(1-p)}(b_{12u})^{p}p_1+(b_{21l})^{(1-p)}(b_{21u})^{p}p_2\}^2> \hbox {or}<\nonumber \\&\!\!\! 4p_1p_2(b_{11l})^{(1-p)}(b_{11u})^{p}(b_{22l})^{(1-p)}(b_{12u})^{p}. \end{aligned}$$
(15)

So, we came to the following theorem:

Theorem 6

The optimal steady state solution \((x_{\delta },y_{\delta })\) lies in the first quadrant of the phase plane iff the condition (15) is satisfied.

Now, the Hamiltonian function for the dynamic optimization problem is

$$\begin{aligned} H&= \lambda _0 e^{-\delta t}[p_1q_1x+p-2q_2y-c]E\nonumber \\&+\,\lambda _1[x\{(r_{1l})^{(1-p)}(r_{1u})^{p}-(b_{11l})^{(1-p)}(b_{11u})^{p}x\nonumber \\&-\,(b_{12l})^{(1-p)}(b_{12u})^{p}y\}-q_1Ex]\nonumber \\&+\,\lambda _2[y\{(r_{2l})^{(1-p)}(r_{2u})^{p}-(b_{22l})^{(1-p)}(b_{22u})^{p}y\nonumber \\&-\,(b_{21l})^{(1-p)}(b_{21u})^{p}x\}-q_2Ey] \end{aligned}$$
(16)

where \(\lambda _0, \lambda _1\) and \(\lambda _2\) are adjoint variables. All the adjoint variables must not be zero simultaneously for the existence of an optimal control \(E=E_{\delta }(t)\) and the corresponding responses \(x=x_{\delta }(t), y=y_{\delta }(t).\) We will proceed with the case \(\delta =0\) in the subsequent analysis [3, 14].

The adjoint equations are

$$\begin{aligned} \frac{d\lambda _1}{dt}&= -\frac{\partial H}{\partial x}=-\lambda _0p_1q_1E-\lambda _1[(r_{1l})^{(1-p)}(r_{1u})^{p}\nonumber \\&-\,2(b_{11l})^{(1-p)}(b_{11u})^{p}x\nonumber \\&-\,(b_{12l})^{(1-p)}(b_{12u})^{p}y-q_1E]\nonumber \\&-\,\lambda _2(b_{21l})^{(1-p)}(b_{21u})^{p}y \end{aligned}$$
(17)

and

$$\begin{aligned} \frac{d\lambda _2}{dt}&= -\frac{\partial H}{\partial y}=-\lambda _0p_2q_2E-\lambda _1(b_{12l})^{(1-p)}(b_{12u})^{p}x\nonumber \\&-\,\lambda _2[(r_{2l})^{(1-p)}(r_{2u})^{p}-2(b_{22l})^{(1-p)}(b_{22u})^{p}y\nonumber \\&-\,(b_{21l})^{(1-p)}(b_{21u})^{p}x-q_2E]. \end{aligned}$$
(18)

The optimal control and its responses must satisfy the following condition [20]:

$$\begin{aligned} H(x_{\delta }(t),y_{\delta }(t),E_{\delta }(t),\lambda _1(t),\lambda _2(t))=0. \end{aligned}$$
(19)

As the optimal control \(E^*(t)\) maximises \(H(x_{\delta }(t),y_{\delta }(t), E_{\delta }(t),\lambda _1(t),\lambda _2(t))\) along an optimal trajectory with respect to all admissible controls, we must have

$$\begin{aligned} \frac{\partial H}{\partial E}=H_E>0 \Rightarrow E_{\delta }(t)=E_{\max }, \end{aligned}$$
(20)
$$\begin{aligned} \frac{\partial H}{\partial E}=H_E<0 \Rightarrow E_{\delta }(t)=0. \end{aligned}$$
(21)

The Hamiltonian \(H\) is a linear function of \(E,\) so the singular control exists if

$$\begin{aligned} H_E&= \lambda _0[p_1q_1x+p_2q_2y-c]\nonumber \\&-\,\lambda _1q_1x-\lambda _2q_2y=0. \end{aligned}$$
(22)

Now,

$$\begin{aligned} DH_E&= \lambda _0p_1q_1x\{(r_{1l})^{(1-p)}(r_{1u})^{p}\nonumber \\&-\,(b_{11l})^{(1-p)}(b_{11u})^{p}x\!-\!(b_{12l})^{(1-p)}(b_{12u})^{p}y\}\nonumber \\&+\,\lambda _0p_2q_2y\{(r_{2l})^{(1-p)}(r_{2u})^{p}\nonumber \\&-\,(b_{22l})^{(1-p)}(b_{22u})^{p}y\!-\!(b_{21l})^{(1-p)}(b_{21u})^{p}x\}\\&-\,\lambda _1q_1(b_{11l})^{(1-p)}(b_{11u})^{p}x^2\nonumber \\&-\,\lambda _2q_2(b_{22l})^{(1-p)}(b_{22u})^{p}y^2\nonumber \\&+\,[\lambda _1(b_{12l})^{(1-p)}(b_{12u})^{p}q_2\nonumber \\&+\,\lambda _2(b_{21l})^{(1-p)}(b_{21u})^{p}q_1]xy, \end{aligned}$$
(23)

where \(D\equiv \frac{d}{dt}.\)

Here, \(DH_E=0\) gives

$$\begin{aligned}&\lambda _0p_1q_1x\{(r_{1l})^{(1-p)}(r_{1u})^{p}-(b_{11l})^{(1-p)}(b_{11u})^{p}x\nonumber \\&-\,(b_{12l})^{(1-p)}(b_{12u})^{p}y\}\nonumber \\&+\,\lambda _0p_2q_2y\{(r_{2l})^{(1-p)}(r_{2u})^{p}\nonumber \\&-\,(b_{22l})^{(1-p)}(b_{22u})^{p}y-(b_{21l})^{(1-p)}(b_{21u})^{p}x\}\nonumber \\&-\,\lambda _1q_1(b_{11l})^{(1-p)}(b_{11u})^{p}x^2\nonumber \\&-\,\lambda _2q_2(b_{22l})^{(1-p)}(b_{22u})^{p}y^2\nonumber \\&+\,[\lambda _1(b_{12l})^{(1-p)}(b_{12u})^{p}q_2\nonumber \\&+\,\lambda _2(b_{21l})^{(1-p)}(b_{21u})^{p}q_1]xy=0. \end{aligned}$$
(24)

We take \(\lambda _0>0\) and without any loss of generality we will proceed with \(\lambda _0=1.\) Now, (22) and (24) can be written as

$$\begin{aligned} \lambda _1q_1x+\lambda _2q_2y-A=0 \end{aligned}$$
(25)

and

$$\begin{aligned}&\lambda _1[q_1(b_{11l})^{(1-p)}(b_{11u})^{p}x^2\nonumber \\&-\,q_2(b_{12l})^{(1-p)}(b_{12u})^{p}xy]\nonumber \\&-\,\lambda _2[q_2(b_{22l})^{(1-p)}(b_{22u})^{p}y^2\nonumber \\&-\,q_1(b_{21l})^{(1-p)}(b_{21u})^{p}xy]-B=0 \end{aligned}$$
(26)

where

$$\begin{aligned} A=p_1q_1x+p_2q_2y-c \end{aligned}$$

and

$$\begin{aligned} B&= p_1q_1x\{(r_{1l})^{(1-p)}(r_{1u})^{p}\nonumber \\&-\,(b_{11l})^{(1-p)}(b_{11u})^{p}x-(b_{12l})^{(1-p)}(b_{12u})^{p}y\}\nonumber \\&+\,p_2q_2y\{(r_{2l})^{(1-p)}(r_{2u})^{p}\nonumber \\&-\,(b_{22l})^{(1-p)}(b_{22u})^{p}y-(b_{21l})^{(1-p)}(b_{21u})^{p}x\}. \end{aligned}$$

Solving (25) and (26), we get

$$\begin{aligned} \lambda _1&= \frac{A[q_2(b_{22l})^{(1-p)}(b_{22u})^{p}y-q_1(b_{21l})^{(1-p)}(b_{21u})^{p}x]-Bq_2}{q_1[q_2(b_{22l})^{(1-p)}(b_{22u})^{p}y-q_1(b_{21l})^{(1-p)}(b_{21u})^{p}x]-q_2[q_1(b_{11l})^{(1-p)}(b_{11u})^{p}x-q_2(b_{12l})^{(1-p)}(b_{12u})^{p}y]},\end{aligned}$$
(27)
$$\begin{aligned} \lambda _2&= \frac{A[q_1(b_{11l})^{(1-p)}(b_{11u})^{p}x-q_2(b_{12l})^{(1-p)}(b_{12u})^{p}y]-Bq_1}{q_2[q_1(b_{11l})^{(1-p)}(b_{11u})^{p}x-q_2(b_{12l})^{(1-p)}(b_{12u})^{p}y]-q_1[q_2(b_{22l})^{(1-p)}(b_{22u})^{p}y-q_1(b_{21l})^{(1-p)}(b_{21u})^{p}x]}. \end{aligned}$$
(28)

Now,

$$\begin{aligned} D^2H_E=\lambda _1K+\lambda _2L+EM+N=0 \end{aligned}$$
(29)

where

$$\begin{aligned} K&= (b_{12l})^{(1-p)}(b_{12u})^{p}x[q_2(b_{22l})^{(1-p)}(b_{22u})^{p}y^2\\&-\,q_1(b_{21l})^{(1-p)}(b_{21u})^{p}xy]\\&+\,[q_1(b_{11l})^{(1-p)}(b_{11u})^{p}x^2\\&-\,q_2(b_{12l})^{(1-p)}(b_{12u})^{p}xy ][(r_{1l})^{(1-p)}(r_{1u})^{p}\\&-\,2(b_{11l})^{(1-p)}(b_{11u})^{p}x\\&-\,(b_{12l})^{(1-p)}(b_{12u})^{p}y]\\&+\,(b_{12l})^{(1-p)}(b_{12u})^{p}q_2xy[\{(r_{1l})^{(1-p)}(r_{1u})^{p}\\&+\,(r_{2l})^{(1-p)}(r_{2u})^{p}\}\\&-\,x\{(b_{11l})^{(1-p)}(b_{11u})^{p}\\&+\,(b_{21l})^{(1-p)}(b_{21u})^{p}\}\\&-\,y\{(b_{22l})^{(1-p)}(b_{22u})^{p}\\&+\,(b_{12l})^{(1-p)}(b_{12u})^{p}\}]\\&-\,2q_1(b_{11l})^{(1-p)}(b_{11u})^{p}x^2[(r_{1l})^{(1-p)}(r_{1u})^{p}\\&-\,(b_{11l})^{(1-p)}(b_{11u})^{p}x-(b_{12l})^{(1-p)}(b_{12u})^{p}y],\\ L&= (b_{21l})^{(1-p)}(b_{21u})^{p}y[q_1(b_{11l})^{(1-p)}(b_{11u})^{p}x^2\\&-\,q_2(b_{12l})^{(1-p)}(b_{12u})^{p}xy]\\&+\,[q_2(b_{22l})^{(1-p)}(b_{22u})^{p}y^2\\&-\,q_1(b_{21l})^{(1-p)}(b_{21u})^{p}xy] [(r_{2l})^{(1-p)}(r_{2u})^{p}\\&-\,2(b_{22l})^{(1-p)}(b_{22u})^{p}y\\&-\,(b_{21l})^{(1-p)}(b_{21u})^{p}x]\\&+\,(b_{21l})^{(1-p)}(b_{21u})^{p}q_1xy[\{(r_{1l})^{(1-p)}(r_{1u})^{p}\\&+\,(r_{2l})^{(1-p)}(r_{2u})^{p}\}\\&-\,x\{(b_{11l})^{(1-p)}(b_{11u})^{p}\\&+\,(b_{21l})^{(1-p)}(b_{21u})^{p}\}-y\{(b_{22l})^{(1-p)}(b_{22u})^{p}\\&+\,(b_{12l})^{(1-p)}(b_{12u})^{p}\}]\\&-\,2q_2(b_{22l})^{(1-p)}(b_{22u})^{p}y^2[(r_{2l})^{(1-p)}(r_{2u})^{p}\\&-\,(b_{22l})^{(1-p)}(b_{22u})^{p}y-(b_{21l})^{(1-p)}(b_{21u})^{p}x],\\ M&= (p_1-\lambda _1)q_1[q_1(b_{11l})^{(1-p)}(b_{11u})^{p}x^2\\&-\,q_2(b_{12l})^{(1-p)}(b_{12u})^{p}xy]-\lambda _1(q_1+q_2)\\&\times \, q_2(b_{12l})^{(1-p)}(b_{12u})^{p}xy\\&+\,2\lambda _1q_1^2(b_{11l})^{(1-p)}(b_{11u})^{p}x^2\\&+\,(p_2-\lambda _2)q_2[q_2(b_{22l})^{(1-p)}(b_{22u})^{p}y^2\\&-\,q_1(b_{21l})^{(1-p)}(b_{21u})^{p}xy]\\&-\,\lambda _2(q_1+q_2)q_1(b_{21l})^{(1-p)}(b_{21u})^{p}xy\\&+\,2\lambda _2q_2^2(b_{22l})^{(1-p)}(b_{22u})^{p}y^2\\&-\,q_1x[p_1q_1(r_{1l})^{(1-p)}(r_{1u})^{p}\\&-\,2p_1q_1(b_{11l})^{(1-p)}(b_{11u})^{p}x]\\&-\,q_2y[p_2q_2(r_{2l})^{(1-p)}(r_{2u})^{p}\\&-\,2p_2q_2(b_{22l})^{(1-p)}(b_{22u})^{p}y]\nonumber \\&+\,xy(q_1+q_2)[p_1q_1(b_{12l})^{(1-p)}(b_{12u})^{p}\\&+\,p_2q_2(b_{21l})^{(1-p)}(b_{21u})^{p}] \end{aligned}$$

and

$$\begin{aligned} N&= x[(r_{1l})^{(1-p)}(r_{1u})^{p}\\&-\,(b_{11l})^{(1-p)}(b_{11u})^{p}x\\&-\,(b_{12l})^{(1-p)}(b_{12u})^{p}y][p_1q_1(r_{1l})^{(1-p)}(r_{1u})^{p}\\&-\,2p_1q_1(b_{11l})^{(1-p)}(b_{11u})^{p}x]\\&+\,y[(r_{2l})^{(1-p)}(r_{2u})^{p}\\&-\,(b_{22l})^{(1-p)}(b_{22u})^{p}y\\&-\,(b_{21l})^{(1-p)}(b_{21u})^{p}x]\\&\times \,[p_2q_2(r_{2l})^{(1-p)}(r_{2u})^{p}-2p_2q_2(b_{22l})^{(1-p)}(b_{22u})^{p}y]\\&-\,xy[p_1q_1(b_{12l})^{(1-p)}(b_{12u})^{p}\\&+\,p_2q_2(b_{21l})^{(1-p)}(b_{21u})^{p}]\\&\times \,[\{(r_{1l})^{(1-p)}(r_{1u})^{p}+(r_{2l})^{(1-p)}(r_{2u})^{p}\}\\&-\,x\{(b_{11l})^{(1-p)}(b_{11u})^{p}\\&+\,(b_{21l})^{(1-p)}(b_{21u})^{p}\}-y\{(b_{22l})^{(1-p)}(b_{22u})^{p}\\&+\,(b_{12l})^{(1-p)}(b_{12u})^{p}\}]. \end{aligned}$$

Hence

$$\begin{aligned} (D^2H_E)_E&= p_1q_1^2x[(b_{11l})^{(1-p)}(b_{11u})^{p}x\nonumber \\&+\,(b_{12l})^{(1-p)}(b_{12u})^{p}y-(r_{1l})^{(1-p)}(r_{1u})^{p}]\nonumber \\&+\,p_2q_2^2y[(b_{22l})^{(1-p)}(b_{22u})^{p}y\nonumber \\&+\,(b_{21l})^{(1-p)}(b_{21u})^{p}x-(r_{2l})^{(1-p)}(r_{2u})^{p}]\nonumber \\&+\,2p_1q_1^2(b_{11l})^{(1-p)}(b_{11u})^{p}x^2\nonumber \\&+\,2p_2q_12^2(b_{22l})^{(1-p)}(b_{22u})^{p}y^2\nonumber \\&+\,q_2^2y[\lambda _2(b_{22l})^{(1-p)}(b_{22u})^{p}y\nonumber \\&-\,\lambda _1(b_{12l})^{(1-p)}(b_{12u})^{p}x]\nonumber \\&+\,q_1^2x[\lambda _1(b_{11l})^{(1-p)}(b_{11u})^{p}x\nonumber \\&-\,\lambda _2(b_{21l})^{(1-p)}(b_{21u})^{p}y]. \end{aligned}$$
(30)

In order to ensure the existence of an optimal singular control, it is required to satisfy the generalised Legendre condition

$$\begin{aligned} (D^2H_E)_E\ge 0. \end{aligned}$$
(31)

Now, the condition (31) will be satisfied if and only if the following constraints hold:

$$\begin{aligned}&(i)(b_{11l})^{(1-p)}(b_{11u})^{p}x+(b_{12l})^{(1-p)}(b_{12u})^{p}y\nonumber \\&\quad -\,(r_{1l})^{(1-p)}(r_{1u})^{p}\ge 0,\nonumber \\&(ii)(b_{22l})^{(1-p)}(b_{22u})^{p}y+(b_{21l})^{(1-p)}(b_{21u})^{p}x\nonumber \\&\quad -\,(r_{2l})^{(1-p)}(r_{2u})^{p}\ge 0,\nonumber \\&(iii)(b_{11l})^{(1-p)}(b_{11u})^{p}(b_{22l})^{(1-p)}(b_{22u})^{p}\nonumber \\&\quad \ge \, (b_{12l})^{(1-p)}(b_{12u})^{p}(b_{21l})^{(1-p)}(b_{21u})^{p}. \end{aligned}$$
(32)

The constraints \((i)\) and \((ii)\) of (32) imply that the bionomic optimal equilibrium solution \((x_{\delta },y_{\delta })\) is established at a stage when both the populations exibit a decelining trend.

Using (19) and (22), the singular extremal trajectory obtained as

$$\begin{aligned}&\lambda _1x[(r_{1l})^{(1-p)}(r_{1u})^{p}\nonumber \\&-\,(b_{11l})^{(1-p)}(b_{11u})^{p}x-(b_{12l})^{(1-p)}(b_{12u})^{p}y]\nonumber \\&\lambda _2y[(r_{2l})^{(1-p)}(r_{2u})^{p}\nonumber \\&-\,(b_{22l})^{(1-p)}(b_{22u})^{p}y-(b_{21l})^{(1-p)}(b_{21u})^{p}x]=0.\nonumber \\ \end{aligned}$$
(33)

Now, the equation

$$\begin{aligned} D^2H_E=0 \end{aligned}$$
(34)

with (27) and (28) gives the optimal singular control \(E_{\delta }(t)\) in terms of the optimal population levels of the two species.

8 Numerical simulations

We first consider the case when \(q_1=0.2, q_2=0.5, E=15, p=0\) with the imprecise biological parameter values given in Table 1 and the initial conditions \((x(0),y(0))=(0.5,0.5).\) Then the condition of Theorem 1 is satisfied, and the trivial equilibrium point \(E_0(0,0)\) is locally asymptotically stable. Using these parameter values and the initial condition the dynamics of the model is graphically presented in Fig. 4. This figure shows that both the species population \((x,y)\) decline to zero, i.e. approaches the trivial equilibrium \(E_0,\) which supports our mathematical result given in Theorem 1. Next, we consider the case when \(q_1=0.2, q_2=0.5, E=10, p=0\) with the imprecise biological parameter values given in Table 1 and the initial conditions \((x(0),y(0))=(0.5,0.5).\) Then the condition stated in Theorem 2 is satisfied, which implies that the axial equilibrium \(E_1(\bar{x},0)\) is locally asymptotically stable, other axial equilibrium \(E_2(0,\tilde{y})\) does not exist, and the trivial equilibrium \(E_0(0,0)\) becomes unstable. The dynamics of the model according to this case is graphically presented in Fig. 5, which shows that the first species population \((x)\) exists, and the second species population \((y)\) goes to extinct, i.e. the system approaches the axial equilibrium \(E_1.\) This result supports our analytical results stated in Theorem 2.

Fig. 4
figure 4

Time series plot of the two species population (\(x,y\)) using the imprecise parameter values given in Table 1 with \(q_1=0.2, q_2=0.5, E=15, p=0\) and initial conditions \((x(0),y(0))=(0.5,0.5)\)

Full size image
Fig. 5
figure 5

Time series plot of the two species population (\(x,y\)) using the imprecise parameter values given in Table 1 with \(q_1=0.2, q_2=0.5, E=10, p=0\) and initial conditions \((x(0),y(0))=(0.5,0.5)\)

Full size image
Table 1 Parameter values for Figs. 4–7 & 8–13
Full size table

Considering \(q_1=0.5, q_2=0.3, E=6, p=0\) with the imprecise biological parameter values given in Table 1 and the initial conditions \((x(0),y(0))=(0.5,0.5),\) we find that the condition of Theorem 3 is satisfied. This implies that using these parameter values the axial equilibrium \(E_2(0,\tilde{y})=(0,2)\) is locally asymptotically stable, other axial equilibrium \(E_1(\bar{x},0)\) does not exist, and the trivial equilibrium \(E_0(0,0)\) becomes unstable. This case is graphically presented in Fig. 6, which shows that the first species \((x)\) declines to zero and the second species \((y)\) exists, i.e. the system approaches the axial equilibrium \(E_2.\) This numerical verification is in good agreement with our analytical result stated in Theorem 3. Finally, we consider \(q_1=0.2, q_2=0.5, E=3, p=0\) with the imprecise biological parameter values given in Table 1 and the initial condition \((x(0),y(0))=(0.5,0.5).\) Using these values, we find that the conditions given in Theorem 4 are satisfied, which imply that the interior equilibrium \(E^*(x^*,y^*)=(7.66667,1.22222)\) becomes locally asymptotically stable. The dynamics of the model is graphically presented in Fig. 7, which shows that both the species population \((x,y)\) exist, i.e. the population tends to the interior equilibrium \(E^*.\) This supports our analytical results stated in Theorem 4.

Fig. 6
figure 6

Time series plot of the two species population (\(x,y\)) using the imprecise parameter values given in Table 1 with \(q_1=0.5, q_2=0.3, E=6, p=0\) and initial conditions \((x(0),y(0))=(0.5,0.5)\)

Full size image
Fig. 7
figure 7

Time series plot of the two species population (\(x,y\)) using the imprecise parameter values given in Table 1 with \(q_1=0.2, q_2=0.5, E=3, p=0\) and initial conditions \((x(0),y(0))=(0.5,0.5)\)

Full size image

Next, we consider the imprecise biological parameter values given in Table 2 with \(q_1=0.5, q_2=0.6, E=4.8, p=0.\) Using these values, \(xy\)-plane projection of the solution for various initial values is presented in Fig. 8. This figure shows that all the four equilibria of the system exist. But only the axial equilibria \(E_1(\bar{x},0)=(0.5,0)\) and \(E_2(0,\tilde{y})=(0,0.4)\) are locally asymptotically stable, and the trivial equilibrium \(E_0(0,0)\) and the interior equilibrium \(E^*(x^*,y^*)=(0.0882353,0.164706)\) are unstable.

Fig. 8
figure 8

\(xy\)-plane projection of the solution using the imprecise parameter values given in Table 2 with \(q_1=0.5, q_2=0.6, E=4.8, p=0\) with various initial conditions

Full size image
Table 2 Parameter values for Fig. 8
Full size table

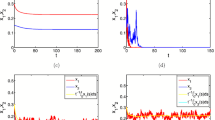
Considering the biological parameters as given in Table 1, \(q_1=0.2, q_2=0.5, E=15\) and the initial condition \((x(0),y(0))=(0.5,0.5)\), we present the dynamics of the model for different values of \(p\ (p=0,0.3,0.5,0.8,1)\) in Fig. 9a–e. These figures show that the trivial equilibrium point \(E_0(0,0)\) always exists for all values of \(p \in [0,1].\) Considering the parameter values as in the previous case with \(E=10\), we present the dynamics of the model for different values of \(p\ (p=0,0.3,0.5,0.8,1)\) in Fig. 10a–e. These figures show that the axial equilibrium \(E_1\) exists for all values of \(p \in [0,1].\) But the values are different for different values of \(p.\) Fig. 9f shows that the value of \(x\) species is decreasing with increasing \(p.\)

Fig. 9
figure 9

Time series plot of the two species population (\(x,y\)) using the imprecise parameter values given in Table 1 with \(q_1=0.2, q_2=0.5, E=15\) and initial conditions \((x(0),y(0))=(0.5,0.5)\) for a \(p=0\), b \(p=0.3\), c \(p=0.5\), d \(p=0.8\) and e \( p=1\)

Full size image
Fig. 10
figure 10

Time series plot of the two species population (\(x,y\)) using the imprecise parameter values given in Table 1 with \(q_1=0.2, q_2=0.5, E=10\) and initial conditions \((x(0),y(0))=(0.5,0.5)\) for a \(p=0\), b \(p=0.3\), c \(p=0.5\), d \(p=0.8\), e \(p=1\) and f Dynamical behaviour of the two species population (\(x,y\)) with respect to \(p\) when the values of other parameters are same

Full size image

In the Fig. 11a–e, we present the dynamics of the model for different values of \(p\ (p=0,0.3,0.5,0.8,1)\) using the parameter values given in Table 1 with \(q_1=0.5, q_2=0.3, E=6\) and the initial condition \((x(0),y(0))=(0.5,0.5).\) These figures show that the axial equilibrium \(E_2\) exists for all values of \(p \in [0,1].\) But the values are different for different values of \(p.\) Fig. 10f shows that the value of \(y\) species is decreasing very slowly with increasing \(p.\) The dynamics of the model with \(q_1=0.5, q_2=0.3, E=3,\) the imprecise biological parameter values given in Table 1 and the initial conditions \((x(0),y(0))=(0.5,0.5),\) is presented in Fig. 12a–e for different values of \(p\ (p=0,0.3,0.5,0.8,1).\) These figures show that the interior equilibrium \(E^*\) exists for all values of \(p \in [0,1],\) but the values are different for different values of \(p.\) Fig. 11f shows that both the species population decrease with increasing \(p,\) but \(x\) species is decreasing rapidly where as \(y\) species is decreasing slowly.

Fig. 11
figure 11

Time series plot of the two species population (\(x,y\)) using the imprecise parameter values given in Table 1 with \(q_1=0.5, q_2=0.3, E=6\) and initial conditions \((x(0),y(0))=(0.5,0.5)\) for a \(p=0\), b \(p=0.3\), c \(p=0.5\), d \(p=0.8\), e \(p=1\) and f Dynamical behaviour of the two species population (\(x,y\)) with respect to \(p\) when the values of other parameters are same

Full size image
Fig. 12
figure 12

Time series plot of the two species population (\(x,y\)) using the imprecise parameter values given in Table 1 with \(q_1=0.2, q_2=0.5, E=3\) and initial conditions \((x(0),y(0))=(0.5,0.5)\) for a \(p=0\), b \(p=0.3\), c \(p=0.5\), d \(p=0.8\), e \(p=1\) and f. Dynamical behaviour of the two species population (\(x,y\)) with respect to \(p\) when the values of other parameters are same

Full size image

Figure 13 shows the dynamical behaviour of the two species population \((x,y)\) with respect to the harvesting effort \(E\) considering the biological parameters as given in Table 1 with \(q_1=0.2, q_2=0.5, p=0\) and the initial condition \((x(0),y(0))=(0.5,0.5).\) This figure shows that the equilibrium point changes for different values of \(E.\) In this figure, we observe that for small value of \(E\ (0<E\le 6)\) both the species population exist. When \(E\) takes large values \((6<E\le 12.5),\) only \(x\) species exists and \(y\) species goes to extinct. For higher values of \(E\ (E>12.5)\) both the species decline to zero. So, we can conclude that the combined harvesting effort \((E)\) plays a key role in the stability of the equilibrium points of our system.

Fig. 13
figure 13

Dynamical behaviour of the two species population (\(x,y\)) with respect to \(E\) when the imprecise parameter values given in Table 1 with \(q_1=0.2, q_2=0.5, p=0\) and initial conditions \((x(0),y(0))=(0.5,0.5)\)

Full size image

9 Discussions and conclusions

In this Paper, we have developed a two species competition model with harvesting. The equations of the model are obtained from the classical equations (Gause’s Model) using combined harvesting effort \(E.\) Most of the harvesting models are generally based on the assumption that the biological parameters are precisely known. But in reality the scenario is different as always it is not possible to know the values of all biological parameters precisely. In this paper, we have developed a method to discuss the dynamical behaviour of the two species competition model with harvesting using some imprecise parameters. Here, we have developed the concept of imprecise parameters to the model by considering the population growth rates (\(r_{1l},r_{1u},r_{2l},r_{2u}\)), the coefficients of intraspecific competition (\(b_{11l},b_{11u},b_{22l},b_{22u}\)), the rate at which presence of the first species affects the growth of the second species (\(b_{21l},b_{21u}\)), and the rate at which presence of the second species affects the growth of the first species (\(b_{12l},b_{12u}\)) are imprecise in nature for the lack of precise numerical information.

We have discussed the existence and stability of various equilibrium points of our system. We have also analysed the bionomic equilibrium of the harvesting model. It is observed that the exploited system may have a stable bionomic equilibrium with positive population levels for both the species. There also may exists a bionomic equilibrium with positive population level only for first species and another bionomic equilibrium with positive population level only for second species. We may also notice that the existence of such a bionomic equilibrium depends critically on the biological parameters \((r_{1l},r_{1u},r_{2l},r_{2u},b_{11l},b_{11u},b_{12l},b_{12u}, b_{21l},b_{21u},b_{22l},b_{22u})\), technological parameters \((q_1, q_2)\) and the economical parameters \((p_1,p_2,c).\)

The most important part of this paper is to set up an optimal control problem with the harvesting effort \(E(t)\) as the control variable so as to maximise the objective functional \(J\) given in (17). We have derived the equilibrium solution of the control problem. Dynamical optimization of the harvest policy is then carried out taking \(E(t)\) as a dynamic variable. Next the singular optimal control \(E^*(t)\) is derived in terms of the optimal population levels of the two species by invoking Pontryagin’s Maximum Principle.

The important mathematical results for the dynamical behaviour of the two species competition model with harvesting are also numerically verified using MATLAB with some imprecise parameter values. The ability of calculating the biological equilibrium points, bionomic equilibrium points and discussing their nature, then developing optimal harvesting policy with some imprecise parameter values and finally verifying all the mathematical results using numerical simulation with some imprecise parameters are no doubt very realistic and helpful in both mathematical and ecological points of view.

Finally, we conclude that our system of two competing species with combined harvesting exhibits very interesting dynamics. But the mathematical model presented in this paper should be treated with circumspection due to the assumptions made and the difficulty in the estimation of the model parameters. In this paper some of the model parameters are taken imprecise in nature, which makes the situation more realistic as always it is not possible to know the parameter values precisely. In this paper we have considered impreciseness only in the biological parameters. But impreciseness of fishing cost and price per unit biomass of the two species of the harvesting model are also possible and reasonable. So, as a part of future work we can incorporate the impreciseness of the technological and economic parameters to improve our model.