1 Introduction

Chaotic dynamics is an interesting topic in nonlinear science which has been intensively studied during the last three decades. Chaotic phenomena can be found in many scientific and engineering fields such as biological systems, electronic circuits, power converters, chemical systems, and so on [1]. A chaotic system has complex dynamical behaviors that possess some special features, such as high sensitivity to initial conditions, broad spectrums of Fourier transform, bounded and fractal properties of the motion in the phase space, etc. [2]. Pecora and Carroll in 1990 [3] addressed the synchronization of chaotic systems using the drive–response concept. Also, in the same year Ott et al. [4] succeeded in controlling chaos using OGY method. Several researches have been carried out theoretically and experimentally on chaos control and synchronization due to its great potential applications in many areas like information science, medicine, biology, economics, social science, engineering, etc. [5–7]. In search of better methods for chaos control and synchronization several variety of methods have been developed for chaos control and chaos synchronization of identical and non identical systems such as linear feedback [8], optimal control [9], adaptive control [10], active control [11], active sliding control [12], passive control [13], impulsive control [14], backstepping control [15–18], etc. Of the several nonlinear control techniques mentioned above, the backstepping technique stands out of these nonlinear control methods as a result of its flexibility in the construction of control law and its ability to control chaos, and to synchronize chaos in identical and non identical chaotic systems [19, 20]. This is our fundamental reason for choosing backstepping technique in this work.

As a result of fast growing interest in chaos control and synchronization various synchronization types and schemes have been proposed and reported, such as complete synchronization [21], phase synchronization [22], generalized synchronization [23], lag synchronization [24], anti-synchronization [25], projective synchronization [26], modified projective synchronization [27], function projective synchronization [28], modified-function projective synchronization [29], and hybrid synchronization [30–32]. It has been discovered a few years ago that some other important form of synchronization like the increased-order synchronization [33] and reduced-order synchronization abound in biological systems [34].

In hybrid synchronization of chaotic systems [35], one part of the systems is completely synchronized and the other part is anti-synchronized so that complete synchronization (CS) and anti-synchronization (AS) coexist in the systems. The coexistence of CS and AS is very useful in applications such as secure communication, chaotic encryption schemes, etc. [30]. For hybrid projective synchronization of chaotic systems, one part of the system synchronizes to a positive scaling factor while the other part synchronizes to a negative scaling factor where the transformation scaling factors between the drive and the response state variables are not equal to one. Hybrid projective synchronization could be used to achieve higher security than projective synchronization in the application to secure communications, because the unpredictability of the vector function factor in hybrid synchronization is higher than that of the same scaling factor in projective synchronization [26]. Also, the co-existence of projective synchronization and projective anti-synchronization in hybrid synchronization offers the opportunity of transforming digital signals through the continuous transformation between synchronization and anti-synchronization which will enhance security in communication and chaotic encryption schemes [36]. Furthermore, the proportionality between the synchronized dynamical states could be used to achieve fast communication [37].

Specifically, synchronization of nonlinear dynamical systems gives the capability to gain an accurate and deep understanding of collective dynamical behavior in physical, chemical, and biological systems. The presence of synchronous behavior has been observed in different mathematical, physical, sociological, physiological, biological, and other systems [38]. In general, synchronization of nonlinear dynamical systems has great practical significance and potential applications in secure communication, laser dynamics, neuron systems, biological systems, chemical systems, power converters, and information science [39]. Synchronization of parallel array of coupled Josephson junctions linked together by inductors has been used to fabricate highly sensitive detectors [22, 40, 41]. Also, synchronization of the superconducting Josephson junction arrays is important for the purpose of generating reasonably large output power [42, 43]. Anti-synchronization of chaotic systems also, has very important applications. For example anti-synchronization of lasers, may be used to generate short pulses of high intensity, which gives some new ways for producing pulses of special shapes [36]. So, investigation of co-existence of synchronization and anti-synchronization known as hybrid synchronization will be an interesting and challenging subject.

Most researches on chaos synchronization are based on one drive to one response system, whereas in the real life situations chaos synchronization also occurs in more than two systems. Only very few research papers have been published on combination synchronization of three or four chaotic systems [44–46]. Combination synchronization scheme presented in this paper is generalized in such a way that other forms of synchronization scheme can be achieved from it. So, the usual one drive system to one response system synchronization scheme is special case of combination synchronization. As a result, combination synchronization scheme is more flexibility and applicability to the real world systems. In addition, the combination synchronization also gives better insight into the complex synchronization and several pattern formations that take place in real world systems since synchronization in real world systems are complex. The generalized reduced-order hybrid projective combination synchronization scheme presented in this paper could be used to vary the Josephson junction signal to any desired level and to achieve a desired synchronization scheme through appropriate choice of the scaling parameters. Moreover, it also gives a more suitable understanding of synchronization in biological systems wherein different organs of different dynamical structures and orders are involved. In general, combination synchronization enhances the security of information transmission better than the usual one master to one slave synchronization. For instance, we split the transmitted signals into several parts, each part loaded in different systems; or divide time into different intervals, the signals in different intervals loaded in different systems. Then, the transmitted signals may have stronger anti-attack ability and anti-translated capability than that transmitted by the usual one drive to one response secure communication scheme. Furthermore, Combination synchronization scheme could be use in a communication network, where many users (slave) but one control (master) connects different users to one another. So, the combination synchronization scheme presented in this paper is an appropriate synchronization scheme for these purposes.

The distinctive attribute of reduced-order synchronization in a master–slave configuration is that the order of the slave is less than the order of the master, where the number of first-order differential equations is referred to as order. So reduced-order synchronization is achieved if two or more dynamical systems of different orders in a master–slave arrangement is such that all the states variables of the slave system are synchronized with the projection of the state variables of the master. There is increasing interest in the study of chaotic synchronization with different structures and different orders due to its wide existence in biological science and social science [33, 35, 47–49]. For instance, the order of the thalamic neurons can be different from the hippocampal neurons [50]. Another example is the synchronization that occurs between heart and lungs, where one can observe that circulatory and respiratory systems synchronize with different orders [51]. Despite the excellent application and importance of reduced-order synchronization only a few research works have reported [52–55]. In general, reduced-order combination synchronization gives a more desirable description of synchronization in biological systems wherein different dynamical structures and orders are involved. The original reduced-order synchronization is a special case of the reduced-order combination synchronization and thus, the original reduced-order synchronization has limited flexibility and applicability to real world systems. The reduced-order combination synchronization is very interesting because the systems consist of different complex dynamical structures and orders as well as parameter mismatches which can further boost the security of information transmission. To the best of our knowledge, reduced order hybrid combination synchronization is not yet investigated.

Meanwhile, Josephson junctions have been used to reproduce many characteristic behaviors of biological neurons like action potentials, refractory periods, and firing thresholds. So Josephson junction can be coupled in ways that mimic electrical and chemical synapses [56]. Josephson junction is a good physical model for the investigation of reduced-order hybrid combination synchronization for two reasons: (i) the reduced-order synchronization is a common phenomenon in biological systems and Josephson junction could be used to simulate biological model, (ii) Josephson neurons are not difficult to design and are not expensive to fabricate; a thousand could be placed on a single chip. Josephson junctions operate fully in parallel, meaning a single Josephson neuron in isolation would run just as quickly as a thousand fully interconnected ones which are several orders of magnitude faster than either computer simulations of neurons or actual biological neural network [56]. Motivated by the above discussion, we present generalized reduced-order hybrid synchronization of three chaotic Josephson junctions via backsteping technique.

The rest of this paper is organized as follows: Sect. 2 gives the description of the systems. Section 3 presents generalized reduced-order hybrid combination synchronization between two third-order Josephson junctions as the drive and one second order Josephson junction as the slave via active backstepping technique. In Sect. 4, we present generalized reduced-order hybrid combination synchronization between one third-order Josephson junction as the drive and two second-order Josephson junction as the slave via active backstepping technique. Section 5 concludes the paper.

2 Description of Josephson junctions

2.1 Resistive–capacitive–inductive shunted Josephson junction (RCLSJJ)

The resistive–capacitive–inductive shunted Josephson junction in dimensionless form is described by the set of first-order differential equations below

$$\begin{aligned} \dot{x}&= y \nonumber \\ \dot{y}&= \frac{1}{\beta _C}(i-g(y)y-\sin x -z) \\ \dot{z}&= \frac{1}{\beta _L} (y-z),\nonumber \end{aligned}$$
(1)

where \(g(y)\) is the nonlinear damping function approximated by current–voltage relation between the junctions and is defined by

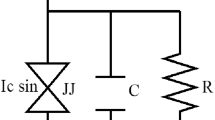
$$\begin{aligned} g(y) = \left\{ \begin{array}{l} 0.366 \,\, \hbox {if } \, |y| > 2.9 \\ 0.061 \,\, \hbox {if } \, |y| \le 2.9 \end{array}\right. \end{aligned}$$

\(x,\,y\), and \(z\) represent the phase difference, the voltage in the junction, and the inductive current, respectively. \(\beta _C\) and \(\beta _L\) are capacitive and inductive constant, respectively. \(i\) is the external direct current. Figure 1 shows the chaotic attractor of the RCL-shunted Josephson junction for the following set of parameters: \(i=1<i<1.3,\,\beta _C=2.6\) and \(\beta _L=0.707\) with the initial conditions \((x, y, z)=(0, 0, 0)\). The RCL-shunted Josephson has been found to be more appropriate in high frequency applications. In RCL Josephson junction chaotic oscillation has modulated in response to both the amplitude and frequency of an external sinusoidal signal.

Fig. 1
figure 1

Phase portrait of chaotic attractors of resistive–capacitive–inductive Josephson junction

Full size image

2.2 Resistive–capacitive-shunted Josephson junction (RCSJJ)

The resistive–capacitive Josephson junction under the external periodic force is given by the second-order differential equation below

$$\begin{aligned} \ddot{\phi }= -\alpha \dot{\phi }-\sin \phi +a +b\sin \omega t, \end{aligned}$$
(2)

where \(\phi \) is the phase difference between quantum mechanical wave function of two superconductors junction separated by some non-superconducting material or barrier. \(\alpha \) and \(a\) are the dimensionless damping and applied current. \(b\sin \omega t\) is the external periodic sinusoidal force. \(b\) and \(\omega \), respectively are the amplitude and frequency of the external periodic sinusoidal force. The second-order differential equation in (2) can be transformed into a set of first-order differential equation as follows.

$$\begin{aligned} \begin{aligned} \dot{x}&= y\\ \dot{y}&= -\alpha y-\sin x +a +b\sin \omega t. \end{aligned} \end{aligned}$$
(3)

Figure 2 shows the chaotic attractor for resistive–capacitive-shunted Josephson junction using the following parametervalues: \(\alpha =0.5,\,a=0.89,\,b=0.4\) and \(\omega =0.25.\)

Fig. 2
figure 2

Phase portrait of chaotic attractors of resistive–capacitive Josephson junction

Full size image

3 Generalized reduced-order hybrid combination synchronization of two third-order and one second-order Josephson junctions

3.1 Design of controller via active backstepping technique

In this section, two third-order Josephson junction in (4) and (5) are taken as the drive systems, while one second- order non-autonomous Josephson junction (6) is taken as the response system in order to achieve generalized reduced-order hybrid projective combination synchronization among the three chaotic Josephson junctions. The first drive system is

$$\begin{aligned} \begin{aligned} \dot{x}_1&= x_2 \\ \dot{x}_2&= \frac{1}{\beta _C}(i-g(x_2)x_2-\sin x_1 -x_3) \\ \dot{x}_3&= \frac{1}{\beta _L} (x_2-x_3) \end{aligned} \end{aligned}$$
(4)

and the second drive system is

$$\begin{aligned} \begin{aligned} \dot{y}_1&= y_2 \\ \dot{y}_2&= \frac{1}{\beta _C}(i-g(y_2)y_2-\sin y_1 -y_3) \\ \dot{y}_3&= \frac{1}{\beta _L} (y_2-y_3), \end{aligned} \end{aligned}$$
(5)

while the response system is given as

$$\begin{aligned} \begin{aligned} \dot{z}_1&= z_2 +u_1\\ \dot{z}_2&= -\alpha z_2-\sin z_1 +a +b\sin \omega t +u_2, \end{aligned} \end{aligned}$$
(6)

where \(u_1\), and \(u_2\) are the controllers to be designed. We define the error systems as follows

$$\begin{aligned} \begin{aligned} e_1&= \gamma _1 z_1 -(\alpha _1 x_1 +\beta _1 y_1 +\alpha _3 x_3 + \beta _3 y_3) \\ e_2&= \gamma _2 z_2 +(\alpha _2 x_2 +\beta _2 y_2) \end{aligned} \end{aligned}$$
(7)

Using the error systems defined in (7) with systems defined in (4)–(6) yields the following error dynamics

$$\begin{aligned} \dot{e}_1&= \gamma _1 z_2 +\gamma _1 u_1 -\alpha _1 x_2 -\beta _1 y_2 \\&-\frac{\alpha _3}{\beta _L}(x_2-x_3)-\frac{\beta _3}{\beta _L}(y_2-y_3) \\&= \frac{\gamma _1}{\gamma _2}(e_2-\alpha _2 x_2-\beta _2 y_2)-\alpha _1 x_2 -\beta _1 y_2 \\&-\frac{\alpha _3}{\beta _L}(x_2-x_3)-\frac{\beta _3}{\beta _L}(y_2-y_3)+\gamma _1 u_1 \\ \dot{e}_2&= \gamma _2 (-\alpha z_2 -\sin z_1 + a + b\sin \omega t + u_2)\\&+\frac{\alpha _2}{\beta _C}(i-g(x_2)x_2-\sin x_1 -x_3) \\&+\frac{\beta _2}{\beta _C}(i-g(y_2)y_2-\sin y_1 -y_3) \\&= -\alpha (e_2 - \alpha _2 x_2 - \beta _2 y_2)\\&+\gamma _2 (-\sin z_1 + a + b\sin \omega t + u_2)\\&+\frac{\alpha _2}{\beta _C}(i-g(x_2)x_2-\sin x_1 -x_3)\\&+\frac{\beta _2}{\beta _C}(i-g(y_2)y_2-\sin y_1 -y_3).\\ \end{aligned}$$

Thus, the error dynamics of the system can be written as:

$$\begin{aligned} \dot{e}_1&= \frac{\gamma _1}{\gamma _2}e_2 +\gamma _1 u_1 + A_1\end{aligned}$$
(8)
$$\begin{aligned} \dot{e}_2&= -\alpha e_2 + \gamma _2 u_2 + A_2, \end{aligned}$$
(9)

where

$$\begin{aligned} A_1&= -\frac{\gamma _1}{\gamma _2}(\alpha _2 x_2+\beta _2 y_2)-\alpha _1 x_2\\&-\beta _1 y_2 -\frac{\alpha _3}{\beta _L}(x_2-x_3)-\frac{\beta _3}{\beta _L}(y_2-y_3)\\ A_2&= \alpha (\alpha _2 x_2 +\beta _2 y_2)+\gamma _2 (-\sin z_1 + a + b\sin \omega t)\\&+\frac{\alpha _2}{\beta _C}(i-g(x_2)x_2-\sin x_1 -x_3)\\&+\frac{\beta _2}{\beta _C}(i-g(y_2)y_2-\sin y_1 -y_3) \end{aligned}$$

then we have the following results.

Theorem 1

If the controllers are chosen as

$$\begin{aligned} U_1&= \frac{1}{\gamma _1}\left( \frac{\gamma _1}{\gamma _2}(\alpha _2 x_2+\beta _2 y_2)+\alpha _1 x_2 +\beta _1 y_2\right. \nonumber \\&\left. +\frac{\alpha _3}{\beta _L}(x_2-x_3)+\frac{\beta _3}{\beta _L}(y_2-y_3)-k q_1\right) \nonumber \\ U_2&= \frac{1}{\gamma _2}\Big ((\alpha -k)q_2-\alpha (\alpha _2 x_2 +\beta _2 y_2)\nonumber \\&-\gamma _2 (-\sin z_1 + a + b\sin \omega t) -\frac{\gamma _1}{\gamma _2}q_1 \nonumber \\&-\frac{\alpha _2}{\beta _C}(i-g(x_2)x_2-\sin x_1 -x_3)\nonumber \\&\left. -\frac{\beta _2}{\beta _C}(i-g(y_2)y_2-\sin y_1 -y_3)\right) , \end{aligned}$$
(10)

where \(q_1=e_1\) and \(q_2=e_2\) then, the drive systems (4) and (5) will achieve generalized reduced-order hybrid combination synchronization with the response systems (6).

Proof

Our goal is to find the control functions which will enable the systems (4), (5), and (6) to realize generalized reduced-order hybrid combination synchronization via active backstepping technique. The design procedures includes three steps as shown below:

Step 1

Let \(q_1=e_1\), its time derivative is

$$\begin{aligned} \dot{q}_1 = \dot{e}_1 = \frac{\gamma _1}{\gamma _2}e_2 +\gamma _1 u_1 + A_1, \end{aligned}$$
(11)

where \(e_2=\alpha _1 (q_1)\) can be regarded as virtual controller. In order to stabilize \(q_1\)-subsystem, we choose the following Lyapunov function \(v_1 = \frac{1}{2}q_1^2\). The time derivative of \(v_1\) is

$$\begin{aligned} \dot{v}_1 = q_1 \dot{q}_1 = q_1\left( \frac{\gamma _1}{\gamma _2}\alpha _1 (q_1) +\gamma _1 u_1 + A_1\right) \end{aligned}$$
(12)

Suppose \(\alpha _1 (q_1)=0\) and the control function \(u_1\) is chosen as

$$\begin{aligned} u_1 = -\frac{1}{\gamma _1}(A_1+k q_1) \end{aligned}$$
(13)

then \(\dot{v}_1 = -k q_1^2 < 0\), where \(k\) is positive constant which represent the feedback gain. Then, \(\dot{v}_1\) is negative definite and the subsystem \(q_1\) is asymptotically stable. Since, the virtual controller \(\alpha _1 (q_1)\) is estimative, the error between \(e_2\) and \(\alpha _1 (q_1)\) can be denoted by \(q_2=e_2-\alpha _1 (q_1)\). Thus, we have the following \((q_1,q_2)\)-subsystems

$$\begin{aligned} \begin{aligned} \dot{q}_1&= \frac{\gamma _1}{\gamma _2}q_2-k q_1 \\ \dot{q}_2&= -\alpha q_2 + \gamma _2 u_2 + A_2 \end{aligned} \end{aligned}$$
(14)

Step 2

In order to stabilize subsystem (14), the following Lyapunov function can be chosen as \(v_2 = v_1 + \frac{1}{2}q_2^2\). The time derivative of \(v_2\) is

$$\begin{aligned} \dot{v}_2 = -k q_1^2 + q_2\left( \frac{\gamma _1}{\gamma _2}q_1-\alpha q_2 + \gamma _2 u_2 + A_2\right) \end{aligned}$$
(15)

If the control function \(u_2\) is chosen as

$$\begin{aligned} u_2 = \frac{1}{\gamma _2}\left( -A_2-k q_2+\alpha q_2-\frac{\gamma _1}{\gamma _2}q_1\right) \end{aligned}$$
(16)

then \(\dot{v}_2 = -k q_1^2 -k q_2^2< 0\), where k is a positive constant which represent the feedback gain. Then, \(\dot{v}_2\) is negative definite and the subsystem \((q_1, q_2)\) (14) is asymptotically stable. This implies that generalized reduced-order hybrid combination synchronization of the drive systems (4) and (5) and the response system (6) is achieved. Finally, we have the following subsystem

$$\begin{aligned} \begin{aligned} \dot{q}_1&= \frac{\gamma _1}{\gamma _2}q_2-k q_1 \\ \dot{q}_2&= -\frac{\gamma _1}{\gamma _2}q_1 -k q_2 \end{aligned} \end{aligned}$$
(17)

so this completes the prove. \(\square \)

The following Corollaries can easily be obtained from Theorem 1, the proofs of these Corollaries are similar to Theorem 1 so, they are omitted.

Let \(\alpha _1=\alpha _2=\alpha _3=0,\,\gamma _1=\gamma _2=\gamma _3=1\), then, we have Corollary 1.

Corollary 1

If the controllers are chosen as

$$\begin{aligned} u_1&= \beta _1 y_2+\beta _2 y_2+\frac{\beta _3}{\beta _L}(y_2-y_3) \nonumber \\ u_2&= (\alpha -k)q_2-q_1-\alpha \beta _2 y_2+\sin z_1 - a - b\sin \omega t \nonumber \\&- \frac{\beta _2}{\beta _C}(i-g(y_2)y_2-\sin y_1 -y_3), \end{aligned}$$
(18)

where \(q_1 = z_1 -\beta _1 y_1 -\beta _3 y_3,\,q_2 = z_2 +\beta _2 y_2\) then the drive system (5) achieve reduced-order-modified projective hybrid synchronization with the response system (6).

Let \(\gamma _1=\gamma _2=\gamma _3=1,\,\beta _1=\beta _2=\beta _3=0\), then we obtain Corollary 2.

Corollary 2

If the controllers are chosen as

$$\begin{aligned} u_1&= \alpha _1 x_2+\alpha _2 x_2+\frac{\alpha _3}{\beta _L}(x_2-x_3) \nonumber \\ u_2&= (\alpha -k)q_2-q_1-\alpha \alpha _2 x_2+\sin z_1 - a - b\sin \omega t \nonumber \\&- \frac{\alpha _2}{\beta _C}(i-g(x_2)x_2-\sin x_1 -x_3), \end{aligned}$$
(19)

where \(q_1 = z_1 -\alpha _1 x_1 -\alpha _3 x_3,\,q_2 = z_2 +\alpha _2 x_2 \) then the drive system (4) achieve reduced-order-modified projective hybrid synchronization with the response system (6).

Suppose \(\gamma _1=\gamma _2=\gamma _3=1,\,\alpha _1=\alpha _2=\alpha _3=0,\,\beta _1=\beta _2=\beta _3=0\), then, we obtain Corollary 3.

Corollary 3

If the controllers are chosen as

$$\begin{aligned} \begin{aligned} u_1&= 0 \\ u_2&= (\alpha -k)q_2-q_1+\sin z_1 - a - b\sin \omega t, \end{aligned} \end{aligned}$$
(20)

where \(q_1 = z_1 ,\,q_2 = z_2\) then the equilibrium point \((0, 0, 0)\) of the response system (6) is asymptotically stable.

Suppose \(\gamma _1=\gamma _2=\gamma _3=1,\,\beta _1=\beta _2=\beta _3=1\), and \(\alpha _1=\alpha _2=\alpha _3=1\) then, we obtain Corollary 4.

Corollary 4

If the controllers are chosen as

$$\begin{aligned} \begin{aligned} u_1&= \frac{1}{\beta _L}(x_2-x_3+y_2-y_3)+2(x_2+y_2) \\ u_2&= (\alpha -k)q_2-q_1-\alpha ( x_2+y_2)\\&\quad +\sin z_1 \!-\! a \!-\! b\sin \omega t\!+\!\frac{1}{\beta _C}(g(x_2)x_2 \!+\! g(y_2)y_2 \\&\quad +\sin x_1+\sin y_1 +x_3+y_3-2i), \end{aligned} \end{aligned}$$
(21)

where \(q_1 = z_1 -(x_1+y_1+x_3+y_3),\,q_2 = z_2 +(x_2+y_2)\) then, the drive systems (4) and (5) achieve reduced-order hybrid combination synchronization with the response system (6).

Let \(\alpha _1=\alpha _2=\alpha _3=1,\,\beta _1=\beta _2=\beta _3=1\), then we obtain Corollary 5.

Corollary 5

If the controllers are chosen as

$$\begin{aligned} \begin{aligned} u_1&= \frac{1}{\gamma _1}\left( \frac{\gamma _1}{\gamma _2}( x_2+ y_2)+x_2+y_2 \right. \\&\quad \left. +\frac{1}{\beta _L}(x_2-x_3+y_2-y_3)\right) \\ u_2&= \frac{1}{\gamma _2}((\alpha -k)q_2-\frac{\gamma _1}{\gamma _2}q_1-\alpha (x_2+y_2)\\&\quad +\gamma _2(\sin z_1 - a - b\sin \omega t)\\&\quad -\frac{1}{\beta _C}(2i-g(x_2)x_2-\sin x_1 -x_3\\&\quad -g(y_2)y_2-\sin y_1 -y_3), \end{aligned} \end{aligned}$$
(22)

where \(q_1 = \gamma z_1 -( x_1+y_1+ x_3+y_3),\,q_2 = \gamma z_2 +(x_2+y_2)\) then the drive system (4) and (5) achieve reduced-order-modified hybrid projective combination synchronization with the response system (6).

3.2 Numerical simulation results

To verify the effectiveness of the designed controllers we used ode45 fourth-order Runge–Kutta algorithm run on Matlab. In the numerical simulation procedure the system parameters are chosen to ensure chaotic dynamics of the state variables as shown in Figs. 1 and 2. Assume that (i) \(\gamma _1=\gamma _2=\gamma _3= \alpha _1=\alpha _2=\alpha _3=\beta _1=\beta _2=\beta _3=1\) in accordance with Corollary 4. The initial conditions of the drive systems and response system are given as \((x_1,x_2,x_3)=(0, 0, 0),\,(y_1,y_2,y_3)=(1 1 1 ),\,(z_1,z_2)=(0, 1)\), thus we have the initial conditions of the error systems as \((10, 5)\). Corresponding numerical results are as follows: Figure 3 shows that reduced order hybrid combination synchronization among systems (4), (5), and (6) is achieved as indicated by the convergence of the error state variables to zero as soon as the controllers are switched on for \(t\ge 100\). Figure 4 shows the trajectory of drive and the response state variables when the controllers are activated for \(t\ge 100\) this again confirms reduced-order hybrid combination synchronization among systems (4), (5), and (6). (ii) We assume that \(\gamma _1=\gamma _2=\gamma _3=0.5,\,\alpha _1=\alpha _2=\alpha _3=\beta _1=\beta _2=\beta _3=1\) in accordance with Corollary 5 with the same initial conditions as given above and the same set of system parameters. The corresponding numerical results are as follows: Figure 5 shows that reduced order hybrid projective combination synchronization among systems (4), (5), and (6) is achieved as indicated by the convergence of the error state variables to zero as soon as the controllers are switched on for \(t\ge 100\). Figure 6 shows the projection of drive and the response state variables when the controllers are activated for \(t\ge 100\) this again confirms reduced-order hybrid projective combination synchronization among systems (4), (5), and (6).

Fig. 3
figure 3

Error dynamics among the drives and the response system with controllers deactivated for \(0<t<100\) and activated for \(t\ge 100\), where \(e_1= z_1 - x_1 -y_1 -( x_3 + y_3),\,e_2 = z_2 -x_2 -y_2\) and \(e=\sqrt{e_1^2+e_2^2}\)

Full size image
Fig. 4
figure 4

Dynamics of the drives (dashed line)and the response (solid line) variables with controllers deactivated for \(0<t<100\) and activated for \(t\ge 100\)

Full size image
Fig. 5
figure 5

Error dynamics among the drives and the response system with controllers deactivated for \(0<t<100\) and activated for \(t\ge 100\), where \(e_1= \gamma _1 z_1 - x_1 -y_1 -( x_3 + y_3),\,e_2 = \gamma _2 z_2 -x_2 -y_2,\,e=\sqrt{e_1^2+e_2^2}\) and \(\gamma _1 = \gamma _2 = \gamma _3=0.5\)

Full size image
Fig. 6
figure 6

Dynamics of the drives (dashed line) and the response (solid line) variables with controllers deactivated for \(0<t<100\) and activated for \(t\ge 100\)

Full size image

4 Generalized reduced-order hybrid combination synchronization of one third-order and two second-order Josephson junctions

4.1 Design of controller via active backstepping technique

In this section, one third-order Josephson junction in (4) is taken as the drive system while two second-order non-autonomous Josephson junction in (23) and (24) are taken as the response systems in order to achieve generalized reduced-order hybrid combination synchronization among the three chaotic Josephson junctions.

$$\begin{aligned} \begin{aligned} \dot{y}_1&= y_2 +u_1 \\ \dot{y}_2&= -\alpha y_2-\sin y_1 +a +b\sin \omega t+u_2, \end{aligned} \end{aligned}$$
(23)
$$\begin{aligned} \begin{aligned} \dot{z}_1&= z_2 +u_3 \\ \dot{z}_2&= -\alpha z_2-\sin z_1 +a +b\sin \omega t +u_4, \end{aligned} \end{aligned}$$
(24)

where \(u_1, u_2, u_3\), and \(u_4\) are the controllers to be designed. We define the error systems as follows

$$\begin{aligned} \begin{aligned} e_1&= \gamma _1 z_1+\beta _1 y_1 -(\alpha _1 x_1 + \alpha _3 x_3) \\ e_2&= \gamma _2 z_2 +(\beta _2 y_2+\alpha _2 x_2) \end{aligned} \end{aligned}$$
(25)

Using the error systems defined in (25) with systems defined in (4), (23), and (24) yields the following error dynamics

$$\begin{aligned} \dot{e}_1&= \gamma _1 z_2 +\gamma _1 u_3 -\alpha _1 x_2 +\beta _1 (y_2+u_1)\\&-\frac{\alpha _3}{\beta _L}(x_2-x_3) \\&= \frac{\gamma _1}{\gamma _2}(e_2-\alpha _2 x_2-\beta _2 y_2)-\alpha _1 x_2 +\beta _1 y_2 \\&-\frac{\alpha _3}{\beta _L}(x_2-x_3)+\gamma _1 u_3+\beta _1 u_1\\ \dot{e}_2&= \gamma _2 (-\alpha z_2 -\sin z_1 + a + b\sin \omega t + u_4)\\&+\beta _2 (-\alpha y_2 -\sin y_1 + a + b\sin \omega t + u_2)\\&+\frac{\alpha _2}{\beta _C}(i-g(x_2)x_2-\sin x_1 -x_3)\\&= -\alpha (e_2-\beta _2 y_2-\alpha _2 x_2)\\&+\gamma _2 ( -\sin z_1 + a + b\sin \omega t) +\gamma _2 u_4\\&+\beta _2 (-\alpha y_2 -\sin y_1 + a + b\sin \omega t)\\&+ \beta _2 u_2 +\frac{\alpha _2}{\beta _C}(i-g(x_2)x_2-\sin x_1 -x_3) \end{aligned}$$

Thus, the error dynamics of the system can be written as:

$$\begin{aligned} \dot{e}_1&= \frac{\gamma _1}{\gamma _2}e_2 + U_1 + B_1 \end{aligned}$$
(26)
$$\begin{aligned} \dot{e}_2&= -\alpha e_2 + U_2 + B_2, \end{aligned}$$
(27)

where

$$\begin{aligned} B_1&= -\frac{\gamma _1}{\gamma _2}(\alpha _2 x_2+\beta _2 y_2)-\alpha _1 x_2\\&+\beta _1 y_2 -\frac{\alpha _3}{\beta _L}(x_2-x_3) \\ B_2&= \alpha (\beta _2 y_2+\alpha _2 x_2)+ \gamma _2 ( -\sin z_1 + a + b\sin \omega t)\\&+\beta _2 (-\alpha y_2 -\sin y_1 + a + b\sin \omega t)\\&+\frac{\alpha _2}{\beta _C}(i-g(x_2)x_2-\sin x_1 -x_3)\\ U_1&= \beta _1 u_1 + \gamma _1 u_3\\ U_2&= \beta _2 u_2 + \gamma _2 u_4 \end{aligned}$$

then we have the following results.

Theorem 2

If the controllers are chosen as

$$\begin{aligned} U_1&= \frac{\gamma _1}{\gamma _2}(\alpha _2 x_2+\beta _2 y_2)+\alpha _1 x_2 \nonumber \\&-\beta _1 y_2 +\frac{\alpha _3}{\beta _L}(x_2-x_3) \nonumber \\ U_2&= (\alpha - k)q_2-\gamma _2 ( -\sin z_1 + a + b\sin \omega t) \nonumber \\&-\beta _2 (-\alpha y_2 -\sin y_1 + a + b\sin \omega t) \nonumber \\&-\alpha (\beta _2 y_2+\alpha _2 x_2)\nonumber \\&-\frac{\alpha _2}{\beta _C}(i-g(x_2)x_2-\sin x_1 -x_3) -\frac{\gamma _1}{\gamma _2}q_1, \end{aligned}$$
(28)

where \(q_1=e_1\) and \(q_2=e_2\) then, the drive systems (4) and (23) will achieve generalized reduced-order hybrid combination synchronization with the response systems (24).

Proof

Our goal is to find the control functions which will enable the systems (4), (23), and (24) to realize generalized reduced-order hybrid combination synchronization via active backstepping technique. The design procedures includes three steps as shown below:

Step 1

Let \(q_1=e_1\), then its time derivative is

$$\begin{aligned} \dot{q}_1 = \dot{e}_1 = \frac{\gamma _1}{\gamma _2}e_2 +U_1 + B_1, \end{aligned}$$
(29)

where \(e_2=\alpha _1 (q_1)\) can be regarded as virtual controller. In order to stabilize \(q_1\)-subsystem, we choose the following Lyapunov function \(v_1 = \frac{1}{2}q_1^2\). The time derivative of \(v_1\) is

$$\begin{aligned} \dot{v}_1 = q_1 \dot{q}_1 = q_1 \left( \frac{\gamma _1}{\gamma _2}\alpha _1 (q_1) +U_1 + B_1\right) \end{aligned}$$
(30)

Suppose \(\alpha _1 (q_1)=0\) and the control function \(U_1\) is chosen as

$$\begin{aligned} U_1 = -(B_1+k q_1) \end{aligned}$$
(31)

then \(\dot{v}_1 = -k q_1^2 < 0\) where \(k\) is positive constant which represent the feedback gain. Then, \(\dot{v}_1\) is negative definite and the subsystem \(q_1\) is asymptotically stable. Since, the virtual controller \(\alpha _1 (q_1)\) is estimative, the error between \(e_2\) and \(\alpha _1 (q_1)\) can be denoted by \(q_2= e_2 -\alpha _1 (q_1)\). Thus, we have the following \((q_1,q_2)\)-subsystems

$$\begin{aligned} \begin{aligned} \dot{q}_1&= \frac{\gamma _1}{\gamma _2}q_2-k q_1 \\ \dot{q}_2&= -\alpha q_2 + U_2 + B_2. \end{aligned} \end{aligned}$$
(32)

Step 2

In order to stabilize system (32), a Lyapunov function can be chosen as \(v_2 = v_1 + \frac{1}{2}q_2^2\). Its time derivative is

$$\begin{aligned} \dot{v}_2 = -k q_1^2 + q_2 \left( \frac{\gamma _1}{\gamma _2}q_1-\alpha q_2 + U_2 + B_2 \right) . \end{aligned}$$
(33)

If the control function \(u_2\) is chosen as

$$\begin{aligned} U_2 = \left( -B_2-k q_2+\alpha q_2-\frac{\gamma _1}{\gamma _2}q_1 \right) \end{aligned}$$
(34)

then \(\dot{v}_2 = -k q_1^2 -k q_2^2< 0\) where \(k\) is a positive constant which represent the feedback gain. Then, \(\dot{v}_2\) is negative definite and the subsystem \((q_1, q_2)\) in (27) is asymptotically stable. This implies that the drive system (4) and the response systems (23) and (24) achieve generalized reduced-order hybrid projective combination synchronization. Finally, we have the following subsystem

$$\begin{aligned} \begin{aligned} \dot{q}_1&= \frac{\gamma _1}{\gamma _2}q_2-k q_1\\ \dot{q}_2&= -\frac{\gamma _1}{\gamma _2}q_1-k q_2. \end{aligned} \end{aligned}$$
(35)

This completes the proof. \(\square \)

Let \(\alpha _1=\alpha _2=\alpha _3=1,\,\beta _1=\beta _2=0\) then, we have Corollary 6.

Corollary 6

If the controllers are chosen as

$$\begin{aligned} u_3&= \frac{1}{\gamma _1}\left( \frac{1}{\beta _L}(x_2-x_3)+\frac{\gamma _1}{\gamma _2}x_2-k q_1\right) \nonumber \\ u_4&= \frac{1}{\gamma _2}\left( (\alpha -k)q_2-\frac{\gamma _1}{\gamma _2}q_1-\alpha x_2\right. \nonumber \\&-\gamma _2(a+b\sin \omega t-\sin z_1) \nonumber \\&\left. -\frac{1}{\beta _C}(i-g(x)x_2-\sin x_1-x_3)\right) , \end{aligned}$$
(36)

where \(e_1 = \gamma _1 z_1 -(x_1 + x_3),\,e_2 = \gamma _2 z_2 + x_2 \) then the drive system (4) achieve modified projective hybrid synchronization with the response system (24).

Let \(\alpha _1=\alpha _2=\alpha _3=0,\,\beta _1=\beta _2=0\), then we obtain Corollary 7.

Corollary 7

If the controllers are chosen as

$$\begin{aligned} u_3&= \frac{1}{\gamma _1}(-k q_1) \nonumber \\ u_4&= \frac{1}{\gamma _2}\Big ((\alpha -k) q_2-\frac{\gamma _1}{\gamma _2}q_1\nonumber \\&-\gamma _2(a+b\sin \omega t-\sin z_1)\Big ), \end{aligned}$$
(37)

where \(e_1 = \gamma _1 z_1,\,e_2 = \gamma _2 z_2\) then the equilibrium \((0, 0, 0)\) of the response system (24) are asymptotically stable.

Suppose \(\gamma _1=\gamma _2=1,\,\alpha _1=\alpha _2=\alpha _3=0\) and \(\beta _1=\beta _2=1\) then, we obtain Corollary 8.

Corollary 8

If the controllers are chosen as

$$\begin{aligned} \begin{aligned} u_1&= u_3 = \frac{1}{2}(-k q_1)\\ u_1&\!=\! u_4 \!=\! \frac{1}{2}\Big ((\alpha -k )q_2\!-\!q_1\!-\!2(a+b\sin \omega t)\\&\quad +\sin z_1+\sin y_1\Big ), \end{aligned} \end{aligned}$$
(38)

where \(q_1 = z_1 + y_1,\,q_2 = z_2 + y_2\) then anti-synchronization is achieved between systems (23) and (24).

Let \(\alpha _1=\alpha _2=\alpha _3=1,\,\beta _1=\beta _2=1,\,\gamma _1=\gamma _2=1\) then, we have Corollary 9.

Corollary 9

If the controllers are chosen as

$$\begin{aligned} \begin{aligned} u_1&= u_3 = \frac{1}{2}\left( \frac{1}{\beta _L}(x_2-x_3)-k q_1+2x_2\right) \\ u_2&= u_4 = \frac{1}{2}\Big ((\alpha -k)q_2-q_1-\alpha x_2 \\&\quad -2(a+b\sin \omega t)+\sin z_1+\sin y_1 \\&\quad -\frac{1}{\beta _C}(i-g(x)x_2-\sin x_1-x_3)\Big ), \end{aligned} \end{aligned}$$
(39)

where \(q_1 = z_1+y_1 -(x_1 + x_3),\,q_2 = z_2 + y_2 +x_2 \) then reduced-order hybrid combination synchronization is achieved among systems (4), (23), and (24).

Let \(\gamma _1=\gamma _2=1,\,\beta _1=\beta _2=1\) then, we have Corollary 10.

Corollary 10

If the controllers are chosen as

$$\begin{aligned} u_1&= u_3 = \frac{1}{2}\left( \frac{\alpha _3}{\beta _L}(x_2-x_3)+(\alpha _2+\alpha _1)x_2-k q_1\right) \nonumber \\ u_2&= u_4 = \frac{1}{2}\Big ((\alpha -k)q_2-q_1-\alpha x_2 \nonumber \\&-2(a+b\sin \omega t)+\sin z_1+\sin y_1 \nonumber \\&-\frac{\alpha _2}{\beta _C}(i-g(x_2)x_2-\sin x_1-x_3)\Big ) \end{aligned}$$
(40)

where \(q_1 = z_1+y_1 -(\alpha _1 x_1 + \alpha _3 x_3),\,q_2 = z_2 + y_2 +\alpha _2 x_2 \) then reduced-order modified projective hybrid combination synchronization is achieved among systems (4), (23) and (24).

4.2 Numerical simulation results

To verify the effectiveness of the designed controllers we used ode45 fourth-order Runge–Kutta algorithm run on Matlab. In the numerical simulation procedure the system parameters are chosen to ensure chaotic dynamics of the state variables as shown in Figs. 1 and 2. Assume that (i) \(\gamma _1=\gamma _2= \beta _1=\beta _2=\alpha _1=\alpha _2=\alpha _3=1\) in accordance with Corollary (9). The initial conditions of the drive systems and response system are given as \((x_1,x_2,x_3)=(0, 0, 0),\,(y_1,y_2,y_3)=(1, 1, 1 ),\,(z_1,z_2)=(0, 1)\), thus we have the initial conditions of the error systems as \((4, 3)\). Corresponding numerical results are as follows: Fig. 7 shows that reduced order hybrid combination synchronization among systems (4), (23) and (24) is achieved as indicated by the convergence of the error state variables to zero as soon as the controllers are switched on for \(t\ge 0\). Figure 8 shows the projection of the drive state variable on response systems when the controllers are activated for \(t\ge 0\) which again confirm reduced order hybrid combination synchronization among systems (4), (23), and (24). (ii) We assumed that \(\alpha _1=\alpha _2=\alpha _3=0.5,\,\gamma _1=\gamma _2=\beta _1=\beta _2=1\) in accordance with Corollary (10) and used the same initial conditions and system parameters as given above. The corresponding numerical results are as follows: Figure 9 shows that reduced order hybrid projective combination synchronization among systems (4), (23), and (24) is achieved as indicated by the convergence of the error state variables to zero as soon as the controllers are switched on for \(t\ge 0\). Figure 10 shows the projection of the drive state variable on response systems when the controllers are activated for \(t\ge 0\) which again confirm reduced-order hybrid projective combination synchronization among systems (4), (23), and (24) with system 4) as the drive systems and systems (23) and (24) as response systems.

Fig. 7
figure 7

Error dynamics among the drive and the response systems with controllers activated for \(t\ge 0\), where \(e_1= z_1 - x_1 -y_1 -(x_3 + y_3),\,e_2 = z_2 -x_2 -y_2\) and \(e=\sqrt{e_1^2+e_2^2}\)

Full size image
Fig. 8
figure 8

Dynamics of the drive (dashed line) and the responses (solid line) variables with controllers activated for \(t\ge 0\)

Full size image
Fig. 9
figure 9

Error dynamics among the drives and the response system with controllers activated for \(t\ge 0\), where \(e_1 = z_1+y_1 -(\alpha _1 x_1 + \alpha _3 x_3),\,e_2 = z_2 + y_2 - \alpha _2 x_2 \) and \(\alpha _1 = \alpha _2 = \alpha _3=0.5\)

Full size image
Fig. 10
figure 10

Dynamics of the drives (dashed line) and the response (solid line) variables with controllers activated for \(t\ge 0\)

Full size image

5 Conclusion

The generalized reduced-order hybrid projective combination synchronization discussed in this paper can be used to improve security of information transmission in two ways: (1) a signal \(f(t)\) can split up into two different signals say, \(f_1 (t)\) and \(f_2(t)\). Each signal \(f_1 (t)\) and \(f_2(t)\) is loaded into each first-drive third-order JJ and, after synchronization has taken place between the response (second-order) JJ and the two third-order drive JJs, the message can be retrieved; (2) another way is to load the split up signals \(f_1 (t)\) into the first-drive third-order JJ at time \(t_1\) and load the second signal \(f_2 (t)\) into the second-drive (third-order) JJ at another time \(t_2\) and after each of the drive JJs has undergone synchronization with the response JJ, the message can retrieved and recombined. Reduced-order hybrid and reduced-order hybrid projective combination synchronization have been achieved for three chaotic systems consisting of: (i) two third-order chaotic Josephson junctions as drives and one second-order chaotic Josephson junction as response system; (ii) one third-order chaotic Josephson junction as the drive and two second-order chaotic Josephson junctions as the slaves via active backstepping technique. We showed from the theoretical analysis that various controllers which are suitable for different type of synchronization scheme can be obtained from the general results. The typical one drive to one response is a special case of combination synchronization hence, it has more potential applications in physics, biology, electrical engineering, communication theory, and many other fields.