1 Introduction

Many identification methods focus on discrete-time systems with same sampling rates [1–4]. However, in many industry applications, the inputs and outputs have different updating rates due to the sensor limits. The systems operating at different input and output sampling rates are called multirate systems [5–7]. Dual-rate systems are a class of multirate systems, where the output sampling period is an integer multiple of the input updating period [8, 9]. Dual-rate systems are often encountered in control, communication, signal processing. There exist several methods to deal with dual-rate system identification, i.e., the lifting technique [10], the polynomial transformation technique [9]. Ding et al. [11] studied the hierarchical least squares identification for linear SISO systems with dual-rate sampled-data and presented a stochastic gradient identification algorithm for estimate the parameters of the dual-rate systems. Liu et al. presented a least squares estimation algorithm for a class of non-uniformly sampled systems based on the hierarchical identification principle [12–14].

Hammerstein systems, which consist of a static nonlinear subsystem followed by a linear dynamic subsystem, can represent many nonlinear dynamic systems [15–22]. There exists a large amount of work on the parametric model identification of Hammerstein systems [23]. Some existing contributions assumed that the nonlinearity is a polynomial combination of a known order in the input [24]. Recently, Li et al. [25] presented a maximum likelihood least squares identification algorithm for input nonlinear finite impulse response moving average systems.

Recursive algorithms are a class of basic parameter estimation approaches which are suitable for on-line applications [26–29]. For decades, recursive algorithms have been used to estimate the parameters of the linear and nonlinear systems [30–32]. Xiao et al. [33] analyzed the convergence of the recursive least squares (RLS) algorithms for controlled auto-regression models. Wang [34] presented a filtering and auxiliary model-based RLS (AM-RLS) identification algorithm to estimate the parameter of output error moving average systems. This paper extends the identification algorithms from the original single-rate Hammerstein model to the dual-rate sampled-data one. The basic idea is, by means of the key-term separation principle, to present a dual-rate Hammerstein model and then derive the AM-RLS algorithm for the proposed model.

The rest of this paper is organized as follows: Sect. 2 presents the identification model of Hammerstein nonlinear systems with dual-rate sampling. Section 3 derives a AM-RLS algorithm for Hammerstein nonlinear systems with dual-rate sampling. Section 4 proves the convergence of the proposed algorithm. Section 5 provides examples to illustrate the effectiveness of the proposed algorithm. Some conclusions are summarized in Sect. 6.

2 Problem formulation

Let us introduce some notation first. The superscript T denotes the matrix transpose; the norm of a matrix \({\varvec{X}}\) is defined by \(\Vert {\varvec{X}}\Vert ^{2}:=\mathrm{tr}[{\varvec{X}}{\varvec{X}}^{\tiny \text{ T }}]\); \(\mathbf{1}_n\) being an \(n\)-dimensional column vector whose elements are all 1; \(\lambda _{\min }[{\varvec{X}}]\) represents the minimum eigenvalue of the symmetric matrix \({\varvec{X}}\); \(f(t)=O(g(t))\) represents that for \(g(t)\geqslant 0\), if there exists a positive constant \(\delta _{1}\) such that \(\Vert f(t)\Vert \geqslant \delta _{1}g(t)\).

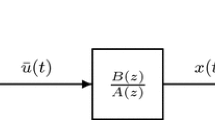
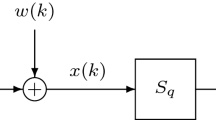
Consider a dual-rate Hammerstein output error system shown in Fig. 1, where \(y(k)\) is the measured output, \(u(k)\) and \(\bar{u}(k)\) are the input and output of the nonlinear subsystem, respectively, \(S_{qh}\) is a sampler with period \(qh\) (\(q\) being a positive integer), which yields a discrete-time signal \(y(kq)\). The input–output data available are \(\{u(k): k=0,1,2,\ldots \}\) at the fast rate, and \(\{y(kq): k=0, 1, 2,\ldots \}\) at the slow rate. Thus, the intersample outputs \(\{y(kq+i), i=1,2,\ldots ,q-1\}\), are not available. Here, we refer to \(\{u(k),y(kq)\}\) as the dual-rate measurement data. \(\bar{u}(k)\) is assumed to be a linear combination of known nonlinear basis functions \({\varvec{f}}:=(f_1,f_2,\ldots ,f_n)\) [35, 36]:

$$\begin{aligned} \bar{u}(k)&= f(u(k))=\gamma _1f_1(u(k)) +\gamma _2f_2(u(k))\nonumber \\&+\cdots + \gamma _{n_{\gamma }}f_{n_{\gamma }}(u(k)),\nonumber \\&= {\varvec{f}}(u(k)){\varvec{\gamma }}, {\varvec{\gamma }}\!:=\!\left[ \gamma _1,\gamma _2,\ldots , \gamma _{n_{\gamma }}\right] ^{\tiny \text{ T }}\in {\mathbb {R}}^{n_{\gamma }}.\nonumber \\ \end{aligned}$$
(1)

\(G(z):=\frac{B(z)}{A(z)}\) is the transfer function of the linear subsystem, and \(A(z)\) and \(B(z)\) are the polynomials in \(z^{-1}\) (\(z^{-1}\) is the unit backward shift operator, i.e., \(z^{-1}u(k)=u(k-1)\)):

$$\begin{aligned} A(z)&:= 1+\alpha _1z^{-1}+\alpha _2z^{-2}+\cdots +\alpha _nz^{-n}, \\ B(z)&:= \beta _0+\beta _1z^{-1}+\beta _2z^{-2}+\cdots +\beta _nz^{-n}. \end{aligned}$$

From Fig. 1, we have

$$\begin{aligned} w(k)&= \frac{B(z)}{A(z)}\bar{u}(k),\end{aligned}$$
(2)
$$\begin{aligned} y(k)&= w(k)+v(k). \end{aligned}$$
(3)

Replacing \(k\) in (2) with \(kq\) gives

$$\begin{aligned} w(kq)=\left[ 1-A(z)\right] w(kq)+B(z)\bar{u}(kq). \end{aligned}$$
(4)

Equation (3) can be expressed as

$$\begin{aligned} y(kq)&= \left[ 1-A(z)\right] w(kq)+B(z)\bar{u}(kq)+v(kq)\nonumber \\&= \beta _0\bar{u}(kq)+\beta _1\bar{u}(kq-1) +\beta _2 \bar{u}(kq-2)\nonumber \\&+\,\cdots +\beta _n\bar{u}(kq-n) -\alpha _1w(kq-1)\nonumber \\&-\,\alpha _2w(kq{-}2) -\cdots -\alpha _nw(kq-n)+v(kq).\nonumber \\ \end{aligned}$$
(5)

Referring to [37], without loss of generality, we set the coefficient of the key-term \(\bar{u}(kq)\) on the right-hand side to be 1 (i.e., \(\beta _0=1\)). Inserting (1) into (5) gives

$$\begin{aligned} y(kq)&= \sum _{i=1}^{n_{\gamma }}\gamma _if_i(u(kq))+\beta _1\bar{u}(kq-1)\nonumber \\&+\,\beta _2\bar{u}(kq-2)+\cdots +\beta _{nq}\bar{u}(kq-n)\nonumber \\&-\,\alpha _1w(kq-1)-\alpha _2w(kq-2)\nonumber \\&-\cdots -\alpha _nw(kq-n)+v(kq). \end{aligned}$$
(6)

The objective of this paper is to present a RLS algorithm to estimate the parameters \(\alpha _i,\,\beta _i\) and \(\gamma _i\) for the dual-rate Hammerstein output error systems using the key-term separation principle and the auxiliary model identification idea.

Fig. 1
figure 1

The Hammerstein system with dual-rate sampling

Full size image

3 The auxiliary model-based RLS algorithm

This section derives the AM-RLS algorithm for the dual-rate sampled-data Hammerstein output error model.

Define the information vector \({\varvec{\varphi }}(kq)\) and the parameter vector \({\varvec{\theta }}\) as

$$\begin{aligned} {\varvec{\varphi }}(kq)&:= \big [-w(kq-1),-w(kq-2),\ldots ,\\&\,-\,w(kq-n),\bar{u}(kq-1),\bar{u}(kq-2)\ldots ,\\&\bar{u}(kq-n), f_1(u(kq)),f_2(u(kq))\ldots ,\\&f_{n_{\gamma }}(u(kq))\big ]^{\tiny \text{ T }}\in {\mathbb {R}}^{n_0},\\ {\varvec{\theta }}&:= \big [\alpha _1,\alpha _2,\ldots ,\alpha _n,\beta _1,\beta _2,\ldots , \beta _n,\gamma _1,\\&\gamma _2,\ldots ,\gamma _{n_\gamma }\big ]^{\tiny \text{ T }}\in {\mathbb {R}}^{n_0},\quad n_0:=2n+n_{\gamma }. \end{aligned}$$

Equation (6) can be written in a regressive form,

$$\begin{aligned} y(kq)={\varvec{\varphi }}^{\tiny \text{ T }}(kq){\varvec{\theta }}+v(kq). \end{aligned}$$
(7)

Define a quadratic criterion function,

$$\begin{aligned} J({\varvec{\theta }}):=\sum _{i=1}^k\left[ y(iq)-{\varvec{\varphi }}^{\tiny \text{ T }}(iq){\varvec{\theta }}\right] ^2. \end{aligned}$$

Let \(\hat{{\varvec{\theta }}}(kq)\) be the estimate of \({\varvec{\theta }}\) at time \(kq\). Minimizing \(J({\varvec{\theta }})\), gives the following RLS algorithm:

$$\begin{aligned} \hat{{\varvec{\theta }}}(kq)&= \hat{{\varvec{\theta }}}(kq-q) +{\varvec{P}}(kq){\varvec{\varphi }}(kq)\nonumber \\&\times \left[ y(kq)-{\varvec{\varphi }}^{\tiny \text{ T }}(kq)\hat{{\varvec{\theta }}}(kq-q)\right] , \end{aligned}$$
(8)
$$\begin{aligned} \hat{{\varvec{\theta }}}(kq+i)&= \hat{{\varvec{\theta }}}(kq),\quad i=0,1,\ldots ,q-1, \end{aligned}$$
(9)
$$\begin{aligned} {\varvec{P}}(kq)={\varvec{P}}(kq{-}q) {-} \frac{{\varvec{P}}(kq{-}q){\varvec{\varphi }}(kq){\varvec{\varphi }}^{\tiny \text{ T }}(kq) {\varvec{P}}(kq{-}q)}{1+{\varvec{\varphi }}^{\tiny \text{ T }}(kq){\varvec{P}}(kq{-}q){\varvec{\varphi }}(kq)}.\!\!\!\!\nonumber \\ \end{aligned}$$
(10)

Because the information vector \({\varvec{\varphi }}(kq)\) in (8) contains unknown inner variables \(w(kq-j)\) and \(\bar{u}(kq-j)\), the standard least squares method fails to give the estimate of the parameter vector \({\varvec{\theta }}\). The solution is based on the auxiliary model identification idea [38–40]: to replace the unmeasurable term \(w(kq+i)\) in \({\varvec{\varphi }}(kq)\) with its estimate,

$$\begin{aligned} \hat{w}(kq+i)=\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(kq+i)\hat{{\varvec{\theta }}}(kq),\ i=1,2,\ldots ,q-1. \nonumber \\ \end{aligned}$$
(11)

Replacing \(\gamma _i\) in (2) with its estimate \(\hat{\gamma }_i(kq)\), we can get the estimate \(\hat{u}(kq+i)\) of \(\bar{u}(kq+i)\):

$$\begin{aligned} \hat{u}(kq+i)&= \hat{\gamma }_1(kq)f_1(u(kq+i))+\hat{\gamma }_2(kq)\nonumber \\&\times f_2(u(kq+i)) +\cdots +\hat{\gamma }_{n_{\gamma }}(kq)\nonumber \\&\times f_{n_{\gamma }}(u(kq+i)), \quad i=1,2,\ldots ,q-1.\nonumber \\ \end{aligned}$$
(12)

Define the estimate of \({\varvec{\varphi }}(kq)\):

$$\begin{aligned} \hat{{\varvec{\varphi }}}(kq)&:= \Big [-\hat{w}(kq-1),-\, \hat{w}(kq-2),\ldots ,\nonumber \\&\quad -\,\hat{w}(kq-n),\hat{u}(kq-1),\hat{u}(kq-2), \ldots ,\nonumber \\&\quad \hat{u}(kq-n),f_1(u(kq)),f_2(u(kq)) \ldots ,\nonumber \\&\quad f_{n_{\gamma }}(u(kq))\Big ]^{\tiny \text{ T }}. \end{aligned}$$
(13)

Using \(\hat{{\varvec{\varphi }}}(kq)\) in place of \({\varvec{\varphi }}(kq)\) in (8) and (10), we have

$$\begin{aligned} \hat{{\varvec{\theta }}}(kq)&= \hat{{\varvec{\theta }}}(kq-q) +{\varvec{P}}(kq) \hat{{\varvec{\varphi }}}(kq)\nonumber \\&\times \left[ y(kq)-\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(kq) \hat{{\varvec{\theta }}}(kq-q)\right] , \end{aligned}$$
(14)
$$\begin{aligned} {\varvec{P}}(kq)&= {\varvec{P}}(kq{-}q) {-} \frac{{\varvec{P}}(kq{-}q)\hat{{\varvec{\varphi }}}(kq)\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(kq) {\varvec{P}}(kq{-}q)}{1{+}\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(kq){\varvec{P}}(kq{-}q)\hat{{\varvec{\varphi }}}(kq)}\!.\!\!\!\!\nonumber \\ \end{aligned}$$
(15)

Equations (9), (11)–(15) form the AM-RLS algorithm for system by using the key-term separation principle, which can be summarized as

$$\begin{aligned}&\hat{{\varvec{\theta }}}(kq)=\hat{{\varvec{\theta }}}(kq-q) \nonumber \\&\quad +{\varvec{P}}(kq) \hat{{\varvec{\varphi }}}(kq)\left[ y(kq)- \hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(kq)\hat{{\varvec{\theta }}}(kq-q)\right] , \nonumber \\\end{aligned}$$
(16)
$$\begin{aligned}&\hat{{\varvec{\theta }}}(kq+i)=\hat{{\varvec{\theta }}}(kq),\quad i=1,2,\ldots ,q-1, \end{aligned}$$
(17)
$$\begin{aligned}&{\varvec{P}}(kq)={\varvec{P}}(kq{-}q) {-} \frac{{\varvec{P}}(kq{-}q)\hat{{\varvec{\varphi }}}(kq) \hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(kq){\varvec{P}}(kq{-}q)}{1+\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(kq) {\varvec{P}}(kq{-}q)\hat{{\varvec{\varphi }}}(kq)}, \nonumber \\ \end{aligned}$$
(18)
$$\begin{aligned}&\hat{{\varvec{\varphi }}}(kq)=\Big [{-}\hat{w}(kq{-}1),{-}\hat{w}(kq{-}2), \ldots , {-}\hat{w}(kq{-}n), \nonumber \\&\hat{u}(kq{-}1),\hat{u}(kq{{-}}2),\ldots , \hat{u}(kq{-}n), f_1(u(kq)),\!\!\!\!\nonumber \\&f_2(u(kq)),\ldots , f_{n_{\gamma }}(u(kq))\Big ]^{\tiny \text{ T }}, \end{aligned}$$
(19)
$$\begin{aligned}&\hat{u}(kq+i)=\hat{\gamma }_1(kq)f_1(u(kq+i)) + \hat{\gamma }_2(kq)f_2(u(kq+i))\nonumber \\&+\cdots +\hat{\gamma }_{n_{\gamma }}(kq)f_{n_{\gamma }}(u(kq+i)),\!\!\!\nonumber \\&\quad i=1,2,\ldots ,q-1, \end{aligned}$$
(20)
$$\begin{aligned}&\hat{w}(kq+i)=\hat{\varvec{\varphi }}^{\tiny \text{ T }}(kq+i)\hat{{\varvec{\theta }}}(kq)\quad i=1,2,\ldots ,q-1.\nonumber \\ \end{aligned}$$
(21)

To initialize the algorithm, we take \(\hat{{{\varvec{\theta }}}}(0)\) to be a small real vector, e.g., \(\hat{{{\varvec{\theta }}}}(0)=\mathbf{1}_{n_0}/p_0\) and with \(p_0\) normally a large positive number (e.g., \(p_0=10^6\)), and \({\varvec{P}}(0)=p_0{\varvec{I}}\) with \({\varvec{I}}\) representing an identity matrix of appropriate dimension.

4 Convergence of parameter estimation

In this section, we focus on analyzing the convergence properties of the proposed RLS algorithm which is under weak conditions. Assume that \(\{v(kq),\mathcal {F}_{kq}\}\) is a martingale difference sequence defined on a probability space \(\{\varOmega ,\mathcal {F},P\}\), where \(\{\mathcal {F}_{kq}\}\) is the \(\sigma \) algebra sequence generated by \(\{v(kq)\}\). The noise sequence \(\{v(kq)\}\) satisfies the following assumptions [41, 42]:

$$\begin{aligned}&(\mathrm{{A}}1)\quad E[v(kq)|{\mathcal {F}}_{kq-q}]={0},\ \mathrm{a.s.}, \\&(\mathrm{{A}}2)\quad E[\Vert v(kq)\Vert ^2|{\mathcal {F}}_{kq-q}]\leqslant \sigma ^2_v<\infty . \end{aligned}$$

Defining \(r(kq)=\mathrm{tr}[{\varvec{P}}^{-1}(kq)]\), it follows that

$$\begin{aligned} \ln |{\varvec{P}}^{-1}(kq)|=O(\ln r(kq)). \end{aligned}$$
(22)

Theorem 1

For the systems in (7) and the algorithm (16)–(21), if assumptions (A1) and (A2) hold, for any \(c>1\), the parameter estimation error associated with the AM-LS algorithm for the dual-rate sampled-data Hammerstein output error model satisfies:

$$\begin{aligned} \Vert \tilde{{\varvec{\theta }}}(kq)\Vert ^{2}=O\left( \frac{\ln \Vert r(kq)\Vert ]^{c}}{\lambda _{\min }[{\varvec{P}}^{-1}(kq)]}\right) . \end{aligned}$$
(23)

Proof

Define the parameter estimation error vector

$$\begin{aligned} \tilde{{\varvec{\theta }}}(kq)&:= \hat{{\varvec{\theta }}(}kq)-{\varvec{\theta }}\nonumber \\&= \tilde{{\varvec{\theta }}}(kq-q)+{\varvec{P}}(kq)\hat{{\varvec{\varphi }}}(kq)\nonumber \\&\left[ \hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(kq){\varvec{\theta }}(kq) \right. \left. +v(kq)-\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(kq)\hat{{\varvec{\theta }}}(kq-q)\right] \nonumber \\&=: \tilde{{\varvec{\theta }}}(kq-q)+{\varvec{P}}(kq) \hat{{\varvec{\varphi }}}(kq)\left[ -\tilde{y}(kq)+v(kq)\right] , \nonumber \\ \end{aligned}$$
(24)

where

$$\begin{aligned} \tilde{y}(kq)&:= \hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(kq)\hat{{\varvec{\theta }}}(kq-q)-\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(kq){\varvec{\theta }}(kq)\nonumber \\&= \hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(kq)\tilde{{\varvec{\theta }}}(kq-q). \end{aligned}$$
(25)

Define a non-negative definite function

$$\begin{aligned} T(kq)=\tilde{{\varvec{\theta }}}^{\tiny \text{ T }}(kq){\varvec{P}}^{-1}(kq)\tilde{{\varvec{\theta }}}(kq). \end{aligned}$$
(26)

Using (7), (24), and (25), we have

$$\begin{aligned} T(kq)&= \big \{\tilde{{\varvec{\theta }}}(kq-q)+{\varvec{P}}(kq) \hat{{\varvec{\varphi }}}(kq)\big [-\tilde{y}(kq) \\&+\,v(kq)\big ]\big \}^{\tiny \text{ T }} {\varvec{P}}^{-1}(kq)\big \{\tilde{{\varvec{\theta }}}(kq-q) \\&+\,{\varvec{P}}(kq)\hat{{\varvec{\varphi }}}(kq)\left[ -\tilde{y}(kq)+v(kq)\right] \big \} \\&= \tilde{{\varvec{\theta }}}^{\tiny \text{ T }}(kq-q){\varvec{P}}^{-1}(kq)\tilde{{\varvec{\theta }}}(kq-q) \\&+\,2\tilde{{\varvec{\theta }}}^{\tiny \text{ T }}(kq-q) \hat{{\varvec{\varphi }}}(kq)\left[ -\hat{y}(kq)+v(kq)\right] \\&+\,\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(kq){\varvec{P}}(kq)\hat{{\varvec{\varphi }}}(kq)[-\hat{y}(kq)+v(kq)]^{2} \\&= T(kq-q)\\&-\,\left[ 1-\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(kq){\varvec{P}}(kq) \hat{{\varvec{\varphi }}}(kq)\right] \tilde{y}^{2}(kq) \\&+\,\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(kq){\varvec{P}}(kq)\hat{{\varvec{\varphi }}}(kq)v^{2}(kq) \\&+\,2\left[ 1-\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(kq){\varvec{P}}(kq)\hat{{\varvec{\varphi }}}(kq) \right] \tilde{y}(kq)v(kq) \\&\leqslant T(kq-q)+\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(kq) {\varvec{P}}(kq)\hat{{\varvec{\varphi }}}(kq)v^{2}(kq)\\&+\,2\left[ 1-\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(kq){\varvec{P}}(kq) \hat{{\varvec{\varphi }}}(kq)\right] \tilde{y}(kq)v(kq). \end{aligned}$$

Here, we have used the relation

$$\begin{aligned}&\left[ 1-\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(kq){\varvec{P}}(kq)\hat{{\varvec{\varphi }}}(kq) \right] \nonumber \\&\quad =\left[ 1{+}\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(kq){\varvec{P}}(kq) \hat{{\varvec{\varphi }}}(kq)\right] ^{-1}>0. \end{aligned}$$
(27)

Since \(\tilde{y}(kq),\,\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(kq){\varvec{P}}(kq)\hat{{\varvec{\varphi }}}(kq)\), and \(T(kq-q)\) are uncorrelated with \(v(kq)\) and \({\mathcal {F}}_{kq-q}\) are measurable, taking the conditional expectation on both sides with respect to \({\mathcal {F}}_{kq-q}\) and using (A1) and (A2) give

$$\begin{aligned}&E\left[ T(kq)|{\mathcal {F}}_{kq-q}\right] \nonumber \\&\quad \leqslant T(kq-q) +2\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(kq){\varvec{P}}(kq) \hat{{\varvec{\varphi }}}(kq)\sigma ^{2}_{v},\ \mathrm{a.s.}\end{aligned}$$
(28)

Let

$$\begin{aligned} V(kq)=\frac{T(kq)}{\left[ \ln \Vert {\varvec{P}}^{-1}(kq)\Vert \right] ^{c}},\quad c>1. \end{aligned}$$

Since \({\varvec{P}}^{-1}(kq)\) is non-decreasing, we have

$$\begin{aligned} E[T(kq)|{\mathcal {F}}_{kq-q}]&\leqslant \frac{T(kq-q)}{\left[ \ln \Vert {\varvec{P}}^{-1}(kq)\Vert \right] ^{c}} \\&+\frac{2\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(kq){\varvec{P}}(kq) \hat{{\varvec{\varphi }}}(kq)}{\left[ \ln \Vert {\varvec{P}}^{-1}(kq)\Vert \right] ^{c}}\sigma ^{2}_{v} \\&= V(kq-q) \\&+\frac{2\hat{{\varvec{\varphi }}}^{\tiny \text{ T }}(kq) {\varvec{P}}(kq)\hat{{\varvec{\varphi }}}(kq)}{\left[ \ln \Vert {\varvec{P}}^{-1}(kq)\Vert \right] ^{c}}\sigma ^{2}_{v}, \ \mathrm{a.s.}\end{aligned}$$

Applying the martingale convergence theorem to the above inequality, we conclude that \(V(kq)\) converges a.s. to a finite random variable \(V_{0}\), i.e.,

$$\begin{aligned} V(kq)&= \frac{T(kq)}{[\ln \Vert {\varvec{P}}^{-1}(kq)\Vert ]^{c}}\rightarrow V_{0} < \infty ,\ \mathrm{a.s.},\;\mathrm{{or}}\nonumber \\ T(kq)&= O\left( \left[ \ln \Vert {\varvec{P}}^{-1}(kq)\Vert \right] ^{c}\right) ,\ \mathrm{a.s.}\end{aligned}$$
(29)

From the definition of \(V(kq)\), we have

$$\begin{aligned} \Vert \tilde{{\varvec{\theta }}}(kq)\Vert ^{2}&\leqslant \frac{\mathrm{tr}\left[ {\varvec{\theta }}^{\tiny \text{ T }}(kq) {\varvec{P}}^{-1}(kq){\varvec{\theta }}(kq)\right] }{\lambda _{\min } \left[ {\varvec{P}}^{-1}(kq)\right] } \nonumber \\&= \frac{T(kq)}{\lambda _{\min }\left[ {\varvec{P}}^{-1}(kq)\right] }. \end{aligned}$$
(30)

Using (29) and (22) gives

$$\begin{aligned} \Vert \tilde{{\varvec{\theta }}}(kq)\Vert ^{2}&= O\left( \frac{\ln \Vert {\varvec{P}}^{-1}(kq)\Vert ]^{c}}{\lambda _{\min } \left[ {\varvec{P}}^{-1}(kq)\right] }\right) \\&= O\left( \frac{\ln \Vert r(kq)\Vert ]^{c}}{\lambda _{\min } \left[ {\varvec{P}}^{-1}(kq)\right] }\right) . \end{aligned}$$

This gives the conclusion of Theorem 1. \(\square \)

Remark

Theorem 1 shows that if the noise has a bounded variance, then the parameter estimates converge to the true values.

5 Numerical examples

In this section, three examples are given to illustrate effectiveness of the AM-RLS algorithm.

Example 1

Consider the following Hammerstein system with dual-rate sampling,

$$\begin{aligned} y(kq)&= \left[ 1-A(z)\right] w(kq)+B(z)\bar{u}(kq)+v(kq),\\ A(z)&= 1-0.24z^{-1}+0.36z^{-2},\\ B(z)&= 1+0.78z^{-1}+0.24z^{-2},\\ \bar{u}(k)&= \gamma _1u(k)+\gamma _2u^{2}(k)+ \gamma _3u^{3}(k) \\&= u(k)+0.5u^{2}(k)+0.25u^{3}(k). \end{aligned}$$

In simulation, \(\{u(k)\}\) is taken as a persistent excitation signal sequence with zero mean and unit variance, and \(\{v(k)\}\) as a white noise sequence with zero mean and variance \(\sigma ^{2}=0.50^{2}\) and \(\sigma ^{2}=2.00^{2}\), respectively. Applying the proposed algorithm in (16)–(21) to estimate the parameters \((\alpha _i,\beta _i,\gamma _i)\) of this system, the parameter estimates and their errors with different noise variances are shown in Tables 1 and 2. The parameter estimation errors \(\delta :=\Vert \hat{{\varvec{\theta }}}(kq)-{\varvec{\theta }}\Vert /\Vert {\varvec{\theta }}\Vert \) versus \(k\) are shown in Fig. 2.

Table 1 The parameter estimates and their errors \((\sigma ^2=2.00^2)\) for Example 1
Full size table
Table 2 The parameter estimates and their errors \((\sigma ^2=0.50^2)\) for Example 1
Full size table
Fig. 2
figure 2

The estimation errors \(\delta \) versus \(k\) with \(\sigma ^2=0.50^2\) and \(\sigma ^2=2.00^2\) in Example 1

Full size image
Fig. 3
figure 3

The estimation errors \(\delta \) versus \(k\) with \(\sigma ^2=0.50^2\) for Example 2

Full size image

Example 2

Consider a Hammerstein system in Example 1 with

$$\begin{aligned} \left\{ \begin{array}{ccl} A(z)&{}=&{}1+0.44z^{-1}+0.36z^{-2}+0.14z^{-3}\\ &{}&{}+\, 0.21z^{-4}+0.12z^{-5}, \\ B(z)&{}=&{}1+0.58z^{-1}-0.54z^{-2}+0.34z^{-3}\\ &{}&{} +\, 0.25z^{-4}+0.13z^{-5}, \\ \bar{u}(k)&{}=&{}u(k)+0.5u^{2}(k)+0.25u^{3}(k). \end{array}\right. \end{aligned}$$

Example 3

Consider a nonlinear subsystem in Example 1 with

$$\begin{aligned} \left\{ \begin{array}{ccl} A(z)&{}=&{}1+0.54z^{-1}-0.36z^{-2}, \\ B(z)&{}=&{}1+0.48z^{-1}+0.14z^{-2}, \\ \bar{u}(k)&{}=&{}u(k)+0.70u^{2}(k)+0.65u^{3}(k)\\ &{}&{} +\, 0.55u^{4}(k)+0.45u^{5}(k). \end{array}\right. \end{aligned}$$

The simulation conditions of Examples 2 and 3 are the same as in Example 1 with the noise variance \(\sigma ^{2}=0.50^{2}\). The parameter estimation errors \(\delta \) versus \(k\) are shown in Figs. 3 and 4.

Fig. 4
figure 4

The estimation errors \(\delta \) versus \(k\) with \(\sigma ^2=0.50^2\) for Example 3

Full size image

From Tables 1 and 2 and Figs. 2, 3, and 4, we can draw the following conclusions:

  • It is clear that the estimation errors become smaller (in general) as the recursive step \(k\) increases—see Tables 1 and 2.

  • A higher noise level results in a slower convergence rate of the parameter estimates; after about \(k=5000\), the parameter estimates converge to their true values—see the error curves in Fig. 2 and the estimation errors of the last columns of Tables 1 and 2.

  • Under the same noise level, a complex model structure results in a slower convergence rate—see Figs. 3 and 4.

  • Increasing the complexity of the nonlinear subsystem causes a slower convergence rate than increasing the complexity of the linear subsystem—see Figs. 3 and 4.

6 Conclusions

In this paper, we present a RLS identification algorithm for dual-rate sampled-data Hammerstein nonlinear systems. Using the key-term separation principle, we construct the identification model of Hammerstein nonlinear systems with dual-rate sampling. All the model parameters can be estimated by the AM-RLS algorithm. The simulation results verified the effectiveness of the proposed algorithm. The method in the paper can combine iterative methods [43–47] to study identification problems for other linear or nonlinear systems [48–52].