1 Introduction

The gear system is distinguished by its compact configuration, extensive load and speed transmission capacity, high operational efficiency, and prolonged service life. Consequently, its application is pervasive across diverse mechanical apparatuses, including but not limited to automobiles, maritime vessels, and wind turbines. The dynamic characteristics of gear systems are directly correlative to the performance and dependability of mechanical apparatuses [1,2,3]. Manufacturing and installation inaccuracies, TVMS, tooth backlash, transmission discrepancies, bearing forces, and additional nonlinear excitations invariably precipitate vibrational and acoustic disturbances in gear systems [4, 5]. Excessive vibration can result in premature degradation and failure of the transmission system; thus, there is a significant engineering requirement to devise gear transmission systems characterized by minimal vibrational output and enhanced reliability.

Within the domain of gear dynamics, two principal methodologies are employed to enhance the system's vibrational characteristics. The first is active vibration mitigation [6], which entails the suppression of vibratory phenomena through the selection of suitable materials or the optimization of gear design parameters prior to manufacturing, including enhancements in machining precision [7] and tooth profile adjustments [8, 9]. Nevertheless, the active vibration mitigation approach incurs increased manufacturing costs, involves intricate calculation and design processes, and presents challenges in identifying optimal optimization parameters. This complexity is further amplified in the context of practical engineering applications. Conversely, passive vibration attenuation [10] employs supplementary damping mechanisms to dissipate systemic energy, thereby mitigating vibrational and acoustic emissions during gear engagement, exemplified by the use of elastic supports [11, 12], damping rings [13, 14], and SFD [15,16,17]. The amalgamation of squirrel-cage elastic supports with SFDs, as a proven and efficacious damping solution, has been extensively adopted in rotor systems to attenuate nonlinear dynamical behaviors [18,19,20]. Squirrel-cage elastic supports diminish the radial stiffness of rolling bearings and modulate the system's natural frequency and critical velocity. SFDs function by introducing damping forces to dissipate energy within the system.

As a distinctive subset of sliding bearings, extensive scholarly research has been dedicated to investigating the damping properties of SFDs and the dynamic responses of rotor systems buttressed by such dampers. Inayat-Hussain [16] delved into the unbalanced response phenomena of rigid rotors supported by SFDs, considering configurations both with and without centering springs. Sun [21] scrutinized the impact of film temperature on the rotor-bearing system dynamics, employing the Leibniz integral law for analytical precision. Bonello [22] introduced a receptance harmonic balance method tailored for the nonlinear analysis of integrated systems, substantiating the methodology with experimental validation. Hemmati [23] conducted an in-depth study into the linear and nonlinear stability of flexible rotor-bearing systems under varying flow regimes, deriving turbulent pressure distributions and forces from the modified Reynolds equation. Lin and Naduvinamani [24, 25] engaged in a theoretical exploration of the hydrodynamic behavior of squeezed films under the influence of coupled stresses. Chang-Jian [26, 27] advanced a nonlinear support model predicated on linear damping, nonlinear elastic restoring forces, and assumptions of turbulent flow dynamics. Chen [5, 17] established a general mathematical model of SFD and proposed two numerical strategies for solving the oil-film forces of SFD based on the finite element method and finite difference method. Meanwhile, the author [28] also derived the Reynolds equation of the elastic ring squeeze film damper and proposed a semi-analytical method for the deformation of the elastic ring. Farshidianfar [29] employed Melnikov's analytical technique to dissect the global homoclinic bifurcations and the ensuing transition into chaotic dynamics within gear systems. Huang [30] conducted a comparative analysis of the bifurcation and chaotic behaviors in gear systems with fixed backlash versus those with fractal backlash characteristics. He [31], Lu [32], and Wang [33] have analyzed the response of dynamic systems using the maximum Lyapunov exponent, but the dynamic models established only contain one degree of freedom, which belonged to the low-dimensional system. Chang-Jian [18, 34,35,36,37] also established models with porous squeeze film dampers and hybrid squeeze-film dampers, analyzing the system's chaotic characteristics using the largest Lyapunov exponent. The models only contain four degrees of freedom, and no computational details regarding the Lyapunov exponents are provided. For SFD supported systems, the published literature only includes single-stage gear transmissions, and research is mainly focused on rotor-SFD systems rather than gear-SFD systems. Research into stability and bifurcation has predominantly concentrated on first-stage gear transmission systems, characterized by their lower dimensionality. There exists a paucity of literature on the investigation of vibrational stability and the taxonomy of bifurcations within high-dimensional gear-rotor-SFD systems. Additionally, Khatri [38] considers the lubricant as a non-Newtonian fluid during the modeling process of journal bearings. Liu [39] employs composite Poincaré maps to capture non-classical local bifurcations induced by double grazing, observing a path from stable periodic motion to chaos. Zheng [40] takes into account gear lightweighting and gear body flexibility, establishing a dynamic model that can reflect the structure of thin-walled gears.

Addressing the aforementioned challenges, this work computes the nonlinear oil-film forces exerted by the SFD employing the finite element method. Predicated upon lumped parameter theory, this inquiry meticulously derives the motion equations for a two-stage spur gear system pertinent to a delineated class of mechanical apparatus. A nonlinear dynamical model incorporating SFD is constructed by integrating the nonlinear oil-film force with the system’s motion equations and is subsequently solved utilizing the fourth-order Runge–Kutta numerical method. Based on the Gram-Schmidt QR decomposition, a computational strategy for calculating the Lyapunov spectrum of high-dimensional gear-rotor-SFD systems is proposed, which involves computing the Floquet multipliers of the system by solving the eigenvalues of the Monodromy matrix. A detailed calculation process is provided, and this method can be extended to the calculation of the Lyapunov spectrum and characteristic multipliers of other dynamical systems. This study conducts a comprehensive analysis of the vibration stability and bifurcation phenomena in two-stage spur gear systems, both with and without the inclusion of the SFD. Furthermore, the study delves into the vibration attenuation capabilities of the SFD, providing a detailed evaluation of its performance.

The subsequent structure of the manuscript is outlined as follows: In Sect. 2, the mathematical model of the SFD is meticulously developed, and the nonlinear oil-film forces are calculated employing the finite element method. Taking into account the oil-film forces, a nonlinear dynamic model of the system is rigorously established. Section 3 delineates a strategic approach for computing the Lyapunov exponents and Floquet characteristic multipliers pertinent to high-dimensional gear-rotor-SFD systems. Section 4 undertakes a detailed examination of the vibration stability and bifurcation types characteristic of systems both equipped with and devoid of SFD. Section 5 encapsulates the principal conclusions derived from the study.

2 System dynamic models

2.1 Mathematical model of SFD

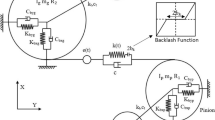
The SFD mainly consists of a bearing housing, gear-shaft, squirrel-cage elastic support, oil-film, and rolling bearings. Figure 1 shows a schematic diagram of the SFD structure with squirrel-cage elastic support and Fig. 1b is a sectional view of Fig. 1a taken along line A-A. The rolling bearing is selected as a cylindrical roller bearing. The gear-shaft is interference-fitted with the inner ring of the rolling bearing and the outer ring of the rolling bearing is transition-fitted with the inner ring of squirrel-cage elastic support. The right end of the squirrel-cage elastic support is fixedly connected to the casing, and the left end serves as the journal for the oil-film. The structure of the journal is similar to a cantilever beam, which can only move laterally but cannot rotate. When the journal is subjected to an external force and lateral displacement occurs, it squeezes the oil-film to produce a damping force that dissipates system energy, which is the vibration-damping mechanism of the SFD. Table 1 provides the design parameters of the SFD.

Fig. 1
figure 1

Schematic illustration of SFD with squirrel-cage elastic support

Full size image
Table 1 Design parameters of SFD
Full size table

The generalized Reynolds equation, governing hydrodynamic lubrication in bearings, can be deduced from the interplay of the continuity equation and the Navier–Stokes equation. The derivation of the generalized Reynolds equation for the SFD is predicated on a set of foundational assumptions. Building on the foundations laid by Refs. [41,42,43], we proceed under the assumption that the fluid is a continuous, Newtonian, and exhibits laminar flow characteristics, the inertial forces within the oil-film are considered negligible, the oil-film's thickness is considerably less than its length and breadth, relative motion between the fluid and the wall is considered absent, and the effects of temperature variations in the oil-film are disregarded.

The generalized Reynolds equation of hydrodynamic lubricated bearings is

$$\begin{aligned} \frac{\partial }{\partial x}\left( {\frac{{\rho h^{3} }}{12\mu }\frac{\partial p}{{\partial x}}} \right) + \frac{\partial }{\partial z}\left( {\frac{{\rho h^{3} }}{12\mu }\frac{\partial p}{{\partial z}}} \right) &=\,h\left[ {\frac{{\partial (\rho U_{2} )}}{\partial x} + \frac{{\partial (\rho W_{2} )}}{\partial z}} \right] - \frac{\partial }{\partial x}\left[ {\frac{{\rho h\left( {U_{2} - U_{1} } \right)}}{2}} \right] \\ &\quad- \frac{\partial }{\partial z}\left[ {\frac{{\rho h\left( {W_{2} - W_{1} } \right)}}{2}} \right] + h\frac{\partial \rho }{{\partial t}} + \rho \left( {V_{2} - V_{1} } \right) \\ \end{aligned}$$
(1)

where the thickness of the oil-film is \(h \approx c\left( {1 + \varepsilon \cos \left( \theta \right)} \right)\). The radial clearance of the oil-film is c = R2 − R, and R2 and R are the radii of the inner hole of the bearing housing and journal, respectively. The eccentricity of the journal is \(\varepsilon = {{\sqrt {x^{2} \left( t \right) + y^{2} \left( t \right)} } \mathord{\left/ {\vphantom {{\sqrt {x^{2} \left( t \right) + y^{2} \left( t \right)} } c}} \right. \kern-0pt} c}\), as shown in Fig. 1b, x(t) and y(t)) are the displacement components of the journal in the x- and y- directions, respectively. μ and p are the fluid dynamic viscosity and oil-film distribution pressure, respectively. Figure 2 shows a cross-sectional schematic of the SFD, where U1, V1, and W1 are the velocity components on the journal surface in the tangential, radial, and axial directions, respectively; U2, V2, and W2 are the velocity components on the bearing housing surface. The hatch marking on the outer surface of the bearing housing indicated that it is fixed, so there exists U2 = V2 = W2 = 0. Connecting points Ob and Oj, the line between Ob and Oj represents the location of maximum oil-film thickness, where Ob and Oj are the centers of the bearing housing and journal, respectively. In defining θ, the position of maximum oil-film thickness is taken as the baseline for θ. Concurrently, the counterclockwise direction is considered the positive direction for θ (green arrow in Fig. 2) and θ represents the angle between any circumferential position and the baseline. At the baseline position, the oil-film thickness \(h_{\max }\) is \(c\left( {1 + \varepsilon } \right)\) and θ is 0°.

Fig. 2
figure 2

Cross-sectional schematic of the SFD

Full size image

In the present investigation, the finite element method, predicated on Galerkin's principle, is meticulously employed to compute the nonlinear oil-film distribution pressure of the SFD in real-time. Subsequently, the oil-film reaction forces (Fx and Fy) of the SFD are ascertained by performing an integration across the entirety of the oil-film region. During the computation of the oil-film forces, the oil-film region is discretized into meshes using triangular elements, and within this computational framework, the deformation of the mesh is neglected to simplify the governing equation of oil-film pressure. A comprehensive elucidation of the calculation methodology is provided in our preceding study [5].

2.2 Nonlinear dynamics model

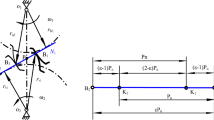
Figure 3 illustrates a schematic diagram of a two-stage spur gear system supported by SFD, and the entire transmission system includes four spur gears, three gear-shafts, and six rolling bearings. The squirrel-cage elastic support and SF D are only installed on the side near gear 1 and gear 3, with the rest supported by rolling bearings. The red arrow in the diagram indicates the input torque, and the blue arrow indicates the output torque.

Fig. 3
figure 3

Two-stage spur gear system supported by SFD

Full size image

STE is delineated as the discrepancy between the actual and the theoretical transmission ratios of a gear pair under static load conditions (absent dynamic loads), arising from factors such as manufacturing inaccuracies, assembly deviations, and material non-uniformities. Under a constant torque, the gear operates at an exceedingly slow rotational speed, where the gear vibration is negligible, and the STE encompasses the sum of the gear's elastic deformation and the cumulative meshing error. Considering TVMS \(k_{ms}\), STE \(e_{s}\), and backlash \(2b_{s}\), the spur gear system supported by SFD is modeled by the lumped mass method, where s represents the s-th gear pair (s = 1,2).

Figure 4 shows the dynamic model of the two-stage spur gear system, which shows the detailed modeling process. The spur gear is considered as a rigid body, and the meshing action between the driving and driven gears is simulated by stiffness elements and damping elements. Each gear contains 3 degrees of freedom, namely lateral displacement \(x_{i}\), \(y_{i}\), and rotational displacement around the gear shaft \(\theta_{i}\). Considering the intermediate shaft as a rigid shaft, gear 2 and gear 3 have the same vibration displacement. \(R_{bi}\) is the base circle radius of the gear. \(T_{1}\) and \(T_{2}\) are the input and output torques respectively. \(k_{bi}\) and \(c_{bi}\) are the stiffness and damping of support bearings, respectively. \(k_{ei}\) and \(c_{ei}\) are the stiffness and damping of squirrel-cage elastic supports, respectively. In Fig. 1a, the squirrel-cage elastic support and rolling bearing are connected in series, and their radial equivalent support stiffness is \(k_{ai} = 1/\left( {1/k_{bi} + 1/k_{ei} } \right)\), (i = 1, 2, 3, 4). Given that the stiffness of the squirrel-cage elastic support is substantially lower than that of the rolling bearings, the lateral displacement of the gear is predominantly governed by the former. Consequently, this study employs the stiffness of the squirrel-cage elastic support as a surrogate for the equivalent support stiffness in all ensuing analyses. Table 2 delineates the fundamental parameters of the spur gear pair and their support mechanisms. The number of teeth, module, pressure angle, backlash, and elastic support stiffness are design parameters; mass and moment of inertia can be directly obtained through three-dimensional software modeling; TVMS and STE are obtained through loading contact analysis [8]; bearing support stiffness can be exported from Romax software; damping is an empirical value, and the selection of its value mainly depends on the reference literature [9, 15, 44, 45].

Fig. 4
figure 4

Dynamics model of two-stage spur gear system

Full size image
Table 2 Parameters of the spur gear set and supports
Full size table

The generalized coordinate vector of the system is

$$\left\{ q \right\} = \left\{ {x_{1} ,y_{1} ,\theta_{1} ,x_{2} ,y_{2} ,\theta_{2} ,x_{4} ,y_{4} ,\theta_{4} } \right\}$$
(2)

According to Fig. 4 and D 'Alembert's principle, the motion equation of the system can be written as

$$m_{1} \frac{{{\text{d}}^{2} x_{1} }}{{{\text{d}}t^{2} }} + c_{e1} \frac{{{\text{d}}x_{1} }}{{{\text{d}}t}} + k_{e1} x_{1} + F_{m1} \sin (\alpha_{1} ) - F_{x1} = 0$$
(3)
$$m_{1} \frac{{{\text{d}}^{2} y_{1} }}{{{\text{d}}t^{2} }} + c_{e1} \frac{{{\text{d}}y_{1} }}{{{\text{d}}t}} + k_{e1} y_{1} + F_{m1} \cos (\alpha_{1} ) - F_{y1} = 0$$
(4)
$$I_{1} \frac{{{\text{d}}^{2} \theta_{1} }}{{{\text{d}}t^{2} }} + F_{m1} R_{b1} = T_{1}$$
(5)
$$m_{23} \frac{{{\text{d}}^{2} x_{2} }}{{{\text{d}}t^{2} }} + c_{e2} \frac{{{\text{d}}x_{2} }}{{{\text{d}}t}} + k_{e2} x_{2} - F_{m1} \sin (\alpha_{1} ) + F_{m2} \sin (\alpha_{2} ) - F_{x2} = 0$$
(6)
$$m_{23} \frac{{{\text{d}}^{2} y_{2} }}{{{\text{d}}t^{2} }} + c_{e2} \frac{{{\text{d}}y_{2} }}{{{\text{d}}t}} + k_{e2} y_{2} - F_{m1} \cos (\alpha_{1} ) + F_{m2} \cos (\alpha_{2} ) - F_{y2} = 0$$
(7)
$$I_{23} \frac{{{\text{d}}^{2} \theta_{2} }}{{{\text{d}}t^{2} }} + F_{m1} R_{b2} - F_{m2} R_{b3} = 0$$
(8)
$$m_{4} \frac{{{\text{d}}^{2} x_{4} }}{{{\text{d}}t^{2} }} + c_{b4} \frac{{{\text{d}}x_{4} }}{{{\text{d}}t}} + k_{b4} x_{4} - F_{m2} \sin (\alpha_{2} ) = 0$$
(9)
$$m_{4} \frac{{{\text{d}}^{2} y_{4} }}{{{\text{d}}t^{2} }} + c_{b4} \frac{{{\text{d}}y_{4} }}{{{\text{d}}t}} + k_{b4} y_{4} - F_{m2} \cos (\alpha_{2} ) = 0$$
(10)
$$I_{4} \frac{{{\text{d}}^{2} \theta_{4} }}{{{\text{d}}t^{2} }} - F_{m2} R_{b4} = - T_{2}$$
(11)

where \(m_{i}\) and \(I_{i}\) are the mass and moment of inertia of the gears, respectively; \(m_{23} = m_{2} + m_{3}\), \(I_{23} = I_{2} + I_{3}\); and \(\alpha_{s}\) is the pressure angle of the s-th stage gear pair.

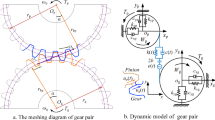
Figure 5 shows the meshing diagram of involute spur gear profiles. In Fig. 5a, let Cp and Cg be a pair of involute gear profiles that mesh with each other, where Op and Og are the centers of the driving and driven gears. The base circle radii of the driving and driven gears are Rbp and Rbg, and the index circle radii are Rp and Rg, with P as the pitch point. For standard involute spur gears, when the two gears are installed with the standard center distance, the pitch circle and the index circle coincide with each other. When Cp and Cg mesh at any point K, the common normal of the pair of tooth profiles through point K is NpNg. According to the characteristics of involute gears, this common normal must also be tangent to the base circles of both gears. When a pair of involute gear profiles mesh at any position, the common normal passing through the contact point is the same straight line NpNg. From the beginning of engagement to disengagement, all the engagement points are on a straight line, so the straight line NpNg is the trajectory of the tooth profile contact point in a fixed plane, so it is also called the line of action. The line of action NpNg is the common tangent to the base circles of the driving and driven gears, not the common tangent to the pitch circles. During the gear transmission process, the dynamic meshing forces between the two meshing profiles always act along the line of action, pointing from the contact point on the driving gear to the contact point on the driven gear (red arrow in Fig. 5b); hence in the motion equations, the lever arm is defined using the base circle radius rather than the pitch circle radius.

Fig. 5
figure 5

Involute tooth profile meshing diagram

Full size image

The dynamic meshing force of the s-th stage can be written as

$$F_{ms} = k_{ms} f(x_{rs} ) + c_{ms} \frac{{{\text{d}}x_{rs} }}{{{\text{d}}t}}$$
(12)

where \(x_{rs}\) is the relative displacement of the gear pair along the line of action, and \(f(x_{rs} )\) is the nonlinear backlash function caused by the relative displacement. \(f(x_{rs} )\) can be expressed as

$$f\left( {x_{rs} } \right) = \left\{ {\begin{array}{*{20}c} {x_{rs} - b_{s} ,} & {x_{rs} \ge b_{s} } \\ {0,} & { - b_{s} < x_{rs} < b_{s} } \\ {x_{rs} + b_{s} ,} & {x_{rs} \le - b_{s} } \\ \end{array} } \right.$$
(13)

Eq. (13) is used to determine the engaging state of gear pairs, and \(b_{s}\) is half of the gear backlash of the s-th gear pair along the line of action. When \(x_{rs} \ge b_{s}\), the gear is in a normal meshing state; When \(- b_{s} < x_{rs} < b_{s}\), the gear is in an unmeshed state, and there is no dynamic meshing force at this time; when \(x_{rs} \le - b_{s}\), a reverse impact occurs.

The obtained TVMS and STE can be transformed from time-domain results to frequency-domain results through the Fourier transform. In the frequency domain, the frequency components include \(\omega_{ms}\), \(2\omega_{ms}\), \(3\omega_{ms}\), etc., where \(\omega_{ms}\) is the meshing frequency and the fundamental frequency. Significant fluctuations of TVMS and STE occur under medium and heavy loads (≥ 200 Nm), while the fluctuations are minimal under light loads (≤ 100 Nm) [46]. In this paper, the spur gear model analyzed operates under an input torque of 100 Nm, which is classified as a light load condition, under which the variations in TVMS and STE can be considered negligible. The first-order meshing frequency plays a dominant role in the excitation of TVMS and STE [47,48,49], and TVMS and STE can be represented as

$$k_{ms} (t) = k_{os} + k_{mas} \sin (\omega_{ms} t + \phi_{ks} )$$
(14)
$$e_{s} (t) = e_{mas} \sin (\omega_{ms} t + \phi_{es} )$$
(15)

where \(k_{os}\) is the average value of TVMS; \(k_{mas}\) and \(e_{mas}\) are the amplitudes corresponding to the first harmonic frequency components of TVMS and STE, respectively. \(\phi_{ks}\) and \(\phi_{es}\) represent the initial phase angles, there is \(\phi_{ks} = \phi_{es} = 0\).

The relative displacement of the gear pair along the line of action is

$$x_{r1} = (x_{1} - x_{2} )\sin (\alpha_{1} ) + (y_{1} - y_{2} )\cos (\alpha_{1} ) + R_{b1} \theta_{1} - R_{b2} \theta_{2} - e_{1}$$
(16)
$$x_{r2} = (x_{2} - x_{4} )\sin (\alpha_{2} ) + (y_{2} - y_{4} )\cos (\alpha_{2} ) + R_{b3} \theta_{3} - R_{b4} \theta_{4} - e_{2}$$
(17)

After combining Eqs. (5), (8) and (16) can be written as

$$\frac{{{\text{d}}^{2} x_{{r1}} }}{{{\text{d}}t^{2} }} - \left( {\frac{{{\text{d}}^{2} x_{1} }}{{{\text{d}}t^{2} }} - \frac{{{\text{d}}^{2} x_{2} }}{{{\text{d}}t^{2} }}} \right)\sin (\alpha _{1} ) - \left( {\frac{{{\text{d}}^{2} y_{1} }}{{{\text{d}}t^{2} }} - \frac{{{\text{d}}^{2} y_{2} }}{{{\text{d}}t^{2} }}} \right)\cos (\alpha _{1} ) + F_{{m1}} \left( {\frac{{R_{{b1}}^{2} }}{{I_{1} }} - \frac{{R_{{b2}}^{2} }}{{I_{{23}} }}} \right) + F_{{m2}} \frac{{R_{{b2}} R_{{b3}} }}{{I_{{23}} }} - \frac{{T_{1} R_{{b1}} }}{{I_{1} }} + \frac{{{\text{d}}^{2} e_{1} }}{{{\text{d}}t^{2} }} = 0$$
(18)

Similarly, Eqs. (8), (11) and (17) can be written as

$$\frac{{{\text{d}}^{2} x_{{r2}} }}{{{\text{d}}t^{2} }} - \left( {\frac{{{\text{d}}^{2} x_{2} }}{{{\text{d}}t^{2} }} - \frac{{{\text{d}}^{2} x_{4} }}{{{\text{d}}t^{2} }}} \right)\sin (\alpha _{2} ) - \left( {\frac{{{\text{d}}^{2} y_{2} }}{{{\text{d}}t^{2} }} - \frac{{{\text{d}}^{2} y_{4} }}{{{\text{d}}t^{2} }}} \right)\cos (\alpha _{2} ) + F_{{m2}} \left( {\frac{{R_{{b4}}^{2} }}{{I_{4} }} - \frac{{R_{{b3}}^{2} }}{{I_{{23}} }}} \right) + F_{{m1}} \frac{{R_{{b2}} R_{{b3}} }}{{I_{{23}} }} - \frac{{T_{2} R_{{b4}} }}{{I_{4} }} + \frac{{{\text{d}}^{2} e_{2} }}{{{\text{d}}t^{2} }} = 0$$
(19)

Through Eqs. (18) and (19), the angular displacements (\(\theta_{1}\), \(\theta_{2}\), \(\theta_{4}\)) are transformed into linear displacements (\(x_{r1}\), \(x_{r2}\)), reducing the number of degrees of freedom, decreasing programming complexity, and improving computational efficiency. At this point, the generalized coordinates of the system have changed from \(\left\{ {x_{1} ,y_{1} ,\theta_{1},\,x_{2} ,y_{2} ,\theta_{2}, x_{4} ,y_{4},\, \theta_{4} } \right\}\) to \(\left\{ {x_{1} ,y_{1} ,x_{2} ,y_{2} ,x_{4} ,y_{4} ,x_{r1} ,x_{r2} } \right\}\).

Half of the backlash of the first-stage gear pair b1 and natural frequency ωn1 are used for dimensionless parameters. Let \(X_{1} = {{x_{1} } \mathord{\left/ {\vphantom {{x_{1} } {b_{1} }}} \right. \kern-0pt} {b_{1} }}\), \(Y_{1} = {{y_{1} } \mathord{\left/ {\vphantom {{y_{1} } {b_{1} }}} \right. \kern-0pt} {b_{1} }}\), \(X_{2} = {{x_{2} } \mathord{\left/ {\vphantom {{x_{2} } {b_{1} }}} \right. \kern-0pt} {b_{1} }}\), \(Y_{2} = {{y_{2} } \mathord{\left/ {\vphantom {{y_{2} } {b_{1} }}} \right. \kern-0pt} {b_{1} }}\), \(X_{4} = {{x_{4} } \mathord{\left/ {\vphantom {{x_{4} } {b_{1} }}} \right. \kern-0pt} {b_{1} }}\), \(Y_{4} = {{y_{4} } \mathord{\left/ {\vphantom {{y_{4} } {b_{1} }}} \right. \kern-0pt} {b_{1} }}\), \(X_{r1} = {{x_{r1} } \mathord{\left/ {\vphantom {{x_{r1} } {b_{1} }}} \right. \kern-0pt} {b_{1} }}\),

\(X_{r2} = {{x_{r2} } \mathord{\left/ {\vphantom {{x_{r2} } {b_{1} }}} \right. \kern-0pt} {b_{1} }}\), dimensionless time \(\tau = \omega_{n1} t\) and Eq. (13) is rewritten as

$$f\left( {X_{r1} } \right) = \left\{ {\begin{array}{*{20}c} {X_{r1} - 1,\;\;\;X_{r1} \ge 1} \\ {0 \, , \, else} \\ {X_{r1} + 1,\;\;X_{r1} \le - 1} \\ \end{array} } \right., \quad f\left( {X_{r2} } \right) = \left\{ {\begin{array}{*{20}c} {X_{r2} - b_{2} /b_{1} ,\;X_{r2} \ge 1} \\ {0 \, , \, else} \\ {X_{r2} + b_{2} /b_{1} ,\;X_{r2} \le - 1} \\ \end{array} } \right.$$
(20)

The dimensionless equation of motion is

$$\begin{aligned} & \frac{{{\text{d}}^{2} X_{1} }}{{{\text{d}}\tau ^{2} }} + c_{1} \frac{{{\text{d}}X_{1} }}{{d\tau }} + k_{1} X_{1} + \left( {c_{2} \frac{{{\text{d}}X_{{r1}} }}{{{\text{d}}\tau }} + k_{2} f\left( {X_{{r1}} } \right)} \right)\sin (\alpha _{1} ) - {{F_{{x1}} } \mathord{\left/ {\vphantom {{F_{{x1}} } {coe_{1} }}} \right. \kern-\nulldelimiterspace} {coe_{1} }} = 0 \\ & \frac{{{\text{d}}^{2} Y_{1} }}{{{\text{d}}\tau ^{2} }} + c_{1} \frac{{{\text{d}}Y_{1} }}{{{\text{d}}\tau }} + k_{1} Y_{1} + \left( {c_{2} \frac{{{\text{d}}X_{{r1}} }}{{{\text{d}}\tau }} + k_{2} f\left( {X_{{r1}} } \right)} \right)\cos (\alpha _{1} ) - {{F_{{y1}} } \mathord{\left/ {\vphantom {{F_{{y1}} } {coe_{1} }}} \right. \kern-\nulldelimiterspace} {coe_{1} }} = 0 \\ & \frac{{{\text{d}}^{2} X_{2} }}{{{\text{d}}\tau ^{2} }} + c_{3} \frac{{{\text{d}}X_{2} }}{{{\text{d}}\tau }} + k_{3} X_{2} - \left( {c_{4} \frac{{{\text{d}}X_{{r1}} }}{{{\text{d}}\tau }} + k_{4} f\left( {X_{{r1}} } \right)} \right)\sin (\alpha _{1} ) + \left( {c_{5} \frac{{{\text{d}}X_{{r2}} }}{{{\text{d}}\tau }} + k_{5} f\left( {X_{{r2}} } \right)} \right)\sin (\alpha _{2} ) \\ & - {{F_{{x2}} } \mathord{\left/ {\vphantom {{F_{{x2}} } {coe_{2} }}} \right. \kern-\nulldelimiterspace} {coe_{2} }} = 0 \\ & \frac{{{\text{d}}^{2} Y_{2} }}{{{\text{d}}\tau ^{2} }} + c_{3} \frac{{{\text{d}}Y_{2} }}{{{\text{d}}\tau }} + k_{3} Y_{2} - \left( {c_{4} \frac{{{\text{d}}X_{{r1}} }}{{{\text{d}}\tau }} + k_{4} f\left( {X_{{r1}} } \right)} \right)\cos (\alpha _{1} ) + \left( {c_{5} \frac{{{\text{d}}X_{{r2}} }}{{{\text{d}}\tau }} + k_{5} f\left( {X_{{r2}} } \right)} \right)\cos (\alpha _{2} ) \\ & - {{F_{{y2}} } \mathord{\left/ {\vphantom {{F_{{y2}} } {coe_{2} }}} \right. \kern-\nulldelimiterspace} {coe_{2} }} = 0 \\ & \frac{{{\text{d}}^{2} X_{4} }}{{{\text{d}}\tau ^{2} }} + c_{6} \frac{{{\text{d}}X_{4} }}{{{\text{d}}\tau }} + k_{6} X_{4} - \left( {c_{7} \frac{{{\text{d}}X_{{r2}} }}{{{\text{d}}\tau }} + k_{7} f\left( {X_{{r2}} } \right)} \right)\sin (\alpha _{2} ) = 0 \\ & \frac{{{\text{d}}^{2} Y_{4} }}{{{\text{d}}\tau ^{2} }} + c_{6} \frac{{{\text{d}}Y_{4} }}{{{\text{d}}\tau }} + k_{6} Y_{4} - \left( {c_{7} \frac{{{\text{d}}X_{{r2}} }}{{{\text{d}}\tau }} + k_{7} f\left( {X_{{r2}} } \right)} \right)\cos (\alpha _{2} ) = 0 \\ & \frac{{{\text{d}}^{2} X_{{r1}} }}{{{\text{d}}\tau ^{2} }} - \left( {\frac{{{\text{d}}^{2} X_{1} }}{{{\text{d}}\tau ^{2} }} - \frac{{{\text{d}}^{2} X_{2} }}{{{\text{d}}\tau ^{2} }}} \right)\sin (\alpha _{1} ) - \left( {\frac{{{\text{d}}^{2} Y_{1} }}{{{\text{d}}\tau ^{2} }} - \frac{{{\text{d}}^{2} Y_{2} }}{{{\text{d}}\tau ^{2} }}} \right)\cos (\alpha _{1} ) - f_{1} + f_{3} \left( {c_{8} \frac{{{\text{d}}X_{{r1}} }}{{{\text{d}}\tau }} + k_{8} f\left( {X_{{r1}} } \right)} \right) \\ & + f_{5} \left( {c_{9} \frac{{{\text{d}}X_{{r2}} }}{{{\text{d}}\tau }} + k_{9} f\left( {X_{{r2}} } \right)} \right) = 0 \\ & \frac{{{\text{d}}^{2} X_{{r2}} }}{{{\text{d}}\tau ^{2} }} - \left( {\frac{{{\text{d}}^{2} X_{2} }}{{{\text{d}}\tau ^{2} }} - \frac{{{\text{d}}^{2} X_{4} }}{{{\text{d}}\tau ^{2} }}} \right)\sin (\alpha _{2} ) - \left( {\frac{{{\text{d}}^{2} Y_{2} }}{{{\text{d}}\tau ^{2} }} - \frac{{{\text{d}}^{2} Y_{4} }}{{{\text{d}}\tau ^{2} }}} \right)\cos (\alpha _{2} ) - f_{2} + f_{4} \left( {c_{9} \frac{{{\text{d}}X_{{r2}} }}{{{\text{d}}\tau }} + k_{9} f\left( {X_{{r2}} } \right)} \right) \\ & + f_{5} \left( {c_{8} \frac{{{\text{d}}X_{{r1}} }}{{{\text{d}}\tau }} + k_{8} f\left( {X_{{r1}} } \right)} \right) = 0 \\ \end{aligned}$$
(21)

where \(c_{1} = \frac{{c_{e1} }}{{m_{1} \omega_{n} }}\), \(c_{2} = \frac{{c_{m1} }}{{m_{1} \omega_{n} }}\), \(c_{3} = \frac{{c_{e2} }}{{m_{23} \omega_{n} }}\), \(c_{4} = \frac{{c_{m1} }}{{m_{23} \omega_{n} }}\), \(c_{5} = \frac{{c_{m2} }}{{m_{23} \omega_{n} }}\), \(c_{6} = \frac{{c_{b4} }}{{m_{4} \omega_{n} }}\), \(c_{7} = \frac{{c_{m2} }}{{m_{4} \omega_{n} }}\), \(c_{8} = \frac{{c_{m1} }}{{\omega_{n} }}\), \(c_{9} = \frac{{c_{m2} }}{{\omega_{n} }}\); \(k_{1} = \frac{{k_{e1} }}{{m_{1} \omega_{n}^{2} }}\), \(k_{2} = \frac{{k_{m1} }}{{m_{1} \omega_{n}^{2} }}\), \(k_{3} = \frac{{k_{e2} }}{{m_{23} \omega_{n}^{2} }}\), \(k_{4} = \frac{{k_{m1} }}{{m_{23} \omega_{n}^{2} }}\), \(k_{5} = \frac{{k_{m2} }}{{m_{23} \omega_{n}^{2} }}\), \(k_{6} = \frac{{k_{b4} }}{{m_{4} \omega_{n}^{2} }}\), \(k_{7} = \frac{{k_{m2} }}{{m_{4} \omega_{n}^{2} }}\), \(k_{8} = \frac{{k_{m1} }}{{\omega_{n}^{2} }}\), \(k_{9} = \frac{{k_{m2} }}{{\omega_{n}^{2} }}\); \(coe_{1} = m_{1} b_{1} \omega_{n}^{2}\), \(coe_{2} = m_{2} b_{1} \omega_{n}^{2}\); \(f_{1} = \frac{{T_{1} R_{b1} }}{{I_{1} b_{1} \omega_{n}^{2} }} + \frac{1}{{b_{1} }} \times \frac{{{\text{d}}^{2} e_{1} }}{{{\text{d}}\tau^{2} }}\), \(f_{2} = \frac{{T_{2} R_{b4} }}{{I_{4} b_{1} \omega_{n}^{2} }} + \frac{1}{{b_{1} }} \times \frac{{{\text{d}}^{2} e_{2} }}{{{\text{d}}\tau^{2} }}\), \(f_{3} = (\frac{{R_{b1}^{2} }}{{I_{1} }} - \frac{{R_{b2}^{2} }}{{I_{23} }})\), \(f_{4} = (\frac{{R_{b4}^{2} }}{{I_{4} }} - \frac{{R_{b3}^{2} }}{{I_{23} }})\), \(f_{5} = \frac{{R_{b2} R_{b3} }}{{I_{23} }}\); \(\omega_{n} = \omega_{n1} = \sqrt {\frac{{k_{m1} }}{{M_{12} }}}\), \(M_{12} = \frac{{m_{1} m_{2} }}{{m_{1} + m_{2} }}\).

3 Nonlinear analysis method for gear-rotor-SFD systems

3.1 The calculation method of the Lyapunov exponent

The gear-rotor assembly, undergirded by SFD, constitutes a prototypical nonlinear system with pronounced sensitivity to initial conditions. The Lyapunov exponent is recognized as an efficacious tool for investigating the stability of transient states in ordinary differential equations [50], and its application is pervasive in the analysis of dynamical systems. Specifically, the maximum Lyapunov exponent serves as a quantitative benchmark for discerning the chaotic behavior within the dynamic system's response [35, 51, 52]. Leveraging the Gram-Schmidt QR decomposition, this study introduces a comprehensive strategy for the computation of all Lyapunov exponents within a gear-rotor-SFD high-dimensional system.

Eq. (21) can be written as

$$\frac{{{\text{d}}^{2} {\mathbf{x}}}}{{{\text{d}}\tau^{2} }} = {\mathbf{k}}({\mathbf{x}},\tau )$$
(22)

Prior to resolution, the second-order differential equation necessitates reduction to a first-order state equation, thereby expanding the system's degrees of freedom from eight to sixteen

$$\frac{{{\text{d}}{\mathbf{y}}}}{{{\text{d}}\tau }} = {\mathbf{f}}({\mathbf{y}},\tau )$$
(23)

where \({\mathbf{y}} = \left\{ {X_{1} ,\frac{{{\text{d}}X_{1} }}{{{\text{d}}\tau }},Y_{1} ,\frac{{{\text{d}}Y_{1} }}{{{\text{d}}\tau }},X_{2} ,\frac{{{\text{d}}X_{2} }}{{{\text{d}}\tau }},Y_{2} ,\frac{{{\text{d}}Y_{2} }}{{{\text{d}}\tau }},X_{4} ,\frac{{dX_{4} }}{{{\text{d}}\tau }},Y_{4} ,\frac{{{\text{d}}Y_{4} }}{{{\text{d}}\tau }},X_{r1} ,\frac{{{\text{d}}X_{r1} }}{{{\text{d}}\tau }},X_{r2} ,\frac{{{\text{d}}X_{r2} }}{{{\text{d}}\tau }}} \right\}^{T}\) indicates the generalized coordinate vector.

Given a group of initial values g,

$$\left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}{\mathbf{y}}}}{{{\text{d}}\tau }} = {\mathbf{f}}({\mathbf{y}},\tau )} \hfill \\ {{\mathbf{y}}(0) = {\mathbf{g}}} \hfill \\ \end{array} } \right.$$
(24)

The steady-state solution of Eq. (24) is related to the initial value g and dimensionless time τ, and the steady-state solution can be written as \({\mathbf{y}}_{1} (\tau ) = {{\varvec{\uppsi}}}(\tau ,{\mathbf{g}})\).

Using another group of initial values g + δy(0) near the initial value g,

$$\left\{ {\begin{array}{*{20}l} {\frac{{d{\mathbf{y}}}}{d\tau } = {\mathbf{f}}({\mathbf{y}},\tau )} \hfill \\ {{\mathbf{y}}(0) = {\mathbf{g}} + \delta {\mathbf{y}}(0)} \hfill \\ \end{array} } \right.$$
(25)

the steady-state solution of Eq. (25) is \({\mathbf{y}}_{2} (\tau ) = {{\varvec{\uppsi}}}(\tau ,{\mathbf{g}} + \delta {\mathbf{y}}(0))\). The variational equation is

$$\delta {\mathbf{y}}(\tau ) = {{\varvec{\uppsi}}}(\tau ,{\mathbf{g}} + \delta {\mathbf{y}}(0)) - {{\varvec{\uppsi}}}(\tau ,{\mathbf{g}}) = \frac{{\partial {{\varvec{\uppsi}}}(\tau ,{\mathbf{g}})}}{{\partial {\mathbf{g}}}}\delta {\mathbf{y}}(0)$$
(26)

which indicates that the Monodromy matrix of the system

$${\mathbf{S}} = \frac{{\partial {{\varvec{\uppsi}}}(\tau ,{\mathbf{g}})}}{{\partial {\mathbf{g}}}}$$
(27)

determines the distance between two neighboring trajectories.

Since \({{\varvec{\uppsi}}}(\tau ,{\mathbf{g}})\) is a solution of Eq. (23), it can be obtained as

$$\frac{{{\text{d}}{{\varvec{\uppsi}}}(\tau ,{\mathbf{g}})}}{{{\text{d}}\tau }} = {\mathbf{f}}({{\varvec{\uppsi}}}(\tau ,{\mathbf{g}}),\tau )$$
(28)

For \({{\varvec{\uppsi}}}(\tau ,{\mathbf{g}})\), the evolution time τ and the initial value g are two independent variables. The evolution of τ does not affect g, the value of g is not related to τ, and the results of solving partial derivatives and total derivatives for g and τ are the same; thus, there exist \(\frac{{\partial {{\varvec{\uppsi}}}(\tau ,{\mathbf{g}})}}{{\partial {\mathbf{g}}}} = \frac{{d{{\varvec{\uppsi}}}(\tau ,{\mathbf{g}})}}{{d{\mathbf{g}}}}\), \(\frac{{\partial {{\varvec{\uppsi}}}(\tau ,{\mathbf{g}})}}{\partial \tau } = \frac{{d{{\varvec{\uppsi}}}(\tau ,{\mathbf{g}})}}{d\tau }\), \(\frac{{{\text{d}}{\mathbf{S}}}}{{{\text{d}}{\mathbf{g}}}} = \frac{{\partial {\mathbf{S}}}}{{\partial {\mathbf{g}}}}\), and \(\frac{{{\text{d}}{\mathbf{S}}}}{{{\text{d}}\tau }} = \frac{{\partial {\mathbf{S}}}}{\partial \tau }\).

Differentiating Eq. (27) with respect to τ gives \(\frac{{{\text{d}}{\mathbf{S}}}}{{{\text{d}}\tau }} = \frac{{\partial {\mathbf{S}}}}{\partial \tau } = \frac{{\partial \left( {\frac{{\partial {{\varvec{\uppsi}}}(\tau ,{\mathbf{g}})}}{{\partial {\mathbf{g}}}}} \right)}}{\partial \tau } = \frac{{\partial^{2} {{\varvec{\uppsi}}}(\tau ,{\mathbf{g}})}}{{\partial {\mathbf{g}}\partial \tau }} = \frac{{\partial^{2} {{\varvec{\uppsi}}}(\tau ,{\mathbf{g}})}}{{\partial \tau \partial {\mathbf{g}}}}\). Taking the partial derivative of Eq.  (28)with respect to g gives.

\(\frac{{\partial \left( {\frac{{d{{\varvec{\uppsi}}}(\tau ,{\mathbf{g}})}}{d\tau }} \right)}}{{\partial {\mathbf{g}}}} = \frac{{\partial \left( {\frac{{\partial {{\varvec{\uppsi}}}(\tau ,{\mathbf{g}})}}{\partial \tau }} \right)}}{{\partial {\mathbf{g}}}} = \frac{{\partial^{2} {{\varvec{\uppsi}}}(\tau ,{\mathbf{g}})}}{{\partial {\mathbf{g}}\partial \tau }} = \frac{{\partial^{2} {{\varvec{\uppsi}}}(\tau ,{\mathbf{g}})}}{{\partial \tau \partial {\mathbf{g}}}}\). Therefore, it can be obtained that

$$\frac{{{\text{d}}{\mathbf{S}}}}{{{\text{d}}\tau }} = \frac{{\partial {\mathbf{f}}({{\varvec{\uppsi}}}(\tau ,{\mathbf{g}}),\tau )}}{{\partial {{\varvec{\uppsi}}}}}\frac{{\partial {{\varvec{\uppsi}}}(\tau ,{\mathbf{g}})}}{{\partial {\mathbf{g}}}} = \frac{{\partial {\mathbf{f}}({{\varvec{\uppsi}}}(\tau ,{\mathbf{g}}),\tau )}}{{\partial {\mathbf{y}}}}\frac{{\partial {{\varvec{\uppsi}}}(\tau ,{\mathbf{g}})}}{{\partial {\mathbf{g}}}} = {\mathbf{J}}\frac{{\partial {{\varvec{\uppsi}}}(\tau ,{\mathbf{g}})}}{{\partial {\mathbf{g}}}} = {\mathbf{JS}}$$
(29)

where \({\mathbf{J}} = \frac{{\partial {\mathbf{f}}}}{{\partial {\mathbf{y}}}}\) is the Jacobian matrix, the coefficient matrix of the independent variables in the equation of state, which can be derived from Eqs. (22) and (23). And

$${\mathbf{J}} = \left[ {\begin{array}{*{20}c} 0 &\quad 1 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ {J_{11} - k_{1} } &\quad {J_{12} - c_{1} } &\quad {J_{13} } &\quad {J_{14} } &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 1 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ {J_{21} } &\quad {J_{22} } &\quad {J_{23} - k_{1} } &\quad {J_{24} - c_{1} } &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 1 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad {J_{31} - k_{3} } &\quad {J_{32} - c_{3} } &\quad {J_{33} } &\quad {J_{34} } &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 1 &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad {J_{41} } &\quad {J_{42} } &\quad {J_{43} - k_{3} } &\quad {J_{44} - c_{3} } &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 1 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad { - k_{6} } &\quad { - c_{6} } &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 1 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad { - k_{6} } &\quad { - c_{6} } \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ {e_{1} } &\quad {e_{2} } &\quad {e_{3} } &\quad {e_{4} } &\quad {e_{5} } &\quad {e_{6} } &\quad {e_{7} } &\quad {e_{8} } &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad {g_{5} } &\quad {g_{6} } &\quad {g_{7} } &\quad {g_{8} } &\quad {g_{9} } &\quad {g_{10} } &\quad {g_{11} } &\quad {g_{12} } \\ \end{array} } \right.$$
$$\left. {\begin{array}{*{20}c} 0 &\quad 0 &\quad 0 &\quad 0 \\ { - k_{2} {\text{d}}f_{x1} \sin (\alpha_{1} )} &\quad { - c_{2} \sin (\alpha_{1} )} &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 \\ { - k_{2} {\text{d}}f_{x1} \cos (\alpha_{1} )} &\quad { - c_{2} \cos (\alpha_{1} )} &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 \\ {k_{4} {\text{d}}f_{x1} \sin (\alpha_{1} )} &\quad {c_{4} \sin (\alpha_{1} )} &\quad { - k_{5} {\text{d}}f_{x2} \sin (\alpha_{2} )} &\quad { - c_{5} \sin (\alpha_{2} )} \\ 0 &\quad 0 &\quad 0 &\quad 0 \\ {k_{4} {\text{d}}f_{x1} \cos (\alpha_{1} )} &\quad {c_{4} \cos (\alpha_{1} )} &\quad { - k_{5} {\text{d}}f_{x2} \cos (\alpha_{2} )} &\quad { - c_{5} \cos (\alpha_{2} )} \\ 0 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad {k_{7} {\text{d}}f_{x2} \sin (\alpha_{2} )} &\quad {c_{7} \sin (\alpha_{2} )} \\ 0 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad {k_{7} {\text{d}}f_{x2} \cos (\alpha_{2} )} &\quad {c_{7} \cos (\alpha_{2} )} \\ 0 &\quad 1 &\quad 0 &\quad 0 \\ {e_{13} } &\quad {e_{14} } &\quad {e_{15} } &\quad {e_{16} } \\ 0 &\quad 0 &\quad 0 &\quad 1 \\ {g_{13} } &\quad {g_{14} } &\quad {g_{15} } &\quad {g_{16} } \\ \end{array} } \right]$$

where \({\text{d}}f_{x1} = \frac{{{\text{d}}f\left( {X_{r1} } \right)}}{{{\text{d}}t}} = \left\{ {\begin{array}{*{20}c} {1,} &\quad {X_{r1} \ge 1} \\ {0,} &\quad {else} \\ {1,} &\quad {X_{r1} \le - 1} \\ \end{array} } \right.\), \(\quad df_{x2} = \frac{{df\left( {X_{r2} } \right)}}{dt} = \left\{ {\begin{array}{*{20}c} {1,} &\quad {X_{r2} \ge 1} \\ {0,} &\quad {else} \\ {1,} &\quad {X_{r2} \le - 1} \\ \end{array} } \right.\);

\(\left[ {\begin{array}{*{20}c} {J_{11} } &\quad {J_{12} } &\quad {J_{13} } &\quad {J_{14} } \\ {J_{21} } &\quad {J_{22} } &\quad {J_{23} } &\quad {J_{24} } \\ {J_{31} } &\quad {J_{32} } &\quad {J_{33} } &\quad {J_{34} } \\ {J_{41} } &\quad {J_{42} } &\quad {J_{43} } &\quad {J_{44} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{{\partial F_{x1} }}{{\partial X_{1} }}} &\quad {\frac{{\partial F_{x1} }}{{\partial \frac{{dX_{1} }}{d\tau }}}} &\quad {\frac{{\partial F_{x1} }}{{\partial Y_{1} }}} &\quad {\frac{{\partial F_{x1} }}{{\partial \frac{{dY_{1} }}{d\tau }}}} \\ {\frac{{\partial F_{y1} }}{{\partial X_{1} }}} &\quad {\frac{{\partial F_{y1} }}{{\partial \frac{{dX_{1} }}{d\tau }}}} &\quad {\frac{{\partial F_{y1} }}{{\partial Y_{1} }}} &\quad {\frac{{\partial F_{y1} }}{{\partial \frac{{dY_{1} }}{d\tau }}}} \\ {\frac{{\partial F_{x2} }}{{\partial X_{1} }}} &\quad {\frac{{\partial F_{x2} }}{{\partial \frac{{dX_{1} }}{d\tau }}}} &\quad {\frac{{\partial F_{x2} }}{{\partial Y_{1} }}} &\quad {\frac{{\partial F_{x2} }}{{\partial \frac{{dY_{1} }}{d\tau }}}} \\ {\frac{{\partial F_{y2} }}{{\partial X_{1} }}} &\quad {\frac{{\partial F_{y2} }}{{\partial \frac{{dX_{1} }}{d\tau }}}} &\quad {\frac{{\partial F_{y2} }}{{\partial Y_{1} }}} &\quad {\frac{{\partial F_{y2} }}{{\partial \frac{{dY_{1} }}{d\tau }}}} \\ \end{array} } \right]\), the partial differential can be obtained by the forward finite difference method; \(e_{1} = \left( {J_{11} - k_{1} } \right)*\sin \alpha_{1} + J_{21} *\cos \alpha_{1}\), \(e_{2} = \left( {J_{12} - c_{1} } \right)*\sin \alpha_{1} + J_{22} *\cos \alpha_{1}\), \(e_{3} = J_{13} *\sin \alpha_{1} + \left( {J_{23} - k_{1} } \right)*\cos \alpha_{1}\), \(e_{4} = J_{14} *\sin \alpha_{1} + \left( {J_{24} - c_{1} } \right)*\cos \alpha_{1}\), \(e_{5} = - \left( {J_{31} - k_{3} } \right)*\sin \alpha_{1} - J_{41} *\cos \alpha_{1}\), \(e_{6} = - \left( {J_{32} - c_{3} } \right)*\sin \alpha_{1} - J_{42} *\cos \alpha_{1}\), \(e_{7} = - J_{33} *\sin \alpha_{1} - \left( {J_{43} - k_{3} } \right)*\cos \alpha_{1}\), \(e_{8} = - J_{34} *\sin \alpha_{1} - \left( {J_{44} - c_{3} } \right)*\cos \alpha_{1}\), \(e_{13} = \left( { - k_{2} - k_{4} - f_{3} *k_{8} } \right)*df_{x1}\), \(e_{14} = \left( { - c_{2} - c_{4} - f_{3} *c_{8} } \right)\), \(e_{15} = \left( {k_{5} *\cos \left( {\alpha_{1} - \alpha_{2} } \right) - k_{9} *f_{5} } \right)*df_{x2}\), \(e_{16} = \left( {c_{5} *\cos \left( {\alpha_{1} - \alpha_{2} } \right) - c_{9} *f_{5} } \right)\), \(g_{5} = \left( {J_{31} - k_{3} } \right)*\sin \alpha_{2} + J_{41} *\cos \alpha_{2}\), \(g_{6} = \left( {J_{32} - c_{3} } \right)*\sin \alpha_{2} + J_{42} *\cos \alpha_{2}\)\(g_{7} = J_{33} *\sin \alpha_{2} + \left( {J_{43} - k_{3} } \right)*\cos \alpha_{2}\), \(g_{8} = J_{34} *\sin \alpha_{2} + \left( {J_{44} - c_{3} } \right)*\cos \alpha_{2}\), \(g_{9} = k_{6} *\sin \alpha_{2}\), \(g_{10} = c_{6} *\sin \alpha_{2}\), \(g_{11} = k_{6} *\cos \alpha_{2}\), \(g_{12} = c_{6} *\cos \alpha_{2}\), \(g_{13} = \left( {k_{4} *\cos \left( {\alpha_{1} - \alpha_{2} } \right) - k_{8} *f_{5} } \right)*df_{x1}\), \(g_{14} = \left( {c_{4} *\cos \left( {\alpha_{1} - \alpha_{2} } \right) - c_{8} *f_{5} } \right)\), \(g_{15} = \left( { - k_{5} - k_{7} - f_{4} *k_{9} } \right)*df_{x2}\), \(g_{16} = \left( { - c_{5} - c_{7} - f_{4} *c_{9} } \right)\).

Furthermore, from the initial value \({\mathbf{y}}(0) = {{\varvec{\uppsi}}}(0,{\mathbf{g}}) = {\mathbf{g}}\), we obtain

$$\left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}{\mathbf{S}}}}{{{\text{d}}\tau }} = {\mathbf{JS}}} \hfill \\ {{\mathbf{S}}(0) = {\mathbf{I}}} \hfill \\ \end{array} } \right.$$
(30)

where S and J are 16 × 16 matrices and I is the unit matrix of 16 × 16.

The algorithmic steps to determine the Lyapunov exponent spectrum for the gear-rotor-SFD system are succinctly delineated as follows:

  1. 1.

    The fourth-order Runge–Kutta method is used to solve Eq. (23). At the same time, the initial value \({\mathbf{y}}_{0} = \left\{ {0.1, \cdots ,0.1} \right\}_{16 \times 1}^{T}\), time \(\tau = 300T_{m}\) (\(T_{m}\) denotes one meshing cycle), absolute error Abstol = 1 × 10−8, relative error Reltol = 1 × 10−8 are set to obtain the steady-state solution \({\mathbf{y}}_{\tau }\).

  2. 2.

    Eq. (23) has 16 degrees of freedom, and the calculation of Eq.  (30) requires solving 16 × 16 differential equations, so the calculation of the Lyapunov exponent requires solving a total of 16 × (16 + 1) differential equations. Therefore, the dimension of the extended vectors dh and h is 272 × 1.

    $$\begin{gathered} {\mathbf{dh}}\left[ {1:16} \right] = {\mathbf{f}}({\mathbf{h}}\left[ {1:16} \right],\tau ) \hfill \\ {\mathbf{dh}}\left[ {17:272} \right] = {\mathbf{JS}} \hfill \\ \end{gathered}$$
    (31)
    1. a.

      where S = \(\left[\begin{array}{ccc}\mathbf{h}[17]&\quad \cdots &\quad \mathbf{h}[257]\\ \vdots &\quad \ddots &\quad \vdots \\ \mathbf{h}[32]&\quad \cdots &\quad \mathbf{h}[272]\end{array}\right]\).

  3. 3.

    Take the steady-state solution \({\mathbf{y}}_{\tau }\) obtained in the first step and the unit matrix \(\bf I_{16\times16}\) as the initial values, namely \({\mathbf{h}}_{0} \left[ {1:16} \right] = {\mathbf{y}}_{\tau }\) and \({\mathbf{h}}_{0} \left[ {17:272} \right] = {\mathbf{I}}\left[ {17:272} \right]\).

  4. 4.

    Take \({\mathbf{h}}_{0}\) as the initial value to solve Eq.  (31) to time T to obtain the steady-state solution \({\mathbf{h}}_{T}\), update the initial value \({\mathbf{h}}_{0}\) with the first 16 elements, that is \({\mathbf{h}}_{0} \left[ {1:16} \right] = {\mathbf{h}}_{T} \left[ {1:16} \right]\), and construct the transition matrix A with the remaining elements,

    $${\mathbf{A}} = \left[ {\begin{array}{*{20}c} {{\mathbf{h}}_{T} \left[ {17} \right]} &\quad \cdots &\quad {{\mathbf{h}}_{T} \left[ {257} \right]} \\ \vdots &\quad \ddots &\quad \vdots \\ {{\mathbf{h}}_{T} \left[ {32} \right]} &\quad \cdots &\quad {{\mathbf{h}}_{T} \left[ {272} \right]} \\ \end{array} } \right]_{16 \times 16}$$
    (32)
  5. 5.

    Based on Gram-Schmidt orthogonalization, QR decomposition of matrix A is obtained,

    $${\mathbf{A}} = \left[ {\begin{array}{*{20}c} {{\mathbf{q}}_{1} , \cdots ,{\mathbf{q}}_{16} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {r_{1,1} } &\quad {r_{1,2} } &\quad \cdots &\quad {r_{1,16} } \\ {} &\quad {r_{2,2} } &\quad \cdots &\quad {r_{2,16} } \\ {} &\quad {} &\quad \ddots &\quad \vdots \\ {} &\quad {} &\quad {} &\quad {r_{16,16} } \\ \end{array} } \right]_{16 \times 16}$$
    (33)
    1. a.

      Set \({\mathbf{h}}_{0} = \left[ {17:272} \right] = \left[ {\begin{array}{*{20}c} {{\mathbf{q}}_{1} \user2{ }, \cdots ,{\mathbf{q}}_{16} } \\ \end{array} } \right]\) and construct the vector \({\mathbf{N}}_{1} = \left\{ {r_{i,i} } \right\}_{16 \times 1}\), i = 1,2,…16.

  6. 6.

    Repeat steps 4 and 5 k times to obtain the vectors N1, N2,…, Nk, and the Lyapunov exponent of the system can be calculated by the following formula:

    $$\lambda = \left[ {_{1} ,\user2{ }_{2} , \cdots ,_{16} } \right]^{T} = \mathop {\lim }\limits_{k \to \infty } \frac{{\mathop \sum \nolimits_{1}^{k} {\text{log}}{\mathbf{N}}_{i} }}{kT}$$
    (34)

3.2 The calculation method of Floquet characteristic multipliers

Floquet characteristic multipliers can be used to identify the stability and bifurcation types of the system and to analyze the nonlinear behavior of the system [53, 54]. For a gear-rotor-SFD system, the characteristic multiplier of the system is the eigenvalue of the Monodromy matrix S, which can be constructed from the steady-state solution of Eq.  (30).

The computational methodology for deriving the characteristic multipliers of the gear-rotor-SFD system is concisely outlined as follows:

  1. 1.

    Using the fourth-order Runge–Kutta method to solve Eq. (23), set the initial value \({\mathbf{y}}_{0} = \left\{ {0.1, \cdots ,0.1} \right\}_{16 \times 1}^{T}\), time τ = 300Tm (Tm denotes one meshing cycle), absolute error Abstol = 1 × 10−8, relative error Reltol = 1 × 10−8, and obtain the steady-state solution \({\mathbf{y}}_{\tau }\).

  2. 2.

    According to Eqs. (23) and (30), the extended ordinary differential equations are

    $$\begin{gathered} {\mathbf{dh}}\left[ {1:16} \right] = {\mathbf{f}}({\mathbf{y}},\tau ) \hfill \\ {\mathbf{dh}}\left[ {17:32} \right] = {\mathbf{J}}_{16 \times 16} {\mathbf{V}}_{16 \times 1} \hfill \\ \end{gathered}$$
    (35)
  3. 3.

    where \(\mathbf{V}={\left\{\mathbf{h}\left[17\right], \mathbf{h}\left[18\right],\cdots ,\mathbf{h}\left[32\right]\right\}}_{16}^{T}\).

  4. 4.

    Take the steady-state solution \({\mathbf{y}}_{\tau }\) calculated in the first step and the i-th column vector \({\mathbf{e}}_{i}\) of the unit matrix \(\bf I_{16\times16}\) as the initial value of Eq.  (35), and use the Runge–Kutta method to calculate the steady-state solution \({\mathbf{h}}_{T}\), and construct the i-th column vector \({\mathbf{S}}_{i}\) of Monodromy matrix S with the last 16 elements in \({\mathbf{h}}_{T}\), that is \({\mathbf{h}}_{0} \left[ {1:16} \right] = {\mathbf{y}}_{\tau }\), \({\mathbf{h}}_{0} \left[ {17:32} \right] = {\mathbf{e}}_{i}\), \({\mathbf{S}}_{i} = {\mathbf{h}}_{T} \left[ {17:32} \right]\).

  5. 5.

    The step 3 is repeated 16 times (i = 1,2,…,16) to obtain the Monodromy matrix

    $${\mathbf{S}} = \left[ {{\mathbf{S}}_{1} ,\user2{ }{\mathbf{S}}_{2} , \cdots ,{\mathbf{S}}_{16} } \right]_{16 \times 16}$$
    (36)
  6. 6.

    Solving for the eigenvalues of the Monodromy matrix S yields the characteristic multipliers of the system.

The amplitude of the characteristic multiplier \((m_{i} )\) determines whether the neighboring trajectories are contracting \((\left| {m_{i} } \right| < 1)\) or diverging \((\left| {m_{i} } \right| > 1)\), and the phase angle determines the rotation frequency [12]. The stability and bifurcation type of the periodic solution can be judged by the properties of the characteristic multipliers [12, 53]:

  1. 1.

    If the amplitude of all characteristic multipliers is less than 1 \((\left| {m_{i} } \right| < 1)\), the periodic solution is gradually stable.

  2. 2.

    If there is a real number for which the characteristic multiplier is less than − 1 \((m_{i} < - 1)\), the periodic solution appears as a period-doubling bifurcation.

  3. 3.

    If there is a real number for which the characteristic multiplier is greater than 1 \((m_{i} > 1)\), the periodic solution appears as a saddle-node bifurcation.

  4. 4.

    If there is a pair of conjugate characteristic multipliers crossing the unit circle, the periodic solution appears as a generalized Hopf bifurcation.

4 Nonlinear characteristic analysis

Figure 6 presents the bifurcation diagram both with and without the inclusion of SFD. Utilizing the input shaft speed n as a bifurcation parameter, this study analyzes the system's stability and bifurcation characteristics by computing the characteristic multipliers according to the method delineated in Sect. 3.2. Concurrently, Fig. 7 delineates the characteristic multipliers in the absence of SFD at various rotational speeds.

Fig. 6
figure 6

Bifurcation diagram of lateral vibration without and with SFD: a Forward speed sweep; b Backward speed sweep

Full size image
Fig. 7
figure 7

Floquet characteristic multipliers without SFD at different rotation speeds: a 4400 rpm; b 4600 rpm; c 4800 rpm; d 5000 rpm; e 5400 rpm; f 6000 rpm; g 6400 rpm; h 8600 rpm; i 9000 rpm; j 11,000 rpm; k 11,400 rpm; l 12,800 rpm

Full size image

For rotational speeds below 4400 rpm, all characteristic multipliers reside within the unit circle (Fig. 7a), signifying a progressive stabilization of the periodic solution. At a rotational speed of 4600 rpm, the characteristic multiplier with the maximum modulus traverses the unit circle via the positive real axis (Fig. 7b), signifying a destabilization of the system owing to a saddle-node bifurcation. When the input shaft speed reaches 4800 rpm, a conjugate pair of characteristic multipliers with the maximum magnitude exits the unit circle (Fig. 7c), suggesting the occurrence of a Hopf bifurcation within the system. Consequently, the periodic solution becomes unstable as a result of the Hopf bifurcation, and the peak-to-peak value (PPV) curve for lateral displacement exhibits a jump phenomenon (Fig. 8). At a rotational speed of 5000 rpm, the characteristic multipliers possessing the maximal modulus cross the unit circle on the negative real axis, concurrently with a pair of complex conjugate characteristic multipliers leaving the unit circle (Fig. 7d), which is indicative of the coexistence of period-doubling and Hopf bifurcations. At a rotational speed of 5400 rpm, the system's periodic solution undergoes a Hopf bifurcation (Fig. 7e). At a rotational speed of 6400 rpm, all characteristic multipliers return to the unit circle (Fig. 7g), and subsequently, the periodic solution evolves into a steady state. For a rotational speed of 8600 rpm, the system exhibits a quasi-periodic solution as the conjugate characteristic multiplier departs from the unit circle (Fig. 7h). At a rotational speed of 9000 rpm, the periodic solution incrementally achieves stability (Fig. 7i). Upon reaching a rotational speed of 11,000 rpm, the characteristic multiplier exhibiting the greatest modulus departs from the unit circle along the positive real axis (Fig. 7j). Figure 6 clearly illustrates that the periodic solution transitions to a period-2 motion via a period-doubling bifurcation. At a rotational speed of 11,400 rpm, the characteristic multiplier re-enters the unit circle (Fig. 7k), resulting in the periodic solution stabilizing into a period-1 motion (Fig. 6). At 12,800 rpm, the system undergoes a Hopf bifurcation (Fig. 7l).

Fig. 8
figure 8

PPV curve of lateral vibration without SFD

Full size image

As depicted in Fig. 8, the PPV curve for lateral displacement, in the absence of SFDs, exhibits a pronounced jump phenomenon. Throughout the acceleration phase, the system's periodic solution demonstrates a 'jump-up' behavior approaching 5000 rpm, whereas in the deceleration phase, a 'jump-down' behavior is observed in proximity to 4600 rpm. Consequently, the dynamic response of the system in the vicinity of 4800 rpm is characterized as a bistable response. Similarly, the speed intervals of 9800 to 11,200 rpm, in the region proximal to 12,400 rpm, and between 16,400 and 17,200 rpm constitute bistable response domains. The rotational speed corresponding to the maximum displacement peak is identified as 12,400 rpm.

Lyapunov exponent is used to identify the chaotic properties of the system. “DynamicalSystems.jl” in Julia is an excellent open-source library, that uses the "H2" method in Ref. [55] to calculate the Lyapunov exponent spectrum of the system, but the library cannot calculate the Lyapunov exponent spectrum with SFD. To verify the accuracy of the proposed method in Sect. 3.1, the Lyapunov exponent spectrum of the gear system without SFD is calculated by these two methods for comparison.

Figure 9a and b shows the maximum and minimum Lyapunov exponents without SFD for forward and backward velocity sweeps, respectively. As shown in Fig. 9, the calculation results of the proposed method and the "H2" method (DS in Fig. 9) are very consistent, indicating that the method proposed in this paper is correct. Upon acceleration, the system exhibits chaotic behavior within the rotational speed range of 16,400 to 16,600 rpm. Localized chaotic features are discernible at rotational speeds of approximately 10,600 rpm, 13,400 rpm, and 14,200 rpm. During the deceleration phase, chaotic dynamics manifest within the speed intervals of 15,000 to 15,400 rpm, 16,400 to 16,600 rpm, and 18,000 to 18,200 rpm. In a similar vein, localized chaotic behavior is also observed at approximate rotational speeds of 10,000 rpm, 13,800 rpm, and 14,400 rpm.

Fig. 9
figure 9

Lyapunov exponent spectrum of the system without SFD: a Forward speed sweep; b Backward speed sweep

Full size image

Time-domain diagrams, phase diagrams, and Poincare section are employed to classify the system's motion. Figure 10 presents the time-domain diagrams for the system without SFDs at rotational speeds of 4800 rpm, 8600 rpm, 10,600 rpm, 11,000 rpm, 12,200 rpm, and 16,400 rpm, while Fig. 11 depicts the corresponding phase diagram and Poincare section. At rotational speeds of 4800 and 8600 rpm, the time-domain diagrams exhibit regular, periodic-like waveforms (Fig. 10a, b), and the Poincaré sections reveal closed loops (Fig. 11a, b), signifying a quasi-periodic motion of the system. Figure 10c and f display irregular periodic waveforms. The Poincaré sections (Fig. 11c, f) show a scattered distribution of points, indicative of chaotic motion. Figures 10d and 11d demonstrate that the system's response at 11,000 rpm is characteristic of period-2 motion. Likewise, Figs. 10e and 11e reveal that the system's response at 12,200 rpm conforms to period-1 motion.

Fig. 10
figure 10

Time domain diagram of the system without SFD at different rotation speeds: a 4800 rpm; b 8600 rpm; c 10,600 rpm; d 11,000 rpm; e 12,200 rpm; f 16,400 rpm

Full size image
Fig. 11
figure 11

Phase diagrams and Poincaré sections of the system without SFD at different rotation speeds: a 4800 rpm; b 8600 rpm; c 10,600 rpm; d 11,000 rpm; e 12,200 rpm; f 16,400 rpm

Full size image

Also taking the input shaft speed n as the bifurcation parameter, Fig. 12 illustrates the characteristic multipliers with the inclusion of SFDs at various rotational speeds. Within the speed interval of 2000 to 3800 rpm, all characteristic multipliers of the system reside within the unit circle (Fig. 12a), indicating a progressive stabilization of the periodic solutions. At n = 4000 rpm, the characteristic multipliers with the greatest modulus exit the unit circle along the positive real axis (Fig. 12b), signifying that the periodic solution experiences a saddle-node bifurcation. At n = 4200 rpm, the characteristic multipliers re-enter the unit circle (Fig. 12c), and the periodic solution progressively attains a steady state. Upon reaching a speed of 9600 rpm, a conjugate pair of characteristic multipliers departs from the unit circle (Fig. 12d), precipitating a Hopf bifurcation in the periodic solution. Subsequently, the system's solution reestablishes stability at 9800 rpm (Fig. 12e).

Fig. 12
figure 12

Floquet characteristic multipliers with SFD at different rotation speeds: a 3800 rpm; b 4000 rpm; c 4200 rpm; d 9600 rpm; e 9800 rpm; f 12,800 rpm

Full size image

Figure 13 illustrates that the PPV curve of lateral displacement when equipped with SFDs, also demonstrates a jump phenomenon. During acceleration, the system's periodic response undergoes a jump-up transition near 8800 rpm, whereas in the deceleration phase, a jump-down transition occurs near 9400 rpm. The speed interval between 9000 and 9200 rpm constitutes a region of bistable response. Additionally, the maximum displacement peak is observed at a rotational speed of 2800 rpm.

Fig. 13
figure 13

PPV curve of lateral vibration with SFD

Full size image

Figure 14 presents the maximum and minimum Lyapunov exponents for the system with SFDs. Irrespective of whether the speed sweep is forward or reverse, the maximum Lyapunov exponent remains negative, signifying the absence of chaotic regions within the system.

Fig. 14
figure 14

Lyapunov exponent spectrum of the system with SFD: a Forward speed sweep; b Backward speed sweep

Full size image

Figure 15 depicts the time-domain responses of the system with SFDs at rotational speeds of 2800 rpm, 4000 rpm, 4800 rpm, 10,600 rpm, 11,000 rpm, and 16,400 rpm, while Fig. 16 presents the phase diagram and Poincaré sections at these respective speeds. At 2800 rpm and 4000 rpm, the time-domain diagrams exhibit regular periodic behavior (Fig. 15a, b), and the corresponding Poincaré sections consist of an isolated point (Fig. 16a, b), indicative of period-1 motion. For rotational speeds of 4800 rpm, 10,600 rpm, 11,000 rpm, and 16,400 rpm, the time-domain diagrams demonstrate consistent period-like behavior (Fig. 15c, d, e, f), the trajectories in the Poincaré sections form closed loops (Fig. 16c, d, e, f), characterizing the motion as quasi-periodic.

Fig. 15
figure 15

Time domain diagram of the system with SFD at different rotation speeds: a 2800 rpm; b 4000 rpm; c 4800 rpm; d 10,600 rpm; e 11,000 rpm; f 16,400 rpm

Full size image
Fig. 16
figure 16

Phase diagrams and Poincaré sections of the system with SFD at different rotation speeds: a 2800 rpm; b 4000 rpm; c 4800 rpm; d 10,600 rpm; e 11,000 rpm; f 16,400 rpm

Full size image

A comparative analysis of the stability and bifurcation types, both with and without the incorporation of SFDs, elucidates the influence of SFDs on the system's dynamic response. Comparison of the bifurcation diagrams (Fig. 6) and Lyapunov exponents (Figs. 9, 14) reveals that after applying SFDs for the model studied in this paper the system exists only in period-1 and quasi-period motions, and the region of chaotic motions and unsteady vibrations are greatly narrowed, which improves the system's dynamic behavior.

Analysis of the PPV curves (Figs. 8, 13) indicates that the implementation of SFDs eliminates the system's bistable response at speeds near 4800 rpm and 12,400 rpm, between 9800 and 11,200 rpm, and from 16,400 to 17,200 rpm. The bistable response is now confined to a narrow speed range of 9000–9200 rpm. Concurrently, the incorporation of SFD notably diminishes the incidence of saddle-node bifurcations (Fig. 7b), Hopf bifurcations (Fig. 7c, d, e, h, i), and period-doubling bifurcations (Fig. 7d, j) throughout the acceleration phase. Correspondingly, the bifurcation diagram and PPV curve associated with the SFD system exhibit enhanced smoothness compared to those without SFD, and the system's nonlinear characteristics are markedly attenuated.

5 Conclusion

This study incorporates time-varying meshing stiffness, static transmission error, and backlash into the analysis, establishing the motion equations for a two-stage spur gear system grounded in lumped parameter theory. The first-stage gear pair is supported by SFD and squirrel-cage elastic support, with the SFD's nonlinear oil-film force calculated via the finite element method and Galerkin's principle. A nonlinear dynamic model of the gear-rotor-SFD system is developed by coupling the nonlinear oil-film force with the motion equations, which is then resolved utilizing the fourth-order Runge–Kutta numerical method. The analysis delineates the vibration stability and bifurcation characteristics of two-stage spur gear systems, both with and without the integration of SFD. Furthermore, the study examines the vibration attenuation properties afforded by the SFD. The principal findings of this investigation are summarized as follows:

  1. 1.

    Leveraging the Gram-Schmidt QR decomposition, a novel methodology is proposed for computing the Lyapunov exponent spectrum and Floquet characteristic multipliers of complex high-dimensional gear-rotor-SFD systems, subsequently corroborating its efficacy through rigorous validation.

  2. 2.

    In the model examined herein, the application of the SFD results in the system exhibiting solely period-1 and quasi-periodic motions, while the domain of chaotic and unstable vibrations is substantially constricted, thereby enhancing the system's dynamic performance.

  3. 3.

    Upon the integration of the SFD, the system's bistable responses observed in the vicinities of 4800 rpm and 12,400 rpm, between 9800 and 11,200 rpm, and from 16,400 to 17,200 rpm are eliminated, with the bistable behavior confined solely to the range of 9000–9200 rpm.

  4. 4.

    With the help of SFD, the occurrence of saddle-node bifurcation, Hopf bifurcation, and period-doubling bifurcation is effectively reduced. The bifurcation diagrams and PPV curves of the system with SFD are smoother than those without SFD, and the nonlinear characteristics of the system are significantly suppressed.

Increasing the degrees of freedom of the system significantly complicates the calculation of Lyapunov exponent and Floquet multipliers. Mastering effective computational methods for Lyapunov exponents and Floquet multipliers in high-dimensional gear systems remains a goal for our future research.