1 Introduction

1.1 Literature review

Fuzzy control is a practical alternative for a variety of challenging control applications since it provides a convenient method for constructing nonlinear controllers via the use of heuristic knowledge. A human operator of a process, or a control engineer, may have a heuristic knowledge. This knowledge also can come from after applying a controller on the system [1]. Thus, in comparison to other controllers, several authors confirm that fuzzy controllers result in a far simpler laws, require minimal modeling of the system, and are robust to the variations in the system dynamics [2–8].

Fuzzy logic was first proposed by Zadeh [9]. However, the first fuzzy control application is referred to Mamdani [10], where he controlled a steam engine. The main problems with using fuzzy logic, however, are twofold. First, except for very few cases, the stability of fuzzy controllers has not been proven [1]. Second, the literature typically only shows the design of fuzzy controllers for second-order systems. The extension of these techniques to higher-order systems is not clear, and in many cases it is cumbersome.

To improve the control performance and to overcome drawbacks of fuzzy controllers, it is common to combine them with other control schemes. Incorporation of fuzzy controllers with PI, PD, or PID controllers results in control performance improvements [11–13]. Inserting a supervisory sliding mode controller to fuzzy controllers improves the stability and robustness of the system [14–16]. Various optimal fuzzy controllers have been achieved by inserting genetic algorithms [17–19] or neural networks [20–22] into the main fuzzy control systems. Likewise, some other robust fuzzy controllers have been designed [23–25].

In another note, the systematic study of Padé approximants was the subject of the Doctoral Thesis of Henri Padé defended in 1892. Padé approximant has been widely used to solve different mathematical problems, and it is the best approximation of a function by a rational function of given order [26–28]. In many cases the traditional Padé technique can greatly increase the convergence region and rate of a given series.

In this paper, we introduce and formalize the fuzzy-Padé controllers, which benefit the inherent stability of Padé approximants and also can be easily applied to high-order systems. As noted, fuzzy-Padé controllers are based on Padé approximants. This is the first time that Padé approximants, which are commonly used to approximate a function, are utilized as controllers. The fuzzy-Padé controller has a simple and intuitively understandable structure.

Fuzzy-Padé controllers are designed to put the expert’s control knowledge into rule bases. Therefore, Heuristic knowledge is a common starting point for both fuzzy and fuzzy-Padé controllers. Fuzzy singleton rules, which are based on the heuristic knowledge and are a special class of fuzzy rules, make the rule base of the fuzzy-Padé controllers. As a result, in the fuzzy-Padé controllers, inference engine, fuzzification and defuzzification levels, which are generally time consuming, are omitted. Instead, the highly convergent Padé approximant is replaced. Despite fuzzy controllers, fuzzy-Padé controllers are suitable to be utilized in high-order systems, as illustrated in the case studies. With fuzzy-Padé designs, simple controllers are obtained which are robust to model variations and besides do not require extensive modeling of the plant.

1.2 Padé approximants

Some techniques exist to increase the convergence of a given series. Among them, the so-called Padé technique is widely applied [26]. A Padé approximant often gives better approximation of the function than truncating its Taylor series, and it may still work where the Taylor series does not converge. For these reasons, Padé approximants are used extensively in mathematics and computer calculations.

Suppose that a function f(x) is represented in a power series \({\sum_{i=0}^{\infty}}c_{i}x^{i}\), so that

$$ f(x)=\sum_{i=0}^{\infty}c_ix^i. $$
(1)

This expansion is the fundamental starting point of any analysis using the Padé approximants. A Padé approximant with single variable is a rational fraction

$$ \mbox{Pad\'{e}}[m,n]=\frac{a_0+a_1x+\cdots+a_mx^m}{\overline{a}_0+\overline{a}_1x+\cdots+\overline{a}_nx^n}, $$
(2)

which has a Maclaurin expansion which agrees with (1) as far as possible [29]. To make (2) definite, we take \(\overline{a}_{0}=1\). The coefficients of its numerator and its denominator are obtained directly from the approximation through-order property of the approximant [30]. Equating right sides of (1) and (2) results in

$$ \sum_{i=0}^{\infty}c_ix^i=\frac{a_0+a_1x+\cdots+a_mx^m}{1+\overline{a}_1x+\cdots+\overline{a}_nx^n}+O(x^{m+n+1}). $$
(3)

One can simply derive the unknown coefficients of the Padé approximant in (3), by cross-multiplying and then equating the coefficients of x 0, x 1,…,x m+n.

[m,n] padé approximant means the order of the variable in numerator is m, and the order of it in denominator is n. However, it is common that in most cases, these two orders are equal, leading to an [m,m] padé approximant. For a single variable [m,n] Padé approximant, there exist m+n+1 unknowns to be determined.

Baker and Gammel [31] prove that the Padé approximant approximates a function, and Baker et al. [32] conclude that the Padé approximants converge uniformly to the desired function, which is out of singularity. Figure 1 demonstrates the convergence rate of the Padé approximant compared to the Taylor series expansion.

Fig. 1
figure 1

Illustration of convergence of Padé approximants. Solid line: \(f(z)=\sqrt{(}(1+z)/(1+4z))\); dashed line: [1, 1] Padé approximant of f(z); dash-dotted line: Maclurin series of f(z) up to the second order

Full size image

This paper is organized as follows. Section 2 is devoted to the formalization of the fuzzy-Padé controllers, and discusses its similarities and differences with fuzzy controllers. In Sects. 3, 4, and 5, three classic problems, the single inverted pendulum, ball and beam, and parallel double inverted pendulum systems are stabilized, by implementing the proposed controller. In each of the Sects. 3, 4, and 5, a fuzzy controller is also represented to make a comparison between the two controllers. Finally, Sect. 6 gives a conclusion.

2 The fuzzy-Padé controller

In this paper, we aim to use the Padé approximant as a controller. To construct the controller, we should determine the Padé unknown coefficients based on some certain rules. To this end, we define fuzzy singleton rules as the basis of the controller. Combined together, we call the constructed controller as the fuzzy-Padé controller. As we will show in three case studies, the proposed controller is efficient and accurate. More accurate results can be obtained with higher-order Padé approximants.

Fuzzy-Padé controllers are based on heuristic knowledge, similar to fuzzy controllers (Fig. 2). It should be noted that fuzzy singleton membership functions have only one member with the degree of membership equal to 1. So, fuzzy singleton rules which are based on fuzzy singleton membership functions are crisp rules, making some data pairs. We use these data pairs to shape the Padé unknown parameters. Since the rules in the fuzzy-Padé controller are crisp, despite the fuzzy controller, fuzzification and defuzzification levels will not be needed any more.

Fig. 2
figure 2

Heuristic knowledge constructs the rule-base for fuzzy and fuzzy-Padé controllers

Full size image

In Fig. 3, the structures of the fuzzy and the fuzzy-Padé controllers are shown and compared. As it can be seen from Fig. 3(a), in fuzzy controllers, fuzzy rules construct the inference engine, which itself needs the fuzzification and defuzzification levels to obtain outputs from the given inputs. On the other hand, in the fuzzy-Padé controllers (as seen in Fig. 3(b) fuzzy singleton rules generate the data pairs, which subsequently shape the Padé approximants by determining the Padé constants. One of the main differences between the two controllers is that the inference engine, fuzzification and defuzzification levels, which are generally time consuming, are omitted from fuzzy-Padé controller. Instead, the highly convergent Padé approximant is replaced. The input rules of the two controllers have a same origin, which is heuristic knowledge of an expert.

Fig. 3
figure 3

Structures of the fuzzy and the fuzzy-Padé controllers

Full size image

By making use of the fuzzy rules, defined by Zadeh [33], we construct the rule base of the controller. Fuzzy singleton rules, which are derived from fuzzy singleton membership functions, shape the governing data pairs. The unknown coefficients of the fuzzy-Padé controller are found in such a way to satisfy these data pairs.

Figure 4 is demonstrating the differences between fuzzy rules and fuzzy singleton rules. Despite general fuzzy membership functions which span in a wide region and have infinite members, fuzzy singleton membership functions have only a single member with the highest degree of membership, 1. Based on this difference, fuzzy singleton membership functions are crisp rules. For convenience, we also represent the fuzzy singleton rule in Fig. 4 as \((x_{1}^{*},x_{2}^{*},u^{*})\).

Fig. 4
figure 4

Demonstration of fuzzy singleton membership functions which are used in the fuzzy-Padé controller

Full size image

Mostly, the dynamic systems which are supposed to be controlled have more than one state variable. So, to construct the fuzzy-padé controller, we use the generalized padé approximant with multiple variables. If we consider a system of order q≥1, with the input variable u, we construct the generalized [m,n] Padé approximant based on (2). Without losing the generality, in the rest of this section, we assume that m=n=3. Therefore, (4) is a general [3, 3] Padé approximant, for a system of arbitrary order q,

(4)

where x=[x 1,x 2,…,x q ]. Letting M and N to be the number of unknown coefficients in the numerator and denominator of (4), respectively, it makes a total number of M+N unknown coefficients in (4). M and N can be obtained as follows:

$$ \left\{ \begin{array}{l} {M={\displaystyle\sum_{i=0}^m}\left(\begin{array}{c}q+i-1\\q-1\end{array}\right),}\\[10pt] {N={\displaystyle\sum_{i=1}^n}\left(\begin{array}{c}q+i-1\\q-1\end{array}\right),} \end{array} \right. $$
(5)

where is denoting the binomial coefficient of the two numbers q+i−1 and q−1.

It is to be noted that we can reduce (4) to a [2, 2] Padé approximant by setting \(d_{ijk}=\overline{d}_{ijk}=0\); and accordingly to a [1, 1] Padé approximant by setting \(c_{ij}=\overline{c}_{ij}=0\) and \(d_{ijk}=\overline{d}_{ijk}=0\).

By replacing a given fuzzy singleton rule, \((x^{*}_{1},x^{*}_{2}, \ldots,x^{*}_{q},u^{*})\), in (4) and by cross-multiplying it, we reach to

(6)

Assume R fuzzy singleton rules in the form

$$ \left\{ \begin{array}{l} \mbox{Rule }1\!:\quad{}(x^{(1)}_1,x^{(1)}_2,\ldots,x^{(1)}_q,u^{(1)}),\\[4pt] \mbox{Rule }2\!:\quad{}(x^{(2)}_1,x^{(2)}_2,\ldots,x^{(2)}_q,u^{(2)}),\\ \quad\vdots\\ \mbox{Rule }R\!:\quad{}(x^{(R)}_1,x^{(R)}_2,\ldots,x^{(R)}_q,u^{(R)}), \end{array} \right. $$
(7)

where R≥M+N. By replacing each rule of (7) into (6) we can construct the following linear matrix equation:

$$ \textbf{A}_{R\times(M+N)}\left[\begin{array}{c}a\\[2pt]\{b_i\}\\[2pt]\{c_{ij}\}\\[2pt]\{d_{ijk}\}\\[2pt]\{\overline{b}_{i}\}\\[2pt]\{\overline{c}_{ij}\}\\[2pt]\{\overline{d}_{ijk}\}\\[2pt]\end{array}\right]_{(M+N)\times1}=\textbf{B}_{R\times1}, $$
(8)

where {b i }={b 1,b 2,…,b q }T, {c ij }={c 11,c 21,…,c qq }T (j≤i), {d ijk }={d 111,d 211,…,d qqq }T (j≤i and k≤j), and so on.

Each row of the matrices A and B in (8) is

$$ \left\{ \begin{array}{l} \textbf{A}_{1\times(M+N)}=[1\ \ \{x^*_i\}\ \ \{x^*_ix^*_j\}\ \ \{x^*_ix^*_jx^*_k\}\\\quad\quad\quad\quad\quad\ \ {-}u^*\{x^*_i\}\ \ {-}u^*\{x^*_ix^*_j\}\ \ {-}u^*\{x^*_ix^*_jx^*_k\}],\\ \textbf{B}_{1\times1}=[u^*], \end{array} \right. $$
(9)

where \(\{x^{*}_{i}\}=\{x^{*}_{1},x^{*}_{2},\ldots,x^{*}_{q}\}\), \(\{x^{*}_{i}x^{*}_{j}\}=\{(x^{*}_{1})^{2},x^{*}_{2}x^{*}_{1}, \ldots,(x^{*}_{q})^{2}\}\) (j≤i), \(\{x^{*}_{i}x^{*}_{j}x^{*}_{k}\}=\{(x^{*}_{1})^{3},x^{*}_{2}(x^{*}_{1})^{2},\ldots, (x^{*}_{q})^{3}\}\) (j≤i and k≤j).

To ensure that the denominator of the designed fuzzy-Padé controller, (4), is always nonzero, we define the constraint

(10)

Finally, by using the standard least square technique we solve Eq. (8) subject to the constraint (10) to derive the M+N unknown coefficients of the fuzzy-Padé controller (4). In what follows, we present the stability theorem of the fuzzy-Padé controller.

Theorem 1

The fuzzy-Padé controller u(x): \(\mathcal{L}^{q}_{\infty}{}\longrightarrow{}\mathcal{L}^{1}_{\infty}\) is \(\mathcal{L}_{\infty}\) stable, and there exist a function α, defined on [0,∞), and a nonnegative constant β such that

for all \(\boldsymbol{x}\in{}\mathcal{L}^{q}_{\infty}\).

Proof

Since \(\boldsymbol{x}\in{}\mathcal{L}^{q}_{\infty}\), suppose that

where r is a positive constant. Thus, it results in the following inequalities:

$$\sup_{t\geq0}\left|{\sum_{i=1}^qb_ix_i}\right|\leq\left(\begin{array}{c}q\\q-1\end{array}\right)|b|r,$$
$$\sup_{t\geq0}\left|{\sum_{i=1}^{q}\sum_{j=1}^{q (j\leq{}i)}c_{ij}x_ix_j}\right|\leq\left(\begin{array}{c}q+1\\q-1\end{array}\right)|c|r^2,$$
$$\sup_{t\geq0}\left|{\sum_{i=1}^{q}\sum_{j=1}^{q (j\leq{}i)}\sum_{k=1}^{q (k\leq{}j)}d_{ijk}x_ix_jx_k}\right|\leq\left(\begin{array}{c}q+2\\q-1\end{array}\right)|d|r^3.$$

It is to be noted that b=max{b i }, c=max{c ij } and d=max{d ijk } for i, j and k ranging from 1 to q. Taking the constraint (10) into consideration, by choosing

and by choosing the bias term \(\beta=\dfrac{a}{D}\) we reach to

$$\sup_{t\geq0}\big|u(\boldsymbol{x})\big|{}\leq{}\alpha(r)+\beta.$$

 □

Since fuzzy-Padé is highly dependent to the fuzzy singleton rules, designing a good rule base is key to obtaining a satisfactory controller for a particular application. Also, we should be careful in selecting the number of rules. This number can be any number more than the unknown coefficients in the fuzzy-Padé controller, M+N, but we should only include the essential ones. Extra rules or even insufficient rules may lead to incorrect determination of fuzzy-Padé parameters.

As we will show in the three case studies, fuzzy-Padé controllers are fast convergent, reduce the oscillations, can be operated in real time, and are suitable for high-order nonlinear systems.

3 The single inverted pendulum system

Inverted pendulum systems are often among the benchmarks for verifying the usefulness of a novel control method. Single inverted pendulum systems, series double inverted pendulum systems and parallel double inverted pendulum systems are all in this category. In this section, we control the single inverted pendulum system, and in Sect. 5 we control the parallel double inverted pendulum system.

Implementing different control methods on the single inverted pendulum system has always been an attractive problem since 1950s [34–38]. The objective is to stabilize the pole around its unstable equilibrium point. When the pendulum is raised from the rest position to its upright one, the system is strongly nonlinear with the pendulum angle. The input to the system is the force applied to the cart, which is free to move.

In this section, we apply the fuzzy-Padé controller to the single inverted pendulum system, and then the results are compared to a fuzzy controller with a similar rule base.

3.1 System dynamics and the fuzzy controller

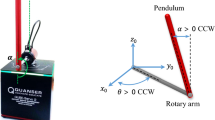
The single inverted pendulum system is composed of two bodies: a cart and a pendulum (Fig. 5). The pendulum is attached to the cart by a revolute joint and the goal of the controller is to stabilize the pendulum in its unstable upright position without taking the cart position into consideration.

Fig. 5
figure 5

Inverted pendulum system; an inverted pendulum is pinned to a moving cart

Full size image

The dynamic model of this second-order system in the state space form can be written as [39]

$$ \left[\begin{array}{c}\dot{x}_1\\\dot{x}_2\end{array}\right]= \left[\begin{array}{c}x_2\\[4pt]\frac{g\sin{x_1}-kmlx_2^2\sin(2x_1)/2+ku\cos{x_1}}{4l/3-kml\cos^2{x_1}}\end{array}\right], $$
(11)

where k=1/(M+m). In the above equation, x 1=θ and \(x_{2}=\dot{\theta}\) are the rotation angle and angular velocity of the pendulum, respectively. u is the force applied to the cart. The parameters M, m, l, and g denote the cart mass, mass and the length of the pendulum, and gravity, respectively. The design parameters are set as M=1 (kg), m=0.1 (kg), l=0.5 (m), and g=9.8 (m/s2).

The fuzzy controller has four main components: (1) the fuzzy rule base keeps the knowledge, in the form of a set of rules, (2) the inference engine evaluates which control rules are relevant at the current point and decides what the input to the plant should be, (3) the fuzzification level converts the plant output data as fuzzy inputs to the inference engine and, (4) the defuzzification level converts the fuzzy conclusions reached by the inference engine into the inputs to the plant. In other words, the fuzzy controller acts as an artificial decision maker that collects plant output data, and then decides what the plant input should be to ensure that the performance goals will be achieved [1].

In this system, 9 fuzzy rules are applied. Three membership functions for each of the states x 1 and x 2 have been defined (Fig. 6(a) and (b); input to the plant, u, has five membership functions shown in Fig. 6(c). Note that in Fig. 6, N, Z, and P represent negative, zero, and positive fuzzy sets, respectively. NG is negative great and PG is positive great.

Fig. 6
figure 6

Membership functions (μ’s) used in the fuzzy controller for the single inverted pendulum system; (a) fuzzy sets N, Z, and P for x 1; (b) fuzzy sets N, Z, and P for x 2; (c) fuzzy sets NG, N, Z, P, and PG for u

Full size image

The 9 fuzzy rules based on the membership functions (Fig. 6) are shown in Table 1.

Table 1 Fuzzy rules used in the fuzzy controller for the inverted pendulum system
Full size table

Beside the above rules, we use Mamdani fuzzy reasoning method [40] and centroid defuzzifier to construct the fuzzy controller.

3.2 The fuzzy-Padé controller

The fuzzy-Padé controller is utilized to stabilize the single inverted pendulum system with 2 state variables and 1 control input. By converting fuzzy membership functions (Fig. 6), and consequently fuzzy rules (Table 1), to fuzzy singleton membership functions and fuzzy singleton rules, we build the rule base for the fuzzy-Padé controller. This rule base is shown in Table 2.

Table 2 Fuzzy singleton rules used in the fuzzy-Padé controller for the inverted pendulum system
Full size table

Each rule in Table 2 represents a fuzzy rule in Table 1. For instance, based on the membership functions in Fig. 6, the rule

is converted to the fuzzy singleton rule

or (−0.3,−0.1,40).

The order of the Padé approximant we use here is [1,1]. Referring to (4), the [1,1] Padé approximant with two variables is

$$ u(\boldsymbol{x})=\frac{{a+\sum_{i=1}^2b_ix_i}}{{1+\sum_{i=1}^2\overline{b}_ix_i}}. $$
(12)

With m=n=1 and i=2, referring to (5), results in M=3 and N=2. Thus, there exist M+N=5 unknown coefficients in (12). We use the 9 rules, R=9, in Table 2 to build (8) and to determine the 5 unknowns in (12). The derived coefficients are shown in Table 3. It is notable that D=1.00 (see (10)).

Table 3 Values of the coefficients of the [1, 1] Padé approximant for the inverted pendulum system
Full size table

3.3 Results and comparisons

The simulated results which compare the fuzzy and fuzzy-Padé controllers are depicted in Figs. 7 and 8. In the simulation, the initial conditions are x 1(0)=40 ∘ and x 2(0)=0. Figure 7 shows that although both controllers converge to the origin, fuzzy-Padé response is smoother. As it can be seen in Fig. 8, the fuzzy-Padé controller has reduced the actuation effort. In this paper, we have used Matlab R2009a [41] for our simulations.

Fig. 7
figure 7

Simulated results for the single inverted pendulum system (initial conditions: x 1(0)=2π/9 (rad) and x 2(0)=0). Dashed-line: fuzzy controller; solid line: fuzzy-Padé controller. (a) angular rotation, x 1, versus time, t; (b) angular velocity, x 2, versus t

Full size image
Fig. 8
figure 8

Input force to the inverted pendulum system, u, versus time, t. Dashed-line: fuzzy controller; solid line: fuzzy-Padé controller

Full size image

A general comparison between these two controllers can be seen in Table 4. CPU-time is the time spent for the overall simulation. The PC used for the experiments has an Intel Quad Core Processor i7 Q820 (1.73 GHz 1066 MHz 8MBL3), and 8 GB DDR3 RAM. CPU-time and input momentum in Table 4 belong to the simulations in Figs. 7 and 8.

Table 4 A comparison between fuzzy and fuzzy-Padé controllers in three areas; convergence region, CPU-time and input momentum to the system
Full size table

High performance of the fuzzy-Padé controller is evident in Table 4. Fuzzy-Padé controller has greatly increased the convergence region; CPU-time in fuzzy-Padé controller is about 3.8 times less than fuzzy controller. Besides, input momentum has also been reduced in the proposed controller. Therefore, we can conclude that the fuzzy-Padé controller perfectly stabilizes the single inverted pendulum system.

It is notable that, in this system, changing the fuzzy membership functions from Gaussian to trapezoid will reduce the convergence region of the fuzzy controller from ±44.80 ∘ to ±37.40 ∘.

4 The ball and beam system

The familiar ball and beam system is a popular textbook example in control theory. Beside nonlinear control methods, several researchers have applied the fuzzy logic to control the ball and beam system [42–45].

Nguyen and Huynh [46] developed their fuzzy controller based on shuffled frog leaping algorithm (SFLA). They have brought the rule base of the fuzzy controller by expert experience, and then they have optimally tuned the parameters of the controller. By imposing constraints on the fuzzy rules in a hierarchical structure, Joo and Lee [47] could control the ball and beam system with fewer fuzzy rules than the rules in a centralized fuzzy controller.

Glower and Munighan [3, 48] designed their controller based on connecting fuzzy controllers and variable structures controllers. They have shown that, through this connection, simpler fuzzy rules can be obtained for higher-order systems with less effort.

In this section, we design a fuzzy-Padé controller for the ball and beam system. To compare with the novel fuzzy-Padé controller, a pure fuzzy controller, similar to Sect. 3, is also developed. Then we discuss about the performance of the two controllers. It is interesting to see that the fuzzy-Padé controller has superior performance compared to the fuzzy controller.

4.1 System dynamics and the fuzzy controller

The ball and beam system is built with two moving parts, a ball and a beam. The ball is free to move along the beam’s direction, and the beam can rotate about the fixed point (Fig. 9). The input to the system is the angular acceleration of the beam.

Fig. 9
figure 9

The ball and beam system. Two variables are the beam’s angle (θ), and the ball’s distance (r). Input u is the angular acceleration of the beam

Full size image

One can control the position of the ball by applying a force to the beam to rotate it. Both the angel of the beam and the position of the ball are measured. Therefore, the model of the system has four states. Those include the position of the ball, r, its velocity, \(\dot{r}\), the angle of the bar, θ, and its angular velocity, \(\dot{\theta}\). The controller uses these variables to derive an error signal used for feedback. The angle of the beam is reduced as the ball nears its desired position, in order to bring the ball to a stop at its desired position with as little overshoot as possible. Let \(\boldsymbol{x}=[r,\dot{r},\theta,\dot{\theta}]^{T}\) be the state of the system, and u be the input force which is angular acceleration of the beam. The state space model of this system is [49]

$$ \left[\begin{array}{c}\dot{x}_1\\[3pt]\dot{x}_2\\[3pt]\dot{x}_3\\[3pt]\dot{x}_4\end{array}\right]= \left[\begin{array}{c}x_2\\[3pt]0.714\left(x_1x_3^2-g\sin{x_3}\right)\\[3pt]x_4\\[3pt]u\end{array}\right]. $$
(13)

In this system, 135 rules are applied to construct the fuzzy controller. Five membership functions are used for position, x 1, and three membership functions are used for other states (i.e. x 2, x 3, x 4). These membership functions are achieved after trials and errors on shape of membership functions and their domains. Figures 10 and 11 show the membership functions for the states of the system (x 1, x 2, x 3, x 4) and for the input force u, respectively. Note that in Figs. 10 and 11, N, Z, and P represent negative, zero, and positive fuzzy sets, respectively. NG is negative great and PG is positive great.

Fig. 10
figure 10

Membership functions (μ’s) used in the fuzzy controller for the ball and beam system; (a) fuzzy sets NG, N, Z, P, and PG for x 1; (b) fuzzy sets N, Z, and P for x 2; (c) fuzzy sets N, Z, and P for x 3; (d) fuzzy sets N, Z, and P for x 4

Full size image
Fig. 11
figure 11

Membership functions (μ’s) used in the fuzzy controller for the ball and beam system; Z, N, and P for u

Full size image

Table 5 shows the fuzzy rules used in the ball and beam system. It should be noted that due to the symmetry of the system, each rule in Table 5 has a complement, which is not shown in the table. For example, the complement of the rule (P,Z,N,Z,P) is (N,Z,P,Z,N).

Table 5 Fuzzy rules used in the fuzzy controller for the ball and beam system
Full size table

Afterward, by using Mamdani’s fuzzy reasoning method [40] and centroid defuzzifier, the fuzzy controller is shaped.

4.2 The fuzzy-Padé controller

The fuzzy-Padé controller is utilized to stabilize the ball and beam system with 4 state variables and 1 control input. Table 6 demonstrate the rules used in the fuzzy-Padé controller. The 41 fuzzy singleton rules in Table 6 are based on membership functions in Fig. 10, and the control input u is based on the fuzzy saturating algorithm given by Glower and Munighan [3].

Table 6 Fuzzy singleton rules used in the fuzzy-Padé controller for the ball and beam system
Full size table

To increase the accuracy of the Padé approximant, we have used the [2,2] Padé approximant in this case study. Referring to (4), a general [2,2] Padé approximant with four variables is as

$$ u(\boldsymbol{x})=\frac{{a+\sum_{i=1}^4b_ix_i}+\sum_{i=1}^{4}\sum_{j=1}^{4 (j\leq{}i)}c_{ij}x_ix_j}{1+{\sum_{i=1}^4\overline{b}_ix_i}+{\sum_{i=1}^{4}\sum_{j=1}^{4 (j\leq{}i)}\overline{c}_{ij}x_ix_j}}. $$
(14)

With m=n=2 and i=4, referring to (5), results in M=15 and N=14. Thus, there exist M+N=29 unknown coefficients in (14). We use the 41 rules, R=41, in Table 6 to build (8) and to determine the 29 unknowns in (14).

If we consider that in (14) we should have u(0)=0, it results in a=0, and since u(−x)=−u(x), it gives us \(c_{ij}=\overline{b}_{i}=0\). The other derived coefficients are shown in Table 7. It is notable that D=0.11 (see (10)).

Table 7 Values of the coefficients of the [2, 2] Padé approximant for the ball and beam system
Full size table

4.3 Results and comparisons

The simulated results which compare the fuzzy and fuzzy-Padé controllers are depicted in Figs. 12 and 13. Figure 12 which compares the response of the states of the systems, shows that despite the fuzzy controller, fuzzy-Padé controller converges asymptotically to the origin at a short settling time. As it can be seen in Fig. 13 the fuzzy-Padé controller has greatly reduced the actuation effort. There is less fluctuations in the response, and the response is quite smoother.

Fig. 12
figure 12

Simulated results for the ball and beam system (initial conditions: x 1(0)=0.1 (m), x 2(0)=0, x 3(0)=0, and x 4(0)=0). Dashed-line: fuzzy controller; solid line: fuzzy-Padé controller. (a) ball’s distance, x 1, versus time, t; (b) ball’s velocity, x 2, versus t; (c) beam’s angle, x 3, versus t; (d) beam’s angular velocity, x 4, versus t

Full size image
Fig. 13
figure 13

Input force to the ball and beam system, u, versus time, t. Dashed-line: fuzzy controller; solid line: fuzzy-Padé controller

Full size image

The initial conditions considered for the simulations are x 1(0)=0.1 (m), x 2(0)=0, x 3(0)=0, and x 4(0)=0.

Simulation results show that the ball is stabilized near to the equilibrium in fuzzy-Padé controller quickly, which is not easy to be achieved in fuzzy controller. As seen from the figures, the fuzzy-Padé technique has greatly accelerated the convergence of the solution of the system. CPU-time and the energy consumption have also been compared in Table 8. CPU-time and energy consumption in Table 8 belong to the simulations in Figs. 12 and 13.

Table 8 A comparison between fuzzy and fuzzy-Padé controllers in two areas; CPU-time and energy consumption of the system
Full size table

Superiority of the fuzzy-Padé controller is clear in Table 8. CPU-time in fuzzy-Padé controller is about 317 times less than fuzzy controller. Besides, the proposed controller has reduced the energy consumption rate near 420 times. We summarize this section that the fuzzy-Padé controller can successfully stabilize the ball and beam system.

5 The parallel double inverted pendulum system

For stabilizing the parallel double inverted pendulum system, several approaches have been studied in the literature. Based on the singleton-type reasoning method and genetic algorithm, Fujita and Mizumoto [50] developed a fuzzy controller only for balancing the two pendulums, ignoring the position of the cart. It needs a long rail for the cart to move in, which is not feasible. Kawatani and Tamaguchi [51] first linearized the system and then designed their controller. This controller is valid only for small initial angles of the pendulums. Sugie and Okada [52] succeeded to design a stabilizing controller based on the H ∞ procedure. However, the asymptotic convergence was not reached and a lasting vibration of about 3∘ of the pendulums remained. Yi et al. [53] could entirely stabilize the double inverted pendulum system using a fuzzy controller. Their controller is based on the single-input rule modules dynamically connected fuzzy inference model.

In this section, we are applying the fuzzy-Padé controller on the parallel double inverted pendulum system. The proposed controller has mostly removed the drawbacks of the above stated controllers. Compared with the fuzzy controller proposed by Yi et al. [53], which is among the best fuzzy controllers designed for this system, our controller is shown to have higher performance.

5.1 System dynamics

It is impossible to control the parallel double inverted pendulum systems with the same natural frequency of the pendulums. By changing the lengths of the pendulums, we can overcome this problem. By taking the cart movements into consideration, and its intensive effects especially on the shorter pendulum with higher frequency, it is accepted that the parallel inverted pendulum systems are the most difficult to be stabilized in the inverted pendulums category [51].

As shown in Fig. 14, the parallel double inverted pendulum system consists of a cart moving on a rail, a longer pendulum 1 hinged on the right side of the cart, and a shorter pendulum 2 hinged on the left side of the cart. An input force is driving the cart.

Fig. 14
figure 14

Parallel double inverted pendulum system; two inverted pendulums are pinned to a moving cart

Full size image

The parameters M, m 1, and m 2 are the masses of the cart, pendulum 1, and pendulum 2, respectively. l 1 and l 2 denote the half lengths of the pendulums 1 and 2, respectively. Here, M=1.0 (kg), m 1=0.3 (kg), m 2=0.1 (kg), l 1=0.6 (m), l 2=0.2 (m), and g=9.8 (m/s2) which is the gravity.

The position of the cart is denoted by x. θ 1 and θ 2 are the angles of pendulums 1 and 2 from their upright positions, respectively. The clockwise direction is positive for both angles. The input force applied on the cart is denoted by u. The nonlinear equations of motion of the system can be achieved by Lagrange method as [53]

$$ \left\{ \begin{array}{l} 4m_1l_1^2\ddot{\theta_1}/3+m_1l_1\cos{\theta_1}\ddot{x}=m_1l_1g\sin{\theta_1},\\[4pt] 4m_2l_2^2\ddot{\theta_2}/3+m_2l_2\cos{\theta_2}\ddot{x}=m_2l_2g\sin{\theta_2},\\[4pt] m_1l_1\cos{\theta_1}\ddot{\theta_1}+m_2l_2\cos{\theta_2}\ddot{\theta_2}+(M+m_1+m_2)\ddot{x}\\[2pt]\quad=u+m_1l_1\dot{\theta_1}^2\sin{\theta_1}+m_2l_2\dot{\theta_2}^2\sin{\theta_2}. \end{array} \right. $$
(15)

The state space variables of this sixth-order system are: x 1=θ 1, \(x_{2}=\dot{\theta_{1}}\), x 3=θ 2, \(x_{4}=\dot{\theta_{2}}\), x 5=x, and \(x_{6}=\dot{x}\).

5.2 The fuzzy-Padé controller

The fuzzy-Padé controller is utilized to stabilize the parallel double inverted pendulum system with 6 state variables and 1 control input. Similar to the ball and beam system, the order of the Padé approximant we use here is [2, 2]. Referring to (4), the [2, 2] Padé approximant with 6 variables is

$$ u(\boldsymbol{x})=\mbox{\fontsize{9.8}{12.0}\selectfont$\displaystyle \frac{{a+\sum_{i=1}^6b_ix_i+\sum_{i=1}^{6}\sum_{j=1}^{6 (j\leq{}i)}c_{ij}x_ix_j}}{{1+\sum_{i=1}^6\overline{b}_ix_i+\sum_{i=1}^{6}\sum_{j=1}^{6 (j\leq{}i)}\overline{c}_{ij}x_ix_j}}$.} $$
(16)

With m=n=2 and i=6, referring to (5), results in M=28 and N=27. Thus, there exist M+N=55 unknown coefficients in (16). We use 144 rules, R=144, to build (8) and to determine the 55 unknowns in (16).

These rules are based on Yi et al. [53] and at the points x 1={−10∘,0,10∘}, x 2={−2,2}, x 3={−10∘,0,10∘}, x 4={−2,2}, x 5={−1,0,1} and x 6={−1,1}.

If we consider that in (16) we should have u(0)=0, it results in a=0, and since u(−x)=−u(x), it gives us \(c_{ij}=\overline{b}_{i}=0\). The other derived coefficients are shown in Table 9. It is notable that D=0.62 (see (10)).

Table 9 Values of the coefficients of the [2, 2] Padé approximant for the double inverted pendulum system
Full size table

5.3 Results and comparisons

To verify the effectiveness of the proposed fuzzy-Padé controller, several simulations are done. At first, Figs. 15 and 16 show fuzzy-Padé results compared to the fuzzy controller proposed by Yi et al. [53].

Fig. 15
figure 15

Simulated results for the double inverted pendulums on a cart (initial conditions: x 1(0)=5 ∘, x 2(0)=−0.1 (deg/s), x 3(0)=10 ∘, x 4(0)=−0.1 (deg/s), x 5(0)=−2 (m), and x 6(0)=0 (m/s)). Dashed-line: fuzzy controller; solid line: fuzzy-Padé controller; (a) angle of pendulum 1, x 1, versus time, t; (b) angular velocity of pendulum 1, x 2, versus t; (c) angle of pendulum 2, x 3, versus t; (d) angular velocity of pendulum 2, x 4, versus t; (e) position of the cart, x 5, versus t; (f) velocity of the cart, x 6, versus t

Full size image
Fig. 16
figure 16

Input force to the double inverted pendulum system, u, versus time, t. Dashed line: fuzzy controller; solid line: fuzzy-Padé controller

Full size image

In Table 10, the two controllers are compared in terms of CPU-time and energy consumption of the system. Data in Table 10 belong to the simulations in Figs. 15 and 16. Table 10 shows that the fuzzy-Pad]é controller is superior to the fuzzy controller designed by Yi et al. [53].

Table 10 A comparison between fuzzy and fuzzy-Padé controllers in two areas; CPU-time and energy consumption of the system
Full size table

Figure 17 shows the convergence regions of the initial angle of the pendulums for both fuzzy and fuzzy-Padé controllers. It is shown that the convergence region of the fuzzy-Padé controller is much larger than that of the fuzzy controller, %348.74 larger.

Fig. 17
figure 17

Comparison of convergence regions for the two controllers. Fuzzy-Padé convergence region is %348.74 larger than that of the fuzzy controller proposed by Yi et al. [34]

Full size image

Figure 18 shows the fuzzy-Padé simulation results with different initial angles, where the fuzzy controller solutions diverge in these cases.

Fig. 18
figure 18

Simulated results for the double inverted pendulums on a cart; non-zero initial conditions: (a) x 1(0)=0, x 3(0)=15 ∘; (b) x 1(0)=10 ∘, x 3(0)=30 ∘; solid line: fuzzy-Padé controller; fuzzy controller does not converge in these cases (not shown in the figure)

Full size image

In Fig. 18, the left and the right axes separately represent the angle of the two pendulums and the position of the cart.

In summary, the simulation results show that the proposed fuzzy-Padé controller can completely stabilize the parallel double inverted pendulum system within a wide range of the initial angles of the two pendulums.

6 Conclusion

The presented fuzzy-Padé controller was shown to be a novel controller, which dramatically affects the quality of the closed-loop behavior. Similar to the fuzzy controllers, fuzzy-Padé controllers use the heuristic knowledge of an expert. Unlike the fuzzy controllers, in which the rules are fuzzy sets, the rule base for fuzzy-Padé controllers which are called fuzzy singleton rules are expressed as crisp sets. One can derive the unknown coefficients of the Padé approximants using these rules to build the fuzzy-Padé controller.

The proposed control method, can be utilized in many real-world complex applications, especially where heuristic information is available. Based on the three case studies, we summarize some properties of the fuzzy-Padé controllers compared to the fuzzy controllers, as follows. In fuzzy-Padé controllers: (1) fewer rules are needed to construct the controller; (2) accurate results can be achieved using even low-order Padé approximants; (3) it is suitable for high-order systems; (4) convergence region is greatly enlarged; (5) by dramatically reducing the CPU-time, real time control is achieved; (6) energy consumption is reduced; and (7) by reducing the oscillations around the equilibrium point, the response of the system asymptotically converges to zero.

As a future work, it is possible to make the fuzzy-Padé controller more efficient by optimizing the values of its parameters. In this way, the controller’s constants, which are derived based on the rule base, will be the initial estimation. Then, an optimization algorithm will tune the constants so that to minimize a control goal such as the settling time, energy consumption, convergence region, etc. Finally, as another future work, it would be interesting to study the robustness of the proposed controller on the model variations, model uncertainties and system noises.