Keywords

1 Introduction

The inverted pendulum is an interesting topic to researchers for its strong degrees of nonlinearity and inherent instability and yet simplicity of structure. So it can efficiently be used for determining the effectiveness of a control algorithm. Its basic structure consists of one/two flexible pendulum arms mounted to a cart on a moving rail. In the absence of a stabilizing controller, the pendulum arms, which have its center of mass above its pivot point, are unable to maintain their upright position. Thus, the control objective is to apply a force to move the cart so that the pendulum arms remain in the vertical unstable position while simultaneously being driven to the desired cart location. Furthermore, it should also include a swing up control aspect if initially the pendulum hangs freely in the vertical position. Control of an inverted pendulum is a very common control engineering problem based on flight simulation of rockets and missiles during the initial stages of flight, wherein the aim was to stabilize the inverted pendulum such that the position of the carriage on the track was controlled quickly and accurately. The pendulum should remain erected in its inverted position during such movements.

The proportional integral derivative (PID) controller though known to operate on a majority of industrial process and control applications, they exhibit poor performance in case the system under study is nonlinear and ill-defined. Moreover, conventional controllers require system model, which may not always be available. Researchers have thus employed newer approaches of genetic algorithms, fuzzy logic [1, 2], neural networks [3], or a combination of any of the above to solve this nonlinear control problem. A few of the earlier methods involved the use of various linearization techniques to account for the nonlinearities of the system model [4]. However, application of fuzzy logic for inverted pendulum control still by far remains most popular, as they do not require precise knowledge of the system parameters. Attempts are persistent in the research world to obtain a superior optimal controller, as choosing the correct set of rules and scaling factor is not an easy task in order to fine tune the fuzzy logic controller (FLC) [5]. A number of approaches have been proposed to implement hybrid control structures that combine the robustness of conventional controllers with the intelligence of fuzzy logic techniques to control the nonlinear systems. Performance of PI-type FLC for higher order nonlinear systems is not satisfactory due to large overshoot, excessive oscillation, and slower response. PD-type FLCs are suitable for a certain class of nonlinear systems [6, 7]. PID-type FLCs are rarely used due to the difficulties in generation of a complicated three-dimensional rule base [8].

As already stated, the inverted pendulum model is nonlinear in nature and its parameters may vary with time. Different operator defined fuzzy tuning schemes have been proposed earlier to control such complex and nonlinear systems [9–12]. This type of fuzzy-based tuning scheme usually decreases the overshoot, but the system response may be delayed for its additional rule base. To overcome this shortcoming, in this paper, we propose a non-fuzzy self-adaptive scheme for tuning of fuzzy PD-type controllers.

2 Inverted Pendulum Description

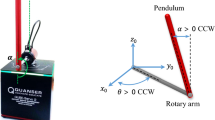
Figure 1 shows the schematic of an inverted pendulum moving on a track of length 1 m [13]. The cart has a shaft to which two pendulums are attached and are able to rotate freely. The cart is driven by a DC motor attached at the end of the rail. The force with which the cart is pulled is controlled by applying a voltage to the motor. This voltage is our control signal u. The two variables that are read from the pendulum (using optical encoders) are the pendulum angle \( \theta \) and the cart position on the rail x. The system is interfaced to a personal computer by means of a data acquisition card and is driven by MATLAB-/Simulink-based real-time software. The equations of motion for the inverted pendulum system are given by Eqs. 1 and 2.

$$ \left( {{M} + {m}} \right){x}^{\prime\prime } + {kx}^{\prime } = {u} + ({\text{mlsin}}\theta )\theta^{{\prime } 2} - \, ({\text{mlcos}}\theta )\theta^{\prime\prime } $$
(1)
$$ \left( {{I} + {\text{ml}}^{ 2} } \right){\theta }^{\prime\prime } = {{{\text{mglsin}}\theta }} - \, ({{{\text{mlcos}}\theta }}){x}^{\prime\prime } - { b\theta }^{\prime } $$
(2)
Fig. 1
figure 1

Schematic of the inverted pendulum system

Full size image

3 Controller Design

The proposed hybrid controller, for efficient control of cart position and inverted pendulum angle, is a PD-type fuzzy logic controller (FPDC). As already mentioned, the inverted pendulum control problem is divided into two separate control schemes. First is the swing up control, which allows the pendulum to reach the upright position with as minimal angular velocity as possible; and second is the inverted pendulum stabilization around the equilibrium point within a specified accuracy. Both these control objectives have to be attained simultaneously. A logical switch is used to change over between the swing up control mode and the inverted pendulum stabilization mode. The stabilization mode comes into effect once the pendulum reaches [−20°, +20°] of the final vertical upright position. The control action begins in the swing up control mode if initially the pendulum arms are hanging free. Here, zone detection signals in combination with a position controller act on the inverted pendulum system to achieve desired sway of the arms. Once in the stabilization mode, the system is acted upon by twin controllers, viz. position controller and angle controller (Fig. 2).

Fig. 2
figure 2

Block diagram of FPDC twin controller for inverted pendulum stabilization

Full size image

Each of the FLC used for performing the control action consists of five symmetrical triangular membership functions (MFs) of equal base and 50 % overlap, hence generating a set of 52 = 25 fuzzy rules (given by Table 1). The inputs to the controller are the amount of deviation in the cart position or pendulum angle from the desired set point at a sampling instant k (denoted by e) and their corresponding change of error (denoted by \( {\Delta} e \)). Depending upon these two input parameters, each of the FLC is capable of generating a control voltage (denoted by u) that will effectively drive the system toward stability. The various input and output scaling factors play a role very similar to the gain coefficients in a conventional controller. The appropriate selection of these scaling factors is done based on the operator’s knowledge of the system under study to obtain the best performance of the control system. The relationships between scaling factors (\( G_{e} ,G_{{{\Delta} e}} ,G_{u} \)) and the input and output variables (\( e, \, {\Delta} e,u \) e, \( {\Delta} e \), u) are given by Eqs. 4–6. The MFs of \( e_{x}, {\Delta} e_{x} ,u_{x} \) for position controller are given by Fig. 3 and MFs of \( e_{\theta } , \, {\Delta} e_{\theta } ,u_{\theta } \) for angle controller are given by Fig. 4. Figure 5 shows the block diagram of FPDC for swing up control.

$$ {\Delta} {e}\left( {k} \right) \, = {e}\left( {k} \right) - {e}\left( {{k} - 1} \right) $$
(3)
$$ {e}_{N} = {G}_{e} \ast {e} $$
(4)
$$ {\Delta} {e}_{N} = {G}_{{{\Delta} {e}}} *{\Delta} {e} $$
(5)
$$ {u} = {G}_{u} *{u}_{N} $$
(6)
Table 1 Fuzzy rules for position and angle control
Full size table
Fig. 3
figure 3

MFs of \( e_{x} ,{\Delta} e_{x} ,u_{x} \)

Full size image
Fig. 4
figure 4

MFs of \( e_{\theta } ,{\Delta} e_{\theta } ,u_{\theta } \)

Full size image
Fig. 5
figure 5

Block diagram of FPDC for swing up control

Full size image

The output scaling factor (G u ) should be determined very carefully for the proper implementation of control logic, since it is directly related to the stability of the system. Authors in [9–12] have proposed a self-tunable fuzzy-based inference system to adjust the gain G u online according to the current states of controlled processes. A very similar scheme is applied here for tuning of the FPDC position controller which is expected to give a better swing up control by modifying the controller gain by a factor α, which is now given by Eq. 7. This self-tuning mechanism for FPDC will be denoted as STFPDC in our discussion henceforth (see Fig. 6).

$$ u = \alpha \cdot {G}_{u} *{u}_{N} $$
(7)

where α is a function of error(e) and change of error(\( {\Delta} e \)) of the system response. The fuzzy rule base for computation of the gain updating factor α consists of seven symmetrical triangular MFs of equal base and 50 % overlap, hence generating a set of 72 = 49 fuzzy rules given by Table 2. The MFs of e, \( {\Delta} e \), and α are given by Figs. 7 and 8, respectively.

Fig. 6
figure 6

Block diagram of STFPDC for swing up control

Full size image
Table 2 Fuzzy rules for computation of α
Full size table
Fig. 7
figure 7

MFs of \( e\,{\text{and}}\,{\Delta} e \)

Full size image
Fig. 8
figure 8

MFs for computation of α

Full size image

4 Proposed Tuning Scheme

Our idea here is to implement a certain non-fuzzy adaptive module to alter the output scaling factor online, to achieve a better performance. Such a scheme will reduce the design complexity by eliminating the need of multiple FLCs and the number of MFs while being able to exercise a similar control on the system [14]. The proposed scheme given by Fig. 9 is a self-adaptive PD-type fuzzy logic controller (SAFPDC) where a dynamic multiplying factor β is incorporated to adjust the controller gain (given by Eqs. 8 and 9).

$$ {u} = \beta \cdot {G}_{u} *{u}_{N} $$
(8)
$$ \beta = {\delta} \cdot {e}^{{{\text{sqrt}}({\Delta} {e})}} $$
(9)
Fig. 9
figure 9

Block diagram of SAFPDC for swing up control

Full size image

The value of β is computed at each sampling instant depending on the value of \( {\Delta} e \) which then automatically operates on the effective gain and thus on the system response. δ in the above expression is a factor that takes positive integer values to be decided by the operator, depending on the design specifications.

5 Results

In this section, we present the simulation results of each of the control scheme discussed above and perform a comparative study to illustrate the effectiveness of our proposed scheme over the others. Figure 10 shows the plot of pendulum cart position (in meter) against time (in second). The results show that the pendulum cart is stabilized within approximately 8 s in case of SAFPDC, while it takes much longer time in case of FPDC and STFPDC. The pendulum cart oscillation is also limited to 0.02 m above the set point during swing up. The various performance indices of the system response such as IAE, ISE, and ITAE have significantly reduced for SAFPDC when compared to STFPDC and FPDC. Figures 11, 12, and 13 show the plot of the inverted pendulum angle (in radian) against time (in second) for each of the control scheme separately for the sake of easy analysis. They very clearly reveal that in case of SAFPDC, the system takes the least time to reach and remain in its vertical upright position. The performance indices and the dynamic response characteristics have been tabulated in Table 3.

Fig. 10
figure 10

Plot of pendulum cart position against time (dotted FPDC; dashed STFPDC; solid SAFPDC)

Full size image
Fig. 11
figure 11

Plot of inverted pendulum angle against time for FPDC

Full size image
Fig. 12
figure 12

Plot of inverted pendulum angle against time for STFPDC

Full size image
Fig. 13
figure 13

Plot of inverted pendulum angle against time for SAFPDC

Full size image
Table 3 Performance analysis of the proposed controllers for inverted pendulum control
Full size table

6 Conclusion

In this paper, we proposed a simple non-fuzzy self-adaptive scheme for PD-type FLCs. Here, the controller gain (output SF) has been updated online through a gain modifying parameter β defined on the change of error (Δe). Our proposed SAFPDC scheme exhibited effective and improved performance compared to its conventional fuzzy counterpart and also outperforms controllers based on fuzzy self-tuning scheme. The proposed twin control scheme for inverted pendulum control reduces the computational complexity. By applying the proposed non-fuzzy tuning method and dual control scheme, the control objectives have been rightly achieved.