1 Introduction

Electrical bursting in electrically excitable cells is characterized by alternation of fast spiking oscillations with silent periods. As a very complex bursting pattern, episodic or compound bursting is exhibited as a transition between a burst episode composed of a few bursts and a long silent phase or “desert”. As reported in pancreatic islets the compound bursting is responsible for pulsatile insulin secretion, since its period is considerably longer than a single simple burst [1, 2].

In a variety of bursting models, the variables can typically be classified as either “fast” or “slow,” and there is usually a single slow variable determining the period of bursting [3–8]. Instead the compound bursting can be represented in some bursting models with two or more disparate-time-scale slow variables, and the burst period is determined by some combination of the slow variable time constants [9, 10].

It is usually thought that independent glycolytic oscillations play a key role in producing the compound bursting [11–13]. A minimal model for electrical activity and independent glycolysis oscillation demonstrates the occurrence of compound bursting [11]. More realistic models for both the electrical and the glycolytic components including the participation of mitochondria describe this mechanism for compound bursting in pancreatic β-cells [12, 13]. As data have been gradually accumulated and some biological phenomena to be explained have expanded, the models become more and more complex, culminating in the so-called dual oscillator model [14, 15], where slow oscillations in glycolysis are combined with an already complex model of electrical activity. At this level of complexity, the classical fast-slow approach becomes intractable due to the large number of slow variables. For consideration of simplification, Bertram et al. [16] uses a minimal and generic phantom bursting model [9] to produce episodic or compound bursting in some parameter settings. It is obtained from time courses of a moderate and a slower slow variable and membrane potential that dynamics of the moderate slow variable is responsible for fast bursts, while dynamics of the slower slow variable clusters bursts together with intervening deserts. So, the compound bursting oscillation is examined by a fast/slow analysis treating the slower slow variable as the sole slow variable in [16]. Nevertheless, the compound bursting pattern is driven by a combination of these two slow variables with different time scales, which can commonly or separately play an important but distinct role in different aspects of the compound bursting. It is obviously not enough to explain dynamic behavior of the complex compound bursting only considering the slower slow variable. Moreover, one needs to investigate some unknown questions associated with the occurrence of the compound bursting listed as follows. What underlies the initiating and terminating of every burst, which is same or not to that of the beginning and ending of a burst episode? What leads to shape of the bursts in the burst episode? Why to a certain extent of amplitude the first burst in the burst episode can continue for a long time and appears to be long while the other bursts have to end very soon and be short? Also, why subthreshold oscillation exists in the quiescent state between the burst episodes, but not between the bursts in the burst episode? In this work, different fast/slow analysis for the moderate and the slower slow variables, respectively, are exhibited in a three-dimensional space so as to investigate preferably how these two different-time-scale slow variables commonly or separately give rise to the compound bursting.

On the other hand, synchronization of bursting activity in pancreatic islets when pancreatic β-cells are coupled together by gap junctions plays an important role in the insulin secretion [17, 18]. In addition, an impact of the channel noise in the important ATP-sensitive K+ channels can be reduced when shared by all the cells in the islet [18–20]. The phenomenon of synchronization via gap junctions has been extensively investigated in the pancreatic β-cell models [21–24] and even in some other coupled biological oscillators [25–27]. However, compound bursting induced by electrical coupling is little studied and is still a challenging problem because of complexity of two or more disparate-time-scale slow variables. Here, the minimal phantom bursting model of two electrical coupling pancreatic β-cells is applied to examine for the first time compound bursting synchronization phenomena with antiphase spikes. In particular, it is more concerned with what evokes a change of the number of the short bursts within a burst episode in different compound bursting.

The structure of this paper is settled as follows. Following this brief introduction in Sect. 1, the phantom bursting model is presented in Sect. 2. Numerical investigations and fast/slow analysis for both the single cell model and the two coupled cells model are described in Sects. 3 and 4, respectively. Finally, conclusions and discussions are given in Sect. 5.

2 The phantom bursting model

An important feature of the minimal compound bursting model [9] is two slow variables with different time scales that interact with a fast subsystem. The fast subsystem is composed of two differential equations

(1)
(2)

In Eq. (1), C m is the membrane capacitance and V is membrane potential. A fast Ca2+ current I Ca, a fast delayed rectifier current I Kdr, a constant-conductance leakage current I Leak, and two slow K+ currents I K1 and I K2 with slowly changing conductances are expressed as follows, respectively:

(3)
(4)
(5)
(6)
(7)

where V Ca, V K, and V Leak are the Nernst potentials of the Ca2+ current, the K+ current and the leakage current, respectively, and g Ca,g Kdr,g Leak,g K1, and g K2 are the maximum conductances of the respective ionic currents. An equilibrium function m ∞(V) for the Ca2+ current activates very rapidly, and an activation variable n for the delayed rectifier current I Kdr satisfies Eq. (2) with an equilibrium function n ∞(V) and a time scale function τ n (V).

The other two activation variables s 1 and s 2 changing very slowly in virtue of large time constants \(\tau_{s_{1}}\) and \(\tau_{s_{2}}\), constitute the slow subsystem as described in the following differential equations:

(8)
(9)

Moreover, a big difference in values of \(\tau_{s_{1}}\) and \(\tau_{s_{2}}\) can induce disparate time scales of these two slow processes.

The equilibrium functions m ∞(V), n ∞(V), s 1∞(V), and s 2∞(V) have the form of x ∞(V) below:

$$ x_{\infty}(V)=\frac{1}{1+\exp((v_{x}-V)/s_{x})} $$
(10)

Parameter values are fixed as shown in [16], except for the maximum conductance of the moderate slow K+ current g K1 as a key parameter. All numerical simulations and bifurcation diagrams were calculated with Matlab and XPPAUT [28] software packages.

3 Compound bursting in the single β-cell model

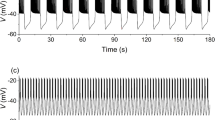
Compound bursting consisting of bursts episodes followed by long silent phases can appear in the minimal phantom bursting model (1)–(10) in Fig. 1, due to the impact of these two slow variables with different time scales. Just as the time course of the membrane potential V for g K1=21.5 pS shown in Fig. 1(a), a burst episode in the compounding bursting is composed of a long burst with many spikes, several short bursts with a few spikes, and subthreshold oscillation with large amplitude on both sides but small on the middle during a long silent phase. In the meantime, the membrane potential of the compounding bursting is accompanied with a no-spike compound mode of the moderate slow variable s 1 in Fig. 1(b) and a relatively large jagged oscillation of the slower slow variable s 2 in Fig. 1(c).

Fig. 1
figure 1

Time courses of the membrane potential V (a), the moderate slow variable s 1 (b) and the slower slow variable s 2 (c) for g K1=21.5 pS in the single cell model

Full size image

The slow variables s 1 and s 2 with different time scales may commonly or separately contribute to complex dynamic of the compound bursting. So, two different fast/slow analyses for the slow variables s 1 and s 2 are given in three-dimensional V–s 1–s 2 spaces in Figs. 2 and 3, respectively, are combined to explore the dynamic behavior of the compound bursting.

Fig. 2
figure 2

(a) The fast/slow analysis of the compound bursting for g K1=21.5 pS in the single β-cell model in the three-dimensional V–s 1–s 2 space, when the moderate variable s 1 is treated as the bifurcation parameter of the fast subsystems (1) and (2), and the slower slow variable s 2 is considered as a constant. The s 1-nullcline surface (blue) and trajectory of the compound bursting (red) are overlapped; (b) is obtained when rotating (a) 90∘ and making it bigger; (c) is a projection of (a) in the V–s1 plane (Color figure online)

Full size image
Fig. 3
figure 3

The fast/slow analysis of the compound bursting for g K1=21.5 pS in the single β-cell model in the three-dimensional V–s 1–s 2 space, when the slower variable s 2 is treated as the bifurcation parameter of the fast subsystems (1), (2), and (8), where H1 and H2 appear in upper and lower branches, respectively; (b) and (c) are enlargements of two different parts in (a), respectively

Full size image

In the fast/slow analysis in Fig. 2, the moderate variable s 1 is treated as a bifurcation parameter of the fast subsystems (1) and (2) and the slower slow variable s 2 is fixed at different values between 0.40 and 0.47 presented in the oscillatory range in Fig. 1(c). A slow manifold surface is composed of multiple Z-shaped bifurcation curves of the fast subsystem with respect to the bifurcation parameter s 1 for these different values of s 2. Stable nodes on the lower branches and saddles on the middle branches of the Z-shaped curves coalesce via fold bifurcation (LP) at left knees. As s 1 increases, the minimum and the maximum of amplitude of stable limit cycles via Hopf bifurcations (H) on upper branches of the Z-shaped curves form a C-shaped surface, since the stable limit cycles hit saddles on middle branches of the Z-shaped curves and disappear via saddle homoclinic bifurcation. The S 1-nullcline surface for the different values of s 2 (blue) and trajectory of the compound bursting (red) are overlapped in Fig. 2. Figure 2(b) is obtained when rotating Fig. 2(a) 90∘ and making it bigger, and Fig. 2(c) is a projection of Fig. 2(a) in the V–s 1 plane.

At the lower level of the s 1, the trajectory jumps up from the stable lower branch to the stable limit cycle branch, and the burst starts to appear in the active phase owing to coalescence of the lower branches and the middle branches via the fold bifurcation. A little tilted form at the start of the burst results when it is located in the C-shaped stable limit cycles, and then the burst terminates and the trajectory returns to the lower branch as the stable limit cycles disappear via saddle homoclinic bifurcation. It follows that these two bifurcations with respect to the fast slow variable s 1 are primarily responsible for the beginning and the ending of every burst in burst episode. However, we wonder if there are same generation mechanisms of the start and end of every burst to those of the whole burst episode. Then why can the burst episode terminate and go into subthreshold oscillation in the quiescent state? In the burst episode, why can the first burst continue for a long time and appear to be long while the other bursts have to end very soon and be short?

It is worth noting that the slower slow variable s 2 gradually increases during the occurrence of the burst episode in the three-dimensional V–s 1–s 2 space in Fig. 2. Therefore, the fast/slow analysis for the moderate slow variable s 1 in Fig. 2 should be combined with that for the slower slow variable s 2 in Fig. 3, where the moderately slow variable s 1 is converted to a fast variable and a fast subsystem consists of (1), (2), and (8). The fast subsystem also forms a Z-shaped bifurcation curve as shown in Fig. 3, where (b) and (c) are enlargements of two different parts in (a), respectively. But differently, the stable limit cycle occurring via a supercritical Hopf bifurcation (H1) on the upper branch loses stability via the period-doubling bifurcation, and then the unstable limit cycle hits saddle on the middle branch and disappears via the saddle homoclinic bifurcation. Apart from that, there is another subcritical Hopf bifurcation (H2) on the lower branch, before which only the unstable limit cycle coexists with a stable focus, and then hits the saddle on the middle branch.

The first burst in the burst episode above both s 1-nullcline in Fig. 2(b) and s 2-nullcline in Fig. 3(b) begins to move from forward to backward along an increasing direction of s 2. When the stable limit cycle hits saddle on the middle branch of the z-shaped bifurcation curve for the bifurcation parameter s 1 in Fig. 2, the trajectory exactly reaches the stable limit cycle around the upper branch of the z-shaped bifurcation curve for the bifurcation parameter s 2 in Fig. 3. Therefore, the fast/slow analysis for the slower slow variable s 2 in Fig. 3 is employed to consider different dynamic behaviors of the long burst and the short bursts before their termination via the saddle homoclinic bifurcation in Fig. 2. The first burst at smaller values of s 2 can continue to possess so many spikes in a very long interval of s 2 until the stable limit cycle becomes unstable at the PD bifurcation point in Fig. 3. However, the other bursts located in the unstable limit cycles at larger values of s 2 are not able to continue and have to become the short bursts. As s 2 continues to rise, the whole burst episode composed of the long burst and the short bursts is totally terminated via the saddle homoclinic bifurcation for the slower slow variable s 2 in Fig. 3. Thus, the initiation of the burst episode, that is, the first burst is induced by fold bifurcation for s 2, while the termination of the burst episode, that is, the last short burst results from collaboration of the different saddle homoclinic bifurcations for s 1 and s 2. Furthermore, the trajectory falls down and stays in gradually decreasing oscillatory mode around the stable focus on the lower branch of the Z-shaped curve for the bifurcation parameter s 2 in Fig. 3. As s 2 decreases, the stable focus becomes unstable through the subcritical Hopf bifurcation (H2) so that the trajectory goes away from the lower branch in a gradually increasing oscillatory mode. That can account for the subthreshold oscillation with large amplitude on both sides and a small one on the middle during the long silent phase.

4 Compound bursting synchronization with the different number of short bursts

Bursting synchronization induced by electrical coupling in the pancreas islet plays an important role in the insulin secretion and it has been explored in many pancreatic β-cell models. However, synchronization of the compound bursting induced by two or more disparate-time-scale slow variables is still a challenging problem. In the present work, the minimal phantom model is extended to two pancreatic β-cells connected by a gap junction to explore synchronization behaviors of the compound bursting evoked by different electrical coupling strength. To model gap junctions of pancreatic β-cells, the two electrical coupling cells model is often handled by adding the following linear coupling term g c (V i −V j ), where g c is the coupling strength between two neighbor identical cells 1 and 2.

(11)
(12)
(13)
(14)

where i, j=1, 2, and i≠j represent the number of the cells. In this work, the coupling strength of gap junctions g c is treated as a free parameter.

The compound bursting with the long burst, the short bursts, and the subthreshold oscillation for g K1=21.5 pS can be presented in the single cell model in Fig. 1. Actually in a certain range of the parameter g K1, the increasing electrically coupled strength g c in the two coupled cells model (11)–(14) can make a transition from fast bursting to compound bursting even to slow bursting. As shown in (g K1,g c )-plane in Fig. 4, compound bursting can dominate a very wide region, especially as it can always exist, no matter whether it is coupled or uncoupled when g K1 varies between 21.3 and 21.7.

Fig. 4
figure 4

The existing ranges of the different bursting patterns in the g K1–g c plane

Full size image

Here, we only consider different bursting behaviors induced by different electrically coupled strength g c for g K1=21.2 pS. As shown in Fig. 5, the fast bursting in the uncoupled case is a square-wave burster. From a dynamic point of view, it is classified as “fold/homolinic” bursting by the fast/slow analysis for the moderate slow variable s 1 and a fixed value of s 2 chosen from its very narrow oscillatory range from 0.47 to 0.48 in Fig. 5(b). Furthermore, all these compound bursting patterns for the different electrically coupled strength g c in the two electrical coupling cells model gradual synchronize in the membrane potential V 1 and V 2, two moderate slow variables s 11 and s 21 and two slower slow variables s 12 and s 22 as shown in Fig. 6. In every burst episode of these different synchronized compound bursting patterns, the number of the short bursts will decrease from 4 to 3, 2 and 1 when the coupled strength g c is fixed as 1.6, 1.95, 2.5, and 3.3, respectively. Additionally, it can be seen in return maps of Inter-Burst Intervals (IBIs) in Fig. 7 that time intervals between two adjacent short bursts have little change but the number of the minimal IBIs decreases from 3 to 2, 1 and 0. That means the different number of the short bursts is decided by the difference in total time durations of all these short bursts. Therefore, the mechanism behind the different durations of all these short bursts in the burst episode for the coupled strength g c =1.6, 1.95, 2.5, and 3.3, respectively, will be deep revealed by the fast/slow analysis of the two coupled β-cells model.

Fig. 5
figure 5

Fast “fold/homoclinic” bursting for g K1=21.2 pS in the single β-cell model, where (a) is time course of the membrane potential V and (b) is the fast/slow analysis for the bifurcation parameter s 1 as s 2 is fixed at 0.483

Full size image
Fig. 6
figure 6

Compound bursting synchronization shown in time courses of the membrane potentials V 1 and V 2, two moderately slow variables s 11 and s 21 and two slower slow variables s 12 and s 22 in the two coupled β-cells model when the coupled strength g c =1.6 (a), 1.95 (b), 2.5 (c), and 3.3 (d), respectively

Full size image
Fig. 7
figure 7

Return maps of Interburst intervals (IBIs) of the compound bursting patterns for g c =1.6 (a), 1.95 (b), 2.5 (c), and 3.3 (d), respectively

Full size image

Without the loss of generality, we only give the fast/slow analysis of the compound bursting synchronization with a long burst and two short bursts for g c =2.5. Just as the time courses of the moderate slower variables and the slower slow variables for cells 1 and 2 in Fig. 6, the moderately slower variable s 11≈s 21=s 1 for different values of s 12≈s 22 and the slower slow variable s 12≈s 22=s 2 are regarded as a bifurcation parameter in the fast/slow analyses in Fig. 8 and Fig. 9, respectively. Stable limit cycles via two Hopf bifurcation points H1 and H2 on upper branch of z-shaped bifurcation curves in the fast/slow analyses in Fig. 8 and Fig. 9, correspond to in-phase (IP) and anti-phase (AP) branches, respectively. Since there is a function relationship between V 1 and V 2, the dynamic behavior of V 1 is only considered here. The stable limit cycle along the AP branch decides anti-phase spike of burst synchronization in a burst, which can be seen in the time courses of V 1 and V 2 in Fig. 10(a) and the V 1–V 2 phase plane in Fig. 10(b). In the fast/slow analysis for the bifurcation parameter s 12≈s 22=s 2 in Fig. 9, the first anti-spike burst along the stable AP limit cycle branch exists in a long interval of s 2 before Torus bifurcation (TR). The other anti-spike bursts lying in the unstable limit cycle after the TR bifurcation can not continue but return to the stable lower branch via the saddle homoclinic bifurcation (HC). It follows that the total time duration of all the short bursts in every compound bursting is determined by the existing range of the unstable limit cycle between the TR bifurcation point and the saddle homoclinic point for the bifurcation parameter s 12≈s 22=s 2. Moreover, it can be seen in Table 1 that the difference of the TR bifurcation points and the saddle homoclinic points gradually decreases with the increasing coupled strength g c , thereby it so that the total time duration of all these short bursts decrease with the increasing coupled strength g c . Based on rough invariability in the time durations of every short burst and in the time intervals between the short bursts, the number of the short bursts gradually decreases from 4 to 3, 2 and 1.

Fig. 8
figure 8

(a) The fast/slow analysis for s 11≈s 21=s 1 as the bifurcation parameter when the coupled strength g c =2.5 in the three-dimensional V–s 1–s 2 space, where stable limit cycles via these two Hopf bifurcations H1 and H2 correspond to in-phase (IP, yellow) and anti-phase (AP, grey) branches, respectively. (b) is gotten when rotating (a) 90∘ and making it bigger. (c) is a projection of (a) in the V 1–s 1 plane (Color figure online)

Full size image
Fig. 9
figure 9

(a) The fast/slow analysis for s 12≈s 22=s 2 as the bifurcation parameter when the coupled strength g c =2.5 in the three-dimensional V–s 1–s 2 space, where stable limit cycles via these two Hopf bifurcations H1 and H2 correspond to in-phase (IP) and anti-phase (AP) branches, respectively. (b) and (c) are enlargements of two different parts in (a), respectively

Full size image
Fig. 10
figure 10

An anti-spike burst synchronization in the compound bursting for g c =2.5 is represented in (a) time courses of V 1 (black) and V 2 (orange) and (b) the trajectory in V 1–V 2 phase plane (Color figure online)

Full size image
Table 1 The difference of the TR bifurcation points and the saddle homoclinic points for the increasing coupled strength g c
Full size table

5 Conclusions and discussions

Episodic or compound bursting is a very complex but important bursting pattern in bursting models with two or more disparate-time-scale slow variables. For consideration of simplification, the minimal and generic phantom bursting model [9] is used to produce episodic or compound bursting, when two slow variables with different time scales commonly or separately play different roles in different aspects of the compound bursting. It is obviously not enough to explain dynamic behavior of the complex compound bursting only considering the slower slow variable. Therefore, different fast/slow analysis for the moderate and the slower slow variables, respectively, are given in a three-dimensional space to reveal complex dynamic of the compound bursting. At first, the beginning and the ending of every burst in burst episode are decided by the fold bifurcation and the saddle homoclinic bifurcation for the moderate slower variable s 1, where the little tilted form at the start is resulted from locating in the C-shaped stable limit cycles. Nonetheless, the burst episode is terminated by common effects of the different saddle homoclinic bifurcations for s 1 and s 2. Then, the first burst exactly reaches the stable limit cycle for the bifurcation parameter s 2, when the stable limit cycle for the bifurcation parameter s 1 hits saddle on the middle branch. So the first burst existing in stable limit cycle for s 2 have many spikes but the others locating in the unstable limit cycles for s 2 are not able to continue and become the short bursts, which can explain different occurrence of the long burst and the short bursts. Finally, during the long silent phase the property of the stable focus on the lower branch for the bifurcation parameter s 2 accounts for the subthreshold oscillation with large amplitude on both sides and small amplitude on the middle.

Furthermore, synchronization of bursting activity plays an important role in the insulin secretion. Using the minimal phantom bursting model of two electrical coupling pancreatic β-cells, we examine for the first time compound bursting synchronization phenomena with anti-phase spikes. Moreover, we also discuss the fundamental mechanism of the change of the number of the short bursts within a burst episode for different compound bursting. Since the total time duration of all the short bursts is decided by the existing range of the unstable limit cycle between the TR bifurcation point and the saddle homoclinic point. So the decrease of the difference between these two points for the increasing coupled strength g c leads to the decreasing durations of all these short bursts. All above can explain the number of the short bursts decreasing from 4 to 3, 2 and 1, in consideration of rough invariability of the time duration of every short burst and the time intervals between the short bursts.

In fact, heterogeneity in the coupled phantom-burster model with heterogeneous electrical coupling can reproduce many aspects of the measured islet electrical dynamics. Furthermore, it would be interesting to study the influence of the topology of the network and the coupling strength between β-cells inside the Langerhans islets. Using complex networks theory, one can investigate under what conditions synchronization emerges for β-cell network models. In addition, periodic insulin secretion appears to be controlled by metabolic oscillations within the cells. To explore the bases of the synchronization phenomenon, both electrical and metabolic features of a mathematical gap junction model will be taken into account to study biological functions of the β-cell cluster.