1 Introduction

The steel jacket type platforms are the most common kind of offshore structures, which play an import role in the oil exploration and drilling operations. The offshore platforms generally involve sophistication of the superstructure in the deep water. The flexibility and complexity of the structure generally induces self-excited nonlinear hydrodynamic force in addition to the nonlinear response, which makes them very vulnerable and unsafe [1–3]. To decrease the vibration of the offshore platforms and thereby guarantee their safety, more and more researchers have engaged in the efforts to the implementation of varieties of control schemes. As one of the effective methods, passive control are often used to enhance the safety by using excessive construction materials to increase the stiffness of the offshore structures [4, 5].

However, due to the huge cost and the limited performance, active control schemes have been aroused extensive concern in recent decades. For instance, the optimal-control-based schemes have been applied to improve the performance of the jacket platforms by using an active mass damper [6–8]. For an offshore steel jacket platforms with an active tuned mass damper (TMD) mechanism, the multi-loop feedback design method [2], the nonlinear control scheme, and the robust state feedback control scheme [3] have been developed to reduce the internal oscillation amplitudes of the offshore platforms. More recently, the dynamic output feedback control scheme [9] and the integral sliding mode control methods [10, 11] have been presented to improve the performance of the offshore platforms. It is indicated that the aforementioned active control schemes are effective ways to deal with the vibration problem of offshore platforms subject to the nonlinear wave force.

Time-delay phenomenon is one of important issues in various engineering systems. It is very common and may cause poor performance and even instability of the systems. The stability analysis and controller synthesis methods for time-delay systems have always been one of the hot topics in the fields of control theory and engineering applications [13–16]. In the active control of the offshore platforms, time-delays may appear in the control channel where it is taken by the actuator to build up the active control force. In the reported works about vibration control of offshore platforms, the designing schemes of active controllers are based on an implicit assumption that there are no time-delays in control inputs [2, 3, 9–11]. However, because of the physical limitations, the time-delays are unavoidable. To avoid the unfavorable effects on the performance of the offshore platforms, the actuator time-delays should be considered.

In this paper, we tend to investigate the effects of actuator time-delays on the stabilization control for the offshore platform, and propose a delay-dependent state feedback stabilization control scheme to reduce the vibration amplitudes of the offshore platform. First, for the offshore platform without actuator timed-delay, a state feedback controller is designed. Then a delay-dependent state feedback controller, which can be solved by using the cone complementarity algorithm, is designed to stabilize the offshore platform in the presence of actuator time-delays. Simulation results are given to illustrate the effectiveness and advantage of the proposed control schemes. In addition, the allowable upper bound of the actuator time-delays of the offshore platform is investigated.

The rest of this paper is organized as follows. Section 2 presents a mathematical model of an offshore steel jacket platform with actuator time-delay. A state feedback controller is proposed in Sect. 3 to stabilize the offshore platform without actuator time-delay. The main results on the designing of the delay-dependent state feedback controller and the algorithm are given in Sect. 4. Section 5 gives some simulation results and Sect. 6 concludes our findings.

Throughout this paper, all the matrices are real matrices. The superscripts “−1” and “T” mean the inverse and transpose of a matrix, respectively; P>0 (P≥0) means that the matrix P is a real symmetric and positive definite (semidefinite) matrix; I is the identity matrix of appropriate dimensions. For simplicity, the symmetric term in a symmetric matrix is denoted by ∗, e.g., .

2 Dynamic model of an offshore platform with actuator time-delay

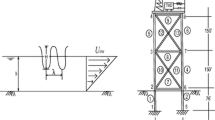
Consider an offshore steel jacket platform with an active tuned mass damper (TMD) shown in Fig. 1 [1–3]. Taking actuator time-delays into consideration, the motion equation of the first two modes of vibration with the coupled TMD can be expressed as

(1)

where z 1(t) and z 2(t) are the generalized coordinates of vibration modes 1 and 2, respectively; ω 1 and ω 2 are the natural frequencies of the first two modes of vibration, respectively; ξ 1 and ξ 2 are the damping ratios in the first two modes of vibration, respectively; ϕ 1 and ϕ 2 are the first and second mode shapes vectors, respectively; C T , m T , and K T are the damping, the mass and the stiffness of the TMD, respectively; z T is the horizontal displacement of the TMD; ω T is the natural frequency of the TMD; ξ T is the damping ratio of the TMD; u is the control action of the system; τ≥0 is the actuator time-delay; f 1, f 2, f 3, and f 4 are nonlinear self-excited force terms.

Fig. 1
figure 1

Steel jacket structure with an active TMD [3]

Full size image

Remark 1

If we take into account of the actuator time-delays in system (3), i.e., τ=0, then the dynamic model (1) reduces to the model in [2] and [3].

Let

(2)

and denote \(x=[ \begin{array}{cccccc} x_{1} & x_{2} & x_{3} & x_{4} & x_{5} & x_{6} \\ \end{array} ]^{T} \). Then the system (1) can be rewritten as

$$ \dot{x}(t)=Ax(t)+Bu(t-\tau)+Df(x,t) $$
(3)

where

$$ \left \{ \begin{array}{l} A =\! \left [ \mbox{\small\selectfont$\displaystyle \begin{array}{c@{\quad}c@{\quad}c} 0 & 1 & 0 \\[4pt] -\omega_1^2- {K_T}\phi_1^2 & -2\xi_1\omega_1- C_T\phi_1^2 & -K_T\phi_1\phi_2 \\[4pt] 0 & 0 & 0 \\[4pt] -K_T\phi_1\phi_2 & -C_T\phi_1\phi_2 & -\omega_2^2 - K_T\phi_2^2 \\[4pt] 0 & 0 & 0 \\[4pt] \omega_T^2\phi_1 & 2\xi_T\omega_T\phi_1 & \omega_T^2\phi_2 \\ \end{array}$} \right.\\ \left.\begin{array}{c@{\quad}c@{\quad}c} 0 & 0 & 0 \\[3pt] -C_T\phi_1\phi_2 & \phi_1K_T & \phi_1C_T\\[3pt] 1 & 0 & 0 \\[3pt] -2\xi_2\omega_2-C_T\phi_2^2 & \phi_2K_T & \phi_2C_T \\[3pt] 0 & 0 & 1 \\[3pt] 2\xi_T\omega_T\phi_2 & -\omega_T^2 & -2\xi_T\omega_T \\ \end{array} \right ]\vspace{1mm} \\ B = \left [ \begin{array}{c} 0 \\ -\phi_1 \\ 0 \\ -\phi_2 \\ 0 \\ \frac{1}{m_T} \\ \end{array} \right ],\qquad D =\left [ \begin{array}{c@{\quad}c} 0 & 0 \\ 1 & 0 \\ 0 & 0 \\ 0 & 1 \\ 0 & 0 \\ 0 & 0 \\ \end{array} \right ] \\ \end{array} \right . $$
(4)

and the nonlinear self-excited wave force f(x,t) is of the form as

$$ f(x,t)=\left [ { \begin{array}{c} f_1(x_1,x_3,t) + f_2(x_1,x_3,t) \\[4pt] f_3(x_1,x_3,t) + f_4(x_1,x_3,t) \\ \end{array} } \right ] \\ $$

which is uniformly bounded and satisfies the following constraint [2, 3]:

$$ \bigl\|f(x,t)\bigr\| \leq\mu\bigl\|x(t)\bigr\| $$
(5)

with μ a positive scalar.

The objective of this paper is to design a state feedback control law

$$ u(t)=Kx(t) $$
(6)

to stabilize the offshore platform (3) and thereby improve the control performance of the offshore platform, where K is a 1×6 real matrix to be determined.

To obtain the main results, the following lemma is needed.

Lemma 1

([13])

For any constant matrix R∈ℝn×n,R=R T>0, a scalar h>0 and a vector-valued function \(\dot{x}:[t-h,t]\rightarrow\mathbb{R}^{n}\) such that the following integration is well defined, then

(7)

3 Design of a state feedback controller

For the ideal case, i.e., τ=0, a state feedback controller of the form (6) is designed first to stabilize the offshore platform in this section. A sufficient condition for the existence of the state feedback controller is stated as the following proposition.

Proposition 1

For a given scalar μ>0, the system (3) with τ=0 is stabilizable via the control law (6) if there exist a 6×6 matrix \(\bar{P}>0\) and a 1×6 matrix \(\bar{K}\) such that

$$ \left [ \begin{array}{c@{\quad}c@{\quad}c} A\bar{P}+\bar{P}A^{T}+B\bar{K}+\bar{K}^{T}B^{T} & D & \mu\bar{P} \\ \ast & -I & 0 \\ \ast & \ast & -I \end{array} \right ]<0 $$
(8)

If the linear matrix inequality (8) is feasible, then the gain matrix K in (6) is given by \(K=\bar{K}\bar{P}^{-1}\).

Proof

Substituting (6) into (3) with τ=0, one yields

$$ \dot{x}(t)=(A+BK)x(t)+Df(x,t) $$
(9)

Let

$$ V_1(x)=x^T (t)Px(t) $$
(10)

be a candidate Lyapunov function for system (9), where P>0 is a 6×6 matrix to be determined. Taking the derivative along the system trajectory, noting that (5) and setting α(t)=[x T(t) f T(x,t)]T, it can be verified that

$$ \dot{V}_1(x)\leq\alpha^T(t)\varPsi \alpha^T(t) $$
(11)

where

$$ \varPsi=\left [ \begin{array}{c@{\ \ \ }c} PA+A^T P+PBK+K^TB^TP+\mu^2I & PD \\ * & -I \\ \end{array} \right ] $$
(12)

By Schur complement, it is straightforward to show that if the linear matrix inequality (8) holds, then we have Ψ<0, which guarantees that \(\dot{V}_{1} (x)<0\) for any x(t)≠0. This completes the proof. □

4 Design of a delay-dependent state feedback controller

In this section, a delay-dependent state feedback controller is presented for the offshore platform with actuator timed-delays. Based on the integral inequality method [13], a sufficient condition for the existence of the control law (6) is given first; then an approximation approach is proposed to solve the gain matrix K.

4.1 Existence of a delay-dependent state feedback controller

The following proposition presents the sufficient conditions for the existence of a delay-dependent state feedback controller.

Proposition 2

For given scalars μ>0 and τ>0, the system (3) is stabilizable via the control law (6) if there exist 6×6 matrices \(\bar{P} > 0, \bar{Q} > 0\), \(\bar{R}>0\), and a 1×6 matrix \(\bar{K}\) such that

(13)

where

$$ \varLambda=A\bar{P} + \bar{P}A^T + \bar{Q} - \bar{R} $$

And if the matrix inequality (13) is feasible, then the gain matrix K is given by \(K= \bar{K} \bar{P}^{ - 1}\).

Proof

From (3) and (6), one yields the closed-loop system as

$$ \dot{x}(t)=Ax(t)+BKx(t-\tau)+Df(x,t) $$
(14)

Choose a Lyapunov–Krasovskii functional as

$$ V(x_t ) =V_1+V_2+V_3 $$
(15)

where V 1 is defined in (10) and

(16)
(17)

with x t =x(t+s),s∈[−τ,0], Q>0 and R>0 are 6×6 matrices to be determined.

Taking the derivative of V(x t ) with respect to t along the trajectory of (14) gives

(18)

Applying Lemma 1 to the integral term in (18), we obtain

(19)

Letting η(t)=[x T(t) x T(t−τ)f T(x,t)]T and noting that (5), it follows from (18) and (19) that

$$ \dot{V} (x_t ) \le\eta^T (t) \bigl( {\varXi + \tau^2 \varGamma^T R\varGamma} \bigr)\eta(t) $$
(20)

where

In order to guarantee \(\dot{V} (x_{t} )<0\) for any x(t)≠0, we require that

$$ \varXi + \tau^2 \varGamma^T R\varGamma < 0 $$
(21)

By applying Schur complement, matrix inequality (21) is equivalent to

(22)

where

$$ \varUpsilon=PA + A^T P + Q - R $$

Pre- and post-multiplying the left-hand side of (22) by diag{P −1,P −1,I,R −1,I} and its transpose, respectively, and setting

we arrive at the condition (13). □

4.2 Numerical algorithm

It is clear that the condition (13) is a nonlinear matrix inequality. In order to derive the controller gain \(\bar{K} \) from the matrix inequality (13), we introduce a new matrix S>0 such that

$$ S \le\bar{P}\bar{R}^{ - 1} \bar{P} $$
(23)

which is equivalent to

$$ \left [ { \begin{array}{c@{\quad}c} {S^{ - 1} } & {\bar{P}^{ - 1} } \\ * & {\bar{R}^{ - 1} } \\ \end{array} } \right ] \ge0 $$
(24)

Let

$$ \bar{S} = S^{ - 1},\qquad \bar{L} = \bar{P}^{ - 1},\qquad \bar{M} = \bar{R}^{ - 1} $$
(25)

Then we have the following proposition.

Proposition 3

The nonlinear matrix inequality (13) holds if the following conditions are satisfied:

(26)
(27)
(28)

The problem formulated by the conditions (26)–(28) is a nonconvex feasibility problem. Based on the cone complementary algorithm [12], the nonconvex feasibility problem can be converted into the following nonlinear minimization problem subject to a set of linear matrix inequalities:

(29)
(30)

By numerically solving the nonlinear minimization problem (29), we can obtain the gain matrix K of the delay-dependent state feedback controller (6).

5 Simulation results

In this section, the effects of actuator time-delays on the stabilization control for the offshore platform are investigated first. Then a delay-dependent state feedback controller is designed to improve the performance of the offshore platform with actuator time-delays.

5.1 Parameters of the offshore platform

In Fig. 1, the parameters of the offshore platform and the wave force are given as follows, which are from [1–3]. The data of the waves are H=12.19 m, h=76.2 m and λ=182.88 m. The TMD parameters are ω T =1.818 revolutions per second (rps), ξ T =0.15, K T =155.15, m T =469.483 kg, and C T =256. The density of steel is 7730.7 kg/m3, the density of water is \(\rho_{\omega }=1025.6~\mathrm{kg/m}^{3}\), the weight of the concrete deck is 6672300 N, and U ow =0.122 m/s. The natural frequencies of the first two modes of vibration are assumed to be ω 1=1.818 rps and ω 2=10.8683 rps, respectively. The structural damping in each mode is supposed to be 0.5 %. The first and second mode shape vectors are ϕ 1=−0.003445 and ϕ 2=0.00344628, respectively. Based on the settings, matrices A and B can be obtained as

$$ \left \{ \begin{array}{l} A = \left [ { \begin{array}{c@{\quad}c@{\quad}c} 0 & 1 & 0 \\ { - 3.3235} & { - 0.0212} & {0.0184} \\ 0 & 0 & 0 \\ {0.0184} & {0.0030} & { - 118.1385} \\ 0 & 0 & 0 \\ { - 0.0114} & { - 0.0019} & {0.0114} \\ \end{array} } \right . \\[40pt] \left . {\; \begin{array}{c@{\quad}c@{\quad}c} 0 & 0 & 0 \\ {0.0030} & { - 5.3449} & { - 0.8819} \\ 1 & 0 & 0 \\ { - 0.1118} & {5.3465} & {0.8822} \\ 0 & 0 & 1 \\ {0.0019} & { - 3.3051} & { - 0.5454} \\ \end{array} } \right ] \\[40pt] B = {\left [ { \begin{array}{c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c} 0 & {0.003445} & 0 & { - 0.00344628} & 0 & {0.00213} \\ \end{array} } \right ]^T} \\ \end{array} \right . $$

Let μ=0.8, the wave frequency be 1.8 rps. The nonlinear self-excited wave force f(x,t) can be computed as Appendix A in [2].

5.2 Effects of actuator time-delays on the performance of the offshore platform

In this subsection, for the case of that the actuator time-delays are not considered, a state feedback controller is first designed via Proposition 1, and the oscillation amplitudes of the three floors and the control force required under the obtained state feedback controller are compared with the ones under the nonlinear controller [3], the dynamic output feedback controller [9] and the integral sliding mode controller [10], respectively. Then, under the state feedback controller, the effects of the actuator time-delays on the performance of the offshore platform are investigated.

First, for comparison purposes, the performance of the offshore platform without control is presented. When no controller is used to the offshore platform, it can be computed that the oscillation amplitudes of the first, second and third floors of the offshore platform are 1.3738 m, 1.4489 m, and 1.5634 m peak to peak, respectively.

Second, for the case of that the actuator time-delay τ=0 in system (3), we design a state feedback controller to reduce the vibration amplitudes of the offshore platform. For this, by Proposition 1, the gain matrix of a state feedback controller (SFC) is obtained as

When the obtained SFC is applied to the offshore platform (3) with τ=0, it can be computed that the controlled vibration amplitudes of the first, second, and third floors of the offshore platform are reduced from 1.3738 m, 1.4489 m, and 1.5634 m to 0.2226 m, 0.2434 m, and 0.2590 m peak to peak, respectively, and the range of the required control force is about 5.73×104 N. The displacement responses of the first, second, and third floors are presented in Figs. 2, 3, 4, respectively, and the response of the control force is given by Fig. 5. It shows that the SFC can able to reduce the vibration amplitudes of the three floors of the offshore platform to about 17 % of those when no active controller is used.

Fig. 2
figure 2

Response of the first floor of the system under the SFC and τ=0

Full size image
Fig. 3
figure 3

Response of the second floor of the system under the SFC and τ=0

Full size image
Fig. 4
figure 4

Response of the third floor of the system under the SFC and τ=0

Full size image
Fig. 5
figure 5

Response of the control force of the system under the SFC and τ=0

Full size image

On the other hand, under the other stabilization controllers, i.e., the nonlinear controller (NLC) [3], the dynamic output feedback controller (DOFC) [9], and the integral sliding mode controller (ISMC) [10], the vibration amplitudes of the three floors of the offshore platform and the control force are listed in Table 1 and compared with the ones under the SFC. From this table, one can see clearly that:

  • the vibration amplitudes of the three floors of the offshore platform under the SFC are smaller than those under the NLC and the DOFC. Furthermore, the required control force by the SFC is significantly reduced. In fact, the control force required by the SFC is reduced to about 28.7 % and 14.3 % of the ones under the NLC and the DOFC, respectively;

  • under the SFC and the ISMC, the controlled oscillation amplitudes of the three floors are almost in the same level, while the control force required by the SFC is much less than that by the ISMC.

Table 1 The ranges of the control force (N) and the vibration amplitudes (m) of the three floors of the offshore platform with τ=0 under the different stabilization controllers, where u r stands for the range of the control force
Full size table

The simulation results show that for the ideal situation, i.e., the actuator time-delay of the offshore platform is considered as zero; the designed SFC is effective to attenuate the vibration amplitudes of the offshore platform, and the controlled performance of the offshore platform under the SFC is better than those under the NLC, the DOFC, and the ISMC. Moreover, the control force required by the SFC is less than the ones by other aforesaid controllers.

Third, we aim to investigate the effects of actuator time-delays on the control performance of the system. When the SFC is used to control the system with actuator time-delays, it can be obtained that for the cases of 0<τ≤0.045, the ranges of the vibration amplitudes of the three floors of the offshore platform are almost in the same level as those in the case of τ=0, while the control force becomes increasingly large, which can be observed from Table 2 and Figs. 6, 7, 8, 9, where the actuator time-delay τ=0.045 s. It shows that as τ≤0.045 s, though the required control force becomes larger over the time-delays, the SFC is still effective to attenuate the vibration of the offshore platform. However, if the value of time-delay τ increases to 0.046 s, it can be found from Fig. 10 that under the SFC, the range of the vibration amplitude of the first floor suddenly increases to about 3.7 m peak to peak. In this case, the obtained SFC is no longer effective.

Fig. 6
figure 6

Response of the first floor of the system under the SFC and τ=0.045 s

Full size image
Fig. 7
figure 7

Response of the second floor of the system under the SFC and τ=0.045 s

Full size image
Fig. 8
figure 8

Response of the third floor of the system under the SFC and τ=0.045 s

Full size image
Fig. 9
figure 9

Response of the control force required by the SFC and τ=0.045 s

Full size image
Fig. 10
figure 10

Response of the first floor of the system under the SFC and τ=0.046 s

Full size image
Table 2 The ranges u r of the control force (N) required by the SFC for the different values of time-delay τ (s)
Full size table

The simulation results show that ignoring the actuator time-delays of the system, the obtained controller is too conservative, and the allowable upper bound of time-delay is too small; on the other hand, the required control force will become larger and larger as actuator time-delay increases gradually.

5.3 Performance of the offshore platform under the delay-dependent state feedback controller

In this subsection, a delay-dependent state feedback controller (DDSFC) is designed to stabilize the offshore platform, and the controlled vibration amplitudes of the offshore platform and the allowable maximum actuator time-delay are presented.

Let actuator time-delay τ=0.08. By Propositions 2 and 3, solving numerically the nonlinear minimization problem (29), one can obtain the gain matrix of the DDSFC as

Under the DDSFC, the response curves of the three floors of the offshore platform and the control force are shown in Figs. 11, 12, 13, 14, respectively. It can be computed that the maximum oscillation amplitudes of the first, second, and third floors of the offshore platform are 0.2244 m, 0.2462 m, and 0.2634 m peak to peak, respectively, the range of the control force is 5.8106×104 N. It shows that as the actuator time-delay τ>0.045, here τ=0.08, the DDSFC is still valid, and it is able to reduce the vibration amplitudes of the offshore platform to about 16 % of those when no controller is applied.

Fig. 11
figure 11

Response of the first floor of the system under the DDSFC and τ=0.08 s

Full size image
Fig. 12
figure 12

Response of the second floor of the system under the DDSFC and τ=0.08 s

Full size image
Fig. 13
figure 13

Response of the third floor of the system under the DDSFC and τ=0.08 s

Full size image
Fig. 14
figure 14

Response of the control force required by the DDSFC and τ=0.08 s

Full size image

Now we turn to investigate the allowable maximum actuator time-delay. When the DDSFC is applied to the offshore platform, the ranges of the vibration amplitudes of the three floors and the control force required for different actuator time-delays are listed in Table 3. It can be seen from this table that when time-delay τ≤0.105 s, the offshore platform can work in a safe environment. As time-delay increases to 0.106 s, the DDSFC is still effective to stabilize the system; however, the range of the control force increases to about 1.5×106 N, which shows that the required control force becomes large suddenly. And as τ=0.107 s, the vibration amplitudes of the three floors suddenly increase to 0.9074 m. Figure 15 presents the response curve of the first floor of the offshore platform as the DDSFC applied to the system with τ=0.107 s. In this situation, the obtained DDSFC will no longer work.

Fig. 15
figure 15

Response of the first floor of the system under the DDSFC and τ=0.107 s

Full size image
Table 3 The ranges u r of the control force (N) and the vibration amplitudes (m) of the three floors of the system under the DDSFC for different values of time-delay τ (s)
Full size table

From Tables 2 and 3, we can clearly see that under the DDSFC, the allowable upper bound of the actuator delay is 0.105 s, which is far greater than the one under the SFC. It indicates that the DDSFC is less conservative than the SFC, and the former is more effective than the latter to reduce the unfavorable effects of the actuator time-delays on stabilization control for the performance of the offshore platform.

6 Conclusions

In this paper, we have developed the problem of stabilization control of the offshore platform. We have proposed the state feedback control scheme and the delay-dependent state feedback control scheme for the offshore platform without and with actuator time-delay, respectively. It is found from the simulation results that the designed delay-dependent state feedback controller is less conservative than the state feedback controller. Moreover, it can effectively improve the control performances of the offshore platform.