Robust non-fragile control for offshore steel jacket platform with nonlinear perturbations

Abstract

This study is concerned with the design of a non-fragile controller for an offshore steel jacket platform with nonlinear perturbations. The delay-dependent sufficient conditions are derived in terms of linear matrix inequalities based on suitable Lyapunov–Krasovskii functional, the second-order reciprocally convex approach and the lower bound lemma. The results indicate asymptotic stability of the offshore steel jacket platform utilizing the proposed non-fragile controller. Besides that, robust stability conditions are derived for an uncertain offshore platform subject to the non-fragile controller. A numerical example is given to illustrate the effectiveness of the proposed theoretical results.

1 Introduction

In our modern world, the oil and gas crisis has become a bottleneck of economy. Therefore, certain offshore structures, especially the oil and gas production platforms, play an increasingly important role. The environment surrounding the offshore platform is harsh and complicated. They have to endure strong dynamic forces caused by wind, sea wave, sea current, sea ice, and even earthquake. Therefore, the structural safety and durability of offshore platforms have raised great concerns in the oil and gas industry. In order to increase stiffness of the offshore platform, many researchers have attempted to design different controllers, and corresponding results were published in the literature (see e.g., [1–10]). As an example, a network-based modeling and active control scheme for offshore steel jacket platforms with tuned mass damper (TMD) mechanisms were investigated in [1]. In [4], a new multi-loop feedback control design was developed and applied to an offshore steel jacket platform. A sliding mode $H_\infty$ controller was designed to reduce the oscillation amplitudes of the offshore platform in [6]. The problem of stabilization control for offshore steel jacket platforms with actuator time delays was investigated in [7]. The authors in [8] studied nonlinear and robust control schemes for offshore steel jacket platforms. A dynamic output feedback controller was proposed to improve the control performance of offshore platform with a TMD mechanism in [9]. Active vibration $H_\infty$ control of offshore steel jacket platforms using delayed feedback was investigated in [10]. More recently, pure delayed non-fragile control was proposed to improve the performance of the offshore steel jacket platform in [11].

On the other hand, it is almost impossible to obtain an exact mathematical model of dynamical systems due to various factors including modeling errors, measurement errors, linearization approximation. Indeed it is reasonable and practical to assume that the system to be controlled has certain amount of uncertainty (see e. g., [12–23]). As an example, robust $H_\infty$ control and non-fragile control problems for Takagi–Sugeno fuzzy systems with linear fractional parametric uncertainties were studied in [12]. An approach to design static output feedback and non-fragile static output feedback $H_\infty$ controllers for active vehicle suspensions by using linear matrix inequalities (LMIs) and genetic algorithms was presented in [16]. Besides that, robust reliable dissipative filtering for networked control systems with sensor failure was discussed in [21]. Very recently, the authors in [24] proposed a new type of uncertainty named randomly occurring uncertainties due to the fact that the uncertainties may be subject to random changes in environmental circumstances, for instance, repairs of components and sudden environmental disturbances. Therefore, the uncertainties occur in a probabilistic way with certain types and intensity. In [25], a non-fragile procedure was introduced to study the problem of synchronization of neural networks with time-varying delay. Robust synchronization of chaotic systems with randomly occurring uncertainties through stochastic sampled-data control was investigated in [26]. The problem of robust state estimator design for a class of uncertain discrete-time genetic regulatory networks with time-varying delays and randomly occurring uncertainties was studied in [27]. In [28], the problem of robust dissipativity analysis for uncertain neural networks with time-varying delay was examined. The design problem of state estimator for genetic regularity networks with time-varying delays and randomly occurring uncertainties was addressed by a delay decomposition approach in [29]. In fact, offshore platforms involve some uncertainties such as unknown system parameters and structure flexibility. In particular, minor variations in some system parameters can bring about undesired effects on the performance of the system in deep water fields. So, designing a robust controller for offshore platforms subject to parameter perturbation is of prime significance.

A controller for which the closed-loop system is destabilized by small perturbations in the controller coefficients is referred to as a ’fragile’ controller. In practice, many controllers are implemented digitally. Therefore, controller implementation is subject to round-off errors and finite word length in numerical computations. Moreover for any controller design, it is necessary to conduct manual tuning to obtain the desired performance of a control system. Therefore, the controller design must be able to tolerate some perturbations in controller coefficients. Such a controller design is nothing other than the non-fragile controller.

In the literature, the problem of non-fragile passive control for uncertain singular time-delay systems with time-invariant norm-bounded uncertainty was investigated in [30]. Robust integral sliding mode control for an offshore steel jacket platforms subject to nonlinear wave-induced force and parameter perturbations was discussed in [31]. The problem of non-fragile $H_\infty$ controller design for linear time-invariant systems with multiplicative controller gain variations was discussed in [32]. In [33], the authors proposed a robust and non-fragile $H_\infty$ state feedback controller design method for discrete systems with multiplicative uncertainty. The problem of non-fragile synchronization control for complex networks with time-varying coupling delay and missing data was addressed in [34]. Exponential synchronization of fractional-order chaotic systems with mixed uncertainties was discussed in [35]. Moreover, the problem of non-fragile synchronization control for complex networks with additive time-varying delays was investigated in [36].

Motivated by the above account, we design a non-fragile controller for an offshore steel jacket platform subject to nonlinear perturbations in this paper. Some sufficient conditions which ensure asymptotic stability of the offshore platform are presented in terms of LMIs. Furthermore, the robust asymptotic stabilization is proposed for an uncertain system by employing the second-order reciprocally convex approach. To the best of authors’ knowledge, no results have been found in the existing literature for asymptotic stabilization of the offshore platform with randomly occurring uncertainties under the non-fragile controller by using the second- order reciprocally convex approach.

The rest of the paper is organized as follows: Preliminaries and problem formulations are given in Sect. 2. In Sect. 3, some sufficient conditions which guarantee the asymptotic stabilization of the considered system under the non-fragile controller are proposed. In addition, the stabilization of the system with random occurring uncertainties is discussed. In Sect. 4, a numerical example is presented to illustrate the effectiveness of the results. Finally, conclusions are drawn in Sect. 5.

2 Notations

Throughout this paper, superscript $T$ stands for matrix transposition. $\mathbb {R}^n$ denotes the $n$-dimensional Euclidean space. $\mathbb {R}^{n\times n}$ denotes the set of all $n\times n$ real matrices. $P>0 \ (P\ge 0)$ means that $P$ is positive definite (positive semi-definite). $I_n$ and $0_n$ stand for $n\times n$ identity matrix and $n\times n$ zero matrix, respectively. The symmetric term in a symmetric matrix is denoted by $\star$. Let Prob $\{\alpha \}$ denote the occurrence probability of an event $\alpha$. The conditional probability of $\alpha$ and $\beta$ is denoted by Prob $\{\alpha |\beta \}$. ${\mathbb {E}}\{x\}$ is the expectation of a stochastic variable $x$, and diag$\{.\}$ stands for a block-diagonal matrix.

3 Preliminaries and problem formulation

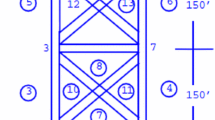
Consider an offshore steel jacket platform model with an TMD mechanism shown in Fig. 1, [8]. The dynamic equation of the model can be expressed as

$$\begin{aligned} \ddot{z}_1(t)= & {} -2\xi _1\omega _1\dot{z}_1-\omega _{1}^2z_1 -\phi _1K_{T}[\phi _1z_1(t)\nonumber \\&+\,\phi _{2}z_{2}(t)]+\,\phi _{1}K_Tz_T(t)+\phi _{1}K_T\dot{z}_T\nonumber \\&-\,\phi _{1}C_T[\phi _1\dot{z}_1(t)+\phi _{2}\dot{z}_{2}(t)]-\phi _{1}u(t)\nonumber \\&+\,f_1(z_1(t),z_2(t),t)\!+\!f_2(z_1(t),z_{2}(t),t), \ddot{z}_2(t)\nonumber \\ \ddot{z}_2(t)= & {} -2\xi _2\omega _2\dot{z}_2-\omega _{2}^2z_2 -\phi _2K_{T}[\phi _1z_1(t)\nonumber \\&+\,\phi _{2}z_{2}(t)]+\,\phi _{2}K_Tz_T(t)+\phi _{2}K_T\dot{z}_T\nonumber \\&-\,\phi _{2}C_T[\phi _1\dot{z}_1(t)+\phi _{2},\dot{z}_{2}(t)]-\,\phi _{2}u(t)\nonumber \\&+\,f_3(z_1(t),z_2(t),t)+f_4(z_1(t),z_{2}(t),t),\\ \ddot{z}_T(t)= & {} -2\xi _T\omega _{T}[\dot{z}_{T}(t)-\phi _1 \dot{z}_1(t)-\phi _2\dot{z}_2(t)]\nonumber \\&+\,\frac{1}{m_T}u(t)-\,\omega _{T}^2[z_T(t)+\phi _{1}z_1(t)+\phi _2z_2(t)],\nonumber \end{aligned}$$

(1)

where $z_1$ and $z_2$ are the generalized coordinates of vibration modes 1 and 2, respectively; $z_T$ is the horizontal displacement of the TMD; $\xi _1$ and $\xi _2$ are the damping ratios in the first two modes of vibration, respectively; $\omega _1$ and $\omega _2$ represent the natural frequencies of the first two modes of vibration, respectively; $\phi _1$ and $\phi _2$ are the first- and second-mode shape vectors, respectively; $\xi _T$ is the damping ratio of the TMD. Damping, mass, and stiffness of the TMD are denoted by $C_T,m_T$ and $K_T$ respectively; $\omega _T=\sqrt{K_T/m_T}$ is the natural frequency of the TMD; $u$ is the control force; $f_1,f_2,f_3$ and $f_4$ are nonlinear self-excited force terms. By defining

$$\begin{aligned}&x_1(t)=z_1(t), x_2(t)=\dot{z}_1(t), x_3(t)=z_2(t)\nonumber \\&x_4(t)=\dot{z}_2(t), x_5(t)=z_T(t), x_6(t)=\dot{z}_T(t) \end{aligned}$$

(2)

as state variables and vectors

$$\begin{aligned} x(t)&=[x_1(t)\ x_2(t)\ x_3(t)\ x_4(t) \ x_5(t)\ x_6(t)],\\ f(x,t)&=\left[ \begin{array}{c} f_1(x_1,x_3,t)+f_2(x_1,x_3,t)\\ f_3(x_1,x_3,t)+f_4(x_1,x_3,t)\end{array} \right] , \end{aligned}$$

the state space model of system (1) can be written as

$$\begin{aligned} \dot{x}(t)=Ax(t)+Bu(t)+Df(x(t),t),\ x(0)=x_0, \end{aligned}$$

(3)

where

$$\begin{aligned} A= & {} \left[ \begin{array}{ccc} 0 &{}1 &{}0 \\ -\omega _1^2-K_T\phi _T^2 &{} -2\xi _1\omega _1-C_T\phi _1^2 &{} -K_T\phi _1\phi _2 \\ 0 &{} 0 &{}0 \\ -K_T\phi _1\phi _2 &{} -C_T\phi _1\phi _2 &{} -\omega _2^2-K_T\phi _2^2 \\ 0 &{} 0&{} 0\\ \omega _T^2\phi _1 &{} 2\xi _T\omega _T\phi _1 &{} \omega _T^2\phi _2 \end{array}\right. \nonumber \\&\left. \begin{array}{ccc} 0 &{} 0 &{} 0\\ -C_T\phi _1\phi _2 &{} \phi _1K_T &{}\phi _1C_T\\ 1 &{} 0&{} 0\\ -2\xi _2\omega _2-C_T\phi _2^2 &{} \phi _2K_T &{} \phi _2C_T\\ 0&{} 0&{} 1\\ 2\xi _T\omega _T\phi _2 &{} -\omega _T^2 &{} -2\xi _T\omega _T \end{array}\right] ,\nonumber \\ B= & {} \left[ \begin{array}{cccccc} 0&-\phi _1&0&-\phi _2&0&\frac{1}{m_T} \end{array} \right] ^T, \ D=\left[ \begin{array}{cccccc} 0 &{} 1 &{} 0 &{} 0&{} 0&{} 0\\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{}0 \end{array}\right] ^T. \end{aligned}$$

The non-fragile control law can be defined as

$$\begin{aligned} u(t)=[K+\Delta K(t)]x(t-\tau (t)), \end{aligned}$$

(4)

where $0\le \tau _1\le \tau (t)\le \tau _2,\ \tau _{12}=\tau _2-\tau _1,$

$$\begin{aligned} \Delta K(t)= EF(t)H \end{aligned}$$

(5)

with $E$ and $H$ are the known matrices of appropriate dimension, $F(t)$ is the unknown time-varying matrix satisfying $F^T(t)F(t)\le I, \quad t\ge 0$ and $K$ is the gain matrix to be determined. Then the controlled system can be written in the form as

$$\begin{aligned}&\dot{x}(t)=Ax(t)+B[K+\Delta K(t)]x(t-\tau (t))\nonumber \\&\quad +Df(x(t),t), x(0)=x_0. \end{aligned}$$

(6)

Before deriving our main results, the necessary assumption, lemmas and definition are introduced.

Fig. 1

A steel jacket platform with TMD [8]

Assumption 1

The nonlinear wave force $f(x(t),t)$ in (3) is uniformly bounded and satisfies the following constraint

$$\begin{aligned} \Vert f(x(t),t)\Vert \le \alpha _1 \Vert x(t)\Vert . \end{aligned}$$

(7)

Lemma 1

[26] For any constant matrix $X\in \mathbb {R}^{n\times n},$ $X=X^T>0,$ two scalars $h_2\ge 0,h_1>0,$ such that the integrations concerned are well defined, then

$$\begin{aligned}&-\frac{h_2^2-h_1^2}{2} \int _{t-h_2}^{t-h_1}\int _{t+\theta }^{t} x^T(s)Xx(s) \mathrm {d}s\mathrm {d}\theta \nonumber \\&\quad \le -\left( \int _{t-h_2}^{t-h_1}\int _{t+\theta }^{t}x(s)\mathrm {d}s\mathrm {d}\theta \right) ^T X \left( \int _{t-h_2}^{t-h_1}\int _{t+\theta }^{t}x(s)\mathrm {d}s\mathrm {d}\theta \right) , \end{aligned}$$

(8)

$$\begin{aligned}&\quad \quad -(h_2-h_1)\int _{t-h_2}^{t-h_1}x^T(x)Xx(s)\mathrm {d}s \nonumber \\&\quad \le -\left( \int _{t-h_2}^{t-h_1}x(s)\mathrm {d}s\right) ^TX\left( \int _{t-h_2}^{t-h_1}x(s)\mathrm {d}s\right) . \end{aligned}$$

(9)

Lemma 2

[37] (lower bound lemma) Let $f_1,f_2, \ldots ,$ $f_n:\mathbb {R}^{m}\rightarrow \mathbb {R}$ have positive values in an open subset $D$ of $\mathbb {R}^m.$ Then the reciprocally convex combination of $f_i$ over $D$ satisfies

$$\begin{aligned} \min \limits _{\{\alpha _i|\alpha _i>0,\sum _{i}\alpha _i=1\}} \sum \limits _{i}\frac{1}{\alpha _i}f_i(t) \!=\!\!\sum \limits _{i}f_{i}(t)\!+\!\max \limits _{g_{ij}(t)} \sum \limits _{i\not =j}g_{ij}(t) \end{aligned}$$

subject to

$$\begin{aligned} \left\{ g_{ij}:\mathbb {R}^{m}\rightarrow \mathbb {R},\ g_{ij}(t),\left[ \begin{array}{cc}f_i(t) &{} g_{ij}(t)\\ g_{ij}(t)&{} f_j(t)\end{array}\right] \ge 0\right\} . \end{aligned}$$

Lemma 3

[38] For the symmetric matrices $R>0,\ \varOmega$ and matrix $\varGamma$, the following statements are equivalent:

• 1. $\varOmega -\varGamma ^TR\varGamma <0,$

• 2. There exists an appropriate dimensional matrix $\Pi$ such that

  $$\begin{aligned} \left[ \begin{array}{cc} \varOmega +\varGamma ^T\Pi +\Pi ^T\varGamma &{} \Pi ^T\\ \star &{} -R\end{array}\right] <0. \end{aligned}$$

Lemma 4

[39] For a positive definite matrix $M$ and any differentiable function $\bar{w}$ in $[a,b]\rightarrow \mathbb {R}^n$, the following inequality holds:

$$\begin{aligned} \int _{a}^{b}\dot{\bar{w}}^T(u)M\dot{\bar{w}}(u)\mathrm{d}u\ge \frac{1}{b-a}w^T(a,b)\bar{M}w(a,b), \end{aligned}$$

where

$$\begin{aligned} w(a,b)&=\left[ \begin{array}{c} \bar{w}(b)\\ \bar{w}(a)\\ \frac{1}{b-a}\int _{a}^{b}\bar{w}(u)\mathrm {d}u \end{array} \right] ,\\ \bar{M}&=\left[ \begin{array}{ccc} M &{} -M &{} 0\\ \star &{} M &{} 0\\ \star &{} \star &{} 0 \end{array} \right] +\frac{\pi ^2}{4}\left[ \begin{array}{ccc} M &{} M &{} -2M \\ \star &{} M &{} -2M \\ \star &{} \star &{} 4M \end{array} \right] . \end{aligned}$$

Definition 1

Let $\varPhi _1,\varPhi _2,\varPhi _3, \ldots , \varPhi _N:\mathbb {R}^m\rightarrow \mathbb {R}$ be a given finite number of functions that have positive values in an open subset $D$ of $\mathbb {R}^m.$ Then, a second-order reciprocally convex combination of these functions over $D$ is a function of the form

$$\begin{aligned} \frac{1}{\alpha _1^2}\varPhi _1+\frac{1}{\alpha _2^2}\varPhi _2+\cdots +\frac{1}{\alpha _N^2}\varPhi _N:D\rightarrow \mathbb {R}^n, \end{aligned}$$

(10)

where the real numbers $\alpha _i$ satisfy $\alpha _i>0$ and $\sum _{i}\alpha _i=1.$

4 Main results

Now, we are in a position to derive the sufficient conditions for which the considered system (6) can be asymptotically stable, which can be realized through the following theorem.

Theorem 1

Given scalars $0\le \tau _1\le \tau _2$, system (6) is asymptotically stable if there exist matrices $\tilde{P}>0, {\tilde{Q}}_i>0,\ i=1,2,3,\ \tilde{T}_i,\ \tilde{W}_i,\ i=1,2,\ {\tilde{R}}_i>0, {\tilde{S}}_i>0,\ i=1,2,\ldots ,6.$ and $\tilde{\Pi }_1,\ \tilde{\Pi }_2$ with appropriate dimensions such that the following conditions hold:

$$\begin{aligned}&\left[ \begin{array}{ccc} \tilde{\varPhi }_1 &{} \tilde{\Pi }_1^T &{} \tilde{\Pi }_2^T\\ \star &{} -\tilde{T}_1 &{} 0\\ \star &{} \star &{} -\tilde{T}_2 \end{array}\right] <0,\ \end{aligned}$$

(11)

$$\begin{aligned}&\left[ \begin{array}{cccc} 2{\tilde{R}}_5 &{} 0 &{} {\tilde{S}}_1 &{} 0\\ \star &{} {\tilde{R}}_5 &{} 0 &{} {\tilde{S}}_2\\ \star &{}\star &{} 2{\tilde{R}}_5 &{} 0\\ \star &{} \star &{} \star &{} {\tilde{R}}_5 \end{array}\right] >0,\ \left[ \begin{array}{cccc} 2{\tilde{R}}_6 &{} 0 &{} {\tilde{S}}_3&{} 0\\ \star &{} {\tilde{R}}_6 &{} 0 &{} {\tilde{S}}_4\\ \star &{}\star &{} 2{\tilde{R}}_6 &{} 0\\ \star &{} \star &{} \star &{} {\tilde{R}}_6 \end{array}\right] >0, \end{aligned}$$

(12)

$$\begin{aligned}&\left[ \begin{array}{cc} {\tilde{R}}_3+\tau _{12}^2{\tilde{R}}_5 &{} {\tilde{S}}_5\\ \star &{} {\tilde{R}}_3+\tau _{12}^2{\tilde{R}}_5 \end{array}\right] >0, \left[ \begin{array}{cc} {\tilde{R}}_4 &{} {\tilde{S}}_6\\ \star &{} {\tilde{R}}_4 \end{array}\right] >0, \end{aligned}$$

(13)

where

$$\begin{aligned} \varPhi =&\left[ \begin{array}{ccc}\varOmega &{} 2\varGamma _1(t)\tilde{W}_1 &{} 2\varGamma _2(t)\tilde{W}_2\\ \star &{} -2\tilde{W}_1 &{} 0\\ \star &{} \star &{} -2\tilde{W}_2\end{array}\right] +\left[ \begin{array}{c} \varGamma _1^T(t)\\ 0_{2n}\\ 0_{2n} \end{array}\right] \tilde{\Pi }_{1}\\&+\,\tilde{\Pi }_1^T \left[ \begin{array}{c} \varGamma _1^T(t)\\ 0_{2n}\\ 0_{2n} \end{array}\right] ^T+ \left[ \begin{array}{c} \varGamma _2^T(t)\\ 0_{2n}\\ 0_{2n} \end{array}\right] \\&\tilde{\Pi }_2+\tilde{\Pi }_2^T \left[ \begin{array}{c} \varGamma _2^T(t)\\ 0_{2n}\\ 0_{2n} \end{array}\right] ^T\\ \tilde{T}_1=&\left[ \begin{array}{cc} 3{\tilde{R}}_5 &{} {\tilde{S}}_1+{\tilde{S}}_2\\ \star &{} 3{\tilde{R}}_5 \end{array}\right] ,\ \tilde{T}_2=\left[ \begin{array}{cc} 3{\tilde{R}}_6 &{} {\tilde{S}}_3+{\tilde{S}}_4\\ \star &{} 3{\tilde{R}}_6 \end{array}\right] \end{aligned}$$

and $\varOmega =[\varOmega _{ij}]_{14\times 14}, \ \varGamma _1,\ \varGamma _2, \acute{R}_5$ and $\acute{R}_6$ are defined as

$$\begin{aligned} \varOmega _{1,1}= & {} {\tilde{Q}}_1+{\tilde{Q}}_2+{\tilde{Q}}_3-\left( {\tilde{R}}_1+\frac{\pi ^2}{4}{\tilde{R}}_1\right) \nonumber \\&-\left( {\tilde{R}}_2+\frac{\pi ^2}{4}{\tilde{R}}_2\right) +\,A{\tilde{G}}\nonumber \\&+\,{\tilde{G}}A^T+\tau _{12}^2{\tilde{R}}_5+\rho \alpha _1^2,\\ \varOmega _{1,2}= & {} BE,\ \varOmega _{1,3}=\tilde{P}-{\tilde{G}}+A{\tilde{G}},\\ \varOmega _{1,5}= & {} -\!\left( \frac{\pi ^2}{4}{\tilde{R}}_1\!-\!{\tilde{R}}_1\right) ,\ \varOmega _{1,6}\!=\!-\!\left( \frac{\pi ^2}{4}{\tilde{R}}_2-\!{\tilde{R}}_2\right) ,\\ \varOmega _{1,8}= & {} \frac{\pi ^2}{2}{\tilde{R}}_1,\ \varOmega _{1,9}=\frac{\pi ^2}{2}{\tilde{R}}_2,\ \varOmega _{1,14}=D,\ \varOmega _{2,2}=-\frac{1}{\epsilon _1},\\ \varOmega _{3,3}= & {} \tau _{1}^2{\tilde{R}}_1+\tau _2^2{\tilde{R}}_2 +\tau _{12}^2{\tilde{R}}_3+\frac{\tau _{12}^4}{4}{\tilde{R}}_5 +\frac{\tau _{12}^4}{4}{\tilde{R}}_6-2{\tilde{G}},\\ \varOmega _{3,7}= & {} BK,\ \varOmega _{3,14}=D,\ \varOmega _{4,4}=-\frac{1}{\epsilon _2},\\ \varOmega _{5,5}= & {} -{\tilde{Q}}_1-({\tilde{R}}_1+\frac{\pi ^2}{4}{\tilde{R}}_1),\ \varOmega _{5,8}=\frac{\pi ^2}{2}{\tilde{R}}_1,\\ \varOmega _{6,6}= & {} -{\tilde{Q}}_2-({\tilde{R}}_2+\frac{\pi ^2}{4}{\tilde{R}}_2),\ \varOmega _{6,9}=\frac{\pi ^2}{2}{\tilde{R}}_2,\\ \varOmega _{7,7}= & {} -(1-\mu ){\tilde{Q}}_3+\epsilon _1^{-1}H^TH+\epsilon _2^{-1}H^TH,\\ \varOmega _{8,8}= & {} -\pi ^2{\tilde{R}}_1,\ \varOmega _{9,9}=-\pi ^2{\tilde{R}}_2,\ \varOmega _{10,10}=-{\tilde{R}}_4,\\ \varOmega _{10,11}= & {} -{\tilde{S}}_6,\ \varOmega _{11,11}=-{\tilde{R}}_4,\ \varOmega _{12,12}=-{\tilde{R}}_4-\frac{\tau _{12}^2}{2}{\tilde{R}}_5,\\ \varOmega _{12,13}= & {} -{\tilde{S}}_5,\ \varOmega _{13,13}=-{\tilde{R}}_4-\frac{\tau _{12}^2}{2}{\tilde{R}}_5,\ \varOmega _{14,14}=-\rho I \end{aligned}$$

$$\begin{aligned} \varGamma _{11}= & {} \left[ \begin{array}{cccccccccccccc} 0_n &{} 0_n &{} 0_n &{} 0_n&{} 0_n &{}0_n &{} 0_n &{} 0_n &{}0_n&{} -I_n &{} 0_n &{} 0_n &{} 0_n &{}0_n \\ 0_n &{} 0_n &{} 0_n &{} 0_n &{}0_n&{} 0_n&{} \tau _{12}I_n &{}0_n&{} 0_n &{} 0_n&{} -I_n &{}0_n &{}0_n &{} 0_n \end{array}\right] ,\\ \varGamma _{12}= & {} \left[ \begin{array}{cccccccccccccc} 0_n &{} 0_n &{} 0_n &{} 0_n&{} \tau _{12}I_n &{}0_n &{} 0_n&{} 0_n &{}0_n&{} -I_n &{} 0_n &{} 0_n &{} 0_n &{}0_n \\ 0_n &{} 0_n &{} 0_n &{} 0_n &{}0_n&{} 0_n&{} 0_n &{}0_n&{} 0_n &{} 0_n&{} -I_n &{}0_n &{}0_n &{} 0_n \end{array}\right] ,\\ \varGamma _{21}= & {} \left[ \begin{array}{cccccccccccccc} 0_n &{} 0_n &{} 0_n &{} 0_n &{} 0_n &{} 0_n&{} 0_n &{}0_n &{} 0_n &{} I_n &{} 0_n &{} 0_n &{} 0_n &{}0_n \\ 0_n &{} 0_n &{} 0_n &{} 0_n &{}0_n&{} -\tau _{12}I_n &{}0_n &{} 0_n &{} 0_n&{} 0_n&{} 0_n&{} 0_n&{} I_n &{}0_n \end{array}\right] ,\\ \varGamma _{22}= & {} \left[ \begin{array}{cccccccccccccc} 0_n &{} 0_n &{} 0_n &{} 0_n &{} 0_n &{} 0_n &{} -\tau _{12}I_n &{}0_n &{} 0_n &{} I_n &{} 0_n &{} 0_n &{} 0_n &{}0_n \\ 0_n &{} 0_n &{} 0_n &{} 0_n &{} 0_n &{} 0_n &{} 0_n &{} 0_n &{} 0_n&{} 0_n&{} 0_n&{} 0_n&{} I_n &{}0_n \end{array}\right] .\\ \end{aligned}$$

$$\begin{aligned} \tilde{W}_1= & {} \left[ \begin{array}{cc} {\tilde{R}}_5 &{} 0\\ \star &{} {\tilde{R}}_5 \end{array}\right] ,\ \tilde{W}_2=\left[ \begin{array}{cc} {\tilde{R}}_6 &{} 0\\ \star &{} {\tilde{R}}_6 \end{array}\right] . \end{aligned}$$

Moreover, if the above condition is feasible, a desired controller gain matrix is given by $K=L{\tilde{G}}^{-1}$.

Proof

Consider the Lyapunov–Krasovksii functional as

$$\begin{aligned} V(t)=\sum \limits _{i=1}^{7}V_i(t), \end{aligned}$$

(14)

where,

$$\begin{aligned} V_1(t)= & {} x^T(t)Px(t),\\ V_2(t)= & {} \!\int _{t\!-\!\tau (t)}^{t}x^T(s)Q_1x(s)\mathrm {d}s\!+\!\int _{t-\tau _1}^{t}x^T(s)Q_2x(s) \mathrm {d}s\nonumber \\&+ \int _{t-\tau _2}^{t}x^T(s)Q_3x(s)\mathrm {d}s,\\ V_3(t)= & {} \int _{-\tau _1}^{0}\int _{t+\theta }^{t}\dot{x}^T(s)R_1 \dot{x}(s)\mathrm {d}s\mathrm {d}\theta \nonumber \\&+\int _{-\tau _2}^{0}\int _{t+\theta }^{t}\dot{x}^T(s)R_2 \dot{x}(s)\mathrm {d}s\mathrm {d}\theta ,\\ V_4(t)= & {} \tau _{12}\int _{-\tau _2}^{-\tau _1}\int _{t+\theta }^{t} \dot{x}^T(s)R_3\dot{x}(s)\mathrm {d}s\mathrm {d}\theta ,\\ V_5(t)= & {} \tau _{12}\int _{-\tau _2}^{-\tau _1}\int _{t+\theta }^{t} x^T(s)R_4x(s)\mathrm {d}s\mathrm {d}\theta ,\\ V_6(t)= & {} \frac{\tau _{12}^2}{2}\int _{-\tau _2}^{-\tau _1} \int _{\theta }^{-\tau _1}\int _{t+\lambda }^{t}\dot{x}^T(s) R_5\dot{x}(s)\mathrm {d}s\mathrm {d}\lambda \mathrm {d}\theta ,\\ V_7(t)= & {} \frac{\tau _{12}^2}{2}\int _{-\tau _2}^{-\tau _1} \int _{-\tau _2}^{\theta }\int _{t+\lambda }^{t}\dot{x}^T(s)R_6 \dot{x}(s)\mathrm {d}s\mathrm {d}\lambda \mathrm {d}\theta . \end{aligned}$$

Define the infinitesimal operator, $L$ as follows:

$$\begin{aligned} LV(t)=lim_{h\rightarrow 0^+}\frac{1}{h}\{\{V(t+h)|t\}-V(t)\}. \end{aligned}$$

Setting $\lambda =\frac{(\tau (t)-\tau _1)}{\tau _{12}},\ \delta =\frac{(\tau _2-\tau (t))}{\tau _{12}}$, it can be seen that

$$\begin{aligned} LV(t)&=LV_1(t)+LV_2(t)+LV_3(t)+LV_4(t)+LV_5(t)\\&\quad +\,LV_6(t)+LV_7(t), \end{aligned}$$

where

$$\begin{aligned} LV_1(t)= & {} 2x^T(t)P\dot{x}(t), \end{aligned}$$

(15)

$$\begin{aligned} LV_2(t)\le & {} x^T(t)(Q_1+Q_2+Q_3)x(t)\nonumber \\&-x^T(t-\tau _1) Q_1x(t-\tau _1)\nonumber \\&-\,x^T(t-\tau _2)Q_2x(t-\tau _2)\nonumber \\&-\,(1-\mu )x^T(t-\tau (t))Q_3x(t-\tau (t)),\end{aligned}$$

(16)

$$\begin{aligned} LV_3(t)= & {} \tau _1^2\dot{x}^T(t)R_1\dot{x}(t)+\tau _2^2 \dot{x}^T(t)R_2\dot{x}(t)\nonumber \\&-\tau _1\int _{t-\tau _1}^{t}\dot{x}^T(s)R_1\dot{x}(s)\mathrm {d}s \nonumber \\&-\tau _2\int _{t-\tau _2}^{t}\dot{x}^T(s)R_2\dot{x}(s)\mathrm {d}s,\nonumber \\\end{aligned}$$

(17)

$$\begin{aligned} LV_4(t)= & {} \tau _{12}^2\dot{x}^T(t)R_3\dot{x}(t) \nonumber \\&-\tau _{12}\int _{t-\tau _2}^{t-\tau (t)}\dot{x}^T(s) R_3\dot{x}(s)\mathrm {d}s\nonumber \\&-\,\tau _{12}\int _{t-\tau (t)}^{t-\tau _1}\dot{x}^T(s)R_3 \dot{x}(s)\mathrm {d}s,\nonumber \\\le & {} \tau _{12}^2\dot{x}^T(t)R_3\dot{x}(t)\nonumber \\&-\,\frac{1}{\delta }\int _{t-\tau _2}^{t-\tau (t)}\dot{x}^T(s) \mathrm {d}sR_3\int _{t-\tau _2}^{t-\tau (t)}\dot{x}(s)\mathrm {d}s \nonumber \\&-\,\frac{1}{\lambda }\int _{t-\tau (t)}^{t-\tau _1}\dot{x}^T(s) R_3\int _{t-\tau (t)}^{t-\tau _1}\dot{x}(s)\mathrm {d}s,\end{aligned}$$

(18)

$$\begin{aligned} LV_5(t)= & {} \tau _{12}^2x^T(t)R_4x(t)\nonumber \\&-\tau _{12} \int _{t-\tau _2}^{t-\tau (t)}x^T(s)R_4x(s)\mathrm {d}s\nonumber \\&-\,\tau _{12}\int _{t-\tau (t)}^{t-\tau _1}x^T(s)R_4x(s)\mathrm {d}s,\nonumber \\\le & {} \tau _{12}^2x^T(t)R_4x(t)\nonumber \\&-\,\frac{1}{\delta } \int _{t-\tau _2}^{t-\tau (t)}x^T(s)\mathrm {d}sR_4\int _{t-\tau _2}^{t-\tau (t)} x(s)\mathrm {d}s\nonumber \\&-\,\frac{1}{\lambda }\int _{t-\tau (t)}^{t-\tau _1}x^T(s) \mathrm {d}sR_4\int _{t-\tau (t)}^{t-\tau _1}x(s)\mathrm {d}s, \end{aligned}$$

(19)

$$\begin{aligned} LV_6(t)= & {} \frac{\tau _{12}^2}{4}\dot{x}^T(t)R_5\dot{x}(t)\nonumber \\&-\,\frac{\tau _{12}^2}{2}\int _{-\tau _2}^{-\tau _1}\int _{t+\theta }^{t-\tau _1} \dot{x}^T(s)R_5\dot{x}(s)\mathrm {d}s\mathrm {d}\theta ,\nonumber \\= & {} \frac{\tau _{12}^2}{4}\dot{x}^T(t)R_5\dot{x}(t)\nonumber \\&-\,\frac{\tau _{12}^2}{2}\int _{-\tau _2}^{-\tau (t)}\int _{t+\theta }^{t-\tau _1} \dot{x}^T(t)R_5\dot{x}(t)\mathrm {d}s\mathrm {d}\theta \nonumber \\&-\,\frac{\tau _{12}^2}{2}(\tau _2-\tau (t))\int _{t-\tau (t)}^{t-\tau _1} \dot{x}^T(t)R_5\dot{x}(t)\mathrm {d}s\nonumber \\&-\,\frac{\tau _{12}^2}{2}\int _{-\tau (t)}^{-\tau _1}\int _{t+\theta }^{t-\tau _1} \dot{x}^T(t)R_5\dot{x}(t)\mathrm {d}s\mathrm {d}\theta \nonumber \\\le & {} \frac{\tau _{12}^2}{4}\dot{x}^T(t)R_5\dot{x}(t)\nonumber \\&-\,\frac{\tau _{12}^2}{2}\frac{\delta }{\lambda }\int _{t-\tau (t)}^{t-\tau _1} \dot{x}^T(s)\mathrm {d}sR_5\int _{t-\tau (t)}^{t-\tau _1}\dot{x}(s) \mathrm {d}s\nonumber \\&-\,\frac{1}{\lambda ^2}\int _{-\tau (t)}^{-\tau _1}\int _{t+\theta }^{t-\tau _1} \dot{x}^T(s)\mathrm {d}s\mathrm {d}\theta R_5\nonumber \\&\int _{-\tau (t)}^{-\tau _1}\int _{t+\theta }^{t-\tau _1}\dot{x}(s) \mathrm {d}s\mathrm {d}\theta \nonumber \\&-\,\frac{1}{\delta ^2}\int _{-\tau _2}^{-\tau (t)} \int _{t+\theta }^{t-\tau (t)}\dot{x}^T(s)\mathrm {d}s\mathrm {d} \theta R_5\nonumber \\&\times \int _{-\tau _2}^{-\tau (t)}\int _{t+\theta }^{t-\tau (t)}\dot{x}(s) \mathrm {d}s\mathrm {d}\theta , \end{aligned}$$

(20)

$$\begin{aligned} LV_7(t)= & {} \frac{\tau _{12}^4}{4}\dot{x}^T(t)R_6\dot{x}(t)\nonumber \\&-\frac{\tau _{12}^2}{2}\int _{-\tau _2}^{-\tau _1}\int _{t-\tau _2}^{t+\theta } \dot{x}^T(s)R_6\dot{x}(s)\mathrm {d}s\mathrm {d}\theta \nonumber \\= & {} \frac{\tau _{12}^4}{4}\dot{x}^T(t)R_6\dot{x}(t)\nonumber \\&-\,\frac{\tau _{12}^2}{2}\int _{-\tau (t)}^{-\tau _1}\int _{t-\tau (t)}^{t+\theta } \dot{x}^T(s)R_6\dot{x}(s)\mathrm {d}s\mathrm {d}\theta \nonumber \\&-\,\frac{\tau _{12}^2}{2}(\tau (t)-\tau _1)\int _{t-\tau _2}^{t-\tau (t)} \dot{x}^T(s)R_6\dot{x}(s)\mathrm {d}s\nonumber \\&-\,\frac{\tau _{12}^2}{2}\int _{-\tau _2}^{\tau (t)}\int _{t-\tau _2}^{t+\theta } \dot{x}^T(s)R_6\dot{x}(s)\mathrm {d}s\mathrm {d}\theta \nonumber \\\le & {} \frac{\tau _{12}^4}{4}\dot{x}^T(t)R_6\dot{x}(t)\nonumber \\&-\,\frac{\tau _{12}^2}{2}\frac{\lambda }{\delta }\int _{t-\tau _2}^{t-\tau (t)} \dot{x}^T(s)\mathrm {d}sR_6\int _{t-\tau _2}^{t-\tau (t)}\dot{x}(s) \mathrm {d}s \nonumber \\&-\,\frac{1}{\lambda ^2}\int _{-\tau (t)}^{-\tau _1}\int _{t-\tau (t)}^{t+\theta } \dot{x}^T(s)\mathrm {d}s \mathrm {d}\theta R_6\nonumber \\&\times \int _{-\tau (t)}^{-\tau _1}\int _{t-\tau (t)}^{t+\theta }\dot{x}(s) \mathrm {d}s \mathrm {d}\theta \nonumber \\&-\,\frac{1}{\delta ^2}\int _{-\tau _2}^{-\tau (t)}\int _{t-\tau _2}^{t+\theta } \dot{x}^T(s) \mathrm {d}s \mathrm {d}\theta R_6\nonumber \\&\times \int _{-\tau _2}^{-\tau (t)}\int _{t-\tau _2}^{t+\theta }\dot{x}(s) \mathrm {d}s\mathrm {d}\theta . \end{aligned}$$

(21)

Let us define $\eta (t)=\left[ x(t)\ \dot{x}(t)\ x(t-\tau _1)\right.$ $\left. x(t-\tau _2)\ x(t-\tau (t)) \frac{1}{\tau _1}\int _{t-\tau _1}^{t}x(s)\mathrm {d}s\ \frac{1}{\tau _2}\right.$ $\left. \int _{t-\tau _2}^{t}x(s)\mathrm {d}s\right.$ $\left. \int _{t-\tau (t)}^{t-\tau _1}x(s)\mathrm {d}s \int _{t-\tau _2}^{t-\tau (t)}x(s)\mathrm {d}s \int _{t-\tau (t)}^{t-\tau _1}\dot{x}(s)\mathrm {d}s \int _{t-\tau _2}^{t-\tau (t)}\dot{x}(s)\right.$ $\left. \mathrm {d}s\ f(x(t),t)\right] .$ By using Lemma 1, the integral term of $LV(t)$ can be bounded as:

$$\begin{aligned}&-\tau _1\int _{t-\tau _1}^{t}\dot{x}^T(s)R_1\dot{x}(s)\mathrm {d}s\nonumber \\&\le -\left[ \begin{array}{c} x(t)\\ x(t-\tau _1)\\ \frac{1}{\tau _1}\int _{t-\tau _1}^{t}x(s)\mathrm {d}s \end{array}\right] ^T \left\{ \left[ \begin{array}{ccc} R_1 &{} -R_1 &{} 0\\ \star &{} R_1 &{} 0\\ \star &{} \star &{} 0 \end{array} \right] \right. \nonumber \\&\left. \quad +\,\frac{\pi ^2}{4}\left[ \begin{array}{ccc} R_1 &{} R_1 &{} -2R_1\\ \star &{} R_1 &{} -2R_1\\ \star &{} \star &{} 4R_1 \end{array}\right] \right\} \left[ \begin{array}{c} x(t)\\ x(t-\tau _1)\\ \frac{1}{\tau _1}\int _{t-\tau _1}^{t}x(s)\mathrm {d}s \end{array}\right] , \end{aligned}$$

(22)

$$\begin{aligned}&\quad -\,\tau _2\int _{t-\tau _2}^{t}\dot{x}^T(s)R_2\dot{x}(s)\mathrm {d}s\nonumber \\&\le -\left[ \begin{array}{c} x(t)\\ x(t-\tau _2)\\ \frac{1}{\tau _2}\int _{t-\tau _2}^{t}x(s)\mathrm {d}s\end{array}\right] ^T \left\{ \left[ \begin{array}{ccc} R_2 &{} -R_2 &{} 0\\ \star &{} R_2 &{} 0\\ \star &{} \star &{} 0 \end{array} \right] \right. \nonumber \\&\left. \quad +\,\frac{\pi ^2}{4}\left[ \begin{array}{ccc}R_2 &{} R_2 &{} -2R_2\\ \star &{} R_2 &{} -2R_2\\ \star &{} \star &{} 4R_2\end{array}\right] \right\} \left[ \begin{array}{c}x(t)\\ x(t-\tau _2)\\ \frac{1}{\tau _2}\int _{t-\tau _2}^{t}x(s)\mathrm {d}s\end{array}\right] . \end{aligned}$$

(23)

From Lemma 1, if there exist matrices $S_5$ and $S_6$ such that (13) holds, then we can obtain

$$\begin{aligned}&-\frac{1}{\lambda }\int _{t-\tau (t)}^{t-\tau _1}\dot{x}^T(s)\mathrm {d}s R_3\int _{t-\tau (t)}^{t-\tau _1}\dot{x}(s)\mathrm {d}s\nonumber \\&-\frac{1}{\delta }\int _{t-\tau _2}^{t-\tau (t)}\dot{x}^T(s)\mathrm {d}s R_3 \int _{t-\tau _2}^{t-\tau (t)}\dot{x}(s)\mathrm {d}s\nonumber \\&-\frac{\tau _{12}^2}{2}\frac{\delta }{\lambda }\int _{t-\tau (t)}^{t-\tau _1} \dot{x}^T(s)\mathrm {d}s R_5 \int _{t-\tau (t)}^{t-\tau _1}\dot{x}(s)\mathrm {d}s\nonumber \\&-\frac{\tau _{12}^2}{2}\frac{\lambda }{\delta }\int _{t-\tau _2}^{t-\tau (t)} \dot{x}^T(s)\mathrm {d}sR_6\int _{t-\tau _2}^{t-\tau (t)}\dot{x}(s) \mathrm {d}s\nonumber \\&\le - \left[ \begin{array}{c}\int _{t-\tau (t)}^{t-\tau _1} \dot{x}(s)\mathrm {d}s\\ \int _{t-\tau _2}^{t-\tau (t)}\dot{x}(s)\mathrm {d}s\end{array}\right] ^T \left[ \begin{array}{cc} R_3+\frac{\tau _{12}^2}{2}R_5 &{} S_5\\ \star &{}R_3+\frac{\tau _{12}^2}{2}R_5 \end{array}\right] \nonumber \\&\qquad \left[ \begin{array}{c}\int _{t-\tau (t)}^{t-\tau _1}\dot{x}(s)\mathrm {d}s\\ \int _{t-\tau _2}^{t-\tau (t)}\dot{x}(s)\mathrm {d}s\end{array}\right] \end{aligned}$$

(24)

and

$$\begin{aligned}&-\frac{1}{\lambda }\int _{t-\tau (t)}^{t-\tau _1}x^T(s)\mathrm {d}s R_4\int _{t-\tau (t)}^{t-\tau _1}x(s)\mathrm {d}s\nonumber \\&-\frac{1}{\delta }\int _{t-\tau _2}^{t-\tau (t)}x^T(s)\mathrm {d}s R_4 \int _{t-\tau _2}^{t-\tau (t)}x(s)\mathrm {d}s\nonumber \\&\le -\left[ \begin{array}{c}\int _{t-\tau (t)}^{t-\tau _1}x(s)\mathrm {d}s\\ \int _{t-\tau _2}^{t-\tau (t)}x(s)\mathrm {d}s\end{array}\right] ^T \left[ \begin{array}{cc} R_4 &{} S_6 \\ \star &{} R_4 \end{array}\right] \left[ \begin{array}{c} \int _{t-\tau (t)}^{t-\tau _1}x(s)\mathrm {d}s\\ \int _{t-\tau _2}^{t-\tau (t)}x(s)\mathrm {d}s\end{array}\!\!\right] \!. \end{aligned}$$

(25)

If $\tau (t)=\tau _1$ or $\tau (t)=\tau _2,$ we have

$$\begin{aligned} \int _{t-\tau (t)}^{t-\tau _1}\dot{x}(s)\mathrm {d}s=\int _{t-\tau (t)}^{t-\tau _1}x(s)\mathrm {d}s=0 \text{ or } \\ \int _{t-\tau _2}^{t-\tau (t)}\dot{x}(s)\mathrm {d}s=\int _{t-\tau _2}^{t-\tau (t)}x(s)\mathrm {d}s=0, \end{aligned}$$

respectively. So inequalities (24) and (25) still hold.

Similarly, we can derive the upper bounds of the second-order reciprocally convex combinations in (20) and (21) for the matrices $S_1,\ S_2,\ S_3$ and $S_4$ satisfying (12) as

$$\begin{aligned}&-\frac{1}{\lambda ^2}\int _{-\tau (t)}^{-\tau _1}\int _{t+\theta }^{t-\tau _1}\dot{x} ^T(s)\mathrm {d}s \mathrm {d}\theta R_5\nonumber \\&\int _{-\tau (t)}^{-\tau _1}\int _{t+\theta }^{t-\tau _1}\dot{x}(s)\mathrm {d}s\mathrm {d}\theta \nonumber \\&-\frac{1}{\delta ^2}\int _{-\tau _2}^{-\tau (t)}\int _{t+\theta }^{t-\tau (t)}\dot{x}^T(s)\mathrm {d}s\mathrm {d}\theta R_5 \nonumber \\&\int _{-\tau _2}^{-\tau (t)}\int _{t+\theta }^{t-\tau (t)}\dot{x}(s)\mathrm {d}s\mathrm {d}\theta \nonumber \\&\le -\left[ \begin{array}{c}\int _{-\tau (t)}^{-\tau _1}\int _{t+\theta }^{t-\tau _1}\dot{x}(s)\mathrm {d}s\mathrm {d}\theta \\ \int _{-\tau _2}^{-\tau (t)}\int _{t+\theta }^{t-\tau (t)}\dot{x}(s)\mathrm {d}s\mathrm {d}\theta \end{array}\right] ^T \left[ \begin{array}{cc}R_5 &{} S_1+S_2\\ \star &{} R_5\end{array}\right] \nonumber \\&\left[ \begin{array}{c}\int _{-\tau (t)}^{-\tau _1}\int _{t+\theta }^{t-\tau _1}\dot{x}(s)\mathrm {d}s\mathrm {d}\theta \\ \int _{-\tau _2}^{-\tau (t)}\int _{t+\theta }^{t-\tau (t)}\dot{x}(s)\mathrm {d}s\mathrm {d}\theta \end{array}\right] \end{aligned}$$

(26)

and

$$\begin{aligned}&-\frac{1}{\lambda ^2}\int _{-\tau (t)}^{-\tau _1}\int _{t-\tau (t)}^{t+\theta } \dot{x}^T(s)\mathrm {d}s\mathrm {d}\theta R_6\nonumber \\&\int _{-\tau (t)}^{-\tau _1}\int _{t-\tau (t)}^{t+\theta }\dot{x}(s) \mathrm {d}s\mathrm {d}\theta \nonumber \\&-\frac{1}{\delta ^2}\int _{-\tau _2}^{-\tau (t)}\int _{t-\tau _2}^{t+\theta } \dot{x}^T(s)\mathrm {d}s\mathrm {d}\theta R_6\nonumber \\&\int _{-\tau _2}^{-\tau (t)}\int _{t-\tau _2}^{t+\theta }\dot{x}(s) \mathrm {d}s\mathrm {d}\theta \nonumber \\&\le - \left[ \begin{array}{c}\int _{-\tau (t)}^{-\tau _1} \int _{t-\tau (t)}^{t+\theta }\dot{x}(s)\mathrm {d}s\mathrm {d}\theta \\ \int _{-\tau _2}^{-\tau (t)}\int _{t-\tau _2}^{t+\theta } \dot{x}(s)\mathrm {d}s\mathrm {d}\theta \end{array}\right] ^T\left[ \begin{array}{cc} R_6 &{} S_3+S_4 \\ \star &{} R_6 \end{array}\right] \nonumber \\&\left[ \begin{array}{c} \int _{-\tau (t)}^{-\tau _1}\int _{t-\tau (t)}^{t+\theta } \dot{x}(s)\mathrm {d}s\mathrm {d}\theta \\ \int _{-\tau _2}^{-\tau (t)}\int _{t-\tau _2}^{t+\theta } \dot{x}(s)\mathrm {d}s\mathrm {d}\theta \end{array}\right] . \end{aligned}$$

(27)

When $\tau (t)=\tau _1$ or $\tau (t)=\tau _2,$ we have

$$\begin{aligned}&\int _{-\tau (t)}^{-\tau _1}\int _{t+\theta }^{t-\tau _1}\dot{x}(s) \mathrm {d}s\mathrm {d}\theta \\&=\int _{-\tau (t)}^{-\tau _1}\int _{t+\theta }^{t-\tau _1} \dot{x}(s)\mathrm {d}s\mathrm {d}\theta =0 \text{ or } \\&\int _{-\tau _2}^{-\tau (t)}\int _{t+\theta }^{t-\tau (t)}\dot{x}(s) \mathrm {d}s\mathrm {d}\theta \\&=\int _{-\tau _2}^{-\tau (t)}\int _{t-\tau _2}^{t+\theta } \dot{x}(s)\mathrm {d}s\mathrm {d}\theta =0 \end{aligned}$$

respectively. Therefore, the conditions (26) and (27) still hold.

For any appropriately dimensioned symmetric matrix $G$, the following equation holds:

$$\begin{aligned}&2\left[ x^T(t)+\dot{x}^ T(t)\right] G\left[ -\dot{x}(t)+Ax(t)\right. \nonumber \\&\left. \quad +\,B(K+\Delta K(t))x(t-\tau (t))+Df(x(t),t)\right] =0, \end{aligned}$$

(28)

Now, by using the fact that $2a^Tb\le \epsilon a^T a+\epsilon ^{-1}b^Tb$ for any real vectors $a,\ b$ and a positive scalar $\epsilon ,$ as well as positive scalars $\epsilon _1,\ \epsilon _2$ and equation $F^T(t)F(t)\le I$, we have:

$$\begin{aligned}&2x^T(t)GBEF(t)H x(t-\tau (t))\nonumber \\&\le x^T(t)(\epsilon _1GBEE^TB^TG)x(t)\nonumber \\&+\,x^T(t-\tau (t))\epsilon _1^{-1}H^THx(t-\tau (t)) \end{aligned}$$

(29)

$$\begin{aligned}&2\dot{x}^T(t)GBEF(t)Hx(t-\tau (t)) \nonumber \\&\le \dot{x}^T(t)(\epsilon _2GBEE^TB^TG)\dot{x}(t)\nonumber \\&\quad +\,x^T(t-\tau (t))\epsilon _2^{-1}H^THx(t-\tau (t)). \end{aligned}$$

(30)

From (15)–(30) and the Schur complement, we have

$$\begin{aligned}&LV(t)\le \eta ^T(t)\left\{ \varOmega -\varGamma _1^T(t)\left[ \begin{array}{cc} R_5 &{} S_1+S_2\\ \star &{} R_5\end{array}\right] \varGamma _1(t)\right. \nonumber \\&\left. -\,\varGamma _2^T(t)\left[ \begin{array}{cc} R_6 &{} S_3+S_4\\ \star &{} R_6\end{array}\right] \varGamma _2(t)\right\} \eta (t), \end{aligned}$$

where

$$\begin{aligned} \varGamma _1(t)= & {} \left[ \begin{array}{cccccccccccccc} 0 &{} 0 &{} 0 &{} 0&{} (\tau (t)-\tau _1) &{}0 &{} 0 &{} 0 &{}0&{} -I_n &{} 0 &{} 0 &{} 0 &{}0 \\ 0 &{} 0 &{} 0 &{} 0 &{}0&{} 0&{} (\tau _2-\tau (t)) &{}0&{} 0 &{} 0&{} -I_n &{}0 &{}0 &{} 0 \end{array}\!\right] ,\\ \varGamma _2(t)= & {} \left[ \begin{array}{cccccccccccccc} 0 &{} 0 &{} 0 &{} 0&{} 0 &{} 0&{} -(\tau (t)-\tau _1) &{}0 &{} 0 &{} I_n &{} 0 &{} 0 &{} 0 &{}0 \\ 0 &{} 0 &{} 0 &{} 0 &{}0&{} -(\tau _2-\tau (t)) &{}0&{} 0 &{} 0&{} 0&{} 0&{} 0&{} I_n &{}0 \end{array}\!\right] . \end{aligned}$$

Furthermore, the condition that

$$\begin{aligned}&\varOmega -\varGamma _1^T(t)\left[ \begin{array}{cc} R_5 &{} S_1+S_2\\ \star &{} R_5\end{array}\right] \varGamma _1(t)\nonumber \\&-\,\varGamma _2^T(t)\left[ \begin{array}{cc} R_6 &{} S_3+S_4\\ \star &{} R_6\end{array}\right] \varGamma _2(t)< 0 \end{aligned}$$

(31)

is intrinsically linear in $\tau (t)$ from the Schur complement and lemma as

$$\begin{aligned} \left[ \begin{array}{ccc} \varPhi (t) &{} \Pi _1^T &{} \Pi _2^T\\ \star &{} -T_1 &{} 0 \\ \star &{} \star &{} -T_2\end{array}\right] <0, \end{aligned}$$

where

$$\begin{aligned} \varPhi (t)=&\left[ \begin{array}{ccc} \varOmega &{} 2\varGamma _1(t)W_1 &{} 2\varGamma _2(t)W_2\\ \star &{} -2W_1 &{} 0\\ \star &{} \star &{} \!-\!2W_2\end{array}\right] \!+\!\left[ \begin{array}{c} \varGamma _1^T(t)\\ 0_{2n}\\ 0_{2n} \end{array}\right] \Pi _{1}\\&+\,\Pi _1^T\left[ \begin{array}{c} \varGamma _1^T(t)\\ 0_{2n}\\ 0_{2n} \end{array}\right] ^T\!+\!\left[ \begin{array}{c} \varGamma _2^T(t)\\ 0_{2n}\\ 0_{2n} \end{array}\right] \Pi _2\!+\!\Pi _2^T\left[ \begin{array}{c} \varGamma _2^T(t)\\ 0_{2n}\\ 0_{2n} \end{array}\right] ^T\!. \end{aligned}$$

Pre- and post-multiplying matrix $\varPhi (t)$ by $diag \{G^{-1},$ $I,G^{-1},I,G^{-1},G^{-1},G^{-1},G^{-1},G^{-1},G^{-1},G^{-1},I,$ $G^{-1},$ $G^{-1},G^{-1},G^{-1},G^{-1},G^{-1},G^{-1},G^{-1}\}$, with ${\tilde{G}}=G^{-1},$ ${\tilde{Q}}_1=G^{-1}Q_1G^{-1},\ {\tilde{Q}}_2=G^{-1}Q_2G^{-1},$ ${\tilde{Q}}_3=G^{-1}Q_3G^{-1},$ ${\tilde{R}}_1=G^{-1}R_1G^{-1},\ {\tilde{R}}_2=G^{-1}R_2G^{-1},\ {\tilde{R}}_3=G^{-1}R_3G^{-1},$ ${\tilde{R}}_4=G^{-1}R_4G^{-1},$ $\ {\tilde{R}}_5=G^{-1}R_5G^{-1},\ {\tilde{R}}_6=G^{-1}R_6G^{-1},$ ${\tilde{S}}_1=G^{-1}S_1G^{-1},\ {\tilde{S}}_2=G^{-1}S_2G^{-1},\ {\tilde{S}}_3\!=\!G^{-1}S_3G^{-1},$ ${\tilde{S}}_4\!=\!G^{-1}S_4G^{-1},\ {\tilde{S}}_5\!=\!G^{-1}S_5G^{-1},\ {\tilde{S}}_6=G^{-1}S_6G^{-1},$ $\tilde{\Pi }_{11}=G^{-1}\Pi _{11}G^{-1},\ \tilde{\Pi }_{12}=G^{-1}\Pi _{12}G^{-1}.$ Therefore, (31) can be treated non-conservatively by two corresponding boundary LMIs (11): one for $\tau (t)=\tau _1$ and the other for $\tau (t)=\tau _2$, which imply $LV(t)<0.$ This completes the proof.

If we consider some uncertainties in the system parameter of (6), it can be written as:

$$\begin{aligned}&\dot{x}(t)=[A+\gamma (t)\Delta A(t)]x(t)+B[K+\gamma (t)\Delta K(t)]\nonumber \\&\ \ \ \ \qquad \times x(t-\tau (t))+Df(x(t),t),\ x(0)=x_0.\nonumber \\ \end{aligned}$$

(32)

The real-valued matrices $\Delta A(t)$ and $\Delta K(t)$ represent the parameter uncertainty that satisfies

$$\begin{aligned} \left[ \begin{array}{cc}\Delta A&\Delta K\end{array}\right] =E F(t) \left[ \begin{array}{cc}H_1&H_2\end{array}\right] , \end{aligned}$$

(33)

where, $E,\ H_1$ and $H_2$ are known constant matrices and the time-varying nonlinear function $F(t)$ satisfies $F^T(t)F(t)\le I.$

To account for the phenomena of randomly occurring uncertainties, we introduce a stochastic variable $\gamma (t)$ which is a mutually independent Bernoulli-distributed white sequence. A natural assumption of $\gamma (t)$ is as follows:

$$\begin{aligned} \text{ Prob }\{\gamma (t)=1\}=\gamma ,\ \text{ Prob }\{\gamma (t)=0\}=1-\gamma \end{aligned}$$

where $\gamma \in [0,1]$ is known constant.

Theorem 2

Given scalars $0\le \tau _1\le \tau _2,\ \gamma$, system (6) is asymptotically stable if there exist matrices $\check{P}>0,\ \check{Q}_i>0,\ i=1,2,3,\ \check{T}_i>0,\ \check{W}_i>0, \ i=1,2,\ \check{R}_i>0,\ \check{S}_i>0,\ i=1,2,\ldots ,6$ and $\check{\Pi }_1,\ \check{\Pi }_2$ with appropriate dimensions such that the following conditions hold:

$$\begin{aligned}&\left[ \begin{array}{ccc} \check{\varPhi }_1 &{} \check{\Pi }_1^T &{} \check{\Pi }_2^T\\ \star &{} -\check{T}_1 &{} 0\\ \star &{} \star &{} -\check{T}_2 \end{array}\right] <0,\ \end{aligned}$$

(34)

$$\begin{aligned}&\left[ \begin{array}{cccc} 2\check{R}_5 &{} 0 &{} \check{S}_1 &{} 0\\ \star &{} {\tilde{R}}_5 &{} 0 &{} \check{S}_2\\ \star &{}\star &{} 2\check{R}_5 &{} 0\\ \star &{} \star &{} \star &{} \check{R}_5 \end{array}\right] \!>\!0,\ \left[ \begin{array}{cccc} 2\check{R}_6 &{} 0 &{} \check{S}_3&{} 0\\ \star &{} \check{R}_6 &{} 0 &{}\check{S}_4\\ \star &{}\star &{} 2\check{R}_6 &{} 0\\ \star &{} \star &{} \star &{} \check{R}_6 \end{array}\right] >0, \end{aligned}$$

(35)

$$\begin{aligned}&\left[ \begin{array}{cc} \check{R}_3+\tau _{12}^2\check{R}_5 &{} \check{S}_5\\ \star &{} \check{R}_3+\tau _{12}^2\check{R}_5 \end{array}\right] \!>\!0, \left[ \begin{array}{cc} \check{R}_4 &{} \check{S}_6\\ \star &{} \check{R}_4 \end{array}\right] >0, \end{aligned}$$

(36)

where

$$\begin{aligned} \varPhi =&\left[ \begin{array}{ccc} \varOmega &{} 2\varGamma _1(t)\check{W}_1 &{} 2\varGamma _2(t)\check{W}_2\\ \star &{} -2\check{W}_1 &{} 0\\ \star &{} \star &{} -2\check{W}_2\end{array}\right] \\&+\left[ \begin{array}{c}\varGamma _1^T(t)\\ 0_{2n}\\ 0_{2n} \end{array}\right] \tilde{\Pi }_{1} +\check{\Pi }_1^T\left[ \begin{array}{c}\varGamma _1^T(t)\\ 0_{2n}\\ 0_{2n} \end{array}\right] ^T\\ {}&+\left[ \begin{array}{c}\varGamma _2^T(t)\\ 0_{2n}\\ 0_{2n} \end{array}\right] \check{\Pi }_2+\check{\Pi }_2^T\left[ \begin{array}{c}\varGamma _2^T(t)\\ 0_{2n}\\ 0_{2n} \end{array}\right] ^T, \end{aligned}$$

$$\begin{aligned} \check{T}_1=\left[ \begin{array}{cc} 3\check{R}_5 &{} \check{S}_1+\check{S}_2\\ \star &{} 3\check{R}_5 \end{array}\right] ,\ \check{T}_2=\left[ \begin{array}{cc} 3\check{R}_6 &{} \check{S}_3+\check{S}_4\\ \star &{} 3\check{R}_6 \end{array}\right] \end{aligned}$$

and $\varOmega =[\varOmega _{ij}]_{16\times 16}, \ \varGamma _1,\ \varGamma _2, \check{W}_1$ and $\check{W}_2$ are defined as

$$\begin{aligned} \varOmega _{1,1}= & {} \check{Q}_1+\check{Q}_2+\check{Q}_3-\left( \check{R}_1+\frac{\pi ^2}{4}\check{R}_1\right) \\&-\left( \check{R}_2+\frac{\pi ^2}{4}\check{R}_2\right) \nonumber \\&+\,A\check{G}+\check{G}A^T+\tau _{12}^2\check{R}_5+\rho \alpha _1^2\nonumber \\&+\,\gamma \epsilon _1^{-1}H_1^TH_1+\gamma \epsilon _2^{-1}H_1^TH_1,\\ \varOmega _{1,2}= & {} \!\gamma BE,\ \varOmega _{1,3}\!=\! \gamma E,\ \varOmega _{1,4} \!=\!\check{P}\!-\!\check{G}+A\check{G},\\ \varOmega _{1,7}= & {} -\!\left( \frac{\pi ^2}{4}\check{R}_1\!-\!\check{R}_1\right) , \varOmega _{1,8}\!=\!-\!(\frac{\pi ^2}{4}\check{R}_2\!-\!\check{R}_2),\\ \varOmega _{1,10}= & {} \frac{\pi ^2}{2}\check{R}_1,\ \varOmega _{1,11} =\frac{\pi ^2}{2}\check{R}_2,\ \varOmega _{1,16}=D,\\ \varOmega _{2,2}= & {} -\frac{1}{\epsilon _1}, \varOmega _{3,3}\!=\!-\!\frac{1}{\epsilon _2}, \varOmega _{4,4}\!=\!\tau _{1}^2\check{R}_1+\tau _2^2\check{R}_2\nonumber \\&+\, \tau _{12}^2\check{R}_3+\frac{\tau _{12}^4}{4}\check{R}_5\nonumber \\&+\frac{\tau _{12}^4}{4}\check{R}_6-2\check{G},\ \varOmega _{4,5}=\gamma BE,\\ \varOmega _{4,6}= & {} \gamma E, \varOmega _{4,9}\!=\!BK, \varOmega _{4,16}\!=\!D, \varOmega _{5,5}\!=\!-\!\frac{1}{\epsilon _3},\\ \varOmega _{6,6}= & {} -\!\frac{1}{\epsilon _4},\ \varOmega _{7,7}=-\check{Q}_1-\left( \check{R}_1+\frac{\pi ^2}{4}\check{R}_1\right) ,\\ \varOmega _{7,10}= & {} \frac{\pi ^2}{2}\check{R}_1,\ \varOmega _{8,8}=-\check{Q}_2-\left( \check{R}_2+\frac{\pi ^2}{4}\check{R}_2\right) ,\\ \varOmega _{8,11}= & {} \frac{\pi ^2}{2}\check{R}_2, \varOmega _{9,9}=\!-\!(1\!-\!\mu )\check{Q}_3\!+\!\gamma \!\epsilon _3^{-1}\!H_2^T\!H_2\nonumber \\&+\,\gamma \epsilon _4^{-1}H_2^TH_2,\ \varOmega _{10,10}=-\pi ^2\check{R}_1,\\ \varOmega _{11,11}= & {} -\pi ^2\check{R}_2,\ \varOmega _{12,12}\!=\!-\!\check{R}_4,\ \varOmega _{12,13}=-\check{S}_6,\\ \varOmega _{13,13}= & {} -\check{R}_4,\ \varOmega _{14,14}=-\check{R}_4-\frac{\tau _{12}^2}{2}\check{R}_5,\ \nonumber \\&\varOmega _{14,15}=-\check{S}_5,\\ \varOmega _{15,15}= & {} -\check{R}_4-\frac{\tau _{12}^2}{2}\check{R}_5,\ \varOmega _{16,16}=-\rho I\\ \end{aligned}$$

$$\begin{aligned} \varGamma _1= & {} \left[ \begin{array}{cccccccccccc} 0_n &{} 0_n &{} 0_n &{}0_n&{} 0_n&{} 0_n&{} 0_n&{}0_n &{} 0_n &{} 0_n &{}0_n&{} -I_n \\ 0_n &{} 0_n &{} 0_n &{} 0_n&{}0_n &{}0_n&{}0_n&{} 0_n&{} \tau _{12}I_n &{}0_n&{} 0_n &{} 0_n \end{array}\right. \\&\left. \begin{array}{cccc} 0_n &{} 0_n &{} 0_n &{}0_n \\ -I_n &{}0_n &{}0_n &{} 0_n \end{array}\right] , \\ \varGamma _1= & {} \left[ \begin{array}{cccccccccccc} 0_n &{} 0_n &{} 0_n &{}0_n&{} 0_n&{} 0_n&{}\tau _{12}I_n &{}0_n &{} 0_n &{} 0_n &{}0_n&{} -I_n \\ 0_n &{} 0_n &{} 0_n &{} 0_n&{}0_n &{}0_n&{}0_n&{} 0_n&{} 0_n &{}0_n&{} 0_n &{} 0_n \end{array}\right. \\&\left. \begin{array}{cccc} 0_n &{} 0_n &{} 0_n &{}0_n \\ -I_n &{}0_n &{}0_n &{} 0_n \end{array}\right] ,\\ \varGamma _2= & {} \left[ \begin{array}{cccccccccccc} 0_n &{} 0_n &{} 0_n &{} 0_n&{} 0_n &{}0_n&{} 0_n&{}0_n&{} 0_n &{}0_n &{} 0_n &{} I_n \\ 0_n &{} 0_n &{} 0_n &{} 0_n&{}0_n &{}0_n&{}0_n&{} -\tau _{12}I_n &{}0_n &{} 0_n &{} 0_n&{} 0_n \end{array}\right. \\&\left. \begin{array}{cccc} 0_n &{} 0_n &{} 0_n &{}0_n \\ 0_n&{} 0_n&{} I_n &{}0_n \end{array}\right] ,\\ \varGamma _2= & {} \left[ \begin{array}{cccccccccccc} 0_n &{} 0_n &{} 0_n &{} 0_n&{} 0_n &{}0_n&{} 0_n&{}0_n&{} -\tau _{12}I_n &{}0_n &{} 0_n &{} I_n \\ 0_n &{} 0_n &{} 0_n &{} 0_n&{}0_n &{}0_n&{}0_n &{}0_n&{}0_n &{} 0_n &{} 0_n \end{array}\right. \\&\left. \begin{array}{cccc} 0_n &{} 0_n &{} 0_n &{}0_n \\ 0_n&{} 0_n&{} I_n &{}0 \end{array}\right] , \end{aligned}$$

$$\begin{aligned} \check{W}_1= & {} \left[ \begin{array}{cc} \check{R}_5 &{} 0\\ \star &{} \check{R}_5 \end{array}\right] ,\ \check{W}_2=\left[ \begin{array}{cc} \check{R}_6 &{} 0\\ \star &{} \check{R}_6 \end{array}\right] . \end{aligned}$$

Moreover, if the above condition is feasible, a desired controller gain matrix is given by $K=L\check{G}^{-1}$.

Proof

Consider the Lyapunov–Krasovskii functional defined by

$$\begin{aligned} V(t)=\sum \limits _{i=1}^{7}V_i(t), \end{aligned}$$

where, $V_{i}(t),\ i=1,2,\ldots , 7$ are defined as in Theorem 1. For any appropriately dimensioned symmetric matrix $G$, the following equation holds:

$$\begin{aligned}&{\mathbb {E}}\left\{ 2\left[ x^T(t)\!+\!\dot{x}^ T(t)\right] G\left[ -\!\dot{x}(t)\!+\!(A\!+\!\gamma (t)\Delta A(t))x(t)\right. \right. \nonumber \\&\left. \left. +\,B(K+\gamma (t)\Delta K(t))x(t\!-\!\tau (t))\!+\!Df(x(t),t)\right] \right\} \!=\!0, \end{aligned}$$

(37)

Now by using the fact that $2a^Tb\le \epsilon a^T a+\epsilon ^{-1}b^Tb$ for any real vectors $a,\ b$ and a positive scalar $\epsilon ,$ as well as positive scalars $\epsilon _1,\ \epsilon _2,\ \epsilon _3,\ \epsilon _4$ and $F^T(t)F(t)\le I$, we have:

$$\begin{aligned}&{\mathbb {E}}\{2\gamma (t)x^T(t)GEF(t)H_1x(t)\}\nonumber \\&\le {\mathbb {E}}\{\gamma (t) x^T(t)(\epsilon _1GEE^TG)x(t)\nonumber \\&+\gamma (t)x^T(t)\epsilon _1^{-1}H_1^TH_1x(t)\} \end{aligned}$$

(38)

$$\begin{aligned}&{\mathbb {E}}\{2\gamma (t)\dot{x}^T(t)GEF(t)H_1x(t)\}\nonumber \\&\le {\mathbb {E}}\{\gamma (t) \dot{x}^T(t)(\epsilon _2GEE^TG)\dot{x}(t)\nonumber \\ {}&+\gamma (t)x^T(t)\epsilon _2^{-1}H_1^TH_1x(t)\}\end{aligned}$$

(39)

$$\begin{aligned}&{\mathbb {E}}\{2\gamma (t)x^T(t)GBEF(t)H_2 x(t-\tau (t))\}\nonumber \\&\le {\mathbb {E}}\{ \gamma (t) x^T(t)(\epsilon _3GBEE^TB^TG)x(t)\nonumber \\&+\gamma (t)x^T(t-\tau (t))\epsilon _3^{-1}H_2^TH_2x(t-\tau (t))\}\end{aligned}$$

(40)

$$\begin{aligned}&{\mathbb {E}}\{2\gamma (t)\dot{x}^T(t)GBEF(t)H_2x(t-\tau (t))\}\nonumber \\&\le {\mathbb {E}}\{\gamma (t) \dot{x}^T(t)(\epsilon _4GBEE^TB^TG)\dot{x}(t)\nonumber \\&+\gamma (t)x^T(t-\tau (t))\epsilon _4^{-1}H_2^TH_2x(t-\tau (t))\}. \end{aligned}$$

(41)

From (15)–(30) and by using the above equations similarly as in the proof of Theorem 1, we can obtain

$$\begin{aligned}&{\mathbb {E}}\{LV(t)\}\!\le \!{\mathbb {E}}\!\left\{ \!\eta ^T(t)\left\{ \varOmega -\varGamma _1^T(t)\!\left[ \begin{array}{cc} R_5 &{} S_1\!+\!S_2\\ \!\star &{} R_5\end{array}\right] \varGamma _1(t)\right. \right. \nonumber \\&\left. \left. -\,\varGamma _2^T(t)\left[ \begin{array}{cc} R_6 &{} S_3+S_4\\ \star &{} R_6\end{array}\right] \varGamma _2(t)\right\} \eta (t)\right\} , \end{aligned}$$

(42)

where

$$\begin{aligned} \varGamma _1(t)= & {} \left[ \begin{array} {ccccccccccc} 0 &{} 0 &{} 0&{}0 &{} 0&{}0&{} (\tau (t)-\tau _1) &{}0 &{} 0 &{} 0 &{}0\\ 0 &{} 0 &{} 0 &{} 0&{}0 &{}0&{}0&{} 0&{} (\tau _2-\tau (t)) &{}0&{} 0 \end{array}\right. \\&\left. \begin{array} {ccccc} -I_n &{} 0 &{} 0 &{} 0 &{}0 \\ 0&{} -I_n &{}0 &{}0 &{} 0 \end{array}\right] ,\\ \varGamma _2(t)= & {} \left[ \begin{array} {ccccccccccc} 0 &{} 0 &{} 0 &{} 0&{} 0&{} 0 &{}0 &{} 0&{} -(\tau (t)-\tau _1) &{}0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0&{} 0&{} 0 &{}0 &{} -(\tau _2-\tau (t)) &{} 0 &{}0 &{} 0 \end{array}\right. \\&\left. \begin{array} {ccccc} I_n &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} I_n &{} 0 \end{array}\right] . \end{aligned}$$

Furthermore, the condition that

$$\begin{aligned} \varOmega -\varGamma _1^T(t)\left[ \begin{array}{cc} R_5 &{} S_1+S_2\\ \star &{} R_5\end{array}\right] \varGamma _1(t)\nonumber \\ \quad -\,\varGamma _2^T(t)\left[ \begin{array}{cc} R_6 &{} S_3+S_4\\ \star &{} R_6\end{array}\right] \varGamma _2(t)< 0 \end{aligned}$$

(43)

is intrinsically linear in $\tau (t)$ from the Schur complement and lemma as

$$\begin{aligned} \left[ \begin{array}{ccc} \varPhi (t) &{} \Pi _1^T &{} \Pi _2^T\\ \star &{} -T_1 &{} 0 \\ \star &{} \star &{} -T_2\end{array}\right] <0, \end{aligned}$$

where

$$\begin{aligned} \varPhi (t)=&\left[ \begin{array}{ccc}\varOmega &{} 2\varGamma _1(t)W_1 &{} 2\varGamma _2(t)W_2\\ \star &{} -2W_1 &{} 0\\ \star &{} \star &{} -2W_2\end{array}\right] \\&+\left[ \begin{array}{c} \varGamma _1^T(t)\\ 0_{2n}\\ 0_{2n} \end{array}\right] \Pi _{1} +\Pi _1^T\left[ \begin{array}{c} \varGamma _1^T(t)\\ 0_{2n}\\ 0_{2n} \end{array}\right] ^T\\&+\left[ \begin{array}{c}\varGamma _2^T(t)\\ 0_{2n}\\ 0_{2n} \end{array}\right] \Pi _2+\Pi _2^T\left[ \begin{array}{c} \varGamma _2^T(t)\\ 0_{2n}\\ 0_{2n} \end{array}\right] ^T. \end{aligned}$$

Pre- and post-multiplying matrix $\varPhi (t)$ by $diag \{G^{-1},I,$ $G^{-1}, I,G^{-1},I,I,G^{-1},G^{-1},G^{-1},G^{-1},G^{-1},G^{-1},I,$ $G^{-1},$ $G^{-1},G^{-1},G^{-1},G^{-1},G^{-1},G^{-1},G^{-1}\},$ with $\check{G}=G^{-1},$ $\check{Q}_1\!=\!G^{-1}Q_1G^{-1},\ \check{Q}_2=G^{-1}Q_2G^{-1},$ $\check{Q}_3=G^{-1}Q_3G^{-1},$ $\check{R}_1=G^{-1}R_1G^{-1},\ \check{R}_2=G^{-1}R_2G^{-1},\ \check{R}_3=G^{-1}R_3G^{-1},$ $\check{R}_4=G^{-1}R_4G^{-1},$ $\check{R}_5=G^{-1}R_5G^{-1},\ \check{R}_6=G^{-1}R_6G^{-1},$ $\check{S}_1=G^{-1}S_1G^{-1},\ \check{S}_2=G^{-1}S_2G^{-1}, \check{S}_3=G^{-1}S_3G^{-1},$ $\check{S}_4=G^{-1}S_4G^{-1},\ \check{S}_5=G^{-1}S_5G^{-1}, \check{S}_6=G^{-1}S_6G^{-1},$ $\check{\Pi }_{11}=G^{-1}\Pi _{11}G^{-1},\ \check{\Pi }_{12}=G^{-1}\Pi _{12}G^{-1}.$ Therefore (43) can be treated non-conservatively by two corresponding boundary LMIs (34): one for $\tau (t)=\tau _1$ and the other for $\tau (t)=\tau _2$, which imply ${\mathbb {E}}\{LV(t)\}<0.$ This completes the proof.

Remark 1

From the application point of view, it is of great significance to investigate stability with uncertainty for system (6). Randomly occurring uncertainties have been introduced to deal with uncertain parameters that vary in a random manner. Therefore, in this paper, we have studied asymptotic stabilization of system (6) with randomly occurring uncertainties. Random variable $\gamma (t)$ that satisfies ${\mathbb {E}}\{\gamma (t)\}=\gamma$ and ${\mathbb {E}}\{(\gamma (t)-\gamma )^2\}=\gamma (1-\gamma ),$ is used to model the probability distribution of the randomly occurring uncertainties, which was introduced in [29].

Remark 2

In [25], the problem of non-fragile synchronization of neural networks with time-varying delay and randomly occurring controller gain fluctuations was addressed. The problem of robust sliding mode control for discrete stochastic systems with mixed time delays, randomly occurring uncertainties and randomly occurring nonlinearities has been investigated in [40]. Robust non-fragile decentralized controller design for uncertain Large-scale interconnected systems with time delays was investigated in [41]. In [42], the authors addressed fuzzy filtering with randomly occurring parameter uncertainties with interval delays and channel fadings.

In the literature, many control methods have been developed for offshore structures such as sliding mode control, optimal tracking control, active vibration $H_\infty$ control, and multi-loop feedback control to improve the performance of the structure. Sliding mode control with mixed current and delayed states for offshore steel jacket platforms was considered in [43]. Optimal tracking control problem with feedforward compensation for offshore steel jacket platforms with active mass damper was studied in [44]. However, investigation on stabilization of offshore platforms with uncertainties through a non-fragile controller has yet to be found in the literature. Motivated by the above discussion, a robust non-fragile controller for asymptotic stability of the offshore steel jacket platform, which is different from other existing literature, has been developed in this paper.

5 Numerical simulations

In this section, a numerical example is given to demonstrate the effectiveness of the proposed control scheme. We consider two cases. Case 1 discusses the result of the conventional system, while case 2 deals with the system with random occurring uncertainties.

We consider an offshore steel jacket platforms with the following parameter values: the wave height is 12.19 m, the wave length is 182.88 m, and the depth of the water is 76.2 m. The TMD parameters are $m_T=469.4836\,\hbox {kg},\omega _T=1.8180\,\hbox {rps}, \xi _T=0.15, K_T=1551.5$ and $C_T=256.$ The density of steel is $7730.7 \hbox {kg}/\hbox {m}^3$, the density of water is $1025.6\,\hbox {kg}/\hbox {m}^3,$ the weight of the concrete deck is $6672300 \hbox {N}$ and the current velocity at the water surface is $0.122$ m/s. The natural frequencies of the first two modes of vibration are assumed to be $\varOmega _1=1.818\,\hbox {rps}$ and $\omega _2=10.8683\,\hbox {rps}$, respectively. The structural damping in each mode is assumed to be 0.5 %. The first- and second-mode shape vectors are $\phi _1=-0.003445$ and $\phi _2=0.00344628$ respectively. Based on the above settings, we can obtain matrices A and B as follows:

$$\begin{aligned} A= & {} \left[ \begin{array}{cccccc} 0 &{} 1&{} 0&{} 0&{} 0&{}0 \\ -3.3235 &{} -0.0212 &{} 0.0184 &{} 0.0030 &{} -5.3449 &{} -0.8819\\ 0&{} 0&{} 0 &{} 1&{} 0&{} 0\\ 0.0184&{} 0.0030 &{} -118.1385 &{} -0.1118 &{} 5.3465 &{} 0.8822\\ 0&{}0 &{} 0&{} 0&{} 0&{} 1\\ -0.0114&{} -0.0019 &{} 0.0114 &{} 0.0019 &{} -3.3501 &{} -0.5454 \end{array}\right] \\ B= & {} \left[ \begin{array}{cccccc} 0&0.003445&0&-0.00344628&0&0.00213\end{array}\right] ^T,\\ D= & {} \left[ \begin{array}{cccccc} 0 &{} 1 &{} 0 &{}0 &{} 0 &{} 0\\ 0&{} 0&{} 0&{}1 &{} 0&{} 0\end{array}\right] ^T. \end{aligned}$$

Let the wave frequency to be $1.8$ rps. The nonlinear wave force can be computed as in [8].

Case 1: In this case, we design a non-fragile controller for the given system. By solving the LMIs in Theorem 1, with ${\tau _1=0.3,\ \tau _2=0.5,\ F(t)=0.9\sin (t),}$

$$\begin{aligned} E=\left[ \begin{array}{cccccc} 0&0.15&0&0.15&0&0.15 \end{array}\right] \end{aligned}$$

(44)

and $H{=}diag\{-0.1,\ -0.1,\ -0.1,\ -0.1,\ -0.1,\ -0.1\},$ the following controller gain is obtained

$$\begin{aligned}&K {=} 10^4\times \big [-0.1247\ 0.0345\ 3.8983\ 1.3768 -0.4356 \\&\quad \qquad -0.7681 \big ]. \end{aligned}$$

When the designed control law is applied to the considered system, displacements of three floors of the system and control responses of the system are shown in Fig. 2.

Fig. 2

State and control response of the nominal system

Case 2: In this case, we consider randomly occurring uncertainties which obey certain mutually uncorrelated Bernoulli-distributed white noise sequences. The parameter uncertainties are defined (as follows) and the stochastic variable is defined as $\gamma =0.1$. By solving the LMIs in Theorem 2, with ${\tau _1=0.3,\ \tau _2=0.5,}\$

$$\begin{aligned}&H_1=H_2=diag\{-0.1,\ -0.1,\\&\quad \qquad -0.1,\ -0.1,\ -0.1,\ -0.1\}. \end{aligned}$$

We can obtain the corresponding gain matrix as

$$\begin{aligned}&K=10^5\times \big [ -0.9800\ 0.5673\ 1.4211 \ 2.6547\\&\quad \qquad -0.7213 -0.1072 \big ]. \end{aligned}$$

When the designed control law is applied to the considered system, displacements of three floors of the system and control responses of the system are shown in Fig. 3. In Fig. 4, time evolutions of $\gamma (t)$, which switch between values $0$ to $1$, are in shown.

Fig. 3

State and control response of the uncertain system

Fig. 4

Time evolutions of $\gamma (t)$; $\gamma (t)$ switch from values $0 \ \text{ and } \ 1$ according to their expectations

6 Conclusions

In this paper, we have designed a non-fragile controller for an offshore steel jacket platform with randomly occurring uncertainties. The randomly occurring uncertainties in the underlying offshore structure have been assumed to obey certain mutually uncorrelated Bernoulli-distributed white noise sequences. Based on suitable Lyapunov–Krasovskii functional and the second- order reciprocally convex approach, the sufficient conditions have been derived in terms of LMIs, which guarantee the asymptotic stability of the offshore steel jacket platforms. It has been shown that the design of a proper non-fragile controller is directly accomplished by means of the feasibility of LMIs. Finally, a numerical example is given to ascertain the validity of the proposed results.