1 Introduction

The problem of delayed neural networks has been focused on in the last decades due to their potential applications in various field such as pattern recognition, static image processing, associative memory and combinatorial optimization [1–3]. In such applications, it is of prime importance to ensure that the designed neural network is stable. Therefore, the issue on the stability analysis of neural networks with time delay has received great attention during the past years and a number of remarkable results have been proposed, see for example [4–12].

According to the modeling approaches, the neural networks can be classified into two types, static neural networks and local field neural networks. The former uses the neuron states as basic variables in order to characterize the dynamical evolution rule. In the latter, the local field states of neurons are taken as basic variables. In this regard, the work [13, 14] dealt with the detailed relationship between static neural networks and local field neural networks. The Hopfield neural network is a typical example of the local field neural network. It has modeled a continuous time-dynamical neural networks containing n dynamic neural units (DNUs) by an analog RC (resistance capacitance) network circuit. Further, a time delay was introduced in the above model by Marcus and Westervelt [15] for Hopfield neural networks to describe the dynamics equation

where x=[x 1,…,x n ]T, \(B= \operatorname{diag}(b_{1},\ldots, b_{n})\) with \(b_{i}=\frac{1}{R_{i}C_{i}}\), the n×n irreducible connection matrix A=(a ij ) in which \(a_{ij}=\frac{w_{ij}}{C_{i}}\), σ(x)=[σ 1(x 1),…,σ n (x n )]T and J=[J 1,…,J n ]T with \(J_{i}=\frac{s_{i}}{C_{i}}\) for i,j=1,2,…,n. In practical points of view, Hopfield [16] realized that in hardware implementation, time delays occur due to finite switching speed of the amplifiers. The existence of time delay may take the neural networks to exhibit complex dynamic behavior and thus is one of the main sources leading to instability, oscillation and poor performance [3]. Therefore, the study of dynamical behavior of neural networks with time delays is an active research topic and has received considerable attention in recent years. Some results on the dynamical behavior have been reported for delayed neural networks in [17–20].

For the dynamical behavior analysis of delayed neural networks, there are two types of time-delay analysis, one is delay-independent approach and the other is delay-dependent approach. The former does not include any information on the size of delay while the latter employs such information. For the delay-dependent type, much attention has been paid to reduce conservatism of stability conditions [18–22].

Generally, a neural network is a highly interconnected network with a large number of neurons. Moreover, in modeling complicated nonlinear systems, the connections between neurons are vitally important. However, due to the complexity of high order and large-scale networks [23] only partial information about the neuron states of the key nodes is available in the network output which is not the case in many practical performances. Thus one often needs to estimate the neuron states through available measurements and then utilizes the estimated neuron states to achieve certain design objectives such as system modeling and state feedback control, refer to works [24–32] for various applications. In the recent trends, the state estimation problem has drawn a remarkable research interest and a lot of research issues have emerged [25]. For instance, a recurrent neural network was presented in [33] to model an unknown nonlinear system, and the neuron states were utilized to implement a control law. Recently, the state estimation for static neural networks with time-varying delay was proposed in [34, 35]. Therefore, it is of both theoretical and practical importance to study the state estimation problem of neural networks.

Markovian jump systems were first introduced by Krasovskii and Lidskii [36]. This class of systems is the hybrid systems with two components in the state. The first one refers to the model which is described by a continuous-time finite-state Markovian process, and the second one refers to the state which is represented by a system of differential equations [37]. On the other hand, neural networks in real life often have a phenomenon of information latching. It is recognized that a way of dealing with this information latching problem is to extract finite-state representations (also called modes or clusters). Actually, such a neural network with information latching may have finite modes, and the modes may switch (or jump) from one to another at different times, and the switching (or jumping) between two arbitrarily different mode can be governed by a continuous-time Markov chain [38]. Therefore, many significant results on Markovian jump systems have been reported in the literature [36–43]. Recently, the authors of [44, 45] have proposed the problem of state estimation for neural networks with Markovian jumping parameters. Initially, Ahn [46] has investigated the problem of switched exponential state estimation of neural networks based on passivity theory by employing an augmented Lyapunov–Krasovskii functional, Jensen’s equality and LMI framework. Inspired by this work, in this paper, we have taken into account the problem of state estimation of neural networks with time-varying delay and Markovian jumping parameters based on passivity theory.

Beginning in the early 1970s, the concept of passivity was studied for state representation of nonlinear systems allowing for a more geometric interpretation of notions such as available, stored and dissipated energy in terms of Lyapunov functions. Thus, the passivity framework is a promising approach to the stability analysis of delayed neural networks. As a powerful tool, passivity has played an important role in synchronization [47], fuzzy control [48] and signal processing [49]. During the recent years, although a number of research activities have been concerned with the problem of passivity analysis of neural networks [50–54], only little attention has been paid to the problem of state estimation of delayed neural networks by using passivity theory [46]. This motivates us to carry out this work.

Based on the above discussions, in this paper, we propose a new state estimator for neural networks with time-varying delays and Markovian jumping parameters based on passivity theory. By constructing a new Lyapunov–Krasovskii functional and employing some analysis techniques, sufficient conditions for the network are derived in terms of LMIs, which can be easily calculated by MATLAB LMI control toolbox. A numerical example is given to illustrate the effectiveness of the proposed method.

Notation

Throughout this paper, ℝn and ℝn×n denote, respectively, the n-dimensional Euclidean space and the set of all n×n real matrices. The superscript T denotes the transposition and the notation X≥Y (respectively, X>Y), where X and Y are symmetric matrices, means that X−Y is positive semi-definite (respectively, positive definite). I n is the n×n identity matrix. |⋅| is the Euclidean norm in ℝn. \(\operatorname{diag}\{\cdots\}\) stands for a block diagonal matrix. Moreover, let \((\varOmega,{\mathcal{F}},{\mathcal{P}})\) be a complete probability space with a filtration \(\{\mathcal{F}_{t}\}_{t\geq0}\) satisfying the usual conditions. That is the filtration contains all \({\mathcal{P}}\)-null sets and is right continuous. The notation ∗ always denotes the symmetric block in one symmetric matrix. Sometimes, arguments of a function or a matrix will be omitted in the analysis when no confusion can arise.

2 Problem description and preliminaries

Consider the neural network with time-varying delays described by

(1)
(2)

where x(t)=[x 1(t),x 2(t),…,x n (t)]T∈ℝn is the state vector of the neural networks, y(t)=[y 1(t),y 2(t),…,y m (t)]T∈ℝm is the output of the networks, \(A= \operatorname{diag}(a_{1}, a_{2},\ldots, a_{n})\) is a diagonal matrix with positive entries a ı >0, B=(b ıȷ ) n×n and W=(w ıȷ ) n×n denote, respectively, the connection weight matrix and the delayed connection weight matrix, g(x(t))=[g 1(x 1(t)),g 2(x 1(t)),…,g n (x n (t))]T denotes the neuron activation, C, D are known constant matrices with appropriate dimensions, and J(t)=[J 1(t),J 2(t),…,J n (t)]T is an external input vector.

Assumption (A)

The neuron activation function g(⋅) is bounded and there exist two constant matrices \(\varphi^{-}=\operatorname{diag}\{\varphi_{1}^{-}, \varphi_{2}^{-}, \ldots, \varphi_{n}^{-}\}\), \(\varphi^{+}=\operatorname{diag}\{\varphi_{1}^{+}, \varphi_{2}^{+}, \ldots, \varphi_{n}^{+}\}\), such that

$$ \varphi_{l}^{-} \leq \frac{g_{l}(a)-g_{l}(b)}{a-b} \leq \varphi_{l}^{+}, $$
(3)

for all a,b∈ℝ, a≠b, l=1,2,…,n.

Also, the time-varying delays τ(t) satisfy

$$ 0 \leq\tau(t) \leq\bar{\tau}, \quad\dot{\tau}(t) \leq \mu, $$

where \(\bar{\tau}\) and μ are constants.

As discussed in the previous section, delayed neural networks with Markovian jumping parameters are more appropriate to describe a class of neural networks with finite-state representation, where the network dynamics can switch from one to another with the switch law being a Markov law. In this regard, we now introduce the Markovian jumping neural networks with time-varying delays. Let {r(t),t≥0} be a right-continuous Markov process on the probability space which takes values in the finite space S={1,2,…,N} with generator Γ=(γ ij )(i,j∈S) given by

(4)

where Δ>0, \(\lim_{\Delta t \rightarrow0}(\frac{o(\Delta )}{\Delta})=0\) and γ ij is transition rate from mode i to mode j satisfying γ ij ≥0 for i≠j with \(\gamma_{ii}=-\sum_{j=1, j \neq i}^{N}\gamma_{ij},i,j \in{S}\).

In this paper, we will focus on the following delayed neural networks with Markovian jumping parameters:

(5)
(6)

It should be noted that the Markov process {r(t),t≥0} takes values in the finite space S={1,2,…,N}. For notation simplicity, we denote

The main objective of this paper is to develop state estimator for neural networks with Markovian jumping parameters (5)–(6) as follows:

(7)
(8)

where \(\hat{x}(t)\) is the estimation of the neuron state, \(\hat{y}(t)\) is the output vector of the state estimator, u(t) is the control input vector, K i is the estimation gain matrix, and G i , F i are known constant matrices.

Define the estimation error \(e(t)=x(t)-\hat{x}(t)\) and the output error \(\tilde{y}(t)=y(t)-\hat{y}(t)\). Then the error-state system can be expressed by

(9)
(10)

where \(\varphi(t)=g(x(t))-g(\hat{x}(t))\).

From Assumption (A), we easily obtain the following inequalities:

The main purpose of this paper is to design a state estimator with Markovian jumping parameter (7)–(8) for the estimation of the state vector x(t) based on passivity theory.

Next, the passivity condition for the estimation error system (9)–(10) is given in the following definition.

Definition 2.1

The estimation error system (9)–(10) is called passive if it satisfies the following passivity inequality:

where β is a nonnegative constant and Φ(e(s)) is a positive semi-definite storage function.

We end this section with the following lemmas, which are useful in proving the main results.

Lemma 2.2

(Schur complement)

Given constant matrices Ω 1, Ω 2 and Ω 3 with appropriate dimensions, where \(\varOmega_{1}^{T}=\varOmega_{1}\) and \(\varOmega_{2}^{T}=\varOmega_{2}>0\), then

$$ \varOmega_{1}+\varOmega_{3}^{T} \varOmega_{2}^{-1}\varOmega_{3}<0 $$

if and only if

$$ \left [ \begin{array} {c@{\quad}c}\varOmega_{1} & \varOmega_{3}^{T} \\ \ast& -\varOmega_{2} \end{array} \right ]<0, \quad \mathrm{or} \quad \left [ \begin{array} {c@{\quad}c} -\varOmega_{2} & \varOmega_{3} \\ \ast & \varOmega_{1} \end{array} \right ] < 0. $$

Lemma 2.3

(Jensen inequality)

For any n×n constant matrix M>0, any scalars a and b with a<b and a vector function x(t):[a,b]⟶ℝn such that integrations concerned are well defined, then the following inequality holds:

3 Main results

This section is devoted to develop a passivity-based approach dealing with the state estimation problem for delayed neural networks with Markovian jumping parameter. A delay-dependent condition is derived such that the resulting estimation error system (9) is passive and asymptotically stable in the mean square.

We shall establish our main results based on LMI framework. For representation convenience, the following notations are introduced:

Theorem 3.1

Assume that there exist matrices \(P_{i}=P_{i}^{T}>0\), \(R_{1}=R_{1}^{T}>0\), \(R_{2}=R_{2}^{T}>0\), \(Q_{1}=Q_{1}^{T}>0\), Q 2, \(Q_{3}=Q_{3}^{T}>0\), \(U_{1}=U_{1}^{T}>0\), \(U_{2}=U_{2}^{T}>0\), S=S T>0, \(S_{1}=S^{T}_{1}>0 \), any matrices N 1,N 2,N 3,V,X i and diagonal matrices L 1>0 and L 2>0 such that the following LMIs are feasible:

(11)
(12)

Then, the estimation error system (9)–(10) is passive from the control input u(t) to the output error \(\tilde{y}(t)\) and the gain matrix of the state estimator (7)–(8) is given by \(K_{i}=P_{i}^{-1}X_{i}\).

Here,

$$ \tilde{\varXi}_{i}= (\tilde{\varXi}_{k,l,i}), \quad k,l=1,2, \ldots,10 $$

with

Proof

Consider the Lyapunov–Krasovskii functional as follows:

(13)

where \(\eta(t)=[e^{T}(t) \ \ \dot{e}^{T}(t) ]^{T}\).

Let \(\mathbb{L}\) be the weak infinitesimal generator of random process {e(t),r(t),t≥0}.

We obtain

(14)

From Lemma 2.3, we have

(15)
(16)

It is noted that

By Lemma 2.3, it follows that

(17)

It is clear from [55, 56] that

(18)

which implies that

(19)

Then, we get

(20)

Note that when τ(t)=0 or \(\tau(t)=\bar{\tau}\), we have β 1(t)=0 or β 2(t)=0, respectively, and thus (20) still holds. It is clear that (20) implies

(21)

where

For positive diagonal matrices L 1 and L 2, we get from Assumption (A) that

(22)
(23)

The following two zero equations with any matrices N 1,N 2, and N 3 are chosen:

(24)
(25)
(26)

Here, we have

where

Using (15)–(21) in (14), subtracting (22)–(23) from (14) and adding (24)–(26) with (14), we have

(27)

where

$$ \varXi_{i}= (\varXi_{k,l,i}), \quad k,l=1,2,\ldots,10 $$

with

Now,

where

$$ \check{\varXi}_{i}= \varXi_{i}+\operatorname{diag} \{S_{1},0,0,0,0,0,0,0,0,0\}. $$

If

$$ \check{\varXi}_{i}+\frac{1}{2}\bar{ \tau}^{2}NS^{-1}N^{T}< 0, $$
(28)

then we have

(29)

Taking expectation on both sides of (29) and integrating from 0 to t and then applying Dynkin’s formula, we have

Let \(\beta=\mathbb{E}[V(0)]\). Since \(\mathbb{E}[V(t)]\geq0\), we have

which is equivalent to the passivity condition given in Definition 2.1. This yields the result that the estimation error system (9)–(10) is passive from the control input u(t) to the output error \(\tilde{y}(t)\) under the state estimator (7)–(8).

Applying Lemma 2.2, the inequality (28) is equivalent to

(30)

Letting X i =P i K i gives the result that the inequality (30) is equivalent to the LMI (12). Then the gain matrix of the state estimator is given by \(K_{i}=P_{i}^{-1}X_{i}\). Hence the proof is completed. □

Remark 3.2

Switched exponential state estimation of neural networks based on passivity theory was proposed in [46]. However, the state estimation of neural networks with time-varying delays and Markovian jumping parameter has not been considered yet in the literature. Based on the new Lyapunov–Krasovskii functional with triple integral terms and some integral inequalities, a new delay-dependent stability criterion for state estimator design of the network with time-varying delays and Markovian jumping parameter is established for the first time. Further, when the control input u(t) is zero, then from Theorem 3.1 we can easily show that the error system (9)–(10) is asymptotically stable in the mean square.

Remark 3.3

The literature for the state estimation [32, 46] proposed conditions which is only for the constant delays. However, we derived the stability conditions for time-varying delays, it contributes more than ones in the literature [32, 46]. In addition, it should be pointed out the traditional assumptions on the boundedness and monotonicity have been removed in this paper.

Remark 3.4

In hardware implementation of neural networks, stochastic disturbances are inevitable due to thermal noise in electronic devices. However, the stochastic disturbance on the state estimation of neural networks have not yet been considered in the previous existing literature [29–31]. In future work, we will design the state estimation of neural networks with stochastic perturbations to take this realistic problem into account.

Now, we will investigate a delay-dependent stability criterion of the following error system without Markovian jumping parameter:

(31)
(32)

For system (31) and (32), we have the following result.

Corollary 3.5

Assume that there exist matrices P=P T>0, \(R_{1}=R_{1}^{T}>0\), \(R_{2}=R_{2}^{T}>0\), \(Q_{1}=Q_{1}^{T}>0\), Q 2, \(Q_{3}=Q_{3}^{T}>0\), \(U_{1}=U_{1}^{T}>0\), \(U_{2}=U_{2}^{T}>0\), S=S T>0, \(S_{1}=S^{T}_{1}>0 \), any matrices N 1,N 2,N 3,V,X and diagonal matrices L 1>0 and L 2>0 such that the following LMIs hold:

(33)
(34)

Then the estimation error system (31)–(32) is passive from the control input u(t) to the output error \(\tilde{y}(t)\) and the gain matrix of the state estimator is given by K=P −1 X.

Here,

$$ \varOmega= (\varOmega_{k,l}), \quad k,l=1,2,\ldots,10 $$

with

Proof

The remaining proof is similar to that of Theorem 3.1 and is thus omitted. □

When there is no control input, that is, u(t)=0 for the neural network (5)–(6) with Markovian jumping parameters, the corresponding state estimator can be described as follows:

(35)
(36)

Accordingly, we get the following error system for (35)–(36):

(37)

Now, the stability results for the above system (37) can be summarized in the following corollary.

Corollary 3.6

For given scalars \(\bar{\tau}\) and μ<∞, error dynamics (37) is globally asymptotically stable in mean square if there exist matrices \(P_{i}=P_{i}^{T}>0\), \(R_{1}=R_{1}^{T}>0\), \(R_{2}=R_{2}^{T}>0\), \(Q_{1}=Q_{1}^{T}>0\), Q 2, \(Q_{3}=Q_{3}^{T}>0\), \(U_{1}=U_{1}^{T}>0\), \(U_{2}=U_{2}^{T}>0\), S=S T>0, any matrices N 1,N 2,N 3,V,X i and positive diagonal matrices L 1 and L 2 such that the following LMIs hold:

(38)
(39)

with

and the other entries of Π i are 0.

Moreover, the gain matrix of state estimator is given by

Proof

Taking u(t)=0 and following the similar argument as in the proof of Theorem 3.1, we obtain the following inequality from (27):

(40)

where

Taking the mathematical expectation on both sides of (40) and proceeding as in Theorem 3.1, it is concluded that the error dynamics (37) is globally asymptotically stable in the mean square. □

Remark 3.7

It is well known that Lyapunov function theory is the most general and useful approach for studying stability of various control systems. However, it can be found that the existing Lyapunov functional introduced in the available literature only contains some integral terms such as \(\int_{t-\tau}^{t} e^{T}(s)Qe(s)\,ds\) and some double integral terms such as \(\int_{-\tau }^{0}\int_{t+\theta}^{t}\dot{e}^{T}(s) Z\dot{e}(s)\,ds\,d\theta\) (see for example [26–31]). In this paper, we considered a new form of the Lyapunov functional that contains triple integral term such as \(\int_{-\bar{\tau}}^{0}\int_{\theta}^{0}\int_{t+\lambda}^{t}\dot{e}^{T}(s) S\dot{e}(s)\,ds\,d\lambda \,d\theta\) which play an important role in further reduction of conservatism.

Remark 3.8

In this paper, the stability for the error dynamics (9)–(10) is derived without any uncertainties. However, it is easy to extend to the system with both parameter norm bounded uncertainties and linear fractional uncertainties.

4 Numerical example

In this section, we will give a numerical example showing the effectiveness of established theoretical results.

Consider the following neural networks with Markovian jumping parameters and time-varying delay:

where

Let the activation function be \(g(x(t))=\frac{1}{5} [|x(t)+1|-|x(t)-1| ]\) and then, Assumption (A) yields ϕ −=−0.5I,ϕ +=0.4I. Thus, we get the following parameters:

We assume τ=0.5,μ=0.3. By using the MATLAB LMI control Toolbox to solve the LMIs in Theorem 3.1, we obtain following feasible solutions matrices

and the corresponding filter gain matrix as follows:

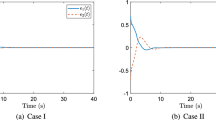
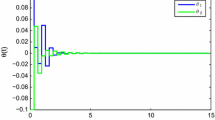
This implies that the error system (9)–(10) with the above given parameters is passive in the sense of Definition 2.1. The responses of error dynamics (9)–(10) which converges to zero with the gain K can be seen from Fig. 1 when u(t)=0.

Fig. 1
figure 1

State trajectories

Full size image

5 Conclusions

In this paper, the state estimation problem is addressed for neural networks with time-varying delays, and Markovian jumping parameter based on passivity theory. By the proposed method, it has been shown that the estimation error system is asymptotically stable in the mean square and passive from the control input to the output error. The gain matrix of the proposed state estimator has been determined by solving the LMI problem. Based on some integral inequalities and a new Lyapunov–Krasovskii functional containing triple integral terms, new delay-dependent stability criteria for designing a state estimator of the considered neural networks have been established in terms of LMIs. The effectiveness of the proposed criteria is demonstrated through a numerical example with simulation results. We would like to point out that it is possible to extend our main results to more general complex dynamical network with mixed time delays and randomly occurring uncertainties by using a delay partitioning approach and the corresponding results will appear in the near future.