1 Introduction

Symmetries and conserved quantities which are of considerable theoretical significance have made great developments in recent years [1–8]. Mei symmetry is a new kind of symmetry proposed by Mei [5] in 2000. It is different from the Noether symmetry [1] and Lie symmetry [2, 3], with which we are familiar. The Noether symmetry is an invariance of the Hamiltonian action functional under infinitesimal transformation groups of time and coordinates. The Lie symmetry is an invariance of the motion of differential equations under infinitesimal transformation groups. For Mei symmetry, the definition has two expressions. The first type is that Mei symmetry is the form of the differential equations of motion of systems keeping invariance under infinitesimal transformation groups [9]. The second is that Mei symmetry is an invariance of the dynamical functions of differential equations of motion of systems under infinitesimal transformation groups [10]. A series of important results have been obtained on the study of the Mei symmetries and the conserved quantities for mechanical systems [4–7, 9–13]. Mei symmetry is one of the most important methods of solving practical problems by obtaining the first integrals from a certain kind of symmetries of systems.

Symmetries are intrinsic and fundamental features of the differential equations of mathematical physics, and symmetries are also the basis of modeling a given mechanical system of differential equations with the use of difference equations and meshes. This is one of the sources of the interest in continuous symmetries of discrete equations [14]. Cadzow [15] proposed a discrete variational principle and obtained discrete Euler–Lagrange equation in 1970. Three years later, Logan [16] constructed the first integrals of discrete Euler–Lagrange equation by studying the invariance of discrete Lagrangian, which is called the discrete Noether theorem. Levi and Winternitz [17–19] proposed approaches on the applications of Lie group theory to difference equations and discrete mechanical systems, in which the Lie group transformations act on the equation but not on the lattice. Dorodnitsyn [20, 21] gave a different approach by which the Lie group transformations act both on the difference equations and the lattice. Based on these two philosophies, several authors [22–26] generalized these theories to many kinds of mechanical systems. However, there are many evolution equations without appropriate or natural Lagrangian formulation. For these equations one may prefer to use the Hamiltonian viewpoint. The Hamiltonian dynamics systems are widespread in modern physics, engineering science, and nonlinear science, and have been thoroughly developed recently [27–31]. Studies on the Hamiltonian difference system are to be considered. Ahlbrandt [32] studied the equivalence of discrete Euler equations and discrete Hamiltonian systems. Chen et al. [33] used the total variation in Hamiltonian formalism and symplectic-energy integrators. Zhang et al. [34] obtained the discrete variational principle in Hamiltonian formalisms and first integrals. Lall and West [35] constructed the discrete variational Hamiltonian mechanics. Dorodnitsyn and Kozlov [36, 37] developed a similar mathematical formalism for discrete Hamiltonian equations. They considered the relation between symmetries and first integrals for the systems. Wang et al. [38] gave the discrete version of Noether’s identity and the forms of Noether conserved quantity of the non-conservative and nonholonomic Hamiltonian system. However, the applications of Mei symmetries to non-conservative Hamiltonian difference systems with irregular lattice have not been investigated. In this paper, we apply the second definition of Mei symmetries to the non-conservative Hamiltonian systems and combine to the two discrete approaches of Levi [17–19] and Dorodnitsyn [20, 21].

This article is organized as follows. In Sect. 2, we give the equations of motion of the non-conservative Hamiltonian systems. In Sect. 3 we consider the Lie group transformations acting both on the difference equations and on the lattice, obtain the determining equations of Mei symmetries, and construct the discrete version of Noether conserved quantity for the systems. In Sect. 5 we draw the conclusion of the present paper and give some problems for future research after an illustrated example being presented in Sect. 4.

2 Hamiltonian difference equations and energy equations of the systems

Lagrangian mechanics provides a description of motion of a mechanical system constrained on a configuration space. We are familiar with the language of Lagrangian formulation of most mechanical systems. There are evolution equations without appropriate or natural Lagrangian formulation of some kinds of mechanical systems. Because of that, one may prefer another point of view to describe some mechanical systems: the Hamiltonian. For the non-conservative Hamiltonian systems, the equations of motion of the systems will be obtained on the basis of the Lagrangian type. We consider a mechanical system whose configuration is determined by n generalized coordinates q i (i=1,…,n). The differential equations of motion of the system can be written in the form [39]:

$$ \frac{\mathrm {d}}{\mathrm {d}t}\frac{\partial L}{\partial \dot{q}_{i}} - \frac{\partial L}{\partial q_{i}} = Q_{i} \quad (i = 1, \ldots,n), $$
(1)

where \(L = L(t,q_{i},\dot{q}_{i})\) is the Lagrangian, \(Q_{i} = Q_{i}(t,q_{i},\dot{q}_{i})\) are the non-potential generalized forces, and the repeated subscripts represent the summation.

Introducing the generalized momentum and Hamiltonian function

$$ p_{i} = \frac{\partial L}{\partial \dot{q}_{i}}, \qquad H = p_{i} \dot{q}_{i} - L $$
(2)

and the canonical form of Eq. (1) in phase space is

$$ \dot{q}_{i} = \frac{\partial H}{\partial p_{i}}, \qquad \dot{p}_{i} = -\frac{\partial H}{\partial q_{i}} + \overline{Q}_{i}, $$
(3)

where \(\overline{Q}_{i}\) are the non-potential generalized forces as functions of t, q i and p i .

We first introduce the transformation operators in the space of discrete Hamiltonians, and then obtain the discrete Hamiltonian equations and energy equations of the systems on the basis of the discretization theory of Eq. (3).

We consider the space z of sequences (t,q,p), and denote by D the first-order linear discrete operator

$$ D = \frac{\partial}{\partial t} + \dot{q}_{i}\frac{\partial}{\partial q_{i}} + \dot{p}_{i}\frac{\partial}{\partial p_{i}} + \cdots. $$
(4)

We fix arbitrary parameter value h>0, and we form a pair of the operators of discrete transformation to the right and left:

$$ \everymath{\displaystyle }\begin{array}{@{}l} S_{ + h} = e^{hD} = \sum_{i = 0}^{\infty} \frac{h^{i}}{s!} D^{i},\\ \noalign {\vspace {5pt}} S_{ - h} = e^{ - hD} = \sum_{i =0}^{\infty} \frac{( - h)^{i}}{s!} D^{i}, \end{array} $$
(5)

where D is a derivation in z. The operators S +h and S −h commute with each other and satisfy S +h S −h =S −h S +h =1.

Using S +h and S −h , we define a pair of left and right discrete (finite-difference) differentiation operators by setting

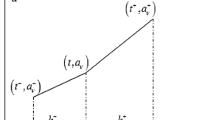
$$ \everymath{\displaystyle }\begin{array}{@{}l} D_{ - h} = \frac{1 - S_{ - h}}{h} = \sum_{i = 1}^{\infty} \frac{h^{i - 1}}{s!} D^{i}, \\ \noalign {\vspace {5pt}} D_{ + h} = \frac{S_{ + h} - 1}{h} = \sum_{i = 1}^{\infty} \frac{( - h)^{i - 1}}{s!} D^{i}. \end{array} $$
(6)

The operators S +h ,S −h ,D +h and D −h commute in any combination, while D +h =D −h S +h ,D −h =D +h S −h . Consider Hamiltonian difference equations at some lattice points (t,q,p). Generally, the lattice is irregular. The notation is given in Fig. 1.

Fig. 1
figure 1

Elementary schematic for a three-point difference equation

Full size image

The regular lattice is with the same invariance meshes in the t-direction. Now the irregular lattices are considered. The method of introducing shift operators and the corresponding discrete differentiation operators is identical to that of regular lattice. The expressions are also the same as in Eqs. (5) and (6). But different results appear while they are applied to variables. For regular lattice,

(7)
(8)

For irregular lattice,

(9)
(10)

Now we consider non-conservative Hamiltonian difference equation at some lattice points (t,q,p). Suppose we have an n-dimensional configuration manifold q={q 1,…,q n },p={p 1,…,p n } and Hamiltonian discrete function H=H(t,t +,q,p +). Hamiltonian equations can be obtained by the variational principle from the finite-difference functional Hamiltonian action

(11)

and

(12)

where is the discrete force, δq i is the discrete virtual placement satisfying

$$ \delta q_{i} = \Delta q_{i} - \frac{q_{i}^{ +} - q_{i}}{h^{ +}} \Delta t. $$
(13)

The variation of the function H h along a curve q i =ϕ i (t), p i =ψ i (t) at some point (t,q,p) will affect only two terms of the sum (11):

(14)

So

(15)

Substituting Eq. (13) into Eq. (15), we obtain

(16)

With the help of Eq. (14), we obtained the expression

(17)

where H=H(t,t +,q,p +) and H −=H −(t −,t,q −,p).

For the stationary value of the discrete Hamiltonian action (12), the systems of 2n+1 equations can be derived:

(18)
(19)
(20)

According to the total left shift and right shift operators and the discrete derivation operators, the expressions (18)–(20) can be written as

(21)
(22)
(23)

Note that the first 2n equations (Eqs. (21) and (22)) are the first-order difference equations, which are the generalized non-conservative canonical Hamiltonian difference equations. Equation (23), which is the energy equation, is of the second order, and it defines the lattice on which the non-conservative canonical Hamiltonian equations are discretized. The above results are built upon the continuous canonical non-conservative Hamiltonian equations, but in the continuous limit, the lattice equation disappears. Equations (21)–(23) require the discrete equations of non-conservative Hamiltonian systems.

3 Noether conserved quantities and Mei symmetries

3.1 Mei symmetries of equations of non-conservative Hamiltonian difference systems

For dynamical systems, Mei gives a modern method of searching conserved quantities. It is the form invariance (Mei symmetry) which has very important practical significance in mathematics, mechanics and physics. Mei symmetry is an invariance of the differential equation satisfied by physical quantities such as Lagrangian, non-potential generalized forces and generalized constrained forces under the infinitesimal transformation of time and generalized coordinates. On the basis of Mei’s theory, we generalize Mei symmetry to the discrete non-conservative Hamiltonian equations and try to obtain some useful conserved quantities. We introduce the infinitesimal transformations with respect to time, generalized coordinates, and generalized momentum as

(24)

where ε is a small parameter. The infinitesimal generators ξ,η i and ζ i constitute the Lie group of the infinitesimal transformations. The Lie group is completely defined by the operators

(25)

where q={q 1,…,q n } and p={p 1,…,p n }. To consider difference equations, we need three points of a lattice. Prolongation of the Lie group operator (25) for left (t −,q −,p −) and right points (t +,q +,p +) is as follows [40]:

(26)

where ξ −=ξ(t −,q −,p −), , , ξ +=ξ(t +,q +,p +), and .

In this paper we define the symmetries as in Eq. (24); Lie point transformations act simultaneously in difference equations (21), (22) and lattice equation (23). The fact is that the lattice also transforms in the spirit of Dorodnitsyn’s approach to difference equations [20, 21].

Under the transformations (24) defined by the operators (26), the function H becomes H ∗=H(t ∗,t +∗,q ∗,p +∗), H − becomes H −∗=H −(t −∗,t ∗,q −∗,p ∗), and \(\bar{Q}_{i}\) becomes . For non-conservative Hamiltonian difference systems, if the functions H, H − and \(\bar{Q}_{i}\) are replaced by the transformed functions H ∗, H −∗ and \(\bar{Q}_{i}^{*}\), whereas the form of equations of motion (21)–(23) is invariant, the following definition applies:

Definition

Under the transformations (26), if the form of equations of motion (21)–(23) keeps invariant, i.e.,

(27)
(28)
(29)

then invariance is called the Mei symmetry of the discrete non-conservative Hamiltonian systems.

Expanding functions H ∗, H −∗ and \(\bar{Q}_{i}^{*}\), substituting them into Eqs. (27)–(29) and ignoring higher-order small quantities, together with Eqs. (21)–(23), we can get the determining equation of the Mei symmetry for the systems:

(30)
(31)
(32)

Equations (30)–(32) are thus the determining equations for the generators ξ,η i and ζ i .

Criterion

For the non-conservative Hamiltonian difference systems (21)–(23), if the generators ξ,η i and ζ i satisfy Eqs. (30)–(32), then the symmetry is called the Mei symmetry for the systems.

3.2 Noether conserved quantities associated with the Mei symmetries

Mei symmetries are carried over from the continuous case to discrete one in this paper. One of our main aims is to find first integrals through Mei symmetries of discrete equations because the preservation of first integrals in different fields is of great importance. For different kinds of applied problems, an analogous discrete framework would allow one to construct many schemes with conservation laws. In the following, we state the discrete versions of the theorem associated with the Mei symmetry for the non-conservative mechanical systems.

In the non-conservative Hamiltonian formulation, under certain conditions, the Mei symmetry can have Noether conserved quantity.

Just as in the continuous case, the invariance of non-conservative Hamiltonian difference systems on a specified mesh yields first integrals of the difference systems. Based on Refs. [36, 37], Dorodnitsyn and Kozlov gave the discrete Hamiltonian identity for discrete Hamiltonian equations as follows:

$$ \everymath{\displaystyle }\begin{array}[b]{@{}l@{}} \zeta_{i}^{ +} D_{ + h}(q_{i}) + p_{i}^{ +} D_{ + h}(\eta_{i}) - X(H) \\ \noalign {\vspace {9pt}} \qquad {}- HD_{ + h}(\xi) + D_{ + h}(G_{i}) \\ \noalign {\vspace {8pt}} \quad\equiv\xi \biggl( \!D_{ + h}\bigl(H^{ -} \bigr) - \frac{\partial H}{\partial t} - \frac{h^{ -}}{h^{ +}} \frac{\partial H^{ -}}{\partial t} \biggr) \\ \noalign {\vspace {8pt}} \qquad {}- \eta_{i} \biggl(\! D_{ + h}(p_{i}) + \frac{\!\partial H\!}{\partial q_{i}} \biggr) + \zeta_{i}^{ +} \biggl( \!D_{ + h}(q_{i}) - \frac{\partial H}{\!\partial p_{i}^{ +}\!} \biggr) \\ \noalign {\vspace {8pt}} \qquad {} + D_{ + h} \biggl( \eta_{i}p_{i} - \xi\biggl(H^{ -} + h^{ -}\frac{\partial H^{ -}}{\partial t}\biggr) + G_{i} \biggr).\\ \noalign {\vspace {8pt}} \end{array} $$
(33)

Similarly we get the discrete Hamiltonian identity for discrete non-conservative Hamiltonian:

$$ \everymath{\displaystyle }\begin{array}[b]{@{}l@{}} \zeta_{i}^{ +} D_{ + h}(q_{i}) + p_{i}^{ +} D_{ + h}(\eta_{i}) -X(H) - HD_{ + h}(\xi) \\ \noalign {\vspace {8pt}} \qquad {}+ \bar{Q}_{i}\bigl[ \eta_{i} - D_{ + h}(q_{i})\xi \bigr] +D_{ + h}(G_{i}) \\ \noalign {\vspace {6pt}} \quad\equiv\xi \biggl( D_{ + h}\bigl(H^{ -} \bigr) - \frac{\partial H}{\partial t} - \frac{h^{ -}}{h^{ +}} \frac{\partial H^{ -}}{\partial t} - \bar{Q}_{i}D_{ + h}(q_{i}) \biggr) \\ \noalign {\vspace {6pt}} \qquad {} - \eta_{i} \biggl(D_{ + h}(p_{i}) + \frac{\partial H}{\partial q_{i}} - \bar{Q}_{i} \biggr) \\ \noalign {\vspace {6pt}} \qquad {}+ \zeta_{i}^{ +} \biggl( D_{ + h}(q_{i}) - \frac{\partial H}{\partial p_{i}^{ +}} \biggr) + D_{ + h}\biggl(\eta^{i}p_{i} \\ \noalign {\vspace {6pt}} \qquad {} - \xi\biggl(H^{ -} + h^{ -} \frac{\partial H^{ -}}{\partial t}\biggr) + G_{i} \biggr). \\ \noalign {\vspace {6pt}} \end{array} $$
(34)

The method is identical to that in Dorodnitsyn and Kozlov’s [36, 37] paper and we will not reproduce it here. If the left-hand side of Eq. (34) equals zero, i.e.

(35)

then it is called the discrete version of generalized Noether-type identity for the systems. If the right-hand side of Eq. (34) equals zero, when there exist some other equations,

(36)
(37)
(38)

which are called the generalized quasi-extremal equations for this non-conservative Hamiltonian systems, then the systems possess the discrete version of conservation law:

$$ D_{ + h}\biggl( \eta_{i}p_{i} - \xi\biggl(H^{ -} + h^{ -} \frac{\partial H^{ -}}{\partial t}\biggr) + G_{i} \biggr) = 0, $$
(39)

namely

$$ I = \eta_{i}p_{i} - \xi\biggl(H^{ -} + h^{ -} \frac{\partial H^{ -}}{ \partial t}\biggr) + G_{i} = \mathrm{const}. $$
(40)

The discrete equations (40) are called the difference version of Noether conservation laws associated with a non-conservative Hamiltonian difference system.

Theorem

If a discrete gauge function G i =G i (t,t +,q,p +) exists such that the infinitesimal transformation generators ξ,η i ,ζ i or the symmetry operators X satisfy the discrete Noether identity (35), then the non-conservative Hamiltonian systems (21)–(23) possess the discrete conserved quantities (40).

This theorem is the difference version of generalized Noether theorem associated with non-conservative Hamiltonian systems.

4 An example

We give an example to illustrate how Mei symmetry of non-conservative Hamiltonian systems can be reduced and how to obtain conservation laws of the systems. The dynamical system with Hamiltonian and the non-conservative force are, respectively,

(41)
(42)

The Hamiltonian equations and the lattice can be rewritten as

(43)
(44)
(45)

Using the prolongation equation of the Lie group operator for the left and right points, we will check the invariance of the determining equations (30)–(32) of the Mei symmetry for the systems with the operators

$$ X = \frac{\partial}{\partial p_{1}} - \frac{\partial}{\partial p_{2}}. $$
(46)

The operator (46) satisfies the determining equations of Mei symmetries of the non-conservative Hamiltonians. The symmetry (46) is called the Mei symmetry of the discrete non-conservative Hamiltonians.

The symmetry operator (46) fulfills the equations (30)–(32) and the Noether identity (35) with the functions

$$ G = - t^{2}. $$
(47)

Using Eq. (40), we can obtain the discrete version of Noether conserved quantity of the systems:

$$ I = p_{1} - p_{2} - t^{2} = \mathrm{const}. $$
(48)

It should be noted that the Lie symmetries can lead to conserved quantities as well. The determining equations of Lie point symmetry of difference equations and lattices were obtained in Ref. [41]. Similarly, the determining equations of Lie point symmetry of discrete non-conservative Hamiltonian systems are

(49)
(50)

In the present example, the operator \(X = \frac{\partial}{\partial p_{1}} - \frac{\partial}{\partial p_{2}}\) is not satisfied with the determining equation of Lie symmetries. Therefore, it is not the Lie symmetry for the system. However, the operator is satisfied with the determining equations of Mei symmetries. The conserved quantity I=p 1−p 2−t 2 can be obtained when it satisfies the theorem of Sect. 3.2. In short, this symmetry operator is the Mei symmetry, but not the Lie symmetry.

5 Conclusion

In this paper, the Mei symmetries and the Noether’s theorem are proposed for non-conservative Hamiltonian difference systems. The form invariance (the Mei symmetry) of a non-conservative Hamiltonian functional and its relation to first integrals of the systems are introduced. For Mei symmetries of non-conservative Hamiltonian, the determining equations (30)–(32) and Noether identity (35) are sufficient conditions of getting Noether conserved quantities (40). One needs to have the appropriate Lie group operators to satisfy them, as well as make sure the Noether conserved quantities are nontrivial, the operators of Mei symmetry for the systems are of significance. That is why not every infinitesimal transformation of Mei symmetry of the non-conservative Hamiltonian equations can provide a conserved quantity.

The present approach might also be extended on the Hamiltonian systems with nonholonomic constraints. The Appell–Chetaev condition and restriction equations should be considered. So it is harder to find the infinitesimal generators and the regular functions to obtain conserved quantities than the non-conservative Hamiltonian systems.