1 Introduction

In recent years, there has been a rapidly growing interest in using teams of mobile robots for automatically covering unknown environments. This interest is mainly motivated by the broad spectrum of potential civilian and military applications of multi-robot surveillance systems. Triggered by this interest, today automated surveillance is a well established topic in multi-robot research which is considered to be of particular practical relevance. Currently, available theoretical and algorithmic approaches to multi-robot coverage are typically based on unrealistic assumptions. Examples of such unrealistic assumptions are idealized sensors/actuators or sensors with infinite range [1], convexity and/or stationarity of the environment [2], and the availability of unlimited communication bandwidth or direct communication links [3]. For these reasons, there is a strong need for robust coverage methods which can adapt to environmental changes, computation limitations, and measurement noises.

The proposed robust coverage approach in this article, addresses this need and wants to explore a novel perspective on covering dynamically changing environments which is based on an established control principle known as robust control technique. According to this principle, the coverage strategy is robust to measurement noises and environmental disturbances. In addition, this control technique can cover dynamically changing environments as well.

Such robust control techniques has been founded to be an effective solution to treat robust stabilization and tracking problems, in presence of external disturbances and system uncertainties [4–10]. In the traditional H ∞ control the exact model of the system must be known. However in order to propose a robust control method, an integration between this robust scheme with fuzzy logic approximators can propose effective controllers for uncertain dynamic models [11, 12].

In this research, coverage of a dynamic environment is considered as the main goal and based on the work of Pimenta et al. in [13] a simple coverage controller is defined to guide the robots through their Voronoi centroids. After adopting unknown coverage error dynamics to each 2-DOF robot, inspired by the work of Ranjbar-Sahraei et al. in [14], an adaptive fuzzy approximator is combined with H ∞ robust control technique to propose a novel adaptive fuzzy coverage control methodology, with robust characteristics. The main advantage of this control strategy is insensitivity to measurement noises and no need to high computational efforts, where to the best of authors’ knowledge, no robust control design of this form has been reported before to address such a problem in multi-robot systems.

The rest of this paper is organized as follows: In Sect. 2, we review former research related to the problem at hand, and a background on coverage control preliminaries is presented. Problem formulation and design of robust control technique are discussed in Sect. 3. Stability of the robust control technique is proved in Sect. 4. Finally, simulation results are included in Sect. 5 and concluding remarks are provided in Sect. 6.

2 Coverage control background

Distributed coverage control of networked robots have attracted remarkable attention from the mathematics and robotics community. Butler and Rus first developed a set of algorithms based on Voronoi diagrams of the sensor positions that enable the sensors to maintain coverage of their environment [15]. In [16], decentralized coverage algorithms which are adaptable to changes in the environment and provably convergent are addressed carefully and in [2, 17], sensory information is propagated from every robot throughout the network, for driving the network to an optimal sensing configuration. However, all of these decentralized algorithms require a group of robots with the capability of direct communication and mathematical computations. There are also a number of other notions for multi-robot surveillance [18, 19], which are presented based on Graph theory and unrealistic assumptions (e.g. ideal sensors, convex environment, etc.).

The major goal in this study is to solve a swarm coverage control problem (i.e. proper deployment of robots for monitoring some quantity of interest over an environment). One of the effective solutions for this problem is locational optimization of a cost function designed based on the Voronoi diagrams concept. This optimization guides the robots through continuous smooth paths in order to form the desired deployment. Such a cost function design has been discussed in various papers (e.g. [17, 20–23]).

In this section, we will explain a simple cost function design for solving the coverage control problem of a group of N robots in a convex region Q∈R 2, where dynamics of the ith robot is considered as

$$ \dot{z}_{i} = u_{i},$$
(1)

in which, z i ∈ℝ2 is the coordinate matrix (for a robot with 2-DOF) and u i ∈ℝ2 denotes the control inputs.

To propose the proper control law for the ith robot, we define the Voronoi region of ith robot as

$$V_i= \{q\in Q |\ \|q-z_i\|\leq\|q-z_j\|,\forall j \neq i \},$$

the sensory function is defined as a scalar function ϕ(.):Q→ℝ+, and the unreliability of the sensor measurement is denoted by \(\frac{1}{2}\|q-z_{i}\|^{2}\) (∥.∥ denotes the l 2-norm). Now, the cost function can be represented by

$$ H(Z) = \sum _{i=1}^{N}\int_{V_i} \frac{1}{2} \|q-z_i\|^2\phi(q)\,dq,$$
(2)

where Z={z 1,…,z 2} denotes the set of all robot coordinates.

Minimization of the cost function defined in (2) will conclude to an optimal deployment of robotic swarm. This optimization is due to the minimization of both unreliability and sensory information.

To propose a solution for optimization of this swarm coverage control problem, based on the gradient method, the steepest descent direction for the ith robot motion [2] is chosen as

(3)

where \(M_{V_{i}}\), \(L_{V_{i}}\), and \(C_{V_{i}}\) are the mass, first mass-moment and centroid of V i respectively, defined as

(4)
(5)
(6)

Note that \(M_{V_{i}}> 0, \forall V_{i}\neq\{\emptyset\}\).

Based on (3), the solution for minimization of H is a deployment such that \(z_{i}= C_{V_{i}}, \forall i\) (i.e. each robot is deployed at the centroid of its Voronoi region).

Therefore, the control is designed to drive each robot to what is called a centroidal Voronoi configuration:

(7)

It is intuitively clear that the simple controller (7) can satisfy the centroidal Voronoi configuration for a massless robot with dynamic model of (1). However, in practice, a static coverage control strategy (7) is not the main goal in coverage missions, rather researchers have focused on simultaneous coverage of dynamic environments and tracking of intruders/events. Consider the event density of a dynamic environment represented by the sensory function ϕ(.) to be time-dependent (i.e. ϕ(q,t)). This dependence is a result of changing environments and intruder detection scenarios. Therefore, our main goal is defined as simultaneous coverage control and tracking in dynamic environments. In the next section, a fuzzy adaptive robust control scheme will be proposed for achieving this goal.

3 Problem formulation and robust control design

In this section, a time-dependent cost function for coverage control of dynamic environments is addressed. This cost function has been previously used in the research of Pimenta et al. in [13].

The time-dependent form of our previous cost function (2), can be rewritten as

$$ H(Z,t) = \sum _{i=1}^{N}\int_{V_i} \frac{1}{2} \|q-z_i\|^2\phi(q,t)\,dq.$$
(8)

Later in this section, the coverage error will be introduced. Then, a robust controller will be designed and a fuzzy logic system will be utilized to approximate the unknown parts of our cost function. The main feature of the proposed novel control scheme is its decentralized characteristic, and its robust stability (i.e. robustness of results in presence of external disturbances, calculation inaccuracy, and measurement noises).

We know that if the centroids of Voronoi regions are perfectly tracked, the cost function in (8) reaches a local minimum. Based on this, the ith coverage error is defined as

$$ E_i(t)=M_{V_i}\|C_{V_i}-Z_i\|^2.$$
(9)

Then the overall coverage error for robotic swarm of N robots is defined as

$$ E(t)= \sum _{i=1}^{N}E_i(t) =\sum _{i=1}^{N}M_{V_i}\|C_{V_i}-Z_i\|^2.$$
(10)

For designing our robust controller, we need to calculate the first derivative of coverage error E. It is straightforward to write the first derivatives of (10) as

$$ \dot{E}(t)= \sum _{i=1}^{N}\biggl(\frac{\partial E^T}{\partial Z_i}\dot{Z}_i + F_i \biggr),$$
(11)

where F i is a result of time-varying sensory information ϕ(q,t):

$$ F_i= (C_{V_i}-Z_i)^T\int_{V_i}(2q-C_{V_i}-Z_i)\dot{\phi}(q,t)\,dq.$$
(12)

The first term of (11) is calculated in [13] and reported as

$$\frac{\partial E}{\partial Z_i} = -2 ( L_{V_i} + R_i - M_{V_i}Z_i)$$
(13)

where

(14)

with

(15)
(16)

Our design goal is to propose a controller so that

$$ \underline{\dot{E}}_i + k\underline{E}_i=0$$
(17)

is achieved, where k is chosen to make (17) asymptotically stable (i.e. k>0). Using the feedback linearization method, the controller can be proposed as

$$ u_i = \frac{L_{V_i}+R_i-M_{V_i} Z_i}{2\|L_{V_i}+R_i-M_{V_i} Z_i\|^2}\bigl(kM_{V_i}\|C_{V_i}-p_i\|^2+F_i\bigr).$$
(18)

The controller proposed in (18), results in an exponentially decay of the coverage error E(t) as

$$ E(t)=E(0)e^{-kt}.$$
(19)

In order to use this control law, the functions R i and F i (i.e. \(\mathcal{M}_{ij}, \mathcal{L}_{ij}, \dot{\phi}(q,t)\)) must be computable. However, in practice, due to limited-processing ability of our small real robots and measurement noises, calculation of these functions is almost impossible in a decentralized form. To overcome this, we make use of two fuzzy approximators \(\hat{F}_{i} \in\mathbb{R}\) and \(\hat{G}_{i} \in\mathbb{R}^{2}\) for approximation of the terms F i and \(G_{i} = -2(L_{V_{i}}+R_{i}-M_{V_{i}}p_{i})\), respectively.

Based on definition of G i , let us rewrite the first derivative of coverage error (11) as

$$\dot{E}(t) = \sum_{i=1}^{N}\bigl(F_i + G_i^T u_i \bigr).$$
(20)

Therefore, based on the adaptive fuzzy H ∞ control design proposed in [11, 14, 24], we propose overall robust control law as

$$ u_i = \frac{\hat{G}_i}{\|\hat{G}_i\|^2}\bigl (-\hat{F}_i + k E(t) - u_{ai} \bigr)$$
(21)

where u ai is engaged to attenuate the fuzzy logic approximation error and measurement noises. Effectiveness of this controller will be proved in next subsection.

4 Stability proof

A Fuzzy Logic System (FLS) can be employed in adaptive control of nonlinear systems, due to its inherent capabilities of nonlinear function approximation. The basic configuration of an FLS consists of a fuzzifier, rule-base, fuzzy inference engine, and defuzzifier. Generally, the rule-base can be constructed by the following K fuzzy rules:

$$\begin{aligned}[b]R_i :& \textsc{IF}\ x_1\ \textsc{is}\ F^i_1\ \textsc{AND}\ \dots\ \textsc{AND}\ x_n \textsc{is}\ F^i_n\\&\textsc{THEN}\ y_i\ \textsc{is}\ G^i ,\quad i=1,2,\dots,K\end{aligned}$$
(22)

where x 1,x 2,…,x n are FLS inputs, y i is ith rule output. \(F^{i}_{j}\), j=1,2,…,n and G i are fuzzy sets characterized by fuzzy membership functions \(\mu_{F^{i}_{j}}(x_{j})\) and \(\mu_{G^{i}}(y_{i})\), respectively and K is the number of rules in the fuzzy rule base.

Lemma 1

By using the singleton fuzzifier, product inference, and weighted average defuzzifier, the output of the FLS can be expressed as

$$ y(x)=\frac{\sum^{K}_{i=1}\bar{y}_i (\prod^{n}_{j=1}\mu _{F_j^i(x_j)} )}{\sum^{K}_{i=1} \prod^{n}_{j=1} \mu_{F_j^i(x_j)}}$$
(23)

where \(\bar{y}_{i}\) is the point at which \(\mu_{G^{i}}(y_{i})=1\) (for more information refer to [25]).

By defining \(\mu_{F^{i}_{j}}(x_{j})\) as a fixed membership function and considering \(\bar{y}_{i}\) as an adjustable parameter, (23) can be rewritten as

$$ y(\underline{x})=\underline{\theta}^T \underline{\zeta}(\underline{x}),$$
(24)

where \(\underline{\theta}= [\bar{y}_{1}, \bar{y}_{2},\allowbreak\ldots ,\allowbreak \bar{y}_{K}]^{T}\) is a vector grouping all adjustable parameters, and \(\underline{\zeta}(\underline{x}) = [\zeta_{1}(\underline{x}),\zeta_{2}(\underline{x}),\allowbreak\ldots ,\zeta_{K}(\underline{x} )]^{T} \) is a set of fuzzy basis functions defined as

$$\zeta_i(\underline{x})=\frac{\prod^{n}_{j=1} \mu_{F_j^i(x_j)}}{\sum ^{K}_{i=1} \prod^{n}_{j=1} \mu_{F_j^i(x_j)}}.$$
(25)

It has been proved in [25] that fuzzy systems in the form of (24) can approximate continuous functions over a compact set to an arbitrary degree of accuracy provided that enough number of rules are considered.

This section presents the stability proof of the proposed adaptive fuzzy controller (21). A Lyapunov candidate will be proposed and then an adaptation law and a robust compensator control input will be derived to satisfy the robust coverage performance.

To derive the adaptive laws for adjusting θ Fi and θ Gi , we first define the optimal parameter vector \({\theta }_{Fi}^{*}\) and \({\theta}_{Gi}^{*}\) as

(26)
(27)

where Ω Fi and Ω Gi are proper compact sets defined as

(28)
(29)

The minimum approximation error is defined as

(30)

where w i ∈L ∞ [25].

It should be mentioned that, Ω Fi and Ω Gi in (28)–(29) do not need to be known in advance. If the robust controller is designed well, then the robots position z i will follow the Voronoi centroids \(C_{V_{i}}\) well. In addition, based on the universal approximation theorem, w i remains bounded. Therefore, the robots position z i remains bounded, also.

By choosing the control input as (21) after simple manipulations, the coverage error dynamic can be expressed as

$$ \dot{E} = k E + \sum_{i=1}^N\bigl[ \bigl( F_i - \hat{F}_i \bigr) + \bigl( G_i^T- \hat{G}_i^T \bigr) u_i \bigr].$$
(31)

By replacing \(\hat{F}_{i} = \theta_{Fi}^{T} \zeta\) and \(\hat{G}_{i} = \theta _{Gi}^{T} \zeta\), the first derivative of coverage error (31) can be rewritten as

$$ \dot{E} = k E + \sum_{i=1}^N\bigl[u_{ai} + w_i -\tilde{\theta}_{Fi}^T\zeta- \zeta^T\tilde{\theta}_{Gi} u_i \bigr]$$
(32)

where \(\tilde{\theta}_{Fi} = {\theta}_{Fi} - {\theta}^{*}_{Fi}\) and \(\tilde{\theta}_{Gi} = {\theta}_{Gi} - {\theta}^{*}_{Gi}\).

In the following theorem, it will be proved that the proposed control law (21) guarantees the robust stability of our coverage problem.

Theorem 1

Consider a group of N fully autonomous robots with the integrator dynamic represented in (1), and with the control law in (21). The robust compensator of ith robot u ai and the fuzzy adaptation laws are chosen as

(33)
(34)
(35)

where r, γ 1, and γ 2 are positive constants and β is the positive solution of the following quadratic equation:

$$ \biggl( \frac{1}{\rho^2} -\frac{2}{r} \biggr)\beta^2 + 2\beta k + \alpha=0,$$
(36)

where ρ is an attenuation level denoted by the designer, and α is a positive scalar.

Therefore, the robust coverage performance can be achieved for a prescribed attenuation level ρ:

(37)

where \(w = \sum_{i=1}^{N} w_{i}^{2}\).

Proof

In order to derive the adaptive law for adjusting θ Fi , and θ Gi the Lyapunov candidate is chosen as

$$ V=\frac{1}{2}\beta E^2 + \sum _{i=1}^N \biggl[\frac{1}{2\gamma_1}\tilde{\theta}_{Fi}^2 + \frac{1}{2\gamma_2}\operatorname{trace}\bigl (\tilde{\theta}^T_{Gi}\tilde{\theta}_{Gi}\bigr) \biggr].$$
(38)

Time derivative of V is written as

$$ \dot{V} = \beta E \dot{E} + \sum _{i=1}^N \biggl[ \frac{1}{\gamma_1}\tilde{\theta}_{Fi} \dot{\tilde{\theta}}_{Fi} + \frac{1}{\gamma_2}\operatorname{trace}\bigl(\tilde{\theta}_{Gi}^T \dot{\tilde{\theta}}_{Gi}\bigr) \biggr].$$
(39)

Using (32), the time derivative of V can be rewritten as

(40)

Substituting (33) in (40) and using the fact that \({\dot{\tilde{\theta}}}_{Fi}={\dot{\theta}}_{Fi}\) and \({\dot {\tilde {\theta}}}_{Gi}={\dot{\theta}}_{Gi}\), after some algebraic effort, we get

(41)

Using adaptation laws (34)–(35) and the quadratic equation (36), the above equation becomes

(42)

Integrating the above inequality from t=0 to T yields to

$$ V(T)-V(0) \le-\frac{1}{2}\alpha\int _{0}^T E^2 \,dt +\frac{1}{2}\rho^2 \int _{0}^Tw^2 \,dt.$$
(43)

Using the fact that V(T)≥0, the following inequality is implied:

$$ \frac{1}{2}\alpha\int _{0}^TE^2 \,dt \le V(0) + \frac{1}{2}\rho^2 \int _{0}^T w^2 \,dt$$
(44)

and from (38), (44) can be rewritten in the following form:

(45)
(46)

This is (37). □

The proposed control methodology for the ith robot is summarized in Algorithm 1.

Algorithm 1
figure 1

Simultaneous Coverage and Tracking Control for the ith robot

Full size image

Remark 1

The solvability of robust coverage performance (37) by the adaptive fuzzy controller (21), and adaptation laws (34)–(35) depends on the existence of a positive solution β of (36). Based on elementary mathematics, for guaranteed existence of such solution we should have

$$(2k)^2 - 4 \biggl(\frac{1}{\rho^2}-\frac{2}{r}\biggr)(\alpha)\geq0.$$

Therefore, our quadratic equation has a positive solution if and only if

$$\biggl(\frac{1}{\rho^2}-\frac{2}{r}\biggr) \leq0\quad \mbox{or}\quad r \leq 2\rho^2.$$

As a conclusion for a prescribed ρ in our robust coverage performance, the coefficient r in (33) should satisfy the above inequality.

5 Simulation results

This section presents three simulation examples to illustrate the effectiveness and robustness of the proposed control scheme. The first example presents the coverage of an unknown environment with 5 Robots and 1 Intruder (5R1I). In this example, a mobile intruder circles in the environment and one robot track it while maintaining the optimal coverage simultaneously. In the second example, the same robotic swarm is covering the environment while 2 mobile intruders roam in the environment (5R2I). Finally, the third complex coverage problem consists of 9 Robots and 3 Intruders (9R3I) with different motion trajectories.

All the simulation results are implemented in MATLAB® with 0.01s as the stepsize.

In order to make the results comparable with existing works, authors have tried to make all simulation conditions (e.g. initial positions, intruding trajectories, etc.) similar to the simulation results presented in [13].

In all simulations, robots compute the function ϕ in (4), (5) locally by considering the tracking distance:

(47)

where [x,y]T is the position of robot, [x i ,y i ]T is the position of the ith detected intruder, A=0.64 and σ=0.5. This radial basis function is centered at the intruder position and can be a good representation for the sensory function used in (8).

Each robot is simulated with the simple kinematic single integrator model represented in (1), and the robust controller of (21) is used to force robots to simultaneously cover the environment and track the intruders. Each controller needs two fuzzy approximators for approximating F i , and G i . Gaussian membership functions are defined as the following:

where x and y are the position coordinate of an individual robot.

Using the aforementioned 10 membership functions, 13 fuzzy rules are designed as

where y′ is the output of each rule.

The output of the fuzzy system is achieved by choosing singleton fuzzification, center average defuzzification, Mamdani implication in the rule base, and product inference engine [25] as

where

are adjustable parameters.

All θs are initialized from zero vectors and the learning rate in (34)–(35) are set to γ 1=γ 2=15.

The prescribed attenuation level (ρ), r and α in (36), are chosen to be 0.1, 0.015, and 100, respectively.

In the first and second simulation examples (i.e. 5R1I and 5R2I), k=40 and the initial positions for robots and intruders are presented in Table 1. Initial positions for the third example 9R3I are presented in Table 2 with k=20.

Table 1 Initial positions for 5R1I and 5R2I
Full size table
Table 2 Initial positions for 9R3I
Full size table

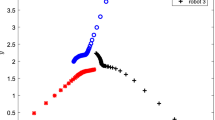
Figures 1, 2 and 3, clearly demonstrate the effectiveness and robustness of our designed controller. In each scenario, intruders are tracked by their nearest robot (i.e. the robot in the same Voronoi region) and still the optimal coverage in maintained regarding to (8).

Fig. 1
figure 2

(Color online) Simultaneous coverage and tracking of five robots and one intruder (The positions of the robots are given by the blue circles. The positions of the intruders are given by red circles. The margins denote the Voronoi regions.)

Full size image
Fig. 2
figure 3

(Color online) Simultaneous coverage and tracking of five robots and two intruder. (The positions of the robots are given by the blue circles. The positions of the intruders are given by red circles. The margins denote the Voronoi regions.)

Full size image
Fig. 3
figure 4

(Color online) Simultaneous coverage and tracking of nine robots and three intruder. (The positions of the robots are given by the blue circles. The positions of the intruders are given by red circles. The margins denote the Voronoi regions.)

Full size image

In order to compare our results with the existing method of Pimenta et al. in [13], the overall coverage error of third example (9R3I), is computed for both methods and results are illustrated in Fig. 4. In this figure, E(t)=40e −20t is the theoretical lower bound of coverage error (based on (19)).

Fig. 4
figure 5

Coverage error E(t). Method I is proposed by Pimenta et al. in [13]; Method II is the proposed method of this article

Full size image

Error comparisons depict the fact that the performance of our method is very similar to the method proposed in [13]. Instead, in our method, due to using fuzzy approximator, there is no need to directly compute (16) and its components. Therefore, the computation complexity of our method is much lower than the method proposed in [13], while performance results are comparable.

6 Conclusion

In this paper, the coverage control problem of a class of multi-robot systems with limited computation ability was investigated, in which centroidal Voronoi configuration was achieved in presence of mobile intruders. On the basis of the Lyapunov stability theory, a novel decentralized adaptive fuzzy controller with corresponding parameter update laws was developed and the stability of the system was proved. All the theoretical results were verified by simulation examples and good performance of the proposed controller was shown even in the case of multiple intruders.