1 Introduction

A swarm system can be found in species such as ant colonies, bird flocking, animal herding, bacteria molding [1, 2], which is an aggregation of multiple agents. The agents in swarm systems interact with each other through attractions and repulsions. Based on the relatively simple strategies, they mimic some complex global behaviors. Such exotic collective behavior is called “swarm intelligence” or “collective intelligence,” which has fascinated the interest of researchers for many years. With the development of the technology such as sensing, information processing and computation, the swarm concept has been applied in engineering. As a result, there are swarm mechanical systems, including systems composed of multiple robots, satellites and vehicles.

Control design is the key to determine the motion of system. Hence, it is crucial in the study of swarm mechanical systems. There are two approaches for the control design of swarm mechanical systems: kinematic approaches and dynamic approaches. The kinematic approaches concern the formulation and analysis of the ideal performance unaware of its implementation. In [3], a kinematic control for platoons of autonomous vehicles is proposed based on the definition of suitable task functions, which are handled in the framework of singularity-robust task-priority kinematics. In [4], a kinematic model for swarm aggregations is built. It suggests that this model can be viewed as an approximation for some swarms with point mass dynamics. In [5], the properties and modeling of self-organized fish schools are investigated. In [6], the control law based on a distributed swarm aggregation algorithm is designed for multiple kinematic robots. The dynamic approaches, on the other hand, emphasize on how to achieve the performance by taking the dynamic characteristics of agents into account. In [7], a sliding-mode control for swarms is proposed to force the motion to meet the kinematic model. In [8], issues in both the kinematic and dynamic domains of swarm systems are addressed. In [9], a novel robust decentralized adaptive control based on fuzzy logic is proposed for the multi-agent systems. In [10], the dynamics and control for robot swarms are considered.

In practice, the uncertainty is an unavoidable plague. Hence, it is inevitable in dynamic modeling. Since the uncertainty enters the line of sight, the description of the uncertainty has become a major task. In this paper, the uncertainty is possibly fast time varying and bounded with unknown bound. The only known information is that the bound lies within a prescribed and compact fuzzy set. That is, only the bound of the uncertainty is fuzzy. Instead of Takagi–Sugeno (T–S)-type fuzzy or other if–then rules-based fuzzy, the fuzzy set theory is employed to describe the uncertainty bound. Based on the fuzzy uncertainty description, we consider a swarm robot system consisting of N robots and devote to the control design problem.

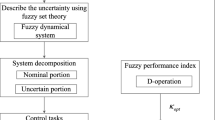
The main contributions of this paper are fourfold. First, we creatively introduce the swarm intelligence into the multi-robot systems (thereby the swarm robot systems), which is accomplished by the design of the function \(G_{ij}\). Based on this, we design the kinematic and dynamic models for the swarm robot systems. Second, we treat the kinematic performance as a constraint and then obtain the analytic (i.e., closed form) constraint force by employing Udwadia–Kalaba approach. The constraint force obeys the Lagrange’s form of d’Alembert’s principle, and it can be adopted as the ideal control input. Motivated by the constraint force, we propose the nominal control actions of the swarm robot systems. Third, in combination with the fuzzy description of the uncertainty, an adaptive robust control is proposed to compensate the uncertainty. The resulting control is deterministic, which renders the system uniform boundedness and uniform ultimate boundedness regardless of the uncertainty. Fourth, the optimal design of the adaptive robust control is completed by choosing a control parameter to minimize a fuzzy-based performance index. This optimization problem is proven to be tractable, with the solution to be existent, unique and in closed form.

2 Fuzzy Swarm Robot System

2.1 Kinematic Model

Consider a swarm system consisting of N robots moving on the ground. For robot \(i\in {{\mathcal {N}}}\), \({{\mathcal {N}}}=\left\{ 1,2,\ldots ,N\right\}\), the position is described by the coordinate \(q_i=[x_i, y_i]^{\mathrm{T}}\), the velocity is described by \(\dot{q}_i=[\dot{x}_i, \dot{y}_i]^{\mathrm{T}}\), the kinematic model of robot i is governed by

$$\begin{aligned} \dot{q}_{i}(t)= -\,\sum ^{N}_{j=1,j\ne {i}}\nabla _{q_{i}}G_{ij}(q_{i}(t),q_{j}(t)), \end{aligned}$$
(1)

where t is the time, and the function \(G_{ij}(q_{i},q_{j}): {{\mathbf{R}}^{n}}\times {{\mathbf{R}}^{n}}\rightarrow {{\mathbf{R}}}\) is \(C^{1}\) (i.e., the first-order derivative of \(G_{ij}\) exists). Let \(g_{ij}(q_{i},q_{j}):=\nabla _{q_{i}}G_{ij}(q_{i},q_{j})\), where the function \(g_{ij}: {{\mathbf{R}}^{n}}\rightarrow {{\mathbf{R}}}\) can represent the attraction and repulsion between agents i and j [4]. The functions \(G_{ij}(q_{i},q_{j})\) and \(g_{ij}(q_{i},q_{j})\) comply with the properties and performances in [8, 11].

2.2 Dynamic Model

Suppose the acceleration is described by \(\ddot{q}_i=[\ddot{x}_i, \ddot{y}_i]^{\mathrm{T}}\), the mass is described by \(m_i\), the dynamic model of robot i is governed by

$$\begin{aligned} M_i(\sigma _i)\ddot{q}_i&= F_i(\sigma _i)+\tau _{i}(t), \end{aligned}$$
(2)
$$M_i(\sigma _i)= \left[ \begin{array}{cc}m_i(\sigma _i)&{}0\\ 0&{}m_i(\sigma _i)\end{array}\right] ,$$
(3)

where \(\sigma _{i}\in {\varSigma _{i}}\subset {{\mathbf{R}}^{p_{i}}}\) is the uncertain parameter with \(\varSigma _{i}\) (the possible bound of \(\sigma _{i}\)) compact but unknown, \(F_i(\sigma _i)\) is the drag force, \(\tau _{i}(t)\) is the control input.

Assumption 1

The inertia matrix \(M_i(\sigma _i)\) is positive definite: For each \(\sigma _{i}\), \(M_i(\sigma _i)>0\).

Assumption 2

(1) Let \(x^i=[{{q_i}^{\mathrm{T}}}\;{{\dot{q}_i}^{\mathrm{T}}}]^{\mathrm{T}}\). Its initial condition is denoted by \(x^i_0.\) For each entry of \(x^i_{0}\), namely \(x^i_{0j}\), \(j=1,2,\ldots ,2n\), there exists a fuzzy set \(X^i_{0j}\) in a universe of discourse \(\varXi ^i_{j} \subset \mathbf{R}\) characterized by a membership function \(\mu _{\varXi ^i_{j}}\): \(\varXi ^i_{j} \rightarrow [0,1]\). That is

$$\begin{aligned} X^i_{0j}=\left\{ \left( x^i_{0j},\mu _{\varXi ^i_j}\left( x^i_{0j}\right) \right) \vert x^i_{0j} \in \varXi ^i_{j}\right\} . \end{aligned}$$
(4)

Here \(\varXi ^i_{j}\subset \mathbf{R}\) is compact and is known. (2) For each entry of vector \(\sigma _i\), namely \(\sigma _{ij}\), \(j=1,2,\ldots ,p_i\), the function \(\sigma _{ij}(\cdot )\) is Lebesgue measurable. (3) For each \(\sigma _{ij}\), there exists a fuzzy set \(S_{ij}\) in a universe of discourse \(\varSigma _{ij} \subset \mathbf{R}\) characterized by a membership function \(\mu _{\varSigma _{ij}}\): \(\varSigma _{ij} \rightarrow [0,1]\). That is

$$\begin{aligned} S_{ij}=\left\{ \left( \sigma _{ij}, \mu _{\varSigma _{ij}}(\sigma _{ij})\right) \vert \sigma _{ij} \in \varSigma _{ij} \right\} . \end{aligned}$$
(5)

Remark 1

The system, in which the uncertainty is described by fuzzy theory, is called fuzzy system. Assumption 2 suggests to use fuzzy theory to describe the possible value of the uncertainty. This method of uncertainty description is different from probability theory, Takagi–Sugeno fuzzy model, Mamdani fuzzy model or other fuzzy inference if–then rule-based models. We call system (2) under the description of Assumption 2 fuzzy swarm robot system.

3 Ideal Control of Swarm Robot System

Employing Udwadia–Kalaba approach [12,13,14,15,16,17], we treat kinematic performance (1) of robot i as a constraint of system (2); then, the ideal control of swarm robot system can be obtained as follows.

First, we differentiate (1) with respect to t; then, we have

$$\begin{aligned} \ddot{q}_{i}(t)&= -\,\frac{d}{{\hbox {d}}t}\sum ^{N}_{j=1,j\ne {i}}\nabla _{q_{i}}G_{ij}(q_{i}(t),q_{j}(t))\nonumber \\&=:\phi _{i}(q(t),\dot{q}(t),t). \end{aligned}$$
(6)

By creatively treating (6) as a second-order constraint, the control input can be selected as

$$\begin{aligned} \tau _{i}(t)=M^{\frac{1}{2}}_{i}(\sigma _{i})[M^{-\frac{1}{2}}_{i}(\sigma _{i})]^{+}\left[ \varPhi _{i}-M^{-1}_{i}(\sigma _{i})F_i(\sigma _i)\right] . \end{aligned}$$
(7)

This control assures agent i to meet kinematic performance (1). It is model-based and can be implemented as a feedback control. This control is ideal. One only can use it under the following two provisions. First, the initial condition of robot i must be the same as (1). Second, the model of robot i must be known, including the value of the uncertain parameter \(\sigma _i(t)\). In practice, however, the provisions are likely not met. Therefore, an adaptive robust control design is needed.

4 Adaptive Robust Control Design

Taking the uncertainty into account, we first decompose the system parameters \(M_{i}(\sigma _{i})\) and \(F_{i}(\sigma _{i})\). We consider \({\bar{M}}_i\), \(\Delta M_i(\sigma _i)\), \({\bar{F}}_{i}\) and \(\Delta F_i(\sigma _i)\) such that

$$\begin{aligned} M_{i}(\sigma _{i})&=\bar{M}_{i}+\Delta {M_{i}(\sigma _{i})},\nonumber \\ F_{i}(\sigma _{i})&=\bar{F}_{i}+\Delta {F_{i}(\sigma _{i})}, \end{aligned}$$
(8)

where \(\bar{M}_{i}\) and \(\bar{F}_{i}\) are the “nominal” portions of the system parameters, and \(\Delta {M}_{i}\) and \(\Delta {F}_{i}\) are the corresponding uncertain portions. We assume that \(\bar{M}_{i}\) is positive definite (since the nominal portion \(\bar{M}_{i}\) is the designer’s direction, \(\bar{M}_{i}>0\) is always feasible). Furthermore, the functions \(\bar{M}_{i}(\cdot )\), \(\Delta {M_{i}}(\cdot )\), \(\bar{F}_{i}(\cdot )\), \(\Delta {F_{i}}(\cdot )\) are all continuous.

Let \(D_{i}(\sigma _{i}):={M}^{-1}_{i}(\sigma _{i})\), \(\bar{D}_{i}:=\bar{M}^{-1}_{i}\), \(\Delta {D_{i}}(\sigma _{i}):=D_{i}(\sigma _{i})-\bar{D}_{i}\), \(E_{i}(\sigma _{i}):=\bar{M}_{i}M^{-1}_{i}(\sigma _{i})-I_{i}\), we further have \(\Delta {D_{i}}(\sigma _{i}):=\bar{D}_{i}E_{i}(\sigma _{i})\), \(D_{i}=\bar{D}_{i}+\Delta {D_{i}}\). For given constant matrix \(P_{i}\in {\mathbf{R}^{n\times {n}}}\), \(P_i>0\), let

$$\begin{aligned} W_{i}(\sigma _{i}):=P_{i}\bar{D}_{i}E_{i}(\sigma _{i})\bar{M}_{i}P^{-1}_{i}. \end{aligned}$$
(9)

Assumption 3

  1. 1.

    There exists a (possibly unknown) scalar \(\rho _{E_{i}}>-\,1\) such that,

    $$\begin{aligned} \min _{\sigma _i\in \varSigma _i}\lambda _{\min } \left( W_{i}(\sigma _{i})+W^{\mathrm{T}}_{i}(\sigma _{i}) \right) \ge {2\rho _{E_{i}}}>-2. \end{aligned}$$
    (10)
  2. 2.

    The unknown scalar \(\rho _{E_{i}}\) belongs to a known fuzzy number.

Let

$$\begin{aligned} S_i:=\sum ^{N}_{j=1,j\ne {i}}\nabla _{q^{i}}G_{ij}(q^{i}(t),q^{j}(t)). \end{aligned}$$
(11)

We now propose a performance measure:

$$\begin{aligned} \beta _i:=\dot{q}_{i}+S_{i}. \end{aligned}$$
(12)

Our adaptive robust control consists of three portions: \(\tau _{i1}\), \(\tau _{i2}\) and \(\tau _{i3}\). \(\tau _{i1}\) and \(\tau _{i2}\) are proposed based on the nominal system (no uncertain parameters involved), which is given by

$$\begin{aligned} \tau _{i1}&=\bar{M}_{i}\left( \phi _{i}-\bar{M}^{-1}_{i}\bar{F}_{i}\right) , \end{aligned}$$
(13)
$$\begin{aligned} \tau _{i2}&= -\,\kappa _{i}\bar{M}_{i}P^{-1}_{i}(\dot{q}_{i}+S_{i})\nonumber \\&= -\,\kappa _{i}\bar{M}_{i}P^{-1}_{i}\beta _{i}, \end{aligned}$$
(14)

where \(\kappa _{i}>0\) is a scalar parameter. \(\tau _{i1}\) is motivated by (7).

Assumption 4

(1) There are a (possibly unknown) constant vector \(\alpha _{i}\in {\mathbf{R}^{k_{i}}}\) and a known function \(\varPi _{i}(\cdot )\) such that

$$\begin{aligned}&(1+\rho _{E_{i}})^{-1}\max \limits _{\sigma _{i}\in {\varSigma _{i}}}\left\| P_{i}\Delta {D_{i}}(\sigma _{i})[F_{i}(\sigma _{i})+\tau _{i1}+\tau _{i2}]\right. \nonumber \\&\quad \left. +\,P_{i}\bar{D}_{i}\Delta {F}_{i}(\sigma _{i})\right\| \le \varPi _{i}(\alpha _{i}), \end{aligned}$$
(15)

where the function \(\varPi _{i}(\alpha _{i})\) is (i) \(C^{1}\); (ii) concave [11]; (iii) nondecreasing with respect to each component of its argument \(\alpha _{i}\). (2) Each entry of \(\alpha _{i}\) (namely \(\alpha _{ij}\), \(j=1, 2,\ldots , k_{i}\)) belongs to a known fuzzy number.

Remark 2

The \(\rho _{E_{i}}\) and \(\alpha _{ij}\) (\(j=1, 2,\ldots , k_{i}\)) are relative to the uncertain parameter \(\sigma _{i}\). As fuzzy numbers, \(\rho _{E_{i}}\) and \(\alpha _{ij}\) are described by their corresponding membership functions. Their membership functions can be determined by fuzzy arithmetic and decomposition theorem. Based on Assumption 3 and the fact that the universes of discourse \(\varSigma _{ij}\) (\(j=1, 2,\ldots , p_i\)) are known, we can evaluate the value of \(\rho _{E_{i}}\).

The adaptive parameter vector \(\hat{\alpha }_i\) is governed by the following adaptive law

$$\begin{aligned} \dot{\hat{\alpha }}_{i}= \kappa _{i}\left[ \frac{\partial {\varPi }^{\mathrm{T}}_{i}}{\partial {\alpha _{i}}}(\hat{\alpha }_{i})\left\| \beta _{i}\right\| -\bar{\kappa }_{i}\hat{\alpha }_{i}\right] , \end{aligned}$$
(16)

where \(\bar{\kappa }_{i}\in {\mathbf{R}}>0\), \(\hat{\alpha }_{ij}(t_{0})>0\) (\(\hat{\alpha }_{ij}\) denotes the j-th component of the vector \(\hat{\alpha }_{i}\), \(j=1,2,\ldots ,\kappa _{i}\)). Notice that the parameter \(\kappa _{i}\) determines not only control \(\tau _{i2}\) but also the adaptive parameter. The third portion of the control is proposed as

$$\begin{aligned} \tau _{i3}&= -\,\bar{M}_{i}P^{-1}_{i}{\gamma _{i}}\mu _{i}\varPi _{i}(\hat{\alpha }_{i}), \end{aligned}$$
(17)

where \({\gamma _{i}}=l_i\Vert \mu _{i}\Vert ^{\omega _i}\), \(\mu _{i}=\beta _{i}\varPi _{i}(\hat{\alpha }_{i})\). Both \(\omega _i\in \mathbf{R}>0\) and \(l_i\in \mathbf{R}>0\) are design parameters. Therefore, the adaptive robust control is given by

$$\begin{aligned} \tau _{i}&= \tau _{i1}+\tau _{i2}+\tau _{i3}. \end{aligned}$$
(18)
$$\begin{aligned} \delta _{i}:&= \left[ \beta ^{\mathrm{T}}_{i}\quad \left( \hat{\alpha }_{i}-\alpha _{i}\right) ^{\mathrm{T}}\right] ^{\mathrm{T}}\in {\mathbf{R}^{{n}+k_{i}}} \end{aligned}$$
(19)
$$\begin{aligned} \delta:&= \left[ \delta ^{\mathrm{T}}_{1}\quad \delta ^{\mathrm{T}}_{2} \cdots \delta ^{\mathrm{T}}_{N}\right] ^{\mathrm{T}}\in {\mathbf{R}^{{\sum _{i=1}^N} \left( {n}+k_{i}\right) }}. \end{aligned}$$
(20)

Theorem 1

Subject to Assumptions 1, 2, 3, 4, control (18) renders system (2) uniformly bounded (i.e., for\(\Vert \delta (t_0)\Vert <r\), there is a\(d(r)>0\)such that\(\Vert \delta (t)\Vert <d(r)\)for all\(t\ge t_0\)) and uniformly ultimately bounded (i.e., for\(\Vert \delta (t_0)\Vert <r\), there exists a\({\underline{d}}>0\)such that for all\({\bar{d}}>{\underline{d}}\), there is a time interval\(T({\bar{d}}, r)<\infty\) with \(\Vert \delta (t)\Vert <{\bar{d}}\)for all\(t\ge t_0+T({\bar{d}}, r)\)).

Proof

Consider the Lyapunov function candidate

$$\begin{aligned} V(\delta )&= \sum ^{N}_{i=1}V_{i}(\beta _{i},\hat{\alpha }_{i}-\alpha _{i}), \end{aligned}$$
(21)
$$\begin{aligned} V_{i}&= \beta ^{\mathrm{T}}_{i}P_{i}\beta _{i}+(1+\rho _{E_{i}})(\hat{\alpha }_{i}-\alpha _{i})^{\mathrm{T}}\kappa ^{-1}_{i}(\hat{\alpha }_{i}-\alpha _{i}). \end{aligned}$$
(22)

The derivative of \(V_{i}\) is given by

$$\begin{aligned} \dot{V_{i}}=2\beta ^{\mathrm{T}}_{i}P_{i}\dot{\beta }_{i}+2(1+\rho _{E_{i}})(\hat{\alpha }_{i}-\alpha _{i})^{\mathrm{T}}\kappa ^{-1}_{i}\dot{\hat{\alpha }}_{i}. \end{aligned}$$
(23)

For the term \(2\beta ^{\mathrm{T}}_{i}P_{i}\dot{\beta }_{i}\), according to (2), (8), (13), (14), (17) and the definition of \(D_i\), \(\bar{D}_{i}\), \(\Delta {D}_{i}\), \(E_i\), we have

$$\begin{aligned}&2\beta ^{\mathrm{T}}_{i}P_{i}\dot{\beta }_{i}=2\beta ^{\mathrm{T}}_{i}P_{i}(\ddot{q}_{i}+\dot{S}_i)\nonumber \\&\quad =2\beta ^{\mathrm{T}}_{i}P_{i}[M^{-1}_{i}(F_i+\tau _{i1}+\tau _{i2}+\tau _{i3})-\phi _{i}]\nonumber \\&\quad =2\beta ^{\mathrm{T}}_{i}[P_{i}\Delta {D}_{i}({F}_{i}+\tau _{i1}+\tau _{i2})+P_{i}\bar{D}_{i}\Delta {F}_{i}]\nonumber \\&\quad \quad +\,2\beta ^{\mathrm{T}}_{i}P_{i}[\bar{D}_{i}(\bar{F}_{i}+\tau _{i1})-\phi _{i}]+2\beta ^{\mathrm{T}}_{i}P_{i}\bar{D}_{i}\tau _{i2}\nonumber \\&\quad \quad +\,2\beta ^{\mathrm{T}}_{i}P_{i}\bar{D}_{i}\tau _{i3}+2\beta ^{\mathrm{T}}_{i}P_{i}\Delta {D}_{i}\tau _{i3}\nonumber \\&\quad \le 2\left\| \beta _{i}\right\| \max \limits _{\sigma _{i}\in {\varSigma _{i}}}\left\| P_{i}\Delta {D}_{i}({F}_{i}+\tau _{i1}+\tau _{i2})+P_{i}\bar{D}_{i}\Delta {F}_{i}\right\| \nonumber \\&\quad \quad +\,2\beta ^{\mathrm{T}}_{i}P_{i}\left\{ \bar{M}^{-1}_{i}\bar{F}_{i}+\bar{M}^{-1}_{i}[\bar{M}_i(\phi _{i}-\bar{M}^{-1}_{i}\bar{F}_{i})]-\phi _{i}\right\} \nonumber \\&\quad \quad -\,2\beta ^{\mathrm{T}}_{i}P_{i}\bar{D}_{i}(-\kappa _{i}\bar{M}_{i}P^{-1}_{i}\beta _{i})-2\gamma _{i}[\beta _{i}\varPi _{i}(\hat{\alpha }_{i})]^{\mathrm{T}}\mu _{i}\nonumber \\&\quad \quad -\,2\gamma _{i}[\beta _{i}\varPi _{i}(\hat{\alpha }_{i})]^{\mathrm{T}}(P_{i}\bar{D}_{i}E_{i}\bar{M}_{i}P^{-1}_{i}\mu _{i}) \end{aligned}$$
(24)

Since \(\mu _{i}=\beta _{i}\varPi _{i}(\hat{\alpha }_{i})\), by (9) and (15), we further have

$$\begin{aligned}&2\beta ^{\mathrm{T}}_{i}P_{i}\dot{\beta }_{i}\le 2(1+\rho _{E_{i}})\left\| \beta _{i}\right\| \varPi _{i}(\alpha _{i})-2\kappa _{i}\left\| \beta _{i}\right\| ^{2} \nonumber \\&\quad \quad -\,2\gamma _{i}{\left\| \mu _{i}\right\| }^{2}-2\gamma _{i}\mu ^{\mathrm{T}}_{i}(P_{i}\bar{D}_{i}E_{i}\bar{M}_{i}P^{-1}_{i})\mu _{i}\nonumber \\&\quad \le -2\kappa _{i}\left\| \beta _{i}\right\| ^{2}+2(1+\rho _{E_{i}})\left\| \beta _{i}\right\| \varPi _{i}(\alpha _{i}) -2\gamma _{i}{\left\| \mu _{i}\right\| }^{2}\nonumber \\&\quad \quad -\,\gamma _{i}\mu ^{\mathrm{T}}_{i}[P_{i}\bar{D}_{i}E_{i}\bar{M}_{i}P^{-1}_{i}+(P_{i}\bar{D}_{i}E_{i}\bar{M}_{i}P^{-1}_{i})^{\mathrm{T}}]\mu _{i}\nonumber \\&\quad \le -2\kappa _{i}\left\| \beta _{i}\right\| ^{2}+2(1+\rho _{E_{i}})\left\| \beta _{i}\right\| \varPi _{i}(\alpha _{i}) -2\gamma _{i}{\left\| \mu _{i}\right\| }^{2}\nonumber \\&\quad \quad -\,\gamma _{i}\mu ^{\mathrm{T}}_{i}(W_{i}+W^{\mathrm{T}}_{i})\mu _{i}\nonumber \\ \end{aligned}$$
(25)

According to (10) and Rayleigh’s inequality, we have

$$\begin{aligned}&-\mu ^{\mathrm{T}}_{i}(W_{i}+W^{\mathrm{T}}_{i})\mu _{i}\le -\lambda _{\min }(W_{i}+W^{\mathrm{T}}_{i}){\left\| \mu _{i}\right\| }^{2}\nonumber \\&\quad \le \min _{\sigma _i\in \varSigma _i}\lambda _{\min }(W_{i}(\sigma _{i})+W^{\mathrm{T}}_{i}(\sigma _{i})){\left\| \mu _{i}\right\| }^{2}\nonumber \\&\quad \le -2\rho _{E_{i}}{\left\| \mu _{i}\right\| }^{2} \end{aligned}$$
(26)

As a result, we have

$$\begin{aligned} 2\beta ^{\mathrm{T}}_{i}P_{i}\dot{\beta }_{i} \le&-2\kappa _{i}{\left\| \beta _{i}\right\| }^{2}+2(1+\rho _{E_{i}})\left\| \beta _{i}\right\| \varPi _{i}(\alpha _{i})\nonumber \\&-2\gamma _{i}(1+\rho _{E_{i}})\left\| \mu _{i}\right\| ^2. \end{aligned}$$
(27)

By \({\gamma _{i}}=l_i\Vert \mu _{i}\Vert ^{\omega _i}\) and \(\mu _{i}=\beta _{i}\varPi _{i}(\hat{\alpha }_{i})\),

$$\begin{aligned}&2\beta ^{\mathrm{T}}_{i}P_{i}\dot{\beta }_{i} \nonumber \\&\quad \le -2\kappa _{i}{\left\| \beta _{i}\right\| }^{2}+2(1+\rho _{E_{i}})\left\| \beta _{i}\right\| \varPi _{i}(\alpha _{i})\nonumber \\&\quad \quad -2l_i(1+\rho _{E_{i}})\left\| \mu _{i}\right\| ^{2+\omega _i}\nonumber \\&\quad = -\,2\kappa _{i}{\left\| \beta _{i}\right\| }^{2} +2(1+\rho _{E_{i}})\left\| \beta _{i}\right\| \varPi _{i}(\alpha _{i})\nonumber \\&\quad \quad -2l_i(1+\rho _{E_{i}})\left\| \mu _{i}\right\| ^{2+\omega _i}\nonumber \\&\quad \quad \,\underbrace{-2(1+\rho _{E_{i}})\left\| \beta _{i}\right\| \varPi _{i}(\hat{\alpha }_{i}) +2(1+\rho _{E_{i}})\left\| \beta _{i}\right\| \varPi _{i}(\hat{\alpha }_{i})}_{=0}\nonumber \\&\quad = -\,2\kappa _{i}{\left\| \beta _{i}\right\| }^{2} +\left[ 2(1+\rho _{E_{i}})\left\| \beta _{i}\right\| \varPi _{i}({\hat{\alpha }}_{i}) -2l_i(1+\rho _{E_{i}})\right. \nonumber \\&\quad \quad \left. \times \left\| \mu _{i}\right\| ^{2+\omega _i}\right] + 2(1+\rho _{E_{i}})\left\| \beta _{i}\right\| \left[ \varPi _{i}({\alpha }_{i})-\varPi _{i}(\hat{\alpha }_{i}) \right] \nonumber \\&\quad = -\,2\kappa _{i}{\left\| \beta _{i}\right\| }^{2} +2(1+\rho _{E_{i}})[\Vert \mu _i\Vert -l_i\Vert \mu _i\Vert ^{2+\omega _i}]\nonumber \\&\quad \quad + 2(1+\rho _{E_{i}})\left\| \beta _{i}\right\| \left[ \varPi _{i}({\alpha }_{i})-\varPi _{i}(\hat{\alpha }_{i}) \right] . \end{aligned}$$
(28)

A simple algebra shows that

$$\begin{aligned}&\Vert \mu _i\Vert -l_i\Vert \mu _i\Vert ^{2+\omega _i}\le {\bar{\xi }}_i, \end{aligned}$$
(29)
$$\begin{aligned}&{\bar{\xi }}_i:= -\,l_i[l_i(2+\omega _i)]^{-\frac{2+\omega _i}{1+\omega _i}}+[l_i(2+\omega _i)]^{-\frac{1}{1+\omega _i}}\nonumber \\&\quad =[l_i(2+\omega _i)]^{-\frac{1}{1+\omega _i}}\frac{1+\omega _i}{2+\omega _i}>0. \end{aligned}$$
(30)

According to the concavity of \(\varPi _{i}(\alpha _{i})\), we have

$$\begin{aligned} \varPi _{i}({\alpha }_{i})-\varPi _{i}(\hat{\alpha }_{i}) \le \frac{\partial {\varPi _{i}}}{\partial {\alpha _{i}}} (\hat{\alpha }_{i})(\alpha _{i}-\hat{\alpha }_{i}). \end{aligned}$$
(31)

Therefore, we have

$$\begin{aligned} 2\beta ^{\mathrm{T}}_{i}P_{i}\dot{\beta }_{i} \le&-2\kappa _{i}{\left\| \beta _{i}\right\| }^{2}+2(1+\rho _{E_{i}}){\bar{\xi }}_i\nonumber \\&+2(1+\rho _{E_{i}}) \left\| \beta _{i}\right\| \frac{\partial {\varPi _{i}}}{\partial {\alpha _{i}}} (\hat{\alpha }_{i})(\alpha _{i}-\hat{\alpha }_{i}). \end{aligned}$$
(32)

For the term \(2(1+\rho _{E_{i}})(\hat{\alpha }_{i}-\alpha _{i})^{\mathrm{T}}\kappa ^{-1}_{i}\dot{\hat{\alpha }}_{i}\), by substituting adaptive law (16), we have

$$\begin{aligned}&2(1+\rho _{E_{i}})(\hat{\alpha }_{i}-\alpha _{i})^{\mathrm{T}}\kappa ^{-1}_{i}\dot{\hat{\alpha }}_{i}\nonumber \\&\quad =[2(1+\rho _{E_{i}})(\hat{\alpha }_{i}-\alpha _{i})^{\mathrm{T}}\frac{\partial {\varPi }^{\mathrm{T}}_{i}}{\partial {\alpha _{i}}}(\hat{\alpha }_{i})\left\| \beta _{i}\right\| ]^{\mathrm{T}}\nonumber \\&\quad \quad -\,2(1+\rho _{E_{i}})(\hat{\alpha }_{i}-\alpha _{i})^{\mathrm{T}}\bar{\kappa }_{i}\hat{\alpha }_{i}\nonumber \\&\quad =2(1+\rho _{E_{i}})\left\| \beta _{i}\right\| \frac{\partial {\varPi _{i}}}{\partial {\alpha _{i}}}(\hat{\alpha }_{i})(\hat{\alpha }_{i}-\alpha _{i})\nonumber \\&\quad \quad -\,2(1+\rho _{E_{i}})(\hat{\alpha }_{i}-\alpha _{i})^{\mathrm{T}}\bar{\kappa }_{i}\hat{\alpha }_{i}. \end{aligned}$$
(33)

Substituting (32) and (33) into (23), we have

$$\begin{aligned} \dot{V}_{i}&\le -2k_{i}{\left\| \beta _{i}\right\| }^{2}+2(1+\rho _{E_{i}}){\bar{\xi }}_i\nonumber \\&\qquad -2(1+\rho _{E_{i}})(\hat{\alpha }_{i}-\alpha _{i})^{\mathrm{T}}\bar{\kappa }_{i}\hat{\alpha }_{i}\nonumber \\&=-2k_{i}{\left\| \beta _{i}\right\| }^{2}+2(1+\rho _{E_{i}}){\bar{\xi }}_i-2(1+\rho _{E_{i}})(\hat{\alpha }_{i}-\nonumber \\&\qquad \alpha _{i})^{\mathrm{T}}\bar{\kappa }_{i}(\hat{\alpha }_{i}-\alpha _{i})-2(1+\rho _{E_{i}})(\hat{\alpha }_{i}-\alpha _{i})^{\mathrm{T}}\bar{\kappa }_{i}\alpha _{i}\nonumber \\&\le -2k_{i}{\left\| \beta _{i}\right\| }^{2}+2(1+\rho _{E_{i}}){\bar{\xi }}_i-2(1+\rho _{E_{i}})\bar{\kappa }_{i}{\left\| \hat{\alpha }_{i}-\alpha _{i}\right\| }^{2}\nonumber \\&\qquad +2(1+\rho _{E_{i}})\bar{\kappa }_{i}\left\| \alpha _{i}\right\| \left\| \hat{\alpha }_{i}-\alpha _{i}\right\| . \end{aligned}$$
(34)

Let \(\bar{\eta }_{1i}=\min \{2k_{i}, 2(1+\rho _{E_{i}})\bar{\kappa }_{i}\}\), \(\bar{\eta }_{2i}=2(1+\rho _{E_{i}})\bar{\kappa }_{i}\times \left\| \alpha _{i}\right\|\), \(\bar{\eta }_{3i}=2(1+\rho _{E_{i}}){\bar{\xi }}_i\), \(\eta _{1i}=\frac{3\bar{\eta }_{1i}}{4}\), \(\eta _{2i}=\frac{\bar{\eta }^2_{2i}}{\bar{\eta }_{1i}}+\bar{\eta }_{3i}\). Based on \(({\sqrt{\bar{\eta }_{1i}}}\left\| \delta _{i}\right\| /2-{\bar{\eta }_{2i}}/{\sqrt{\bar{\eta }_{1i}}})^2\ge 0\), we have

$$\begin{aligned} \dot{V}_{i}&\le -\bar{\eta }_{1i}{\left\| \beta _{i}\right\| }^{2}-\bar{\eta }_{1i}{\left\| \hat{\alpha }_{i}-\alpha _{i}\right\| }^{2}+\bar{\eta }_{2i}\left\| \hat{\alpha }_{i}-\alpha _{i}\right\| +\bar{\eta }_{3i}\nonumber \\&\le -\bar{\eta }_{1i}({\left\| \beta _{i}\right\| }^{2}+{\left\| \hat{\alpha }_{i}-\alpha _{i}\right\| }^{2})\nonumber \\&\qquad +\bar{\eta }_{2i}\sqrt{{\left\| \beta _{i}\right\| }^{2}+{\left\| \hat{\alpha }_{i}-\alpha _{i}\right\| }^{2}}+\bar{\eta }_{3i}\nonumber \\&=-\bar{\eta }_{1i}{\left\| \delta _{i}\right\| }^{2}+\bar{\eta }_{2i}\left\| \delta _{i}\right\| +\bar{\eta }_{3i}\nonumber \\&\le -\bar{\eta }_{1i}{\left\| \delta _{i}\right\| }^{2}+\frac{\bar{\eta }_{1i}}{4}{\left\| \delta _{i}\right\| }^{2} +\frac{\bar{\eta }^2_{2i}}{\bar{\eta }_{1i}}+\bar{\eta }_{3i}\nonumber \\&=-\eta _{1i}{\left\| \delta _{i}\right\| }^{2}+\eta _{2i}. \end{aligned}$$
(35)

Let \(\eta _{1}=\min \nolimits _{i\in {{\mathcal {N}}}}{\eta _{1i}}\), \(\eta _{2}=\max \nolimits _{i\in {{\mathcal {N}}}}{\eta _{2i}}\). Then we have

$$\begin{aligned} \dot{V}&=\sum ^{N}_{i=1}{\dot{V}_{i}}\le \sum ^{N}_{i=1}{(-\eta _{1i}{\left\| \delta _{i}\right\| }^{2}+\eta _{2i})}\nonumber \\ \le&\sum ^{N}_{i=1}{(-\eta _{1}{\left\| \delta _{i}\right\| }^{2}+\eta _{2})}= -\,\eta _{1}\sum ^{N}_{i=1}{\left\| \delta _{i}\right\| }^{2}+N\eta _{2}\nonumber \\&=-\eta _{1}{\left\| \delta \right\| }^{2}+N\eta _{2}= -\,\eta {\left\| \delta \right\| }^{2}+\theta , \end{aligned}$$
(36)

where \(\eta =\eta _{1}\), \(\theta =N\eta _{2}\). According to the result of (36), we conclude that \(\dot{V}\) is negative definite for all \(\left\| \delta \right\|\) such that

$$\begin{aligned} \left\| \delta \right\| >\sqrt{\frac{\theta }{\eta }}. \end{aligned}$$
(37)

Since each universe of discourse \(\varSigma _{ij}\) is compact (hence closed and bounded), the uncertainty \(\sigma _i\) is bounded. Thus, both \(\eta\) and \(\theta\) are bounded. Therefore, \(\dot{V}\) is negative definite when \(\left\| \delta \right\|\) is sufficiently large. According to [18], we conclude that the solution of system (2) under control (18) is uniformly bounded and uniformly ultimately bounded. According to (22) and Rayleigh’s inequality, we have

$$\begin{aligned}&\lambda _{\min }(P_{i})\left\| \beta _{i}\right\| ^{2}+(1+\rho _{E_{i}})\kappa ^{-1}_{i} \left\| \hat{\alpha }_{i}-\alpha _{i}\right\| ^{2}\nonumber \\&\quad \le V_{i}\nonumber \\&\quad \le \lambda _{\max }(P_{i})\left\| \beta _{i}\right\| ^{2}+(1+\rho _{E_{i}})\kappa ^{-1}_{i} \left\| \hat{\alpha }_{i}-\alpha _{i}\right\| ^{2}. \end{aligned}$$
(38)

Let \(\xi _{1i}=\min \{\lambda _{{\mathrm{min}}}(P_{i}),(1+\rho _{E_{i}})\kappa ^{-1}_{i}\}\), \(\xi _{2i}=\max \{\lambda _{\max }(P_{i}), (1+\rho _{E_{i}})\kappa ^{-1}_{i}\}\). Thus, we have

$$\begin{aligned} \xi _{1i}\left\| \delta _{i}\right\| ^2\le {V_{i}}\le & {} {\xi _{2i}\left\| \delta _{i}\right\| ^2}, \end{aligned}$$
(39)
$$\begin{aligned} \sum ^{N}_{i=1}{\xi _{1i}\left\| \delta _{i}\right\| ^2}\le & {} {V}\le {\sum ^{N}_{i=1}{\xi _{2i}\left\| \delta _{i}\right\| ^2}}. \end{aligned}$$
(40)

Let \(\xi _{1}=\min \nolimits _{i\in {{\mathcal {N}}}}{\xi _{1i}}\), \(\xi _{2}=\max \nolimits _{i\in {{\mathcal {N}}}}{\xi _{2i}}\), we have

$$\begin{aligned} \xi _{1}\left\| \delta \right\| ^2\le {V} \le {\xi _{2}\left\| \delta \right\| ^2}, \left\| \delta \right\| ^2=\sum \limits ^{N}_{i=1}{\left\| \delta _{i}\right\| ^2}. \end{aligned}$$
(41)

According to [19], we conclude the uniform boundedness with

$$d(r)= \left\{ \begin{array}{ll} \sqrt{\frac{\xi _{2}}{\xi _{1}}}R, &{}\quad {\mathrm{if}}\,r\le {R},\\ \sqrt{\frac{\xi _{2}}{\xi _{1}}}r, &{}\quad {\mathrm{if}} \,r>{R}, \end{array} \right.$$
(42)
$$\begin{aligned} R&= \sqrt{\frac{\theta }{\eta }}. \end{aligned}$$
(43)

The uniform ultimate boundedness is also proven by taking \({\underline{d}}=R\sqrt{{\xi _{2}}/{\xi _{1}}}\). For given \(\overline{d}>{\underline{d}}\),

$$\begin{aligned} \Vert \delta (t)\Vert \le&{\bar{d}}, \quad \forall \,t\ge t_0+T(\overline{d},r). \end{aligned}$$
(44)
$$T(\overline{d},r)=\left\{ \begin{array}{ll} 0, &{}\quad \mathrm{if}{\quad }r\le {\overline{R}},\\ \frac{\xi _{2}r^{2}-\xi _{1}{\overline{R}}^{2}}{\eta {\overline{R}}^{2}-\theta }, &{}\quad \mathrm{if} \quad r>{\overline{R}}, \end{array} \right.$$
(45)
$$\begin{aligned} \overline{R}&=\sqrt{\frac{\xi _{1}}{\xi _{2}}}\overline{d}. \end{aligned}$$
(46)

□

Remark 3

The uniform boundedness and uniform ultimate boundedness of the controlled system are guaranteed deterministically regardless of the uncertainty. Since the design parameter \(\kappa _i\) impacts on both control \(\tau _{i2}\) and \(\tau _{i3}\) (\(\kappa _i\) determines the rate of adaptation and \(\tau _{i3}\) is relative to adaptive parameter), the optimization of \(\kappa _i\) will be very important to system performances. In the next section, we will find the optimal choice of \(\kappa _i\).

5 Control Parameter Optimization

According to (34) and Rayleigh’s inequality,

$$\begin{aligned} \dot{V}_{i}&\le -\frac{2\kappa _{i}}{\lambda _{\max }(P_{i})}\beta ^{\mathrm{T}}_{i}P_{i}\beta _{i}+2(1+\rho _{E_{i}}){\bar{\xi }}_i-2(1+\rho _{E_{i}})\times \nonumber \\&\qquad \bar{\kappa }_{i}{\left\| \hat{\alpha }_{i}-\alpha _{i}\right\| }^{2}+(1+\rho _{E_{i}})\bar{\kappa }_{i}\left( {\left\| \alpha _{i}\right\| }^2+{\left\| \hat{\alpha }_{i}-\alpha _{i}\right\| }^2\right) \nonumber \\&=-\frac{2\kappa _{i}}{\lambda _{\max }(P_{i})}\beta ^{\mathrm{T}}_{i}P_{i}\beta _{i}-(1+\rho _{E_{i}})\bar{\kappa }_{i}{\left\| \hat{\alpha }_{i}-\alpha _{i}\right\| }^{2}\nonumber \\&\quad +(1+\rho _{E_{i}})\bar{\kappa }_{i}{\left\| \alpha _{i}\right\| }^2+2(1+\rho _{E_{i}}){\bar{\xi }}_i\nonumber \\&=-\frac{2\kappa _{i}}{\lambda _{\max }(P_{i})}\beta ^{\mathrm{T}}_{i}P_{i}\beta _{i}-\kappa _i\bar{\kappa }_i(1+\rho _{E_{i}})(\hat{\alpha }_{i}-\alpha _{i})^{\mathrm{T}}\kappa ^{-1}_{i}\times \nonumber \\&\qquad (\hat{\alpha }_{i}-\alpha _{i})+(1+\rho _{E_{i}})\bar{\kappa }_{i}{\left\| \alpha _{i}\right\| }^2+2(1+\rho _{E_{i}}){\bar{\xi }}_i. \end{aligned}$$
(47)

Let \(\hat{\eta }=\min \{\frac{2}{\lambda _{\max }(P_{i})},\bar{\kappa }_i\}\), \(\hat{\theta }_i=(1+\rho _{E_{i}})\bar{\kappa }_{i}{\left\| \alpha _{i}\right\| }^2+2(1+\rho _{E_{i}}){\bar{\xi }}_i\). According to (22), then we have

$$\begin{aligned} \dot{V}_{i} \le -\kappa _i\hat{\eta }_iV_i+\hat{\theta }_i. \end{aligned}$$
(48)

Notice that (48) is a differential inequality, not a differential equation. Next, we will analyze (48) according to the procedure in [21].

Definition 1

[20] Let \(\omega (\psi ,t)\) be a scalar function of the scalar \(\psi\) and t in some open-connected set \({\mathcal {D}}\). A function \(\psi (t)\), \(t_{0}\le t \le {\bar{t}}\), \({\bar{t}} > t_{0}\) is a solution to the differential inequality

$$\begin{aligned} {\dot{\psi }} (t) \le \omega (\psi (t),t), \end{aligned}$$
(49)

on \([t_{0},{\bar{t}})\) if \(\psi (t)\) is continuous on \([t_{0},{\bar{t}})\) and its derivative on \([t_{0},{\bar{t}})\) satisfies (49).

In general, the solution to differential inequality (49) is not unique and not available. Thus, the analysis will be more difficult.

Theorem 2

[20] Let\(\omega (\phi (t),t)\)be continuous on an open-connected set\({{\mathcal {D}}}\in \mathbf{R}^2\)such that the initial value problem for the scalar equation

$$\begin{aligned} {\dot{\phi }}(t)=\omega (\phi (t),t), \quad \phi (t_0) = \phi _0, \end{aligned}$$
(50)

has a unique solution. If\(\phi (t)\)is a solution of (50) on\(t_0 \le t \le {\bar{t}}\)and\(\psi (t)\)is a solution of (49) on\(t_0 \le t \le {\bar{t}}\)with\(\psi (t_0) \le \phi (t_0)\), then\(\psi (t) \le \phi (t)\)for\(t_0 \le t \le {\bar{t}}\).

Theorem 2 provides an upper bound for the nonunique solution of (49). Since the solution of (49) is not unique and not available and the solution of (50) is unique, we often explore the upper bound of the solution to differential inequality (49) instead of the solution itself.

Theorem 3

[21] Consider differential inequality (49) and differential equation (50). Suppose that for some constant\(L>0\), the function\(\omega (\cdot )\)satisfies the Lipschitz condition

$$\begin{aligned} \vert \omega (\nu _{1},t) - \omega (\nu _{2},t) \vert \le L \vert \nu _{1} - \nu _{2} \vert , \end{aligned}$$
(51)

for all points\((\nu _{1},t)\), \((\nu _{2},t) \in {\mathcal {D}}\). Then, any function\(\psi (t)\)that satisfies differential inequality (49) for\(t_0 \le t \le {\bar{t}}\)also satisfies the inequality

$$\begin{aligned} \psi (t) \le \phi (t), \end{aligned}$$
(52)

for\(t_0 \le t \le {\bar{t}}\).

In order to solve differential inequality (48), we consider the differential equation

$$\begin{aligned} \dot{r}_{i}(t)= -\,\kappa _i\hat{\eta }_i r_i+\hat{\theta }_i,\quad r_{i}(t_{0})=V_{i0}=V_i(t_0). \end{aligned}$$
(53)

The function \(-\kappa _i\hat{\eta }_i r_i+\hat{\theta }_i\) satisfies the Lipschitz condition with \(L=\kappa _i\hat{\eta }_i\). Solving (53), then we get

$$\begin{aligned} r_{i}(t)=\left( V_{i0} - \frac{\hat{\theta }_i}{\kappa _i\hat{\eta }_i}\right) \exp \left[ -\kappa _i\hat{\eta }_i(t-t_0)\right] +\frac{\hat{\theta }_i}{\kappa _i\hat{\eta }_i}. \end{aligned}$$
(54)

By Theorems 2 and 3, we have

$$\begin{aligned} V_{i}(t)\le \left( V_{i0} - \frac{\hat{\theta }_i}{\kappa _i\hat{\eta }_i}\right) \exp \left[ -\kappa _i\hat{\eta }_i(t-t_0)\right] +\frac{\hat{\theta }_i}{\kappa _i\hat{\eta }_i}, \end{aligned}$$
(55)

for all \(t\ge t_0\).

Similarly, for any \(t_{s}\) and any \(\tau \ge t_{s}\), we can get

$$\begin{aligned} V_{i}({\tau })&\le \left( V_{is} - \frac{\hat{\theta }_i}{\kappa _i\hat{\eta }_i}\right) \exp \left[ -\kappa _i\hat{\eta }_i(\tau -t_s)\right] +\frac{\hat{\theta }_i}{\kappa _i\hat{\eta }_i}. \end{aligned}$$
(56)

Here \(V_{is}=V_{i}(t_{s})=\beta ^{\mathrm{T}}_{i}(t_{s})P_{i}\beta _{i}(t_{s})+(1+\rho _{E_{i}})\,[\hat{\alpha }_{i}(t_{s})-\alpha _{i}]^{\mathrm{T}}\kappa ^{-1}_{i}[\hat{\alpha }_{i}(t_{s})-\alpha _{i}]\), \(t_{s}\) is the time when control (18) is activated, which is not necessary to be \(t_0\). Let

$$\begin{aligned} \varGamma _{i} (\kappa _i, \tau , t_s)&:=\left( V_{is} - \frac{\hat{\theta }_i}{\kappa _i\hat{\eta }_i}\right) \exp \left[ -\kappa _i\hat{\eta }_i(\tau -t_s)\right] , \end{aligned}$$
(57)
$$\begin{aligned} \varGamma _{i{\infty }}(\kappa _i)&:=\frac{\hat{\theta }_i}{\kappa _i\hat{\eta }_i}. \end{aligned}$$
(58)

In (57), the \(\varGamma _i(\kappa _i, \tau , t_s)\) is a reflection of the system’s transient performance. For each \(\kappa _i\), \(t_s\), as \(\tau\) approaches to \(\infty\), \(\varGamma _{i} (\kappa _i, \tau , t_s)\) approaches to zero. In (58), the \(\varGamma _{i\infty }(\kappa _i)\) is relevant to the steady-state portion of the system’s performances.

Definition 2

For a fuzzy set \({\mathcal {A}}=\{\upsilon , \mu _{N}(\upsilon ) \mid \upsilon \in {A}\}\) and any function \(f(\upsilon ): A\rightarrow {\mathbf{R}}\), the D-operation of \(f(\upsilon )\) is defined as

$$\begin{aligned} {D[f(\upsilon )]}=\frac{\int _{A} f(\upsilon ) \mu _{A}(\upsilon ) d \upsilon }{\int _{A} \mu _{A} (\upsilon ) {\hbox {d}} \upsilon }. \end{aligned}$$
(59)

Remark 4

For any crisp constant \(c \in \mathbf{R}\), \(D[c f(\upsilon )]=c D[f(\upsilon )]\). The D-operation represents a defuzzification algorithm or a fuzzy-theoretic average. In the special case that \(f(\upsilon )=\upsilon\), the expression of D-operation is identical to the center of gravity defuzzification method.

We now propose the following performance index: For any \(t_s\), let

$$\begin{aligned} J_{i}(\kappa _i, t_s):&= \bar{\alpha }_{i} J_{i1}(\kappa _i, t_s) +\bar{\beta }_{i}J_{i2} (\kappa _i), \end{aligned}$$
(60)
$$\begin{aligned} J_{i1}(\kappa _i, t_s):&= D\left[ \int ^{\infty }_{t_s} \varGamma _{i}^2 (\kappa _i, \tau , t_s){\hbox {d}} \tau \right] , \end{aligned}$$
(61)
$$\begin{aligned} J_{i2}(\kappa _i)&= D\left[ \varGamma ^2_{i{\infty }}(\kappa _i)\right] . \end{aligned}$$
(62)

Here, the performance index is composed of two portions: \(J_{i1}\) and \(J_{i2}\). \(\bar{\alpha }_{i}>0\) is the weighting factor of \(J_{i1}\), and \(\bar{\beta }_{i}>0\) is the weighting factor of \(J_{i2}\). By the D-operation, \(J_{i1}\) can represent the average of the system’s overall transient performance and \(J_{i2}\) can represent the average of the steady-state performance.

Our optimal design problem can be stated as follows: For given \(P_i\), \(\bar{\kappa }_i\), \(\bar{\alpha }_{i}\) and \(\bar{\beta }_{i}\), choose the optimal value of the parameter \(\kappa _i>0\) such that the performance index \(J_{i}(\kappa _i, t_s)\) is minimized. By the integral operation, we have

$$\begin{aligned}&\int ^{\infty }_{t_s} \varGamma _{i}^2 (\kappa _i, \tau , t_s){\hbox {d}} \tau \nonumber \\&\quad =\left( V_{is} - \frac{\hat{\theta }_i}{\kappa _i\hat{\eta }_i}\right) ^2\int ^{\infty }_{t_s} \exp \left[ -2\kappa _i\hat{\eta }_i(\tau -t_s)\right] {\hbox {d}} \tau \nonumber \\&\quad =\left( V_{is} - \frac{\hat{\theta }_i}{\kappa _i\hat{\eta }_i}\right) ^2\left( \frac{1}{2\kappa _i\hat{\eta }_i}\right) . \end{aligned}$$
(63)

Taking the D-operation of (63), we have

$$\begin{aligned} J_{i1}(\kappa _i, t_s)&=D\left[ \int ^{\infty }_{t_s} \varGamma _{i}^2 (\kappa _i, \tau , t_s){\hbox {d}} \tau \right] \nonumber \\&=D\left[ \left( V_{is} - \frac{\hat{\theta }_i}{\kappa _i\hat{\eta }_i}\right) ^2\left( \frac{1}{2\kappa _i\hat{\eta }_i}\right) \right] \nonumber \\&=\frac{1}{2\kappa _i\hat{\eta }_i}D\left[ V^2_{is}\right] +\frac{1}{2\kappa ^3_i\hat{\eta }^3_i}D\left[ \hat{\theta }^2_i\right] \nonumber \\&\qquad -\frac{1}{\kappa ^2_i\hat{\eta }^2_i}D\left[ V_{is}\hat{\theta }_i\right] , \end{aligned}$$
(64)
$$\begin{aligned} J_{i2}(\kappa _i)&=D\left[ \varGamma ^2_{i{\infty }}(\kappa _i)\right] =\frac{1}{\kappa _i^2\hat{\eta }^2_i}D\left[ \hat{\theta }^2_i\right] . \end{aligned}$$
(65)

Substituting (64) and (65) into (60), then we get

$$\begin{aligned} J_{i}(\kappa _i, t_s)&=\frac{\bar{\alpha }_{i}}{2\kappa _i\hat{\eta }_i}D\left[ V^2_{is}\right] +\frac{\bar{\alpha }_{i}}{2\kappa ^3_i\hat{\eta }^3_i}D\left[ \hat{\theta }^2_i\right] \nonumber \\&\qquad -\frac{\bar{\alpha }_{i}}{\kappa ^2_i\hat{\eta }^2_i}D\left[ V_{is}\hat{\theta }_i\right] +\frac{\bar{\beta }_{i}}{\kappa _i^2\hat{\eta }^2_i}D\left[ \hat{\theta }^2_i\right] . \end{aligned}$$
(66)

Let \(\lambda _{i1}=\frac{1}{2\hat{\eta }_i}D\left[ V^2_{is}\right]\), \(\lambda _{i2}=\frac{1}{2\hat{\eta }^3_i}D\left[ \hat{\theta }^2_i\right]\), \(\lambda _{i3}=\frac{1}{\hat{\eta }^2_i}\times D\left[ V_{is}\hat{\theta }_i\right]\), \(\lambda _{i4}=\frac{1}{\hat{\eta }^2_i}D\left[ \hat{\theta }^2_i\right]\), then we can rewrite (66) as

$$\begin{aligned} J_{i}(\kappa _i, t_s)&=\lambda _{i1}\bar{\alpha }_{i}\kappa ^{-1}_{i}+\lambda _{i2}\bar{\alpha }_{i}\kappa ^{-3}_{i} -\lambda _{i3}\bar{\alpha }_{i}\kappa ^{-2}_{i}\nonumber \\&\qquad +\lambda _{i4}\bar{\beta }_{i}\kappa ^{-2}_{i}. \end{aligned}$$
(67)

The optimal design problem can be stated as follows: For any \(t_{s}\),

$$\begin{aligned} \min _{\gamma _{i}} J_{i}(\kappa _i, t_s), \qquad {\mathrm{subject\; to\;}} \gamma _{i}>0. \end{aligned}$$
(68)

To solve this problem, we take the first-order derivative of \(J_{i}\) with respect to \(\kappa _i\); then, we have

$$\begin{aligned} \frac{\partial {J_{i}}}{\partial {\kappa _{i}}}= -\,\frac{1}{\kappa ^{4}_{i}}\left[ \lambda _{i1}\bar{\alpha }_{i}\kappa ^{2}_{i}-\left( 2\lambda _{i3}\bar{\alpha }_{i} -2\lambda _{i4}\bar{\beta }_{i}\right) \kappa _i+3\lambda _{i2}\bar{\alpha }_{i}\right] . \end{aligned}$$
(69)

Let \(\tilde{a}:=\lambda _{i1}\bar{\alpha }_{i}\), \(\tilde{b}= -\,2\left( \lambda _{i3}\bar{\alpha }_{i}-\lambda _{i4}\bar{\beta }_{i}\right)\), \(\tilde{c}=3\lambda _{i2}\bar{\alpha }_{i}\). Then we rewrite (69) in the form of

$$\begin{aligned} \frac{\partial {J_{i}}}{\partial {\kappa _{i}}}= -\,\frac{1}{\kappa ^{4}_{i}}\left[ \tilde{a}\kappa ^{2}_{i}+\tilde{b}\kappa _i+\tilde{c}\right] . \end{aligned}$$
(70)

The stationary condition

$$\begin{aligned} \frac{\partial {J_{i}}}{\partial {\kappa _{i}}}=0 \end{aligned}$$
(71)

leads to the following algebraic quadratic equation:

$$\begin{aligned} \tilde{a}\kappa ^{2}_{i}+\tilde{b}\kappa _i+\tilde{c}=0. \end{aligned}$$
(72)

Theorem 4

Suppose\(D\left[ V^2_{is}\right] \ne 0\), \(D\left[ V_{is}\hat{\theta }_i\right] \ne 0\), \(D\left[ \hat{\theta }^2_i\right] \ne 0\), \(\tilde{b}<0\), \(\tilde{b}^2-4\tilde{a}\tilde{c}\ge 0\). For given\(\lambda _{i1}\), \(\lambda _{i2}\), \(\lambda _{i3}\), \(\lambda _{i4}\), the optimal solution\(\kappa _{{\mathrm{iopt}}}\)exists and is unique, which globally minimizes performance index (66).

Proof

Since \(D\left[ V^2_{is}\right] \ne 0\), then we have \(\lambda _{i1}\ne 0\). According to \(\lambda _{i1}\ne 0\), we get \(\tilde{a}\ne 0\). Therefore, the solutions of algebraic quadratic equation (72) are given by

$$\begin{aligned} \kappa _{i1}&=\frac{-\,\tilde{b}-\sqrt{\tilde{b}^2-4\tilde{a}\tilde{c}}}{2\tilde{a}}, \end{aligned}$$
(73)
$$\begin{aligned} \kappa _{i2}&=\frac{-\,\tilde{b}+\sqrt{{\tilde{b}}^2-4\tilde{a}\tilde{c}}}{2\tilde{a}}. \end{aligned}$$
(74)

Since \(\tilde{b}^2-4\tilde{a}\tilde{c}\ge 0\), we conclude that the solutions \(\kappa _{i1}\) and \(\kappa _{i2}\) are real solutions. Taking the second-order derivative of \(J_{i}\) with respect to \(\kappa _i\) yields

$$\begin{aligned} \frac{\partial {J^2_{i}}}{\partial {\kappa ^2_{i}}}&=2\tilde{a}\kappa ^{-3}_i+3\tilde{b}\kappa ^{-4}_i+4\tilde{c}\kappa ^{-5}_i\nonumber \\&=\frac{1}{\kappa ^5_i}\left( 2\tilde{a}\kappa ^2_i+3\tilde{b}\kappa _i+4\tilde{c}\right) . \end{aligned}$$
(75)

Substituting \(\kappa _i=\kappa _{i1}=\left( {-\,\tilde{b}-\sqrt{\tilde{b}^2-4\tilde{a}\tilde{c}}}\right) /{2\tilde{a}}\) into \(\frac{\partial {J^2_{i}}}{\partial {\kappa ^2_{i}}}\) yields

$$\begin{aligned} \frac{\partial {J^2_{i}}}{\partial {\kappa ^2_{i}}}\mid _{\kappa _i=\kappa _{i1}}&=\frac{1}{\kappa ^5_{i1}}\left[ 2\left( \tilde{a}\kappa ^2_{i1}+\tilde{b}\kappa _{i1}+\tilde{c}\right) +\tilde{b}\kappa _{i1}+2\tilde{c}\right] \nonumber \\&=\frac{1}{\kappa ^5_{i1}}\left( \tilde{b}\kappa _{i1}+2\tilde{c}\right) \nonumber \\&=\frac{1}{\kappa ^5_{i1}}\frac{-\,\tilde{b}^2-\,\tilde{b}\sqrt{\tilde{b}^2-4\tilde{a}\tilde{c}}+4\tilde{a}\tilde{c}}{2\tilde{a}}\nonumber \\&=\frac{\sqrt{\tilde{b}^2-4\tilde{a}\tilde{c}}}{\kappa ^4_{i1}}>0. \end{aligned}$$
(76)

Substituting \(\kappa _i=\kappa _{i2}=\left( {-\,\tilde{b}+\sqrt{\tilde{b}^2-4\tilde{a}\tilde{c}}}\right) /{2\tilde{a}}\) into \(\frac{\partial {J^2_{i}}}{\partial {\kappa ^2_{i}}}\) yields

$$\begin{aligned} \frac{\partial {J^2_{i}}}{\partial {\kappa ^2_{i}}}\mid _{\kappa _i=\kappa _{i2}}&=\frac{1}{\kappa ^5_{i2}}\left[ 2\left( \tilde{a}\kappa ^2_{i1}+\tilde{b}\kappa _{i2}+\tilde{c}\right) +\tilde{b}\kappa _{i2}+2\tilde{c}\right] \nonumber \\&=\frac{1}{\kappa ^5_{i2}}\left( \tilde{b}\kappa _{i2}+2\tilde{c}\right) \nonumber \\&=\frac{1}{\kappa ^5_{i2}}\frac{-\,\tilde{b}^2+\tilde{b}\sqrt{\tilde{b}^2-4\tilde{a}\tilde{c}}+4\tilde{a}\tilde{c}}{2\tilde{a}}\nonumber \\&=-\frac{\sqrt{\tilde{b}^2-4\tilde{a}\tilde{c}}}{\kappa ^4_{i2}}<0. \end{aligned}$$
(77)

Therefore, the optimal \(\kappa _{{\mathrm{iopt}}}\) [i.e., the solution \(\kappa _i\) of (68)] is given by

$$\begin{aligned} \kappa _{{\mathrm{iopt}}}=\frac{-\,\tilde{b}-\sqrt{\tilde{b}^2-4\tilde{a}\tilde{c}}}{2\tilde{a}}. \end{aligned}$$
(78)

The minimal performance index is given by

$$\begin{aligned} J_{i\min }&=\lambda _{i1}\bar{\alpha }_{i}\kappa ^{-1}_{{\mathrm{iopt}}}+\lambda _{i2}\bar{\alpha }_{i}\kappa ^{-3}_{{\mathrm{iopt}}} -\lambda _{i3}\bar{\alpha }_{i}\kappa ^{-2}_{{\mathrm{iopt}}}\nonumber \\&\qquad +\lambda _{i4}\bar{\beta }_{i}\kappa ^{-2}_{{\mathrm{iopt}}}. \end{aligned}$$
(79)

□

The optimal design problem is completely solved.

Remark 5

The current setting also applies in the special case that the fuzzy sets are crisp (i.e., \(D\left[ V^2_{is}\right] =V^2_{is}\), \(D\left[ \hat{\theta }^2_i\right] =\hat{\theta }^2_i\), \(D\left[ V_{is}\hat{\theta }_i\right] =V_{is}\hat{\theta }_i\)). With the optimal \(\kappa _{{\mathrm{iopt}}}\), adaptive robust control (18) renders system (2) uniform boundedness and uniform ultimate boundedness. Furthermore, the optimal design of the parameter \(\kappa _i\) globally minimizes the performance index \(J_{i}(\kappa _i, t_s)\).

6 Simulation Results

We consider a swarm robot system consisting of three robots to verify the effectiveness of proposed control. Each robot moves in a two-dimensional space. The position is described by \(q_i=[x_i, y_i]^{\mathrm{T}}, i=1,2,3\). The equation of motion of robot i is given by

$$\left[ \begin{array}{cc} m_i &{}\quad 0\\ 0&{}\quad m_i \end{array} \right] \left[ \begin{array}{c} \ddot{x}_i\\ \ddot{y}_i \end{array} \right] =F_i+\tau _i.$$
(80)

Here, \(M_i=\left[ \begin{array}{cc}m_i(\sigma _i)&{}\quad 0\\ 0&{}\quad m_i(\sigma _i)\end{array}\right]\).

For comparison purpose, we consider two types of control for the swarm robot system: adaptive robust control (18) and the linear-quadratic regulator (LQR) control. We chose LQR for comparison because it has been used as a benchmark for many new controls for comparisons in the past. The most common robustness measures attributed to the LQR are a one-half gain reduction in any input channel, an infinite gain amplification in any input channel or a phase error of plus or minus sixty degrees in any input channel. In addition, the LQR is also robust with respect to uncertainty in the real coefficients of the model (e.g., coefficients in the system matrix) and certain nonlinearities, including control switching and saturation.

For the adaptive robust controller,

$$\begin{aligned} \tau _{i}=\tau _{i1}+\tau _{i2}+\tau _{i3}. \end{aligned}$$
(81)

We decompose the mass \(m_i\) as \(m_i={\bar{m}}_i+\Delta m_i\). \({\bar{m}}_i\) is the nominal portion, and \(\Delta m_i\) is the uncertain portion. Then we have

$$\bar{M}_{i}=\left[ \begin{array}{cc} \bar{m}_{i}&{}\quad 0\\ 0&{}\quad \bar{m}_{i}\end{array}\right] ,\quad \Delta {M}_{i}=\left[ \begin{array}{cc} \Delta {m}_{i}&{}0\quad \\ 0&{}\quad \Delta {m}_{i}\end{array}\right] .$$
(82)

In the same concept, \(F_i\) is decomposed as

$$F_i = \bar{F}_i+\Delta F_i= \left[ \begin{array}{cc} \bar{f}_i\\ \bar{f}_i \end{array}\right] +\left[ \begin{array}{cc} \Delta {f}_i\\ \Delta {f}_i \end{array}\right] .$$
(83)

Suppose \(\Delta {m}_{i}\) is “close to 5” (belongs to a fuzzy set). Its associated membership function (triangular type) is given by

$$\mu _{\Delta m_i}(\nu ) = {\left\{ \begin{array}{ll} \frac{10}{50}\nu , &{} \quad 0\le \nu \le 5, \\ -\frac{10}{50}\nu +2, &{} \quad 5\le \nu \le 10, \\ \end{array}\right. }$$
(84)

Suppose \(\Delta {f}_{i}\) is “close to 0.2” (belongs to a fuzzy set). Its associated membership function (triangular type) is given by

$$\begin{aligned} \mu _{\Delta f_i}(\nu ) = {\left\{ \begin{array}{ll} \frac{10}{2}\nu , &{} \quad 0\le \nu \le 0.2, \\ -\frac{10}{2}\nu +2, &{} \quad 0.2\le \nu \le 0.4. \\ \end{array}\right. } \end{aligned}$$
(85)

For the adaptive law, Assumption 4 is met by choosing

$$\begin{aligned} \varPi _i(\alpha _i,q_i,\dot{q}_i,t)&= \alpha _{i1}\Vert \dot{q}_i\Vert ^2+\alpha _{i2}\Vert \dot{q}_i\Vert +\alpha _{i3} \nonumber \\&= [\alpha _{i1}\quad \alpha _{i2} \quad \alpha _{i3}]\left[ \begin{array}{c} \Vert \dot{q}_i\Vert ^2 \\ \Vert \dot{q}_i\Vert \\ 1 \end{array}\right] \nonumber \\=: & {} \alpha _i^{\mathrm{T}}\tilde{\varPi _i}(q_i,\dot{q}_i,t), \end{aligned}$$
(86)

where \(\alpha _{i1}, \alpha _{i2}, \alpha _{i3}\) are unknown constant parameters. For simplicity without loosing validity, an alternative choice of \(\varPi _i\) can be given as

$$\begin{aligned} \alpha _{i1}\Vert \dot{q}_i\Vert ^2+\alpha _{i2}\Vert \dot{q}_i\Vert +\alpha _{i3}\le & {} \alpha _i(\Vert \dot{q}_i\Vert ^2+\Vert \dot{q}_i\Vert +1) \nonumber \\&= \alpha _i(\Vert \dot{q}_i\Vert +1)^2 \nonumber \\=: & {} \alpha _i\tilde{\varPi _i}(q_i,\dot{q}_i,t), \end{aligned}$$
(87)

where \(\alpha _1 = \max \{\alpha _{i1}, \alpha _{i2}, \alpha _{i3}\}\). Then we have adaptive law for the i-th vehicle as follows:

$$\begin{aligned} \dot{\hat{\alpha }}_i = \kappa _i\left[ (\Vert \dot{q}_i\Vert +1)^2\Vert \beta _i\Vert -\bar{\kappa }_i\hat{\alpha }\right] . \end{aligned}$$
(88)

Here \(\beta _i\) is defined as (12). Following steps (13), (14) and (17), we finally have control (18). We firstly choose Condition 1 for simulations: \(\bar{m}_{i}=50\), \(\Delta {m}_{i}(t)=5\sin {t}\), \(\kappa _{i}=\bar{\kappa }_i=1\), \(\omega _i=1\), \(l_i=1\), \(P_i = I\), \(\bar{f}_i=10\), \(\Delta {f}_{i}(t)=2\sin {t}\). The initial values are: \(x_{1}(0) =0\), \(y_{1}(0)=0\), \(x_{2}(0)=3\), \(y_{2}(0)=4\), \(x_{3}(0)=5\), \(y_{3}(0)=0\), \(\dot{x}_{1}(0)=0.1\), \(\dot{y}_{1}(0)=0.1\), \(\dot{x}_{2}(0)=0.2\), \(\dot{y}_{2}(0)=0.2\), \(\dot{x}_{3}(0)=0.3\), \(\dot{y}_{3}(0)=0.3\), \(\hat{\alpha }_{1}(0)=0.2\), \(\hat{\alpha }_{2}(0)=0.2\), \(\hat{\alpha }_{3}(0)=0.2\). Then, we have \(V_{1s} = 49.58\), \(V_{2s} = 104.06\), \(V_{3s} = 89.87\), \(\tilde{a}_1 = 1229.1, \tilde{b}_1 = -\,87.1, \tilde{c}_1 = 1.2\), \(\tilde{a}_2 = 5414.2, \tilde{b}_2 = -\,184.6, \tilde{c}_2 = 1.2\), \(\tilde{a}_3 = 4038.1, \tilde{b}_3 = -\,159.2, \tilde{c}_3 = 1.2\). Thus, the algebraic quadratic equations are given by (\(\bar{\alpha }_i=\bar{\beta }_i=1\))

$$\begin{aligned} {\left\{ \begin{array}{ll} 1229.1\kappa _1^2- 87.1\kappa _1+1.2 = 0, \\ 5414.2\kappa _2^2-184.6\kappa _2+1.2 = 0, \\ 4038.1\kappa _3^2-159.2\kappa _3+1.2 = 0. \end{array}\right. } \end{aligned}$$
(89)

The optimal \(\kappa _{1{\mathrm{opt}}},\kappa _{2{\mathrm{opt}}},\kappa _{3{\mathrm{opt}}}\) is given by

$$\begin{aligned} \kappa _{1{\mathrm{opt}}}= 0.0189,\quad \kappa _{2{\mathrm{opt}}}= 0.0088,\quad \kappa _{3{\mathrm{opt}}}= 0.0103. \end{aligned}$$
(90)

Therefore, the adaptive robust controller is completely designed.

Figure 1 shows the trajectories of three robots under the optimal control [proposed control (81) with optimal parameters (90)]. The robots aggregate toward the center when they are far away from the center. They never collide with each other. In Fig. 2, we show the trajectories of three robots under the nonoptimal control (proposed control (81) with nonoptimal parameters \(\kappa _{1}= 1,\kappa _{2}= 0.8,\kappa _{3}= 0.85\)). It can be seen that, even though the behaviors of three robots are similar to those with optimal parameters: aggregations and repulsions, the performance is inferior to the optimal control. Figure 3 depicts the trajectories of robots under LQR control, and all the robots move to the lower left, which departs from the swarm performance.

Fig. 1
figure 1

The trajectories of three robots under optimal control

Full size image
Fig. 2
figure 2

The trajectories of three robots under nonoptimal control

Full size image
Fig. 3
figure 3

The trajectories of three robots under LQR control

Full size image

Next, we explore the control effort (i.e., \(\Vert \tau \Vert\)) and following error (i.e., \(\Vert \beta \Vert\)) for three cases: (i) with the optimal adaptive robust control, (ii) with the nonoptimal adaptive robust control, (iii) with the LQR control. Here,

$$\begin{aligned} \Vert \tau \Vert = \sqrt{\tau _1^2+\tau _2^2+\tau _3^2}, \qquad \Vert \beta \Vert = \sqrt{\beta _1^2+\beta _2^2+\beta _3^2}. \end{aligned}$$
(91)

In Figs. 4 and 5, the system performances under optimal adaptive robust control, nonoptimal adaptive robust control and LQR control are compared. As shown in Fig. 4, there is no significant difference of \(\Vert \tau \Vert\) between optimal control and nonoptimal control. The maximum value under optimal parameters is about 62, while the maximum value under nonoptimal is about 74. Both maximum values of \(\Vert \tau \Vert\) under adaptive controls (optimal and nonoptimal) are higher than that under LQR control. This is simply because that a learning process is necessary to adjust the adaptive parameters. When the adaptive parameters are close to their real value adequately, the performances are better. Although \(\Vert \tau \Vert\) under LQR control is smaller than that under optimal control at the very beginning, it decreases much more slowly than the other two controls. Figure 5 depicts the history of \(\Vert \beta \Vert\) under different controls. The errors under the adaptive controls are much more smaller than the error under LQR control. Meanwhile, the errors under the optimal adaptive robust control and nonoptimal adaptive robust control quickly fall in a very small region, while LQR control error decreases much more slowly. Compared with the performance under nonoptimal control, the optimal control is superior.

Fig. 4
figure 4

The comparison of control effort under optimal control, nonoptimal control and LQR control

Full size image
Fig. 5
figure 5

The comparison of the following error under optimal control, nonoptimal control and LQR control

Full size image

To show the robustness of the proposed optimal control, we apply the control to another different initial condition. Condition 2: \(\Delta {m}_{i}(t)=5\sin {10t}\), \(\Delta {f}_{i}(t)=2\sin {10t}\). \(x_{1}(0) =0\), \(y_{1}(0)=5\), \(x_{2}(0)=5\), \(y_{2}(0)=3\), \(x_{3}(0)=0\), \(y_{3}(0)=0\), \(\dot{x}_{1}(0)= -\,0.1\), \(\dot{y}_{1}(0)= -\,0.1\), \(\dot{x}_{2}(0)=0.3\), \(\dot{y}_{2}(0)=0.1\), \(\dot{x}_{3}(0)= -\,0.4\), \(\dot{y}_{3}(0)=0.2\). The comparisons of control effort \(\Vert \tau \Vert\) and the following error \(\Vert \beta \Vert\) are shown in Fig. 6a, b, respectively. Obviously, although the initial condition (position and velocity) is changed under Condition 2 and the uncertainties are in a higher frequency, the system performances are consistent to those under Condition 1. Both of \(\Vert \tau \Vert\) and \(\Vert \beta \Vert\) converge to a steady status quite soon.

Fig. 6
figure 6

The comparisons of control effort \(\Vert \tau \Vert\) and the following error \(\Vert \beta \Vert\) under optimal control with respect to different initial conditions

Full size image

Since the uncertainty in system is time varying, we may not have much information about it. The magnitude and the frequency of the variation of the uncertainty will certainly affect the control effort and system performance. Suppose the uncertainty in the mass is \(\Delta m_i = A\sin (\omega t)\), \(A\in [0,10], \omega \in [0,5]\). Let

$$\begin{aligned} \bar{\tau }&= \frac{\int _0^{\mathrm{T}}\tau (t){\hbox {d}}t}{T}|_{(A,\omega )}, \end{aligned}$$
(92)
$$\begin{aligned} \bar{\beta }&= \frac{\int _0^{\mathrm{T}}\beta (t){\hbox {d}}t}{T}|_{(A,\omega )}, \end{aligned}$$
(93)
$$\begin{aligned} \beta _{\max }&= \mathop {\max } \limits _{t}\Vert \beta (t)\Vert \Big |_{(A,\omega )}. \end{aligned}$$
(94)

Here, \(T = 5\) is the simulation time. The relations between \(\bar{\tau },\bar{\beta },\beta _{\max }\) and \(A,\omega\) are shown in Figs. 7, 8 and 9, respectively. The conclusions of these results are twofold: i) The magnitude of the uncertainty and the frequency of the variation of the uncertainty have influences on the \(\bar{\tau },\bar{\beta }\) and \(\beta _{\max }\). These indices increase as A and \(\omega\) increase. ii) The influences due to A and \(\omega\) are limited. The magnitudes of variations of \(\bar{\tau },\bar{\beta },\beta _{\max }\) are tiny. Their percentages are only 1.45%, 0.75%, 2.05%, respectively. This means the proposed optimal control has strong robustness.

For comparison, we investigate the performance index \(\bar{\tau }\) under LQR control. The result is shown in Fig. 10. It can be seen that the average control torque under LQR control is almost double of that under the proposed control with optimal parameters.

Fig. 7
figure 7

The average control effort \(\bar{\tau }\) with respect to A and \(\omega\)

Full size image
Fig. 8
figure 8

The average following error \(\bar{\beta }\) with respect to A and \(\omega\)

Full size image
Fig. 9
figure 9

The maximum following error \(\beta _{\max }\) with respect to A and \(\omega\)

Full size image
Fig. 10
figure 10

The average control effort \(\bar{\tau }\) under LQR control with respect to A and \(\omega\)

Full size image

7 Conclusion

Taking the uncertainty into account, we propose an optimal adaptive robust control design for the swarm robot system, which is deterministic. The uncertainty in the system is assumed to be fast time varying and bounded. Fuzzy set theory is introduced to describe the uncertainty of the system. Here the fuzzy set theory is not if–then rule-based, which is different from the fuzzy logic theory. The desired system performance is twofold: deterministic and fuzzy. The deterministic performance is to render the system uniform boundedness and uniform ultimate boundedness. The fuzzy performance consists of transient performance and steady-state performance, which is guaranteed by a fuzzy-based performance index. The control design parameter \(\kappa _{i}\) is selected as the optimization parameter such that the performance index is minimized. By solving the optimization problem, the closed-form expressions of the solution and the minimized performance index are obtained.