Rapid prediction of alongshore run-up distribution from near-field tsunamis

Abstract

Rapid prediction of the spatial distribution of the run-up from near-field tsunamis is critically important for tsunami hazard characterization. Even though significant advances have been made over the last decade, physics-based numerical models are still computationally intensive. Here, we present a response surface methodology (RSM)-based model called the tsunami run-up response function (TRRF). Derived from a discrete set of tsunami simulations, TRRF can produce a rapid prediction of a near-field tsunami run-up distribution that takes into account the influence of variable local topographic and bathymetric characteristics in a given region. This new method reduces the number of simulations required to build an RSM model by separately modeling the leading order contribution and the residual part of the tsunami run-up distribution. Using the northern region of Puerto Rico as a case study, we investigated the performance (accuracy, computational time) of the TRRF. The results reveal that the TRRF achieves reliable prediction while reducing the prediction time by six orders of magnitude (computational time: $< 1$ s per earthquake).

1 Introduction

Tsunamis are some of the most destructive and costly natural hazards for coastal areas around the world. The 2004 Indian Ocean tsunami and the 2011 Tohoku tsunami are prime examples of how tsunamis can cause extensive damage to coastal communities, especially in near-field areas (Titov et al. 2005; Wei et al. 2013). A near-field tsunami, which is a tsunami generated close to the coastline, involves a high risk for coastal communities because the first waves can arrive on shore in minutes (National Research Council 2011). To mitigate damage and build resilient coastal communities, it is critically important to develop rapid prediction capacities for a near-field tsunami run-up distribution along the coastlines. Physics-based numerical simulation is currently the most accurate method for predicting a tsunami run-up distribution. Though significant advances have been made over the last decade (LeVeque et al. 2011; Lin et al. 2015; Popinet 2015; Shi et al. 2012), these physics-based numerical models still remain time consuming. For example, robust probabilistic tsunami hazard assessment (PTHA) requires tsunami run-up estimates for a large number of scenarios to allow for accurate quantification of the hazard and related uncertainty (Mori et al. 2018). However, due to the computational burden associated with physics-based numerical simulation, a logic-tree approach is typically employed: it limits the number of scenarios based on historical earthquake characteristics (e.g., magnitude, recurrence interval) used to evaluate uncertainty in tsunami hazard (Annaka et al. 2007; Park and Cox 2016; Park et al. 2018). The issue with the logic-tree approach is that it relies on expert judgment, which is difficult to quantify reliability. On the other hand, to carry out a large number of scenario simulations, several studies applied an amplification factor method that can rapidly estimate the maximum inundation height from the simulated offshore tsunami amplitude (Davies et al. 2018; Glimsdal et al. 2019). However, limitations of the amplification factor approach are that the choice of the offshore reference point is somewhat subjective and that the approach still requires numerical simulation to obtain offshore tsunami amplitude. The computational burden associated with physics-based numerical simulation—especially for near-field tsunami forecasting—is a major obstacle. For this reason, pre-computed simulation databases are widely used. These databases can provide fast prediction by selecting the best-matched simulation or by interpolating between simulations immediately after the source mechanism is known (Kamigaichi 2011; Mulia et al. 2018; Setiyono et al. 2017). A problem with the database approach is that it can have substantial errors in real-world scenarios that do not exist in the selected databases.

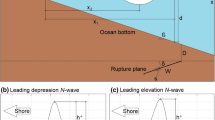
The response surface methodology (RSM) is an effective statistical-based approach for establishing a relationship between a set of input variables and the output of a system (Box and Wilson 1951; Myers et al. 2016). Once the RSM model is built, output can be rapidly estimated across the continuum of input spaces. However, because high-dimensional input requires a large number of simulations—which is prohibitively expensive—the RSM has not been used to predict a tsunami run-up distribution. For example, a tsunamigenic–earthquake (the input in an RSM model) is usually represented by nine fault parameters (Fig. 1). A full factorial design is one of the most widely employed designs of experiments (DoE) used to measure the response of every possible combination of independent variables. If we design the synthetic tsunami scenarios using a three-level full factorial approach with nine fault parameters, 19,683 ($=3^9$) simulations are required. Moreover, if the input/output relationship shows large nonlinearity, a higher level of DoE may be needed, which would necessitate exponentially more simulations.

Fig. 1

Schematic sketch of earthquake fault parameters: epicenter latitude (LAT), epicenter longitude (LON), fault length (LEN), fault width (WID), top-edge fault depth (DEP), strike angle (STR), dip angle (DIP), rake angle (RAK) and slip (SLP)

Here, we present a new methodology to rapidly predict the near-field tsunami run-up distribution: the tsunami run-up response function (TRRF). It is based on RSM but requires only 729 ($=3^6$) simulations through reducing input dimensionality. Input dimensionality is reduced through a decomposition of the leading order tsunami run-up contribution and the residual part of the run-up distribution. We demonstrated the TRRF approach in northern Puerto Rico, where a significant tsunami generated by an earthquake along the Puerto Rico Trench could devastate coastal communities on the northern shore (Grilli et al. 2010; López-Venegas et al. 2015; Reid and Taber 1919) (Fig. 2).

Fig. 2

Map of northern Puerto Rico. Open black circles represent the epicenters of historical earthquakes [$M_w\ge 4.5$, (USGS 2017)]. The filled black circles and dashed black lines represent the epicenters of NOAA’s pre-defined unit sources and fault orientation, respectively (Gica et al. 2008). The dashed red line represents the contour line where the water depth is 8 km. The blue dashed square represents the region where the National Geophysical Data Center (NGDC)’s 3-sec topographic grid (NGDC 2005) is used for numerical simulation

2 Tsunami run-up response function (TRRF)

The main concept of TRRF is to decompose the tsunami run-up distribution R(x) into source run-up S(x) and topographic run-up T(x) (Fig. 3):

$$\begin{aligned} R(x)=S(x)+T(x) \end{aligned}$$

(1)

where the x-axis is parallel to the coastline.

Fig. 3

Example of a tsunami run-up distribution, b source run-up and c topographic run-up. The fault parameter condition is as follows: $LON = 66.4^{{\circ }}$ W, $LAT =19.3^{{\circ }}$ N, $STR=90^{{\circ }}$, $DIP=20^{{\circ }}$, $RAK=90^{{\circ }}$, $LEN=90$ km, $WID=40$ km, $SLP=2$ m, $DEP=30$ km. The a, b and c on the second panel are the coefficients of the OS formula (Eq. 2)

The source run-up S(x) is a leading order contribution that can be represented by Okal and Synolakis (2004)’s empirical formula (hereafter OS formula):

$$\begin{aligned} S(x)=\frac{b}{\left[ \frac{x-c}{a}\right] ^2+1} \end{aligned}$$

(2)

where the coefficient a is related to the width of the source run-up, b is the maximum source run-up, and c is the distance from the x-axis origin to the location of the maximum source run-up.

The topographic run-up T(x) is the residual run-up remaining after subtracting S(x) from R(x). It represents the local (de)amplification of the incoming tsunami wave and the resulting run-up arising from topographic variation. The T(x) can be normalized as follows, hereafter called normalized topographic run-up ${\mathrm{NT}}(x)$.

$$\begin{aligned} {\mathrm{NT}}(x)=\frac{T\left( x\right) }{S\left( x\right) } \end{aligned}$$

(3)

The default axis of the TRRF approach is oriented as follows: x-axis is east–west direction ($x_{\mathrm{E}}$) and y-axis is north–south direction ($y_{\mathrm{N}}$). Thus, if the coastline is not aligned east–west, the axis should be rotated based on the east–west direction until the x-axis is parallel to the coastline as follows:

$$\begin{aligned}&{x=x_{\mathrm{E}} \cos \delta + y_{\mathrm{N}} \sin \delta } \end{aligned}$$

(4)

$$\begin{aligned}&{y=-x_{\mathrm{E}} \sin \delta + y_{\mathrm{N}} \cos \delta } \end{aligned}$$

(5)

where $\delta$ is an angle between the east–west direction and the coastline in a counterclockwise direction from East, x is a rotated x-axis, and y is a rotated y-axis. Also, the TRRF approach is defined based on a Cartesian coordinate system while the epicenters are defined in a spherical coordinate system. To align the coordinate systems, the unit of the epicenter should be converted from degrees (LON, LAT) to kilometers (X, Y) where X is shortest distance from the rotated y-axis to the epicenter and Y is shortest distance from the rotated x-axis to the epicenter.

Based on the main concept, the TRRF can predict a tsunami run-up distribution $R^p (x)$ by putting the source run-up $S^p(x)$ and the normalized topographic run-up ${\mathrm{NT}}^p(x)$ (where superscript p represents prediction) to the following equation:

$$\begin{aligned} R^p(x)=S^p(x)\left[ 1+{\mathrm{NT}}^p(x)\right] \end{aligned}$$

(6)

where ${\mathrm{NT}}^p(x)$ is the 50th percentile (or median) of ${\mathrm{NT}}(x)$ among all the simulations used to build the TRRF. Note that the ${\mathrm{NT}}^p(x)$ is independent of the earthquake fault parameters. The source run-up $S^p(x)$ can be estimated by inputting the OS formula coefficients a, b, and c into Eq. 2. The RSM approach is applied to estimate the OS formula coefficients a and b from six parameters (hereafter RSM parameters):

$$\begin{aligned} a= f_a({Y}, LEN, WID, DIP, SLP, DEP) \end{aligned}$$

(7)

$$\begin{aligned} b= f_b({Y}, LEN, WID, DIP, SLP, DEP) \end{aligned}$$

(8)

where $f_a$ and $f_b$ are the best-fitting curves to these coefficients; hereafter, these curves are called RSM functions. Since the RSM function inputs consist of six parameters, 729 ($=3^6$) simulations are required to derive RSM functions following a three-level full factorial design (see Appendix 1).

The epicenter location along the x-axis, X, is excluded in the RSM function inputs because x-axis runs parallel to the coastline. In this condition, the coefficients a and b are independent of X, and the coefficient c is equal to X by the definition of the OS formula (see Eq. 2):

$$\begin{aligned} {c=X} \end{aligned}$$

(9)

The strike angle STR and rake angle RAK are also not included in the RSM function inputs because the OS formula (Okal and Synolakis 2004) is only applicable to an earthquake fault oriented in shore-parallel strike direction with $90 ^{{\circ }}$ rake angle. Since this is not the only case that occurs in nature, we developed a method that can represent a fault where strike direction is not parallel to the coastline and rake angle is not $90 {^{\circ }}$ as a series of hypothetical faults where the strike direction is parallel to the coastline and the rake angle is $90 {^{\circ }}$, hereafter, called the angle projection (AP) method.

Section 2.1 will describe the procedures of building a TRRF. Section 2.2 will explain the AP method, and Sect. 2.3 will describe the procedures of predicting a tsunami run-up distribution once the TRRF is built.

Fig. 4

Computational flow of TRRF development. The inputs, the processing steps and the outputs are represented in light red box, white dashed box and light blue box, respectively. The red lines represent the process where the response surface methodology (RSM) approach is applied

2.1 TRRF development

Figure 4 shows the procedure of TRRF development. The first step is to simulate 729 tsunamigenic–earthquake scenarios using a physics-based numerical model. The second step is to extract the run-up and apply the OS formula (Eq. 2) to obtain the normalized topographic run-up ${\mathrm{NT}}^p(x)$ (Eq. 3). The last step is to fit the earthquake fault parameters and the OS formula coefficients (a and b) to the second-order polynomial model to obtain the RSM functions (Eqs. 7 and 8). Once the ${\mathrm{NT}}^p(x)$ and the RSM functions are derived, this procedure does not have to be repeated to predict the tsunami run-up distribution.

2.2 Angle projection (AP) method

The AP method comprises three steps: adjustment of strike angle and rake angle, fault rotation and decomposition of slip.

2.2.1 Adjustment of strike angle and rake angle

The direction of near-field tsunami propagation is related to the interaction between the strike angle STR and the rake angle RAK. To consider the interaction between STR and RAK, the first step involves adjusting the STR and the RAK as follows (Fig. 5):

$$\begin{aligned} \theta= & {} {\alpha [f_{AP}(STR, \delta )-90^{{\circ }} ] + 90^{{\circ }}+\beta (RAK-90^{{\circ }})} \end{aligned}$$

(10)

$$\begin{aligned} \lambda= & {} \gamma (RAK-90^{{\circ }})+90^{{\circ }} \end{aligned}$$

(11)

where $\theta$ is the adjusted strike angle ($0< \theta <180$) and $\lambda$ is the adjusted rake angle ($0< \lambda <180$) based on the rotated axes. The $\alpha$, $\beta$ and $\gamma$ are the site-specific coefficients that should be calibrated in advance (see Sect. 4). The $f_{AP}$ is a function of $STR \ (0^{{\circ }} - 360^{{\circ }})$ and $\delta \ (0^{{\circ }} - 360^{{\circ }})$ defined as follows:

$$\begin{aligned} {f_{AP}(STR, \delta )= {\left\{ \begin{array}{ll} {STR+\delta , \quad \ 0^{{\circ }} \le STR+\delta < 360^{{\circ }}} \\ {STR+\delta -360^{{\circ }}, \quad \ 360^{{\circ }} \le STR+\delta }. \end{array}\right. } } \end{aligned}$$

(12)

Fig. 5

Schematic sketch of step 1 of AP method. The yellow-filled rectangle is the original fault where STR is strike angle and RAK is rake angle. The red rectangle represents the adjusted fault where $\theta$ is the adjusted strike angle and $\lambda$ is the adjusted rake angle based on the rotated axis (blue). The arrows represent the slip direction

2.2.2 Fault rotation

If the adjusted strike direction is parallel to the coastline ($\theta = 90 ^{{\circ }}$) and the adjusted rake angle $\lambda$ is $90 ^{{\circ }}$, the maximum source run-up will be located at the epicenter location along the x-axis, X. On the other hand, if the adjusted strike direction is not parallel to the coastline ($\theta \ne 90 ^{{\circ }}$), the location of the maximum source run-up will be shifted to a direction perpendicular to the adjusted strike direction. To consider the location of the maximum source run-up depending on the adjusted strike angle, the second step involves rotating the adjusted fault ($\theta \ne 90^{{\circ }}$) until $\theta$ becomes $90 ^{{\circ }}$ (Fig. 6). The epicenter of the rotated fault ($X_1^p$, $Y_1^p$) can be calculated as follows:

Fig. 6

Schematic sketch of step 2 of AP method. The red rectangle is the adjusted fault where the epicenter is (X, Y). The green rectangle represents the rotated fault where the epicenter is ($X^p_1$, $Y^p_1$). The two red lines are of the same length. One line is perpendicular to the strike direction spanning from the epicenter of the adjusted fault to the point where it meets the coastline. The other line is the vertical distance from the epicenter of the rotated fault to the coastline

$$\begin{aligned} X_1^p= & {} X+\frac{Y}{{\rm tan} (\theta )} \end{aligned}$$

(13)

$$\begin{aligned} Y_1^p= & {} \frac{Y}{|{\rm sin} (\theta )|} \end{aligned}$$

(14)

2.2.3 Decomposition of slip

If the adjusted rake angle $\lambda$ is not $90 ^{{\circ }}$, the run-up will be spread in the slip direction. To consider the spread of run-ups depending on the adjusted rake angle, the third step involves representing the rotated fault ($\lambda \ne 90^{{\circ }}$) as a series of hypothetical faults having slips perpendicular to the coastline ($\lambda =90^{{\circ }}$) (Fig. 7). Since the tsunami energy is proportional to SLP, we assume that the source run-up will be spread proportionally to a component of SLP parallel to the coastline. Based on this assumption, while the LEN, WID, DEP and DIP are identical to the original fault, the epicenter ($X_i^p$, $Y_i^p$) and $SLP_i^p$ of the ith hypothetical fault ($i=1,2,\ldots ,n$) is defined as follows:

$$\begin{aligned} X_i^p= & {} X_1^p+\frac{X_n^p-X_1^p}{n-1}(i-1) \end{aligned}$$

(15)

$$\begin{aligned} Y_i^p= & {} Y_1^p+\frac{Y_n^p-Y_1^p}{n-1}(i-1) \end{aligned}$$

(16)

$$\begin{aligned} SLP_i^p= & {} SLP_1^p+\frac{SLP_n^p-SLP_1^p}{n-1}(i-1) \end{aligned}$$

(17)

where n is the total number of hypothetical faults, which should be calibrated in advance (see Sect. 4). The $SLP_1^p$ and $SLP_n^p$ are the slips of the first and last hypothetical faults, respectively, defined as follows:

Fig. 7

Schematic sketch of step 3 of AP method. The green rectangle represents the first hypothetical fault where the epicenter is ($X^p_1$, $Y^p_1$) and the slip is $SLP^p_1$. The blue rectangle represents the last hypothetical fault among a series of hypothetical faults where the epicenter is ($X^p_n$, $Y^p_n$) and slip is $SLP^p_n$. Gray circles and arrows represent the epicenters and the slips of the hypothetical faults, respectively; these are linearly distributed between the first hypothetical fault and the last hypothetical fault. Two red lines are of the same length. One line is parallel to the slip direction spanning from the epicenter of the rotated fault to the point where it meets the coastline. The other line is the vertical distance from the epicenter of the last hypothetical fault to the coastline

$$\begin{aligned} SLP_1^p= & {} SLP|{\rm sin}(\lambda )| \end{aligned}$$

(18)

$$\begin{aligned} SLP_n^p= {} SLP|{\rm cos}(\lambda )| \end{aligned}$$

(19)

The ($X_n^p$, $Y_n^p$) are the epicenter of the last hypothetical fault and can be calculated based on a geometric setup (see two red lines in Fig. 7):

$$\begin{aligned} X_n^p= & {} X_1^p-\frac{Y_1^p}{{\rm tan}(\lambda )} \end{aligned}$$

(20)

$$\begin{aligned} Y_n^p= & {} \frac{Y_1^p}{|{\rm sin} (\lambda )|} \end{aligned}$$

(21)

Following this procedure, a fault where strike direction is not parallel to the coastline and/or rake angle is not $90^{{\circ }}$ can be converted into a series of hypothetical faults where the strike direction is parallel to the coastline and rake angle is $90^{{\circ }}$.

2.3 TRRF application for prediction

Figure 8 shows the procedure for how the TRRF predicts a tsunami run-up distribution once the TRRF is built. The first step is to convert the earthquake fault into a series of hypothetical faults using the AP method. The second step is to estimate the OS formula coefficients $a_i^p$, $b_i^p$ ($i=1,2,\ldots ,n$) of hypothetical faults using the RSM functions (Eqs. 7 and 8). The third step is to estimate the OS formula coefficient $c_i^p$ ($i=1,2,\ldots ,n$) by inputting the $X_i^p$ into Eq. 9. The fourth step is to estimate the final source run-up $S^p(x)$ by inputting the OS formula coefficients ($a_i^p$, $b_i^p$, $c_i^p$) into Eq. 2 and taking the maximum values of the estimated source run-ups for all hypothetical faults. Finally, the tsunami run-up distribution $R^p (x)$ can be estimated by inputting the source run-up $S^p(x)$ and the normalized topographic run-up ${\mathrm{NT}}^p(x)$ to Eq. 6.

Fig. 8

Computational flow of TRRF application for prediction. The inputs, the processing steps and the outputs are represented in light red box, white dashed box and light blue box, respectively. The subscript i represents the ith hypothetical fault and the superscript p represents the prediction. MAX represents the process of extracting the maximum value along the x-axis

3 TRRF development for northern Puerto Rico

3.1 Numerical simulation

In this study, we assumed that the coastline of northern Puerto Rico runs parallel to east–west direction ($\delta =0^{{\circ }}$), and thus the x-axis is parallel to east–west direction and y-axis is parallel to north–south direction (Fig. 2). In this condition, the epicenter location along the x-axis (X) is only related to the epicenter longitude (LON) and the epicenter location along the y-axis (Y) is only related to the epicenter latitude (LAT).

The 729 tsunamigenic–earthquake scenarios were simulated based on the numerical model Basilisk, which solves the Green–Naghdi equations and employs both Adaptive Mesh Refinement (AMR) and parallelization to facilitate efficient computation. The Basilisk model has not only been validated with several benchmark problems but also been applied to several tsunami research (Lane et al. 2017; Popinet 2015; Zainali et al. 2018). The 729 scenarios were designed as shown in Table 1. The range of the epicenter latitude LAT was determined based on National Oceanic and Atmospheric Administration (NOAA)’s pre-defined unit sources and historical earthquake records in northern Puerto Rico (Fig. 2). The range of the fault length LEN, fault width WID and slip SLP was set based on the assumption that the moment magnitude ($M_w$) should be larger than 7.0 for a tsunami to occur. We used the empirical regression of Hanks and Kanamori (1979) and fundamental equation of Aki (1966) to calculate the moment magnitude:

$$\begin{aligned} M_w= & {} \frac{2}{3}\left[ \log {\left( M_0\right) }-9.05\right] \end{aligned}$$

(22)

$$\begin{aligned} M_0= & {} \mu ( {\rm LEN} \times {\rm WID} \times SLP ) \end{aligned}$$

(23)

where $M_0$ is a seismic moment (Nm), $\mu$ is rigidity modulus of the Earth’s crust (${\mathrm{Nm}}^{-2}$), and the units of LEN, WID and SLP are in meters. We assumed that the rigidity modulus $\mu$ is $4.2\times {10}^{10}\,{\mathrm{Nm}}^{-2}$ in northern Puerto Rico following Grilli et al. (2010). We limited the maximum moment magnitude to 8.0 considering the historical seismic events that led to tsunamis in Puerto Rico (Nealon and Dillon 2001). We assumed that the LEN should be longer than the WID, and the range of the LEN and WID should follow the scaling laws introduced by Blaser et al. (2010). The range of the dip angle DIP and the depth of the top edge DEP were determined based on the characteristics of a subduction-interface earthquake that usually causes a tsunami. According to Thingbaijam et al. (2017), subduction-interface earthquakes occur between $10 ^{{\circ }}$ and $30 ^{{\circ }}$ dip angles and within a slip-centroid depth of $50 \ km$. We assumed that the fault rupture occurred instantaneously, where the initial free surface displacement was calculated using the Okada equations (Okada 1985). Nearshore bathymetry and onshore topography in the inundation zone were from the 3 arc-second National Geophysical Data Center data set (NGDC 2005), while the 1 arc-minute ETOPO1 data set (Amante and Eakins 2009) was used for the entire region (Fig. 2). Considering the grid size, the minimum and maximum AMR levels were set to 5 and 11, respectively. The bottom friction was parameterized using a quadratic drag law in which the bottom drag coefficient $C_f$ was set to $10^{-4}$. The numerical model was used to simulate two hours of tsunami propagation to ensure that complete inundation of the onshore areas was captured. The maximum envelope of the water level was interpolated bilinearly onto a regular grid ($0.001 ^{{\circ }}$ interval). We excluded four simulations, which failed to finish the simulations because of instability issue, to build the TRRF. A sensitivity test showed that the impact of building the TRRF without four simulations on the accuracy of the TRRF was negligible (see Appendix 2). We obtained tsunami run-up distribution R(x) by extracting the maximum inundation height along the coastline ranging from $67.100 ^{{\circ }}$ W to $65.620 ^{{\circ }}$ W. The tsunami simulations were conducted in a spherical coordinate system, but the TRRF was defined based on a Cartesian coordinate system. To align the coordinate systems, Vincenty’s formulae (Vincenty 1975) were used to convert the unit of the geometric point from degrees to kilometers. We set the origin at ($18.450 ^{{\circ }}$ N, $66.400 ^{{\circ }}$ W) and used it as a reference point in Vincenty’s formulae.

3.2 RSM functions and ${\mathrm{NT}}^p(x)$

The RSM functions and the normalized topographic run-up ${\mathrm{NT}}^p(x)$ were derived as follows. We calculated the OS formula coefficients a and b by fitting the tsunami run-up distribution R(x) to the OS formula for each simulation (Eq. 2). Here, the OS formula coefficient c was fixed to zero because we set the longitude of the origin and the epicenter longitude of simulations identically (Eq. 9). We derived the RSM functions by fitting the RSM parameters to the OS formula coefficients a and b using second-order polynomial models. The normalized topographic run-up ${\mathrm{NT}}(x)$ was calculated for each simulation following Eqs. 1–3. We derived ${\mathrm{NT}}^p(x)$ by selecting the 50th percentile of ${\mathrm{NT}}(x)$ among all simulations (Fig. 9).

Fig. 9

Normalized topographic run-up ${\mathrm{NT}}^p(x)$ of northern Puerto Rico. The gray represents the range between 1st and 99th percentiles

Table 1 Range of fault parameters used for TRRF development and TRRF prediction

3.3 Fault parameter range for TRRF prediction

We set the fault parameter range for TRRF prediction as shown in Table 1. The range of six fault parameters (LAT, LEN, WID, DIP, SLP, DEP) was set to the same range as the tsunamigenic–earthquake scenarios used in the TRRF development. In order to avoid an extrapolation beyond the inference space of the RSM functions, we only considered cases where all epicenter of the hypothetical faults fell within the range for LAT. The range of LON was set to the extent that the fault does not fall outside the region used in the numerical simulation. The strike angle is usually set in the direction tangential to the subduction zone (Gica et al. 2008), and thus we set the range of STR to be from $50^{{\circ }}$ to $130^{{\circ }}$. Even though some tsunamis are generated by strike-slip earthquakes (Heidarzadeh et al. 2017), most tsunamis are caused by thrust earthquakes. Following this characteristic of RAK, we set the range of RAK to be from $50^{{\circ }}$ to $130^{{\circ }}$.

4 TRRF calibration

To apply the AP method, (1) the site-specific coefficients ($\alpha$, $\beta$ and $\gamma$) of Eqs. 10 and 11 and (2) the number of hypothetical faults (n) must be defined in advance.

Fig. 10

Best $\theta$ values (that show the minimum NRMSE) associated with varying strike angles. Dashed line represents the best-fitting line

To determine the coefficient $\alpha$, we simulated 80 additional cases (hereafter called STR cases) that were not used in building the TRRF. These additional cases had a fixed longitude of $66.400 ^{{\circ }} {\mathrm{W}}$, where 10 sets varying the RSM parameters were randomly selected. For each set, eight different strike angles between $50 ^{{\circ }}$ and $130 ^{{\circ }}$ were selected, at $10^{{\circ }}$ intervals, except $90 ^{{\circ }}$. The rake angle was fixed to $90 ^{{\circ }}$ so that $\theta$ could be independent of $\beta$ and $\lambda$ could be fixed to $90 ^{{\circ }}$ (see Eqs. 10 and 11). The coefficient $\alpha$ was selected by minimizing TRRF error as represented by normalized root mean square error (NRMSE):

$$\begin{aligned} NRMSE=\frac{\sqrt{\frac{1}{N}\sum _{x=1}^{N}\left[ R^p(x)-{\hat{R}}^p(x)\right] ^2}}{{\mathrm{max}}\left[ {\hat{R}}^p(x)\right] -{\mathrm{min}}\left[ {\hat{R}}^p(x)\right] } \times 100 \, (\%) \end{aligned}$$

(24)

where $R^p(x)$ is the tsunami run-up distribution predicted by the TRRF, ${{\hat{R}}^p}(x)$ is the numerically simulated tsunami run-up distribution, and N is the total number of alongshore locations. For each case, we found the $\theta$ value that shows the minimum NRMSE in the range of $45 ^{{\circ }}$ and $135 ^{{\circ }}$. We fixed the number of hypothetical faults (n) to 100, which was large enough to provide a convergent prediction. We set the coefficient $\alpha$ to 0.585 by fitting the STR and the $\theta$ in Eq. 10 (Fig. 10).

To determine the coefficients ($\beta$ and $\gamma$), we simulated 80 additional cases (hereafter called RAK cases) where all fault parameters but the rake angle were set in the same way as the STR cases. Unlike the STR cases, the rake angle was set to the same value as the strike angle. For each case, we found the $\theta$ value that shows the minimum NRMSE in the range of $45 ^{{\circ }}$ and $135 ^{{\circ }}$. At the same time, we found the $\lambda$ value that shows the minimum NRMSE in the range of $90 ^{{\circ }}$ and $179 ^{{\circ }}$ (if $RAK < 90 ^{{\circ }}$) or the $\lambda$ value that shows the minimum NRMSE in the range of $1 ^{{\circ }}$ and $90 ^{{\circ }}$ (if $RAK \ge 90 ^{{\circ }}$). We set the coefficient $\beta$ to $-0.284$ by fitting the RAK and the $\theta$ to Eq. 10 (Fig. 11a). We set the coefficient $\gamma$ to $-0.754$ by fitting the RAK and the $\lambda$ in Eq. 11 (Fig. 11b).

Fig. 11

Best a $\theta$ and b $\lambda$ values (that show the minimum NRMSE) associated with varying rake angles. Dashed line represents the best-fitting line

To determine the number of hypothetical faults (n), we revisited the RAK cases. For each case, we decreased the number of hypothetical faults (n) from 100 to 2 (Fig. 12). Then, we found the minimum value needed for convergence since the computational time increases as n increases. In this study, we set the n to 30, which shows less than $0.1 \%$ difference in NRMSE.

Fig. 12

Relative NRMSE differences as the total number of hypothetical faults (n) increases. $NRMSE_n$ is the NRMSE of the case where n hypothetical faults are considered. $NRMSE_{100}$ is the NRMSE of the case where 100 hypothetical faults are considered

5 TRRF performance

5.1 Accuracy

The accuracy of the TRRF was investigated by comparing TRRF predictions against the direct numerical simulations. We systematically tested the accuracy of the TRRF as follows:

• Test 1: To test whether the RSM functions and the ${\mathrm{NT}}^p(x)$ are valid, we simulated 100 additional cases in which the RSM parameters were randomly selected, while the epicenter longitude was fixed to $66.400 ^{{\circ }} {\mathrm{W}}$ and both the strike and rake angles were fixed to $90 ^{{\circ }}$.

• Test 2: To test whether Eq. 9 is valid, we simulated 100 additional cases in which the fault parameters were selected based on the following conditions. While both the strike and rake angles were fixed to $90 ^{{\circ }}$, 10 sets of the RSM parameters were randomly selected. For each set, 10 longitudes were selected at a uniform interval in the range of $65.800 ^{{\circ }} {\mathrm{W}}$ and $67.000 ^{{\circ }} {\mathrm{W}}$.

• Test 3: To test the performance of the AP method, we investigated the RAK cases defined in Sect. 4.

• Test 4: To test the overall accuracy of the TRRF, we simulated 100 additional cases in which all fault parameters were randomly selected.

Fig. 13

Comparison of OS formula coefficients between Basilisk (simulated) and TRRF (predicted): a OS formula coefficient a, b OS formula coefficient b

Fig. 14

Selected examples of tests: a, b Test 1. c , d Test 2. e and f Test 3. g, h Test 4. Black line and red line are the tsunami run-up distributions predicted by Basilisk and TRRF, respectively. The number inside the bracket above each pane represents the fault parameters in this sequence: $LON (^{{\circ }} {\mathrm{W}})$, $LAT (^{{\circ }} {\mathrm{N}})$, $STR (^{{\circ }})$, $DIP (^{{\circ }})$, $RAK (^{{\circ }})$, $LEN {\mathrm{(km)}}$, $WID {\mathrm{(km)}}$, $SLP {\mathrm{(m)}}$, $DEP {\mathrm{(km)}}$. The blue line in c and d represents the location of epicenter longitude

Figure 13 shows the comparison of the OS formula coefficients based on the 100 cases of Test 1. Note that these 100 cases were never used to derive the RSM functions. The x-axis is the OS formula coefficient obtained by fitting the numerical simulation result to the OS formula. The y-axis is the OS formula coefficient obtained by putting the fault parameters to the RSM functions. The high-correlated results confirm that the RSM functions can predict the OS formula coefficients well.

Figure 14 shows the selected alongshore tsunami run-up predictions for each test. Figure 14a and b shows the best case (minimum NRMSE) and the worst case (maximum NRMSE) of Test 1, respectively. In both cases, the TRRF prediction followed the overall trend of the numerical simulation result well. However, there are a few localities where the TRRF did not predict the run-up well such as the run-ups near $66.2^{{\circ }} {\mathrm{W}}$ in the worst case. Figure 14c and d displays the Test 2 results where all the fault parameter conditions were the same except the epicenter longitude. The results show that the TRRF can effectively capture the influence of the epicenter longitude. Figure 14e and f presents the Test 3 results in which all fault parameter conditions are the same except for the strike and rake angles. Note that the TRRF predictions strongly align with the numerical simulation results while capturing the asymmetrical shape of the tsunami run-up distribution. Figure 14g and h shows the best case (minimum NRMSE) and worst case (maximum NRMSE) of Test 4, respectively. Both examples have a few localities where the TRRF did not predict the run-ups well, but the overall trend of the TRRF predictions agrees well with the numerical simulation results.

Fig. 15

Overall error of TRRF: a Normalized root mean square error (%), b Normalized bias error (m). The violin plot shows the distribution of test results with the box and whisker plot inside where the black box represents the interquartile range, the black lines stretched from the box represent the range of 1.5 times of the interquartile range, and the white dot represents the median. p is a p-value of Welch’s t-test

Figure 15 shows the overall error of the TRRF in each corresponding test where the mean bias error (MBE) is defined as follows:

$$\begin{aligned} {MBE = \frac{1}{N}\sum _{x=1}^{N}\left[ R^p(x)-{\hat{R}}^p(x)\right] } \end{aligned}$$

(25)

where $R^p(x)$ is a TRRF prediction, ${{\hat{R}}^p}(x)$ is a numerically simulated tsunami run-up distribution, and N is the total number of alongshore locations. As shown in Fig. 15a, the overall NRMSE of Test 2 (3.40–9.21%) has only increased slightly compared to Test 1 (3.37–8.80%), and this result confirms that Eq. 9 is valid. Also, the overall NRMSE of Test 3 (3.46–10.02%) increased only slightly from Test 1, and this result confirms the performance of the AP method. The overall NRMSE of Test 4 (3.32–10.11%) shows that the TRRF can produce reliable run-up distribution. Figure 15b shows that the TRRF underestimated the run-up in Test 1 while slightly overestimating the run-up in Test 2 and Test 3. The overall MBE of Test 4 shows that the TRRF can predict run-up distribution without an apparent bias ($MBE={-0.33}\ {\mathrm{m}}-0.24\ {\mathrm{m}}$).

5.2 Computational time

The efficiency of the TRRF was investigated by comparing the computational time between the physics-based numerical model and the TRRF. When the physics-based numerical model (Basilisk) was used to predict the tsunami run-up distribution, the computational time was about one hour (24 CPU hours) on average for each scenario (24 cores, OpenMP, Intel Xeon E5-2680v3). On the other hand, when the TRRF was used to predict the tsunami run-up distribution, the computational time was only 0.01 CPU second per scenario (desktop computer with one core, Intel I7-7700). The TRRF’s CPU time is nearly 9 million times shorter than that of numerical simulation. The difference in computational time between the TRRF and the numerical model would be even greater given higher-resolution grids and larger geographic areas than those used in this study.

6 Discussion

The performance of TRRF was investigated based on total 380 additional simulations in Sect. 5. When the TRRF predictions are compared against the direct numerical simulations, it is clear that the TRRF can produce reliable run-up predictions over real topography, given the computational time. However, as shown in Fig. 14, even though the TRRF predicts the leading order of tsunami run-up distribution well, there are a few localities where the difference of the run-up is more than twofold. We found that these localities are correlated to the uncertainty (or the range of percentiles) of ${\mathrm{NT}}^p(x)$ (Fig. 9). For example, a large uncertainty was commonly found in places with complex topography, such as areas surrounded by mountains (e.g., $65.735^{{\circ }} {\mathrm{W}}$), areas containing a river (e.g., $66.955^{{\circ }} {\mathrm{W}}$), steep cliffs (e.g., $66.444^{{\circ }} {\mathrm{W}}$) and coastal dunes (e.g., $66.239^{{\circ }} {\mathrm{W}}$). Even though it is difficult to fully interpret the physics behind the normalized topographic run-up ${\mathrm{NT}}^p(x)$, we think that this high uncertainty may be attributed to the nonlinear behavior of the tsunami wave as it propagates and inundates complex topography. In its present form, the TRRF does not directly consider potential nonlinearities between the source and topographic run-up components in the hypothesis that the tsunami run-up distribution can be expressed as a sum of the source and topographic run-ups (Eq. 1). Future studies should investigate ways to account for the uncertainty to improve the accuracy of the TRRF approach.

As shown in Fig. 15b, Test 1 shows statistically different MBE compared to other tests ($p<0.05$). The TRRF generally underestimated the run-up in Test 1 where the fault parameters were set based on the following conditions: (1) X is fixed to zero, (2) strike direction is parallel to the coastline and (3) the rake angle is $90^{{\circ }}$. In this condition, the error is only related to the RSM functions and the normalized topographic run-up, ${\mathrm{NT}}^p(x)$. We think that this underestimated run-up may be attributed to the characteristic of ${\mathrm{NT}}^p(x)$ of northern Puerto Rico, for two reasons. First, the RSM functions predicted the OS formula coefficients well (Fig. 13), and second, most of the ${\mathrm{NT}}^p(x)$ ($67.1^{{\circ }}$ W − $65.8^{{\circ }}$ W) was biased toward the lower values within the range of ${\mathrm{NT}}(x)$ (Fig. 9). On the other hand, the TRRF slightly overestimated the run-up in Test 2 and Test 3 which were designed to test the error of Eq. 9 and that of the AP method, respectively. It should be noted that when all fault parameters are randomly selected (Test 4), there was no apparent bias (Median $MBE=1.8$ cm). We think this is because the negative bias caused by ${\mathrm{NT}}^p(x)$ is compensated by the positive bias caused by Eq. 9 and the AP method. Future studies should investigate how to reduce distinct bias in a certain condition like Test 1.

Moreover, future studies should expand the applicability of the TRRF by considering the following limitations. One is that the TRRF is only applicable to uniform slip distribution. Several studies have shown that tsunami prediction can vary depending on heterogeneous slip models even when the earthquake magnitude is the same (Davies 2019; Geist 2002; Li et al. 2016; Ruiz et al. 2015). The other limitation of the TRRF is that it is only applicable to tsunamis generated by seafloor displacements associated with earthquakes. After earthquakes, landslides are the second most common cause of tsunamis (Harbitz et al. 2014). Moderate earthquakes do not always cause tsunamis themselves, but they can, in some instances, trigger large landslides that result in tsunamis (Uri et al. 2009). Though landslide-generated tsunamis are rare, a single occurrence can cause substantial damage and loss of life. For example, in 2017, a landslide-generated tsunami off the western coast of Greenland flooded several villages and resulted in casualties (Paris et al. 2019). A recent study also revealed that the 2018 Indonesian tsunami, which claimed more than 2,000 lives and severely damaged coastal communities, was caused by the combination of an earthquake and a landslide (Sassa and Takagawa 2019). Several other key elements would merit attention in future studies. For example, the arrival time and inundation distance are as important to consider as the run-up. A high tide could enhance tsunami inundation, while a receding tide could dissipate tsunami energy (Tolkova et al. 2015; Zhang et al. 2011). Likewise, a modest amount of sea-level rise could dramatically impact the tsunami run-up distribution (Li et al. 2018). Lastly, the TRRF was able to reduce the input dimensionality by using the OS formula, but the OS formula limits its applicability to straight coastal areas and near-field tsunamis. To generalize the applicability of TRRF, future studies should investigate the effect of a coastline shape and that of a distance between an earthquake source and a coast.

7 Conclusions

In the present study, we presented a new methodology, called TRRF, that can predict the alongshore run-up distribution from a near-field tsunami. We adopted the OS formula and developed what we call the AP method to reduce the number of simulations to build the TRRF. The tsunami run-up distribution was decomposed into source run-up and topographic run-up, that source run-up can be modeled by earthquake fault parameters, and that normalized topographic run-up is associated with local topographic characteristics. Using the northern region of Puerto Rico as a case study, the performance of the TRRF was investigated based on total 380 additional simulations. The results showed that the TRRF can produce rapid near-field tsunami run-up predictions over real topography (3–10% of NRMSE, ${-0.33}\ {\mathrm{m}}-0.24\ {\mathrm{m}}$ of MBE). We expect that future applications of the TRRF will have the potential to save lives and promote resiliency of coastal communities.

Appendices

Appendix 1: Design of experiments

The tsunamigenic–earthquake scenarios were designed in a three-level full factorial. The level of the design of experiments (DoE) was determined based on preliminary simulations where 60 cases were considered as follows. We set a reference case where the fault parameters are as follows: $LON = 66.4^{{\circ }}$ W, $LAT =19.3^{{\circ }}$ N, $STR=90^{{\circ }}$, $DIP=20^{{\circ }}$, $RAK=90^{{\circ }}$, $LEN=90\,{\mathrm{km}}$, $WID=40\,{\mathrm{km}}$, $SLP=3\,{\mathrm{m}}$, $DEP=20\,{\mathrm{km}}$, which are the same as the central level values used in Table 1. Based on the reference case, we performed 60 simulations, varying each of the six fault parameters (LAT, LEN, WID, DIP, SLP, DEP) one at a time through a uniformly distributed array of 10 values within the parameter’s range shown in Table 1. The 60 simulations show that the second-order polynomial model, which requires at least three-level data, is enough to fit the fault parameters to the OS formula’s coefficients a and b (Fig. 16).

Fig. 16

The OS formula coefficients (a and b) variation in terms of RSM parameters: a, b epicenter latitude, c, d dip angle, e, f fault length, g, h fault width, i, j slip, k, l top-edge fault depth. The red dots represent the simulated coefficients and the black line represents the best-fitting curve based on the second-order polynomial model

Appendix 2: Sensitivity test

While developing the TRRF for northern Puerto Rico, we encountered numerical model stability issues with four simulations (0.5% of simulations) among the 729 scenarios. The stability issue occurred when the LAT is $19.6^{{\circ }}$, earthquake magnitude (LEN, WID, SLP) is relatively large, DIP is shallow and DEP is deep (Table 2). Even though it is difficult to fully interpret the reason of this stability problem, we think that one of the reasons may be that some part of the fault lies in the Puerto Rico Trench where the water depth abruptly changes, and the grid resolution used in this study may not be sufficiently resolved for the case when the fault lies in steep slopes (Fig. 2). In order to test whether building the TRRF with 725 instead of 729 simulations affected the accuracy of the TRRF, we conducted a sensitivity test as follows. We randomly chose four simulations among the 725 successful simulations. We built the TRRF with 721 simulations, where the four randomly chosen scenarios were intentionally removed. We tested this TRRF based on the 100 simulation cases used in Test 4, which were never used in developing the TRRF and whose fault parameters were selected randomly. We repeated this procedure 10 different times. The result of the sensitivity test shows that the impact on accuracy of building the TRRF without four additional simulations is negligible (the largest difference of $NRMSE =1.27\%)$.

Table 2 Fault parameter condition of four cases that shows model stability issue