1 Introduction

Tsunamis have been causing enormous loss of lives and assets repeatedly (Synolakis and Bernard 2006; Kânoğlu et al. 2015). Preparedness and timely early warning could mitigate losses for future events. There are a limited number of operational forecasting methodologies such as the ones used at the National Oceanic and Atmospheric Administration (NOAA) (Titov et al. 2016), the Indonesian Meteorology, Climatology, and Geophysical Agency (BKGM) (Rudloff et al. 2009), the Japan Meteorological Agency (JMA) (2013), and the Australia Tsunami Warning Systems (Greenslade et al. 2019).

One significant guiding parameter in tsunami warning is the maximum runup, defined as the difference in elevation between the maximum tsunami penetration and the still water line at the time of an event (Fig. 1). Numerous studies have addressed the long wave runup on a beach through numerical and analytical methods. Numerical models compute tsunami runup solving the nonlinear shallow water-wave (NSW) equations (Imamura 1995; Titov and Synolakis 1995, 1998; Liu et al. 1998; Tinti et al. 2013; Miranda et al. 2014; Titov et al. 2016; Miranda and Luis 2019) or Boussinesq-type equations (Madsen and Sørensen 1992; Chen and Liu 1995; Kirby et al. 1998; Fuhrman and Madsen 2009), mostly validated and verified through Synolakis et al. (2008). Application of these models to field cases employs the half-space elastic theory (Okada 1985; Mansinha and Smylie 1971) to produce the initial waveforms for earthquake-generated tsunamis. These models compute wave propagation and runup using appropriate digital elevation models (DEMs). Numerical models may predict inundation parameters with high accuracy since they solve tsunami propagation on a real bathymetry using waveforms compatible with earthquake parameters. However, at least currently, these models may be unsuitable to be used in real time implementing high-resolution bathymetry and topography in the DEMs since the computation with high-resolution is time-consuming. Besides, such bathymetry and topography data could be proprietary. Runup may be computed using a moving boundary algorithm (Liu et al. 1995, 1998). However, accurate runup computation depends on many factors such as accurate near shore bathymetry and topography, bottom roughness, wave breaking, and energy dissipation. Most numerical tsunami models do not solve wave breaking, but they produce better inundation results if they include some numerical dissipation or using bottom friction including the Manning-coefficient (Burwell et al. 2007; Bricker et al. 2015). However, numerical models allow computation of tsunami impact reasonably well.

Fig. 1
figure 1

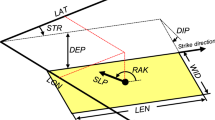
Definition sketch. a The shoreline is located at the origin of the coordinate system. \(R \) shows the maximum runup. \(\beta\) is the beach slope angle, and \(d\) is the ocean depth at maximum amplitude. Wave parameters: \(x_{1}\) and \(x_{2}\) are the distances of the maximum amplitude of the crest \(h^{ + }\) and the minimum amplitude of the trough \(h^{ - }\) to the shore, respectively. \(\lambda \) shows the wavelength. Fault plane parameters: \(D\), \(W\), \(\delta\) and \(s\) are the depth of the fault top to the ocean bottom, the width of the fault, the dip of the fault, and the fault slip amount, respectively; b definition parameters for LDNs; \(l_{{\text{p}}}\) is the horizontal length of the wave face, and \({h}^{+}\) and \({h}^{-}\) are the positive and negative amplitudes, respectively; c definition parameters for LENs; \(l_{{\text{p}}}\) is the horizontal length of the wave face, and \(h^{ + }\) is the positive amplitude

Full size image

On the other hand, analytical methods estimate the runup in the correct order of magnitude (e.g. Synolakis 1987; Pelinovsky and Mazova 1992; Kânoğlu and Synolakis 1998; Kânoğlu 2004; Tinti and Tonini 2005; Didenkulova et al. 2006, 2007a, b; Aydın and Kânoğlu 2017). Indeed, the analytical solutions have some limitations, such as using the shallow water-wave theory and idealized bathymetric profiles. Synolakis (1987) presented a solution to the linear shallow water-wave equation for the canonical problem -a constant depth region connected to a sloping beach- and extended the linear solution to the nonlinear solution using Carrier and Greenspan’s (1958) hodograph transformation. Tadepalli and Synolakis (1994, 1996) proposed leading depression N-waves (LDNs) to be more appropriate to describe a realistic initial tsunami waveform. Tadepalli and Synolakis (1996) include a horizontal length scale and a steepness parameter. They demonstrated that LDNs produce higher runup than solitary and leading elevation N-waves (LENs) with the same amplitude. Later, Madsen et al. (2008) concluded that the solitary wave tie to describe N-waves as proposed by Tadepalli and Synolakis (1994, 1996) does not appropriately represent spatial and temporal scales of realistic geophysical tsunamis. Madsen and Schäffer (2010) presented analytical runup solutions for sinusoidal, single, N, and transient waves to overcome this problem. As also implied in Tadepalli and Synolakis (1994, 1996), they demonstrated that a larger amplitude ratio negative–positive amplitude positively influences the runup. Chan and Liu (2012) studied the runup numerically and analytically, adapting and extending the earlier solutions of Synolakis (1987) and Madsen and Schäffer (2010) for cnoidal and multiple solitary waves. Using profiles from the 2011 Tohoku-Oki, Japan tsunami, they find that the triggered tsunami waveform was different from a solitary wave in near- and far-fields. Moreover, they concluded that the accelerating phase of the incident wave controls the maximum runup.

Further, Kânoğlu (2004) proposed that Carrier and Greenspan’s (1958) hodograph transformation can be linearized for the spatial variable to define the initial condition, a vexing issue. Aydın and Kânoğlu (2017) provided an efficient computational framework using Kânoğlu’s (2004) approach and solved the NSW equations employing eigenfunction expansion on a sloping beach as a classical initial value problem.

Sepúlveda and Liu (2016) expressed maximum runup in terms of earthquake fault plane parameters. They use Okada (1985) to estimate initial source parameters. Further, they identified a general relationship between the maximum runup and earthquake source parameters adopting the boundary and initial value problem solutions of the nonlinear shallow water-wave equations through Madsen and Schäffer (2010) and Kânoğlu (2004), respectively.

Further, McGovern et al. (2018) studied runup using a pneumatic long wave generator. They observed a relationship between the relative slope length and the dimensionless runup and suggested the relative slope length as the explanatory variable for the runup. The relative slope length relates the wavelength with the beach’s wetted length, over which the wave travels. Moreover, they recommended the use of expanded datasets with varying slopes and depths to validate their solution. However, McGovern et al. (2018) do not include the amplitude ratio, as in Madsen and Schäffer (2010), which directly influences the runup. Further, they do not consider Chan and Liu’s (2012) conclusion that the wave’s accelerating phase mainly controls the runup.

In this study, we compute runup numerically and analytically over a constant sloping beach having different slopes for earthquake-generated initial waveforms with different source parameters. We then introduce a new parameter, tsunami runup predictor (TRP), and its relation to the runup. The TRP combines the wave's accelerating phase that we define as the horizontal length of the wave face, the wetted length of the slope, and the amplitude ratio to a single parameter, thus including the findings of the studies summarized previously. Finally, we use the TRP to estimate the runup for past events. We discuss the results compared to the field measurements and observe that the mean- and extreme-field maximum runup measurements are related to the TRP.

2 Runup computation

We produced a database of initial tsunami waveforms (ITWs) of LENs and LDNs, using the half-space elastic theory (Mansinha and Smylie 1971) embedded in MIRONE suite (Luis 2007). It is common practice to assume that the sea surface elevation over the epicentral area mimics the ocean bottom’s co-seismic deformation for earthquake-induced tsunamis. We varied the fault plane parameters -dip, width, depth, and slip, and the distance of the fault to the shore,- and the beach slope (Fig. 1, Table 1) and computed 210 ITWs. We assumed a rake angle of 90° for all cases.

Table 1 Fault plane parameters and slopes used in modelling. Here, D, W, δ and s represent the fault depth, the width, the dip angle, and the slip amount, respectively; x1 is the distance of the initial wave to the shore and β is the nearshore beach slope
Full size table

We first used the numerical model nonlinear shallow water model with nested grids (NSWING) (Miranda and Luis 2019) to evaluate the maximum runup. NSWING solves the NSW equations in a Cartesian or spherical reference system, allows for nested grids, and employs a moving boundary algorithm to track the shoreline motion during the inundation like Cornell multi-grid coupled tsunami model (COMCOT) (Liu et al. 1995, 1998). The code was benchmarked according to the analytical tests presented by Synolakis et al. (2008) and applied in Miranda et al. (2014), Omira et al. (2015), Wronna et al. (2015), Baptista et al. (2017) and Wronna et al. (2017, 2019). We used a synthetic bathymetry with the dimensions of 80 × 520 km2 with a constant slope (Fig. 2). We used a coupled nested grids system from 320 m at offshore up to 5 m resolution at near and onshore.

Fig. 2
figure 2

Definition sketch for the bathymetry used in the numerical model. Quantities are in meters

Full size image

Moreover, we applied the analytical solution of Aydın and Kânoğlu (2017). Their method computes the shoreline elevation and velocity for a given initial waveform with or without initial velocities. We fitted N-waves in exponential waveforms as used in Kânoğlu (2004) and Aydın and Kânoğlu (2017) to each of the ITWs from the database to obtain the profiles as input to the analytical solution.

3 The tsunami runup predictor

McGovern et al. (2018) suggested the relative slope length sl as the primary parameter controlling the maximum runup. They defined \(sl\) as

$$ sl = \frac{\sin \beta }{d}\lambda $$
(1)

where β is the beach slope, d is the water depth, and λ is the wavelength. This relationship describes the length of the wetted slope with respect to the wavelength. Besides, Chan and Liu (2012) suggested that the maximum runup also crucially depends on the wave’s accelerating phase. We also observed the strong influence of the wave steepness on the maximum runup as McGovern et al. (2018). Hence, we propose to use the horizontal length of the wave face lp (Fig. 1) to describe the accelerating phase of the wave since we reach a similar conclusion from the runup results. We define lp as the distance between the maximum and the minimum amplitudes for LDNs and the distance from the maximum height to the 5% tail of the positive amplitude for LENs (Fig. 1b and c). We also include the amplitude ratio \(\tilde{\mu } = h^{ - } /h^{ + }\), where \(h^{ - }\) is the minimum amplitude of the trough and \(h^{ + }\) is the maximum amplitude of the crest, to distinguish between LENs and LDNs (Madsen and Schäffer 2010). Since the accelerating phases for LENs do not include negative amplitude, using the amplitude ratio for LEN becomes irrelevant. Hence, we present the TRP \(\tilde{\phi }\) as,

$$ \tilde{\phi }_{{{\text{LEN}}}} = \frac{1}{{l_{{\text{p}}} }}\frac{d}{\sin \beta }{\text{ and }}\tilde{\phi }_{{{\text{LDN}}}} = \frac{{\tilde{\mu }}}{{l_{{\text{p}}} }}\frac{d}{\sin \beta } $$
(2)

for LENs and LDNs, respectively. Here, d is the water depth at the maximum wave height. We also define the dimensionless maximum runup as,

$$ \mathop {\tilde{R}}\nolimits_{{{\text{LEN}}}} = \frac{R}{h^{ + }}\,{\text{and}}\mathop {\tilde{R}}\nolimits_{{{\text{LEN}}}} = \frac{R}{H/\tilde{\mu }} $$
(3)

where R is the maximum runup and \(H = h^{ + } + \left| {h^{ - } } \right|\). Further, we search for a relationship between the maximum runup and TRP in the form of \(\tilde{R} = a\,\tilde{\phi }^{\text{b}}\) to fit our numerical and analytical data set. We approximately identify maximum runup as,

$$ \tilde{R}_{{{\text{LEN}}}} = 2.15 \; \tilde{\phi }_{{{\text{LEN}}}}^{0.5} {\text{ and }}\tilde{R}_{{{\text{LDN}}}} = 1.1 \; \tilde{\phi }_{{{\text{LDN}}}}^{0.7} $$
(4)

for LEN and LDN, and present the results in Figs. 3 and 4, respectively.

Fig. 3
figure 3

The maximum runup in respect to the TRP for LENs. The circles and dots show analytical and numerical maximum runup results, respectively. The dashed line shows Eq. 4. The initial waveform for the Illapel tsunami is a LEN. The dark and the light diamonds show the mean- and extreme-field maximum runup measurements along the target coastline for the Illapel tsunami, respectively

Full size image
Fig. 4
figure 4

The maximum dimensionless runup in respect to the TRP for LDNs. The circles and dots show the analytical and numerical maximum runup results, respectively. The dashed line shows a fit to the numerical and analytical runup results (Eq. 4). The dotted line depicts the fitted law (Eq. 5) for the extreme runup \(\tilde{R}_{{{\text{LDN}},\; {\text{Ext}}}}\) values from the field measurements. Each symbol depicts runup values for one event; the mean- and extreme-field maximum runup measurements are presented in dark and light, respectively

Full size image

4 The application of the TRP to the field observations

We set down to use field data to test the new runup formulation based on TRP. We use Nicaragua 1992 (Dziewonski et al. 1995; Piatanesi et al. 1996; Okal and Synolakis 2004); Indonesia, Java 1994 (Dziewonski et al. 1995; Abercrombie et al. 2001; Okal and Synolakis 2004); Mexico, Colima 1995 (Dziewonski et al. 1997; Mendoza and Hartzell 1999; Okal and Synolakis 2004); Chile, Maule 2010 (Delouis et al. 2010; Hayes 2010; Sepúlveda and Liu 2016); Japan, Tohoku-Oki, 2011 (Ammon et al. 2011; Wei et al. 2012; Yue and Lay 2013); Chile, Iquique 2014 (Wei 2014) and Chile, Illapel 2015 (Okuwaki et al. 2017) events to test our empirical solutions. Table 2 lists the source models we have used for these events. We use the centroid moment tensor (CMT) and inversion models to compute the ITW through Mansinha and Smylie (1971). We then trace a profile along the maximum sea level elevation orthogonal to the ITW to identify the parameters \(h^{ + }\), \(h^{ - }\), and \(l_{{\text{p}}}\). We approximate the target beach slope angle β and the water depth d at the maximum \(h^{ + }\) using the GEBCO (2014) bathymetry. We then use these parameters to compute dimensionless runup \(\tilde{R}\), using Eqs. 2, 3 and 4, depending on initial wave polarity, i.e. LDN or LEN, for all the cases listed in Table 2, and present the results in Figs. 3 and 4, and Table 3. Then, we compare the estimates to the mean- and extreme-field maximum runup measurements for each event (National Geophysical Data Center / World Data Service NGDC/WDS 2019) in Figs. 3 and 4. Analysing Fig. 4, reluctant to have a conclusion from a few data points, we observe that the dimensionless extreme maximum runup heights, \(\tilde{R}_{{{\text{LDN}}, \;{\text{Ext}}}}\), for the cases Java, Mexico, Maule, Tohoku-Oki, and Iquique, follow

$$ \tilde{R}_{{{\text{LDN}},\; {\text{Ext}}}} = 2.8\;\tilde{\phi }_{{{\text{LDN}}}}^{0.7} $$
(5)
Table 2 The source parameters and beach slopes used for the field cases. Here, \(M_{{\text{w}}}\) represents the moment magnitude; \(\delta\), \(W\), \(D\) and s represent the fault dip angle, the width, the depth, and the slip amount, respectively; and \(\beta\) is the nearshore beach slope
Full size table
Table 3 The waveform parameters, TRP and dimensionless runup values for the field cases. The observed mean and extreme runup values are also tabulated. Here, \(h^{ - }\) is the minimum amplitude of the trough, \(h^{ + }\) is the maximum amplitude of the crest, \(H = h^{ + } + \left| {h^{ - } } \right|\) and \(\tilde{\mu } = h^{ - } /h^{ + }\). \(l_{p}\) is the horizontal length of the wave face, \(\beta\) is the target beach slope angle and d is the water depth at the maximum wave height. \(\tilde{\phi }\) is calculated from Eq. 2, \(\tilde{R}\) and corresponding R from Eqs. 4 and 3, respectively, depending on the polarity of the initial wave, i.e. LEN or LDN. The mean (\(\tilde{R}_{mean}\)) and extreme (\(\tilde{R}_{{{\text{Ext}}}}\)) runup values are calculated based on field data using Eq. 3. Refer to Table 2 for the references of the source models
Full size table

This result indicates that even extreme runup might follow a similar law to Eq. 4, with a factor of about 2.5. Our results are compatible with the mean- and extreme-field maximum runup measurements.

Specifically, we have the following observations regarding the field application of the TRP.

The TRP estimate using the waveform based on the inversion by Piatanesi et al. (1996) is within the field observation range for the 1992 Nicaragua event (Table 3).

In the 1994 Java, post-event field surveys report the measured tsunami runup in only four locations (Maramai and Tinti 1997, NGDC/WDS 2019). The TRP model underestimates the mean- and extreme-field maximum runup measurements for this event. A possible explanation is that the rupture originated at a locked subducting seamount (Abercrombie et al. 2001), resulting in the concentration of maximum slip distribution along a small area. Hence, this produces a relatively short length of the accelerating phase of the wave lp that is not well reproduced when using CMT parameters to compute the ITW.

The co-seismic deformation occurs partially onshore, resulting in shoreline subsidence or uplift for the 2010 Maule, 2014 Iquique, and 2015 Illapel, Chile events (Omira et al. 2016). Fritz et al. (2011) measured a maximum runup height of 29 m decaying fast from this maximum value to values between 5 and 10 m for the Maule event. Both of our predictions are in line with their observations. For the Iquique event, the post-event field survey reported runup heights ranging 2–3 m with a maximum value of 4.6 m (Catalán et al. 2015). The prediction of the runup is 1.8 m for the Iquique event. For the Illapel event, our prediction lies within the range of most of the measurements between 2 and 6 m (Aránguiz et al. 2016). However, it underestimates the extreme runup of 13.6 m (Contreras-López et al. 2016). Aránguiz et al. (2016) found an extreme runup of 10.8 m for the Illapel event and used numerical modelling to explain the runup distribution. Their modelled values represent well the tide gauge recordings and mostly the measured runup values between 2 and 6 m. However, they do not reproduce their maximum measured runup; the authors attribute this extreme value to the deep offshore bathymetry and the pocket beach morphology.

We considered 3 different inversion models and obtained very different results ranging between 15.1 and 47.4 m (Table 3) for the Japan, Tohoku-Oki, 2011 event. The differences in the inversion models and their corresponding wave height profiles may explain the diversity of different results obtained. We overestimate the maximum runup about 20% for an ITW produced for the Tohoku-Oki case based on Yue and Lay (2013) inversion model (Fig. 4, Tables 2 and 3). Ammon et al. (2011) and Wei et al. (2012) inversion models of the Tohoku-Oki event results in an underestimation of the maximum runup of about 28 and 60%, respectively (Table 3). However, we overestimate the mean runup values for the Tohoku-Oki event independently from the inversion models used here. The overestimation of the runup for the Tohoku-Oki inversion through Yue and Lay (2013) possibly results because of the extreme values of the ITW where we calculate a wave height H of more than 25 m in the open ocean and a relatively large amplitude ratio \(\tilde{\mu }\) close to 0.6, i.e. larger values of \(\stackrel{\sim }{\mu }\) result in higher runup (Madsen and Schäffer 2010).

Considering the 1995 Colima, Mexico event, different solutions for the tsunami source in the empirical model produced considerable discrepancies. The model using the CMT solution profile produces a 4 m runup. In comparison the inversion model profile produces a runup of 8 m, which is much closer to the maximum measured runup (Fig. 4, Tables 2 and 3).

5 Final remarks

We used numerical and analytical methods to compute the runup on constant sloping beaches. We generated the ITW dataset, including the maximum runup using different earthquake fault parameters and constant sloping bathymetries with different beach slopes. We introduced a new dimensionless parameter TRP and further, we present relation to the maximum runup for LEN and LDN initial waveforms separately. Our results suggest a strong correlation between these parameters (Figs. 3 and 4).

Further, we applied the empirical model for past tsunamis and compare the runup predictions to the field measurements. We hypothesize that underestimating the maximum runup in the real events may result from the fact that the empirical model considers simplified 1-D bathymetric profiles. We speculate that the fact that our model does not account for changes in coastal bathymetry and topography may explain some of the discrepancies of the runup predictions (Tang et al. 2009; Aránguiz et al. 2016) and needs some further investigation. However, the local bathymetric effects on the runup are beyond the scope of this study.

We also developed a formulation (Eq. 5) for the extreme-field measured maximum runup that produces reliable results for all events tested here (Fig. 4). The multiplication factor is about 2.5 compared to the mean runup, even though this needs further validation with more cases. However, we speculate that heterogeneous slip distribution may account for some of the differences in the runup estimates. Distribution of slip along the faults may lead to a larger runup. Concentrated areas of slip influence the length of the wave’s accelerating phase, thus may lead to a higher runup. Consequently, runup estimates depend crucially on the quality of the estimated/measured wave shape. Interestingly, Geist and Dmowska (1999) and Geist (2002) found that heterogeneous slip distribution may greatly influence tsunami wave steepness and runup. Geist (2002) found that the nearshore tsunami amplitude can vary a factor of 3 when considering variable heterogeneous slip distribution patterns. Recent studies (Baglione et al. 2017; Melgar et al. 2019) discuss the importance of the heterogeneous slip distribution to nearshore tsunami runup. Rapidly available earthquake parameters based on CMT solutions do not contain information on heterogeneous slip distribution along the fault. The conclusion for the cases 2011 Tohoku-Oki, Japan, and 1995 Colima, Mexico events, where we tested more than one ITW, confirm that the sources used for the field observations are approximate solutions and may include uncertainties. This fact highlights the need for an efficient sea level observation system to measure the waveform offshore; thus, the runup can be estimated in real-time, independently from the generation mechanism.

We conclude that the empirical method presented here allows for a quick estimate of the runup in coastal stretches where no high-resolution terrain models are available. Once the waveform is estimated, the empirical runup estimation method based on the TRP could be a powerful tool for a tsunami early warning system.