1 Introduction

Comprehension of wave run-up on beaches is essential for prediction of beach erosion, coastal impact of tsunamis, and storm surges. This is one reason for the lasting attention that run-up topics have required in the literature of hydrodynamics and coastal engineering (Pedersen 2008).

The problem of the run-up of long non-breaking and breaking waves on a plane beach is well described mathematically within the framework by a nonlinear shallow water theory. This approach leads to an analytical solution based on the Carrier–Greenspan transformation (Carrier and Greenspan 1958). Various shapes of the periodic incident wavetrains, such as the sine wave (Kaistrenko et al. 1991; Madsen and Fuhrman 2008; Belega 2013), cnoidal wave (Synolakis 1991), and nonlinear deformed periodic wave (Didenkulova et al. 2006, 2007) have been treated in the literature. The relevant analysis has also been performed for a variety of solitary waves and single pulses, such as soliton (Padersen and Gjevik 1983; Synolakis 1987; Knouglou 2004), sine pulse (Mazova et al. 1991), Lorentz pulse (Pelinovsky and Mazova 1992), Gaussian pulse (Carrier et al. 2003; Knouglou and Synolakis 2006), N-waves (Tadepalli and Synolakis 1994), “characterized tsunami waves” (Tinti and Tonini 2005), and the random set of solitons (Brocchini and Gentile 2001). As is often the case in nonlinear problems, reaching an analytical solution is seldom possible. Run-up of solitary pulses is, however, easily implemented experimentally in measuring flumes, and various experimental expressions about run-up of long waves on plane beach are available (Synolakis 1987; Briggs et al. 1995; Hsiao et al. 2008) (see Didenkulova et al. 2009).

Due to the simulation simplicity and similarity of wave hydrodynamics, solitary-type long waves have been used for decades to investigate tsunami behavior (Liu et al. 1991; Synolakis and Bernard 2006). Particularly, solitary waves interacting with coastal objects have garnered considerable attention in terms of wave run-up on a uniform slope (Lin et al. 1999; Carrier et al. 2003; Li and Raichlen 2003; Hsiao et al. 2008; Chang et al. 2009; Hsiao and Lin 2010; Wu et al. 2012; Jianhong et al. 2013), disintegration and transmission properties of waves over an abrupt topography (Losada et al. 1989; Liu and Cheng 2001; Lin 2004), wave–structure interaction between a wave/bore and a vertical/floating barrier (Ramsden 1996; Liu and Al-banaa 2004; Xiao and Huang 2008), vortex shedding and advection around a submerged obstacle or a subaerial plate (Chang et al. 2001; Lin et al. 2005), and free surface kinematics of a wave passing over and through a porous structure (Lee and Lan 1996; Lan and Lee 2010; Wu et al. 2014; in Hsiao and Lin 2010).

This study investigates behavior of tsunami solitary waves impinging and overtopping a submerged trapezoidal obstacle on a 1:19.85 sloping beach, and the effects of a submerged obstacles on run-up value. Several series of experiments were carried out in medium-size wave flume for four different depths of obstacle’s peak. New laboratory data of maximum run-up height of wave under submerged obstacle effect are presented and discussed. A numerical modeling of the same case is employed using the FD computing code namely COULWAVE. A description, of the bottom bathymetry, the experimental set, and the numerical model, is presented in Sect. 2. Section 3 shows the different results obtained by numerical and experimental investigations, and also the comparison between the two. Using least squares method estimation, we established a regression model of maximum run-up according to wave height and obstacle peak depth. The principal findings are drawn in Sect. 4.

2 Method

2.1 Bottom profile

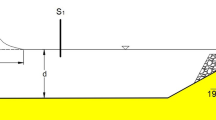
The present bottom profile is used to reproduce (Synolakis 1987) cases for non-breaking and breaking solitary wave climbing up a plane beach; however, we have added to this beach a submerged obstacle. The bottom profile is one-dimensional, and regular horizontal bathymetry comes to end (ended) by a 1:19.85 sloping beach as shown in Fig. 1. The beach contains in its middle a trapezoidal obstacle, which has a slope on both sides equal to 1:2.5, where d is water depth, L and H are length and amplitude of solitary wave, respectively, P is obstacle peak depth, and R is run-up value. S 1, S 2, and S 3 are the gauges which measure water elevation variation in time. Note that the obstacle peak width is equal to d/10, and \(\cot \beta =19.85\).

Fig. 1
figure 1

Definition sketch of bottom profile and the definitions of physical variables

Full size image

2.2 Experimental setup

The experiments were carried out in a medium-size flume at Civil Engineering Faculty’s Hydraulics Laboratory of University of Sciences and technology Houari Boumediene (USTHB) Algiers. This flume has a dimension of 22 m long, 75 cm wide, and 90 cm deep. Target solitary waves were generated at one end of the flume by a guillotine system wavemaker (Goring and Raichlen 1980). A plane beach with 1 vertical to 19.85 horizontal, consisting of a wooden skeleton covered with plastic, starts 12 m from the vertical bulkhead wave generator. A mobile trapezoidal obstacle is mounted in a way that its peak is always in the middle of the submerged part of the slope. The obstacle slopes on both sides are equal to 1:2.5, and its peak width is equal to 3 cm.

Figure 2 shows a photograph of the laboratory flume and the measurement facilities employed in the present experiments. The arrangement of measurement apparatus was deployed with wave gauges and camera. The elevation of local water surface was recorded by three wave gauges located at (S 1) 5 m, (S 2) 10 m, and (S 3) 16 m from the wavemaker. It is noted that the wave probe S 2 located 10 m from the wave generator is referred to the reference gauge in all experiments. We note that each wave gauge was mounted at the middle of the flume width, and thus the viscous effect is negligible. All wave gauges were calibrated through a standard method which concerns the change of water level to adjust the response voltage of each gauge before and after the experiments to ensure its linearity and stability. The linearity of gauge response was given by a correlation coefficient of 0.9999. Note that to write this subsection we followed the same methods used in Hsiao et al. (2008).

Fig. 2
figure 2

Prospective view of the flume and the obstacle. (a) Plane beach, (b) obstacle, (c) wave gauge

Full size image

2.3 Numerical model

The model used in this study is the Cornell University Long and Intermediate Wave Modeling package (COULWAVE) (Lynett and Liu 2002). COULWAVE was developed to model the propagation and run-up of long and intermediate length waves, using fully nonlinear and dispersive wave theory (i.e., the nonlinear Boussinesq equations) as described by many authors (Lynett and Liu 2002, 2005; Lynett et al. 2002; Lynett 2006). Because this wave modeling package is computationally intensive, there are also options to use different approximations, such as weakly nonlinear, linear, and non-dispersive forms of the wave equations. On the basis of initial tests, the weakly nonlinear “extended” equations [termed WNL-EXT in Lynett and Liu (2002)] were used to simulate solitary waves overtopping obstacles even with steep slopes of obstacle (1/2.08) (Tsung et al. 2012), and fully nonlinear equations in tsunami simulation on real topography (Geist et al. 2009). The WNL-EXT form of the wave equations described by Lynett and Liu (2002) are derived from the fully nonlinear form by assuming that the wavelength is much greater than the water depth and that the wave amplitude and vertical seafloor displacement are much smaller than the water depth. Specifically, for the dimensionless parameters: [from Geist et al. (2009)]

Continuity of mass (COM):

$$\eta _{t}+\nabla \cdot M=0$$
(1)

where

$$\begin{aligned} M&=(h+\delta \eta )\left\{ {\mathbf{u}}_{\alpha }+\mu ^{2}\left[ \frac{1}{2}z_{\alpha }^{2}-\frac{1}{6}(h^{2}-h\delta \eta +\delta ^{2}\eta ^{2})\right] \nabla (\nabla \cdot {\mathbf{u}}^{2})\right. \\&\quad \left. \mu ^{2}\left[ z_{\alpha }+\frac{1}{2}(h+\delta \eta )\right] \nabla [\nabla \cdot (h{\mathbf{u}}_{\alpha })]\right\} +O (\mu ^{4}) \end{aligned}$$
(2)

Equation of motion (EOM):

$${\mathbf{u}}_{\alpha t}+\delta ({\mathbf{u}}_{\alpha }\cdot \nabla ){\mathbf{u}}_{\alpha }+\nabla \eta +\mu ^{2}V_{1}+\delta \mu ^{2}V_{2}=O (\mu ^{4})$$
(3)

where

$$V_{1}=\frac{1}{2}z^{2}_{\alpha }\nabla (\nabla \cdot {\mathbf{u}}_{\alpha t})+z_{\alpha }\nabla [\nabla \cdot (h{\mathbf{u}}_{\alpha t})]-\nabla \left[ \frac{1}{2}(\delta \eta )^{2}\nabla \cdot {\mathbf{u}}_{\alpha t}+\delta \eta \nabla \cdot (h{\mathbf{u}}_{\alpha t})\right]$$
(4)
$$\begin{aligned} V_{2}&=\nabla \left\{ (z_{\alpha }-\delta \eta )({\mathbf{u}}_{\alpha }.\nabla )[\nabla \cdot (h{\mathbf{u}}_{\alpha })]+\frac{1}{2}\left( z_{\alpha }^{2}-\delta ^{2}\eta ^{2}\right) ({\mathbf{u}}_{\alpha }\cdot \nabla )(\nabla \cdot {\mathbf{u}}_{\alpha })\right\} \\&\quad +\frac{1}{2}\nabla \left\{ [\nabla \cdot (h{\mathbf{u}}_{\alpha })+\delta \eta \nabla \cdot {\mathbf{u}}_{\alpha }]^{2}\right\} \end{aligned}$$
(5)

\(\delta =\frac{a_{0}}{h_{0}},\mu =k_{0}h_{0}\) are scales of nonlinearity and dispersion respectively, where a 0 and h 0 are typical amplitude and still water depth, respectively.

$$z_{\alpha }= \left[ (1+2\alpha )^{\frac{1}{2}}-1\right] h\approx -0.531h$$
(6)
$$\alpha= \frac{1}{2}\left( \frac{z_{\alpha }}{h}^{2}+\frac{z_{\alpha }}{h}\right) \approx -0.39$$
(7)

\({\mathbf{u}}_{\alpha }\) is the horizontal velocity at \(z=z_{\alpha }\) and \({\mathbf{u}}_{\alpha }=(\nabla \phi )_{z=z_{\alpha }}\)

3 Results

3.1 Wave shape and amplitude evolution

The obstacle has a steep slope 1:2.5, and thus a significant vertical velocity will be induced around the obstacle, or even a vortex may be formed behind. To verify the applicability of the model to the present problem, the comparison of the time histories of the free surface elevation between mean measurements and numerical results must be demonstrated. As can be seen in Figs. 3 and 4, one measured wave gauge datum for non-breaking and breaking wave at downstream of the obstacle (S 3 16 m from the wavemaker), is chosen to compare with numerical results. We only present results for two cases as a mean of verifying the applicability of the model, one for non-breaking wave and another for breaking wave. Note that for both non-breaking and breaking wave, the water depth is (d = 0.3 m) and the depth of the obstacle peak is (P = 0.027 m). Figure 3 shows the comparison of numerical time history of free surface vertical displacement with laboratory gauge recording of non-breaking wave (H = 0.025 m). There is no significant difference among the two profiles, except the perturbations after the mean wave in the experimental gauge recordings. These perturbations are due to the wave generation device. Figure 4 shows the comparison of numerical time history of free surface vertical displacement with laboratory gauge recording of the breaking wave (H = 0.1 m). The agreement for the main wave form is acceptable. However, discrepancies exist for the small trailing waves, especially the presence of a small wave just before the main one. This small wave exists also for non-breaking wave in Fig. 3, and it is due to the volume of water flowing from the bottom during the opening of the vertical wall of the wave maker.

Fig. 3
figure 3

Gauge recording of non-breaking wave (H = 0.025 m) for obstacle depths (P = 0.027 m) in water depth (d = 0.3 m). Experimental results (solid line), numerical results (dashed line)

Full size image
Fig. 4
figure 4

Gauge recording of breaking wave (H = 0.1 m) for obstacle depths (P = 0.027 m) in water depth (d = 0.3 m). Experimental results (solid line), numerical results (dashed line)

Full size image

To obtain a better understanding the effect of submerged obstacle on solitary wave shape, we made several numerical simulations of non-breaking wave (H/d = 0.0185). The choice of the non-breaking wave is mainly due to the absence of discrepancies comparing to the breaking wave, making it easier to distinguish changes in shape due to the obstacle. We vary the depth of the obstacle peak in each simulation, and we compare the time histories of the free surface elevation for the gauge (S 3), just behind the obstacle, with the recording of the same gauge, without obstacle. The obtained results are illustrated in Fig. 5.

Fig. 5
figure 5figure 5

Time series of (H/d = 0.0185) wave for obstacle depths a P/d = 0.01, b P/d = 0.02, c P/d = 0.03, d P/d = 0.06, e P/d = 0.08, f P/d = 0.09, g P/d = 0.12, h P/d = 0.17. Without obstacle (dotted line). In presence of obstacle (solid line)

Full size image

Figure 5 shows the comparison of the numerical gauge recording of (S 3) (Fig. 1) in presence and without submerged obstacle, for non-breaking solitary wave (H/d = 0.0185). The profiles are plotted according to the dimensionless time for different depths of the submerged obstacle peak, (P/d = 0.01 to P/d = 0.17). The recordings of simulations without obstacle are presented in dotted line and those of simulations with obstacle are presented in solid line.

From Fig. 5, the effect of the obstacle on all wave characteristics is obvious, in particular, on the amplitude. Figure 5a–c shows that the presence of the obstacle clearly reduces the amplitude of the wave. It is apparent from the profiles shape that the wave is broken approaching the obstacle. This effect decreases with increasing depth of the obstacle peak until it disappears completely in Fig. 5d. Figure 5e-f shows an adverse effect on the amplitude comparing to the previous figures. The only explanation is that going up the slope of the obstacle, and under the effect of the abrupt decrease in depth, the amplitude of wave (the potential energy) increases, and it is called the dispersion effect. We can see also the effect of dispersion caused by the obstacle in the difference between the time made by the wave to reach the gauge location in presence of obstacle and without obstacle (the difference between the peaks). This difference becomes smaller when the depth of the obstacle peak increases, but it still exists even for the large depths. Excepting the effect of dispersion which goes until the depth P/d = 0.17 (Fig. 5h), all the effects disappear beyond the depth P/d = 0.9, and the shape of the profiles becomes substantially the same. Note also the presence of the disturbances after the two main peaks (incident and reflected wave), and this is due to the reflection of the wave on the downstream slope of the obstacle and the slope of the plan beach.

3.2 Wave run-up

In the practical cases, the obstacles present a barrier against the devastative force of the tsunami waves which appears in the floods of the continent, because of the run-up. Thus the effect of the obstacle peak depth on the run-up could guide us in the protection of the beaches against the floods by the tsunamis. In this fact, we studied the influence of the obstacle peak depth on the run-up.

Figure 6 presents experimental results of the evolution of the run-up according to the amplitude of wave for several obstacle peak depths. The x-axis presents the dimensionless value of the amplitude (H/d), and the y-axis presents the dimensionless value of the maximum run-up (R/d).

Fig. 6
figure 6

Experimental results of run-up evolution according to the amplitude of solitary wave for several obstacle peak depths. Without obstacle (plus symbol), experimental results (Synolakis 1987) (times symbol), P/d = 0.03 (filled diamond), P/d = 0.06 (filled triangle), P/d = 0.09 (filled circle), P/d = 0.12 (filled square)

Full size image

The data represented in Fig. 6 encompass the results obtained for the obstacle dimensionless peak depths P/d = 0.03, P/d = 0.06, P/d = 0.09, P/d = 0.12, P/d = 0.5 (without obstacle) and the experimental results obtained by Synolakis (1987). Figure 6 shows clearly the effect of the submerged obstacle on the run-up values, and this effect is presented by reducing run-up values in the presence of submerged obstacle comparing to those without obstacle. As can be seen also in Fig. 6, the peak depth has a great effect on reducing the run-up. For the small obstacle peak depth, the reduction of run-up value is very important and vice versa. This effect is limited to the small wave amplitudes, and for the large wave amplitudes, it becomes insignificant. In another sense, there is obviously no concordance between the results we have obtained (without obstacle) and the results obtained by Synolakis (1987). This is probably due to the roughness of the materials used in the construction of the slope. Synolakis (1987) used aluminum plates, whereas we used plates of plexiglass. In this case, the friction was able to reduce the value of the run-up by approximately 20%.

Following validation of the present model, numerical simulations are performed to reproduce the same cases studied in the experimental investigation. Figure 7 plots the numerical results of the dimensionless maximum run-up data (R/d) against the dimensionless wave amplitude (H/d). Because of the ease of controlling the wave amplitude using COULWAVE, Fig. 7 gives us clearer view of the submerged obstacle effect on the run-up. The obtained numerical results confirm what has been said about the experimental ones in Fig. 6. Note that the bed friction coefficient used for all numerical calculations is 10−2.

Fig. 7
figure 7

Numerical results of run-up evolution according to amplitude of solitary wave for several obstacle peak depths. Without obstacle (plus symbol), P/d = 0.03 (filled diamond), P/d = 0.06 (filled triangle), P/d = 0.09 (filled circle), P/d = 0.12 (filled square)

Full size image

For a good discussion of the results, and to give further clarification, we just have to separate the graphs by putting each obstacle peak depth in its own graph. Figure 8a–d compares the numerical results of maximum vertical run-up to the measured experimental ones in four cases, representing each one a different obstacle peak depth. A regression model performed by Eq. (8) is also plotted on the same graphs.

$$\frac{R}{d}= 1.012\left( \sin \left( \frac{P}{d}\right) \right) ^{0.1036} \left( \sin \left( \frac{H}{d}\right) \right) ^{0.6594}$$
(8)

Equation (8) is a multiple nonlinear model representing the correlation of run-up dimensionless values (R/d) against the dimensionless values of the obstacle peak depth (P/d) and the dimensionless wave amplitude (H/d). The model has been determined using nonlinear least squares estimation method with a determination coefficient \(R^{2}=0.981\). From the results illustrated in Fig. 8a–d, it is conspicuous that the present laboratory measurements of run-up heights are in good agreement with the numerical predictions. We could also clearly see that the model presented by Eq. (8) can well describe the run-up heights evolution for both breaking and non-breaking wave.

Fig. 8
figure 8

Experimental and numerical results comparison to regression model of run-up evolution according to amplitude of solitary wave for several obstacle peak depths. Experimental results (filled triangle), numerical results (filled square), regression model of Eq. (8) (dashed line). a P/d = 0.03, b P/d = 0.06, c P/d = 0.09, d P/d = 0.12

Full size image

The significant difference observed between the experimental results obtained by Synolakis (1987) and our own experimental results without obstacle led us to make an additional numerical investigation using a bottom friction coefficient \(f = 10^{-3}\). According to Lynett et al. (2002), which is by the way demonstrated in this case (Fig. 9), the bottom friction has very important effect on the run-up value. Figure 9 presents the run-up evolution according to amplitude of solitary wave, comparing the experimental results obtained by Synolakis (1987) to the numerical results using a friction coefficient \(f=10^{-2}\), and the experimental results of the present study to the numerical results using friction coefficient \(f=10^{-2}\). The bottom friction change explains the difference we have observed in Fig. 6, especially for the big values of wave amplitude. Figure 9 shows a satisfying agreement between the experimental and numerical results according to the bottom friction coefficient, and this agreement comforts what was said before concerning the roughness of the slope. Note that we tried to make another simulations using bottom friction coefficient \(f=10^{-4}\), but it was difficult to ensure the numerical stability.

Fig. 9
figure 9

Comparison between experimental results (Synolakis 1987, present study) and numerical results (friction coefficient \(f=10^{-2},\, f=10^{-3}\)) of run-up evolution according to amplitude of solitary wave. Present study experimental results (plus symbol), experimental results (Synolakis 1987) (times symbol), numerical results for (\(f=10^{-3}\)) (solid line), numerical results for (\(f=10^{-2}\)) (dashed line)

Full size image

Based on the previous results, the applicability of the numerical model to the present problem is verified. Next, we will focus on the effect of obstacle peak depth on non-breaking wave run-up height. Figure 10 shows the evolution of the run-up according to the obstacle peak depth. The x-axis presents the dimensionless depth value of obstacle’s peak “P/d,” and in the y-axis the dimensionless value of the run-up “R/d.” The rhombuses (run-up) represent the values of the run-up corresponding to a defined peak depth for the same non-breaking wave (H/d = 0.0185), and the series represented by a dashed line is the formula shown in Eq. (9).

$$\frac{R}{d}= 0.3469 \left( \frac{P}{d}\right) +0.0916$$
(9)

Equation (9) is obtained by linear regression; it presents the line of tendency equation of the ascending part of the run-up series. The coefficient of determination of the regression model and the results is \(R^{2}=0.981\). Note that the graph contains two essential parts: The first ascending part represented by Eq. (9) is explained by the effect of the obstacle on the run-up (P/d = 0.01 to P/d = 0.12), and therefore beyond this depth the obstacle almost does not have an effect on the wave. The second part is the horizontal part, where the obstacle does not have an effect, and therefore the run-up is almost equal to the value without obstacle (P/d = 0.5).

Fig. 10
figure 10

Run-up evolution according to the obstacle peak depth for non-breaking wave (H/d = 0.0185). Run-up value (filled diamond), regression model of Eq. (9) (dashed line)

Full size image

4 Conclusion

In this paper, tsunami-like breaking and non-breaking solitary waves on 1:19.85 uniform slope which contains a submerged obstacle are investigated. New laboratory experiments are presented for five different obstacle peak depths including the slope without obstacle. The COULWAVE model is successfully validated by experimental data. Numerical simulation is employed to examine certain wave amplitude, obstacle peak depths, and bottom friction unavailable in experiments. The experimental and numerical results include detailed free surface vertical displacement evolution in time, gauge records with and without obstacle, and maximum run-up height.

In the analysis of evolution of free surface vertical displacement in times (gauge records), it is clearly demonstrated that the submerged obstacles have a very important effect on solitary wave shape and run-up. This effect disappears beyond a certain obstacle peak depth.

It is observed that for non-breaking wave, the evolution of run-up varies linearly with obstacle peak depth. Using a simple linear regression, we found that it follows this formula:

$$\frac{R}{d}= 0.3469 \left( \frac{P}{d}\right) +0.0916$$

A predictive method to estimate breaking solitary wave run-up is also examined in this study. However, reasonably good agreements between this predictive method and the experimental and numerical results are found. Based on the available results, we proposed a simple predictive model for solitary wave run-up heights with a wide range of obstacle peak depth (\(P/d =0.01-0.5\)) using nonlinear least squares estimation regression as :

$$\frac{R}{d}= 1.012\left( \sin \left( \frac{P}{d}\right) \right) ^{0.1036} \left( \sin \left( \frac{H}{d}\right) \right) ^{0.6594}$$

Finally, according to this work, it is obvious that the submerged obstacles have a very important effect in the reduction of the run-up and thus in the reduction of the risk of floods and inundations in the coastal areas, without affecting the activity of navigation in these zones.