1 Introduction

Understanding the mechanism of tsunami generation and propagation is of the utmost importance to predict flooding in coastal areas. A tsunami is created when a large body of water is moved; this can be the case during a major earthquake, when the level of the ocean floor along a fault depresses or upsurges suddenly, during a coastal or underwater landslide, or during a meteoritic impact. The nature and extent of the damage caused by a tsunami depends mainly on the specific characteristics of each coastal region, as well as on its morphological configuration, its use and its urban development.

It is obvious that the tragedy caused by the tsunamis was mainly due to the flood. Therefore, the forecast of wave motion offshore and nearshore is very important for the reduction of danger (risk) of tsunami and coastal protection. Protection of coastal areas against natural hazards can be ensured by natural barriers such as reefs and vegetation or artificial barriers such as walls and dikes. One of the most effective coastal protections, are breakwaters and submerged obstacles, they constitute a sort of barrier facing and reducing the risk of inundation by waves. Various studies have been conducted on wave-structure interaction between a wave/bore and a vertical/floating barrier; Losada et al. (1989) describes physical and numerical experiments that were carried out to investigate the scattering of non-breaking solitary waves of moderate amplitude on encountering an abrupt discontinuity. Ramsden (1996) performed an experimental study on the forces and overturning moments on a vertical wall due to the reflection of solitary waves, undular bores, turbulent bores, and surges on a dry bed. Liu and Al-banaa (2004) investigated experimentally the interaction between a solitary wave and a thin vertical barrier. Xiao and Huang (2008) described a numerical wave model based on the incompressible Reynolds-averaged Navier–Stokes (RANS) and K–ε equations to estimate the impact of a solitary wave on an idealized beach-front house located at different elevations on a plane beach.

Other studies focused on submerged obstacle or a subaerial plate; Chang et al. (2001) investigated both experimentally and numerically the interactions between a solitary wave and a submerged rectangular obstacle using PIV and numerical model, based on the Reynolds Averaged Navier–Stokes (RANS) equations with a K–ε turbulence model. Lin et al (2005) conducted an experimental study on the vortex shedding process induced by the interaction between a solitary wave and a submerged vertical plate using particle image velocimetry (PIV). Touhami and Khellaf (2017) presented laboratory experiments and numerical simulations using COULWAVE model, on effects of submerged obstacles peak depth on tsunami-like solitary wave and its run-up. In Yao et al (2018) tsunami-like solitary wave transformation and run-up over various fringing reef profiles were investigated experimentally.

Also, the study of a wave passing over and through a porous structure to determine its kinematics and energy, its reflection and transmission and its effect on the wave shape; Dalrymple et al. (1991) examined a linear theory for water waves impinging obliquely on a vertically sided porous structure. Lee and Lan (1996) used a generalized potential theory to describe both the internal and external water flows with an implicit nonlinear model to define flow mechanism inside the porous medium. Harada et al. (2002) performed experiments for the tsunami of two different amplitudes with five kinds of models; mangrove, coastal forest, wave dissipating block, rock breakwater, houses, with different structure and porosities. Lan and Lee (2010) studied theoretically the problem of incident waves propagating over a submerged poro-elastic structure. Wu et al. (2014) proposed a three-dimensional large-eddy-simulation model with macroscopic model equations of porous flow to investigate solitary waves interacting with permeable breakwaters. Sasikumar et al. (2020) studied the interaction of waves with porous coastal structures using a computational fluid dynamics (CFD) model. Francis et al. (2020) focusses on energy dissipation of the interaction and run-up of solitary waves on coastal protection structures in the form of thin, rigid vertical porous barriers.

Because of their low cost compared to impermeable structures and their ability to dissipate more energy, submerged permeable breakwaters are widely used to reduce the impact of waves and currents along the coast. The shape and size of the blocks that make up these structures condition their porosity and therefore their ability to dissipate wave energy. To highlight the effectiveness of submerged structures reducing wave energy as a function of their porosity, we have performed the present work. In this study, we will examine the comportment of tsunami-like solitary waves striking and overtopping a porous submerged trapezoidal obstacle on a 1:19.85 sloping beach, to determine the effects of a low-crested structures-like submerged obstacles on the wave shape and the run-up value. Numerous experiments were conducted in medium-size wave channel for four different obstacle’s porosities. Original laboratory data of maximum run-up height of wave under porous submerged obstacle effect are presented and discussed. A report on the bottom bathymetry and the experimental set, is given in Sect. 2. In Sect. 3, we illustrated the different results found by experimental investigations, we also be able to establish a regression model of maximum run-up according to wave height and obstacle porosity using least squares method estimation. The major conclusions are summarized in Sect. 4.

2 Research methods

2.1 Flume bottom layout

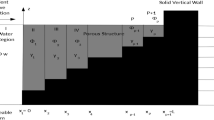
The bottom profile of the wave flume presented in this study is used to investigate the behavior of breaking and non-breaking solitary wave mounting up on a plane beach; yet, we have added a porous submerged obstacle to this beach. The existing bottom profile is one-dimensional regular horizontal bathymetry which comes to end (ended) by a 1:19.85 sloping beach as shown in Fig. 1. The beach contains in its middle a trapezoidal and porous obstacle. The slopes of the obstacle on both sides equal to 1:2.5, where d is water depth, L and H are length and amplitude of solitary wave, respectively, and R is run-up value. To measure water elevation variation in time, the gauges S1, S2, and S3 are mounted in different positions. Note that the obstacle peak width is equal to d/10 and its peak depth is d/15.

Fig. 1
figure 1

Definition sketch of bottom profile and the definitions of physical variables

Full size image

2.2 Experimental setup and measurement facilities

The experiments were conducted in a medium-size flume at Civil Engineering Faculty’s Hydraulics Laboratory of University of Sciences and technology Houari Boumediene (USTHB) Algiers. This flume is 22 m long, 75 cm wide and 90 cm deep. The wavemaker is located at one end of the flume and consists of a guillotine system (designated in Fig. 1 by Bulkhead). This system is used to generate target solitary waves by isolating an amount of water which has a higher free surface than the rest of the channel, this amount of water is then released to give rise to the solitary wave (Goring and Raichlen 1980). A wooden skeleton covered with plastic takes the shape of a plane beach with 1 vertical to 19.85 horizontal. This ramp starts 12 m from the vertical bulkhead wave generator. A removable trapezoidal obstacle, is mounted in a way that its peak is always in the middle of the submerged part of the slope. The obstacle slopes on both sides equal to 1:2.5, and its peak width equals to 3 cm, it is located at 2 cm depth. Two types of obstacles were made: the first one (Fig. 2a) has a wooden skeleton covered with plastic, which makes it completely waterproof; and the second one (Fig. 2b) consists of a steel cage which will contain different permeable materials (gravel) to vary the porosity. We used three different gravel grain sizes, namely: 3–8 mm for porosity ξ = 0.34, 8–15 mm for porosity ξ = 0.38, and 15–25 mm for porosity ξ = 0.44. The porosities of the three permeable obstacles were determined using a pycnometer.

Fig. 2
figure 2

Prospective view of the flume and the obstacle. (1) Plane beach, (2) obstacle, (3) wave gauge. a impermeable obstacle, b permeable obstacle

Full size image

Figure 2 shows a prospective view of the laboratory flume and the obstacles, also the measurement apparatus employed in the present experiments. The arrangement of measurement apparatus was deployed with wave gauges to record free surface variation in time, and camera to determine the run-up value. The local free surface elevation was recorded by three wave gauges located, from the wavemaker, at (S1) 11 m (4 m upstream of the obstacle peak), (S2) 15.25 m (25 cm downstream of the obstacle peak) and (S3) 15.6 m (60 cm downstream of the obstacle peak). To avoid the viscous effect, each wave gauge was mounted at the middle of the flume width. The calibration of all wave gauges was done through a standard method which concerns the change of water level to adjust the response voltage of each gauge before and after the experiments to ensure its linearity and stability. The calibration results give a straight line with a correlation coefficient of 0.9999. It is noted that in all experiments, the wave gauge S1 located 11 m from the wave generator is referred as a reference gauge.

3 Results and discussions

To study the impact of the porosity of the obstacle on tsunami run-up, we performed several experiments and measured the characteristic wave parameters according to the variation of porosity. The main results obtained in our experimental study will be presented in this section. In the first part we will focus on the wave shape given by gauge recording. A comparison between the cases with and without obstacle is made for breaking and non-breaking waves. In the second part we will focus on the maximum run-up of the waves and the effect of the obstacle’s porosity on it. We will also present a comparison between the experimental results that we obtained and multiple nonlinear models that we were able to obtain by the method of least squares.

3.1 Gauge recording

The wave propagation is recorded using three gauges, one placed at the horizontal part of the channel and two on the ramp, as can be seen in Fig. 1. The gauge recording represents the vertical variation of water free surface in time at the location of the gauge. The results obtained are used to describe the wave shape. To better understand the effect of the porosity of a submerged obstacle on the shape of the solitary wave, we performed several laboratory experiments on different variants of obstacles. Based on the results obtained, a comparison of the wave shape in the presence and absence of obstacle is made using gauge recordings for non-breaking waves (H/d = 0.09) and breaking waves (H/d = 0.4). The profiles are plotted for different submerged obstacle porosity (ξ = 0 (impermeable), ξ = 0.34 (3–8 mm), ξ = 0.38 (8–15 mm), ξ = 0.44 (15–25 mm)). In this section, the gauges S2 and S3, located respectively 25 cm and 60 cm downstream of the obstacle, are chosen as reference to determine the wave shape change under effect of obstacle porosity variation. We will present in what follows the recordings given by the gauges S2 and S3 to compare the shape of the waves in the two cases with and without obstacle for both breaking and not breaking wave, and this for different obstacle porosities.

3.1.1 Non-breaking wave

First, we performed several experiments on non-breaking wave (H/d = 0.09). We vary the obstacle porosity in each test and compare the vertical displacements of the free surface recorded by the gauges S2 and S3, installed respectively at a distance of 0.25 m and 0.6 m from the crest downstream of the obstacle, to the recording of the same gauges without obstacle. The results obtained are shown in Figs. 3 and 4. Figures 3 and 4 show the vertical displacement of the free surface recorded by the gauges S2 and S3, which presents solitary waves shape in both a, b, c and d plots. These waves are followed by interference due to the generation mechanism and successive reflections on the slope and the obstacle. In one hand, we notice that the comparison between the case without obstacle and presence of obstacle shows clearly a difference in wave shape, in particular the wave amplitude, which induces to say that the presence of the obstacle clearly reduces the wave height. In the other hand the obstacle porosity has a significant effect on the wave shape. This effect is summarized in the fact that the high values of obstacle porosities are more effective in reducing the wave amplitude. If we compare the changes in wave shape caused by the presence of obstacles, the recordings from gauge S2 show a clear superiority in the effect of the submerged obstacle in the area just behind it (25 cm after). This effect decreases in the recordings of gauge S3 (60 cm downstream of submerged obstacle) where the wave shapes in presence and without obstacle are closer. We also found that there is a slight dispersion effect, caused by the presence of the plane ramp. This effect is reflected in the difference of maximum wave heights, noticed between the recordings of the gauge S2 and the gauge S3 in the case without obstacle. Obviously, the amplitude recorded by the gauge S3, is greater than that of the gauge S2 in this particular case.

Fig. 3
figure 3

Gauge S2 recordings of non-breaking wave (H/d = 0.09) for obstacle porosity a ξ = 0, b ξ = 0.34, c ξ = 0.38 and d ξ = 0.44, without obstacle (dashed line). In presence of obstacle (solid line)

Full size image
Fig. 4
figure 4

Gauge S3 recordings of non-breaking wave (H/d = 0.09) for obstacle porosity a ξ = 0, b ξ = 0.34, c ξ = 0.38 and d ξ = 0.44, without obstacle (dashed line). In presence of obstacle (solid line)

Full size image

3.1.2 Breaking wave

In a second step, we carried out several experiments on breaking wave for (H/d = 0.4). We varied the obstacle porosity in each experiment and compared the vertical displacements of the free surface recorded by the gauges S2 and S3, located respectively at 0.25 m and 0.6 m downstream from the obstacle peak, to the recording of the same gauges without obstacle. The results obtained are illustrated in Fig. 5 and 6.

Fig. 5
figure 5

Gauge S2 recordings of breaking wave (H/d = 0.4) for obstacle porosity a ξ = 0, b ξ = 0.34, c ξ = 0.38 and d ξ = 0.44, without obstacle (dashed line). In presence of obstacle (solid line)

Full size image
Fig. 6
figure 6

Gauge S3 recordings of breaking wave (H/d = 0.4) for obstacle porosity a ξ = 0, b ξ = 0.34, c ξ = 0.38 and d ξ = 0.44, without obstacle (dashed line). In presence of obstacle (solid line)

Full size image

Figures 5 and 6 represent the recording of the free surface variation in time at 25 cm downstream of the submerged obstacle crest (gauge S2), as well as at 60 cm downstream of the obstacle (gauge S3). The plots show a main wave followed by perturbations due to the generation mechanism. It is obvious that this main wave in all cases a, b, c and d represents a breaking solitary wave because of the vertical straight rise of the wave ending with a peak, reflecting the passage speed of the wave. As noticed for non-breaking waves, the presence of an obstacle causes a considerable change in the wave shape, even a more significant change than for the non-breaking wave for gauge S2, especially the amplitude. As for the gauge S3 recordings, the effect of submerged obstacles is basically limited to the decrease of the wave amplitude. For the breaking wave, the effect of the porosity is as remarkable as for the non-breaking wave. This one is inversely proportional to the porosity, i.e., when the porosity of the obstacle increases the height of the wave decreases. Note that in the case of breaking wave, the effect of the porosity on the wave amplitude is less significant than for the non-breaking wave. In this case as well, the effect of the presence of an obstacle appears more clearly for gauge S2 than for gauge S3. It looks like the wave undergoes a form of breaking in the area above the obstacle, then it reconstitutes and restabilizes itself further towards the beach. The presence of a small wave just before the main one is also noticed in the plots of gauge S3 recordings, it is may be due to the volume of water flowing from below when the movable bulkhead of the wave generator opens. But anyway, we can say that the presence of this small wave does not have a significant influence on the ensemble of the results obtained.

3.2 Wave run-up

The measurement of the maximum run-up due to a solitary wave is an important parameter to evaluate inundation areas and the effects caused by tsunami. The experimental setup used in the study allows us to determine the run-up value, and thus to have a global view on the effectiveness of low-crested structures in the protection of the coastline and to decrease the surface of the inundable zones. In this regard, we will study the influence of submerged obstacles porosity on the maximum run-up value.

To obtain the maximum run-up value as a function of the wave amplitude, a series of height differences Δh, between the water level in the generator and that of the channel, ranging from Δh = 0.5 cm to Δh = 25 cm with a step of 0.5 cm, were used to generate the different waves. As the wave propagates and reaches the end of the channel, there is a considerable increase in water height and overflow on the sloping ramp (1, 19.85). We placed a graduated ruler on this ramp and a camera to measure the distance covered by the water. The measurement of the run-up was carried out using a test pattern in the form of a fabric tape, graduated every five millimeters. The zero point of the tape measure is set on the free surface when the water is calm. A video camera is placed on a tripod in such a way that it can provide a fairly clear video of the entire area submerged by water. The video is UHD quality (3840 × 2160 pixels). The camera records the video during the whole experiment, to monitor the evolution of the run-up over time. The recorded video will be analyzed frame by frame to determine the exact value of the maximum run-up. The vertical run-up values are calculated knowing the maximum distance traveled by the water and the tangent of the slope. Therefore, the accuracy of this device is estimated to the quarter of a millimeter (2.5 × 10–4 m).

The effect of obstacle porosity on the Run-up could guide us to protect coastline area from tsunami inundation. To better understand the effect of the porosity of a submerged obstacle on the Run-up of solitary waves, we performed series of experiments in the laboratory on different obstacle variants (ξ = 0 (impermeable), ξ = 0.34 (3–8 mm), ξ = 0.38 (8–15 mm) and ξ = 0.44 (15–25 mm)) and thus according to wave amplitude following the procedures explained above. the obtained results are presented in Fig. 7.

Fig. 7
figure 7

Experimental results of run-up evolution according to the amplitude of solitary wave for several obstacle porosity. Without obstacle (filled circle), experimental results (Synolakis 1987) (times symbol), impermeable obstacle (white diamond), obstacle porosity = 0.34 (filled triangle), obstacle porosity = 0.38 (white circle), obstacle porosity = 0.44 (filled diamond)

Full size image

Figure 7 shows the experimental results of run-up evolution as a function of wave amplitude for several obstacle porosities (ξ = 0 (impermeable), ξ = 0.34 (3–8 mm), ξ = 0.38 (8–15 mm), ξ = 0.44 (15–25 mm)) where the x-axis represents the dimensionless value of amplitude (H/d) while the y-axis represents the dimensionless value of maximum run-up (R/d).

The data plotted in Fig. 7 encompass the results obtained for the different obstacle porosities (ξ = 0 (impermeable), ξ = 0.34 (3–8 mm), ξ = 0.38 (8–15 mm), ξ = 0.44 (15–25 mm)), and without obstacle. The experimental results obtained by Synolakis (1987), are also presented for comparison.

From Fig. 7, we can clearly see the effect of submerged obstacle on the obtained run-up values, this effect is presented as the reduction of the run-up values in the presence of obstacle compared to the case without obstacle. It can also be seen that the obstacle porosity plays an important role in the reduction of the run-up values, it is clear that the increase of the submerged obstacles porosity leads to the decrease of the run-up values. It is also remarkable that this effect appears slightly on the waves of small amplitudes (non-breaking waves), but it becomes significant (more visible) for large amplitudes (breaking waves). In another hand, there is an obvious difference (approximately 20%) between the results obtained in this work (without obstacle) and the results obtained by Synolakis (1987). As mentioned by Touhami and Khellaf (2017), this is due to the roughness of the materials used in the construction of the slope. Synolakis (1987) used aluminum plates, whereas we used plates of plexiglass.

By comparing the values of the run-up obtained for the cases in presence of submerged obstacles with the case without submerged obstacle, we will be able to evaluate the effectiveness of obstacle in the reduction of the run-up values and thus the reduction of the risk of inundation, especially the effectiveness of the porosity of obstacle in this specific case. The decrease of the run-up values under the effect of the obstacle porosity, compared to the values without obstacle, expressed in percentage, are as follows:

  • For impermeable obstacle (ξ = 0), the reduction mean equals to 7.9%, and the maximum reduction equals to 11%;

  • For obstacle 3–8 mm (ξ = 0.34), the reduction mean equals to 12.14%, and the maximum reduction equals to 17.44%;

  • For obstacle 8–15 mm (ξ = 0.38), the reduction mean equals to 13.5%, and the maximum reduction equals to 17.4%;

  • For obstacle 15–25 mm (ξ = 0.44), the reduction mean equals to 15.22%, and the maximum reduction equals to 19.32%;

To simplify the estimation of solitary waves maximum run-up value (R/d), under effect of the change of obstacle porosity (ξ), we have suggested three different empirical predictive formulas. Based on the experimental results obtained in this study, and by a nonlinear regression using the least square method, we were able to estimate the parameters of the three predicate equations. Note that two of the three equation that we will demonstrate in the following, was inspired by previous studies on run-up estimation.

$$\frac{R}{d}=1.356\sqrt{\mathrm{sin}\left(\xi \right)}{\left(\frac{H}{d}\right)}^{0.6969}.$$
(1)

The Formula (1) provides an estimation of solitary wave run-up heights (R/d) against obstacle porosity (ξ) and wave amplitude variation (H/d). To obtain the Formula (1), we were inspired by the model established by Synolakis (1987). Based on his laboratory study, Synolakis (1987) proposed an analytic solution and an empirical formula for the predictions of maximum run-up height of non-breaking and breaking solitary waves. The model presented by Formula (1) gives a value of the coefficient of determination equal to ρ2 = 0.9759.

$$\frac{R}{d}=0.8189{\left(\mathrm{sin}\left(\xi \right)\right)}^{-0.05325}{\left(\mathrm{sin}\left(\frac{H}{d}\right)\right)}^{0.7136}.$$
(2)

The Formula (2) has the same form as the one presented in the work conducted by Touhami and Khellaf (2017). In their study, Touhami and Khellaf (2017) addressed a multiple nonlinear model representing the correlation of Run-up dimensionless values against the dimensionless values of the obstacle peak depth and the dimensionless wave amplitude. The model presented by Formula (2) gives a value of the coefficient of determination equal to ρ2 = 0.9928.

$$\frac{R}{d}=0.7948{\left(\xi \right)}^{-0.05036}{\left(\frac{H}{d}\right)}^{0.6975}.$$
(3)

This time we took the initiative to try a simple power equation (Formula (3)) which follows the shape of the run-up variation shown in Fig. 7. The model presented by Formula (3) gives a value of the coefficient of determination equal to ρ2 = 0.9923.

For proper discussion of the results and further clarification, we will separate the graphs by placing the experimental run-up results for each obstacle porosity in its own graph, and compare them to the results obtained by the regression models proposed in this study. Figure 8a–c shows a comparison of the measured experimental run-up results to the results obtained by the calculated regression models in three cases, each representing a different obstacle porosity (ξ = 0.34, ξ = 0.38, ξ = 0.44).

Fig. 8
figure 8

Experimental results comparison to regression models of run-up evolution according to amplitude of solitary wave for several obstacle porosities. Experimental results (filled circles), regression model of Formula (1) (solid line), regression model of Formula (2) (dashed line), regression model of Formula (1) (dotted line). a ξ = 0.34, b ξ = 0.38, c ξ = 0.44

Full size image

From the results shown in Fig. 8, it is obvious that the run-up measurements in the laboratory agree well with the results obtained by the equations of the proposed models, more precisely with the values given by the Formula (2), which induces to say that the model presented by the Formula (2) can describe well the evolution of the run-up for the breaking and non-breaking waves.

Based on the available data, we propose the Formula (2) chosen among the formulas presented above as a predictive model for the run-up values of breaking and non-breaking solitary waves on a 1:19.85 uniform slope.

Formula (2) is a multiple nonlinear model representing the correlation of the dimensionless run-up values (R/d) against to the values of the obstacle porosity (ξ) and the dimensionless wave amplitude (H/d). The model was determined using a nonlinear least squares estimation method with a correlation coefficient ρ2 = 0.9928.

4 Conclusion

In this study, a series of laboratory experiments on breaking and non-breaking solitary waves, traveling on a uniform slope of 1/19.85 that contains a submerged obstacle, were performed in a wave channel with a constant water depth d = 0.3 m for a wave amplitude interval of (0.01 < h/d < 0.6). The laboratory data, including the detailed evolution of amplitude, wave shape and maximum run-up height, are presented and compared with and without obstacle for four different obstacle porosities.

As stated by the examination of the evolution in time of the free surface vertical displacement recorded by the gauges, a very important effect of submerged obstacles on the solitary wave shape and run-up is clearly shown.

The effect of the obstacle on all the wave characteristics is obvious, it clearly reduces the amplitude of the wave. This amplitude is also influenced by the variation of the porosity of the submerged obstacles, the wave height decreases with the increase of the porosity of the obstacle.

Predictive methods facilitating the estimation of solitary wave run-up values are also analyzed in this study. A relatively satisfying correlation was found between those predictive methods and the experimental results. Based on the results obtained in this work, we proposed a simple predictive formula for the estimation of solitary wave run-up heights against obstacle porosity and wave amplitude variation using a nonlinear least squares estimation regression by means of:

$$\frac{R}{d}=0.8189{\left(\mathrm{sin}\left(\xi \right)\right)}^{-0.05325}{\left(\mathrm{sin}\left(\frac{H}{d}\right)\right)}^{0.7136}$$

Finally, from this work, it is clear that low-crested structures porosity has a very significant effect on reducing tsunami momentum, and consequently reducing the risk of flooding in coastal areas, without affecting navigation activity or disturbing aquatic life.