Estimation of lateral force acting on piles to stabilize landslides

Abstract

The lateral force on stabilizing piles due to the movement of the landslide has been studied by many researchers. One of the most widely used methods was proposed by Ito and Matsui in 1975 based on the plastic deformation theory. This paper aims to extend the approach of Ito and Matsui by considering the soil arching effects along the height of the sliding layer between two neighboring piles. The analysis is carried out in two stages. First stage involves the plastic deformation of soil adjacent to piles. In this stage, considering the arching effects along the height of the sliding layer, a typical cross section of the soil is employed to analyze the soil stress in the rear of piles. In the second stage, the plastic deformation theory proposed by Ito and Matsui is adopted to analyze the squeezing effects between two neighboring piles. Moreover, the parametric analysis is performed to investigate the susceptibility of the governing factors, which include the geometric and mechanical parameters. The results show that both the geometric and mechanical parameters impart the significant influence on the lateral force. Finally, both the numerical simulation results and the field experiment data from the literatures are introduced to validate the proposed approach. The comparison charts illustrate that the predictions by the proposed approach are consistent with the experimental results.

1 Introduction

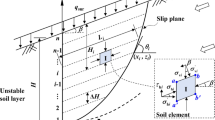
Landslide occurring in both natural and cut slopes often results in serious damage to both human lives and properties (Poulos 1973; Liu and Zhao 2013; Cai and Ugai 2004). Lots of research has been carried out to reduce the damage of landslide disasters. Stabilizing piles, as one of the most widely used countermeasure in reinforcement engineering of slopes, have been proved to be an efficient solution to landslides (Guo 2013). Stabilizing piles as passive piles are embedded into a stable base of slope to provide additional stability. The distributions of the lateral force acting on passive piles are dependent on soil movements. Due to the complex plastic deformation of soil, estimation of the lateral force on passive piles cannot be easily solved.

Several previous researchers have attempted to estimate the lateral force exerted on stabilizing piles. Ito and Matsui (1975) proposed an analysis to evaluate the lateral force acting on a single row of piles due to soil movement. Their analysis was carried out in light of the theory of plastic deformation, and simultaneously, the interaction between piles and soil was considered. It is convenient to estimate the ultimate soil pressure on pile segment embedded in the sliding soil layer using this method, because the pressure depends on only four parameters: the cohesion c, the internal friction angle φ, pile diameter, and spacing between piles. This method has been widely referred by other researchers (Hassiotis et al. 1997; Cai and Ugai 2000; Hazarika et al. 2000). Poulos (1995) presented a method in which a boundary element method was employed to analyze the response of a row of passive piles incorporated in limit equilibrium solutions of slope stability in which the pile is modeled as a simple elastic beam. The method evaluates the maximum shear force that each pile can provide based on an assumed input free field soil movement (Ashour and Ardalan 2012). Poulos (1995) revealed the existence of three modes of failure: (i) the “flow mode,” (ii) “intermediate mode,” and (iii) the “short-pile mode.” These three modes of failure highlighted by Polous definitely promote the application of analysis of stabilizing piles. This classification of failure modes was diffusely adopted by researchers (Chen and Poulos 1997; Ashour and Norris 2000; Ashour et al. 2004; Won et al. 2005; Jeong et al. 2003; Nian et al. 2008; Suleiman et al. 2014). In this paper, a row of piles in the deforming ground with the “flow mode” mechanism is analyzed, and here the soil movement is larger than the pile deflection. In addition, the soil arching effects along the height of the sliding layer between two neighboring piles are considered to provide the nonlinear distribution of lateral force on each pile.

In this study, the lateral force on a row of piles under lateral movement of the sliding layer is analyzed. The analysis is carried out in deforming ground considering the arching effects in the rear of piles. The distribution of the soil stress exerted on the piles is nonlinear based on the soil arching theory. From parametric analysis of the factors utilized in the proposed formulae, it reveals that all the factors including the internal friction angle, the cohesion, the pile diameter, the height of the unstable soil layer influenced the lateral stress enormously. What’s more, the numerical simulation results together with field experiments from literatures are introduced to validate the proposed approach.

2 Force on stabilizing piles undergoing lateral soil movement

2.1 General descriptions

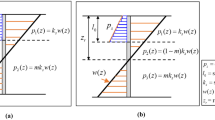
When the sliding layer moves laterally, the soil around the piles deforms. Between two neighboring piles, the soil arching occurs along the height of the sliding layer. In the rear of piles, the direction of major and minor principal stress of the soil rotates in the soil arching zone. In this analysis, the soil arching zone in the rear of piles is shown as the dashed area in Fig. 1. The plane view of soil deforming between two neighboring piles is depicted in Fig. 2. In addition, a typical cross section, UU′, as shown in Fig. 3, is employed to display the soil stress in the rear of the plane AA′ (Fig. 2). In the present paper, the analysis is conducted in two stages. Firstly, the soil pressure acting on the plane AA′ is analyzed based on the soil arching theory. Secondly, considering the squeezing effect between the piles, the lateral force acting on the piles is calculated.

Fig. 1

The soil arching zone in the rear of stabilizing piles

Fig. 2

Plastic deformation of soil between neighboring piles (after Ito and Matsui 1975)

Fig. 3

Cross section of the deformation in soil ground in the rear of piles

2.2 Soil arching effects

Soil arching was described by Terzaghi (1943) as one of the most universal phenomenon in the field of soil mechanics. Transferring of soil pressure from a yielding support to an adjacent non-yielding support is the essence of this phenomenon (Bosscher and Gray 1986). However, as to the geometrical feature of soil arch, Terzaghi used shadow to represent the zone of soil arching instead of drawing a real arch (Terzaghi 1936, 1943). In the present paper, a circle-shaped arch is employed, and the limit equilibrium of the differential element in the soil arching zone is analyzed to investigate the lateral active soil stress.

In silos and ditches, some researchers have set up differential equations to estimate the soil pressure by considering the soil arching effects, without defining the shape of the soil arching (Janssen 1895; Marston and Anderson 1913). However, the shape of the soil arching is crucial for lateral stress analysis. It has been investigated by many researchers, and several geometrical models, such as elliptic, catenary, and parabolic, have been proposed to describe the shape of the arch (Livingston 1961; Walker 1966; Stević et al. 1979; Handy 1985). The trajectory of the arch was examined theoretically by Kingsley (1989). It is shown that the minor principal stress arch can be approximated by a catenary or a circle. Recently, the soil arching theory has been developed to study on retaining wall based on the catenary and circle-shaped arch, respectively (Handy 1985; Wang 2000; Paik and Salgado 2003). In the present paper, some concept of previous study is adopted to evaluate the soil stress behind a row of stabilizing piles. The trajectory of soil arching is assumed to be an arc of a circle. In addition, in order to analyze the soil stress on the plane AA′ (Fig. 2) due to the soil layer deformation, the plane AA′ (Fig. 2) is assumed in active condition. Furthermore, it is assumed that only the area between the two parallel lines AG and A′G′ (Fig. 2) is considered, when the active stress on the plane AA′ is analyzed. It is noted that assumption of the active stress is same to that of Ito and Matsui (1975). Moreover, they assumed that the Rankine’s earth pressure theory was applied on the plane. However, some recent research indicates that the active earth pressure predicted by soil arching theory provides more accurate result than that by Rankine’s theory. It has been proved in the study of silos, ditches, and retaining walls (Janssen 1895; Marston and Anderson 1913; Paik and Salgado 2003). Based on soil arching theory proposed by Paik and Salgado (2003), the active stress on plane AA′ (Fig. 2) in deforming ground is discussed.

When soil layer deforms, the actual soil arching zone would be complicated. In this study, assumption mentioned previously is utilized to simplify the analysis. The cross section UU′ is shown in Fig. 3. The angle between sliding plane and the horizontal is β. In the deforming soil layer, the rotation of the principal stress on the line FF′ (Fig. 3) is described as Fig. 4. In the rear of the line FF′, the shape of the soil arching is an arc of a circle which dips downward instead of upward. The trajectory of minor principal stress on the differential element is represented by the dotted lines, while the direction of major principal stress is the normal of the arch.

Fig. 4

Stress on differential element in the soil arching zone (after Paik and Salgado 2003)

The active earth pressure acted on the line FF′ includes two components: the active lateral stress σ _h and the shear stress τ. A theoretical approach has been proposed by Paik and Salgado (2003) to estimate the active lateral stress σ _h behind a retaining wall for cohesionless soil. This approach is adopted herein and extended for c–φ soil.

Considering the force equilibrium in the triangular element at point A in Fig. 4, the lateral stress is obtained as:

$$\sigma_{h} = \sigma_{1} \cos^{2} \theta + \sigma_{3} \sin^{2} \theta$$

(1)

At an arbitrary point D of the arch, whose original location is point B, a similar equation is given by

$$\sigma_{ah} = \sigma_{1} \cos^{2} \psi + \sigma_{3} \sin^{2} \psi$$

(2)

where ψ is the angle between the normal of the arch at point D and the horizontal, σ _ah is the lateral stress at point D. Considering that the soil is in active state, the Mohr–Coulomb’s yielding criterion is applied:

$$\sigma_{3} = \sigma_{1} N - 2cN^{1/2}$$

(3)

where N = tan²(π/4 − φ/2) and c is the cohesion of soil. Substituting Eq. (3) in Eq. (1), the lateral stress at point D (Fig. 4) is obtained:

$$\sigma_{ah} = (\cos^{2} \psi + N\sin^{2} \psi )\sigma_{1} - 2cN^{1/2} \sin^{2} \psi$$

(4)

Since σ _ah −σ ₃ = σ ₁−σ _av , substitution for σ _ah gives

$$\sigma_{av} = (\sin^{2} \psi + N\cos^{2} \psi )\sigma_{1} - 2cN^{1/2} \cos^{2} \psi$$

(5)

where σ _av is the vertical stress at an arbitrary point D. As depicted by Eq. (5), the vertical stress varies with angle ψ, which changes from θ to π/2. In this problem, it seems impossible to calculate the vertical stress at every point in the analyzing zone, so the average vertical stress $\bar{\sigma }_{v}$ is introduced, which can be expressed as:

$$\bar{\sigma }_{v} = \frac{V}{S}$$

(6)

in which V is the total vertical stress across the differential element and S the width of the differential element. The total vertical stress V of the differential element can be calculated by the following formula:

$$\begin{aligned} V& = \int_{\theta }^{\pi /2} {dV} \hfill \\ &= \int_{\theta }^{\pi /2} {\sigma_{av} dA} \hfill \\& = \int_{\theta }^{\pi /2} {[\sigma_{1} (\sin^{2} \psi + N\cos^{2} \psi )} {\kern 1pt} {\kern 1pt} - 2cN^{1/2} \cos^{2} \psi ](R \cdot d\psi \cdot \sin \psi ) \hfill \\ \end{aligned}$$

(7)

where dV is the differential vertical force on the shaded portion at arbitrary point B and dA the width of the shaded portion at point B.

Substituting Eq. (7) in Eq. (6), and considering S = R × cosθ, the average vertical stress is obtained as follows:

$$\bar{\sigma }_{v} = \int_{\theta }^{\pi /2} {\sigma_{1} } (\sin^{2} \psi + N\cos^{2} \psi )\frac{\sin \psi }{\cos \theta } \cdot d\psi {\kern 1pt} - \int_{\theta }^{\pi /2} {2c} N^{1/2} \cos^{2} \psi \frac{\sin \psi }{\cos \theta } \cdot d\psi$$

(8)

Integrating of Eq. (8) yields

$$\bar{\sigma }_{v} = \sigma_{1} \left(1 - \frac{1 - N}{3}\cos^{2} \theta \right) - \frac{2c}{3}N^{1/2} \cos^{2} \theta$$

(9)

Equation (9) can be rewritten as:

$$\sigma_{1} = \frac{{3\bar{\sigma }_{v} + 2cN^{1/2} \cos^{2} \theta }}{{3 - (1 - N)\cos^{2} \theta }}$$

(10)

Substituting Eqs. (3) and (10) in Eq. (1), the lateral stress is obtained

$$\sigma_{h} = \frac{{3(\cos^{2} \theta + N\sin^{2} \theta )}}{{3 - (1 - N)\cos^{2} \theta }}(\bar{\sigma }_{v} + \frac{2c}{3}N^{1/2} \cos^{2} \theta ) - 2cN^{1/2} \sin^{2} \theta$$

(11)

in which θ = 45° + φ/2 when the line FF′ is in active condition. It is noted that in Paik and Salgado’s research (2003), the angle θ is defined as a function of wall friction angle. However, in this study, the friction force is induced by the soil particles on the line FF′; namely, it is identical to the condition that the wall friction angle equals to 0 in Paik and Salgado’s model. In order to simplify the expression of Eq. (11), let

$$K_{an} = \frac{{3(\cos^{2} \theta + N\sin^{2} \theta )}}{{3 - (1 - N)\cos^{2} \theta }}$$

(12)

and

$$\begin{aligned} T = \frac{{3(\cos^{2} \theta + N\sin^{2} \theta )}}{{3 - (1 - N)\cos^{2} \theta }} \cdot \frac{2c}{3}N^{1/2} \cos^{2} \theta - 2cN^{1/2} \sin^{2} \theta {\kern 1pt} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = 2cN^{1/2} (\frac{1}{3}\cos^{2} \theta \cdot K_{an} - \sin^{2} \theta ) \hfill \\ \end{aligned}$$

(13)

Then, Eq. (11) can be expressed as:

$$\sigma_{h} = K_{an} \bar{\sigma }_{v} + T$$

(14)

Equation (14) shows that the active lateral stress consists of two components: the cohesion effect and non-cohesion effect. In cohesionless soil, the relation between active lateral stress and average vertical stress on the line FF′ is succinct, which can be written as $\sigma_{h} = K_{an} \bar{\sigma }_{v}$.

2.3 Limit equilibrium equation in the soil arching zone

The stress on the differential element in the soil arching zone is shown as Fig. 5. The angle β is assumed to be 45° + φ/2. It has been proved that the right edge of the differential element, namely the triangular area ABC, is in the state of limit equilibrium, so that the stress in this area can be neglected when total stress on the differential element is analyzed. At left edge of the differential element, the shear stress along the line FF′ should be taken into account, which can be expressed as:

$$\tau = \sigma_{h} \tan \varphi + c = (K_{an} \bar{\sigma }_{v} + T)\tan \varphi + c$$

(15)

Fig. 5

Soil stress on differential element

In the vertical direction of Fig. 5, considering the width of soil arching zone, all the vertical force must be in equilibrium. The equation is set up as follows:

$$\gamma S \cdot D_{2} {\text{d}}z = (K_{an} \bar{\sigma }_{v} + T)\tan \varphi \cdot D_{2} {\text{d}}z{\kern 1pt} + cD_{2} {\text{d}}z + S \cdot D_{2} {\text{d}}\bar{\sigma }_{v}$$

(16)

in which $\bar{\sigma }_{v}$ is the average vertical stress, S is the width of the differential element, D ₂ is the clear interval between two neighboring piles, dz is the thickness of the differential element. Dividing by D ₂ in both sides of Eq. (16), and considering S = (H−z)/tanβ (Fig. 5), the general solution of Eq. (16) is obtained:

$$\bar{\sigma }_{v} = (H - z)^{{K_{an} \tan \varphi \tan \beta }} \left[ - \gamma \frac{{(H - z)^{{1 - K_{an} \tan \varphi \tan \beta }} }}{{1 - K_{an} \tan \varphi \tan \beta }}{\kern 1pt} - \frac{(T\tan \varphi + c)\tan \beta }{{K_{an} \tan \varphi \tan \beta }}{\kern 1pt} (H - z)^{{ - K_{an} \tan \varphi \tan \beta }} + C_{1} \right]$$

(17)

where H is the thickness of the sliding soil layer, z is the depth below the surface of the soil, γ is the unit weight of the soil, C ₁ is an integration constant. Considering the condition of overload acting on the surface of the ground (Fig. 6), substituting the boundary condition that $\bar{\sigma }_{v} = q$ when z = 0, the constant C ₁ is obtained

$$C_{1} = qH^{{ - K_{an} \tan \varphi \tan \beta }} + \gamma \frac{{H^{{^{{1 - K_{an} \tan \varphi \tan \beta }} }} }}{{1 - K_{an} \tan \varphi \tan \beta }} + \frac{(T\tan \varphi + c)}{{K_{an} \tan \varphi }}H^{{ - K_{an} \tan \varphi \tan \beta }}$$

(18)

in which q is the overloading exerted on the surface of the ground. The average vertical stress at an arbitrary depth is given by Eq. (19)

$$\bar{\sigma }_{v} = \frac{{\gamma H[(1 - \frac{z}{H})^{{K_{an} \tan \varphi \tan \beta }} - (1 - \frac{z}{H})]}}{{1 - K_{an} \tan \varphi \tan \beta }} + \frac{(T\tan \varphi + c)}{{K_{an} \tan \varphi }}\left[\left(1 - \frac{z}{H}\right)^{{K_{an} \tan \varphi \tan \beta }} - 1\right] + q \left(1 - \frac{z}{H}\right)^{{K_{an} \tan \varphi \tan \beta }}$$

(19)

Combining Eq. (14) with Eq. (19), the active lateral stress is obtained

$$\sigma_{h} = \frac{{K_{an} \gamma H[(1 - \frac{z}{H})^{{K_{an} \tan \varphi \tan \beta }} - (1 - \frac{z}{H})]}}{{1 - K_{an} \tan \varphi \tan \beta }} + \frac{(T\tan \varphi + c)}{\tan \varphi } \left[\left(1 - \frac{z}{H}\right)^{{K_{an} \tan \varphi \tan \beta }} - 1\right] + K_{an} q\left(1 - \frac{z}{H}\right)^{{K_{an} \tan \varphi \tan \beta }} +\,T$$

(20)

It is noted that, when Eq. (20) is utilized to estimate the active lateral stress in pure cohesive soil whose internal friction angle equals to zero, the parameter φ should be substituted by a value close to 0, such as 0.01°.

Fig. 6

Soil stress on differential element with overloading on the surface of the ground

2.4 The squeezing effects of the soil between neighboring piles

In order to analyze the lateral force acting on the piles, the squeezing effects of the soil between neighboring piles should be taken into account. Some assumptions have been made by Ito and Matsui (1975) to estimate the squeezing effects. In this analysis, the assumptions of the deforming soil around the piles made by Ito and Matsui are adopted. Based on these assumptions and soil arching theory, the active stress on plane AA′ (Fig. 2) in the theory of plastic deformation proposed by Ito and Matsui (1975) is replaced by Eq. (20). Then, the lateral force acting on a stabilizing pile p per unit thickness of the layer in the direction of x-axis can be estimated by new formula. As derived in “Appendix”, the equations to estimate the lateral force including the squeezing effects between two neighboring piles for cohesionless soil and c−φ soil can be expressed as Eqs. (30) and (31), respectively.

Cohesionless soil (c = 0):

$$\begin{aligned} p & = \left\{ \frac{{\gamma HK_{an} }}{{1 - K_{an} \tan \varphi \tan \beta }} \times \left[\left(1 - \frac{z}{H}\right)^{{K_{an} \tan \varphi \tan \beta }} - \left(1 - \frac{z}{H}\right)\right]+ K_{an} q\left(1 - \frac{z}{H}\right)^{{K_{an} \tan \varphi \tan \beta }} \right\} \\ & \quad \times \left\{ D_{1} (\frac{{D_{1} }}{{D_{2} }})^{{N_{1}^{1/2} \tan \varphi + N_{1} - 1}} \times \exp \left[\frac{{D_{1} - D_{2} }}{{D_{2} }}N_{1} \tan \varphi \tan \left(\frac{\pi }{8} + \frac{\varphi }{4}\right)\right] - D_{2} \right\} \\ \end{aligned}$$

(21)

c–φ soil:

$$\begin{aligned} p & = cD_{1} \left(\frac{{D_{1} }}{{D_{2} }}\right)^{{N_{1}^{1/2} \tan \varphi + N_{1} - 1}} \left\{ \frac{{(2N_{1}^{1/2} \tan \varphi + 1)}}{{N_{1} \tan \varphi }} \times \left[\exp \left(\frac{{D_{1} - D_{2} }}{{D_{2} }}N_{1} \tan \varphi \tan \left(\frac{\pi }{8} + \frac{\varphi }{4}\right)\right) - 1\right] + \frac{{2\tan \varphi + 2N_{1}^{1/2} + N_{1}^{ - 1/2} }}{{N_{1}^{1/2} \tan \varphi + N_{1} - 1}}\right\} \\ & \quad - cD_{1} \frac{{2\tan \varphi + 2N_{1}^{1/2} + N_{1}^{ - 1/2} }}{{N_{1}^{1/2} \tan \varphi + N_{1} - 1}} + \sigma_{h} \times \left[D_{1} \left(\frac{{D_{1} }}{{D_{2} }}\right)^{{N_{1}^{1/2} \tan \varphi + N_{1} - 1}} \times \exp \left(\frac{{D_{1} - D_{2} }}{{D_{2} }}N_{1} \tan \varphi \tan \left(\frac{\pi }{8} + \frac{\varphi }{4}\right)\right) - D_{2} \right] \\ \end{aligned}$$

(22)

in which z is the arbitrary depth of the sliding soil layer, σ _h can be obtained by Eq. (20), and N ₁ = tan²(45° + φ/2).

3 Parameter analysis

Equations (21) and (22) show that the lateral forces exerted on the stabilizing piles vary with many parameters. In both cohesionless soil and c−φ soil, the common parameters are unit weight γ, the height of the unstable soil layer H, the depth of the analyzed soil z, pile diameter D ₁–D ₂, and the interval between two neighboring piles D ₁. Besides, there are two mechanical parameters: the internal friction angle φ and the cohesion c. In the present paper, the effects of all the parameters are evaluated.

3.1 The height of the unstable soil layer

Figure 7 displays the distribution of the lateral force along the normalized depth of unstable soil with respect to different H. In both cohesionless soil and c–φ soil, the height of the sliding soil layer changes from 2 to 8 m, but the shape of distribution of the lateral force does not change much with the variation of H. However, the magnitude of the lateral force increases with the growth of the height H. It is found from Fig. 8 that the magnitude of the lateral force in c–φ soil is greater than that in cohesionless soil in the same depth with the same internal friction angle. In addition, peak value of the force is always in the range of 0.6–0.8H.

Fig. 7

The distribution of lateral force along the unstable soil layer with respect to different height of unstable layer, a cohesionless soil (c = 0 kN/m²) and b c–φ soil (c = 10 kN/m²)

Fig. 8

The distribution of lateral force versus the internal friction angle along the height of the sliding soil for a cohesionless soil (c = 0 kN/m²) and b c–φ soil (c = 10 kN/m²)

3.2 Internal friction angle and cohesion

As the Mohr–Coulomb’s criterion is utilized to estimate the lateral force, the internal friction angle and cohesion are the most affecting parameters for the lateral force. Figure 8 displays the lateral force distribution on pile with the internal friction angle varying from 5° to 40°, and the depth of the sliding layer is 6 m. Figure 8a, b displays the lateral forces on piles in cohesionless soil and c–φ soil, respectively. It reveals that for both cohesionless soil and c–φ soil as the internal friction angle increases, the lateral force acting on the stabilizing pile increases at every depth. The magnitude of the lateral force in both kinds of soils in the same depth is in the same order. The maximum value of the lateral force is in the range of 0.8–0.85H when the internal friction angle is <20°. The height of the point of the peak value decreases, while the internal friction angle increases. When φ = 40°, the maximum value of the force is in the range of 0.6–0.7H.

As mentioned above, the peak value is in the range of 0.6–0.8H, and the lateral forces at depth 0.7H versus ratio D ₂ /D ₁ are shown in Fig. 9. The two figures show that when the ratio D ₂ /D ₁ is less than 0.7, and the internal friction angle φ more than 20°, the lateral force calculated from Eq. (21) and (22) may be a big value. The trend of the lateral force versus internal friction angle on basis of the proposed method is similar to that of Ito and Matsui’s analysis (1975).

Fig. 9

The effect of internal friction angle for a cohesionless soil (c = 0 kN/m²) and b c–φ soil (c = 10 kN/m²)

The effect of the cohesion is shown in Fig. 10. It is found in the figure that the lateral force increases while the cohesion grows. However, the increment of the lateral force due to the effect of cohesion is less than that due to internal friction angle. Note that a value of φ closes to 0° that 0.01° is substituted to calculate the force, and it is because the internal friction angle cannot be zero in Eq. (22).

Fig. 10

The effect of cohesion for a cohesive soil with internal friction angle approximates 0° (φ = 0.01°) and b c–φ soil with φ = 10°

The total lateral force on a stabilizing pile is shown in Fig. 11. It is clear that the total lateral force increases with the increase in internal friction angle φ and the cohesion c of the soil. Note that the four curves in Fig. 11 are nearly parallel to each other. It implies that the increment between two curves is nearly constant. For instance, when φ = 10°, the increment of the force at c = 5 kN/m² and c = 10 kN/m² is about 1.5 t. Comparing that when φ = 30°, the increment is 1.6 t.

Fig. 11

The total lateral force on the stabilizing piles

3.3 Pile diameter

The lateral force on the depth 0.7H with different pile diameter is presented in Fig. 12. In both cohesionless soil and c–φ soil, the increase in the pile diameter leads to the rise of the lateral force. Generally speaking, it means the piles in greater diameter provide more additional resistance than the smaller ones. For instance, Fig. 12b shows that when the diameter is 0.3 m and D ₂/D ₁ = 0.3, the lateral force is nearly 10 t/m; when the diameter is 1.2 m and D ₂/D ₁ = 0.3, the lateral force is nearly 40 t/m, which is 4 times larger than the previous condition. It reveals that the lateral force increases in proportion to the pile diameter.

Fig. 12

The effect of diameter of pile for a cohesionless soil (c = 0 kN/m²) and b c–φ soil (c = 10 kN/m²)

3.4 The range of effective height

A limitation of Eq. (22) may exist when this equation is applied in c–φ soil in which the value of internal friction angle φ is small. It means that when Eq. (22) is utilized to calculate the lateral force acting on a stabilizing pile in c–φ soil with small value of internal friction angle, a negative value might be obtained in the depth that z is very close to the height of the sliding soil layer H. In this paper, the critical depth in which the positive lateral force on piles can be calculated by Eq. (22) is defined as the effective height. What’s more, the depth where the negative value exists is defined as the negative value area. In the negative value area, the lateral force is let equal to 0. That’s because in many field experiments and numerical simulation results (Fukumoto 1972, 1974; Lirer 2012), it is shown that when the depth that z is very close to the height of the sliding soil layer H, the value of lateral force on the piles is small. We will demonstrate in the following section that the negative value area is quite tiny that can be ignored so the treatment of the lateral force in the negative value area does not affect the prediction of the force. The calculated negative value between the effective height and the failure surface is considered to be a limitation of this approach because the prediction of the lateral force on the pile in the ground above the failure plane should be positive. However, this limitation can be neglected because the effective height always approximately equal to the real height of the sliding layer. The value of the effective height is studied as follows.

The ratio H _c/H versus H with respect to different mechanical parameters is shown in Fig. 13, in which H _c is the effective height, H the height of the sliding soil layer. Figure 13 displays that the effective height varies with the mechanical parameters, and the ratio H _c/H changes from 0.99 to 1. The variation of the ratio H _c/H indicates that only a tiny discrepancy exists between effective height and the real height of sliding soil layer. It means that H _c ≈ H.

Fig. 13

Change of effective height with mechanical parameters for a pure cohesive soil with internal friction angle approximates 0º and b c–φ soil with φ = 10°

It should be noted that if the calculated value on the failure plane is positive, it means there is no negative value area in these kinds of soils. In these soils, the effective height H _c equals to H, and there is no need to modify the calculated value on the failure surface.

4 Numerical and experimental verification

4.1 Verification for cohesionless soil

In order to validate the proposed approach for cohesionless soil, the literature data are introduced. A numerical simulation on the response of piles subjected to mudslide was carried out by Lirer (2012). The dimensions of the numerical model are 300 m in length, 8 m in width, and 25 m in height. The sliding soil layer in this model is 4.5 m. The material properties are listed in Table 1. The pile used in the numerical simulation has a diameter of 0.4 m and a length of 10 m. The center-to-center interval between two neighboring piles in a row is 1.3 m. The source reference gives details of the numerical model. The prediction of the lateral force and the numerical results are compared one another as shown in Fig. 14.

Table 1 Material properties in Lirer’s numerical model (Lirer 2012)

Fig. 14

Calculated and numerical simulated lateral force on a pile

Ignoring the negative force within the top few meter of the ground, Fig. 14 displays that in cohesionless soil the prediction by the proposed approach coincides with numerical results. Both the numerical results and the prediction show that the lateral force decreases near the sliding surface after the first gradually increases along the depth of the sliding soil layer. In the depth of 3.5–4 m, both the prediction and the numerical results reach the peak value. The trend of the distribution of the force estimated by the proposed method shows a high degree of consensus with the numerical simulation data.

4.2 Verification for the c–φ soil and cohesive soil

In Ito and Matsui’s research (1975), the theoretical values were compared with the experimental results, which was originally given by Fukumoto (1972, 1974) for the typical landside areas in Japan, including Katamachi, Higashitono, and Kamiyama landside areas. In this research, for the purpose of comparison, the measured data of Fukumoto (1972, 1974) are used again. The conditions of the stabilizing piles in these areas are summarized as follows. In Katamachi landslide area, the hollow concrete piles with diameter of 300 mm and wall thickness of 60 mm were adopted. In the other landslide areas, the steel pipe piles with the diameter of 318.5 mm and wall thickness of 6.9 mm were adopted. All the piles were set up zigzag in two rows at 4-m intervals, and the line space between two rows was 2 m. Furthermore, the head of the Katamachi B pile is 2.17 m depth under the ground, and the Kamiyama No. 2 pile and the Higashitono No. 2 piles are both 1 m depth under the ground.

The soil properties are given in Table 2. Note that the internal friction angles in Kamiyama and Higashitono landslide areas are 0.01°, while the original values of the angles are 0°. As mentioned previously, in the pure cohesive soil, when the internal friction angle equals to zero, a value approximated 0 is substituted.

Table 2 Soil properties of plastically deforming ground

Generally speaking, in Fig. 15a–c the experimental results display the similar trend of the distributions of lateral force. Ignoring the negative force exerted on the pile within the top few meters, the lateral force by the experiment increases gradually and then reduces near the sliding surface after reaching the peak value. The predictions of the lateral forces by the proposed method in several landslides area are almost in line with the experimental results.

Fig. 15

Comparison between the observed and the theoretical values of lateral force acting on stabilizing piles in typical landslide areas in Japan. a Katamachi B pile, height of unstable soil layer H is 8.4 m; effective height H _c is 8.399 m. b Kamiyama No. 2 pile, height of unstable soil layer H is 6.47 m; effective height H _c is 6.452 m. c Higashitono No. 2 pile, height of unstable soil layer H is 6.07 m; effective height H _c is 6.045 m

In Fig. 15a–c, it is obvious that the distributions of the lateral force computed by Ito and Matsui’s approach are linear along the stabilizing piles from top of the soil to the sliding surface. Furthermore, the maximum values calculated by Ito and Matsui’s method are on the sliding surface. However, the experimental results show that the value of the force reduces radically when it reaches the maximum. Especially on the sliding surface, it usually appears to be a small value. The lateral force by the proposed method shows the nonlinear distribution, which results from the soil arching effect. Both the values due to the two theoretical methods are in the same order of magnitude with the observed ones. In Fig. 15a, the maximum force of the experimental result is about 3.18 t/m in the depth of 7 m below the ground, while the prediction of the proposed approach shows a maximum force of 4.97 t/m, which occurs in the depth of 7 m as well, comparing that the maximum force by Ito and Matsui’s method is 6.46 t/m in the depth of 8.4 m, i.e., on the sliding surface. In Fig. 15b, the total lateral force on the pile in the sliding layer by the experiment, the proposed approach, and Ito & Matsui’s method is about 14.85, 19.21, and 20.94 t, respectively. The peak value of the experimental result is about 4.30 t within the depth of 4.6–5.5 m, while the maximum value by the prediction of the proposed approach is about 5.0 t within the depth of 4–5 m, comparing the maximum force of 6.29 t in the depth of 6.47 m by the traditional prediction.

The study of case histories indicates that the predictions by the proposed method are consistent with the field measurements for both c–φ soil and pure cohesive soil. Particularly, the proposed method shows the nonlinear distribution of the force, i.e., the phenomenon of the distribution that decreases after the first gradually increases, which compares well with the measurements.

5 Conclusions

The estimation of the lateral force acting on the stabilizing pile due to the soil layer movement is discussed in this paper. The previous theoretical method shows the linear distribution of the lateral force along the sliding soil layer, which can evaluate the magnitude of the lateral force. In this paper, the plastic deformation theory proposed by Ito and Matsui is modified by considering the soil arching effect between two neighboring piles. The prediction by the modified approach provides the nonlinear distribution of the lateral force, which is more consistent with the field measurement.

For cohesionless and c–φ soil, the lateral forces on the pile are discussed separately, and two new formulae are proposed. The parameters in these formulae are studied for each soil. Generally speaking, the parametric study shows the lateral force increase with the growth of the height of the unstable soil layer H, the internal friction angle φ, the cohesion c, and the pile diameter D ₁–D ₂.

The comparisons for cohesionless soil, c–φ soil and pure cohesive soil are carried out, respectively. The calculated value shows highly consistent with the numerical simulation result. The comparisons in the c–φ soil and pure cohesive soil indicate that the prediction by the proposed approach compares well with the experimental result; particularly, the maximum force and the corresponding position calculated by the proposed method is in line with the field measurement. In addition, all the comparisons in this paper display that in the flow mode the nonlinear distribution of the force on the stabilizing pile in the sliding soil layer is predicted by the proposed approach, which shows a satisfactory agreement with the experimental value. What’s more, the proposed method reveals that the lateral force on the pile segment embedded in the sliding soil layer would increase from the top of the ground surface and then decrease to a small value on the sliding surface after culminates. This behavior of the distribution of the lateral force coincides with the experimental data, ignoring the negative force within the little depth below the ground surface.

Appendix

1.1 The squeezing effects between two neighboring piles [derivation of Eqs. (21) and (22)]

The squeezing effects have been proved by Ito and Matsui (1975). It is summarized as follows.

Firstly, all the assumptions they made are adopted in this paper. In the zone EBB′E′ (Fig. 1), the equilibrium of the forces in x direction on a differential element is considered (as shown in Fig. 16):

$$2{\text{d}}x \left[\sigma_{\alpha } \tan \left(\frac{\pi }{4} + \frac{\varphi }{2}\right) + \sigma_{\alpha } \tan \varphi + c\right] - D{\text{d}}\sigma_{x} - \sigma_{x} {\text{d}}D = 0$$

(23)

Fig. 16

Differential element (EBB′E′) between two neighboring piles (Ito and Matsui 1975)

The normal stress σ _α on the surface EBB′E′ (Fig. 1) is assumed to equal to the principal stress σ _x . The Mohr–Coulomb’s yield criterion is expressed as:

$$\sigma_{\alpha } = \sigma_{x} N_{1} + 2cN_{1}^{1/2}$$

(24)

in which N ₁ = tan²(π/4 + φ/2). The geometrical condition gives:

$$dx = \frac{d(D/2)}{\tan (\pi /4 + \varphi /2)}$$

(25)

Substituting Eq. (24) and (25) in Eq. (23) and then making integration,

$$\sigma_{x} = \frac{{(C_{1} D)^{{(N_{1}^{1/2} \tan \varphi + N_{1} - 1)}} - c(2\tan \varphi + 2N_{1}^{1/2} + N_{1}^{ - 1/2} )}}{{N_{1}^{1/2} \tan \varphi + N_{1} - 1}}$$

(26)

where C ₁ is an integration constant.

Then, in the zone AEE′A′ (Fig. 1), the equilibrium of the forces on a small soil element in x direction is also considered, as shown in Fig. 17.

$$D_{2} {\text{d}}\sigma_{x} = 2(\sigma_{\alpha } \tan \varphi + c){\text{d}}x$$

(27)

Fig. 17

Differential element (AEE′A′) between two neighboring piles (Ito and Matsui 1975)

Substituting Eq. (34) in Eq. (27) and integrating it,

$$\sigma_{x} = \frac{{C_{2} \exp (\frac{{2N_{1} \tan \varphi }}{{D_{2} }}x) - c(2N_{1}^{1/2} \tan \varphi + 1)}}{{N_{1} \tan \varphi }}$$

(28)

where C ₂ is an integration constant.

1.2 The solution for lateral force acting on stabilizing pile in cohesionless ground

For cohesionless soil, the active earth pressure acts on the plane AA′ is obtained by Eq. (20), namely:

$$[\sigma_{x} ]_{x = 0} = \sigma_{h} = \frac{{\gamma HK_{an} }}{{1 - K_{an} \tan \varphi \tan \beta }} \left[\left(1 - \frac{z}{H}\right)^{{K_{an} \tan \varphi \tan \beta }} - \left(1 - \frac{z}{H}\right)\right] + K_{an} q\left(1 - \frac{z}{H}\right)^{{K_{an} \tan \varphi \tan \beta }}$$

(29)

in which z is an arbitrary depth below the ground surface, γ the unit weight of the soil, q the vertical pressure exerted on the surface of the ground. Equation (29) is considered as the boundary condition of Eq. (28), and then,

$$C_{2} = \sigma_{h} N_{1} \tan \varphi$$

(30)

Substituting Eq. (30) in Eq. (28) yields

$$[\sigma_{x} ]_{{x = \frac{{D_{1} - D_{2} }}{2}\tan (\frac{\pi }{8} + \frac{\varphi }{4})}} = (\sigma_{h} N_{1} \tan \varphi )\exp \left[\frac{{D_{1} - D_{2} }}{{D_{2} }} \cdot N_{1} \tan \varphi \tan \left(\frac{\pi }{8} + \frac{\varphi }{4}\right)\right]$$

(31)

The constant C ₁ in Eq. (26) is obtained by considering Eq. (31) as the boundary condition. Then,

$$(C_{1} D_{2} )^{{(N_{1}^{1/2} \tan \varphi + N_{1} - 1)}} = \frac{{(N_{1}^{1/2} \tan \varphi + N_{1} - 1)}}{{N_{1} \tan \varphi }}\left[\sigma {}_{h}N_{1} \tan \varphi \cdot \exp \left(\frac{{D_{1} - D_{2} }}{{D_{2} }}N_{1} \tan \varphi \tan \left(\frac{\pi }{8} + \frac{\varphi }{4}\right)\right)\right]$$

(32)

Equations (26) and (32) are used to obtain the solution of lateral force P _BB′ acting on the plane BB′ per unit thickness of layer in x direction, which is shown as follows:

$$p_{BB'} = D_{1} \left(\frac{{D_{1} }}{{D_{2} }}\right)^{{(N_{1}^{1/2} \tan \varphi + N_{1} - 1)}} \left[\sigma_{h} \cdot \exp \left(\frac{{D_{1} - D_{2} }}{{D_{2} }}N_{1} \tan \varphi \tan \left(\frac{\pi }{8} + \frac{\varphi }{4}\right)\right)\right]$$

(33)

Finally, subtracting the active lateral force acting on the plane AA′ from P _BB′ , the lateral force acting on a pile per unit thickness of layer in x direction is obtained.

$$\begin{aligned} p & = p_{BB'} - D_{2} [\sigma_{x} ]_{x = 0} \\ & = \left\{ \frac{{\gamma HK_{an} }}{{1 - K_{an} \tan \varphi \tan \beta }} \times \left[\left(1 - \frac{z}{H}\right)^{{K_{an} \tan \varphi \tan \beta }} - \left(1 - \frac{z}{H}\right)\right] + K_{an} q\left(1 - \frac{z}{H}\right)^{{K_{an} \tan \varphi \tan \beta }} \right\} \times \left\{ D_{1} \left(\frac{{D_{1} }}{{D_{2} }}\right)^{{N_{1}^{1/2} \tan \varphi + N_{1} - 1}} \right.\\ & \quad \left.\times {\kern 1pt} \exp \left[\frac{{D_{1} - D_{2} }}{{D_{2} }}N_{1} \tan \varphi \tan \left(\frac{\pi }{8} + \frac{\varphi }{4}\right)\right] - D_{2} \right\} \\ \end{aligned}$$

(34)

Equation (34) is the solution for lateral force acting on a pile in the cohesionless ground.

Similarly, in the c–φ soil ground, the solution is obtained,

$$\begin{aligned} p & = cD_{1} \left(\frac{{D_{1} }}{{D_{2} }}\right)^{{N_{1}^{1/2} \tan \varphi + N_{1} - 1}} \left\{ \frac{{(2N_{1}^{1/2} \tan \varphi + 1)}}{{N_{1} \tan \varphi }} \times \left[\exp \left(\frac{{D_{1} - D_{2} }}{{D_{2} }}N_{1} \tan \varphi \tan \left(\frac{\pi }{8} + \frac{\varphi }{4}\right)\right) - 1\right] + \frac{{2\tan \varphi + 2N_{1}^{1/2} + N_{1}^{ - 1/2} }}{{N_{1}^{1/2} \tan \varphi + N_{1} - 1}}\right\} \\ & \quad - cD_{1} \frac{{2\tan \varphi + 2N_{1}^{1/2} + N_{1}^{ - 1/2} }}{{N_{1}^{1/2} \tan \varphi + N_{1} - 1}} + \sigma_{h} \times \left[D_{1} \left(\frac{{D_{1} }}{{D_{2} }}\right)^{{N_{1}^{1/2} \tan \varphi + N_{1} - 1}} \times \exp \left(\frac{{D_{1} - D_{2} }}{{D_{2} }}N_{1} \tan \varphi \tan \left(\frac{\pi }{8} + \frac{\varphi }{4}\right)\right) - D_{2} \right] \\ \end{aligned}$$

(35)