Analysis of the Lateral Force on Stabilizing Piles in c-φ Soil

Abstract

In the past, the lateral force on stabilizing piles has been studied by many researchers. In this study, the lateral force loading on stabilizing piles per unit thickness is analyzed in a semi-infinite c-φ soil ground (φ > 0, c > 0). The soil arching effects between two neighboring piles are considered. A new formula is proposed to estimate the lateral load acting on the stabilizing piles. When the proposed approach is applied on some kinds of c-φ soil, an invalid value would be obtained on the failure plane. However, the invalid value can be ignored since it has little impact on the solution. The in situ observed tests from the literatures are introduced to validate the proposed approach. The comparison charts illustrate that the prediction from the proposed approach shows a better agreement with the test results comparing with the solution from plastic deformation theory.

1 Introduction

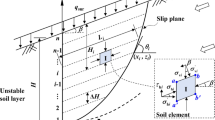
During the past decades, installing rows of drilled shafts for slope stabilization has been proved to be the reliable and effective technique to prevent excessive slope movement (Liang and Zeng 2002; Lirer 2012). Such piles are installed through the unstable soil layer and embedded into the stable layer below the sliding surface. The slope is enhanced by piles, which are able to transfer part of the force from the failing mass to the stable soil layer. For passive piles, the lateral force applied on the piles by the unstable layer is dependent on the soil movement, which is in turn affected by the presence of the piles.

Evaluating the lateral force loading on the stabilizing piles is of great significance for the study of slope stabilization. Referring to the previous research on estimation of the lateral force of the stabilizing piles, an analysis of piles in a single row through plastically deforming ground was described by Ito and Matsui (1975) based on the theory of plastic deformation, simultaneously, the interaction between piles and soil are considered. The approach can roughly agree with the observed values. However, the linear distribution of the lateral force predicted by this method appears different from many experimental results (Chen and Poulos 1997; Lirer 2012; Fukumoto 1972), which present the nonlinear distribution of the force due to arching effects in the soil-piles system. Recently, the soil arching theory has been successfully introduced in soil-structure engineering, such as retaining walls and piles embankments. Authors believe that Ito and Matsui’s method can be got further improvement by soil arching theory as well.

In this study, a new formula is proposed to estimate the lateral load acting on the stabilizing piles in c-φ soil ground. The distribution of the soil stress exerted on the piles is nonlinear based on the soil arching theory. To validate the proposed approach, the in situ tests are introduced. The results indicate that the prediction by the proposed formula agrees with measured data, but some limitation still exists. Nevertheless, comparing to Ito and Matsui’s methods (1975), it shows that the proposed approach has advantage in estimating the lateral force acting on stabilizing piles.

2 Analysis of the Piles

2.1 Soil Arching Effects

In order to estimate the lateral force acting on stabilizing piles, a set of assumptions in the soils between two neighboring piles were developed in plastically deforming ground by Ito and Matsui (1975). In this analysis, comparing with the assumptions of the soil deforming adjacent to piles in Ito and Matsui’s theory, the soil arching zone in the rear of piles is introduced (Fig. 1). As shown in Fig. 1, the deformation in the unstable soil layer of thickness H yields the soil arching, whose area is described by the shaded portion. The plane view of soil deforming between two neighboring piles is depicted in Fig. 2. Furthermore, a typical cross section, UU′, as shown in Fig. 3, is employed to display the state of the soil stress in the rear of the plane AA′ (Fig. 2). In the present paper, the analysis is conducted in two stages. First, the soil pressure acting on the plane AA′ is analyzed based on the soil arching theory. Second, considering the squeezing effect between the piles, the lateral force acting on the piles is calculated.

Fig. 1

The soil arching zone in the rear of stabilizing piles

Fig. 2

Plastic deformation of soil between neighboring piles [after Ito and Matsui (1975)]

Fig. 3

Cross section of deformation in c-φ soil with non-uniform pressure on the top surface

The soil arching theory has been developed to study on retaining wall based on the catenary and circle shaped arch respectively (Handy 1985; Wang 2000; Paik and Salgado 2003). In this paper, some concept of previous study is adopted to investigate the state of soil stress behind a row of stabilizing piles. The trajectory of soil arch is assumed to be an arc of a circle, and the direction of major and minor principal stress in the rear of piles is discussed. Furthermore, in order to inquire into the state of soil stress in the rear of the plane AA′ (Fig. 2), two main assumptions are made as follows:

• 1. When soil layer deforms, the plane AA′ (Fig. 2) is in active condition.

• 2. When the active stress on the plane AA′ is analyzed, only the area between the two parallel lines AG and A′G′ (Fig. 2) is considered, the actual sliding surface between two piles is ignored.

It is noted that assumption 1 is same as that of Ito and Matsui (1975). Furthermore, they assumed that the Coulomb’s active earth pressure was applied on the plane. However, some researches (Janssen 1895; Marston and Anderson 1913; Paik and Salgado 2003) indicate that the active earth pressure predicted by soil arching theory provides more accurate result than that by Coulomb’s method. In this paper, the active stress on plane AA′ (Fig. 2) in c-φ soil is discussed based on soil arching theory.

When soil layer deforms, the actual soil arching zone would be complicated. In this study, assumption 2 is utilized to simplify the analysis. The cross section UU′ is shown in Fig. 3, where the angle between the sliding plane and the horizontal is assumed to be β. It is noted that a nonuniform pressure Q(x) is applied on the top surface FG in Fig. 3, which aims at eliminating the effect of tensile zone in c-φ soil.

The rotation of the principal stress on the line FF′ (Fig. 3) is described as Fig. 4. The trajectory of minor principal stress on the differential element is represented by the dotted lines, while the major principal stress is the normal of the arch.

Fig. 4

State of stress on differential element in the soil arching zone [after Paik and Salgado (2003)]

Considering the force equilibrium in the triangular element at point A in Fig. 4, the lateral stress is obtained as

$$ \sigma_{\text{h}} = \sigma_{1} \cos^{2} \theta + \sigma_{3} \sin^{2} \theta $$

(1)

At an arbitrary point D of the arch, whose original location is point B, a similar equation is given by

$$ \sigma_{\text{ah}} = \sigma_{1} \cos^{2} \psi + \sigma_{3} \sin^{2} \psi $$

(2)

where ѱ is the angle between the normal of the arch at point D and the horizontal, σ _ah the lateral stress at point D. Considering that the soil is in active state, the Mohr–Coulomb’s yielding criterion is applied:

$$ \sigma_{3} = \sigma_{1} K_{\text{a}} - 2cK_{\text{a}}^{1/2} $$

(3)

where, K _a = tan²(π/4 + φ/2), c is the cohesion of soil. Substituting Eq. (3) into Eq. (1), the lateral stress at point D is obtained

$$ \sigma_{\text{ah}} = (\cos^{2} \psi + K_{\text{a}} \sin^{2} \psi )\sigma_{1} - 2cK_{\text{a}}^{1/2} \sin^{2} \psi $$

(4)

Since σ _ah − σ ₃ = σ ₁ − σ _av, substitution for σ _ah gives

$$ \sigma_{\text{av}} = \left( {\sin^{2} \psi + K_{\text{a}} \cos^{2} \psi } \right)\sigma_{1} - 2cK_{\text{a}}^{1/2} \cos^{2} \psi $$

(5)

where σ _av is the vertical stress at an arbitrary point D. As depicted by Eq. (5), the vertical stress varies with angle ѱ, which changes from θ to π/2. In this problem, it seems to be impossible to calculate the vertical stress at every point in the analyzing zone, so the average vertical stress $\bar{\sigma }_{\text{v}}$ is introduced, which can be expressed as

$$ \bar{\sigma }_{\text{v}} = \frac{V}{S} $$

(6)

in which V is the total vertical stress across the differential element and S the width of the differential element. The total vertical stress V of the differential element can be calculated by the following formula:

$$ \begin{aligned} V & = \int\limits_{\theta }^{\pi /2} {{\text{d}}V} \\ & = \int\limits_{\theta }^{\pi /2} {\sigma_{\text{av}} {\text{d}}A} \\ & = \int\limits_{\theta }^{\pi /2} {\left[ {\sigma_{1} (\sin^{2} \psi + K_{\text{a}} \cos^{2} \psi ){\kern 1pt} - 2cK_{\text{a}}^{1/2} \cos^{2} \psi } \right]} \left( {R \cdot {\text{d}}\psi \cdot \sin \psi } \right) \\ \end{aligned} $$

(7)

where dV is the differential vertical force on the shaded portion at arbitrary point B, and dA the width of the shaded portion at point B.

Substituting Eq. (7) into Eq. (6), and considering S = R · cos θ, the average vertical stress is obtained as follows

$$ \bar{\sigma }_{\text{v}} = \int\limits_{\theta }^{\pi /2} {\sigma_{1} \left( {\sin^{2} \psi + K_{\text{a}} \cos^{2} \psi } \right)} \frac{\sin \psi }{\cos \theta } \cdot {\text{d}}\psi - \int\limits_{\theta }^{\pi /2} {2cK_{\text{a}}^{1/2} \cos^{2} \psi \frac{\sin \psi }{\cos \theta } \cdot {\text{d}}\psi } $$

(8)

Integration of Eq. (8) yields

$$ \bar{\sigma }_{\text{v}} = \sigma_{1} \left( {1 - \frac{{1 - K_{\text{a}} }}{3}\cos^{2} \theta } \right) - \frac{2c}{3}K_{\text{a}}^{1/2} \cos^{2} \theta $$

(9)

Equation (9) can be rewritten as

$$ \sigma_{1} = \frac{{3\bar{\sigma }_{\text{v}} + 2cK_{\text{a}}^{1/2} \cos^{2} \theta }}{{3 - (1 - K_{\text{a}} )\cos^{2} \theta }} $$

(10)

Substituting Eqs. (3) and (10) into Eq. (1), the lateral stress is obtained

$$ \sigma_{\text{h}} = \frac{{3\left( {\cos^{2} \theta + K_{\text{a}} \sin^{2} \theta } \right)}}{{3 - (1 - K_{\text{a}} )\cos^{2} \theta }}\left( {\bar{\sigma }_{\text{v}} + \frac{2c}{3}K_{\text{a}}^{1/2} \cos^{2} \theta } \right) - 2cK_{\text{a}}^{1/2} \sin^{2} \theta $$

(11)

in which θ = 45° + φ/2 when the line FF′ is in the active condition. In order to predigest the expression of Eq. (11), let

$$ K_{\text{an}} = \frac{{3\left( {\cos^{2} \theta + K_{\text{a}} \sin^{2} \theta } \right)}}{{3 - (1 - K_{\text{a}} )\cos^{2} \theta }} $$

(12)

and

$$ \begin{aligned} T & = \frac{{3\left( {\cos^{2} \theta + K_{\text{a}} \sin^{2} \theta } \right)}}{{3 - (1 - K_{\text{a}} )\cos^{2} \theta }} \cdot \frac{2c}{3}K_{\text{a}}^{1/2} \cos^{2} \theta - 2cK_{\text{a}}^{1/2} \sin^{2} \theta {\kern 1pt} \\ & = \frac{2c}{3}K_{\text{a}}^{1/2} \cos^{2} \theta \cdot K_{\text{an}} - 2cK_{\text{a}}^{1/2} \sin^{2} \theta \\ \end{aligned} $$

(13)

Then Eq. (11) can be expressed as

$$ \sigma_{\text{h}} = K_{\text{an}} \bar{\sigma }_{\text{v}} + T $$

(14)

2.2 Limit Equilibrium Equation for c-φ Soil

As mentioned previously, when the c-φ soil is in active condition, a tensile zone exists in the soil, which leads to a complicated analysis for the active tress. To simplify the analysis, as shown in Fig. 5, a nonuniform load Q(x) is assumed acting on the top surface of the soil, which would erase the tensile zone. Furthermore, it is assumed that the angle between the yielding plane and the horizontal in the loaded cohesive soil is assumed β = 45° + φ/2.

Fig. 5

Soil stress on differential element in loaded cohesive soil

Figure 5 shows the state of the differential element in loaded c-φ soil. In the vertical direction, considering the effect of cohesion at the left edge, the limit equilibrium equation is set up

$$ \gamma S \cdot D_{2} {\text{d}}z = (K_{\text{an}} \bar{\sigma }_{\text{v}} + T)\tan \varphi \cdot D_{2} {\text{d}}z + cD_{2} {\text{d}}z + S \cdot D_{2} {\text{d}}\bar{\sigma }_{\text{v}} $$

(15)

in which T is calculated by Eq. (13), $\bar{\sigma }_{\text{v}}$ the average vertical stress, S the width of the differential element (S = (H − z)/tan β), D ₂ the clear interval between two neighboring piles, dz the thickness of the differential element. Solving this equation, the average vertical stress at arbitrary depth in the loaded c-φ soil is obtained as follows

$$ \begin{aligned} \bar{\sigma }_{\text{v}} & = \frac{{\gamma H\left[ {\left( {1 - \frac{z}{H}} \right)^{{K_{\text{an}} \tan \varphi \tan \beta }} - \left( {1 - \frac{z}{H}} \right)} \right]}}{{1 - K_{\text{an}} \tan \varphi \tan \beta }} + \frac{(T\tan \varphi + c)}{{K_{\text{an}} \tan \varphi }}\left[ {\left( {1 - \frac{z}{H}} \right)^{{K_{\text{an}} \tan \varphi \tan \beta }} - 1} \right] \\ & \quad + \bar{Q}(x)\left( {1 - \frac{z}{H}} \right)^{{K_{\text{an}} \tan \varphi \tan \beta }}\end{aligned}$$

(16)

Let

$$ \bar{\sigma }_{{{\text{v}}1}} = \frac{{\gamma H\left[ {\left( {1 - \frac{z}{H}} \right)^{{K_{\text{an}} \tan \varphi \tan \beta }} - \left( {1 - \frac{z}{H}} \right)} \right]}}{{1 - K_{\text{an}} \tan \varphi \tan \beta }} + \frac{(T\tan \varphi + c)}{{K_{\text{an}} \tan \varphi }}\left[ {\left( {1 - \frac{z}{H}} \right)^{{K_{\text{an}} \tan \varphi \tan \beta }} - 1} \right] $$

(17)

Eliminating the average nonuniform pressure $\bar{Q}(x)$ with some simplifying method, the active lateral stress on the plane AA′ (Fig. 2) in c-φ soil is presented by

$$ \sigma_{\text{h}} = K_{\text{an}} \left( {[\bar{\sigma }_{{{\text{v}}1}} ]_{{z = z_{i} }} - [\bar{\sigma }_{{{\text{v}}1}} ]_{z = 0} } \right) $$

(18)

in which z _i is the arbitrary depth of the soil layer, $\bar{\sigma }_{{{\text{v}}1}}$ is calculated by Eq. (17).

It is noted that, when Eq. (18) is utilized to estimate the active lateral stress in cohesive soil whose internal friction angle equals to zero, parameter φ should be substituted by a value close to 0, such as 0.01°.

2.3 The Squeezing Effects of the Soil Between Neighboring Piles

Ito and Matsui (1975) have proposed a plastic deformation model to evaluate the squeezing effects between two neighboring piles. In the present paper, the concept used herein is similar to the method used by Ito and Matsui (1975). Furthermore, all the assumptions given by them are adopted. Equation (18) is substituted for Eq. (8) in Ito and Matsui’s research (1975), the lateral forces acting on stabilizing piles in the c-φ soil is expressed as

$$ \begin{aligned} p & = cD_{1} \left( {\frac{{D_{1} }}{{D_{2}}}} \right)^{{N_{\varphi }^{{1/2}} \tan \varphi + N_{\varphi } - 1}} \left\{ {\frac{{(2N_{\varphi }^{{1/2}} \tan \varphi + 1)}}{{N_{\varphi } \tan \varphi }} \times \left[ {\exp \left( {\frac{{D_{1} - D_{2} }}{{D_{2} }}N_{\varphi } \tan \varphi \tan \left( {\frac{\pi }{8} + \frac{\varphi }{4}} \right)} \right) - 1} \right]} \right. \\ & \quad \left. { + \frac{{2\tan \varphi + 2N_{\varphi }^{{1/2}} + N_{\varphi }^{{ - 1/2}} }}{{N_{\varphi }^{{1/2}} \tan \varphi + N_{\varphi } - 1}}} \right\} - cD_{1} \frac{{2\tan \varphi + 2N_{\varphi }^{{1/2}} + N_{\varphi }^{{ - 1/2}} }}{{N_{\varphi }^{{1/2}} \tan \varphi + N_{\varphi } - 1}} + \left( {K_{{{\text{an}}}} \left( {[\bar{\sigma }_{{{\text{v}}1}} ]_{{z = z_{i} }} - [\bar{\sigma }_{{{\text{v}}1}} ]_{{z = 0}} } \right)} \right) \\ & \quad \times \left[ {D_{1} \left( {\frac{{D_{1} }}{{D_{2} }}} \right)^{{N_{\varphi }^{{1/2}} \tan \varphi + N_{\varphi } - 1}} \times \exp \left( {\frac{{D_{1} - D_{2} }}{{D_{2} }}N_{\varphi } \tan \varphi \tan \left( {\frac{\pi }{8} + \frac{\varphi }{4}} \right)} \right) - D_{2} } \right] \\ \end{aligned} $$

(19)

In c-φ soil, when Eq. (19) is utilized to calculate the lateral force acting on a stabilizing pile, an invalid value would be obtained in when z _i is very close to the height of the unstable soil layer H. In other words, the predicted lateral force by Eq. (19) may be as a negative value when z _i approximates to H. It is considered to be limitation of this approach since the lateral force of the pile in the ground between the tensile zone and the failure plane should not be negative. An adjustment for this problem is that, if the calculated value is negative in the invalid-value-area above H, we let it to be 0. That is to say, in a tiny range above the failure plane, the lateral force on the piles would be 0 when the invalid-value-area exists in the soil ground. Since the invalid-value-area is very small and the lateral force on the pile at z _i  = H generally approximate to 0 for rigid piles, this treatment of the negative force is reasonable. Furthermore, the range of the invalid-value-area will be discussed in the following section. On the contrary, if the calculated value on the failure plane is not negative, it means there is no invalid-value-area in this kind of soil. In this soil, the lateral forces around the depth z _i  = H can be calculated by Eq. (19) directly.

3 Parameter Analysis (The Range of Invalid-Value-Area)

As noted previously, in some kinds of c-φ soil, an invalid value would be obtained near the potential failure plane. The area in which the invalid value obtained is called invalid-value-area. Effective height is defined as the accurate height that the positive lateral force on piles can be calculated along by Eq. (19). That is to say, when Eq. (19) is utilized, once the height exceeds effective height the lateral force would be negative. The ratio H _c/H versus H with respect to different mechanical parameters is shown in Fig. 6, in which H _c is the effective height, H the height of the unstable soil layer. Figure 6 displays that the effective height varies with the mechanical parameters, and the ratio H _c/H changes from 0.99 to 1. The variation of the ratio H _c/H indicates that the only a tiny discrepancy exists between effective height and the height of unstable soil layer.

Fig. 6

Change of effective height with mechanical parameters for (a) cohesive soil with internal friction angle approximates to 0° and (b) c-φ soil with φ = 10°. a Change of effective height with cohesion. b Change of effective height with internal friction angle

In some kinds of soil, when Eq. (19) is utilized the invalid-value-area indeed exists, it is the limitation of this approach. However, as shown in Fig. 6, this area is so tiny that it is considered reasonable to neglect it. So in both cohesionless and cohesive soil, the proposed approach is available for estimating the lateral force on pile at every depth within H.

4 Experimental Verification

In Ito and Matsui’s research (1975), the theoretical values were compared with the observed ones, which were obtained by Fukumoto (1972, 1973) in the typical landsides areas in Japan, including Higashitono, Kamiyama landsides areas. In this research, for the purpose of comparison, one of the measured data of Fukumoto (1972, 1973) is used again. The condition of the stabilizing piles in Kamiyama areas is summarized as follows. The steel pipe piles with the diameter of 318.5 mm, and wall thickness of 6.9 mm were adopted. All the piles were set up zigzag in two rows at 4 m intervals, and the line space between two rows was 2 m. The friction angle, cohesion and unit weight of the soil are 0.01°, 0.41 kg/cm², 19 t/m³ respectively. Note that the internal friction angles in Kamiyama landslide area is set 0.01°, while the original values of the angles are 0°. As mentioned previously, in the cohesive soil, when the internal friction angle equals to zero, a value approximated to 0 is substituted. It is a mathematic approach to make sure Eq. (19) can still be used in the case of φ = 0°.

In Fig. 7, it is obvious that the distribution of the lateral force computed by Ito and Matsui’s approach is linear along the stabilizing piles from top of the soil to the sliding surface. Furthermore, the maximum value calculated by Ito and Matsui’s method is on the sliding surface, but the observed data shows that the value on the sliding surface usually is minimum, namely 0. Contrarily, the lateral force from the proposed method shows the nonlinear distribution, which results from the soil arching effect. Both the values due to the two theoretical methods are in the same order of magnitude with the observed ones. Since in the c-φ soil, the angle of the soil arching zone is simply assumed to be 45° + φ/2, and the assumption of tensile zone is simplified, some discrepancies still exist in the solution. Nevertheless, the proposed approach shows a more accurate solution for estimating the lateral force acting in stabilizing piles than Ito and Matsui’s.

Fig. 7

Comparison between the observed and the theoretical values of lateral force acting on stabilizing piles in typical landslide area (Kamiyama No. 2 pile, height of unstable soil layer H is 6.47 m; effective height H _c is 6.460 m)

5 Conclusions

The estimation of the lateral force acting on the stabilizing pile due to the soil layer movement is discussed in this paper. Former theoretical methods proposed by other researchers show the linear distribution of the lateral force along the unstable soil layer, which is quite different from the observed value. In this paper, the plastic deformation theory proposed by Ito and Matsui is modified by considering the soil arching effect between two neighboring piles, which results in the nonlinear distribution of the lateral force.

For the purpose of checking the accuracy of the proposed methods, a comparison is conducted on the cohesive soil between the observed values and this model. The comparison shows that the proposed formula produces satisfactory results for c-φ soil.