1 Introduction

As mentioned by Ait Dads and Ezzinbi in [1], periodically varying environment and almost periodically varying environment are foundations for the theory of nature selection, and it would be of great interest to study the dynamics of pseudo almost periodic systems with time delays. Consequently, the existence and stability of almost periodic solutions or pseudo almost periodic solutions of delayed cellular neural networks has been extensively studied (For example [2,3,4,5,6,7,8,9,10,11], and the references therein).

As well known, in the biochemistry experiments of neural network dynamics, neural information may transfer across chemical reactivity, which results in a neutral-type process. Recently, more attention has been paid to the existence and stability analysis of equilibrium point and pseudo almost periodic solutions for delayed cellular neural networks (CNNs) of neutral type (see [12,13,14,15,16,17,18] and the references therein). In particular, all neutral type CNNs models considered in the above mentioned references can be described as non-operator-based neutral functional differential equations (NFDEs). On the other hand, neutral type CNNs with D operator have more realistic significance than non-operator-based ones in many practical applications of neural networks dynamics [19,20,21]. Based on the complex neural reactions, neutral type CNNs with D operator may be described by the following NFDEs (see [20, 22, 23]):

$$\begin{aligned}&[x _{i} (t)-p_{i}(t)x_{i}(t-r _{i}(t))]^\prime \nonumber \\&\quad = -c_{i}(t)x_{i}(t)+ \sum \limits _{j=1}^{n}a_{ij}(t)f_{j}(x_{j}(t ))+ \sum \limits _{j=1}^{n}b_{ij}(t)g_{j}(x_{j}(t-\tau _{ij}(t))) \nonumber \\&\qquad + \sum \limits _{j=1}^{n}d_{ij}(t) \int _{0}^{\infty }\sigma _{ij}(u) \tilde{g}_{j}(x_{j}(t-u))du+I_{i}(t), i\in J=\{1, 2, \ldots , n\}, \end{aligned}$$
(1.1)

and criteria ensuring the existence of periodic solutions for (1.1) are established in [24,25,26]. Here n corresponds to the number of units in a neural network, \(x_{i}(t)\) corresponds to the state vector, \(c_{i}(t) \) represents the rate with which the ith unit will reset its potential to the resting state in isolation when disconnected from the network and external inputs at the time t. \(p_{i}(t)\), \(a_{ij}(t)\), \( b_{ij}(t) \) and \( d_{ij}(t) \) are the connection weights at the time t, \(\tau _{ij}(t)\ge 0\) and \(r_{i}(t)\ge 0\) correspond to the transmission delays, \(\sigma _{ij }(u) \) corresponds to the transmission delay kernel, \(I_{i}(t)\) denotes the external inputs at time t, \( f_{j}\), \( g_{j}\) and \( \tilde{g}_{j}\) are the activation functions of signal transmission.

It should be mentioned that the global exponential stability of pseudo almost periodic solutions plays a key role in characterizing the dynamical behavior of biological and ecological dynamical systems since the exponential convergence rate can be unveiled [27, 28, 30]. Moreover, the properties of the almost periodic functions do not always hold in the set of pseudo almost periodic functions. For example, if F(t) and \(\tau (t)\) are almost periodic functions, we can show that \(F(t-\tau (t))\) is an almost periodic function. But when F(t) and \(\tau (t)\) are pseudo almost periodic functions, \(F(t-\tau (t))\) may not be a pseudo almost periodic function. For more details, readers may refer to [31]. Meanwhile, it is difficult to construct a suitable Lyapunov functional to study the stability of the neutral type CNNs with D operator. Consequently, to the best of our knowledge, there exist few works on the existence and global exponential stability of pseudo almost periodic solutions of neutral type CNNs with D operator.

Motivated by the above discussions, the aim of this work is to establish a criterion to ensure the existence and global exponential stability of pseudo almost periodic solutions for neutral type CNNs (1.1), which is new and complements previously known results.

The initial condition associated with neutral type CNNs (1.1) is of the form

$$\begin{aligned} x_{i}(s)=\phi _{i}(s), \ s\in (-\infty , \ 0], \ i\in J, \end{aligned}$$
(1.2)

where \(\phi _{i}(\cdot )\) is a real-valued bounded and continuous function defined on \((-\infty , 0]\).

For convenience, we denote by \(\mathbb {R}^{n}\)(\(\mathbb {R}=\mathbb {R}^{1}\)) the set of all n—dimensional real vectors (real numbers). For any \( x=(x_{1} , \ x_{2} , \ldots , x_{ n})^{T} \in \mathbb {R}^{ n}\), we let \(\{x_{i}\}=(x_{1} , \ x_{2} , \ldots , x_{ n})^{T}\), |x| denote the absolute-value vector given by \(|x|=\{|x_{i}|\} \), and define \(\Vert x \Vert =\max \limits _{ i\in J} |x_{i } | \). Given a bounded and continuous function h defined on \(\mathbb {R}\), we denote

$$\begin{aligned} h^{+}=\sup \limits _{t\in \mathbb {R}}|h(t)|\quad \text{ and } \quad h^{-}=\inf \limits _{t\in \mathbb {R}}|h(t)|. \end{aligned}$$

This paper is structured as follows: In Sect. 2, some assumptions and basic definitions are given. In Sect. 3, the results of the existence and global exponential stability of pseudo almost periodic solutions are obtained by employing the fixed point method and constructing a suitable Lyapunov functional. In Sect. 4, numerical simulations are performed to support the analytic results. Finally, conclusions are drawn in Sect. 5.

2 Preliminary Results

In this paper, \(BC(\mathbb {R},\mathbb {R}^{n})\) denotes the set of bounded and continued functions from \(\mathbb {R}\) to \(\mathbb {R}^{n}\). Note that \((BC(\mathbb {R},\mathbb {R}^{n}), \Vert \cdot \Vert _{\infty } )\) is a Banach space where \(\Vert \cdot \Vert _{\infty } \) denotes the sup norm \(\Vert f\Vert _{\infty } := \sup \limits _{ t\in \mathbb {R}} \Vert f (t)\Vert \).

Definition 2.1

(see [28, 29]). Let \(u(t)\in BC(\mathbb {R},\mathbb {R}^{n})\). u(t) is said to be almost periodic on \(\mathbb {R}\) if, for any \(\varepsilon >0\), the set \(T(u,\varepsilon )= \{\delta :\Vert u(t+\delta )-u(t)\Vert <\varepsilon \ \text{ for } \text{ all } \ t\in \mathbb {R}\}\) is relatively dense, i.e., for any \( \varepsilon >0\), it is possible to find a real number \(l=l(\varepsilon )>0\) with the property that, for any interval with length \(l(\varepsilon )\), there exists a number \(\delta =\delta (\varepsilon )\) in this interval such that \(\Vert u(t+\delta )-u(t)\Vert <\varepsilon , \ \text{ for } \text{ all } \ t\in \mathbb {R}.\)

We denote by \(AP(\mathbb {R},\mathbb {R}^{n})\) the set of the almost periodic functions from \(\mathbb {R}\) to \(\mathbb {R}^{n}\). Precisely, define the class of functions \(PAP_{0}(\mathbb {R},\mathbb {R}^{n})\) as follows:

$$\begin{aligned} \big \{f\in BC(\mathbb {R},\mathbb {R}^{n})|\lim \limits _{r\rightarrow +\infty }\frac{1}{2r}\int _{-r}^{r}|f(t)|dt=0\big \}. \end{aligned}$$

A function \(f\in {BC(\mathbb {R},\mathbb {R}^{n})}\) is called pseudo almost periodic if it can be expressed as

$$\begin{aligned} f=h+\varphi , \end{aligned}$$

where \(h\in {AP(\mathbb {R},\mathbb {R}^{n})}\) and \(\varphi \in {PAP_{0}(\mathbb {R},\mathbb {R}^{n})}.\) The collection of such functions will be denoted by \(PAP(\mathbb {R},\mathbb {R}^{n}).\) The functions h and \(\varphi \) in above definition are respectively called the almost periodic component and the ergodic perturbation of the pseudo almost periodic function f. In particular, \((PAP(\mathbb {R},\mathbb {R}^{n}),\Vert .\Vert _{\infty } )\) is a Banach space and \(AP(\mathbb {R},\mathbb {R}^{n})\) is a proper subspace of \(PAP(\mathbb {R},\mathbb {R}^{n})\) [31].

Throughout this paper, it will be assume that \(c_{i}\in AP(\mathbb {R},\mathbb {R} )\), \(p_{i } , r_{i}, \tau _{ij}, a_{ij}, b_{ij}, d_{ij} \in PAP(\mathbb {R},\mathbb {R} )\), \(r_{i}\) and \(p_{i } \) are uniformly continuous on \(\mathbb {R}\), and

$$\begin{aligned} M[c_{i}]=\lim \limits _{T\rightarrow +\infty }\frac{1}{T}\int _{t}^{t+T}c_{i}(s)ds>0 \ \text{ for } \text{ all } t\in \mathbb {R} , \ i,j \in J. \end{aligned}$$

We also make the following assumptions which will be used later.

\((H_0)\) for \(i \in J\), there exist a bounded and continuous function \(\tilde{c}_{i} :\mathbb {R}\rightarrow (0, \ +\infty )\) and a positive constant \(K_{i} \) such that

$$\begin{aligned} e ^{ -\int _{s}^{t}c_{i}(u)du}\le K_{i} e ^{ -\int _{s}^{t}\tilde{c}_{i}(u)du} \ \text{ for } \text{ all } t,s\in \mathbb {R} \text{ and } t-s\ge 0. \end{aligned}$$

\((H_1)\) there exist nonnegative constants \(L^{f}_{j} \), \(L^{g}_{j} \) and \(L^{\tilde{g}}_{j} \) such that

$$\begin{aligned} |f_{j}(u )-f_{j}(v )|\le L ^{f}_{j}|u -v |, |g_{j}(u )-g_{j}(v )| \le L^{g}_{j}|u -v |, \ |\tilde{g}_{j}(u )-\tilde{g}_{j}(v )| \le L^{\tilde{g}}_{j}|u -v |, \end{aligned}$$

\(\text{ for } \text{ all } \ u , \ v \in \mathbb {R}, j\in J\).

\((H_{2})\) for \(i, j \in J\), the delay kernel \(\sigma _{ij } :[0, +\infty )\rightarrow \mathbb {R}\) is continuous, and \(|\sigma _{ij }(t)|e^{\kappa t}\) is integrable on \([0, +\infty )\) for a certain positive constant \(\kappa \).

\((H_3)\) there exist positive constants \(\xi _{1}, \xi _{2},\ldots , \xi _{n} \) and \(\Lambda _{1}, \Lambda _{2},\ldots , \Lambda _{n} \) such that

$$\begin{aligned}&\sup \limits _{t\in \mathbb { R}} \frac{1}{\tilde{c}_{i}(t)} K_{i}\bigg [|c_{i}(t)p_{i}(t)| +\xi _{i}^{-1}\sum ^n_{j=1}|a_{ij}(t)| L^{f}_{j} \xi _j +\xi _{i}^{-1} \sum \limits _{j=1}^{n}|b_{ij}(t)|L^{g}_{j} \xi _j \\&\quad +\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}|d_{ij}(t)| \int _{0}^{\infty }|\sigma _{ij}(u)| du L^{\tilde{g}}_{j} \xi _j \bigg ]<\Lambda _{i},\\&\sup \limits _{t\in \mathbb {R}}\bigg \{ -\tilde{c}_{i}(t)+K_{i}\bigg [\frac{ 1 }{1- p_{i} ^{+} }|c_{i} (t)p_{i} (t)| + \xi _{i}^{-1}\sum ^n_{j=1} |a_{ij} (t)| L^{f}_{j}\xi _{j}\frac{1}{1- p_{j} ^{+}} \\&\quad +\, \xi _{i}^{-1}\sum ^n_{j=1} |b_{ij} (t)| L^{g}_{j}\xi _{j} \frac{1}{1- p_{j} ^{+} } + \xi _{i}^{-1}\sum ^n_{j=1}|d_{ij} (t)| L^{\tilde{g}}_{j} \int _{0}^{+\infty }|\sigma _{ij} (u)| du \xi _{j} \frac{1}{1- p_{j} ^{+} } \bigg ]\bigg \} < 0 , \end{aligned}$$

and

$$\begin{aligned} p_{i} ^{+}+\Lambda _{i}<1, i\in J. \end{aligned}$$

3 Main Results

In this section, we establish some sufficient conditions on the existence and global exponential stability of pseudo almost periodic solutions of (1.1).

Theorem 3.1

Let \((H_{0})\), \((H_{1})\), \((H_{2})\) and \((H_{3})\) hold. Then, there exists a unique pseudo almost periodic solution \( x^{*}(t)\) of (1.1), which is globally exponentially stable, i.e., the solution x(t) of (1.1) with initial condition (1.2) converges exponentially to \( x ^{* }(t )\) as \(t\rightarrow +\infty \).

Proof

From \((H_{3})\), we can choose a constant \(\lambda \in (0, \ \min \{\kappa , \ \min \limits _{i\in J}\tilde{c}_{i} ^{-}\}) \) such that \( p_{j} ^{+}e^{\lambda r_{j} ^{+} }<1\),

$$\begin{aligned}&\sup \limits _{t\in \mathbb { R}} \frac{e^{\lambda }}{\tilde{c}_{i}(t)} K_{i}\bigg [|c_{i}(t)p_{i}(t)| +\xi _{i}^{-1}\sum ^n_{j=1}|a_{ij}(t)| L^{f}_{j} \xi _j +\xi _{i}^{-1} \sum \limits _{j=1}^{n}|b_{ij}(t)|L^{g}_{j} \xi _j \nonumber \\&\quad +\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}|d_{ij}(t)| \int _{0}^{\infty }|\sigma _{ij}(u)| du L^{\tilde{g}}_{j} \xi _j \bigg ] <\Lambda _{i}, \end{aligned}$$
(3.1)

and

$$\begin{aligned}&\sup \limits _{t\in \mathbb {R}}\bigg \{ \lambda -\tilde{c}_{i}(t)+K_{i}\bigg [\frac{ e^{\lambda r_{i} ^{+} } }{1- p_{i} ^{+}e^{\lambda r_{i} ^{+} }}|c_{i} (t)p_{i} (t)| + \xi _{i}^{-1}\sum ^n_{j=1} |a_{ij} (t)| L^{f}_{j}\xi _{j}\frac{1}{1- p_{j} ^{+}e^{\lambda r_{j} ^{+} }} \nonumber \\&\quad +\, \xi _{i}^{-1}\sum ^n_{j=1} |b_{ij} (t)| L^{g}_{j}\xi _{j} e^{\lambda \tau _{ij} ^{+} } \frac{1}{1- p_{j} ^{+}e^{\lambda r_{j} ^{+} }}\nonumber \\&\quad +\, \xi _{i}^{-1}\sum ^n_{j=1}|d_{ij} (t)| L^{\tilde{g}}_{j} \int _{0}^{+\infty }|\sigma _{ij} (u)| e^{ \lambda u } du \xi _{j}\frac{1}{1- p_{j} ^{+}e^{\lambda r_{j} ^{+} }} \bigg ]\bigg \} < 0 , \ i\in J. \end{aligned}$$
(3.2)

Set

$$\begin{aligned} B=\{\varphi |\varphi \in PAP(\mathbb {R},\mathbb {R}^{n}) \ \text{ is } \text{ uniformly } \text{ continuous } \text{ on } \ \mathbb {R} \}. \end{aligned}$$

Then, using a similar way to that in the proof of Lemma 2.3 in [30], we can see that B is a closed subset of \(PAP(\mathbb {R},\mathbb {R}^{n})\).

Let

$$\begin{aligned} y _{i}(t) = \xi _{i}^{-1} x_{i}(t) , \ Y_{i}(t)=y_{i} (t)-p_{i}(t)y_{i} (t-r_{i}(t)), i\in J. \end{aligned}$$

We obtain from (1.1) that

$$\begin{aligned} Y_{i}'(t)= & {} [y_{i} (t)-p_{i}(t)y_{i} (t-r_{i}(t))]'\nonumber \\= & {} -c_{i}(t)Y_i (t )-c_{i}(t)p_{i}(t)y_{i} (t-r_{i}(t)) +\xi _{i}^{-1}\sum ^n_{j=1}a_{ij}(t) f_{j}(\xi _j y_{j}(t )) \nonumber \\&+\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}b_{ij}(t)g_{j}(\xi _j y_{j}(t-\tau _{ij}(t))) \nonumber \\&+\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}d_{ij}(t) \int _{0}^{\infty }\sigma _{ij}(u) \tilde{g}_{j}(\xi _j y_{j}(t-u))du +\xi _{i}^{-1}I_{i}(t),\ i\in J. \end{aligned}$$
(3.3)

Clearly, \((H_{1})\) implies that \(f_{j}, \ g_{j} \) and \(\tilde{g}_{j}\) are uniformly continuous functions on \(\mathbb {R}\) for \(j=1, \ 2, \ \ldots , n\). Let \( \varphi \in B\), and \(F(t,z)=\varphi _{j}(t-z) (j\in J).\) By Theorem 5.3 in [31, p. 58] and Definition 5.7 in [31, p. 59], we can obtain that \(F\in PAP(\mathbb {R}\times \Omega , \mathbb {R})\) and F is continuous in \(z\in K\) and uniformly in \(t\in \mathbb {R}\) for all compact subset K of \(\Omega \subset \mathbb {R}\). This, together with \(\tau _{ij}\in PAP(\mathbb {R},\mathbb {R})\) and Theorem 5.11 in [31, p. 60], implies that

$$\begin{aligned} \varphi _{j}(t-\tau _{ij}(t))\in PAP(\mathbb {R},\mathbb {R}), i,j\in J. \end{aligned}$$

Again from Corollary 5.4 in [31, p. 58], we have

$$\begin{aligned} f_{j}(\xi _{j}\varphi _{j}(t )), \ g_{j}(\xi _{j}\varphi _{j}(t-\tau _{ij}(t)))\in PAP(\mathbb {R},\mathbb {R}), i,j\in J. \end{aligned}$$

From Lemma 2.3 in [18], we can show

$$\begin{aligned} \int _{0}^{\infty }\sigma _{ij}(u)\tilde{ g}_{j}(\xi _{j}\varphi _{j}(t-u))du \ \in PAP(\mathbb {R},\mathbb {R} ), \ i,j\in J. \end{aligned}$$

Now, we consider the following auxiliary pseudo almost periodic differential equations:

$$\begin{aligned} Y_{i}'(t)= & {} -c_{i}(t)Y_i (t )-c_{i}(t)p_{i}(t)\varphi _{i} (t-r_{i}(t)) +\xi _{i}^{-1}\sum ^n_{j=1}a_{ij}(t) f_{j}(\xi _j \varphi _{j}(t )) \nonumber \\&+\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}b_{ij}(t)g_{j}(\xi _j \varphi _{j}(t-\tau _{ij}(t)))\nonumber \\&+\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}d_{ij}(t) \int _{0}^{\infty }\sigma _{ij}(u) \tilde{g}_{j}(\xi _j \varphi _{j}(t-u))du \nonumber \\&+\,\xi _{i}^{-1}I_{i}(t), \ \varphi \in B, \ i\in J. \end{aligned}$$
(3.4)

According to the fact that \( M[c_{i}(t) ]>0 , \ i\in J \), it follows from Theorem 2.3 in [33] that the system (3.4) has exactly one pseudo almost periodic solution:

$$\begin{aligned} x^{\varphi }(t)= & {} \{x^{\varphi }_{i}(t)\}\nonumber \\= & {} \left\{ \int _{-\infty }^{t}e^{-\int _{s}^{t}c_{i}(u) du}[-c_{i}(s)p_{i}(s)\varphi _{i} (s-r_{i}(s)) +\xi _{i}^{-1}\sum ^n_{j=1}a_{ij}(s) f_{j}(\xi _j \varphi _{j}(s )) \right. \nonumber \\&+\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}b_{ij}(s)g_{j}(\xi _j \varphi _{j}(s-\tau _{ij}(s)))\nonumber \\&+\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}d_{ij}(s) \int _{0}^{\infty }\sigma _{ij}(u) \tilde{g}_{j}(\xi _j \varphi _{j}(s-u))du \nonumber \\&\left. +\,\xi _{i}^{-1}I_{i}(s)]ds\}\right. \end{aligned}$$
(3.5)

Consequently,

$$\begin{aligned} \{[x_{i}^{\varphi }(t)]'\}= & {} \{[-c_{i}(t)p_{i}(t)\varphi _{i} (t-r_{i}(t)) +\xi _{i}^{-1}\sum ^n_{j=1}a_{ij}(t) f_{j}(\xi _j \varphi _{j}(t ))\nonumber \\&+\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}b_{ij}(t)g_{j}(\xi _j \varphi _{j}(t-\tau _{ij}(t)))\nonumber \\&+\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}d_{ij}(t) \int _{0}^{\infty }\sigma _{ij}(u) \tilde{g}_{j}(\xi _j \varphi _{j}(t-u))du \nonumber \\&+\,\xi _{i}^{-1}I_{i}(t) ]-c_{i}(t)x_{i}^{\varphi }(t)\}, \end{aligned}$$
(3.6)

which entails that \(\{[x_{i}^{\varphi }(t)]'\}\) is bounded on \(\mathbb {R}\), and \(\{x_{i}^{\varphi }(t)\}\) is uniformly continuous on \(\mathbb {R}\). In view of the uniform continuity of \(r_{i}\) and \(p_{i } \), we can show that \(\{p_{i}(t)\varphi _{i} (t-r_{i}(t))\}\) is uniformly continuous on \(\mathbb {R}\). Thus, \(\{p_{i}(t)\varphi _{i} (t-r_{i}(t))\}+x^{\varphi }\in B\).

Now, we define a mapping \(T:B \rightarrow B\) by setting

$$\begin{aligned} (T\varphi )(t)=\{p_{i}(t)\varphi _{i} (t-r_{i}(t))\}+x^{\varphi }(t), \ \ \ \forall \varphi \in B. \end{aligned}$$

We next prove that the mapping T is a contraction mapping of the B. In fact, in view of (3.1), (3.5), (\(H_{0}\)), (\(H_{1}\)), (\(H_{2}\)) and (\(H_{3}\)), for \( \varphi , \psi \in B \), we have

(3.7)

and

$$\begin{aligned} \Vert T \varphi -T \psi \Vert _{\infty } \le \rho \Vert \varphi -\psi \Vert _{\infty } , \ \ \rho =\max \limits _{i\in J}\{p_{i}^{+} +\Lambda _{i}\}<1, \end{aligned}$$

which implies that the mapping \(T :B \longrightarrow B \) is a contraction mapping. According to Theorem 0.3.1 of [34] and the fact that B is also a Banach space, we obtain that the mapping T possesses a unique fixed point \(x^{**}=\{x_{i}^{**}(t)\}\in B\) such that

$$\begin{aligned} \{x^{**}_{i}(t)\}= & {} x^{**}(t)=(Tx^{**})(t)=\{p_{i}(t)x_{i}^{**}(t-r_{i}(t))\}+x^{x^{**}}(t)\nonumber \\= & {} \{p_{i}(t)x_{i}^{**}(t-r_{i}(t))\}+\{x_{i}^{x^{**}}(t)\}, \end{aligned}$$

and

$$\begin{aligned} x_{i}^{**}(t)= & {} p_{i}(t)x_{i}^{**}(t-r_{i}(t))+x_{i}^{x^{**}}(t)\\= & {} \,p_{i}(t)x_{i}^{**}(t-r_{i}(t))+\int _{-\infty }^{t}e^{-\int _{s}^{t}c_{i}(u) du}\bigg [-c_{i}(s)p_{i}(s)x_{i}^{**} (s-r_{i}(s)) \\&+\,\xi _{i}^{-1}\sum ^n_{j=1}a_{ij}(s) f_{j}(\xi _j x_{j}^{**}(s ))+\xi _{i}^{-1} \sum \limits _{j=1}^{n}b_{ij}(s)g_{j}(\xi _j x_{j}^{**}(s-\tau _{ij}(s)))\\&+\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}d_{ij}(s) \int _{0}^{\infty }\sigma _{ij}(u) \tilde{g}_{j}(\xi _j x_{j}^{**}(s-u))du \\&+\,\xi _{i}^{-1}I_{i}(s)\bigg ]ds, \ i\in J, \end{aligned}$$

which, together with (3.6) leads to

$$\begin{aligned}&[x _{i} ^{**}(t)-p_{i}(t)x_{i}^{**}(t-r _{i}(t))]' \\ {}= & {} -c_{i}(t)x _{i} ^{**}(t) +\,\xi _{i}^{-1}\sum ^n_{j=1}a_{ij}(t) f_{j}(\xi _j x_{j}^{**}(t )) \\&+\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}b_{ij}(t)g_{j}(\xi _j x_{j}^{**}(t-\tau _{ij}(t)))+\xi _{i}^{-1} \sum \limits _{j=1}^{n}d_{ij}(t) \int _{0}^{\infty }\sigma _{ij}(u) \tilde{g}_{j}(\xi _j x_{j}^{**}(t-u))du \\&+\,\xi _{i}^{-1}I_{i}(t), i\in J , \end{aligned}$$

and \(x^{**}(t)\) is a pseudo almost periodic solution of system (3.3). So (1.1) has a pseudo almost periodic solution \(x^{* }(t)=\{\xi _{i}x_{i}^{**}(t)\}\) .

Finally, we prove that \(x^{*}(t)\) is globally exponentially stable. Suppose that \( x(t)=\{x_{i}(t)\} \) is an arbitrary solution of (1.1) associated with initial value \( \phi (t)=\{\phi _{i}(t)\} \) satisfying (1.2).

Let

$$\begin{aligned} y ^{*}_{i}(t) = \xi _{i}^{-1} x_{i}^{*}(t) , \ Y^{*}_{i}(t)=y_{i} ^{*}(t)-p_{i}(t)y_{i} ^{*}(t-r_{i}(t)), \end{aligned}$$

and

$$\begin{aligned} z_{i}(t)=y _{i}(t)-y^{*}_{i}(t), Z_{i}(t)=Y _{i}(t)-Y^{*}_{i}(t), i\in J. \end{aligned}$$

Then

$$\begin{aligned} Z_{i}'(t)= & {} [Y _{i}(t)-Y^{*}_{i}(t)]'\nonumber \\= & {} -c_{i}(t)Z_i (t )-c_{i}(t)p_{i}(t)z_{i} (t-r_{i}(t)) +\xi _{i}^{-1}\sum ^n_{j=1}a_{ij}(t)[ f_{j}(\xi _j y_{j}(t )) - f_{j}(\xi _j y_{j}^{*}(t ))]\nonumber \\&+\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}b_{ij}(t)[g_{j}(\xi _j y_{j}(t-\tau _{ij}(t)))-g_{j}(\xi _j y_{j}^{*}(t-\tau _{ij}(t)))] \nonumber \\&+\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}d_{ij}(t) \int _{0}^{\infty }\sigma _{ij}(u) [\tilde{g}_{j}(\xi _j y_{j}(t-u))-\tilde{g}_{j}(\xi _j y_{j}^{*}(t-u))]du , \ i\in J. \ \ \end{aligned}$$
(3.8)

Let

$$\begin{aligned} \Vert \varphi \Vert _{\xi }= \sup \limits _{t\le 0 }\max \limits _{1\le i\le n }\xi _{i}^{-1}|[\phi _{i} (t)-p_{i}(t)\phi _{i} (t-r_{i}(t))] -[x^{*}_{i} (t)-p_{i}(t)x^{*}_{i} (t-r_{i}(t))] | . \end{aligned}$$
(3.9)

For any \(\varepsilon >0\), we obtain

$$\begin{aligned} \Vert Z(0)\Vert < (\Vert \varphi \Vert _{\xi }+\varepsilon ) , \end{aligned}$$
(3.10)

and

$$\begin{aligned} \Vert Z(t)\Vert< (\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda t}<M(\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda t} \text{ for } \text{ all } t \in (- \infty , \ 0], \end{aligned}$$
(3.11)

where M is a sufficiently large constant such that

$$\begin{aligned} M >1+K_{i } ~ \text{ for } \text{ all } i \in J. \end{aligned}$$
(3.12)

In the following, we will show

$$\begin{aligned} \Vert Z(t)\Vert <M (\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda t} \text{ for } \text{ all } t > 0 . \end{aligned}$$
(3.13)

Otherwise, there must exist \(i\in J\) and \( \theta >0 \) such that

$$\begin{aligned} \left\{ \begin{array}{rcl} |Z_{i} (\theta )|&{}=&{}\Vert Z(\theta )\Vert = M(\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda \theta }, \ \ \\ \ \Vert Z(t)\Vert &{}<&{}M(\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda t} \text{ for } \text{ all } t \in (- \infty , \ \theta ). \end{array} \right. \end{aligned}$$
(3.14)

Furthermore,

$$\begin{aligned} e^{\lambda \nu }|z_{j} (\nu )|\le & {} e^{\lambda \nu }|z_{j} (\nu )- p_{j}(\nu )z_{j} (\nu -r_{j}(\nu ))| +\,e^{\lambda \nu }| p_{j}(\nu )z_{j} (\nu -r_{j}(\nu ))| \nonumber \\\le & {} \, e^{\lambda \nu }|Z_{j} (\nu ) |+ p_{j} ^{+}e^{\lambda r_{j} ^{+} } e^{\lambda (\nu -r_{j}(\nu ))}|z_{j} (\nu -r_{j}(\nu ))| \nonumber \\\le & {} \, M (\Vert \varphi \Vert _{\xi }+\varepsilon ) + p_{j} ^{+}e^{\lambda r_{j} ^{+} }\sup \limits _{s\in (-\infty , \ t]} e^{\lambda s}|z_{j} (s)|, \end{aligned}$$
(3.15)

\(\text{ for } \text{ all }\ \ \nu \in (- \infty , \ t], \ t \in (- \infty , \ \theta ), j\in J, \) which entails that

$$\begin{aligned} e^{\lambda t}|z_{j} (t)| \le \sup \limits _{s\in (-\infty , \ t]} e^{\lambda s}|z_{j} (s)|\le \frac{M (\Vert \varphi \Vert _{\xi }+\varepsilon ) }{1- p_{j} ^{+}e^{\lambda r_{j} ^{+} }} \ \text{ for } \text{ all } \ t \in (- \infty , \ \theta ), j\in J. \end{aligned}$$
(3.16)

Note that

$$\begin{aligned} Z_{i}'(s)+c_{i}(s)Z_i (s ) \nonumber \\= & {} -c_{i}(s)p_{i}(s)z_{i} (s-r_{i}(s)) +\,\xi _{i}^{-1}\sum ^n_{j=1}a_{ij}(s)[ f_{j}(\xi _j y_{j}(s )) - f_{j}(\xi _j y_{j}^{*}(s ))]\nonumber \\&+\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}b_{ij}(s)[g_{j}(\xi _j y_{j}(s-\tau _{ij}(s)))-g_{j}(\xi _j y_{j}^{*}(s-\tau _{ij}(s)))] \nonumber \\&+\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}d_{ij}(s) \int _{0}^{\infty }\sigma _{ij}(u) [\tilde{g}_{j}(\xi _j y_{j}(s-u))-\tilde{g}_{j}(\xi _j y_{j}^{*}(s-u))]du, \nonumber \\&\quad s\in [0, \ t], t\in [0, \ \theta ]. \end{aligned}$$
(3.17)

Multiplying both sides of (3.17) by \(e ^{ \int _{0}^{s}c_{i}(u)du} \), and integrating it on \( [0, \ t]\), we get

$$\begin{aligned} Z_{i} (t)= & {} Z_{i} (0) e ^{-\int _{0}^{t}c_{i}(u)du}+ \int _{0}^{t}e ^{ -\int _{s}^{t}c_{i}(u)du}\bigg \{ -c_{i}(s)p_{i}(s)z_{i} (s-r_{i}(s)) \\&+\,\xi _{i}^{-1}\sum ^n_{j=1}a_{ij}(s)[ f_{j}(\xi _j y_{j}(s )) - f_{j}(\xi _j y_{j}^{*}(s ))]\\&+\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}b_{ij}(s)[g_{j}(\xi _j y_{j}(s-\tau _{ij}(s)))-g_{j}(\xi _j y_{j}^{*}(s-\tau _{ij}(s)))] \\&+\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}d_{ij}(s) \int _{0}^{\infty }\sigma _{ij}(u) [\tilde{g}_{j}(\xi _j y_{j}(s-u))-\tilde{g}_{j}(\xi _j y_{j}^{*}(s-u))]du\bigg \}ds, \nonumber \\&\quad t\in [0, \ \theta ]. \end{aligned}$$

Thus, with the help of (3.2), (3.10), (3.11), (3.12), (3.14) and (3.16), we obtain

$$\begin{aligned} |Z_{i} (\theta )|= & {} \,\bigg | Z_{i} (0) e ^{-\int _{0}^{\theta }c_{i}(u)du}+ \int _{0}^{\theta }e ^{ -\int _{s}^{\theta }c_{i}(u)du}\bigg \{ -c_{i}(s)p_{i}(s)z_{i} (s-r_{i}(s)) \\&+\,\xi _{i}^{-1}\sum ^n_{j=1}a_{ij}(s)[ f_{j}(\xi _j y_{j}(s )) - f_{j}(\xi _j y_{j}^{*}(s ))] \\&+\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}b_{ij}(s)[g_{j}(\xi _j y_{j}(s-\tau _{ij}(s)))-g_{j}(\xi _j y_{j}^{*}(s-\tau _{ij}(s)))] \\&+\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}d_{ij}(s) \int _{0}^{\infty }\sigma _{ij}(u) [\tilde{g}_{j}(\xi _j y_{j}(s-u))-\tilde{g}_{j}(\xi _j y_{j}^{*}(s-u))]du\bigg \}ds \bigg | \\&\,\le | Z_{i} (0)| K_{i}e ^{-\int _{0}^{\theta }\tilde{c}_{i}(u)du}+ \int _{0}^{\theta }e ^{ -\int _{s}^{\theta }\tilde{c}_{i}(u)du}K_{i}\bigg | -c_{i}(s)p_{i}(s)z_{i} (s-r_{i}(s)) \\&+\,\xi _{i}^{-1}\sum ^n_{j=1}a_{ij}(s)[ f_{j}(\xi _j y_{j}(s )) - f_{j}(\xi _j y_{j}^{*}(s ))] \\&+\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}b_{ij}(s)[g_{j}(\xi _j y_{j}(s-\tau _{ij}(s)))-g_{j}(\xi _j y_{j}^{*}(s-\tau _{ij}(s)))] \\&+\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}d_{ij}(s) \int _{0}^{\infty }\sigma _{ij}(u) [\tilde{g}_{j}(\xi _j y_{j}(s-u))-\tilde{g}_{j}(\xi _j y_{j}^{*}(s-u))]du \bigg |ds \\&\le (\Vert \varphi \Vert _{\xi }+\varepsilon )K_{i}e ^{-\int _{0}^{\theta }\tilde{c}_{i}(u)du}+ \int _{0}^{\theta }e ^{ -\int _{s}^{\theta }\tilde{c}_{i}(u)du}K_{i}\bigg [|c_{i} (s)p_{i} (s)||z_{i} (s-r_{i}(s))| \\&+\,\xi _{i}^{-1}\sum ^n_{j=1} |a_{ij} (s)| L^{f}_{j}\xi _{j}|z_{j}(s )| + \xi _{i}^{-1}\sum ^n_{j=1}| b_{ij} (s)| L^{g}_{j}\xi _{j}|z_{j}(s-\tau _{ij}(s))| \\&+\,\xi ^{-1}_{i}\sum \limits ^n_{j=1} |d_{ij } (s)| \int _{0}^{+\infty }|\sigma _{ij} (u)|L^{\tilde{g}}_{j} \xi _{j} |z_{j}(s-u)| du \bigg ] ds \\&\le \, (\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda \theta }K_{i}e ^{-\int _{0}^{\theta }[\tilde{c}_{i}(u)-\lambda ]du}\\&+\, \int _{0}^{\theta }e ^{ -\int _{s}^{\theta }[\tilde{c}_{i}(u)-\lambda ]du} K_{i}\bigg [\frac{ e^{\lambda r_{i} ^{+} } }{1- p_{i} ^{+}e^{\lambda r_{i} ^{+} }}|c_{i} (s)p_{i} (s)| + \xi _{i}^{-1}\sum ^n_{j=1} |a_{ij} (s)| L^{f}_{j}\xi _{j}\frac{1}{1- p_{j} ^{+}e^{\lambda r_{j} ^{+} }} \\&+\,\xi _{i}^{-1}\sum ^n_{j=1} |b_{ij} (s)| L^{g}_{j}\xi _{j} \frac{1}{1- p_{j} ^{+}e^{\lambda r_{j} ^{+} }} e^{\lambda \tau _{ij} ^{+} } \\&+\,\xi _{i}^{-1}\sum ^n_{j=1}|d_{ij} (s)| L^{\tilde{g}}_{j} \int _{0}^{+\infty }|\sigma _{ij} (u)| e^{ \lambda u } du \xi _{j}\frac{1}{1- p_{j} ^{+}e^{\lambda r_{j} ^{+} }} \bigg ]ds M(\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda \theta } \\&\le \, M(\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda \theta }\bigg [(\frac{K_{i}}{M}-1)e ^{-\int _{0}^{\theta }(\tilde{c}_{i}(u)-\lambda )du}+ 1 \bigg ] \\&<\,M(\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda \theta } , \end{aligned}$$

which contradicts the first equation in (3.14). Hence, (3.13) holds. Letting \(\varepsilon \longrightarrow 0^{+}\), we have from (3.13) that

$$\begin{aligned} \Vert Z(t)\Vert \le M\Vert \varphi \Vert _{\xi }e^{-\lambda t} \text{ for } \text{ all } t > 0 . \end{aligned}$$
(3.18)

Then, arguing as in the proof of (3.15) and (3.16), it follows from (3.18) that

$$\begin{aligned} e^{\lambda t}|z_{j} (t)| \le \sup \limits _{s\in (-\infty , \ t]} e^{\lambda s}|z_{j} (s)|\le \frac{M \Vert \varphi \Vert _{\xi } }{1- p_{j} ^{+}e^{\lambda r_{j} ^{+} }}, \end{aligned}$$

and

$$\begin{aligned} |z_{j} (t)| \le \frac{M \Vert \varphi \Vert _{\xi } }{1- p_{j} ^{+}e^{\lambda r_{j} ^{+} }}e^{-\lambda t} \ \text{ for } \text{ all } \ t > 0, \ j\in J, \end{aligned}$$

which ends the proof. \(\square \)

Remark 3.1

In this paper, by using the properties of uniformly continuous functions, we obtain the pseudo almost periodicity of the composite function \( g_{j}(\xi _{j}\varphi _{j}(t-\tau _{ij}(t))) \) under suitable conditions, which provides a possible method to study the existence of pseudo almost periodic on other delayed neural networks models. The inequality techniques involving \(\Vert \varphi \Vert _{\xi }\) might also be used to study the stability problem of other neutral type neural networks models with D operator.

4 An Example and Its Numerical Simulations

Example 4.1

We consider a case of neutral type CNNs as follows:

$$\begin{aligned} \left\{ \begin{array}{rcl} &{}&{}[x_{1} (t)-\frac{\sin t}{100}x_{1} (t-|\sin \sqrt{2}t|)]'\\ {} &{}=&{} - \left( \frac{1}{5}+ \frac{3}{10}\sin 200t\right) x_{1}(t ) +\left( \frac{1}{100}\sin \sqrt{2}t\right) x_{1}(t-2|\sin t|)\\ &{}\;&{} +\left( \frac{1}{100}\sin \sqrt{2}t\right) x_{2}(t-3|\sin t|) + \left( \frac{1}{100}\sin t\right) \int _{0}^{\infty } e^{-u}\arctan x_{1}(t-u) du\\ &{}\;&{}+ \left( \frac{1}{100}\sin t\right) \int _{0}^{\infty } e^{-u} \arctan x_{2}(t-u) du+\sin t+e^{-t^{4} \sin ^{2} t},\\ &{}&{}[x_{2} (t)-\frac{\cos t}{100}x_{2} (t-|\sin \sqrt{3}t|)]'\\ &{}=&{} -\left( \frac{1}{5}+ \frac{3}{10}\cos 200t\right) x_{2}(t ) +\left( \frac{1}{100}\sin \sqrt{2}t\right) x_{1}(t-3|\sin t|) \\ &{}\;&{} +\left( \frac{1}{100}\sin \sqrt{2}t\right) x_{2}(t-4|\sin t|) + (\frac{1}{100}\sin t) \int _{0}^{\infty } e^{-u}\arctan x_{1}(t-u) du\\ &{}\;&{}+ \left( \frac{1}{100}\sin t\right) \int _{0}^{\infty }e^{-u}\arctan x_{2}(t-u) du+2\cos t+e^{-t^{4} \sin ^{2} t}. \end{array} \right. \end{aligned}$$
(4.1)

Clearly,

$$\begin{aligned} \left. \begin{array}{ll} n=2, \ \ f_{i}(x) =0, \ g_{i}(x)=x, \ \tilde{g}_{i}(x)= \arctan x , \\ r_{1 }(t)= |\sin \sqrt{2}t|, \ r_{2 }(t)= |\sin \sqrt{3}t|, \ p_{1}(t)=\frac{\sin t}{100}, \ p_{2}(t)=\frac{\cos t}{100},\\ c_{1}(t)= \frac{1}{5}+ \frac{3}{10}\sin 200t, \ c_{2}(t)= \frac{1}{5}+ \frac{3}{10}\cos 200t, I_{1}(t)=\sin t+e^{-t^{4} \sin ^{2} t}, \\ I_{2}(t)= 2\cos t+e^{-t^{4} \sin ^{2} t}, a _{ij}(t) = 0, b _{ij}(t) = \frac{1}{100}\sin \sqrt{2}t, \\ d _{ij}(t) = \frac{1}{100}\sin t, \ \sigma _{ij } (t) = e^{- t}, \tau _{ij } (t) = (i+j)|\sin t|, i,j=1,2. \end{array}\right. \end{aligned}$$

Then, we can choose

$$\begin{aligned} \tilde{c}_{i} (t)= & {} \frac{1}{5}, \ \xi _{i}= 1, \ \lambda _{0}= \kappa = \frac{1}{2}, \\ L^{f}_{i}= & {} 0, L^{g}_{i}=L^{\tilde{g}}_{i} =1, \ K_{i}=e^{\frac{3}{1000} }, p_{i} ^{+}=\frac{1}{100}, \quad i =1,2, \end{aligned}$$

such that

$$\begin{aligned}&\sup \limits _{t\in \mathbb { R}} \frac{1}{\tilde{c}_{i}(t)} K_{i}\bigg [|c_{i}(t)p_{i}(t)| +\xi _{i}^{-1}\sum ^n_{j=1}|a_{ij}(t)| L^{f}_{j} \xi _j +\xi _{i}^{-1} \sum \limits _{j=1}^{n}|b_{ij}(t)|L^{g}_{j} \xi _j \\&\quad +\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}|d_{ij}(t)| \int _{0}^{\infty }|\sigma _{ij}(u)| du L^{\tilde{g}}_{j} \xi _j \bigg ] < \frac{1}{3}, \end{aligned}$$

and

$$\begin{aligned}&\sup \limits _{t\in \mathbb {R}}\bigg \{ -\tilde{c}_{i}(t)+K_{i}\bigg [\frac{ 1 }{1- p_{i} ^{+} }|c_{i} (t)p_{i} (t)| + \xi _{i}^{-1}\sum ^n_{j=1} |a_{ij} (t)| L^{f}_{j}\xi _{j}\frac{1}{1- p_{j} ^{+}} \\&\quad +\,\xi _{i}^{-1}\sum ^n_{j=1} |b_{ij} (t)| L^{g}_{j}\xi _{j} \frac{1}{1- p_{j} ^{+} } + \xi _{i}^{-1}\sum ^n_{j=1}|d_{ij} (t)| L^{\tilde{g}}_{j} \int _{0}^{+\infty }|\sigma _{ij} (u)| du \xi _{j} \frac{1}{1- p_{j} ^{+} } \bigg ]\bigg \} < -\frac{1}{10}, \end{aligned}$$

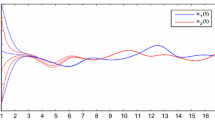
which imply that (4.1) satisfies all the conditions in Theorem 3.1. It follows that system (4.1) has exactly one pseudo almost periodic solution \(x^{*}(t)\). Moreover, all solutions of (4.1) with initial conditions (1.2) converge exponentially to \(x^{*}(t)\) . The exponential convergent rate is about 0.05. The fact is verified by the numerical simulation in Figure 1.

Fig. 1
figure 1

Numerical solutions of system (4.1) with three groups initial values \((\varphi _1(s),\varphi _2(s))=(2,-4), (1,-1), (-3,2) \), respectively, where \( s\in (-\infty ,0]\)

Full size image

Remark 4.1

Since the space of pseudo almost periodic functions properly contains the space of almost-periodic functions and of periodic functions. Thus, our results generalize and improve greatly many previous works on periodic solution of CNNs in [24,25,26] and are therefore very significant. In example 4.1, the exponential convergence of pseudo almost periodic solution for neutral type CNNs with D operator:

$$\begin{aligned} D\left[ \begin{array}{ccc} x_{1 }(t) \\ x_{2 }(t) \end{array} \right] =\left[ \begin{array}{ccc} x_{1} (t)-\frac{\sin t}{100}x_{1} (t-|\sin \sqrt{2}t|) \\ x_{2} (t)-\frac{\cos t}{100}x_{2} (t-|\sin \sqrt{3}t|) \end{array} \right] , \end{aligned}$$

has not been studied before. One can see that all results obtained in [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18] are invalid for example 4.1.

5 Conclusions

In this paper, the existence and global exponential stability of pseudo almost periodic solutions for a class of neutral type cellular neural network model with D operator have been discussed. By employing differential inequality techniques, several sufficient conditions have been obtained to ensure the existence, uniqueness and global exponential stability of pseudo almost periodic solutions for the considered neural networks. Moreover, the exponential convergence rate index is estimated, which depends on the system parameters. Also, an example and its numerical simulations are given to demonstrate our theoretical results. In particular, we employ a novel proof to establish some criteria which guarantee the existence and global exponential convergence of pseudo almost periodic solutions for neutral type cellular neural network model with D operator. The method used in this paper provides a possible method to study the pseudo almost periodic problem of other neutral type neural networks models with D operator.