1 Introduction

Recently, neural networks have been a subject of intensive research activities in the existing literature and have found widespread applications in various fields, such as target tracking, machine learning system identification, associative memories, pattern recognition, solving optimization problems, image processing, signal processing, and so on [1–4]. In particular, it has been recognized that the time delays often occur in various neural networks, and may cause undesirable dynamic behaviors such as oscillation and instability. Therefore, the stability analysis for delayed cellular neural networks (CNNs) has become a topic of great theoretic and practical importance in the literature [5–7]. In addition, neutral-type phenomenon always appears in the study of automatic control, population dynamics and vibrating masses attached to an elastic bar, and so forth. Hence, the stability and other dynamic behaviors for different classes of CNNs with neutral type delays were studied in [8–15]. It should be pointed out that all neutral type CNNs models considered in the aforementioned references can be described as non-operator-based neutral functional differential equations (NFDEs) and D-operator-based NFDEs, respectively. Usually, based on the complex neural reactions, D-operator-based CNNs can be defined as the following NFDEs (see [16–18]):

$$\begin{aligned}{[x _{i} (t)-q_{i}(t)x_{i}(t-r _{i}(t))]}^{\prime}= &-c_{i}(t)x_{i}(t)+ \sum \limits _{j=1}^{n}a_{ij}(t)F_{j}(x_{j}(t ))+ \sum \limits _{j=1}^{n}b_{ij}(t)G_{j}(x_{j}(t-\tau _{ij}(t))) \nonumber \\&+\, \sum \limits _{j=1}^{n}d_{ij}(t) \int _{0}^{+\infty }\sigma _{ij}(u) \tilde{G}_{j}(x_{j}(t-u))du+I_{i}(t), \end{aligned}$$
(1.1)

where \(i\in J=\{1, 2, \ldots , n\},\) \((x_{1}(t), x_{2}(t), \ldots , x_{n}(t))^{T}\) corresponds to the state vector, \(c_{i}(t)\) represents the rate of decay, \(F_{j},\) \(G_{j}\) and \(\tilde{G}_{j}\) are the activation functions of signal transmission. The detailed biological explanation of the coefficients \(a_{ij}(t)\), \(b_{ij}(t)\), \(d_{ij}(t)\) and delays \(\tau _{ij}(t),\) \(r_{i}(t)\), \(\sigma _{ij }(u)\) can be found in [18, 19].

As discussed in [20], when investigating the exponential stability criteria, the exponential convergence rate can be utilized in ascertaining the speed of neural calculations. For this reason, studying the exponential stability has practical significance, and it is useful to estimate and ensure the exponential convergence rate of delayed CNNs [21–25]. On the other hand, anti-periodic phenomenon often occurs in the signal transmission among the neurons, and therefore, the existence and exponential stability of anti-periodic solutions of delayed CNNs have been an attractive subject of research [26–31]. However, it should be mentioned that all above results on anti-periodic problem were obtained only for non-operator-based CNNs. We only found that the reference [18] dealt with the global exponential convergence on the zero vector of CNNs with neutral type delays and D operator. Meanwhile, it is difficult to construct a suitable Lyapunov functional to study the stability of anti-periodic solutions of neutral type CNNs with D operator. Consequently, to the best of our knowledge, there exist few works on the existence and global exponential stability of anti-periodic solutions of neutral type CNNs with D operator.

Inspired by the above discussions, the aim of this paper is to provide a criterion to guarantee that all state vectors of (1.1) converge to a anti-periodic solution with a positive exponential convergence rate.

The initial condition associated with neutral type CNNs (1.1) is of the form

$$\begin{aligned} x_{i}(s)=\phi _{i}(s), \ s\in (-\infty , \ 0], \quad i\in J, \end{aligned}$$
(1.2)

where \(\phi _{i}(\cdot )\) is a real-valued bounded and continuous function defined on \((-\infty , 0]\).

2 Preliminary results

Throughout this paper, we denote by \(\mathbb {R}^{n}\)(\(\mathbb {R}=\mathbb {R}^{1}\)) the set of all \(n-\)dimensional real vectors (real numbers). For any \(x=(x_{1}, \ x_{2}, \ldots , x_{ n})^{\mathbf {T}} \in \mathbb {R}^{ n}\), we let \(\{x_{i}\}=(x_{1}, \ x_{2}, \ldots , x_{ n})^{\mathbf {T}},\) |x| denote the absolute-value vector given by \(|x|=\{|x_{i}|\}\), and define \(\Vert x \Vert =\max \nolimits _{ i\in J} |x_{i } |\). Given a bounded and continuous function h defined on \(\mathbb {R}\), we denote

$$\begin{aligned} h^{+}=\sup \limits _{t\in \mathbb {R}}|h(t)|\quad \text{ and } \quad h^{-}=\inf \limits _{t\in \mathbb {R}}|h(t)|. \end{aligned}$$

Also, \(BC(\mathbb {R},\mathbb {R}^{n})\) denotes the set of bounded and continued functions from \(\mathbb {R}\) to \(\mathbb {R}^{n}\). Note that \((BC(\mathbb {R},\mathbb {R}^{n}), \Vert \cdot \Vert _{\infty } )\) is a Banach space where \(\Vert \cdot \Vert _{\infty }\) denotes the sup norm \(\Vert f\Vert _{\infty } := \sup \nolimits _{ t\in \mathbb {R}} \Vert f (t)\Vert\). Furthermore, let

$$\begin{aligned} AP^{T}(\mathbb {R},\mathbb {R}^{ n}) := \{h\in BC(\mathbb {R},\mathbb {R}^{ n}) | h(t+T)=-h(t) \quad \text{ for } \text{ all } t\in \mathbb {R} \} \end{aligned}$$

designate the set of \(T-\)anti-periodic functions from \(\mathbb {R}\) to \(\mathbb {R}^{ n}\).

Moreover, it will be assumed that \(\tau _{ij}, r_{i} :{\mathbb {R}}\rightarrow [0, \ +\infty ) \in BC(\mathbb {R},\mathbb {R} ),\) \(c_{i}, q_{i}, I_{i}, \ a_{ij}, \ b_{ij }, d_{ij } \in BC(\mathbb {R},\mathbb {R} )\),

$$\begin{aligned} c_{i }(t+T) = c_{i }(t ), \quad q_{i}(t+T) = q_{i}(t ), \quad \ a_{ij} (t+T)F_{j} (u)= -a_{ij} (t)F_{j}(-u),\quad \forall t,u \in \mathbb {R}, \end{aligned}$$
(2.1)
$$\begin{aligned} \left. \begin{array}{rcl} b_{ij}(t+T) = -b_{ij}(t ) , G_{j}(u) = G_{j}(-u)\\ ( \text{or } b_{ij}(t+T) = b_{ij}(t ), G_{j}(u) = - G_{j}(-u)) \end{array} \right\} ,\quad \forall t,u \in \mathbb {R}, \end{aligned}$$
(2.2)
$$\begin{aligned} \left. \begin{array}{rcl} d_{ij}(t+T) = -d_{ij}(t ) , \tilde{G}_{j}(u) = \tilde{G}_{j}(-u)\\ ( \text{or } d_{ij}(t+T) = d_{ij}(t ), \tilde{G}_{j}(u) = - \tilde{G}_{j}(-u)) \end{array} \right\} ,\quad \forall t,u \in \mathbb {R}, \end{aligned}$$
(2.3)

and

$$\begin{aligned} \tau _{ij}(t+T)=\tau _{ij}(t ), \quad r_{i}(t+T)=r_{i}(t ),\quad I_{ij}(t+T)=-I_{ij}(t ), \quad \forall t \in \mathbb {R}, \quad i, j \in J. \end{aligned}$$
(2.4)

For \(i, j \in J\), the following assumptions will be adopted:

  • \((H_0)\) there exist a bounded and continuous function \(\tilde{c}_{i} :\mathbb {R}\rightarrow (0, \ +\infty )\) and a positive constant \(K_{i}\) such that

    $$\begin{aligned} e ^{ -\int _{s}^{t}c_{i}(u)du}\le K_{i} e ^{ -\int _{s}^{t}\tilde{c}_{i}(u)du} \quad \text{ for } \text{ all } t,s\in \mathbb {R}\quad \text{ and } \quad t-s\ge 0. \end{aligned}$$

  • \((H_1)\) there exist nonnegative constants \(L^{f}_{j}\), \(L^{g}_{j}\) and \(L^{\tilde{g}}_{j}\) such that

    $$\begin{aligned} |F_{j}(u )-F_{j}(v )|\le L ^{f}_{j}|u -v |, |G_{j}(u )-G_{j}(v )| \le L^{g}_{j}|u -v |, \ |\tilde{G}_{j}(u )-\tilde{G}_{j}(v )| \le L^{\tilde{g}}_{j}|u -v |, \end{aligned}$$

    \(\text{ for } \text{ all } \ u, \ v \in \mathbb {R}\).

  • \((H_{2})\) the delay kernel \(\sigma _{ij } :[0, +\infty )\rightarrow \mathbb {R}\) is continuous, and \(|\sigma _{ij }(t)|e^{\kappa t}\) is integrable on \([0, +\infty )\) for a certain positive constant \(\kappa\).

  • \((H_3)\) there exist positive constants \(\xi _{1}, \xi _{2},\ldots , \xi _{n}\) and \(\Lambda _{1}, \Lambda _{2},\ldots , \Lambda _{n}\) such that

    $$\begin{aligned}&\sup \limits _{t\in \mathbb { R}} \frac{1}{\tilde{c}_{i}(t)} K_{i}\left[ |c_{i}(t)q_{i}(t)| +\xi _{i}^{-1}\sum ^n_{j=1}|a_{ij}(t)| L^{f}_{j} \xi _j +\xi _{i}^{-1} \sum \limits _{j=1}^{n}|b_{ij}(t)|L^{g}_{j} \xi _j \right. \\&\left. \quad +\xi _{i}^{-1} \sum \limits _{j=1}^{n}|d_{ij}(t)| \int _{0}^{\infty }|\sigma _{ij}(u)| du L^{\tilde{g}}_{j} \xi _j \right] <\Lambda _{i}, \end{aligned}$$
    $$\begin{aligned}&\sup \limits _{t\in \mathbb {R}}\left\{ -\tilde{c}_{i}(t)+K_{i}\left[ \frac{ 1 }{1- q_{i} ^{+} }|c_{i} (t)q_{i} (t)| + \xi _{i}^{-1}\sum ^n_{j=1} |a_{ij} (t)| L^{f}_{j}\xi _{j}\frac{1}{1- q_{j} ^{+}} \right. \right. \\&\quad \left. \left. + \xi _{i}^{-1}\sum ^n_{j=1} |b_{ij} (t)| L^{g}_{j}\xi _{j} \frac{1}{1- q_{j} ^{+} } + \xi _{i}^{-1}\sum ^n_{j=1}|d_{ij} (t)| L^{\tilde{g}}_{j} \int _{0}^{+\infty }|\sigma _{ij} (u)| du \xi _{j} \frac{1}{1- q_{j} ^{+} } \right] \right\} < 0, \end{aligned}$$

    and

    $$\begin{aligned} q_{i} ^{+}+\Lambda _{i}<1. \end{aligned}$$

Remark 2.1

It follows from \((H_{3})\) that we can choose a constant \(\lambda \in (0, \ \min \{\kappa , \ \min \limits _{i\in J}\tilde{c}_{i} ^{-}\})\) such that \(1- p_{j} ^{+}e^{\lambda r_{j} ^{+} }>0,\)

$$\begin{aligned} G_{i}(\lambda )= & \sup \limits _{t\in \mathbb { R}} \frac{e^{\lambda }}{\tilde{c}_{i}(t)} K_{i}\left[ |c_{i}(t)q_{i}(t)| +\xi _{i}^{-1}\sum ^n_{j=1}|a_{ij}(t)| L^{f}_{j} \xi _j +\xi _{i}^{-1} \sum \limits _{j=1}^{n}|b_{ij}(t)|L^{g}_{j} \xi _j \right. \nonumber \\&\left. +\xi _{i}^{-1} \sum \limits _{j=1}^{n}|d_{ij}(t)| \int _{0}^{\infty }|\sigma _{ij}(u)| du L^{\tilde{g}}_{j} \xi _j \right] <\Lambda _{i}, \end{aligned}$$
(2.5)

and

$$\begin{aligned} \Gamma _{i}(\lambda )= \sup \limits _{t\in \mathbb {R}}&\left\{ \lambda -\tilde{c}_{i}(t)+K_{i}\left[ \frac{ e^{\lambda r_{i} ^{+} } }{1- p_{i} ^{+}e^{\lambda r_{i} ^{+} }}|c_{i} (t)q_{i} (t)| + \xi _{i}^{-1}\sum ^n_{j=1} |a_{ij} (t)| L^{f}_{j}\xi _{j}\frac{1}{1- q_{j} ^{+}e^{\lambda r_{j} ^{+} }} \right. \right. \nonumber \\&\quad\left. \left. +\, \xi _{i}^{-1}\sum ^n_{j=1} |b_{ij} (t)| L^{g}_{j}\xi _{j} e^{\lambda \tau _{ij} ^{+} } \frac{1}{1- q_{j} ^{+}e^{\lambda r_{j} ^{+} }}\right. \right. \nonumber \\&\quad\left. \left. +\, \xi _{i}^{-1}\sum ^n_{j=1}|d_{ij} (t)| L^{\tilde{g}}_{j} \int _{0}^{+\infty }|\sigma _{ij} (u)| e^{ \lambda u } du \xi _{j}\frac{1}{1- q_{j} ^{+}e^{\lambda r_{j} ^{+} }} \right] \right\} < 0, \quad i, j\in J. \end{aligned}$$
(2.6)

3 Main results

Theorem 3.1

Let \((H_{0})\), \((H_{1})\), \((H_{2})\) and \((H_{3})\) hold. Then, there exists a unique \(T-\) anti-periodic solution \(x^{*}(t)\) of (1.1), and every solution x(t) of (1.1) with initial condition (1.2) converges exponentially to \(x ^{* }(t )\) as \(t\rightarrow +\infty .\)

Proof

Let

$$\begin{aligned} y _{i}(t) = \xi _{i}^{-1} x_{i}(t), \quad Y_{i}(t)=y_{i} (t)-q_{i}(t)y_{i} (t-r_{i}(t)),\quad i\in J. \end{aligned}$$

We obtain from (1.1) that

$$\begin{aligned} Y_{i}'(t)= & -c_{i}(t)Y_i (t )-c_{i}(t)q_{i}(t)y_{i} (t-r_{i}(t)) +\xi _{i}^{-1}\sum ^n_{j=1}a_{ij}(t) F_{j}(\xi _j y_{j}(t ))\nonumber \\&+\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}b_{ij}(t)G_{j}(\xi _j y_{j}(t-\tau _{ij}(t)))\nonumber \\&+\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}d_{ij}(t) \int _{0}^{\infty }\sigma _{ij}(u) \tilde{G}_{j}(\xi _j y_{j}(t-u))du +\xi _{i}^{-1}I_{i}(t),\ i\in J. \end{aligned}$$
(3.1)

Define

$$\begin{aligned} x^{\varphi }(t)= & \left\{ \int _{-\infty }^{t}e^{-\int _{s}^{t}c_{i}(u) du}[-c_{i}(s)q_{i}(s)\varphi _{i} (s-r_{i}(s)) +\xi _{i}^{-1}\sum ^n_{j=1}a_{ij}(s) F_{j}(\xi _j \varphi _{j}(s )) \right. \nonumber \\&\quad\left. +\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}b_{ij}(s)G_{j}(\xi _j \varphi _{j}(s-\tau _{ij}(s)))\right. \nonumber \\&\quad\left. +\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}d_{ij}(s) \int _{0}^{\infty }\sigma _{ij}(u) \tilde{G}_{j}(\xi _j \varphi _{j}(s-u))du +\xi _{i}^{-1}I_{i}(s)]ds\right\} . \end{aligned}$$
(3.2)

Then, arguing as that in the proof of Lemma 2.1 in [28], from (2.1)–(2.4), we can show that \(x ^{\varphi } \in AP^{T}.\) Moreover, we define a mapping \(Q:AP^{T} \rightarrow AP^{T}\) by setting

$$\begin{aligned} (Q\varphi )(t)=\{q_{i}(t)\varphi _{i} (t-r_{i}(t))\}+x^{\varphi }(t), \quad \forall \varphi \in AP^{T}. \end{aligned}$$
(3.3)

It follows from (2.5), (3.2), (3.3), (\(H_{0}\)), (\(H_{1}\)), (\(H_{2}\)) and (\(H_{3})\) that

$$\begin{aligned}& |(Q\varphi )(t)-(Q\psi )(t)|\\&\quad \le \bigg \{ q_{i}^{+} +\int _{-\infty }^{t}e^{-\int _{s}^{t}\tilde{c}_{i}(u) du}K_{i}\left[ |c_{i}(s)q_{i}(s)| +\xi _{i}^{-1}\sum ^n_{j=1}|a_{ij}(s)| L^{f}_{j} \xi _j\right. \\&\qquad \left. +\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}|b_{ij}(s)|L^{g}_{j} \xi _j+\xi _{i}^{-1} \sum \limits _{j=1}^{n}|d_{ij}(s)| \int _{0}^{\infty }|\sigma _{ij}(u)| du L^{\tilde{g}}_{j} \xi _j \right] ds \bigg \}\Vert \varphi -\psi \Vert _{\infty }\\ & \quad \le \bigg \{ q_{i}^{+} +\Lambda _{i}\int _{-\infty }^{t}e^{-\int _{s}^{t}\tilde{c}_{i}(u) du} \frac{1}{e^{\lambda }}\tilde{c}_{i}(s)ds \bigg \}\Vert \varphi -\psi \Vert _{\infty }\\ & \quad\le \bigg \{ q_{i}^{+} +\Lambda _{i}\frac{1}{e^{\lambda }} \bigg \}\Vert \varphi -\psi \Vert _{\infty }, \end{aligned}$$

and

$$\begin{aligned} \Vert Q \varphi -Q \psi \Vert _{\infty } \le \rho \Vert \varphi -\psi \Vert _{\infty }, \ \ \rho =\max \limits _{i\in J}\{q_{i}^{+} +\Lambda _{i}\}<1, \end{aligned}$$

which implies that the mapping \(Q :AP^{T} \longrightarrow AP^{T}\) is a contraction mapping, and so it possesses a unique fixed point \(x^{**}=\{x_{i}^{**}(t)\}\in AP^{T}\) such that

$$\begin{aligned} \{x^{**}_{i}(t)\}=x^{**}(t)=(Qx^{**})(t)=\left\{ q_{i}(t)x_{i}^{**}(t-r_{i}(t))\}+x^{x^{**}}(t)=\{q_{i}(t)x_{i}^{**}(t-r_{i}(t))\}+\{x_{i}^{x^{**}}(t)\right\} , \end{aligned}$$

and

$$\begin{aligned} x_{i}^{**}(t)= & q_{i}(t)x_{i}^{**}(t-r_{i}(t))+x_{i}^{x^{**}}(t),\quad \ i\in J, \end{aligned}$$

which involves that \(x^{**}(t)\) is a \(T-\)anti-periodic solution of system (3.1). So (1.1) has a \(T-\)anti-periodic solution \(x^{* }(t)=\{\xi _{i}x_{i}^{**}(t)\}\).

Finally, we prove that \(x^{*}(t)\) is globally exponentially stable. Suppose that \(x(t)=\{x_{i}(t)\}\) is an arbitrary solution of (1.1) associated with initial value \(\phi (t)=\{\phi _{i}(t)\}\) satisfying (1.2).

Let

$$\begin{aligned} y ^{*}_{i}(t) = \xi _{i}^{-1} x_{i}^{*}(t), \quad Y^{*}_{i}(t)=y_{i} ^{*}(t)-q_{i}(t)y_{i} ^{*}(t-r_{i}(t)), \end{aligned}$$

and

$$\begin{aligned} z_{i}(t)=y _{i}(t)-y^{*}_{i}(t), \quad Z_{i}(t)=Y _{i}(t)-Y^{*}_{i}(t), i\in J. \end{aligned}$$

Then

$$\begin{aligned} Z_{i}'(t)= & -c_{i}(t)Z_i (t )-c_{i}(t)q_{i}(t)z_{i} (t-r_{i}(t)) +\xi _{i}^{-1}\sum ^n_{j=1}a_{ij}(t)[ F_{j}(\xi _j y_{j}(t )) - F_{j}(\xi _j y_{j}^{*}(t ))]\nonumber \\&+\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}b_{ij}(t)[G_{j}(\xi _j y_{j}(t-\tau _{ij}(t)))-G_{j}(\xi _j y_{j}^{*}(t-\tau _{ij}(t)))] \nonumber \\&+\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}d_{ij}(t) \int _{0}^{\infty }\sigma _{ij}(u) [\tilde{G}_{j}(\xi _j y_{j}(t-u))-\tilde{G}_{j}(\xi _j y_{j}^{*}(t-u))]du, \ i\in J. \end{aligned}$$
(3.4)

Let

$$\begin{aligned} \Vert \varphi \Vert _{\xi }= \sup \limits _{t\le 0 }\max \limits _{1\le i\le n }\xi _{i}^{-1}|[\phi _{i} (t)-q_{i}(t)\phi _{i} (t-r_{i}(t))] -[x^{*}_{i} (t)-q_{i}(t)x^{*}_{i} (t-r_{i}(t))] |. \end{aligned}$$
(3.5)

For any \(\varepsilon>0\), we obtain

$$\begin{aligned} \Vert Z(0)\Vert < (\Vert \varphi \Vert _{\xi }+\varepsilon ), \end{aligned}$$
(3.6)

and

$$\begin{aligned} \Vert Z(t)\Vert< (\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda t}<M(\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda t} \quad \text{ for } \text{ all } t \in (- \infty , \ 0], \end{aligned}$$
(3.7)

where M is a sufficiently large constant such that

$$\begin{aligned} M>1+K_{i } \quad \text{ for } \text{ all } i \in J. \end{aligned}$$
(3.8)

In the following, we will show

$$\begin{aligned} \Vert Z(t)\Vert <M (\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda t} \quad \text{ for } \text{ all } t> 0. \end{aligned}$$
(3.9)

Otherwise, there must exist \(i\in J\) and \(\theta>0\) such that

$$\begin{aligned} \left\{ \begin{array}{ll} |Z_{i} (\theta )|=\Vert Z(\theta )\Vert = M(\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda \theta }, & \\ \ \Vert Z(t)\Vert < M(\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda t} \quad \text{ for } \text{ all } t \in (- \infty , \ \theta ). \end{array} \right. \end{aligned}$$
(3.10)

Furthermore,

$$\begin{aligned} e^{\lambda \nu }|z_{j} (\nu )|\le & M (\Vert \varphi \Vert _{\xi }+\varepsilon ) + q_{j} ^{+}e^{\lambda r_{j} ^{+} }\sup \limits _{s\in (-\infty , \ t]} e^{\lambda s}|z_{j} (s)|, \end{aligned}$$
(3.11)

\(\text{ for } \text{ all }\ \ \nu \in (- \infty , \ t], \ t \in (- \infty , \ \theta ), j\in J,\) which entails that

$$\begin{aligned} e^{\lambda t}|z_{j} (t)| \le \sup \limits _{s\in (-\infty , \ t]} e^{\lambda s}|z_{j} (s)|\le \frac{M (\Vert \varphi \Vert _{\xi }+\varepsilon ) }{1- q_{j} ^{+}e^{\lambda r_{j} ^{+} }} \quad \text{ for } \text{ all } \ t \in (- \infty , \quad \theta ), j\in J. \end{aligned}$$
(3.12)

Note that

$$\begin{aligned}&Z_{i}'(s)+c_{i}(s)Z_i (s ) \nonumber \\&\quad =\, -c_{i}(s)q_{i}(s)z_{i} (s-r_{i}(s)) +\xi _{i}^{-1}\sum ^n_{j=1}a_{ij}(s)[ F_{j}(\xi _j y_{j}(s )) - F_{j}(\xi _j y_{j}^{*}(s ))]\nonumber \\&\qquad +\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}b_{ij}(s)[G_{j}(\xi _j y_{j}(s-\tau _{ij}(s)))-G_{j}(\xi _j y_{j}^{*}(s-\tau _{ij}(s)))] \nonumber \\&\qquad +\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}d_{ij}(s) \int _{0}^{\infty }\sigma _{ij}(u) [\tilde{G}_{j}(\xi _j y_{j}(s-u))-\tilde{G}_{j}(\xi _j y_{j}^{*}(s-u))]du, \quad s\in [0, \ t], t\in [0, \ \theta ]. \end{aligned}$$
(3.13)

Multiplying both sides of (3.13) by \(e ^{ \int _{0}^{s}c_{i}(u)du}\), and integrating it on \([0, \ \theta ]\), with the help of (2.6), (3.1), (3.6)–(3.8), (3.10) and (3.12), we obtain

$$\begin{aligned} |Z_{i} (\theta )|= & \bigg | Z_{i} (0) e ^{-\int _{0}^{\theta }c_{i}(u)du}+ \int _{0}^{\theta }e ^{ -\int _{s}^{\theta }c_{i}(u)du}\Bigg\{ -c_{i}(s)q_{i}(s)z_{i} (s-r_{i}(s)) \\&\left. +\,\xi _{i}^{-1}\sum ^n_{j=1}a_{ij}(s)[ F_{j}(\xi _j y_{j}(s )) - F_{j}(\xi _j y_{j}^{*}(s ))]\right. \\&\left. +\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}b_{ij}(s)[G_{j}(\xi _j y_{j}(s-\tau _{ij}(s)))-G_{j}(\xi _j y_{j}^{*}(s-\tau _{ij}(s)))]\right. \\&\left. +\,\xi _{i}^{-1} \sum \limits _{j=1}^{n}d_{ij}(s) \int _{0}^{\infty }\sigma _{ij}(u) [\tilde{G}_{j}(\xi _j y_{j}(s-u))-\tilde{G}_{j}(\xi _j y_{j}^{*}(s-u))]du\right\} ds \bigg |\\\le & \; (\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda \theta }K_{i}e ^{-\int _{0}^{\theta }[\tilde{c}_{i}(u)-\lambda ]du}\\&+\, \int _{0}^{\theta }e ^{ -\int _{s}^{\theta }[\tilde{c}_{i}(u)-\lambda ]du} K_{i}\left[ \frac{ e^{\lambda r_{i} ^{+} } }{1- q_{i} ^{+}e^{\lambda r_{i} ^{+} }}|c_{i} (s)q_{i} (s)| + \xi _{i}^{-1}\sum ^n_{j=1} |a_{ij} (s)| L^{f}_{j}\xi _{j}\frac{1}{1- q_{j} ^{+}e^{\lambda r_{j} ^{+} }} \right. \\&\left. +\, \xi _{i}^{-1}\sum ^n_{j=1} |b_{ij} (s)| L^{g}_{j}\xi _{j} \frac{1}{1- q_{j} ^{+}e^{\lambda r_{j} ^{+} }} e^{\lambda \tau _{ij} ^{+} }\right. \\&\left. +\, \xi _{i}^{-1}\sum ^n_{j=1}|d_{ij} (s)| L^{\tilde{g}}_{j} \int _{0}^{+\infty }|\sigma _{ij} (u)| e^{ \lambda u } du \xi _{j}\frac{1}{1- q_{j} ^{+}e^{\lambda r_{j} ^{+} }} \right] ds M(\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda \theta } \\\le & \;M(\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda \theta }\bigg [\left( \frac{K_{i}}{M}-1\right) e ^{-\int _{0}^{\theta }(\tilde{c}_{i}(u)-\lambda )du}+ 1 \bigg ]\\ <& \; M(\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda \theta }, \end{aligned}$$

which contradicts the first equation in (3.10). Hence, Eq. (3.9) holds. Letting \(\varepsilon \longrightarrow 0^{+}\), we have from Eq. (3.9) that

$$\begin{aligned} \Vert Z(t)\Vert \le M\Vert \varphi \Vert _{\xi }e^{-\lambda t} \quad \text{ for } \text{ all } t> 0. \end{aligned}$$
(3.14)

Then, by a similar argument as the proof of (3.11) and (3.12), it follows from (3.18) that

$$\begin{aligned} e^{\lambda t}|z_{j} (t)| \le \sup \limits _{s\in (-\infty , \ t]} e^{\lambda s}|z_{j} (s)|\le \frac{M \Vert \varphi \Vert _{\xi } }{1- q_{j} ^{+}e^{\lambda r_{j} ^{+} }}, \end{aligned}$$

and

$$\begin{aligned} |z_{j} (t)| \le \frac{M \Vert \varphi \Vert _{\xi } }{1- q_{j} ^{+}e^{\lambda r_{j} ^{+} }}e^{-\lambda t} \quad \text{ for } \text{ all } \ t> 0, \quad j\in J, \end{aligned}$$

which ends the proof.\(\square\)

Remark 3.1

Because neutral type cellular neural networks with D operator is a class of D-operator-based NFDEs, the stability of its anti-periodic solutions is not easy to be established. Here, the map construction (3.3) and the variable substitution \(Y_{i}(t)=y_{i} (t)-q_{i}(t)y_{i} (t-r_{i}(t))\) play a key role in the proof of Theorem 3.1, which can be used to analyze the anti-periodic solution problem for other D-operator-based NFDEs.

4 An example and its numerical simulations

Example 4.1

Let

$$\begin{aligned} \left\{ \begin{array}{ll} n=2, \ \ F_{i}(x) =\frac{1}{20}x, \ G_{i}(x)=\tilde{G}_{i}(x)=\frac{1}{20}\arctan x, \\ r_{1 }(t)=\frac{1}{2}|\sin t|, \ r_{2 }(t)=\frac{1}{2}|\cos t|, \ q_{1}(t)=\frac{1}{200}|\sin t|, \ q_{2}(t)=\frac{1}{200}|\cos t|,\\ c_{1}(t)= \frac{1}{10}(1+\frac{3}{2}\sin 10 t), \ c_{2}(t)= \frac{1}{10}(1+\frac{3}{2}\cos 10 t), I_{1}(t)=10\sin t, \\ I_{2}(t)= 20\sin t, a _{ij}(t) = \frac{1}{8} \sin 2 t, b _{ij}(t) = \frac{1}{8} \cos 2 t, \\ d _{ij}(t) = \frac{1}{9}\sin 4 t, \ \sigma _{ij } (t) = \frac{1}{10} e^{-2t}, \tau _{ij } (t) = \frac{1}{i+j}|\sin t|. \end{array}\right. \end{aligned}$$
(4.1)

Obviously,

$$\begin{aligned} \tilde{c}_{i} (t)= \frac{1}{10}, \quad \xi _{i}= 1, \quad T= \pi , \quad \kappa =1, \quad L^{f}_{i}=L^{g}_{i}=L^{\tilde{g}}_{i} =\frac{1}{20}, \ K_{i}=e^{\frac{3}{100} }, \quad i,j=1,2, \end{aligned}$$

and the D operator satisfies

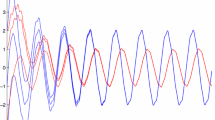
$$\begin{aligned} D\left[ \begin{array}{ccc} x_{1 }(t) \\ x_{2 }(t) \end{array} \right] =\left[ \begin{array}{ccc} x _{1} (t)-\frac{1}{2}|\sin t|x_{1}\left( t-\frac{1}{2}|\sin t|\right) \\ x _{2} (t)-\frac{1}{2}|\cos t|x_{2}\left( t-\frac{1}{2}|\cos t|\right) \end{array} \right] . \end{aligned}$$
(4.2)

This implies that neutral type CNNs (1.1) with parameters (4.1) satisfies all the conditions mentioned in Sect. 2, so it has a unique anti-periodic solution \(x^{*}(t)\in AP^{\pi }(\mathbb {R},\mathbb {R}^{2})\). Moreover, all solutions of system (1.1) with (4.1) and initial value (1.2) converge exponentially to \(x^{*}(t)\) as \(t\rightarrow +\infty.\) Here, the exponential convergence rate \(\lambda \approx 0.01\). This can be seen by the numerical simulations given in Fig. 1.

Fig. 1
figure 1

Numerical solutions of system (1.1) with (4.1) and three groups of different initial values \((1,-3),(2,-1),(-2,1)\), respectively

Full size image

Remark 4.1

In Example (4.1), the problem of global exponential stability of anti-periodic solutions of neutral type CNNs (1.1) with parameters (4.1) and D operator (4.2) has not been studied before. One can see that all results obtained in [8–31] are invalid for Example (4.1).

Remark 4.2

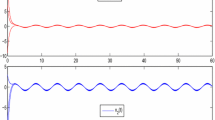
In Example 3.1, replacing \(c_{1}(t)= \frac{1}{10}(1+\frac{3}{2}\sin 10 t)\) and \(c_{2}(t)= \frac{1}{10}(1+\frac{3}{2}\cos 10 t)\) with \(c_{1}(t)=-8\) and \(c_{2}(t)=-13\), respectively, it is easily to see that \((H_{0})\) and \((H_{3})\) are not satisfied. Some numerical simulations in Fig. 2 illustrate that the exponential stability does not exist. This demonstrate the validity of the theoretical result of this paper.

Fig. 2
figure 2

Numerical solutions \(x(t)=(x_1(t),x_2(t))^T\) of system (4.1) with \(c_{1}(t)=-8\) and \(c_{2}(t)=-13\) for initial values \((200,-300)^T\)

Full size image

5 Conclusions

In this paper, a class of neutral type cellular neural networks described by neutral functional differential equations with D operator is considered. By means of fixed point theorem, Lyapunov functional method and differential inequality techniques, it is the first time to derive criteria on the existence and global exponential stability of anti-periodic solutions of the addressed model. Many adjustable parameters are introduced in criteria to provide flexibility for the design and analysis of the system. The results of this paper are new and they supplement previously known results. The method affords a possible method to analyze the global exponential stability of anti-periodic solutions for other neural networks with neutral type delays and D operator.