1 Introduction

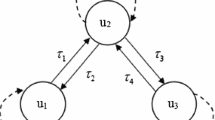
In the last three decades, there has been increasing interest in the dynamical properties of neural networks due to their important applications in many fields such as pattern recognition, classification, optimization, signal and image processing, solving nonlinear algebraic equations, associative memories, cryptography and so on [1]. Many rich mathematical investigations and interesting results on neural networks have been available in the literature (see [2–14]). In particular, the Hopf bifurcation behavior is of great interest. In order to obtain a deep and clear understanding of the Hopf bifurcation nature of neural networks, many authors have focused on the studying of simplified neural networks with two, three or four neurons. For instance, Zou et al. [15] considered the stability and Hopf bifurcation of a three-unit neural network with two delays, Shayer and Campbell [16] studied the stability, bifurcation, and multistability in a system of two coupled neurons with multiple time delays, Guo and Huang [17] focused on the linear stability and Hopf bifurcation of a two-neuron network with three delays, Liao et al. [18] analyzed the stability and bifurcation of a tri-neuron model with time delay, Wang and Jian [3] gave a detailed study on the stability and Hopf bifurcation for a four-neuron BAM neural network with distributed delays, Mao and Hu [19] made a detailed discussion on Hopf bifurcation of a four-neuron network with multiple time delays. Majee and Roy [20] dealt with the temporal dynamics of two-neuron continuous network model with time delay. For more work on this aspect, one can see [2, 21–39]. In 2008, Gupta et al. [40] considered the following three neurons network with distributed delay

$$\begin{aligned} \frac{dx_i}{dt}=-px_i(t)+\sum _{j=1}^3a_{ij}\tanh \left[ \int _{-\infty }^tk(t-s)x_j(s)ds\right] ,\quad i = 1,2,3, \end{aligned}$$
(1.1)

where \(p>0\) is the delay rate of neurons. \(a_{ij}\) is the weight of synaptic connections from neuron j to neuron i and k is the delay kernel assumed to satisfy the following conditions:

$$\begin{aligned}&(\text{ i }) \,k:[0,\infty )\rightarrow [0,\infty ); \\&(\text{ ii }) \,k\; \text{ is } \text{ piecewise } \text{ continuous }; \\&(\text{ iii }) \quad \int _0^{\infty }k(s)ds=1, \int _0^{\infty }sk(s)ds<\infty . \end{aligned}$$

The general form of delay kernel k(s) takes the form:

$$\begin{aligned} k(s)=\beta ^{n+1}\frac{s^ne^{\beta {s}}}{n!},\quad s\in (0,\infty ),\qquad n=0,1,2, \end{aligned}$$

where \(\beta \) is a parameter which stands for the rate of decay of the effects of past memories and it is a positive real number. \(n = 0\) represents weak kernel, whereas \(n =1\) represents strong kernel.

When \(n = 0\), then the delay kernel k(s) reads as

$$\begin{aligned} k(s)=\beta {e^{-\beta {s}}},s\in (0,\infty ). \end{aligned}$$

Then system (1.1) takes the form

$$\begin{aligned} \frac{dx_i}{dt}=-px_i(t)+\sum _{j=1}^3a_{ij}\tanh \left[ \beta \int _{-\infty }^te^{-\beta (t-s)}x_j(s)ds\right] ,\quad \!\! t>0,\quad i=1,2,3. \end{aligned}$$
(1.2)

To make the calculation more tractable, Gupta et al. [40] make the following assumption:

$$\begin{aligned} p=1,a_{11}=a_{22}=a_{33}=0,a_{12}=a_{13}=b,a_{21}=a_{31}=a,a_{23}=a_{32}=0. \end{aligned}$$

Then system (1.2) becomes

$$\begin{aligned} \left\{ \begin{array}{lc} \displaystyle \frac{dx}{dt}=-x(t)+b\tanh \left[ \beta \int _{-\infty }^te^{-\beta (t-s)}y(s)ds\right] +b\tanh \left[ \beta \int _{-\infty }^te^{-\beta (t-s)}z(s)ds\right] ,\\ \displaystyle \frac{dy}{dt}=-y(t)+a\tanh \left[ \beta \int _{-\infty }^te^{-\beta (t-s)}x(s)ds\right] ,\\ \displaystyle \frac{dz}{dt}=-z(t)+a\tanh \left[ \beta \int _{-\infty }^te^{-\beta (t-s)}x(s)ds\right] . \end{array}\right. \end{aligned}$$
(1.3)

With the aid of some auxiliary variables, Gupta et al. [40] focused on the asymptotic stability, orbits stability of Hopf bifurcation periodic solution of system (1.3).

We must point out that in real life, there is transmission delay of the signal along the axon of the neuron. Motivated by the viewpoint, we can modify system (1.3) as follows:

$$\begin{aligned} \left\{ \begin{array}{lc} \displaystyle \frac{dx}{dt}=-x(t)+b\tanh \left[ \beta \int _{-\infty }^te^{-\beta (t-s)}y(s-\tau _2)ds\right] \\ \qquad \qquad +\,b\tanh \left[ \beta \int _{-\infty }^te^{-\beta (t-s)}z(s-\tau _2)ds\right] ,\\ \displaystyle \frac{dy}{dt}=-y(t)+a\tanh \left[ \beta \int _{-\infty }^te^{-\beta (t-s)}x(s-\tau _1)ds\right] ,\\ \displaystyle \frac{dz}{dt}=-z(t)+a\tanh \left[ \beta \int _{-\infty }^te^{-\beta (t-s)}x(s-\tau _1)ds\right] . \end{array}\right. \end{aligned}$$
(1.4)

Here we wold like to point out that human brain is made up of a large number of cells neurons and their interaction, artificial neural networks are information processing systems which have some common characteristics with biological neural networks. System (1.4) can play a important role in the control of regular dynamical functions such as breathing and hear beating of human.

In this paper, we consider the model (1.4). In order to establish the main results for model (1.4), it is necessary to make the following assumption:

$$\begin{aligned} (\text{ H }1)\,\tau _1+\tau _2=\tau . \end{aligned}$$

This paper is organized as follows. In Sect. 2, the stability of the equilibrium and the existence of Hopf bifurcation at the equilibrium are analyzed. In Sect. 3, the direction of Hopf bifurcation and the stability and periods of bifurcating periodic solutions on the center manifold are determined. In Sect. 4, numerical simulations are given to illustrate the validity of the main results. Some main conclusions are drawn in Sect. 5.

2 Stability of the Equilibrium and Local Hopf Bifurcations

Let

$$\begin{aligned} \left\{ \begin{array}{lc} \displaystyle {u(t)}=\beta \int _{-\infty }^te^{-\beta (t-s)}x(s-\tau _1)ds,\quad t>0,\\ \displaystyle {v(t)}=\beta \int _{-\infty }^te^{-\beta (t-s)}x(s-\tau _1)ds,\quad t>0,\\ \displaystyle {w(t)}=\beta \int _{-\infty }^te^{-\beta (t-s)}x(s-\tau _1)ds,\quad t>0. \end{array}\right. \end{aligned}$$
(2.1)

then system (1.4) takes the following equivalent form:

$$\begin{aligned} \left\{ \begin{array}{lc} \displaystyle \frac{dx}{dt}=-x(t)+b\tanh [v(t)]+b\tanh [w(t)],\\ \displaystyle \frac{dy}{dt}=-y(t)+a\tanh [u(t)],\\ \displaystyle \frac{dz}{dt}=-z(t)+a\tanh [u(t)],\\ \displaystyle \frac{du}{dt}=\beta [x(t-\tau _1)-u(t)],\\ \displaystyle \frac{dv}{dt}=\beta [y(t-\tau _2)-v(t)],\\ \displaystyle \frac{dw}{dt}=\beta [z(t-\tau _2)-w(t)]. \end{array}\right. \end{aligned}$$
(2.2)

For notational and computational simplicity, we can rewrite system (2.2) as follows:

$$\begin{aligned} \left\{ \begin{array}{lc} \displaystyle \frac{dx_1}{dt}=-x_1(t)+b\tanh [x_5(t)]+b\tanh [x_6(t)],\\ \displaystyle \frac{dx_2}{dt}=-x_2(t)+a\tanh [x_4(t)],\\ \displaystyle \frac{dx_3}{dt}=-z(t)+a\tanh [x_4(t)],\\ \displaystyle \frac{dx_4}{dt}=\beta [x_1(t-\tau _1)-x_4(t)],\\ \displaystyle \frac{dx_5}{dt}=\beta [x_2(t-\tau _2)-x_5(t)],\\ \displaystyle \frac{dx_6}{dt}=\beta [x_3(t-\tau _2)-x_6(t)]. \end{array}\right. \end{aligned}$$
(2.3)

From the paper [40], if the following condition

$$\begin{aligned} (\text{ H }2) \; ab<\frac{1}{2} \end{aligned}$$

holds, then (2.3) has a unique equilibrium \(E(x_1^*, x_2^*, x_3^*, x_4^*, x_5^*, x_6^*)\). The linear equation of (2.3) at \(E(x_1^*, x_2^*,\, x_3^*, x_4^*, x_5^*, x_6^*)\) takes the form:

$$\begin{aligned} \left\{ \begin{array}{lc} \displaystyle \frac{dx_1}{dt}=-x_1(t)+b\text{ sech }^2(x_5^*)x_5(t)+b\text{ sech }^2(x_6^*)x_6(t),\\ \displaystyle \frac{dx_2}{dt}=-x_2(t)+a\text{ sech }^2(x_4^*)x_4(t),\\ \displaystyle \frac{dx_3}{dt}=-x_3(t)+a\text{ sech }^2(x_4^*)x_4(t),\\ \displaystyle \frac{dx_4}{dt}=\beta [x_1(t-\tau _1)-x_4(t)],\\ \displaystyle \frac{dx_5}{dt}=\beta [x_2(t-\tau _2)-x_5(t)],\\ \displaystyle \frac{dx_6}{dt}=\beta [x_3(t-\tau _2)-x_6(t)]. \end{array}\right. \end{aligned}$$
(2.4)

Then the associated characteristic equation of (2.4) is given by

$$\begin{aligned} \det \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \lambda +1 &{} 0 &{} 0 &{} 0 &{} -b\text{ sech }^2(x_5^*) &{} -b\text{ sech }^2(x_6^*) \\ 0 &{} \lambda +1 &{} 0 &{} -b\text{ sech }^2(x_4^*) &{} 0 &{} 0 \\ 0 &{} 0 &{} \lambda +1 &{} -b\text{ sech }^2(x_4^*) &{} 0 &{} 0 \\ -\beta {e}^{-\lambda \tau _1} &{} 0 &{} 0 &{} \lambda +\beta &{} 0 &{} 0 \\ 0 &{} -\beta {e}^{-\lambda \tau _2} &{} 0 &{} 0 &{} \lambda +\beta &{} 0 \\ 0 &{} 0 &{} -\beta {e}^{-\lambda \tau _2} &{} 0 &{} 0 &{} \lambda +\beta \\ \end{array} \right) =0,\nonumber \\ \end{aligned}$$
(2.5)

which leads to the following form:

$$\begin{aligned} \lambda ^6 +r_5\lambda ^5+ r_4\lambda ^4 + r_3\lambda ^3 + r_2\lambda ^2 + r_1\lambda + r_0 + (s_2\lambda ^2 + s_1\lambda + s_0)e^{-\lambda \tau } =0, \end{aligned}$$
(2.6)

where

$$\begin{aligned} r_0= & {} \beta ^3,r_1=3\beta ^3+3\beta ^2,r_2=3\beta ^3+9\beta ^2+3\beta ,\\ r_3= & {} \beta ^3+9\beta ^2+9\beta +1,r_4=3\beta ^2+9\beta +3,r_5=3\beta +3,\\ s_0= & {} -ab\beta ^3\text{ sech }^2(x_6^*)(\text{ sech }^2(x_4^*)+\text{ sech }^2(x_5^*)),\\ s_1= & {} -ab(\beta +1)\beta ^2\text{ sech }^2(x_6^*)(\text{ sech }^2(x_4^*)+\text{ sech }^2(x_5^*)),\\ s_2= & {} -ab\beta ^2\text{ sech }^2(x_6^*)(\text{ sech }^2(x_4^*)+\text{ sech }^2(x_5^*)). \end{aligned}$$

Let \(\lambda =i\omega _0,\tau =\tau _0\), and substituting this into (2.6), for the sake of simplicity, denote \(\omega _0\) and \(\tau _0\) by \(\omega \) and \(\tau \), respectively, then (2.6) becomes

$$\begin{aligned}&-\omega ^6+r_5\omega ^5i+r_4\omega ^4-r_3\omega ^3i-r_2\omega ^2+r_1\omega {i}+r_0 \nonumber \\&\quad +(-s_2\omega ^2+s_1\omega {i}+s_0)(\cos \omega \tau +i\sin \omega \tau )=0. \end{aligned}$$
(2.7)

Separating the real and imaginary parts leads to

$$\begin{aligned} (s_0-s_2\omega ^2)\cos \omega \tau +s_1\omega \sin \omega \tau= & {} \omega ^6-r_4\omega ^4+r_2\omega ^2-r_0, \end{aligned}$$
(2.8)
$$\begin{aligned} s_1\omega \cos \omega \tau -(s_0-s_2\omega ^2)\cos \omega \tau= & {} r_3\omega ^3-r_5\omega ^5-r_1\omega . \end{aligned}$$
(2.9)

Squaring both sides of (2.8) and (2.9), and adding them up gives

$$\begin{aligned} (s_0-s_2\omega ^2)^2+(s_1\omega )^2=(\omega ^6-r_4\omega ^4+r_2\omega ^2-r_0)^2+(r_3\omega ^3-r_5\omega ^5-r_1\omega )^2, \end{aligned}$$

which is equivalent to

$$\begin{aligned} \omega ^{12} + \theta _5\omega ^{10} +\theta _4\omega ^8 + \theta _3\omega ^6 + \theta _2\omega ^4 + \theta _1\omega ^2 +\theta _0=0, \end{aligned}$$
(2.10)

where

$$\begin{aligned} \theta _0= & {} r_0^2-s_0^2,\theta _1=r_1^2-2r_0r_2+2s_0s_2-s_1^2, \\ \theta _2= & {} r_2^2-2r_0r_4-2r_1r_3-s_2^2, \theta _3=r_3^2+2r_1r_5-2r_0-2r_2r_4, \\ \theta _4= & {} r_4^2+2r_2-2r_3r_5,\theta _5=r_5^2-2r_4. \end{aligned}$$

Let \(z =\theta ^2\). Then (2.10) becomes

$$\begin{aligned} z^{6} + \theta _5z^{5} +\theta _4z^4 + \theta _3z^3 + \theta _2z^2 + \theta _1z +\theta _0=0, \end{aligned}$$
(2.11)

If \(\theta _0<0\), then (2.11) has at least one positive root. Suppose that Eq. (2.11) has positive roots. Without loss of generality, we assume that (2.11) has six positive roots, denoted by \(z_1, z_2, z_3, z_4, z_5, z_6\), Then (2.10) has six positive roots as follows

$$\begin{aligned} \omega _1=\sqrt{z_1},\omega _2=\sqrt{z_2},\omega _3=\sqrt{z_3},\omega _4=\sqrt{z_4},\omega _5=\sqrt{z_5},\omega _6=\sqrt{z_6}. \end{aligned}$$

By (2.8) and (2.9), we have

$$\begin{aligned} \cos \omega _k\tau =\frac{(\omega _k^6-r_4\omega _k^4+r_2\omega _k^2-r_0)(s_0-s_2\omega _k^2)+(r_3\omega _k^3-r_5\omega _k^5-r_1\omega _k)s_1\omega _k}{(s_0-s_2\omega _k^2)^2+(s_1\omega _k)^2}.\qquad \quad \end{aligned}$$
(2.12)

Thus, if we denote

$$\begin{aligned} \tau _k^{(j)}=\frac{1}{\omega _k}\left\{ \arccos \left[ \frac{(\omega _k^6-r_4\omega _k^4+r_2\omega _k^2-r_0)(s_0-s_2\omega _k^2)+(r_3\omega _k^3-r_5\omega _k^5-r_1\omega _k)s_1\omega _k}{(s_0-s_2\omega _k^2)^2+(s_1\omega _k)^2}\right] +2j\pi \right\} ,\nonumber \\ \end{aligned}$$
(2.13)

where \(k =1,2,3,\ldots ,6\) and \(j=0,1,2,\ldots \). Then \(\pm i\omega _k\) are a pair of purely imaginary roots of Eq. (2.6) with \(\tau = \tau _k^{(j)}\). Obviously, in view of (2.13), the sequence \(\{\tau _k^{(j)}\}_{j=0}^{+\infty }\) is increasing, and

$$\begin{aligned} \lim _{j\rightarrow {+\infty }}\tau _k^{(j)}=+\infty ,\quad k=1,2,3,\ldots ,6. \end{aligned}$$

Then we can define

$$\begin{aligned} \tau _0=\tau _{k0}^{(0)}=\min _{1\le {k}\le 6}\{\tau _k^{(0)}\},\qquad \omega _0=\omega _{k0}. \end{aligned}$$
(2.14)

Note that when \(\tau =0,\) (2.6) becomes

$$\begin{aligned} \lambda ^6+r_5\lambda ^5+r_4\lambda ^4+r_3\lambda ^3+(r_2+s_2)\lambda ^2+(r_1+s_1)\lambda +(r_0+s_0)=0. \end{aligned}$$
(2.15)

All roots of (2.15) have a negative real part if the following well-known Routh-Hurwitz criteria hold.

$$\begin{aligned} D_1= & {} r_5>0, \end{aligned}$$
(2.16)
$$\begin{aligned} D_2= & {} \det \left( \begin{array}{cc} r_5 &{}\quad 1 \\ r_3 &{}\quad r_4 \\ \end{array} \right) >0,\end{aligned}$$
(2.17)
$$\begin{aligned} D_3= & {} \det \left( \begin{array}{ccc} r_5 &{}\quad 1 &{}\quad 0 \\ r_3 &{}\quad r_4 &{}\quad r_5 \\ r_1+s_1 &{}\quad r_2+s_2 &{}\quad r_3 \\ \end{array} \right) >0, \end{aligned}$$
(2.18)
$$\begin{aligned} D_4= & {} \left( \begin{array}{cccc} r_5 &{} 1 &{}\quad 0 &{}\quad 0 \\ r_3 &{}\quad r_4 &{}\quad r_5 &{}\quad 1 \\ r_1+s_1 &{}\quad r_2+s_2 &{}\quad r_3 &{}\quad r_4 \\ 0 &{}\quad r_0+s_0 &{}\quad r_1+s_1 &{}\quad r_2+s_2 \\ \end{array} \right) \end{aligned}$$
(2.19)
$$\begin{aligned} D_5= & {} \det \left( \begin{array}{ccccc} r_5 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ r_3 &{}\quad r_4 &{}\quad r_5 &{}\quad 1 &{}\quad 0 \\ r_1+s_1 &{}\quad r_2+s_2 &{}\quad r_3 &{}\quad r_4 &{}\quad r_5 \\ 0 &{}\quad r_0+s_0 &{}\quad r_1+s_1 &{}\quad r_2+s_2 &{}\quad r_3 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad r_0+s_0 &{}\quad r_1+s_1 \\ \end{array} \right) >0, \end{aligned}$$
(2.20)
$$\begin{aligned} D_6= & {} r_0+s_0>0. \end{aligned}$$
(2.21)

In order to obtain the main results in this paper, it is necessary to make the following assumptions:

(H3) If (2.16)–(2.21) hold, (2.15) have six roots with negative real parts when \(\tau =0,\) (2.1) is stable near the equilibrium.

\((\text{ H }4) \text{ Re }\left( \frac{d\lambda }{d\tau }\right) \Big |_{\tau =\tau _0}\ne 0\).

Taking the derivative of \(\lambda \) with respect to \(\tau \) in (2.6), it is easy to obtain:

$$\begin{aligned} \left[ \frac{d\lambda }{d\tau }\right] ^{-1}= & {} \frac{(6\lambda ^5+5r_5\lambda ^4+4r_4\lambda ^3+3r_3\lambda ^2+2r_2\lambda +r_1)e^{\lambda \tau }}{\lambda (s_2\lambda ^2+s_1\lambda +s_0)} \nonumber \\&+\,\frac{2s_2\lambda +s_1}{\lambda (s_2\lambda ^2+s_1\lambda +s_0)}-\frac{\tau }{\lambda }. \end{aligned}$$
(2.22)

Then

$$\begin{aligned} \text{ Re }\left[ \frac{d\lambda }{d\tau }\right] _{\tau =\tau _0}^{-1}= & {} \text{ Re }\Big \{\frac{(6\lambda ^5+5r_5\lambda ^4+4r_4\lambda ^3+3r_3\lambda ^2+2r_2\lambda +r_1)e^{\lambda \tau }}{\lambda (s_2\lambda ^2+s_1\lambda +s_0)}\Big \}_{\tau =\tau _0} \nonumber \\&+\Big \{\frac{2s_2\lambda +s_1}{\lambda (s_2\lambda ^2+s_1\lambda +s_0)}\Big \}_{\tau =\tau _0}. \end{aligned}$$
(2.23)

Thus

$$\begin{aligned} \text{ Re }\left[ \frac{d\lambda }{d\tau }\right] _{\tau =\tau _0}^{-1}=\frac{\Theta _1}{\Theta _2}, \end{aligned}$$
(2.24)

where

$$\begin{aligned} \Theta _1= & {} s_1\omega _0^2[(6\omega _0^5-4r_4\omega _0^3+2r_2\omega _0)\sin \omega _0\tau _0-(5r_4\omega _0^4-3r_3\omega _0^2+r_1)\cos \omega _0\tau _0-s_1\\&+(s_0-s_2\omega _0^2)[(5r_4\omega _0^4-3r_3\omega _0^2+r_1)\sin \omega _0\tau _0+(6\omega _0^2-4r_4\omega _0^3+2r_2\omega _0)\cos \omega _0\tau _0],\\ \Theta _2= & {} (s_1\omega _0)^2+[(s_0-s_2\omega _0^2)\omega _0]^2. \end{aligned}$$

In order to investigate the distribution of roots of the transcendental equation (2.6), the following Lemma that is stated in [41] is useful.

Lemma 2.1

[41] For the transcendental equation

$$\begin{aligned} P(\lambda ,e^{-\lambda \tau _1},\ldots ,e^{-\lambda \tau _m})= & {} \lambda ^n+p_1^{(0)}\lambda ^{n-1}+\cdots +p_{n-1}^{(0)}\lambda +p_n^{(0)}\\&+\left[ p_1^{(1)}\lambda ^{n-1}+\cdots +p_{n-1}^{(1)}\lambda +p_{n}^{(1)}\right] e^{-\lambda \tau _1}+\cdots \\&+\left[ p_1^{(m)}\lambda ^{n-1}+\cdots +p_{n-1}^{(m)}\lambda +p_{n}^{(m)}\right] e^{-\lambda \tau _m}=0, \end{aligned}$$

as \((\tau _1,\tau _2,\tau _3,\ldots ,\tau _m)\) vary, the sum of orders of the zeros of \(P(\lambda , e^{-\lambda \tau _1},\ldots ,e^{-\lambda \tau _m})\) in the open right half plane can change and only if a zero appears on or crosses the imaginary axis.

Remark 2.1

Lemma 2.1 is a generalization of the Lemma in Cooke and Grossman [42] in which a second order degree exponential polynomial was investigated.

In view of Lemma 2.1, it is easy to obtain the following results:

Theorem 2.2

If (H1)–(H4) hold, then

  1. (i)

    for system (2.3), its equilibrium \(E(x_1^*, x_2^*, x_3^*, x_4^*, x_5^*, x_6^*)\) is asymptotically stable for \(\tau \in [0, \tau _0)\)

  2. (ii)

    system (2.3) undergoes a Hopf bifurcation at the equilibrium \(E(x_1^*, x_2^*, x_3^*, x_4^*, x_5^*, x_6^*)\) when \(\tau = \tau _0\), i.e., system (2.3) has a branch of periodic solutions bifurcating from the equilibrium \(E(x_1^*, x_2^*, x_3^*, x_4^*, x_5^*, x_6^*)\) solution near \(\tau = \tau _0\).

3 Direction and Stability of the Hopf Bifurcation

In the previous section, we have obtained some conditions to ensure that system (2.3) undergoes a single Hopf bifurcation at the equilibrium \(E(x_1^*, x_2^*, x_3^*, x_4^*, x_5^*, x_6^*)\) when \(\tau =\tau _1+\tau _2\) passes through certain critical values. In this section, we shall study the direction, stability, and the period of bifurcating periodic solutions. The method we used is based on normal form method and the center manifold theory introduced by Hassard et al. [43].

Without loss of generality, we denote the critical value \(\tau _i(i = 0, 1, 2, \ldots )\) by \(\tilde{\tau } =\tilde{\tau }_1 + \tilde{\tau }_2\) at which system (2.3) undergoes a Hopf bifurcation, where \(\tilde{\tau }_1<\tilde{\tau }_2\) and \(\tau = \tilde{\tau }+ \mu =(\tilde{\tau }_1 + \mu )+\tilde{\tau }_2\), then \(\mu = 0\) is Hopf bifurcation value of system (2.3). We choose the phase space as \(C = C([-\tilde{\tau }_2, 0],C^6)\), where for convenience in computation we use \(C^6\) instead of \({\mathbb {R}}^6\).

Its linear part is given by

$$\begin{aligned} \left\{ \begin{array}{lc} \displaystyle \frac{dx_1}{dt}=-x_1(t)+b\text{ sech }^2(x_5^*)x_5(t)+b\text{ sech }^2(x_6^*)x_6(t), \\ \displaystyle \frac{dx_2}{dt}=-x_2(t)+a\text{ sech }^2(x_4^*)x_4(t), \\ \displaystyle \frac{dx_3}{dt}=-x_3(t)+a\text{ sech }^2(x_4^*)x_4(t), \\ \displaystyle \frac{dx_4}{dt}=\beta [x_1(t-\tau _1)-x_4(t)], \\ \displaystyle \frac{dx_5}{dt}=\beta [x_2(t-\tau _2)-x_5(t)], \\ \displaystyle \frac{dx_6}{dt}=\beta [x_3(t-\tau _2)-x_6(t)]. \end{array}\right. \end{aligned}$$
(3.1)

Its non-linear part is given by

$$\begin{aligned} f(\mu , x_t)=\left( \begin{array}{c} c_{11}x_5^2(0)+c_{12}x_5^3(0)+ c_{13}x_6^2(0)+c_{14}x_6^3(0)+\text{ h.o.t. }\\ c_{21}x_4^2(0)+c_{22}x_4^3(0)+\text{ h.o.t. } \\ c_{21}x_4^2(0)+c_{22}x_4^3(0)+\text{ h.o.t. } \\ 0 \\ 0 \\ 0 \\ \end{array} \right) , \end{aligned}$$
(3.2)

where

$$\begin{aligned} c_{11}= & {} -2b\text{ sech }^2(v^*)\text{ th }(v^*),\\ c_{12}= & {} -b(4\text{ sech }^2(v^*)\text{ th }^2(v^*)-2\text{ sech }^4(v^*)),\\ c_{13}= & {} -2b\text{ sech }^2(w^*)\text{ th }(w^*),\\ c_{14}= & {} -b(4\text{ sech }^2(w^*)\text{ th }^2(w^*)-2\text{ sech }^4(w^*)), \\ c_{21}= & {} -2b\text{ sech }^2(u^*)\text{ th }(u^*),\\ c_{22}= & {} -b(4\text{ sech }^2(u^*)\text{ th }^2(u^*)-2\text{ sech }^4(u^*)) \end{aligned}$$

and

$$\begin{aligned} x_t(\theta )= & {} (x_{1t}(\theta ),x_{2t}(\theta ),x_{3t}(\theta ),x_{4t}(\theta ),x_{5t}(\theta ),x_{6t}(\theta ))^T\\= & {} (x_1(t+\theta ), x_2(t+\theta ),x_3(t+\theta ),x_4(t+\theta ),x_5(t+\theta ),x_6(t+\theta ))^T. \end{aligned}$$

Denote

$$\begin{aligned} C^k[-\tilde{\tau }_2,0]= & {} \{\varphi |\varphi :[-\tilde{\tau }_2,0]\rightarrow {{\mathbb {R}}^6},\\&\text{ each } \text{ component } \text{ of } \varphi \text{ has } k \text{ order } \text{ continuous } \text{ derivative }\}. \end{aligned}$$

For convenience, denote \(C[-\tilde{\tau }_2, 0]\) by \(C^0[-\tilde{\tau }_2, 0]\).

For \(\varphi (\theta )=(\varphi _1(\theta ), \varphi _2(\theta ), \varphi _3(\theta ), \varphi _4(\theta ), \varphi _5(\theta ), \varphi _6(\theta ))^T\in {C([-\tilde{\tau }_2, 0], {\mathbb {R}}^6)}\), define a family of operators

$$\begin{aligned} L_\mu (\varphi )=B \left( \begin{array}{c} \varphi _1(0) \\ \varphi _2(0) \\ \varphi _3(0) \\ \varphi _4(0) \\ \varphi _5(0) \\ \varphi _6(0) \\ \end{array} \right) +B_1 \left( \begin{array}{c} \varphi _1(-\tilde{\tau }_1+\mu ) \\ \varphi _2(-\tilde{\tau }_1+\mu ) \\ \varphi _3(-\tilde{\tau }_1+\mu ) \\ \varphi _4(-\tilde{\tau }_1+\mu ) \\ \varphi _5(-\tilde{\tau }_1+\mu ) \\ \varphi _6(-\tilde{\tau }_1+\mu ) \\ \end{array} \right) +B_2\left( \begin{array}{c} \varphi _1(-\tilde{\tau }_2) \\ \varphi _2(-\tilde{\tau }_2) \\ \varphi _3(-\tilde{\tau }_2) \\ \varphi _4(-\tilde{\tau }_2) \\ \varphi _5(-\tilde{\tau }_2) \\ \varphi _6(-\tilde{\tau }_2) \\ \end{array} \right) , \end{aligned}$$
(3.3)

where \(L_\mu \) is a one-parameter family of bounded linear operators in \(C([-\tilde{\tau }_2, 0], {\mathbb {R}}^6)\rightarrow {{\mathbb {R}}^6}\) and

$$\begin{aligned} B= & {} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} -1 &{} 0 &{} 0 &{} 0 &{} b\text{ sech }^2(v^*) &{} b\text{ sech }^2(w^*) \\ 0 &{} -1 &{} 0 &{} b\text{ sech }^2(u^*) &{} 0 &{} 0 \\ 0 &{} 0 &{} -1 &{} b\text{ sech }^2(u^*) &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} -\beta &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} -\beta &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -\beta \\ \end{array} \right) , \\ B_1= & {} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{}0 &{} 0 &{} 0 \\ 0 &{}0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \beta &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right) , B_2=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{}0 &{} 0 &{} 0 \\ 0 &{}0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} \beta &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} \beta &{} 0 &{} 0 &{} 0 \\ \end{array} \right) . \end{aligned}$$

By the Riesz representation theorem, there exists a matrix whose components are bounded variation functions \(\eta (\theta ,\mu )\) in \([-\tilde{\tau }_2, 0]\rightarrow {{\mathbb {R}}^{6^2}}\), such that

$$\begin{aligned} L_\mu (\varphi )=\int _{-\tilde{\tau }_2}^0d\eta (\theta , \mu )\varphi (\theta ). \end{aligned}$$
(3.4)

In fact, choosing

$$\begin{aligned} \eta (\theta ,\mu )=\left\{ \begin{array}{l@{\quad }l} B, &{} \theta =0,\\ B_1, &{} \theta \in [-\tilde{\tau }_1,0),\\ B_2, &{} \theta \in [-\tilde{\tau }_2,-\tilde{\tau }_1), \end{array}\right. \end{aligned}$$
(3.5)

where \(\delta (\theta )\) is Dirac function, then (3.4) is satisfied. For \((\varphi _1, \varphi _2, \varphi _3, \varphi _4, \varphi _5, \varphi _6 )\in {(C^1[-\tilde{\tau }_2, 0], {\mathbb {R}}^6)}\), define

$$\begin{aligned} A(\mu )\varphi =\left\{ \begin{array}{l@{\quad }l} \frac{d\varphi (\theta )}{d\theta }, &{} -\tilde{\tau }_2\le \theta <0,\\ \int _{-\tilde{\tau }_2}^0d\eta (s, \mu )\varphi (s), &{} \quad \theta =0 \end{array} \right. \end{aligned}$$
(3.6)

and

$$\begin{aligned} R\varphi =\left\{ \begin{array}{l@{\quad }l} 0, &{} -\tilde{\tau }_2\le \theta <0,\\ f(\mu , \varphi ), &{} \theta =0. \end{array} \right. \end{aligned}$$
(3.7)

Then (2.3) is equivalent to the abstract differential equation

$$\begin{aligned} \dot{u_t}=A(\mu )x_t+R(\mu )x_t, \end{aligned}$$
(3.8)

where \(u=(u_1, u_2, u_3, u_4, u_5, u_6)^T,\,u_t(\theta )=u(t+\theta ),\theta \in [-\tilde{\tau }_2, 0]\).

For \(\psi \in {C([0, \tilde{\tau }_2], ({\mathbb {R}}^6)^*)}\), define

$$\begin{aligned} A^*\psi (s)=\left\{ \begin{array}{l@{\quad }c} -\frac{d\psi (s)}{ds}, &{} s\in {(0,\tilde{\tau }_2]}, \\ \int _{-\tilde{\tau }_2}^0d\eta ^T(t,0)\psi (-t),&{} s=0. \end{array}\right. \end{aligned}$$
(3.9)

For \(\phi \in {C([-\tilde{\tau }_2, 0], {\mathbb {R}}^6)}\) and \(\psi \in {C([0, \tilde{\tau }_2], ({\mathbb {R}}^6)^*)}\), define the bilinear form

$$\begin{aligned} \langle \psi ,\phi \rangle =\overline{\psi }(0)\phi (0)-\int _{-\tilde{\tau }_2}^0\int _{\xi =0}^{\theta }\psi ^T(\xi -\theta ) d\eta (\theta )\phi (\xi )d\xi , \end{aligned}$$
(3.10)

where \(\eta (\theta )=\eta (\theta ,0)\). We have the following result on the relation between the operators \(A=A(0)\) and \(A^*\).

Lemma 3.1

\(A=A(0)\) and \(A^*\) are adjoint operators.

Proof

Let \(\phi \in {C^1([-\tilde{\tau }_2, 0], {\mathbb {R}}^6)}\) and \(\psi \in {C^1([0, \tilde{\tau }_2], ({\mathbb {R}}^6)^*)}\). It follows from (3.10) and the definitions of \(A=A(0)\) and \(A^*\) that

$$\begin{aligned} \langle \psi (s), A(0)\phi (\theta )\rangle= & {} \bar{\psi }(0)A(0)\phi (0)-\int _{-\tilde{\tau }_2}^{0}\int _{\xi =0}^{\theta } \bar{\psi }(\xi -\theta )d\eta (\theta )A(0)\phi (\xi )d\xi \\= & {} \bar{\psi }(0)\int _{-\tilde{\tau }_2}^{0}d\eta (\theta )\phi (\theta )-\int _{-\tilde{\tau }_2}^{0}\int _{\xi =0}^{\theta } \bar{\psi }(\xi -\theta )d\eta (\theta )A(0)\phi (\xi )d\xi \\= & {} \bar{\psi }(0)\int _{-\tilde{\tau }_2}^{0}d\eta (\theta )\phi (\theta )-\int _{-\tilde{\tau }_2}^{0}[ \bar{\psi }(\xi -\theta )d\eta (\theta )\phi (\xi )]_{\xi =0}^{\theta } \\&+\int _{-\tilde{\tau }_2}^{0}\int _{\xi =0}^{\theta } \frac{d\bar{\psi }(\xi -\theta )}{d\xi }d\eta (\theta )\phi (\xi )d\xi \\= & {} \int _{-\tilde{\tau }_2}^{0}\bar{\psi }(-\theta )d\eta (\theta )\phi (0)- \int _{-\tilde{\tau }_2}^{0}\int _{\xi =0}^{\theta } \left[ -\frac{d\bar{\psi }(\xi -\theta )}{d\xi }\right] d\eta (\theta )\phi (\xi )d\xi \\= & {} A^*\bar{\psi }(0)\phi (0)-\int _{-\tilde{\tau }_2}^{0}\int _{\xi =0}^{\theta } A^*\bar{\psi }(\xi -\theta )d\eta (\theta )\phi (\xi )d\xi \\= & {} \langle A^*\psi (s), \phi (\theta )\rangle . \end{aligned}$$

This shows that \(A=A(0)\) and \(A^*\) are adjoint operators and the proof is complete. \(\square \)

By the discussions in Sect. 2, we know that \(\pm {i\omega _0}\) are eigenvalues of A(0), and they are also eigenvalues of \(A^*\) corresponding to \(i\omega _0\) and \(-i\omega _0\), respectively. We have the following result.

Lemma 3.2

The vector

$$\begin{aligned} q(\theta )=(1, a_1, a_2, a_3, a_4,a_5)^Te^{i\omega _0\theta }, \quad \theta \in [-\tilde{\tau }_2, 0], \end{aligned}$$

where

$$\begin{aligned} a_1= & {} \frac{a\beta \text{ sech }^2(u^*)e^{-i\omega _0\tilde{\tau }_1}}{(i\omega _0+1)(\beta +i\omega _0)}, a_2=\frac{a\beta \text{ sech }^2(u^*)e^{-i\omega _0\tilde{\tau }_1}}{(i\omega _0+1)(\beta +i\omega _0)}, \\ a_3= & {} \frac{{\beta }e^{-i\omega _0\tilde{\tau }_1}}{\beta +i\omega _0}, a_4=\frac{a\beta \text{ sech }^2(u^*)e^{-i\omega _0\tilde{\tau }}}{(i\omega _0+1)(\beta +i\omega _0)^2},\\ a_5= & {} \frac{(i\omega _0+1)^2(\beta +i\omega _0)^2-a\beta \text{ sech }^2(u^*)e^{-i\omega _0\tilde{\tau }}}{(i\omega _0+1)(\beta +i\omega _0)^2b\text{ sech }^2(w^*)}, \end{aligned}$$

is the eigenvector of A(0) corresponding to the eigenvalue \(i\omega _0\), and

$$\begin{aligned} q^*(s)=D(1, a_1^*, a_2^*, a_3^*, a_4^*, a_5^*)e^{i\omega _0{s}},\quad s\in [0, \tilde{\tau }_2], \end{aligned}$$

where

$$\begin{aligned} a_1^*= & {} \frac{b\beta \text{ sech }^2(u^*)e^{-i\omega _0\tilde{\tau }_2}}{(i\omega _0+1)(\beta +i\omega _0)}, a_2^*=\frac{b\beta \text{ sech }^2(w^*)e^{-i\omega _0\tilde{\tau }_2}}{(i\omega _0+1)(\beta +i\omega _0)},\\ a_3^*= & {} \frac{i\omega _0+1}{{\beta }e^{-i\omega _0\tilde{\tau }_1}}, a_4^*=\frac{b\text{ sech }^2(u^*)}{i\omega _0+\beta },\\ a_5^*= & {} \frac{b\text{ sech }^2(w^*)}{i\omega _0+\beta }, \end{aligned}$$

is the eigenvector of \(A^*\) corresponding to the eigenvalue \(-i\omega _0\), moreover, \(\langle q^*(s), q(\theta )\rangle =1\), where

$$\begin{aligned} D=\frac{1}{1+\sum _{i=1}^5\bar{a}_ia_i^*+a_3^*\beta {e}^{i\omega _0\tilde{\tau }_1}+\bar{a}_1a_4^*\beta {e}^{i\omega _0\tilde{\tau }_2}+ \bar{a}_2a_5^*\beta {e}^{i\omega _0\tilde{\tau }_2}}. \end{aligned}$$

Proof

Let \(q(\theta )\) be the eigenvector of A(0) corresponding to the eigenvalue \(i\omega _0\) and \(q^*(s)\) be the eigenvector of \(A^*\) corresponding to the eigenvalue \(-i\omega _0\), namely, \(A(0)q(\theta )=i\omega _0q(\theta )\) and \(A^*q(s)=-i\omega _0q^*(s)\). From the definitions of A(0) and \(A^*\), we have \(A(0)q(\theta )=dq(\theta )/d\theta \) and \(A^*q(s)=-\frac{dq^*(s)}{ds}\). Thus, \(q(\theta )=q(0)e^{i\omega _0\theta }\) and \(q^*(s)=q(0)e^{i\omega _0s}\). In addition,

$$\begin{aligned} \int _{-\tilde{\tau }_2}^{0}d\eta (\theta )q(\theta )= & {} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} -1 &{} 0 &{} 0 &{} 0 &{} b\text{ sech }^2(v^*) &{} b\text{ sech }^2(w^*) \\ 0 &{} -1 &{} 0 &{} b\text{ sech }^2(u^*) &{} 0 &{} 0 \\ 0 &{} 0 &{} -1 &{} b\text{ sech }^2(u^*) &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} -\beta &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} -\beta &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -\beta \\ \end{array} \right) q(0) \nonumber \\&+\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{}0 &{} 0 &{} 0 \\ 0 &{}0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \beta &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right) q(-\tilde{\tau }_1)+\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{}0 &{} 0 &{} 0 \\ 0 &{}0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} \beta &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} \beta &{} 0 &{} 0 &{} 0 \\ \end{array} \right) q(-\tilde{\tau }_2)\nonumber \\= & {} A(0)q(0)=i\omega _0q(0). \end{aligned}$$
(3.11)

That is

$$\begin{aligned} \left( \begin{array}{c} -1+a_4\text{ sech }^2(v^*)+a_5\text{ sech }^2(w^*) \\ -a_1+a_3\text{ sech }^2(u^*) \\ -a_2+a_3\text{ sech }^2(u^*) \\ \beta {e}^{i\omega _0\tilde{\tau }_1}-a_3\beta \\ \beta {a_1}{e}^{i\omega _0\tilde{\tau }_2}-a_4\beta \\ \beta {a_2}{e}^{i\omega _0\tilde{\tau }_2}-a_5\beta \\ \end{array} \right) =\left( \begin{array}{c} i\omega _0 \\ ia_1\omega _0 \\ ia_2\omega _0 \\ ia_3\omega _0 \\ ia_4\omega _0 \\ ia_5\omega _0 \\ \end{array} \right) . \end{aligned}$$
(3.12)

Therefore, we can easily obtain

$$\begin{aligned} a_1= & {} \frac{a\beta \text{ sech }^2(u^*)e^{-i\omega _0\tilde{\tau }_1}}{(i\omega _0+1)(\beta +i\omega _0)},\qquad a_2=\frac{a\beta \text{ sech }^2(u^*)e^{-i\omega _0\tilde{\tau }_1}}{(i\omega _0+1)(\beta +i\omega _0)},\\ a_3= & {} \frac{{\beta }e^{-i\omega _0\tilde{\tau }_1}}{\beta +i\omega _0}, a_4=\frac{a\beta \text{ sech }^2(u^*)e^{-i\omega _0\tilde{\tau }}}{(i\omega _0+1)(\beta +i\omega _0)^2},\\ a_5= & {} \frac{(i\omega _0+1)^2(\beta +i\omega _0)^2-a\beta \text{ sech }^2(u^*)e^{-i\omega _0\tilde{\tau }}}{(i\omega _0+1)(\beta +i\omega _0)^2b\text{ sech }^2(w^*)}. \end{aligned}$$

On the other hand,

$$\begin{aligned} \int _{-\tilde{\tau }_2}^{0}q^*(-t)d\eta (t)= & {} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} -1 &{} 0 &{} 0 &{} 0 &{} b\text{ sech }^2(v^*) &{} b\text{ sech }^2(w^*) \\ 0 &{} -1 &{} 0 &{} b\text{ sech }^2(u^*) &{} 0 &{} 0 \\ 0 &{} 0 &{} -1 &{} b\text{ sech }^2(u^*) &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} -\beta &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} -\beta &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -\beta \\ \end{array} \right) ^Tq^*(0)\nonumber \\&+\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{}0 &{} 0 &{} 0 \\ 0 &{}0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \beta &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right) ^Tq^*(-\tilde{\tau }_1)+\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{}0 &{} 0 &{} 0 \\ 0 &{}0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} \beta &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} \beta &{} 0 &{} 0 &{} 0 \\ \end{array} \right) ^Tq(-\tilde{\tau }_2)\nonumber \\= & {} A^*q^*(0)=-i\omega _0q^*(0). \end{aligned}$$
(3.13)

Namely,

$$\begin{aligned} \left( \begin{array}{c} -1+\beta {a_3^*}{e}^{i\omega _0\tilde{\tau }_1} \\ -a_1^*+\beta {a_3^*}{e}^{i\omega _0\tilde{\tau }_2} \\ -a_2^*+\beta {a_5^*}{e}^{i\omega _0\tilde{\tau }_2} \\ a_1^*a\text{ sech }^2(u^*)+a_2^*a\text{ sech }^2(u^*)-\beta {a_3^*} \\ b\text{ sech }^2(u^*)-\beta {a_4^*}\\ b\text{ sech }^2(w^*)-\beta {a_5^*}\\ \end{array} \right) =\left( \begin{array}{c} 1 \\ ia_1^*\omega _0 \\ ia_2^*\omega _0 \\ ia_3^*\omega _0 \\ ia_4^*\omega _0 \\ ia_5^*\omega _0 \\ \end{array} \right) . \end{aligned}$$
(3.14)

Therefore, we can easily obtain

$$\begin{aligned} a_1^*= & {} \frac{b\beta \text{ sech }^2(u^*)e^{-i\omega _0\tilde{\tau }_2}}{(i\omega _0+1)(\beta +i\omega _0)}, a_2^*=\frac{b\beta \text{ sech }^2(w^*)e^{-i\omega _0\tilde{\tau }_2}}{(i\omega _0+1)(\beta +i\omega _0)},\\ a_3^*= & {} \frac{i\omega _0+1}{{\beta }e^{-i\omega _0\tilde{\tau }_1}}, a_4^*=\frac{b\text{ sech }^2(u^*)}{i\omega _0+\beta },\\ a_5^*= & {} \frac{b\text{ sech }^2(w^*)}{i\omega _0+\beta }. \end{aligned}$$

In the sequel, we shall verify that \(\langle q^*(s), q(\theta ) \rangle =1\). In fact, from (3.10), we have \(\langle q^*(s), q(\theta )\rangle \)

$$\begin{aligned}= & {} \bar{D}(1, \bar{a_1^*}, \bar{a_2^*}, \bar{a_3^*}, \bar{a_4}, \bar{a_5^*})(1, a_1, a_2, a_3, a_4, a_5)^T\\&-\int _{-\tilde{\tau }_2}^{0}\int _{\xi =0}^{\theta }\bar{D}(1, \bar{a_1^*}, \bar{a_2^*}, \bar{a_3^*}, \bar{a_4}, \bar{a_5^*}) e^{-i\omega _0\tau _0(\xi -\theta )} d\eta (\theta )(1, a_1, a_2, a_3, a_4, a_5)^Te^{i\omega _0\xi }d\xi \\= & {} \bar{D}\left[ 1+\sum _{i=1}^5a_i\bar{a_i^*}- \int _{-\tilde{\tau }_2}^{0}(1, \bar{a_1^*}, \bar{a_2^*}, \bar{a_3^*}, \bar{a_4}, \bar{a_5^*}){\theta }e^{i\omega _0\theta }d\eta (\theta ) (1, a_1, a_2, a_3, a_4, a_5)^T\right] \\= & {} \bar{D}\left\{ 1+\sum _{i=1}^5a_i\bar{a_i^*}+(1, \bar{a_1^*}, \bar{a_2^*}, \bar{a_3^*}, \bar{a_4}, \bar{a_5^*}) \Lambda (1, a_1, a_2, a_3, a_4, a_5)^T\right\} \\= & {} \bar{D}\Bigg [1+\sum _{i=1}^5a_i\bar{a_i^*}+\bar{a_3^*}\beta {e}^{-i\omega _0\tilde{\tau }_1}+a_1\bar{a_4^*}\beta {e}^{-i\omega _0\tilde{\tau }_2} +a_2\bar{a_5^*}\beta {e}^{-i\omega _0\tilde{\tau }_2}\Bigg ]=1. \end{aligned}$$

where

$$\begin{aligned} \Lambda =\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{}0&{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0&{} 0 &{} 0\\ \beta {e}^{-i\omega _0\tilde{\tau }_1} &{} 0 &{} 0&{} 0&{} 0 &{} 0 \\ 0 &{} \beta {e}^{-i\omega _0\tilde{\tau }_1} &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} \beta {e}^{-i\omega _0\tilde{\tau }_1} &{} 0 &{} 0 &{} 0 \\ \end{array} \right) . \end{aligned}$$
(3.15)

Next, we use the same notations as those in Hassard, Kazarinoff and Wan [43], and we first compute the coordinates to describe the center manifold \(C_0\) at \(\mu =0\). Let \(u_t\) be the solution of Eq.(2.3) when \(\mu =0\).

Define

$$\begin{aligned} z(t)=\langle q^*, x_t \rangle ,\;W(t,\theta )=x_t(\theta )-2\text{ Re }\{z(t)q(\theta )\} \end{aligned}$$
(3.16)

on the center manifold \(C_0\), and we have

$$\begin{aligned} W(t, \theta )=W(z(t), \bar{z}(t), \theta ), \end{aligned}$$
(3.17)

where

$$\begin{aligned} W(z(t), \bar{z}(t), \theta )=W(z,\bar{z})=W_{20}\frac{z^2}{2}+W_{11}z\bar{z}+W_{02} \frac{\bar{z}^2}{2}+\cdots \end{aligned}$$
(3.18)

and z and \(\bar{z}\) are local coordinates for center manifold \(C_0\) in the direction of \(q^*\) and \(\bar{q}^*\). Noting that W is also real if \(x_t\) is real, we consider only real solutions. For solutions \(x_t\in {C_0}\) of (2.3),

$$\begin{aligned} \dot{z}(t)= & {} \langle q^*(s), \dot{x}_t \rangle = \langle q^*(s), A(0)x_t+R(0)x_t \rangle \nonumber \\= & {} \langle q^*(s), A(0)x_t \rangle +\langle q^*(s), R(0)x_t \rangle \nonumber \\= & {} \langle A^*q^*(s), x_t \rangle +\bar{q^*}(0)R(0)x_t\nonumber \\&-\int _{-\tilde{\tau }_2}^{0}\int _{\xi =0}^{\theta } \bar{q^*}(\xi -\theta )d\eta (\theta )A(0)R(0)x_t(\xi )d\xi \nonumber \\= & {} \langle i\omega _0q^*(s), x_t \rangle +\bar{q^*}(0)f(0, x_t(\theta )\nonumber \\&\mathop {=}\limits ^{\text {def}}i\omega _0z(t)+\bar{q^*}(0)f_0(z(t), \bar{z}(t)). \end{aligned}$$
(3.19)

That is

$$\begin{aligned} \dot{z}(t)=i\omega _0\tau _0{z}+g(z, \bar{z}), \end{aligned}$$
(3.20)

where

$$\begin{aligned} g(z, \bar{z})=g_{20}\frac{z^2}{2}+g_{11}z\bar{z}+g_{02} \frac{\bar{z}^2}{2}+g_{21}\frac{z^2\bar{z}}{2}+\cdots . \end{aligned}$$
(3.21)

Hence, we have

$$\begin{aligned} g(z, \bar{z})= & {} \bar{q}^*(0)f_0(z, \bar{z})=f(0, u_t)\nonumber \\= & {} \tau _0\bar{D}(1, \bar{a}_1^*, \bar{a}_2^*, \bar{a}_3^*, \bar{a}_4^*, \bar{a}_5^*)\nonumber \\&\times (f_1(0, x_t), f_2(0, x_t), f_3(0, x_t), f_4(0, x_t), f_5(0, x_t), f_6(0, x_t))^T, \end{aligned}$$
(3.22)

where

$$\begin{aligned} f_1(0,x_t)= & {} c_{11}x_{5t}^2(0)+c_{12}x_{5t}^3(0)+ c_{13}x_{6t}^2(0)+c_{14}x_{6t}^3(0)+\text{ h.o.t. }, \\ f_2(0,x_t)= & {} c_{21}x_{4t}^2(0)+c_{22}x_{4t}^3(0)+\text{ h.o.t. }, \\ f_3(0,x_t)= & {} c_{21}x_{4t}^2(0)+c_{22}x_{4t}^3(0)+\text{ h.o.t. }, \\ f_4(0,x_t)= & {} f_5(0,x_t)=f_6(0,x_t)=0. \end{aligned}$$

Noticing that

$$\begin{aligned} x_t(\theta )=(x_{1t}(\theta ), x_{2t}(\theta ), x_{3t}(\theta ), x_{4t}(\theta ), x_{5t}(\theta ),x_{6t}(\theta ))^T =W(t,\theta )+zq(\theta )+\bar{z}\bar{q} \end{aligned}$$

and

$$\begin{aligned} q(\theta )=(1, a_1, a_2, a_3, a_4, a_5)^Te^{i\omega _0\theta }, \end{aligned}$$

we have

$$\begin{aligned} x_{4t}(0)= & {} a_3z+\bar{a}_3\bar{z}+W_{20}^{(4)}(0)\frac{z^2}{2}+W_{11}^{(4)}(0)z\bar{z} +W_{02}^{(4)}(0)\frac{\bar{z}^2}{2}+\cdots , \\ x_{5t}(0)= & {} a_4z+\bar{a}_4\bar{z}+W_{20}^{(5)}(0)\frac{z^2}{2}+W_{11}^{(5)}(0)z\bar{z} +W_{02}^{(5)}(0)\frac{\bar{z}^2}{2}+\cdots , \\ x_{6t}(0)= & {} a_5z+\bar{a}_5\bar{z}+W_{20}^{(6)}(0)\frac{z^2}{2}+W_{11}^{(6)}(0)z\bar{z} +W_{02}^{(6)}(0)\frac{\bar{z}^2}{2}+\cdots . \end{aligned}$$

From (3.21) and (3.22), we can obtain the expression of \(g(z,\bar{z})\) as follows

$$\begin{aligned} g(z,\bar{z})= & {} (c_{11}a_4^2+c_{13}a_5^2+\bar{a_1^*}c_{21}a_3^2+\bar{a_2^*}c_{21}a_3^2)z^2\\&+\, (2c_{11}|a_4|^2+2c_{13}|a_5|^2+2\bar{a_1^*}c_{21}|a_3|^2+2\bar{a_2^*}c_{21}|a_3|^2)z\bar{z}\\&+\, (c_{11}\bar{a}_4^2+c_{13}\bar{a}_5^2+\bar{a_1^*}c_{21}\bar{a}_3^2+\bar{a_2^*}c_{21}\bar{a}_3^2)\bar{z}^2\\&+\,\Big \{c_{11}\left( 2a_4W_{11}^{(5)}(0)+W_{20}^{(5)}(0)\bar{a}_4\right) +3c_{12}a_4^2\bar{a}_4\\&+\,c_{13}\left( 2a_5W_{11}^{(6)}(0)+W_{20}^{(6)}(0)\bar{a}_5\right) +3c_{14}a_5^2\bar{a}_5+(a_1^*+a_2^*)\\&\times \left[ c_{21}\left( 2a_3W_{11}^{(4)}(0)+W_{20}^{(4)}(0)\bar{a}_3\right) +3c_{22}a_3^2\bar{a}_3\right] \Big \}z^2\bar{z}+\text{ h.o.t. }. \end{aligned}$$

It is easy to obtain

$$\begin{aligned} g_{20}= & {} 2\bar{D}(c_{11}a_4^2+c_{13}a_5^2+\bar{a_1^*}c_{21}a_3^2+\bar{a_2^*}c_{21}a_3^2)\\ g_{11}= & {} 2\bar{D}(c_{11}|a_4|^2+c_{13}|a_5|^2+\bar{a_1^*}c_{21}|a_3|^2+\bar{a_2^*}c_{21}|a_3|^2),\\ g_{02}= & {} 2\bar{D}\Big \{c_{11}\left( 2a_4W_{11}^{(5)}(0)+W_{20}^{(5)}(0)\bar{a}_4\right) +3c_{12}a_4^2\bar{a}_4\\&+\,c_{13}\left( 2a_5W_{11}^{(6)}(0)+W_{20}^{(6)}(0)\bar{a}_5\right) +3c_{14}a_5^2\bar{a}_5+(a_1^*+a_2^*)\\&\times \left[ c_{21}\left( 2a_3W_{11}^{(4)}(0)+W_{20}^{(4)}(0)\bar{a}_3\right) +3c_{22}a_3^2\bar{a}_3\right] \Big \}. \end{aligned}$$

Since

$$\begin{aligned} W_{11}^{(4)}(0), W_{11}^{(5)}(0), W_{11}^{(6)}(0), W_{20}^{(4)}(0), W_{20}^{(5)}(0),W_{20}^{(6)}(0) \end{aligned}$$

in \(g_{21}\), we still need to compute them. In view of (3.8) and (3.9), we have

$$\begin{aligned} W^{'}= & {} \left\{ \begin{array}{lc} AW-2\text{ Re }{\{\bar{q}^*(0)f_0q(\theta )\}}, &{} -\tilde{\tau }_2\le \theta <0,\\ AW-2\text{ Re }{\{\bar{q}^*(0)f_0q(\theta )\}}+ f_0, &{}\theta =0. \end{array}\right. \nonumber \\&\quad \mathop {=}\limits ^{\text {def}}AW+H(z, \bar{z}, \theta ), \end{aligned}$$
(3.23)

where

$$\begin{aligned} H(z,\bar{z},\theta )=H_{20}(\theta )\frac{z^2}{2}+H_{11}(\theta )z\bar{z}+H_{02}(\theta ) \frac{\bar{z}^2}{2}+\cdots . \end{aligned}$$
(3.24)

Comparing the coefficients, we obtain

$$\begin{aligned} (A-2i\omega _0)W_{20}=-H_{20}(\theta ), \end{aligned}$$
(3.25)
$$\begin{aligned} AW_{11}(\theta )=-H_{11}(\theta ), \end{aligned}$$
(3.26)

For \(\theta \in [-\tilde{\tau }_2, 0)\),

$$\begin{aligned} H(z,\bar{z}, \theta )=-\bar{q}^*(0)f_0q(\theta )-q^*(0)\bar{f}_0\bar{q}(\theta ) =-g(z, \bar{z})q(\theta )-\bar{g}(z, \bar{z})\bar{q}(\theta ). \end{aligned}$$
(3.27)

Comparing the coefficients of (3.24) with (3.27) gives that

$$\begin{aligned} H_{20}(\theta )= & {} -g_{20}q(\theta )-\bar{g}_{02}\bar{q}(\theta ), \end{aligned}$$
(3.28)
$$\begin{aligned} H_{11}(\theta )= & {} -g_{11}q(\theta )-\bar{g}_{11}\bar{q}(\theta ). \end{aligned}$$
(3.29)

From (3.25), (3.28) and the definition of A, we get

$$\begin{aligned} \dot{W}_{20}(\theta )=2i\omega _0W_{20}(\theta )+g_{20}q(\theta ) +\bar{g_{02}}\bar{q}(\theta ). \end{aligned}$$
(3.30)

Noting that \(q(\theta )=q(0)e^{i\omega _0\theta }\), we have

$$\begin{aligned} W_{20}(\theta )=\frac{ig_{20}}{\omega _0}q(0) e^{i\omega _0\theta }+\frac{i\bar{g}_{02}}{3\omega _0} \bar{q}(0)e^{-i\omega _0\theta } +E_1e^{2i\omega _0\theta }, \end{aligned}$$
(3.31)

where \(E_1\) is a constant vector. Similarly, from (3.26), (3.29) and the definition of A, we have

$$\begin{aligned} \dot{W}_{11}(\theta )= & {} g_{11}q(\theta ) +\bar{g_{11}}\bar{q}(\theta ), \end{aligned}$$
(3.32)
$$\begin{aligned} W_{11}(\theta )= & {} -\frac{ig_{11}}{\omega _0}q(0) e^{i\omega _0\theta }+\frac{i\bar{g}_{11}}{\omega _0} \bar{q}(0)e^{-i\omega _0\theta }+E_2. \end{aligned}$$
(3.33)

where \(E_2\) is a constant vector.

In what follows, we shall seek appropriate \(E_1,\, E_2\) in (3.31), (3.33), respectively. It follows from the definition of A and (3.28), (3.29) that

$$\begin{aligned} \int _{-\tilde{\tau }_2}^0d\eta (\theta )W_{20}(\theta )= 2i\omega _0W_{20}(0)-H_{20}(0) \end{aligned}$$
(3.34)

and

$$\begin{aligned} \int _{-\tilde{\tau }_2}^0d\eta (\theta )W_{11}(\theta )=-H_{11}(0), \end{aligned}$$
(3.35)

where \(\eta (\theta )=\eta (0, \theta )\). It follows from (3.25) that

$$\begin{aligned} H_{20}(0)=-g_{20}q(0)-\bar{g_{02}}\bar{q}(0)+2(H_1, H_2, H_3, H_4, H_5, H_6)^T, \end{aligned}$$
(3.36)

where

$$\begin{aligned} H_1=c_{11}a_4^2+c_{13}a_5^2,H_2=c_{21}a_3^2,H_3=c_{21}a_3^2,H_4=H_4=H_6=0. \end{aligned}$$

From (3.26), we have

$$\begin{aligned} H_{11}(0)=-g_{11}q(0)-\bar{g_{11}}(0)\bar{q}(0)+\tau _0(P_1, P_2, P_3, P_4, P_5, P_6)^T, \end{aligned}$$
(3.37)

where

$$\begin{aligned} P_1=c_{11}|a_4|^2+c_{13}|a_5|^2, P_2=c_{21}|a_3|^2,P_3=c_{21}|a_3|^2,P_4=P_5=P_6=0. \end{aligned}$$

Noting that

$$\begin{aligned} \left( i\omega _0I-\int _{-\tilde{\tau }_2}^0e^{i\omega _0\theta } d\eta (\theta )\right) q(0)= & {} 0, \end{aligned}$$
(3.38)
$$\begin{aligned} \quad \left( -i\omega _0I-\int _{-\tilde{\tau }_2}^0e^{-i\omega _0\theta } d\eta (\theta )\right) \bar{q}(0)= & {} (H_1, H_2, H_3, H_4, H_5, H_6)^T \end{aligned}$$
(3.39)

and substituting (3.31) and (3.36) into (3.34), we have

$$\begin{aligned} \left( 2i\omega _0I-\int _{-\tilde{\tau }_2}^0e^{2i\omega _0\theta } d\eta (\theta )\right) E_1=(H_1, H_2, H_3, H_4, H_5, H_6)^T. \end{aligned}$$
(3.40)

That is

$$\begin{aligned}&\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 2i\omega _0+1 &{} 0 &{} 0 &{} 0 &{} -b\text{ sech }^2(v^*) &{} -b\text{ sech }^2(w^*) \\ 0 &{} 2i\omega _0+1 &{} 0 &{} -b\text{ sech }^2(u^*) &{} 0 &{} 0 \\ 0 &{} 0 &{} 2i\omega _0+1 &{} -b\text{ sech }^2(u^*) &{}0 &{} 0 \\ -\beta {e}^{i\omega _0\tilde{\tau }_1} &{} 0 &{} 0&{} 2i\omega _0+\beta &{} 0 &{} 0 \\ 0 &{} -\beta {e}^{i\omega _0\tilde{\tau }_1} &{} 0 &{} 0 &{} 2i\omega _0+\beta &{} 0 \\ 0 &{} 0 &{} -\beta {e}^{i\omega _0\tilde{\tau }_1} &{} 0 &{} 0 &{} 2i\omega _0+\beta \\ \end{array} \right) \nonumber \\&\quad \times (E_1^{(1)}, E_1^{(2)}, E_1^{(3)}, E_1^{(4)}, E_1^{(5)}, E_1^{(6)})^T=2(H_1, H_2, H_3, 0, 0, 0)^T. \end{aligned}$$
(3.41)

Hence,

$$\begin{aligned} E_1^{(1)}=\frac{\Delta _{11}}{\Delta _1},\,E_1^{(2)}=\frac{\Delta _{12}}{\Delta _1},\, E_1^{(3)}=\frac{\Delta _{13}}{\Delta _1},\,E_1^{(4)}=\frac{\Delta _{14}}{\Delta _1},~E_1^{(5)}=\frac{\Delta _{15}}{\Delta _1},\, E_1^{(6)}=\frac{\Delta _{16}}{\Delta _1},\nonumber \\ \end{aligned}$$
(3.42)

where

$$\begin{aligned} \Delta _1= & {} \det \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 2i\omega _0+1 &{} 0 &{} 0 &{} 0 &{} -b\text{ sech }^2(v^*) &{} -b\text{ sech }^2(w^*) \\ 0 &{} 2i\omega _0+1 &{} 0 &{} -b\text{ sech }^2(u^*) &{} 0 &{} 0 \\ 0 &{} 0 &{} 2i\omega _0+1 &{} -b\text{ sech }^2(u^*) &{}0 &{} 0 \\ -\beta {e}^{i\omega _0\tilde{\tau }_1} &{} 0 &{} 0&{} 2i\omega _0+\beta &{} 0 &{} 0 \\ 0 &{} -\beta {e}^{i\omega _0\tilde{\tau }_1} &{} 0 &{} 0 &{} 2i\omega _0+\beta &{} 0 \\ 0 &{} 0 &{} -\beta {e}^{i\omega _0\tilde{\tau }_1} &{} 0 &{} 0 &{} 2i\omega _0+\beta \\ \end{array} \right) ,\\ \Delta _{11}= & {} 2\det \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} H_1 &{} 0 &{} 0 &{} 0 &{} -b\text{ sech }^2(v^*) &{} -b\text{ sech }^2(w^*) \\ H_2 &{} 2i\omega _0+1 &{} 0 &{} -b\text{ sech }^2(u^*) &{} 0 &{} 0 \\ H_3 &{} 0 &{} 2i\omega _0+1 &{} -b\text{ sech }^2(u^*) &{}0 &{} 0 \\ 0 &{} 0 &{} 0&{} 2i\omega _0+\beta &{} 0 &{} 0 \\ 0 &{} -\beta {e}^{i\omega _0\tilde{\tau }_1} &{} 0 &{} 0 &{} 2i\omega _0+\beta &{} 0 \\ 0 &{} 0 &{} -\beta {e}^{i\omega _0\tilde{\tau }_1} &{} 0 &{} 0 &{} 2i\omega _0+\beta \\ \end{array} \right) ,\\ \Delta _{12}= & {} 2\det \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 2i\omega _0+1 &{} H_1 &{} 0 &{} 0 &{} -b\text{ sech }^2(v^*) &{} -b\text{ sech }^2(w^*) \\ 0 &{} H_2 &{} 0 &{} -b\text{ sech }^2(u^*) &{} 0 &{} 0 \\ 0 &{} H_3 &{} 2i\omega _0+1 &{} -b\text{ sech }^2(u^*) &{}0 &{} 0 \\ -\beta {e}^{i\omega _0\tilde{\tau }_1} &{} 0 &{} 0&{} 2i\omega _0+\beta &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 2i\omega _0+\beta &{} 0 \\ 0 &{} 0 &{} -\beta {e}^{i\omega _0\tilde{\tau }_1} &{} 0 &{} 0 &{} 2i\omega _0+\beta \\ \end{array} \right) ,\\ \Delta _{13}= & {} 2\det \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 2i\omega _0+1 &{} 0 &{} H_1 &{} 0 &{} -b\text{ sech }^2(v^*) &{} -b\text{ sech }^2(w^*) \\ 0 &{} 2i\omega _0+1 &{} H_2 &{} -b\text{ sech }^2(u^*) &{} 0 &{} 0 \\ 0 &{} 0 &{} H_3 &{} -b\text{ sech }^2(u^*) &{}0 &{} 0 \\ -\beta {e}^{i\omega _0\tilde{\tau }_1} &{} 0 &{} 0&{} 2i\omega _0+\beta &{} 0 &{} 0 \\ 0 &{} -\beta {e}^{i\omega _0\tilde{\tau }_1} &{} 0 &{} 0 &{} 2i\omega _0+\beta &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 2i\omega _0+\beta \\ \end{array} \right) ,\\ \Delta _{14}= & {} 2\det \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 2i\omega _0+1 &{} 0 &{} 0 &{} H_1 &{} -b\text{ sech }^2(v^*) &{} -b\text{ sech }^2(w^*) \\ 0 &{} 2i\omega _0+1 &{} 0 &{} H_2 &{} 0 &{} 0 \\ 0 &{} 0 &{} 2i\omega _0+1 &{} H_3 &{}0 &{} 0 \\ -\beta {e}^{i\omega _0\tilde{\tau }_1} &{} 0 &{} 0&{} 0 &{} 0 &{} 0 \\ 0 &{} -\beta {e}^{i\omega _0\tilde{\tau }_1} &{} 0 &{} 0 &{} 2i\omega _0+\beta &{} 0 \\ 0 &{} 0 &{} -\beta {e}^{i\omega _0\tilde{\tau }_1} &{} 0 &{} 0 &{} 2i\omega _0+\beta \\ \end{array} \right) ,\\ \Delta _{15}= & {} 2\det \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 2i\omega _0+1 &{} 0 &{} 0 &{} 0 &{} H_1 &{} -b\text{ sech }^2(w^*) \\ 0 &{} 2i\omega _0+1 &{} 0 &{} -b\text{ sech }^2(u^*) &{} H_2 &{} 0 \\ 0 &{} 0 &{} 2i\omega _0+1 &{} -b\text{ sech }^2(u^*) &{}0 &{} 0 \\ -\beta {e}^{i\omega _0\tilde{\tau }_1} &{} 0 &{} 0&{} 2i\omega _0+\beta &{} H_3 &{} 0 \\ 0 &{} -\beta {e}^{i\omega _0\tilde{\tau }_1} &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} -\beta {e}^{i\omega _0\tilde{\tau }_1} &{} 0 &{} 0 &{} 2i\omega _0+\beta \\ \end{array} \right) ,\\ \Delta _{16}= & {} 2\det \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 2i\omega _0+1 &{} 0 &{} 0 &{} 0 &{} -b\text{ sech }^2(v^*) &{} H_1 \\ 0 &{} 2i\omega _0+1 &{} 0 &{} -b\text{ sech }^2(u^*) &{} 0 &{} H_2 \\ 0 &{} 0 &{} 2i\omega _0+1 &{} -b\text{ sech }^2(u^*) &{}0 &{} H_3 \\ -\beta {e}^{i\omega _0\tilde{\tau }_1} &{} 0 &{} 0&{} 2i\omega _0+\beta &{} 0 &{} 0 \\ 0 &{} -\beta {e}^{i\omega _0\tilde{\tau }_1} &{} 0 &{} 0 &{} 2i\omega _0+\beta &{} 0 \\ 0 &{} 0 &{} -\beta {e}^{i\omega _0\tilde{\tau }_1} &{} 0 &{} 0 &{} 0\\ \end{array} \right) . \end{aligned}$$

Similarly, substituting (3.32) and (3.37) into (3.35), we have

$$\begin{aligned} \left( \int _{-\tilde{\tau }_2}^0 d\eta (\theta )\right) E_2=2(-P_1, -P_2, -P_3, 0, 0, 0)^T. \end{aligned}$$
(3.43)

That is

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} -1 &{} 0 &{} 0 &{} 0 &{} b\text{ sech }^2(v^*)&{} b\text{ sech }^2(w^*) \\ 0 &{} -1 &{} 0 &{} a\text{ sech }^2(u^*)&{} 0 &{} 0\\ 0 &{} 0 &{} -1 &{} a\text{ sech }^2(u^*) &{} 0 &{} 0 \\ \beta &{} 0 &{} 0&{} 0 &{} 0 &{} 0 \\ 0 &{} \beta &{} 0 &{} 0 &{} 0&{} 0 \\ 0 &{} 0 &{} \beta &{} 0 &{} 0 &{} 0 \\ \end{array} \right) \left( \begin{array}{c} E_2^{(1)} \\ E_2^{(2)} \\ E_2^{(3)} \\ E_2^{(4)} \\ E_2^{(5)} \\ E_2^{(6)} \\ \end{array} \right) =2\left( \begin{array}{c} -P_1 \\ -P_2 \\ -P_3 \\ 0 \\ 0 \\ 0 \\ \end{array} \right) .\nonumber \\ \end{aligned}$$
(3.44)

Hence,

$$\begin{aligned} E_2^{(1)}=\frac{\Delta _{21}}{\Delta _2},\,E_2^{(2)}=\frac{\Delta _{22}}{\Delta _2},\, E_2^{(3)}=\frac{\Delta _{23}}{\Delta _2},\,E_2^{(4)}=\frac{\Delta _{24}}{\Delta _2},\,E_2^{(5)}=\frac{\Delta _{25}}{\Delta _2},\, E_2^{(6)}=\frac{\Delta _{26}}{\Delta _2},\nonumber \\ \end{aligned}$$
(3.45)

where

$$\begin{aligned} \Delta _2= & {} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} -1 &{} 0 &{} 0 &{} 0 &{} b\text{ sech }^2(v^*)&{} b\text{ sech }^2(w^*) \\ 0 &{} -1 &{} 0 &{} a\text{ sech }^2(u^*)&{} 0 &{} 0\\ 0 &{} 0 &{} -1 &{} a\text{ sech }^2(u^*) &{} 0 &{} 0 \\ \beta &{} 0 &{} 0&{} 0 &{} 0 &{} 0 \\ 0 &{} \beta &{} 0 &{} 0 &{} 0&{} 0 \\ 0 &{} 0 &{} \beta &{} 0 &{} 0 &{} 0 \\ \end{array} \right) ,\\ \Delta _{21}= & {} 2\det \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} -P_1 &{} 0 &{} 0 &{} 0 &{} b\text{ sech }^2(v^*)&{} b\text{ sech }^2(w^*) \\ -P_2 &{} -1 &{} 0 &{} a\text{ sech }^2(u^*)&{} 0 &{} 0\\ -P_3 &{} 0 &{} -1 &{} a\text{ sech }^2(u^*) &{} 0 &{} 0 \\ 0 &{} 0 &{} 0&{} 0 &{} 0 &{} 0 \\ 0 &{} \beta &{} 0 &{} 0 &{} 0&{} 0 \\ 0 &{} 0 &{} \beta &{} 0 &{} 0 &{} 0 \\ \end{array} \right) =0,\\ \Delta _{22}= & {} 2\det \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} -1 &{} -P_1 &{} 0 &{} 0 &{} b\text{ sech }^2(v^*)&{} b\text{ sech }^2(w^*) \\ 0 &{} -P_2 &{} 0 &{} a\text{ sech }^2(u^*)&{} 0 &{} 0\\ 0 &{} -P_3 &{} -1 &{} a\text{ sech }^2(u^*) &{} 0 &{} 0 \\ \beta &{} 0 &{} 0&{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0&{} 0 \\ 0 &{} 0 &{} \beta &{} 0 &{} 0 &{} 0 \\ \end{array} \right) =0,\\ \Delta _{23}= & {} 2\det \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} -1 &{} 0 &{} -P_1 &{} 0 &{} b\text{ sech }^2(v^*)&{} b\text{ sech }^2(w^*) \\ 0 &{} -1 &{} -P_2 &{} a\text{ sech }^2(u^*)&{} 0 &{} 0\\ 0 &{} 0 &{} -P_3 &{} a\text{ sech }^2(u^*) &{} 0 &{} 0 \\ \beta &{} 0 &{} 0&{} 0 &{} 0 &{} 0 \\ 0 &{} \beta &{} 0 &{} 0 &{} 0&{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right) ,\\ \Delta _{24}= & {} 2\det \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} -1 &{} 0 &{} 0 &{} -P_1 &{} b\text{ sech }^2(v^*)&{} b\text{ sech }^2(w^*) \\ 0 &{} -1 &{} 0 &{} -P_2&{} 0 &{} 0\\ 0 &{} 0 &{} -1 &{} -P_3 &{} 0 &{} 0 \\ \beta &{} 0 &{} 0&{} 0 &{} 0 &{} 0 \\ 0 &{} \beta &{} 0 &{} 0 &{} 0&{} 0 \\ 0 &{} 0 &{} \beta &{} 0 &{} 0 &{} 0 \\ \end{array} \right) ,\\ \Delta _{25}= & {} 2\det \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} -1 &{} 0 &{} 0 &{} 0 &{} -P_1&{} b\text{ sech }^2(w^*) \\ 0 &{} -1 &{} 0 &{} a\text{ sech }^2(u^*)&{} -P_2 &{} 0\\ 0 &{} 0 &{} -1 &{} a\text{ sech }^2(u^*) &{} -P_3 &{} 0 \\ \beta &{} 0 &{} 0&{} 0 &{} 0 &{} 0 \\ 0 &{} \beta &{} 0 &{} 0 &{} 0&{} 0 \\ 0 &{} 0 &{} \beta &{} 0 &{} 0 &{} 0 \\ \end{array} \right) ,\\ \Delta _{26}= & {} 2\det \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} -1 &{} 0 &{} 0 &{} 0 &{} b\text{ sech }^2(v^*)&{} -P_1 \\ 0 &{} -1 &{} 0 &{} a\text{ sech }^2(u^*)&{} 0 &{} -P_2\\ 0 &{} 0 &{} -1 &{} a\text{ sech }^2(u^*) &{} 0 &{}-P_3 \\ \beta &{} 0 &{} 0&{} 0 &{} 0 &{} 0 \\ 0 &{} \beta &{} 0 &{} 0 &{} 0&{} 0 \\ 0 &{} 0 &{} \beta &{} 0 &{} 0 &{} 0 \\ \end{array} \right) . \end{aligned}$$

From (3.31), (3.33), (3.42), (3.45), we can calculate \(g_{21}\) and derive the following values:

$$\begin{aligned} c_1(0)= & {} \frac{i}{2\omega _0}\left( g_{20}g_{11}-2|g_{11}|^2-\frac{|g_{02}|^2}{3}\right) +\frac{g_{21}}{2},\\ \mu _2= & {} -\frac{\text{ Re } \{c_1(0)\}}{\text{ Re }\{\lambda ^{'}(\tau _0)\} },\\ \beta _2= & {} 2\text{ Re }{(c_1(0))},\\ T_2= & {} -\frac{\text{ Im }{\{c_1(0)\}}+\mu _2Im\{\lambda ^{'}(\tau _0)\}}{\omega _0}. \end{aligned}$$

These formulaes give a description of the Hopf bifurcation periodic solutions of (2.3) at \(\tau =\tau _0\) on the center manifold. From the discussion above, we have the following result: \(\square \)

Theorem 3.3

For system (2.3), if (H1)–(H4) hold, the periodic solution is supercritical (subcritical) if \(\mu _2>0\) (\(\mu _2<0\)); The bifurcating periodic solutions are orbitally asymptotically stable with asymptotical phase (unstable) if \(\beta _2<0\) (\(\beta _2>0\)); The periods of the bifurcating periodic solutions increase (decrease) if \(T_2>0\) (\(T_2<0\)).

Remark 3.1

In [44], authors considered the stability switches and bifurcation for a neural networks with continuous delay and strong kernel by regarding the mean time delay as bifurcation parameter. In [45], authors discussed the delay-dependent asymptotic stability for neural networks with distributed delays by employing suitable Lyapunov functionals and delay-dependent criteria. In [46], authors analyzed bifurcation behavior for a two-neuron system with distributed delays by applying frequency domain method. All the analysis methods above are different from those in this paper. Thus our work complements the previous studies.

4 Numerical Examples

To illustrate the analytical results, we consider the following special case of system (2.3).

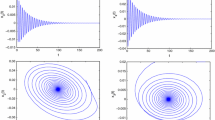
$$\begin{aligned} \left\{ \begin{array}{lc} \displaystyle \frac{dx_1}{dt}=-x_1(t)+0.5\tanh [x_5(t)]+0.5\tanh [x_6(t)],\\ \displaystyle \frac{dx_2}{dt}=-x_2(t)+3\tanh [x_4(t)],\\ \displaystyle \frac{dx_3}{dt}=-x_3(t)+3\tanh [x_4(t)],\\ \displaystyle \frac{dx_4}{dt}=0.5[x_1(t-\tau _1)-x_4(t)],\\ \displaystyle \frac{dx_5}{dt}=0.5[x_2(t-\tau _2)-x_5(t)],\\ \displaystyle \frac{dx_6}{dt}=0.5[x_3(t-\tau _2)-x_6(t)], \end{array}\right. \end{aligned}$$
(4.1)

which has a unique steady state E(0, 0, 0, 0, 0, 0). By means of Matlab 7.0, we obtain \(\omega _0 \approx 0.9059, \tau _0\approx 0.6002, \lambda ^{'}(0) \approx 3.4023-2.6576i\). Thus we can compute these values as follows: \(c_1(0)\approx -4.1128-16 5.5123i, \mu _2 \approx 2.0213> 0, \beta _2\approx -8.2256<0, T_2\approx 16.4719\). Then all the conditions indicated in Theorem 2.2 hold true. From Theorem 2.1, we know that the zero steady state of system (4.1) is asymptotically stable when \(\tau _1+\tau _2 \in [0, 0.6)\) which is illustrated by the numerical simulations shown in Figs. 1, 2 and 3 in which \(\tau _1 = 0.3\) and \(\tau _2 = 0.2\). When \(\tau _1+\tau _2\) is increased to the critical value 0.6, the equilibrium E(0, 0, 0, 0, 0, 0) loses its stability and a Hopf bifurcation occurs. Since \(\mu _2 > 0\) and \(\beta _2 < 0\) it follows from Theorem 3.3 that the Hopf bifurcation is supercritical and bifurcating periodic solution is asymptotically stable which is depicted in Figs. 4, 5 and 6.

Fig. 1
figure 1

Dynamic behavior of system (4.1): times series of \(x_i(i = 1, 2, 3, 4, 5, 6)\). A Matlab simulation of the asymptotically stable origin to system (4.1) with \(\tau \approx 0.6002\). The initial value is (0.1, 0.1, 0.1, 0.1, 0.1, 0.1)

Full size image
Fig. 2
figure 2figure 2

Dynamic behavior of system (4.1): projection on \(x_1-x_2, x_1-x_3, x_1-x_4, x_1-x_5, x_1-x_6, x_2-x_5, x_2-x_6, x_3-x_4, x_3-x_5, x_3-x_6, x_4-x_5, x_4-x_6\) plane, respectively. A Matlab simulation of the asymptotically stable origin to system (4.1) with \(\tau _1=0.3, \tau _2=0.2\) and \(\tau _1 + \tau _2 = \tau = 0.5 < \tau _0\approx 0.6002\). The initial value is (0.1, 0.1, 0.1, 0.1, 0.1, 0.1)

Full size image
Fig. 3
figure 3figure 3

Dynamic behavior of system (4.1): projection on \(x_1-x_2-x_3, x_1-x_2-x_5, x_1-x_2-x_6, x_1-x_3-x_5, x_1-x_3-x_6, x_1-x_4-x_5, x_1-x_4-x_6, x_2-x_4-x_5, x_2-x_4-x_6, x_2-x_5-x_6, x_3-x_5-x_6, x_4-x_5-x_6\) space, respectively. A Matlab simulation of the asymptotically stable origin to system (4.1) with \(\tau _1=0.3, \tau _2=0.2\) and \(\tau _1 + \tau _2 = \tau = 0.5 < \tau _0\approx 0.6002\). The initial value is (0.1, 0.1, 0.1, 0.1, 0.1, 0.1)

Full size image
Fig. 4
figure 4

Dynamic behavior of system (4.1): times series of \(x_i(i = 1, 2, 3, 4, 5, 6)\). A Matlab simulation of the Hopf bifurcation of system (4.1) with \(\tau _1 = 0.8, \tau _2 = 0.3\) and \(\tau _1 + \tau _2 = \tau = 1.1>\tau _0 \approx 0.6002\). The initial value is (0.1, 0.1, 0.1, 0.1, 0.1, 0.1)

Full size image
Fig. 5
figure 5figure 5

Dynamic behavior of system (4.1): projection on \(x_1-x_2-x_3, x_1-x_2-x_5, x_1-x_2-x_6, x_1-x_3-x_5, x_1-x_3-x_6, x_1-x_4-x_5, x_1-x_4-x_6, x_2-x_4-x_5, x_2-x_4-x_6, x_2-x_5-x_6, x_3-x_5-x_6, x_4-x_5-x_6\) space, respectively. A Matlab simulation of the Hopf bifurcation of system (4.1) with \(\tau _1=0.8, \tau _2=0.3\) and \(\tau _1 + \tau _2 = \tau = 1.1 > \tau _0\approx 0.6002\). The initial value is (0.1, 0.1, 0.1, 0.1, 0.1, 0.1)

Full size image
Fig. 6
figure 6figure 6

Dynamic behavior of system (4.1): projection on \(x_1-x_2-x_3, x_1-x_2-x_5, x_1-x_2-x_6, x_1-x_3-x_5, x_1-x_3-x_6, x_1-x_4-x_5, x_1-x_4-x_6, x_2-x_4-x_5, x_2-x_4-x_6, x_2-x_5-x_6, x_3-x_5-x_6, x_4-x_5-x_6\) space, respectively. A Matlab simulation of the Hopf bifurcation of system (4.1) with \(\tau _1=0.8, \tau _2=0.3\) and \(\tau _1 + \tau _2 = \tau = 1.1 > \tau _0\approx 0.6002\). The initial value is (0.1, 0.1, 0.1, 0.1, 0.1, 0.1)

Full size image

5 Conclusions

In this paper, we have investigated three-neuron artificial neural network model with distributed delays. Using Hopf bifurcation theory and numerical method of functional differential equation, we have analyzed the local stability of the equilibrium \(E(x_1^*, x_2^*, x_3^*, x_4^*, x_5^*, x_6^*)\) and oscillatory behavior of the system. We have showed that if some suitable conditions hold and \(\tau \in [0, \tau _0)\), then the equilibrium \(E(x_1^*, x_2^*, x_3^*, x_4^*, x_5^*, x_6^*)\) of system (2.3) is asymptotically stable and unstable when \(\tau >\tau _0\). It is also showed that if some other suitable conditions are fulfilled and when the delay \(\tau \) increases, the equilibrium loses its stability and a sequence of Hopf bifurcations occur around \(E(x_1^*, x_2^*, x_3^*, x_4^*, x_5^*, x_6^*)\), i.e., a family of periodic orbits bifurcate from the equilibrium \(E(x_1^*, x_2^*, x_3^*, x_4^*, x_5^*, x_6^*)\). In addition, explicit algorithm for determining the direction of Hopf bifurcation and the stability of the bifurcating periodic orbits are derived by applying the normal form theory and the center manifold theorem. Numerical simulation results are agreeable with the theoretical findings. In addition, we would like to point out that system (2.3) is obtained using the weak kernel. If we use the general kernel, then it is difficult for us to simplify system (1.4) by the similar variable changes (see (2.1)), then our results obtained in this paper would not hold true. We leave this topic for future work.