1 Introduction

Time delay is ubiquitous due to finite propagation speeds of signals, reaction times, and processing times in various natural systems such as biological systems [1], neural activity [2,3,4], mechanical systems [5], and so on. Marcus and Westervelt [6] pointed out that time delay has a qualitative impact on neural dynamics, even for a tiny time delay that destabilizes systems. Time delay is also an effective tool to adjust the stability of the system and secure communication [7,8,9]. Even if the delay does not affect the asymptotic behavior of the system, it can influence the boundary of the basin of attraction of the stable equilibria [10]. So the effects of time delay are not ignored on dynamics. Recently, some researchers have introduced different [11,12,13,14,15] or more time delays [16,17,18,19,20,21] into various types of neural system models because the communications may be inconsistent among different neurons. It is more realistic and meaningful to consider different time delays in artificial neural networks.

It is well known that mode interactions are very important in the analysis of multi-parameter nonlinear autonomous differential equations. A vital mode interaction is double Hopf singularity, which is characterized by the coexistence of two periodic modes of the linearized differential equations for a certain point in two parameter spaces. Note that double Hopf bifurcations in nonlinear autonomous differential equations have been widely discussed [22,23,24,25,26,27,28]. The bifurcation dynamics of neural networks play an important role in cognitive calculation [15, 29, 30]. Until now, in the existing relative literatures, very few results on the exploration on double Hopf bifurcation mechanism of multi-delay neural network models, which, however, is meaningful and challenging since it is hard to analyze the transcendental characteristic equation with multiple time delays. Hence, some investigation of the mechanism of complex dynamics near double Hopf bifurcation is of great necessity and interest for multi-delayed neural systems.

In 2000, Shayer and Campbell [31] considered the Hopf-Hopf interaction occurring in a two-neuron neural system with multiple delays

$$ \left\{ \begin{gathered} \frac{dx_1 \left( t \right)}{{dt}} = - kx_1 \left( t \right) + af\left( {x_1 \left( {t - s} \right)} \right) + J_{12} f\left( {x_2 \left( {t - \tau_{12} } \right)} \right), \hfill \\ \frac{dx_2 \left( t \right)}{{dt}} = - kx_2 \left( t \right) + af\left( {x_2 \left( {t - s} \right)} \right) + J_{21} f\left( {x_1 \left( {t - \tau_{21} } \right)} \right), \hfill \\ \end{gathered} \right. $$

with the initial function

$$ \begin{gathered} x_1 \left( t \right) = \phi _1 \left( t \right),\;x_2 \left( t \right) = \phi _2 \left( t \right), \hfill \\ t \in \left[ { - \tau _{\max } ,0} \right],\;\tau _{\max } = \max \left\{ {\tau _{12} ,\tau _{21} ,s} \right\} \hfill \\ \end{gathered} $$

by providing numerical simulations, and did not make some bifurcation analysis in the neighbor of double Hopf bifurcation point. Afterwards, Huang et al. studied Hopf bifurcation with the relation \(\tau_{12} + \tau_{21} = 2s\) [32] (i.e., the original system with three delays was transformed into the system with one single time delay). Song et al. analyzed the non-resonant double Hopf bifurcation of the network by applying normal form technique and center manifold method (CMR) [33]. Ma studied the weak resonant double Hopf bifurcation induced by self-connection delay \(s\) and \(k\) with the assumption on coupled weights \(J_{12} J_{21} < 0\) by means of the CMR [34]. We previously have studied the occurrence of a pitchfork-Hopf interaction about the trivial equilibrium point with the identical coupled delays \(\tau_{12} = \tau_{21}\) by performing the perturbation scheme due to its less computation and ease of application [35].

Motivated by the above facts, here we are interested in dealing with double Hopf bifurcations of weak resonance and harmonic analytical solutions without using the CMR. So we consider a multi-delayed model consisting of two coupled neurons including the above mentioned model [31,32,33,34,35], which is described by

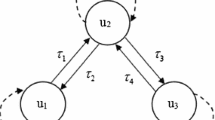
$$ \left\{ \begin{gathered} \frac{dx_1 \left( t \right)}{{dt}} = - k_1 x_1 \left( t \right) + af\left( {x_1 \left( {t - s} \right)} \right) + J_{12} f\left( {x_2 \left( {t - \tau_{12} } \right)} \right), \hfill \\ \frac{dx_2 \left( t \right)}{{dt}} = - k_2 x_2 \left( t \right) + af\left( {x_2 \left( {t - s} \right)} \right) + J_{21} f\left( {x_1 \left( {t - \tau_{21} } \right)} \right), \hfill \\ \end{gathered} \right. $$
(1)

where \(x_j\)\(\left( {j = 1,2} \right)\) represents the voltage of the \(jth\) neuron, the real constants \(k_1\) and \(k_2\) denote the rate with which the neuron resets its potential to the resting state in isolation when disconnected from the network and external inputs; \(a\) denotes the feedback weight; \(J_{12}\) and \(J_{21}\) represent the coupled connection weights; \(s\) is the self- connection delay between one neuron from itself; \(\tau_{12}\) and \(\tau_{21}\) are the signal transmission delays between two coupled neurons; the activation function is chosen as \(f\left( x \right) =\) \(\tanh \left( x \right)\). For the network (1) to make sense physically, \(k_1\),\(k_2\),\(s\),\(\tau_{12}\), and \(\tau_{21}\) should be nonnegative, but the connection weight \(a\),\(J_{12}\) and \(J_{21}\) are unrestricted. The topological connection of the neural network is shown in Fig. 1.

Fig. 1
figure 1

Graph of architecture for two coupled neuron systems with three delays (1)

Full size image

The main contributions in this paper can be summarized as follows.

  1. (1)

    Without any restriction on time delays and system parameters, system (1) is more general and includes the ones in the already literatures [31,32,33,34,35].

  2. (2)

    Not only are three communication delays discussed, but the system (1) is not transformed into a system with a single delay like the traditional way. Compared with the case of a single delay, the direct discussion of multiple delays is more realistic and challenging.

  3. (3)

    Selecting self-connection weight and coupling delay as bifurcation parameters, we mainly concentrate on stability and double Hopf bifurcation of weak resonance, which differs from the previous literature [31,32,33,34,35].

  4. (4)

    The mechanisms of complex dynamics in the vicinity of the weak resonant point are derived by extending the perturbation scheme. The search for the explicit periodic solution is converted to the problem of solving four algebraic equations. The advantage of the perturbation scheme lies in its simplicity and ease of application.

The rest of this paper is organized as follows. In Sect. 2, the existence of resonant double Hopf singularity is obtained by analyzing the corresponding linearization system. Section 3 presents a clear procedure for investigating the double Hopf bifurcation of weak resonance via the perturbation scheme in a general multi-delayed nonlinear differential system. In Sect. 4, employing the perturbation scheme, the classification and bifurcation sets of double Hopf bifurcation of weak resonance are displayed for the system (1). Section 5 contains some numerical examples to verify the theoretical analysis. Finally, conclusions are made in Sect. 6.

2 Existence of double Hopf bifurcation of weak resonance

When the system has only a pair of purely imaginary eigenvalues, system dynamics change from a static stable state to a periodic oscillation or vice versa. The dynamics become quite complicated when the system has two pairs of purely imaginary eigenvalues, which may give rise to double Hopf bifurcations. Here we concentrate on the dynamic stability of the trivial equilibrium to find double Hopf bifurcations at a critical value of time delay by employing Hopf bifurcation. So we let \({\mathop \prod \nolimits_{i = 1}^2} \left( {a - k_i } \right) \ne J_{12} J_{21}\) and \(\lambda = 0\) is not the root of the characteristic equation in the present paper.

The linearization of the system (1) about the origin of the state space is

$$ \left\{ \begin{gathered} \frac{dx_1 \left( t \right)}{{dt}} = - k_1 x_1 \left( t \right) + ax_1 \left( {t - s} \right) + J_{12} x_2 \left( {t - \tau_{12} } \right), \hfill \\ \frac{dx_2 \left( t \right)}{{dt}} = - k_2 x_2 \left( t \right) + ax_2 \left( {t - s} \right) + J_{21} x_1 \left( {t - \tau_{21} } \right). \hfill \\ \end{gathered} \right. $$
(2)

The associated characteristic equation of system (2) is expressed as follows.

\(\left| {\begin{array}{*{20}c} {\lambda + k_1 - a{\text{e}}^{ - \lambda s} } & { - J_{12} {\text{e}}^{ - \lambda \tau_{12} } } \\ { - J_{21} {\text{e}}^{ - \lambda \tau_{21} } } & {\lambda + k_2 - a{\text{e}}^{ - \lambda s} } \\ \end{array} } \right| = 0\), which produces

$$ \left( {\lambda + k_1 - a{\text{e}}^{ - \lambda s} } \right)\left( {\lambda + k_2 - a{\text{e}}^{ - \lambda s} } \right) - J_{12} J_{21} {\text{e}}^{ - 2\lambda \left( {\tau_{21} + \tau_{12} } \right)} = 0. $$

That is,

$$ \begin{gathered} \lambda^2 + \lambda \left( {k_1 + k_2 - 2a{\text{e}}^{ - s\lambda } } \right) + k_1 k_2 + a^2 {\text{e}}^{ - 2s\lambda } \hfill \\ - a{\text{e}}^{ - s\lambda } \left( {k_1 + k_2 } \right) - {\text{e}}^{ - 2\lambda \tau } J_{12} J_{21} = 0. \hfill \\ \end{gathered} $$
(3)

where \(\tau_{12} + \tau_{21} = 2\tau\).

Due to the influences of two delays, the discussion on the stability of the trivial equilibrium is very complicated. We firstly discuss the case of \(s = \tau = 0\), then the case of \(s = 0\) and \(\tau > 0\) with a single delay, and finally the case of \(s > 0\) and \(\tau > 0\). Time delay-induced double Hopf bifurcations are found at some critical values as follows.

Case 1

\(s = \tau = 0\).

When the neural system (1) has no time delay, i.e.,\(s = \tau_{12}\) \(= \tau_{21} = 0\), Eq. (3) is simplified to

$$ \lambda^2 + \lambda \left( {k_1 + k_2 - 2a} \right) + \left( {\left( {a - k_1 } \right)\left( {a - k_2 } \right) - J_{12} J_{21} } \right) = 0 $$
(4)

It is obvious that two roots of Eq. (4) have negative real parts if and only if the following conditions hold.

$$ \begin{gathered} \, k_1 + k_2 - 2a > 0, \hfill \\ \left( {a - k_1 } \right)\left( {a - k_2 } \right) - J_{12} J_{21} > 0. \hfill \\ \end{gathered} $$
(5)

Lemma 1

When the system (1) is absent of time delay, i.e.,\(s = \tau_{12} = \tau_{21} = 0\), the trivial equilibrium point is locally asymptotically stable if the conditions (5) are satisfied. Otherwise, the trivial equilibrium point is unstable.

With a single delay increasing, the trivial equilibrium point may change from a static stable state to a periodic oscillation or vice versa. Here we concentrate on considering the impacts of coupling delay \(\tau\) on the dynamics of the system (1).

Case 2

\(s = 0\) and \(\tau > 0\).

If \(\tau_{12} + \tau_{21} = 2\tau > 0\), then one or two of coupled delays is nonzero, i.e., \(\tau_{12} > 0\) or \(\tau_{21} > 0\). Accordingly, the characteristic Eq. (3) with \(s = 0\) becomes

$$ \begin{gathered} \lambda^2 + \lambda \left( {k_1 + k_2 - 2a} \right) \hfill \\ + \left( {\left( {a - k_1 } \right)\left( {a - k_2 } \right) - {\text{e}}^{ - 2\lambda \tau } J_{12} J_{21} } \right) = 0 \hfill \\ \end{gathered} $$
(6)

Substituting \(\lambda = i\nu\) into Eq. (6) and separating the real and imaginary parts, one haswhich produces

$$ \left\{ \begin{gathered} a^2 - \nu^2 - ak_2 - ak_2 + k_1 k_2 = \cos \left[ {2\tau \nu } \right]J_{12} J_{21} , \hfill \\ \nu \left( {2a - k_1 - k_2 } \right) = \sin \left[ {2\tau \nu } \right]J_{12} J_{21} , \hfill \\ \end{gathered} \right. $$
$$ \begin{gathered} \cos \left[ {2\tau \nu } \right] = \frac{a^2 - \nu^2 - ak_1 - ak_2 + k_1 k_2 }{{J_{12} J_{21} }}, \hfill \\ \sin \left[ {2\tau \nu } \right] = \frac{{\nu \left( {2a - k_1 - k_2 } \right)}}{{J_{12} J_{21} }}. \hfill \\ \end{gathered} $$
(7)

Squaring and adding both equations of Eq. (7) leads to the following equation on \(\nu\)

$$ \begin{gathered} \nu^4 + \nu^2 \left( {\left( {a - k_1 } \right)^2 + \left( {a - k_2 } \right)^2 } \right) \hfill \\ \quad+ \left( {a - k_1 } \right)^2 \left( {a - k_2 } \right)^2 - J_{12}^2 J_{21}^2 = 0. \hfill \\ \end{gathered} $$
(8)

It is no difficulty to obtain that there exists only a positive real root in Eq. (8).

\(\nu = \sqrt {{\frac{{ - \left( {a - k_1 } \right)^2 - \left( {a - k_2 } \right)^2 + \sqrt {\Delta } }}{2}}}\), if \(\left( {a - k_1 } \right)^2 \left( {a - k_2 } \right)^2 < J_{12}^2 J_{21}^2\) where

\(\Delta = 4J_{12}^2 J_{21}^2 + \left( {k_1 - k_2 } \right)^2 \left( { - 2a + k_1 + k_2 } \right)^2 > 0\).

Otherwise, Eq. (8) has no positive real root. The following result is obtained.

Lemma 2

When \(s = 0\) and \(\tau > 0\), the neural system (1) has only a pair of purely imaginary eigenvalues if the condition \(\left( {a - k_1 } \right)^2 \left( {a - k_2 } \right)^2 < J_{12}^2 J_{21}^2\). Otherwise, the system (1) has no purely imaginary eigenvalue.

Based on Lemma 2, it is necessary to discuss two delays to make system (1) have two pairs of purely imaginary eigenvalues, which may give rise to double Hopf bifurcations.

Case 3

\(s > 0\) and \(\tau > 0\).

Substituting the simple eigenvalue \(\lambda = i\omega\) \(\left( {\omega > 0} \right)\) into Eq. (3), one can obtain the following equations

$$ \begin{gathered} \cos \left[ {2\tau \omega } \right] = \frac{{ - \omega^2 + a^2 \cos \left[ {2s\omega } \right] - 2a\omega \sin \left[ {s\omega } \right]}}{{J_{12} J_{21} }} - \hfill \\ \, \frac{{a\cos \left[ {s\omega } \right]k_1 + a\cos \left[ {s\omega } \right]k_2 - k_1 k_2 }}{{J_{12} J_{21} }}, \hfill \\ \sin \left[ {2\tau \omega } \right] = \frac{{\left( {\omega + a\sin \left[ {s\omega } \right]} \right)\left( {2a\cos \left[ {s\omega } \right] - k_1 - k_2 } \right)}}{{J_{12} J_{21} }}. \hfill \\ \end{gathered} $$
(9)

Based on \(\cos^2 \left[ {2\tau \omega } \right] + \sin^2 \left[ {2\tau \omega } \right] = 1\), one can obtain the equation on \(\omega\) as follows.

$$ H\left( \omega \right) = \omega^4 + B_3 \omega^3 + B_2 \omega^2 + B_1 \omega + B_0 = 0, $$
(10)

where

$$ \begin{gathered} B_0 = a^4 \cos \left[ {2s\omega } \right]^2 - J_{12}^2 J_{21}^2 - 2a^3 \cos \left[ {s\omega } \right]\cos \left[ {2s\omega } \right]k_1 \hfill \\ \, + a^2 \cos \left[ {s\omega } \right]^2 k_1^2 - 2a^3 \cos \left[ {s\omega } \right]\cos \left[ {2s\omega } \right]k_2 \hfill \\ \, + 2a^2 \cos \left[ {s\omega } \right]^2 k_1 k_2 + 2a^2 \cos \left[ {2s\omega } \right]k_1 k_2 \hfill \\ \, - 2a\cos \left[ {s\omega } \right]k_1^2 k_2 + a^2 \cos \left[ {s\omega } \right]^2 k_2^2 \hfill \\ \, + a^2 \sin \left[ {s\omega } \right]^2 \left( {2a\cos \left[ {s\omega } \right] - k_1 - k_2 } \right)^2 \, \hfill \\ \, - 2a\cos \left[ {s\omega } \right]k_1 k_2^2 + k_1^2 k_2^2 , \hfill \\ \end{gathered} $$
$$ \begin{gathered} B_1 = - 4a^3 \cos \left[ {2s\omega } \right]\sin \left[ {s\omega } \right] + 4a^2 \cos \left[ {s\omega } \right]\sin \left[ {s\omega } \right]k_1 \hfill \\ \, + 2a\sin \left[ {s\omega } \right]\left( {2a\cos \left[ {s\omega } \right] - k_1 - k_2 } \right)^2 \hfill \\ \, + 4a^2 \cos \left[ {s\omega } \right]\sin \left[ {s\omega } \right]k_2 - 4a\sin \left[ {s\omega } \right]k_1 k_2 , \hfill \\ \end{gathered} $$
$$ \begin{gathered} B_2 = - 2a^2 \cos \left[ {2s\omega } \right] + 4a^2 \sin \left[ {s\omega } \right]^2 + 2a\cos \left[ {s\omega } \right]k_1 \hfill \\ \, + \left( {2a\cos \left[ {s\omega } \right] - k_1 - k_2 } \right)^2 + 2a\cos \left[ {s\omega } \right]k_2 - 2k_1 k_2 , \hfill \\ \end{gathered} $$
$$ B_3 = 4a\sin \left[ {s\omega } \right]. $$

If Eq. (10) has positive and simple roots \(\omega_i\)\(\left( {i = 1,2, \cdots } \right)\), then the critical delay values are computed from Eq. (9)

$$ \tau_i^j = \frac{\varphi_i + 2j\pi }{{2\omega_i }}, \, i = 1,2, \cdots ; \, j = 0,1,2, \cdots , $$

where \(\varphi_i \left( { \in \left[ {0,2\pi } \right)} \right)\) satisfy

$$ \begin{gathered} \cos \varphi_i = \frac{{ - {\omega}_{i}^2 + a^2 \cos \left[ {2\omega_i s} \right] - 2a\omega \sin \left[ {\omega_i s} \right]}}{{J_{12} J_{21} }} - \hfill \\ \, \frac{{a\cos \left[ {\omega_i s} \right]k_1 + a\cos \left[ {\omega_i s} \right]k_2 - k_1 k_2 }}{{J_{12} J_{21} }}, \hfill \\ \sin \varphi_i = \frac{{\left( {{{\omega}_{i}} + a\sin \left[ {\omega_i s} \right]} \right)\left( {2a\cos \left[ {\omega_i s} \right] - k_1 - k_2 } \right)}}{{J_{12} J_{21} }}. \hfill \\ \end{gathered} $$

To make Hopf bifurcation occur, the transversality condition should be satisfied. So differentiating \(\lambda\) on \(\tau\) in Eq. (3), one gets

$$ \lambda^{\prime}\left( \tau \right) = $$
$$ - \frac{\tau }{\lambda } - \frac{{{\text{e}}^{2\lambda \left( { - s + \tau } \right)} \left( {as + {\text{e}}^{s\lambda } \left( {1 + 2\lambda } \right)} \right)\left( { - a + {\text{e}}^{s\lambda } \left( {1 + \lambda + \lambda^2 } \right)} \right)}}{{J_{12} J_{21} }}, $$

which leads to

$$ \left[ {{\text{Re}} \left( {\lambda^{\prime}\left( \tau \right)} \right)} \right]^{ - 1} \left| {_{\lambda = i\omega } } \right. = \frac{h_0 + \omega h_1 + \omega^2 h_2 + \omega^3 h_3 }{{2\omega J_{12}^2 J_{21}^2 }}, $$

where

$$ \begin{gathered} h_0 = \,2a^3 \sin \left[ {s\omega } \right] + a^3 s\sin \left[ {s\omega } \right]k_1 + a^3 s\sin \left[ {s\omega } \right]k_2 \hfill \\ \, + a\sin \left[ {s\omega } \right]k_2^2 + as\sin \left[ {s\omega } \right]k_1 k_2^2 \hfill \\ \, - a^2 \sin \left[ {2s\omega } \right]\left( {k_2 + k_1 \left( {1 + 2sk_2 } \right)} \right) \hfill \\ \, + a\sin \left[ {s\omega } \right]k_1^2 \left( {1 + sk_2 } \right), \hfill \\ \end{gathered} $$
$$ \begin{gathered} h_1 = \,2a^2 + 2a^3 s\cos \left[ {s\omega } \right] + 4a^2 \sin \left[ {s\omega } \right]^2 + k_1^2 + k_2^2 \hfill \\ \, + a\cos \left[ {s\omega } \right]\left( { - 2k_1 + sk_1^2 + k_2 \left( { - 2 + sk_2 } \right)} \right) \hfill \\ \, - 2a^2 s\cos \left[ {2s\omega } \right]\left( {k_1 + k_2 } \right), \hfill \\ \end{gathered} $$
$$ \begin{gathered} h_2 =\, 6a\sin \left[ {s\omega } \right] + 4a^2 s\cos \left[ {s\omega } \right]\sin \left[ {s\omega } \right] \hfill \\ \, + as\sin \left[ {s\omega } \right]\left( {k_1 + k_2 } \right), \hfill \\ \end{gathered} $$

\(h_3 = 2 + 2as\cos \left[ {s\omega } \right].\)

Noticing that

$$ {\text{s}} {\rm{ign}}\left\{ {{\text{Re}} \left( {\lambda^{\prime}\left( \tau \right)} \right)\left| {_{\lambda = i\omega } } \right.} \right\} = {\text{s}} {\rm{ign}}\left\{ {\left[ {{\text{Re}} \left( {\lambda^{\prime}\left( \tau \right)} \right)} \right]^{ - 1} \left| {_{\lambda = i\omega } } \right.} \right\}. $$

The dynamics become quite complex when the system has only two pairs of purely imaginary eigenvalues \(\lambda_1 = \pm i\omega_1\) and \(\lambda_2 = \pm i\omega_2\) \(\left( {0 < \omega_1 < \omega_2 } \right)\) at a critical value of coupling delay. Next, we only focus on such cases.

Remark 1

Two families of delay surfaces denoted by \(\tau_-\) and \(\tau_+\) corresponding to \(\omega_1\) and \(\omega_2\) respectively, can be computed by.

$$ \begin{gathered} \cos \left( {2\omega_1 \tau_- } \right) = \frac{{ - \omega_1^2 + a^2 \cos \left[ {2\omega_1 s} \right] - 2a\omega_1 \sin \left[ {\omega_1 s} \right]}}{{J_{12} J_{21} }} - \hfill \\ \, \frac{{a\cos \left[ {\omega_1 s} \right]k_1 + a\cos \left[ {\omega_1 s} \right]k_2 - k_1 k_2 }}{{J_{12} J_{21} }}, \hfill \\ \cos \left( {2\omega_2 \tau_+ } \right) = \frac{{ - \omega_2^2 + a^2 \cos \left[ {2\omega_2 s} \right] - 2a\omega_2 \sin \left[ {\omega_2 s} \right]}}{{J_{12} J_{21} }} - \hfill \\ \, \frac{{a\cos \left[ {\omega_2 s} \right]k_1 + a\cos \left[ {\omega_2 s} \right]k_2 - k_1 k_2 }}{{J_{12} J_{21} }}. \hfill \\ \end{gathered} $$
(11)

Then a possible double Hopf bifurcation point occurs when two such families of surfaces intersect each other where \(\tau_- = \tau_+\). If \(\frac{\omega_1 }{{\omega_2 }} = \frac{m_1 }{{m_2 }},\)\(m_1 < m_2 ,\)\(m_1 \ne 1,\)\(m_2 \ne 1,\)\(m_1 \in Z^+ ,\) \(m_2 \in Z^+\), then such bifurcation is named the double Hopf bifurcation of weak resonance. The corresponding critical value of time delay is given by

\(\tau_0 = \tau_- = \tau_+\),

which is determined by Eq. (11). So the following theorem is correct.

Theorem 3

If Eq. (10) has only two simple positive real roots \(\omega_1\) and \(\omega_2\) \(\left( {\omega_1 < \omega_2 } \right)\) satisfying the transversal conditions \({\text{Re}} \left( {\lambda^{\prime}\left( \tau \right)} \right)\left| {_{\lambda = i\omega_{1,2} ,\tau = \tau_0 } } \right. \ne 0\), then double Hopf bifurcations arises around the trivial equilibrium point at \(\tau = \tau_0\). Furthermore, if \(\frac{\omega_1 }{{\omega_2 }} = \frac{m_1 }{{m_2 }},\)\(m_1 < m_2 ,\)\(m_1 \ne 1,\)\(m_2 \ne 1,\) \(m_1 \in Z^+ ,\) \(m_2 \in Z^+\), then the double Hopf bifurcations of weak resonance produces at \(\tau = \tau_0\) in the system (1).

Remark 2

In this paper, not only are three communication delays discussed, but also the considered system (1) is not transformed into a system with a single delay like the traditional way. Moreover, without any restriction of time delays and system parameters, selecting the self-connection weight and coupling delay as two bifurcation parameters, we focus on the double Hopf bifurcation of weak resonance, which is different from the previously published results [31,32,33,34,35].

In the next, we mainly discuss the complicated behaviors near the weak resonant double Hopf bifurcation by extending the perturbation scheme [36] when self-connection weight and coupling delay as two bifurcation parameters. The methodology formulation firstly will be presented for reader’s convenience.

3 Double Hopf bifurcation via perturbation scheme (PS)

In [36], Xu et al. proposed a simple and efficient method called a perturbation-incremental scheme (PIS) to investigate weak resonant double Hopf bifurcation in a single delay nonlinear differential system. The scheme is described in two steps, namely, the perturbation step (noted as step one) for bifurcation parameters close to the bifurcation point and the incremental step (noted as step two) for those far away from the bifurcation point.

In this section, we only provide a clear program on step one of PIS to deal with the small-amplitude bifurcating solutions from double Hopf bifurcation of weak resonance for a general multi-delayed nonlinear differential system.

3.1 Critical values of double-Hopf bifurcation

The first-order delayed differential equations (DDEs) with multiple delays and nonlinearities are written in the general form by

$$ \begin{gathered} \dot{X}\left( t \right) = CX\left( t \right) + DX\left( {t - s} \right) + B_1 X\left( {t - \tau_1 } \right) + + B_2 X\left( {t - \tau_2 } \right) \hfill \\ \, \quad+ \varepsilon F\left( {X\left( t \right),X\left( {t - s} \right),X\left( {t - \tau_1 } \right),X\left( {t - \tau_2 } \right)} \right), \hfill \\ \end{gathered} $$

where \(X\left( t \right) = \left( {\begin{array}{*{20}c} {x_1 \left( t \right)} \\ {x_2 \left( t \right)} \\ \vdots \\ {x_n \left( t \right)} \\ \end{array} } \right)\),\(B_1 , \, B_2 , \, C\) and \(D\) are \(n \times n\) real constant matrices, \(s\) denotes the self-feedback delay and \(\tau_i\) \(\left( {i = 1,2} \right)\) coupling delays, a nonlinear function \(F\left( \cdot \right)\) satisfies \(F\left( {0,0, \cdots ,0} \right) = 0\) and \(\varepsilon\) is a parameter representing the coupling degree between nonlinearities.

It is obvious that a zero solution is the trivial point. The characteristic equation around the zero solution reads,

\(\det \left( {\lambda I - C - De^{ - \lambda s} {\rm{ - }}B_1 e^{ - \lambda \tau_1 } - B_2 e^{ - \lambda \tau_2 } } \right) = 0\), where \(I\) is the identity matrix.

Here we mainly discuss the complicated behaviors near the weak resonant double Hopf bifurcation. In order to facilitate analysis, the following assumption is firstly needed.

(A1) The system undergoes double-Hopf bifurcation of weak resonance at the trivial point for bifurcation parameters \(D = D_0\) and \(\tau_1 = \tau_{10}\). That is, all eigenvalues of the above characteristic equation have negative real parts except for two pairs of simple purely imaginary eigenvalues \(\lambda_1 = \pm i\omega_1\) and \(\lambda_2 = \pm i\omega_2\) \(\left( {0 < \omega_1 < \omega_2 } \right)\) with \(\omega_1 = m_1 \omega\) and \(\omega_2 = m_2 \omega\) \(\left( {m_1 \in Z^+ , \, m_2 \in Z^+ } \right)\) at the critical point \(\left( {D_0 ,\tau_{10} } \right)\).

3.2 Bifurcation sets near double-Hopf bifurcation

For two bifurcation parameters \(D\) and \(\tau_1\), make a small perturbation close to the double-Hopf bifurcation point \(\left( {D_0 ,\tau_{10} } \right)\) by setting

\(D = D_0 + \varepsilon D_\varepsilon\), \(\tau = \tau_{10} + \varepsilon \tau_\varepsilon\).

Accordingly, the above system is equivalent to be transformed as

$$ \begin{gathered} \dot{X}\left( t \right) = CX\left( t \right) + D_0 X\left( {t - s} \right) + B_1 X\left( {t - \tau_{10} } \right) \hfill \, + B_2 X\left( {t - \tau_2 } \right) + \hat{F}\left( \cdot \right), \hfill \\ \end{gathered} $$
(12)

where

$$ \begin{gathered} \hat{F}\left( \cdot \right) = \varepsilon D_\varepsilon X\left( {t - s} \right) + B_1 \left[ {X\left( {t - \tau_1 } \right) - X\left( {t - \tau_{10} } \right)} \right] \hfill \\ \, + \varepsilon F\left( {X\left( t \right),X\left( {t - s} \right),X\left( {t - \tau_1 } \right),X\left( {t - \tau_2 } \right)} \right). \hfill \\ \end{gathered} $$

For \(\varepsilon = 0\) in Eq. (12), the periodic solutions are expressed as

$$ X_0 \left( t \right) = \left( {\begin{array}{*{20}c} {\sum_{i = 1}^2 {\left( {a_{i1} \cos \left( {\omega_i t} \right) + b_{i1} \sin \left( {\omega_i t} \right)} \right)} } \\ {\sum_{i = 1}^2 {\left( {a_{i2} \cos \left( {\omega_i t} \right) + b_{i2} \sin \left( {\omega_i t} \right)} \right)} } \\ \vdots \\ {\sum_{i = 1}^2 {\left( {a_{in} \cos \left( {\omega_i t} \right) + b_{in} \sin \left( {\omega_i t} \right)} \right)} } \\ \end{array} } \right). $$
(13)

Bringing (13) into (12) when \(\varepsilon = 0\), using the harmonic balance, it is no difficult to get the coefficients \(a_{ij}\) and \(b_{ij}\) \(\left( {i = 1,2;j = 1,2, \cdots ,n} \right)\) satisfying the following equations

$$ \begin{gathered} \, M_i \left( {\begin{array}{*{20}c} {b_{i1} } \\ {b_{i2} } \\ \vdots \\ {b_{in} } \\ \end{array} } \right) = N_i \left( {\begin{array}{*{20}c} {a_{i1} } \\ {a_{i2} } \\ \vdots \\ {a_{in} } \\ \end{array} } \right), \hfill \\ - M_i \left( {\begin{array}{*{20}c} {a_{i1} } \\ {a_{i2} } \\ \vdots \\ {a_{in} } \\ \end{array} } \right) = N_i \left( {\begin{array}{*{20}c} {b_{i1} } \\ {b_{i2} } \\ \vdots \\ {b_{in} } \\ \end{array} } \right), \hfill \\ \end{gathered} $$
(14)

where

$$ M_i = \omega_i I + D_0 \sin \left( {\omega_i s} \right) + B_1 \sin \left( {\omega_i \tau_{10} } \right) + B_2 \sin \left( {\omega_i \tau_2 } \right), $$
$$ N_i = C + D_0 \cos \left( {\omega_i s} \right) + B_1 \cos \left( {\omega_i \tau_{10} } \right) + B_2 \cos \left( {\omega_i \tau_2 } \right). $$

For a small value \(\varepsilon\)\(\left( { > 0} \right)\), the bifurcation solutions of the system (12) can be seen as a small perturbation of harmonic solution (13) in a polar coordinate by the following

$$ X\left( t \right) = \left( {\begin{array}{*{20}c} {\sum_{i = 1}^2 {r_{i1} \left( \varepsilon \right)\cos \left( {\left( {\omega_i + \sigma_i \left( \varepsilon \right)} \right)t + \theta_i } \right)} } \\ {\sum_{i = 1}^2 {r_{i2} \left( \varepsilon \right)\cos \left( {\left( {\omega_i + \sigma_i \left( \varepsilon \right)} \right)t + \theta_i } \right)} } \\ \vdots \\ {\sum_{i = 1}^2 {r_{in} \left( \varepsilon \right)\cos \left( {\left( {\omega_i + \sigma_i \left( \varepsilon \right)} \right)t + \theta_i } \right)} } \\ \end{array} } \right), $$
(15)

where \(r_{ij} \left( 0 \right) = r_i\),\(\sigma_i \left( 0 \right) = 0\),and \(\theta_i\) are determined by some initial conditions \(\left( {j = 1,2, \cdots ,n} \right).\)

The values of \(r_{ij} \left( \varepsilon \right)\) and \(\sigma_i \left( \varepsilon \right)\)\(\left( {i = 1,2;j = 1,2, \cdots ,n} \right)\) in Eq. (15) can be derived by the following theorem with the aid of the Lemma 1.

Lemma 1

The adjoint system of the linearization of the system (12) is as follows.

$$ \begin{gathered} \dot{Y}\left( t \right) = - C^{\rm{T}} Y\left( t \right) - D_0^{\rm{T}} Y\left( {t + s} \right) \hfill \\ \, - B_1^{\rm{T}} Y\left( {t + \tau_{10} } \right) - B_2^{\rm{T}} Y\left( {t + \tau_2 } \right). \hfill \\ \end{gathered} $$
(16)

If \(Y\left( t \right)\) is the periodic solution of Eq. (16), then \(Y\left( t \right)\) is derived by

$$ Y\left( t \right) = \left( {\begin{array}{*{20}c} {\sum_{i = 1}^2 {\left( {p_{i1} \cos \left( {\omega_i t} \right) + q_{i1} \sin \left( {\omega_i t} \right)} \right)} } \\ {\sum_{i = 1}^2 {\left( {p_{i2} \cos \left( {\omega_i t} \right) + q_{i2} \sin \left( {\omega_i t} \right)} \right)} } \\ \vdots \\ {\sum_{i = 1}^2 {\left( {p_{in} \cos \left( {\omega_i t} \right) + q_{in} \sin \left( {\omega_i t} \right)} \right)} } \\ \end{array} } \right), $$
(17)

with the period \(2\pi /\omega\) where the unknown coefficients are computed by the following equations

$$ \begin{gathered} \, M_i^{\rm{T}} \left( {\begin{array}{*{20}c} {p_{i1} } \\ {p_{i2} } \\ \vdots \\ {p_{in} } \\ \end{array} } \right) = N_i^{\rm{T}} \left( {\begin{array}{*{20}c} {q_{i1} } \\ {q_{i2} } \\ \vdots \\ {q_{in} } \\ \end{array} } \right), \, \hfill \\ - M_i^{\rm{T}} \left( {\begin{array}{*{20}c} {q_{i1} } \\ {q_{i2} } \\ \vdots \\ {q_{in} } \\ \end{array} } \right) = N_i^{\rm{T}} \left( {\begin{array}{*{20}c} {p_{i1} } \\ {p_{i2} } \\ \vdots \\ {p_{in} } \\ \end{array} } \right), \hfill \\ \end{gathered} $$
(18)

where the expressions of \(M_i\) and \(N_i\) are consistent with ones in Eq. (14).

Theorem 2

If \(Y\left( t \right)\) is the periodic solution of Eq. (16), then bifurcation solution \(X\left( t \right)\) in Eq. (12) for a small value \(\varepsilon \left( { > 0} \right)\) may be expressed by.

$$ \begin{gathered} \left[ {Y\left( 0 \right)} \right]^{\rm{T}} C\left[ {X\left( {\frac{2\pi }{\omega }} \right) - X\left( 0 \right)} \right] \hfill \\ - \int_{ - s}^0 {\left[ {Y\left( {t + s} \right)} \right]^{\rm{T}} D_0 \left[ {X\left( t \right) - X\left( {t + \frac{2\pi }{\omega }} \right)} \right]dt} \hfill \\ - \int_{ - \tau_{10} }^0 {\left[ {Y\left( {t + \tau_{10} } \right)} \right]^{\rm{T}} B_1 \left[ {X\left( t \right) - X\left( {t + \frac{2\pi }{\omega }} \right)} \right]dt} \hfill \\ - \int_{ - \tau_2 }^0 {\left[ {Y\left( {t + \tau_2 } \right)} \right]^{\rm{T}} B_2 \left[ {X\left( t \right) - X\left( {t + \frac{2\pi }{\omega }} \right)} \right]dt} \hfill - \int_0^{\frac{2\pi }{\omega }} {Y^{\rm{T}} \left( t \right)\hat{F}\left( \cdot \right)dt} = 0. \hfill \\ \end{gathered} $$
(19)

Proof

Multiplying both sides of Eq. (12) by \(Y^{\rm{T}} \left( t \right)\) and integrating with regard to \(t\), one has.

$$ \begin{gathered} \int_0^{\frac{2\pi }{\omega }} {Y^{\rm{T}} \left( t \right)\dot{X}\left( t \right)dt} \hfill \\ = \int_0^{\frac{2\pi }{\omega }} {Y^{\rm{T}} \left( t \right)\left( {CX\left( t \right) + D_0 X\left( {t - s} \right)} \right)dt} \, \hfill \\ \, + \int_0^{\frac{2\pi }{\omega }} {Y^{\rm{T}} \left( t \right)\left( {B_1 X\left( {t - \tau_{10} } \right) + B_2 X\left( {t - \tau_2 } \right)} \right)dt} \hfill \, + \int_0^{\frac{2\pi }{\omega }} {Y^{\rm{T}} \left( t \right)\hat{F}\left( \cdot \right)dt} , \hfill \\ \end{gathered} $$
(20)

where

$$ \begin{gathered} \int_0^{\frac{2\pi }{\omega }} {Y^{\rm{T}} \left( t \right)\dot{X}\left( t \right)dt} = Y^{\rm{T}} \left( 0 \right)\left[ {X\left( {\frac{2\pi }{\omega }} \right) - X\left( 0 \right)} \right] \hfill \\ + \int_0^{\frac{2\pi }{\omega }} {Y^{\rm{T}} \left( t \right)CX\left( t \right)dt} + \int_0^{\frac{2\pi }{\omega }} {Y^{\rm{T}} \left( {t + s} \right)D_0 X\left( t \right)dt} \hfill \\ + \int_0^{\frac{2\pi }{\omega }} {Y^{\rm{T}} \left( {t + \tau_{10} } \right)B_1 X\left( t \right)dt} \hfill + \int_0^{\frac{2\pi }{\omega }} {Y^{\rm{T}} \left( {t + \tau_2 } \right)B_2 X\left( t \right)dt} . \hfill \\ \end{gathered} $$
(21)
$$ \begin{gathered} \int_0^{\frac{2\pi }{\omega }} {Y^{\rm{T}} \left( t \right)D_0 X\left( {t - s} \right)dt} = \int_0^{\frac{2\pi }{\omega }} {Y^{\rm{T}} \left( {t + s} \right)D_0 X\left( t \right)dt} \hfill \\ \, + \int_{ - s}^0 {Y^{\rm{T}} \left( {t + s} \right)D_0 \left[ {X\left( t \right) - X\left( {t + \frac{2\pi }{\omega }} \right)} \right]dt.} \hfill \\ \end{gathered} $$
(22)
$$ \begin{gathered} \int_0^{\frac{2\pi }{\omega }} {Y^{\rm{T}} \left( t \right)B_1 X\left( {t - \tau_{10} } \right)dt} = \int_0^{\frac{2\pi }{\omega }} {Y^{\rm{T}} \left( {t + \tau_{10} } \right)B_1 X\left( t \right)dt} \hfill \\ \, + \int_{ - \tau_{10} }^0 {Y^{\rm{T}} \left( {t + \tau_{10} } \right)B_1 \left[ {X\left( t \right) - X\left( {t + \frac{2\pi }{\omega }} \right)} \right]dt} . \hfill \\ \end{gathered} $$
(23)
$$ \begin{gathered} \int_0^{\frac{2\pi }{\omega }} {Y^{\rm{T}} \left( t \right)B_2 X\left( {t - \tau_2 } \right)dt} = \int_0^{\frac{2\pi }{\omega }} {Y^{\rm{T}} \left( {t + \tau_2 } \right)B_2 X\left( t \right)dt} \hfill \\ \, + \int_{ - \tau_2 }^0 {Y^{\rm{T}} \left( {t + \tau_2 } \right)B_2 \left[ {X\left( t \right) - X\left( {t + \frac{2\pi }{\omega }} \right)} \right]dt} . \hfill \\ \end{gathered} $$
(24)

Substituting Eqs. (21–24) into Eqs. (20), (19) is derived. The theorem is proved.

Remark 3

To obtain the analytical solution (15), Eq. (19) need to be expanded into \(\varepsilon\) series, neglect high order terms in \(\varepsilon\), and yield four algebraic equations in \(r_i \left( \varepsilon \right)\) and \(\sigma_i \left( \varepsilon \right)\) \(\left( {i = 1,2} \right)\). Therefore, when two control parameters are close to the bifurcation point, the approximate periodic solution is easy to be obtained from four algebraic equations.

4 Complex dynamics near double Hopf bifurcation point

In this section, complex phenomena near double Hopf bifurcation are demonstrated in the system (1) via the above mentioned PS.

System parameters are fixed as

\(k_1 = 1.0\), \(k_2 = 1.0\), \(J_{12} = 2.0\), \(J_{21} = 2.02863\), \(s = 0.5\),

\(a\) and \(\tau\) are chosen as bifurcation parameters.

From Eq. (10), the two frequencies corresponding to Hopf bifurcation are computed as

\(\omega_1 = 5\omega = 1.91085\), \(\omega_2 = 9\omega = 3.43953\),

with \(\omega = 0.38217\).

The bifurcating critical values \(a = a_0 = - 1.59324\) and \(\tau = \tau_0 = 1.4831\). And the corresponding transversal conditions

$$ \begin{aligned}&{\text {Re}}({\lambda^{\prime}}(\tau)) \mathop{\mathop{\Big\vert}\nolimits_{\lambda= i\omega_1}}\limits_{\tau = \tau_{0}}= -0.12<0,\\&{\text {Re}}({\lambda^{\prime}}(\tau)) \mathop{\mathop{\Big\vert}\nolimits_{\lambda= i\omega_2}}\limits_{\tau = \tau_{0}}= 0.11>0.\end{aligned} $$

That is, the characteristic Eq. (3) has only two pairs of simple purely imaginary eigenvalues \(\lambda_1 = \pm i\omega_1\) and \(\lambda_2 = \pm i\omega_2\), and the other eigenvalues with negative real parts. And the critical point \(\left( {a_0 ,\tau_0 } \right) = \left( { - 1.59324, \, 1.4831} \right)\) is a double Hopf bifurcation point of 5:9 weak resonance, which is usually thought as codimesion-two bifurcation. This singularity point is a source of more complicated dynamics, such as the the coexistence of stable periodic behaviors.

By performing the numerical tool DDEBIFTOOL [37] in MATLAB, the partial eigenvalues of Eq. (3) are displayed in Fig. 2 where the green star represents the eigenvalue with negative real part while the red star represents the maximum eigenvalues \(\lambda_1 = \pm i\omega_1\) and \(\lambda_2 = \pm i\omega_2\).

Fig. 2
figure 2

Roots of the characteristic equation in the complex plane at the critical point \(\left( {a_0 ,\tau_0 } \right) = \left( { - 1.59324, \, 1.4831} \right)\) in the system (1) where the red stars denote the rightmost eigenvalues which are two pairs of simple purely imaginary eigenvalues with \(\lambda_1 = \pm 1.91085i\) and \(\lambda_2 = \pm 3.43953i\) and all the eigenvalues with negative real parts in the green

Full size image

According to Eq. (11), we can plot two Hopf bifurcation curves for varying \(a\) on the \(\left( {a,\tau } \right)\) plane shown in Fig. 3. It can be seen that two Hopf bifurcation curves \(\tau_-\) (the red line) and \(\tau_+\) (the green line) intersect at the point \(\left( {a_0 ,\tau_0 } \right) = \left( { - 1.59324,1.4831} \right)\), which is the critical point of double Hopf bifurcation, denoted by the black solid dot.

Fig. 3
figure 3

Variation of the critical values a versus \(\tau\) in the \(\left( {a,\tau } \right)\) parameter plane of the linearized system (2) where the red line denotes Hopf bifurcation curve \(\tau_-\) and the green line \(\tau_+\). The intersection solid dot \(\left( { - 1.59324, \, 1.4831} \right)\) is the double Hopf bifurcation point of weak resonance with the frequencies in the ratio \(\frac{\omega_1 }{{\omega_2 }} = \frac{5}{9}\)

Full size image

To use the above mentioned PS to get the analytical solutions in the neighboring of \(\left( {a_0 ,\tau_0 } \right) = \left( { - 1.59324,1.4831} \right)\) with \(\tau = \tau_{21} = \tau_{12}\), we rescale some variables

\(x_1 \left( t \right) \to \varepsilon x_1 \left( t \right)\), \(x_2 \left( t \right) \to \varepsilon x_2 \left( t \right)\), and two parameter perturbations

\(a = a_0 + \varepsilon^2 \delta_1\), \(\tau = \tau_0 + \varepsilon^2 \delta_2\), where \(\varepsilon^2 \delta_1\) and \(\varepsilon^2 \delta_2\) are very small. System (1) can be transformed as the form like the system (12)

$$ \begin{gathered} X\left( t \right) = \left( {\begin{array}{*{20}c} {x_1 \left( t \right)} \\ {x_2 \left( t \right)} \\ \end{array} } \right),C = \left( {\begin{array}{*{20}c} { - k_1 } & 0 \\ 0 & { - k_2 } \\ \end{array} } \right), \hfill \\ D_0 = \left( {\begin{array}{*{20}c} {a_0 } & 0 \\ 0 & {a_0 } \\ \end{array} } \right),B = B_1 + B_2 = \left( {\begin{array}{*{20}c} 0 & {J_{12} } \\ {J_{21} } & 0 \\ \end{array} } \right), \hfill \\ \, \hat{F}\left( \cdot \right) = \varepsilon D_0 X\left( {t - s} \right) + B\left[ {X\left( {t - \tau } \right) - X\left( {t - \tau_0 } \right)} \right] + \varepsilon F, \hfill \\ F\left( \cdot \right) = \left( {\begin{array}{*{20}c} { - \frac{{\varepsilon^2 J_{12} }}{3}x_2 \left( {t - \tau } \right)^3 + h.o.t.} \\ { - \frac{{\varepsilon^2 J_{21} }}{3}x_1 \left( {t - \tau } \right)^3 + h.o.t.} \\ \end{array} } \right). \hfill \\ \end{gathered} $$
(24)

From Eq. (18), it follows the adjoint periodic solution Eq. (17)

$$ Y\left( t \right) = \left[ {\begin{array}{*{20}c} {\sum_{i = 1}^2 {p_{i1} \cos \left( {\omega_1 t} \right) + q_{i1} \sin \left( {\omega_i t} \right)} } \\ {\sum_{i = 1}^2 {p_{i2} \cos \left( {\omega_1 t} \right) + q_{i2} \sin \left( {\omega_i t} \right)} } \\ \end{array} } \right], $$
(25)

where

$$ \begin{gathered} p_{11} = - 1.00713p_{12} , \, q_{11} = - 1.00713q_{12} , \hfill \\ p_{21} = 1.00713p_{22} , \, q_{21} = 1.00713q_{22} . \hfill \\ \end{gathered} $$
(26)

From Eq. (14), the periodic solution (13) with \(\varepsilon = 0\) is obtained

$$ X_0 \left( t \right) = \left[ {\begin{array}{*{20}c} {\sum_{i = 1}^2 {a_{i1} \cos \left( {\omega_1 t} \right) + b_{i1} \sin \left( {\omega_i t} \right)} } \\ {\sum_{i = 1}^2 {a_{i2} \cos \left( {\omega_1 t} \right) + b_{i2} \sin \left( {\omega_i t} \right)} } \\ \end{array} } \right], $$

where

$$ \begin{gathered} a_{11} = - 0.992919a_{12} , \, b_{11} = - 0.992919b_{12} , \hfill \\ a_{21} = 0.992919r_2 a_{22} , \, b_{21} = 0.992919 \, b_{22} . \hfill \\ \end{gathered} $$
(27)

and the corresponding perturbation solution (15) is rewritten as in polar coordinate

$$ X\left( t \right) = \left( {\begin{array}{*{20}c} \begin{gathered} 0.992919\cos \left( {\theta_2 + \left( {\varepsilon^2 \sigma_2 + \omega_2 } \right)t} \right)r_2 - \hfill \\ 0.992919r_1 \cos \left( {\theta_1 + \left( {\varepsilon^2 \sigma_1 + \omega_1 } \right)t} \right) \hfill \\ \end{gathered} \\ \begin{gathered} r_1 \cos \left( {\theta_1 + \left( {\varepsilon^2 \sigma_1 + \omega_1 } \right)t} \right) + \hfill \\ r_2 \cos \left( {\theta_2 + \left( {\varepsilon^2 \sigma_2 + \omega_2 } \right)t} \right) \hfill \\ \end{gathered} \\ \end{array} } \right), $$
(28)

where

\(\begin{gathered} a_{12} = r_1 \cos \left( {\theta_1 } \right),b_{12} = - r_1 \sin \left( {\theta_1 } \right), \hfill \\ a_{22} = r_2 \cos \left( {\theta_2 } \right), \, b_{22} = - r_2 \sin \left( {\theta_2 } \right) \hfill \\ \end{gathered}\), and \(\theta_1\) and \(\theta_2\) are determined by the initial conditions.

Substituting Eqs. (25–28) into Eq. (19), noting that \(p_{i2}\) and \(q_{i2}\) are independent and \(\cos^2 \left( {\theta_i } \right) + \sin^2 \left( {\theta_i } \right) = 1\) \(\left( {i = 1,2} \right)\), produces the following algebraic equations as

$$ \begin{gathered} \varepsilon^2 r_1 \left( { - 13.2952 + 9.49064a + 19.1599\tau - 4.0812r_1^2 } \right) \hfill \\ + \varepsilon^2 r_1 \left( { - 8.1624r_2^2 + 25.5654\sigma_1 } \right) = 0, \hfill \\ \varepsilon^2 r_1 \left( {68.0562 - 13.4249a - 60.3096\tau - 7.79857r_1^2 } \right) \hfill \\ + \varepsilon^2 r_1 \left( { - 15.5971r_2^2 - 55.6895\sigma_1 } \right) = 0, \hfill \\ \varepsilon^2 r_2 \left( {38.1315 - 16.2587a - 43.1768\tau - 28.0748r_1^2 } \right) \hfill \\ + \varepsilon^2 r_2 \left( { - 14.0374r_2^2 - 37.0022\sigma_2 } \right) = 0, \hfill \\ \varepsilon^2 r_2 \left( {160.211 + 2.44013a - 105.403\tau + 8.1624r_1^2 } \right) \hfill \\ + \varepsilon^2 r_2 \left( {4.0812r_2^2 - 58.4011\sigma_2 } \right) = 0. \hfill \\ \end{gathered} $$
(29)

The search for an explicit periodic solution (28) is converted to the problem of solving four algebraic equations in (29). All local solutions and their stability near a double Hopf bifurcation can be obtained from Eq. (29). All solutions are easily solved as follows

$$ \left( {r_{10} ,r_{20} } \right) = \left( {0,0} \right), $$
$$ \left( {r_{11} ,r_{20} } \right) = \left( {0.659051\sqrt {5.39339 + a - 2.5623\tau } ,0} \right), $$
$$ \left( {r_{10} ,r_{21} } \right) = \left( {0,1.03493\sqrt {1.32579\tau - 3.55952 - a} } \right), $$
$$ \left( {r_{12} ,r_{22} } \right) = \left( \begin{gathered} 0.926733\sqrt {1.53424\tau - 3.86867 - a} , \hfill \\ 0.804109\sqrt {4.38079 + a - 1.87954\tau } \hfill \\ \end{gathered} \right), $$

and

$$ \sigma_1 = 0.894014 - 0.301892a - 0.927111\tau , $$
$$ \sigma_2 = 2.47687 - 0.033067a - 1.70558\tau . $$

It is no difficulty to obtain that four bifurcation lines denoted by different colors in Fig. 4 as follows.

Fig. 4
figure 4

Classification and bifurcation sets near the 5:9 resonant double Hopf bifurcation point \(\left( {a_0 ,\tau_0 } \right) = \left( { - 1.59324,1.4831} \right)\) in the \(\left( {a,\tau } \right)\) plane for the network (1) where the four color lines represent bifurcation boundaries

Full size image

Red: \(\tau = 2.1049 + 0.390274a\).

Green: \(\tau = 2.68483 + 0.754268a\).

Blue: \(\tau = 2.52155 + 0.651788a\).

Cyan: \(\tau = 2.33078 + 0.532045a\).

The six different dynamical regions are divided by the above bifurcation lines as displayed in Fig. 4. The solutions in the same region have the same topological structure. It is easily seen that Eq. (29) has always a zero root \(\left( {r_{10} ,r_{20} } \right) = \left( {0,0} \right)\) and the existence of other roots is only dependent on the location of parameters \(\left( {a,\tau } \right)\). The zero root \(\left( {r_{10} ,r_{20} } \right) = \left( {0,0} \right)\) corresponds to the trivial equilibrium of the origin system. The other three roots \(\left( {r_{11} ,0} \right),\) \(\left( {0,r_{21} } \right),\) and \(\left( {r_{12} ,r_{22} } \right)\) correspond to the limit cycles of the original system. A stable zero root \(\left( {0,0} \right)\) only exists in region I while there are four roots \(\left( {0,0} \right),\)\(\left( {r_{11} ,0} \right),\) \(\left( {0,r_{21} } \right),\) and \(\left( {r_{12} ,r_{22} } \right)\) in region IV where two stable periodic attractors \(\left( {r_{11} ,0} \right)\) and \(\left( {0,r_{21} } \right)\) coexist. Region I is an amplitude death one, i.e., when the parameters are located on this region, there is no vibration with non-zero amplitude in the original system. In region II, there are two roots \(\left( {0,0} \right)\) and \(\left( {r_{11} ,0} \right)\) where the equilibrium \(\left( {0,0} \right)\) is unstable and the periodic attractor \(\left( {r_{11} ,0} \right)\) is stable from Hopf bifurcation at trivial equilibrium point. In region III, there are three roots in which the periodic attractor \(\left( {r_{11} ,0} \right)\) is stable and the other two roots \(\left( {0,r_{21} } \right)\) and \(\left( {0,0} \right)\) are unstable. In region V, system has a stable periodic attractor \(\left( {0,r_{21} } \right)\), unstable periodic motion \(\left( {r_{11} ,0} \right)\) and unstable equilibrium \(\left( {0,0} \right)\). In region VI, there exists only a stable periodic attractor \(\left( {0,r_{21} } \right)\) and unstable equilibrium \(\left( {0,0} \right)\).

In summary, it can be obtained from an analysis of the stability that there exists a unique stable periodic solution in the other four regions except in regions (I) and (IV). All the solutions have been marked in each region in Fig. 4, which are well agreement with that provided by Guckenheimer and Holmes [38].

5 Numerical examples

This section validates the correctness of the theoretical results by providing numerical computations for system (1).

Firstly, with the aid of DDEBIFTOOL [37] in MATLAB, the stability of the trivial equilibrium point is determined from the real parts of the rightmost eigenvalues shown by plotting Fig. 5. In Fig. 5, the green star represents the eigenvalue of negative real part while the red star represents the eigenvalue of positive real part. In Fig. 5a, all the eigenvalues of the characteristic equation denoted by green and have negative real parts. Whereas in Fig. 5b–f, the rightmost eigenvalues are positive real parts. So the trivial equilibrium point is asymptotically stable only in region I, whereas unstable in the other five regions. These agree well with theoretical analysis. The stable trivial equilibrium point in region I can also further be verified by time history (Fig. 6a) and phase portrait (Fig. 6b).

Fig. 5
figure 5figure 5

Eigenvalues in the complex plane in six regions (i.e., I-VI) near the critical point \(\left( {a_0 ,\tau_0 } \right) = \left( { - 1.59324, \, 1.4831} \right)\) in Fig. 4 for system (1) where the red star denotes the rightmost eigenvalue of the characteristic equation with positive real part and the green star with negative real part. The trivial equilibrium point is asymptotically stable only in region I, whereas unstable in other five regions

Full size image
Fig. 6
figure 6

The trivial equilibrium point is locally asymptotically stable in region I displayed by (a) time history of \(x_1\) and (b) phase portrait of \(x_1\) for \(\left( {a,\tau } \right) = \left( { - 1.5,1.54} \right)\) in region I

Full size image

In the next, the Runge–Kutta scheme is adopted to obtain the numerical results in the neighbor of double Hopf bifurcation point of weak resonance.

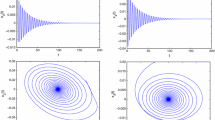
The parameter value \(\left( {a,\tau } \right) = \left( { - 1.5, \, 1.54} \right)\) is located in region I, the system (1) tends to the trivial equilibrium point and is stable displayed by time history of \(x_1\) in Fig. 6a and phase portrait of \(x_1\) in Fig. 6b. Region I is a stability zone, which is called as death zone.

Fix the parameter \(a = - 1.5\) in Fig. 4. With the decreasing of time delay, for example, if \(\left( {a,\tau } \right) = \left( { - 1.5, \, 1.3} \right)\) is located in region II, the trivial equilibrium point becomes unstable and the system (1) undergoes a Hopf bifurcation at the red line shown in Fig. 4 and produces a stable periodic solution \(\left( {r_{11} ,0} \right)\) with low frequency \(\omega_1\) as shown in Fig. 7a.

Fig. 7
figure 7

A stable periodic solution near the trivial equilibruium point in four different regions are shown in phase portrait of \(x_1\) when two parameters \(\left( {a,\tau } \right)\) are chosen as (a) \(\left( {1.5,1.3} \right)\)(b) \(\left( { - 1.7,1.41} \right)\) (c) \(\left( { - 1.7,1.44} \right)\) and (d) \(\left( { - 1.7,1.5} \right)\), respectively

Full size image

Fix the parameter \(a = - 1.7\) in Fig. 4, some numerical results of complex dynamical behaviors are exhibted with the increasing value of time delay. \(\left( {a,\tau } \right) = \left( { - 1.7, \, 1.41} \right)\) in region III, when \(\left( {a,\tau } \right)\) crossing the green line, there exist two periodic solutions and the trivial equilibrium point. Whereas the periodic solution \(\left( {0,r_{21} } \right)\) and trivial equilibrium point are unstable and there only exists a stable periodic solution \(\left( {r_{11} ,0} \right)\) in Fig. 7b. The increasing value of time delay \(\tau = 1.42\) is located in region IV, we can find that there exists two stable limit cycles \(\left( {r_{11} ,0} \right)\) and \(\left( {0,r_{21} } \right)\)(one resulting from each of the primary Hopf bifurcation). When the initial value is chosen as \(\left( {0.5, - 0.5} \right)\), the system tends to a limit cycle. But, when the initial value is used as \(\left( {0.5,0.5} \right)\), the system finally tends to a second limit cycle in Fig. 8. Double Hopf bifurcation produces bistability between two limit cycles of different frequencies. Bistability of periodic solutions is very important dynamical behaviors in neural networks.

Fig. 8
figure 8

Bistability periodic attractors in region IV with different initial conditions displayed by (a) time history of \(x_1\) and (b, c) phase portrait of \(x_1\) for two parameters \(\left( {a,\tau } \right) = \left( { - 1.7,1.42} \right)\) in region IV

Full size image

Increasing delay \(\tau = 1.44\) located in region V, it can be seen that a periodic solution \(\left( {r_{11} ,0} \right)\) lose its stability and emerges a stable limit cycle \(\left( {0,r_{21} } \right)\) with high frequency \(\omega_2\) in Fig. 7c. Increasing delay \(\tau = 1.5\) is located in region VI, the limit cycle \(\left( {0,r_{21} } \right)\) is still stable in Fig. 7d and the unstable limit cycle \(\left( {r_{11} ,0} \right)\) disappears.

When two parameter values are chosen in the neighbor of a double bifurcation point of weak resonance, the numerical simulations in each region are presented by the distribution of eigenvalues, time histories or phase portraits in Figs. 5, 6, 7, 8, respectively. It can be seen that numerical results are in good agreement with the classification sets and dynamical behaviors in Fig. 4.

6 Conclusions

In this paper, we concentrate on weak resonant double Hopf bifurcations of a neural network composed of a pair of neurons with three discrete delays. Compared to prior works [31,32,33,34,35], the considered network cannot be transformed into a system with a single delay like the traditional way. We choose self-connection weight and coupling delay as bifurcation parameters to get the mechanism of complex dynamics near double Hopf bifurcation of weak resonance including classification sets by using the perturbation scheme, which are different from the previous literature. Compared with the CMR, it is simple and valid with less calculation. In the neighborhood of the 5:9 resonant Hopf bifurcations, the neural system can have stable trivial equilibrium, stable periodic and coexistence of two periodic motions. Numerical examples agree well with the analytical results.

The analytical results presented in this paper would guide the researchers to dominate and optimize networks at the right physical parameters to guarantee the good performance of network systems in practical applications. For example, to make the system stable, physical parameters can be chosen in the region I near double Hopf bifurcation point. There are many references that consider the topic. We refer the readers to [39,40,41,42]. Though the two-neuron neural system considered in this paper is relatively simple, it can describe brain dynamics and provide a model for better understanding human activity and memory. Double Hopf bifurcation produces bistability between two limit cycles of different frequencies. This is interesting as it is generally considered that periodic firing is one mechanism for transmitting information in the neural system [43], with the frequencies of the oscillations being the “message” transmitted. Thus, bistability between limit cycles provides a mechanism for the neural system to convey two different “messages” in response to different stimuli, for the same parameter values.

By considering this simple model, one can vividly observe the influences of connection weight and time delay on it. Physically, the system may be regarded as a basic element integrated into a large-scale system. It is no hard that the same method and ideas can be used to discuss bifurcation issues of tri-neuron or more neuron neural systems with multiple time delays. In near further, we will discuss how the PS is used to study other resonances, for example, strong resonance.