Asynchronous Spiking Neural P Systems with Anti-Spikes

Abstract

Spiking neural P systems with anti-spikes (ASN P systems, for short) are a class of distributed parallel computing devices inspired from the way neurons communicate by means of spikes and inhibitory spikes. ASN P systems working in the synchronous manner with standard spiking rules have been proved to be Turing completeness, do what Turing machine can do. In this work, we consider the computing power of ASN P systems working in the asynchronous manner with standard rules. As expected, the non-synchronization will decrease the computability of the systems. Specifically, asynchronous ASN P systems with standard rules can only characterize the semilinear sets of natural numbers. But, by using weighted synapses, asynchronous ASN P systems can achieve the equivalence with Turing machine again. It implies that weighted synapses has some “programming capacity” in the sense of achieving computing power. The obtained results have a nice interpretation: the loss in power entailed by removing the synchronization from ASN P systems can be compensated by using weighted synapses among connected neurons.

1 Introduction

Membrane computing is a new and hot researching field recently emerged as a branch of natural computing. It was initiated in [18] and has developed rapidly. In 2003, it was considered by Institute for Scientific Information (ISI) as a “fast emerging research area in computer science” (for more information, one can refer to http://esi-topics.com). The aim is to find efficient bio-inspired computing models/devices by abstracting ideas from the structure and the functioning of single cell or from tissues and organs, such as brain. The obtained computing models are a class of distributed and parallel bio-inspired computing models, usually called P systems, which provide a group of theoretical computing systems for constructing bio-computing machines with bio-nano-materials, as well as give various of potentially feasible frameworks for designing artificial life systems in nano-scale. Spiking neural P systems (shortly called SN P systems) are a class of neural-like P systems in membrane computing introduced in [8], which are inspired from the way neurons communicate by means of spikes. The aim is to define computing models based on ideas related to spiking neurons, which are currently much investigated in neural computing [6, 9].

Briefly, an SN P system consists of a set of neurons placed in the nodes of a directed graph, where neurons send signals (which are called spikes, denoted by the symbol $a$ in what follows) along synapses (arcs of the graph). Spikes evolve by means of spiking rules, which are of the form $E / a^c \rightarrow a; d$, where $E$ is a regular expression over {a} and $c$, $d$ are natural numbers, $c \ge 1$, $d \ge 0$. In other words, if a neuron contains $k$ spikes such that $a^k \in L(E)$, $k \ge c$, then it can consume $c$ spikes and produce one spike after a delay of $d$ steps. This spike is sent to all neurons connected by an outgoing synapse from the neuron where the rule was applied. There are also forgetting rules, of the form $a^s \rightarrow \lambda$, with the meaning that $s \ge 1$ spikes are removed if the neuron contains exactly $s$ spikes. In the SN P system, a global clock is assumed to mark the time of the whole system. SN P systems work in the synchronous manner, that is, in each time unit, one rule must be applied for each neuron with applicable rules (if there are more than one applicable rules in the neuron, then one of them is non-deterministically chosen). The work in each neuron is sequential: only one rule is applied in each time unit, but for different neurons, their works are in a parallel manner. One neuron is distinguished as the output neuron which also emits spikes out to the environment. The time interval between the first two spikes sent out to the environment by the output neuron contributes the result of the computation.

SN P systems have been proved to be Turing completeness, that is, they can do what Turing machine does. In previous works, SN P systems were used as computing devices mainly in three ways: generating/computing sets of numbers [8, 13, 21], generating string languages [2, 25] and computing functions [17]. SN P systems were also used to (theoretically) solve computationally hard problems, for example SAT problem, in a feasible time (see, e.g., [14, 26]). With different biological motivations, many variants of SN P systems have been investigated, such as SN P systems with weighted synapses were considered in [16], where each connected pair of neurons is endowed with an integer to denote the number of synapses between them; SN P systems with astrocytes [15], where a set of astrocyte cells are used to control the spikes passing along synapses; time-free SN P systems [24], where any rule in the neurons can take any time to apply; asynchronous SN P systems [1], where the enabled spiking or forgetting rule is not obligatorily used in each time unit.

The present work deals with a variant of SN P systems, called SN P systems with anti-spikes (ASN P systems, for short), which are inspired from the way neurons communicate by means of both “positive” spikes and inhibitory spikes [12, 20]. In ASN P systems, besides usual “positive” spikes $a$, anti-spikes denoted by $\bar{a}$ are considered. Spiking rules are of the form $E/b^c\rightarrow b'$, where $E$ is the regular expression over $\{a\}$ or $\{\bar{a}\}$ and $b,b'\in \{a,\bar{a}\}$. Rules of the form $b^s\rightarrow \lambda$ are forgetting rules, by which $s$ spikes or anti-spikes would be removed out of the neuron. The spikes and anti-spikes can participate in the annihilating rule $a\bar{a}\rightarrow \lambda$, by which spikes and anti-spikes in certain neuron will annihilate each other in a maximal manner. The application of the annihilating rule happens immediately and takes no time. Hence, at any moment, there are only spikes or anti-spikes in any neuron but not both of them. ASN P systems working in the synchronous manner can achieve the Turing completeness [12].

In this work, we consider the computing power of ASN P systems working in the asynchronous manner. In asynchronous ASN P systems, in each time unit if a neuron has a spiking or forgetting rule enabled to apply, then this rule is not obligatorily used, that is, the neuron can choose to remain unfired and receive spikes or anti-spikes (maybe both) from its neighboring neurons. In any neuron, if the unused spiking or forgetting rule is enable to used later, then it would be chosen to use without any restriction on the interval of time. If the new coming spikes or anti-spikes (maybe both) make the spiking or forgetting rule unable to use, the computation continues in the new circumstances (maybe other rules are enable now). Note that when spikes and anti-spikes meet in a neuron, the application of the annihilating rule happens immediately and takes no time. At any moment, there are only spikes or anti-spikes in each neuron of asynchronous ASN P systems. The way of non-synchronized use of spiking and forgetting rules also works in the output neuron, thus the distance in time between the spikes sent to the environment by the output neuron can be any long, and it is no longer the result of the computation. For asynchronous ASN P systems, the result of the computation is the total number of spikes sent to the environment by the output neuron.

As expected, non-synchronization will decrease the computing power of the ASN P systems. Specifically, it is proved that ASN P systems working in the asynchronous manner (without using weighted synapses) can only characterize the semilinear sets of natural numbers. If we use weighted synapses (with weights not more than three), the equivalence between asynchronous ASN P systems and Turing machine can be achieved again: the sets of Turing computable numbers can be generated by asynchronous ASN P systems with weighted synapses. It indicates that weighted synapses have some “programming capacity” in the sense of achieving some computing power. The obtained results have a nice interpretation that the loss in power entailed by removing the synchronization from ASN P systems can be compensated by using weighted synapses among connected neurons.

2 Preliminaries

Readers can refer to [19] for very basic notions of formal languages and automata theory. In the following, we mainly recall the structure of register machine [10] and $k$-output monotonic counter machine [7], which are used in the following theories.

By $\textit{SLIN}$ and $\textit{NRE}$, we denote the families of semilinear and Turing computable sets of numbers. ($\textit{SLIN}$ is the family of length sets of regular languages – languages characterized by regular expressions; and $\textit{NRE}$ is the family of length sets of recursively enumerable languages – those recognized by Turing machines.)

In universality proofs, the notion of register machine from [10] is used. A register machine is a construct $M=(m, H, l_0,l_h,R)$, where $m$ is the number of registers, $H$ is the set of instruction labels, $l_0$ is the start label, $l_h$ is the halt label (assigned to instruction HALT), and $R$ is the set of instructions; each label from $H$ labels only one instruction from $R$, thus precisely identifying it. The instructions are of the following forms:

• $l_i : (\mathtt{ADD}(r), l_j,l_k)$ (add 1 to register $r$ and then go to one of the instructions with labels $l_j,l_k$),

• $l_i : (\mathtt{SUB}(r), l_j, l_k)$ (if register $r$ is non-zero, then subtract 1 from it, and go to the instruction with label $l_j$; otherwise, go to the instruction with label $l_k$),

• $l_h : \mathtt{HALT}$ (the halt instruction).

A register machine $M$ generates (computes) a number $n$ in the following way. The register machine starts with all registers empty (i.e., storing the number zero). It applies the instruction with label $l_0$ and proceeds to apply instructions as indicated by labels (and, in the case of SUB instructions, by the content of registers). If the register machine reaches the halt instruction, then the number $n$ stored at that time in the first register (the output register) is said to be generated (computed) by $M$. The set of all numbers computed by $M$ is denoted by $N(M)$. It is known that register machines compute all sets of numbers which are Turing computable, hence they characterize $\textit{NRE}$.

Without loss of generality, it can be assumed that $l_0$ labels an ADD instruction, that in the halting configuration, all registers different from the first one are empty, and that the output register is never decremented during the computation (its content is only added to).

A k-output monotonic counter machine is a specific register machine with $k$ counters, all of which are output counters. All counters are initially zero and can be only incremented by 1 or 0. Hence, the number stored in the $k$ output counters can not be decremented during the computation. Starting with all the $k$ counters zero if the counter machine reaches the halting instruction, the k-tuple of values in the $k$ counters is said to be computed/generated by the k-output monotonic counter machine. The set of vectors (associated with $k$ tuple values) generated by k-output monotonic counter machines is denoted by $N(C_kM)$. It is known that a set $Q\subseteq N^k$ with $k\ge 1$ is semilinear if and only if it can be generated by a k-output monotonic counter machine [7]. Specifically, when $k=1$, a set of numbers can be generated by the 1-output monotonic counter machine, which is denoted by $N(CM)$. A set of numbers is semilinear if and only if it can be generated by a 1-output monotonic counter machine.

Convention: When evaluating or comparing the power of two number generating/accpe- ting devices, number zero is ignored (this corresponds to the usual practice of ignoring the empty string in language and automata theory).

3 Asynchronous ASN P Systems

In this section, we introduce the asynchronous ASN P systems, as well as the family of sets of numbers generated (computed) by the systems. The feature of delay is not used in our research. The definition is complete, but familiarity with the basic elements of classic SN P systems (e.g. from [8]) is helpful.

An asynchronous spiking neural P system (without delay) with anti-spikes of degree $m\ge 1$ is a construct of the form:

$$\begin{aligned} \Pi =(O,\sigma _1,\sigma _2,\dots ,\sigma _m,syn,out), \end{aligned}$$

where

• $O=\{a,\bar{a}\}$ is the alphabet, where $a$ is called spike and $\bar{a}$ is called anti-spike;

• $\sigma _1,\sigma _2,\dots ,\sigma _m$ are neurons of the form $\sigma _i=(n_i,R_i)$ with $1\le i\le m$, where

  • 1. $n_i\in \mathbb {Z}$ is the initial number of spikes contained in neuron $\sigma _i$;

  • 2. $R_i$ is a finite set of rules of following two forms:

    • (a) $E/b^c\rightarrow b'$, where $E$ is the regular expression over $\{a\}$ or $\{\bar{a}\}$,$b,b'\in \{a,\bar{a}\}$ and $c\ge 1$;

    • (b) $b^s\rightarrow \lambda$ for some $s\ge 1$ with the restriction that $b^s\notin L(E)$ for any rule $E/b^c\rightarrow b'$ from $R_i$ and $b\in \{a,\bar{a}\}$;

• $syn\subseteq \{1,2,\dots ,m\}\times \{1,2,\dots ,m\}$ with $(i,i)\notin syn$ is the set of synapses between neurons;

• $out\in \{1,2,\dots ,m\}$ indicates the output neuron.

The rules of the form $E/b^c\rightarrow b'$ are spiking rules. They are applied as follows: if neuron $\sigma _i$ contains $k$ spikes/anti-spikes $b$ with $b^k\in L(E)$ and $k\ge c$, then the rule $E/b^c\rightarrow b'$ is enabled to apply. The application of the rule means $c$ spikes/anti-spikes $b$ are consumed (thus $k-c$ spikes/anti-spikes $b$ remain in neuron $\sigma _i$) and one spike/antispike $b'$ is sent out to all neurons $\sigma _j$ such that $(i,j)\in syn$. For any spiking rule $E/b^c\rightarrow b'$, if $L(E)=b^c$, then it is simply written as $b^c\rightarrow b'$. Every neuron can contain several spiking rules. Because two spiking rules, $E_1/b^{k_1}\rightarrow b'$ and $E_2/b^{k_2}\rightarrow b'$, can have $L(E_1)\cap L(E_2)\ne \emptyset$, it is possible that two or more spiking rules can be used in a neuron at some moment, while only one of them is chosen non-deterministically. It is important to notice that the applicability of a spiking rule is controlled by checking the number of spikes/anti-spikes contained in the neuron against a regular expression over $\{a\}$ or $\{\bar{a}\}$ associated with the rule.

Rules of the form $b^s\rightarrow \lambda$ with $b\in \{a,\bar{a}\}$ and $s\ge 1$ are forgetting rules, by which certain number of spikes or anti-spikes can be removed out of the neuron. Specifically, if neuron $\sigma _i$ contains exactly $s$ spikes/anti-spikes, then the forgetting rule $b^s\rightarrow \lambda ,b\in \{a,\bar{a}\}$ from $R_i$ can be applied. For any regular expression $E$ associated with a spiking rule from $R_i$, it satisfies that $b^s\notin L(E)$. It means if a spiking rule is applicable, then no forgetting rule is applicable, and vice versa.

A global clock is assumed, marking the time for all neurons. The systems work in the asynchronous manner, that is, in each time unit, if a neuron has a applicable spiking/forgetting rule, this rule is not obligatorily used, which means the neuron is free to choose to use the spiking/forgetting rule or not. In other words, the neuron can remain still in spite of the fact that it contains spiking/forgetting rules which are enabled by its contents. If the contents of the neuron are not changed, the spiking/forgetting rule that are enabled at a certain step can be applied later. If the new coming spikes or anti-spikes (maybe both) make the spiking or forgetting rule unable to use, the computation continues in the new circumstances (maybe other rules are enable now).

In asynchronous ASN P systems, any neuron can have either spikes or anti-spikes, but not both of them. When spikes and anti-spikes meet in a neuron, they will immediately annihilate each other, that is, if a neuron contains both spikes and anti-spikes, then the annihilating rule must be applied in a maximal manner without taking any time. Specifically, if a neuron contains $a^r$ spikes and $\bar{a}^s$ anti-spikes inside, then the annihilating rule $a\bar{a}\rightarrow \lambda$ is immediately applied in a maximal manner, ending with $r-s$ spikes or $s-r$ anti-spikes in the neuron. It is the reason why the regular expression $E$ from any spiking rule $E/b^c\rightarrow b'$ is over $\{a\}$ or $\{\bar{a}\}$, but not over $\{a,\bar{a}\}$.

The set of synapses between neurons is denoted by $syn\subseteq \{1,2,\dots ,m\}\times \{1,2,\dots ,m\}$ with $(i,i)\notin syn$. If $(i,j)\in syn$, then there is a synapses from neuron $\sigma _i$ to neuron $\sigma _j$, along which the spike or anti-spike produced by neuron $\sigma _i$ can be sent to neuron $\sigma _j$. We can also use weighted synapses in asynchronous ASN P systems, where each connected pair of neurons is endowed with an integer number, which is called the weight of the synapse, to denote the number of synapses between them. The set of weighted synapses between each pair of neurons is of the form $syn'\subseteq \{1,2,\dots ,m\}\times \{1,2,\dots ,m\}\times \mathbb {N}$. For any $r\in \mathbb {N}$ and $i\in \{1,2,\dots ,m\}$, it holds $(i,i,r)\notin syn$, which means there is no synapse for any neuron to emit spikes or anti-spikes to itself. The function of weighted synapses is as follows: at any moment, if neuron $\sigma _i$ fires and sends one spike/anti-spike along synapse $(i,j,r)\in syn$, then $r$ spikes/anti-spikes will be received by neuron $\sigma _j$.

The configuration of the systems is of the form $\langle c_1,c_2,\dots ,c_m\rangle$ with $c_i\in \mathbb {Z}$. At any moment, if $c_i\ge 0$, it means that there are $c_i$ “positive” spikes in neuron $\sigma _i$; if $c_i<0$, it indicates that neuron $\sigma _i$ contains $c_i$ anti-spikes. By using spiking and forgetting rules, one can define transitions among configurations. A series of transitions starting from the initial configuration is called a computation. A computation is successful if it reaches a halting configuration, where no rule can be applied in any neuron (i.e., the system has halted). Because of working in the asynchronous mode, the output neuron can remain still for any long time between two consecutive spikes. Hence, the result of a computation can no longer be defined in terms of the steps between two consecutive spikes. The result of a computation in the asynchronous ASN P system is defined as the total number of spikes sent into the environment by the output neuron. We impose the restriction that the output neuron produces only spikes, not also anti-spikes; this restriction is only natural/elegant, but not essential. Specifically, a number $x$ is generated by an asynchronous SN P system if there is a successful computation of the system where the output neuron emits exactly $x$ spikes out to the environment. Because of the non-determinism in using the rules, a given system computes in this way a set of numbers. The set of all numbers computed in this way by an asynchronous ASN P system $\Pi$ is denoted by $N(\Pi )$.

By $\textit{NS}pik_{tot}\textit{ASNP}_m^{asyn}(rule_k, forg_l, wei_h)$, we denote the family of sets of numbers generated by asynchronous ASN P systems with at most $m$ neurons, where in any neuron there are at most $k$ rules, any forgetting rule removes at most $l$ spikes/anti-spikes each time and the weight of the synapses is at most $h$. If one of the parameters $m,k,l$ and $h$ is not bounded, then it is replaced with $*$. For any $m,k,l$ and $h$, it holds $\textit{NS}pik_{tot}\textit{ASNP}_m^{asyn}(rule_k, forg_l, wei_h)$ $\subseteq \textit{NS}pik_{tot}\textit{ASNP}_*^{asyn}(rule_*, forg_*, wei_*)$. If the forgetting rules or weighted synapses are not used, the indication of $forg$ or $wei$ will be removed from the notation. The subscript $tot$ reminds us of the fact that we count all spikes sent into the environment as computation results.

4 Computing Power of Asynchronous ASN P Systems

In this section, we consider the computing power of ASN P systems working in the asynchronous manner. We prove that asynchronous ASN P systems can characterize $\textit{SLIN}$ by achieving the equivalence with 1-output monotonic counter machines. Moreover, asynchronous ASN P systems with weighted synapses are proved to be Turing completeness by simulating register machines. Hence, the weighted synapses shows some “programming capacity” in the sense of achieving computing power.

Asynchronous ASN P systems are represented graphically, which maybe easier to understand than in a symbolic way. We use an oval with rules and initial spikes inside to represent a neuron, and a directed graph to represent the structure of the system: the neurons are placed in the nodes of the graph and the edges represent the synapses; the output neuron has an outgoing arrow, suggesting their communication with the environment.

4.1 Computing Power of ASN P systems using General Synapses

Lemma 1

$\textit{NS}pik_{tot}\textit{ASNP}_*^{asyn}(rule_*, forg_*)\subseteq N(C$ $M)$.

Let $\Pi$ be an asynchronous ASN P system. In the following, we will prove that there exists a 1-output monotonic counter machine $M$, which can simulate the computations of $\Pi$. Without losing generality, it is assumed that the number in the counter of $M$ never decreases before the computation halting. In the simulation, the function of the output neuron $\sigma _{out}$ in $\Pi$ can be simulated by the unique counter of $M$, and the transitions among configurations of $\Pi$ is simulated by the configuration transitions of $M$.

In the proof, besides using the configurations of $\Pi$, the number of spikes emitting to the environment by the output neuron is also considered to describe the instantaneous state of the asynchronous ASN P system $\Pi$ in each time unit. Specifically, at certain step $t$, if the configuration of $\Pi$ is $C_i$ and the output neuron emits one spike out, then the instantaneous state of $\Pi$ is $\langle C_i,1 \rangle$; if no spike is emitted out to the environment at that moment, then the instantaneous state of $\Pi$ is $\langle C_i,0 \rangle$. Note that in each time unit, at most one spike can be emitted out by the output neuron of $\Pi$. At certain moment, suppose that system $\Pi$ is in configuration $C_i$, and according to the transitions among configurations of asynchronous ASN P systems, $\Pi$ can do only one of the following five operations in each time unit.

Proof

• 1. $C_i \Rightarrow \langle C_i,0\rangle$:system $\Pi$ keeps in configuration $C_i$ with output neuron emitting no spike out to the environment. This is possible due to the asynchronous working manner of $\Pi$.

• 2. $C_i \Rightarrow \langle C_j,0\rangle$:system $\Pi$ proceeds to configuration $C_j$ from configuration $C_i$ with output neuron emitting no spike out to the environment. It means that some rules are applied in certain neurons, but no spiking rule is applied in the output neuron $\sigma _{out}$.

• 3. $C_i \Rightarrow \langle C_j,1\rangle$:system $\Pi$ proceeds to configuration $C_j$ from configuration $C_i$ with output neuron emitting one spike out to the environment.It means that some rules are used in certain neurons, where neuron $\sigma _{out}$ uses a spiking rule and sends one spike out to the environment.

• 4. $C_i \Rightarrow \langle C_h,0\rangle$:system $\Pi$ proceeds to the halt configuration $C_h$ from configuration $C_i$ with output neuron emitting no spike out to the environment.The total number of spikes emitted out to the environment by the output neuron contributes the result of the computation of $\Pi$.

• 5. $C_i \Rightarrow \langle C_h,1\rangle$:system $\Pi$ proceeds to the halt configuration $C_h$ from configuration $C_i$ with output neuron emitting one spike out to the environment. The total number of spikes emitted out to the environment by the output neuron contributes the result of the computation $\Pi$.

The state of the 1-output monotonic counter machine $M$ in each time unit is composed of its configuration and the numbers stored in the counter. Specifically, at any moment, if the configuration of $M$ is $q_i$ and the number in the output counter is $n_i$, then state of $M$ is of the form $q_i[n_i]$. In each time unit, the above five possible operations of asynchronous ASN P system $\Pi$ can be simulated by $M$ as follows.

Operation 1 can be simulated by the transition of $M$: $q_i[n_i]\Rightarrow q_i[n_i]$, which means that $M$ keeps in configuration $q_i$ without using any instruction.

Operation 2 can be simulated by the transition of $M$: $q_i[n_i]\Rightarrow q_j[n_i]$, which means that $M$ proceeds to configuration $q_j$ from $q_i$ by using an instruction of adding 0 to the output counter.

Operation 3 can be simulated by the transition of $M$: $q_i[n_i]\Rightarrow q_j[n_i+1]$, which means that $M$ proceeds to configuration $q_j$ from $q_i$ by using an ADD instruction of adding 1 to the output counter.

Operation 4 is simulated by the transition of $M$: $q_i[n_i]\Rightarrow q_f[n_i]$, which means that $M$ reaches the halting configuration $q_f$ from configuration $q_i$ by using an instruction of adding 0 to the output counter. The number stored in the output counter contributes the result of the computation of $M$.

Operation 5 is simulated by the transition of $M$: $q_i[n_i]\Rightarrow q_f[n_i+1]$, which means that $M$ reaches the halting configuration $q_f$ from configuration $q_i$ by using an ADD instruction of adding 1 to the output counter. The number stored in the output counter contributes the result of the computation of $M$.

From the previous simulation, it is obtained that any number generated by the asynchronous ASN P system $\Pi$ can also be generated by the 1-output monotonic counter machine $M$. In the asynchronous ASN P system, We don’t use any restriction on the number of neurons, the number of rules in any neuron and the most number of spikes/anti-spikes removed each time by a forgetting rule. Therefore, it is obtained that $\textit{NS}pik_{tot}\textit{ASNP}_*^{asyn}(rule_*,forg_*)\subseteq N(CM)$. $\square$

Lemma 2

$N(CM)\subseteq \textit{NS}pik_{tot}\textit{ASNP}_*^{asyn}(rule_2)$.

Let $M$ be a 1-output monotonic counter machine with properties specified in Section 2. In the following proofs, an asynchronous ASN P system $\Pi '$ is constructed to simulate the computation of $M$. The system $\Pi '$ consists of two types of modules – ADD modules and a FIN module. These modules will be given in graphical forms indicating neurons, initial number of spikes and the set of rules present in each neuron. The annihilating rule will not be indicted, since it is applicable in any neuron. The ADD modules are used to simulate the ADD instructions of $M$, and the FIN module is used to halt the computation of $\Pi '$. In general, a neuron $\sigma _{out}$ is associated with the output counter of $M$. The number stored in the output counter is represented by the number of spikes emitted by the neuron $\sigma _{out}$. Specifically, during the simulation, if the number in the output counter of $M$ increases one, then the number of spikes emitted out to the environment by the neuron $\sigma _{out}$ is increased by one.

With each instruction $l_i$ in $M$, a neuron $\sigma _{l_i}$ of $\Pi '$ is associated. In the initial configuration, all neurons are empty, with the exception of neuron $\sigma _{l_0}$ associated with the initial instruction $l_0$ of $M$ and neuron $\sigma _{l^{(1)}_h}$, which contain one spike, respectively. During a computation, a neuron $\sigma _{l_i}$ having one spike inside will become active and starts to simulate an instruction $l_i:(\mathtt{ADD}(r),l_i,l_j)$ of $M$: starting with neuron $\sigma _{l_i}$ activation, neuron $\sigma _{out}$ emits one spike to the environment to simulate that the number in the output counter is increased by one, then one spike is non-deterministically sent to neuron $\sigma _{l_j}$ or neuron $\sigma _{l_k}$, which becomes active in this way. When neuron $\sigma _{l_h}$ (associated with the halting instruction $l_h$ of $M$) is activated, a computation in $M$ is completely simulated in $\Pi '$; the FIN module will halt the computation of $\Pi '$. (If neuron $\sigma _{l_h}$ is not activated, the computation of $\Pi '$ can never halt, thus with no computing results.)

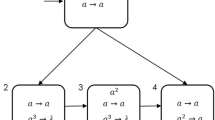
Module ADD (shown in Fig. 1) – simulating an ADD instruction $l_i: (\mathtt{ADD}$ $(r),l_j, l_k)$.

The initial instruction of $M$, the one with label $l_0$, is an ADD instruction. Let us assume that at step $t$, an instruction $l_i : (\mathtt{ADD}(r), l_j , l_k)$ has to be simulated, with one spike present in neuron $\sigma _{l_i}$ (like neuron $\sigma _{l_0}$ in the initial configuration). Having one spike inside, neuron $\sigma _{l_i}$ can fire at some time and send a spike to neuron $\sigma _{l^{(1)}_i}$. By using the rule $a\rightarrow \bar{a}$ at certain step, neuron $\sigma _{l^{(1)}_i}$ fires sending an anti-spike to neurons $\sigma _{l^{(2)}_i}$ and $\sigma _{l^{(4)}_i}$. With the anti-spike, neuron $\sigma _{l^{(2)}_i}$ can fire by using the rule $\bar{a}\rightarrow a$, and one spike is sent to neurons $\sigma _{l^{(3)}_i}$, $\sigma _{l^{(5)}_i}$ and $\sigma _{out}$, respectively. Neuron $\sigma _{out}$ can fire at some moment by the rule $a\rightarrow a$, sending one spike to the environment, which simulates the number in the output counter of $M$ is increased by one. Neuron $\sigma _{out}$ also sends one spike to neuron $\sigma _{l^{(3)}_i}$, which can fire by using one of its two spiking rules. There are the following two cases in neuron $\sigma _{l^{(3)}_i}$.

Fig. 1

Module ADD of $\Pi '$ (simulating $l_i: (\mathtt{ADD}(r), l_j, l_k)$)

Proof

• (1) In neuron $\sigma _{l^{(3)}_i}$, if rule $a^2\rightarrow a$ is chosen to be applied, then neuron $\sigma _{l^{(3)}_i}$ emits one spike to neurons $\sigma _{l^{(4)}_i}$ and $\sigma _{l^{(5)}_i}$, respectively. Having two spikes, neuron $\sigma _{l^{(5)}_i}$ will become active at some time and emits a spike to neuron $\sigma _{l_j}$. Hence, neuron $\sigma _{l_j}$ will be eventually activated, which simulates that $M$ reaches instruction $l_j$. Moreover, in neuron $\sigma _{l^{(4)}_i}$, the anti-spike will be annihilated as soon as the spike from neuron $\sigma _{l^{(3)}_i}$ arrives. When neuron $\sigma _{l_j}$ fires, all the neurons neurons are in the initial configuration. The system $\Pi '$ proceeds to a new configuration of the computation.

• (2) In neuron $\sigma _{l^{(3)}_i}$, if rule $a^2\rightarrow \bar{a}$ is chosen to be applied, then neuron $\sigma _{l^{(3)}_i}$ sends an anti-spike to neurons $\sigma _{l^{(4)}_i}$ and $\sigma _{l^{(5)}_i}$. With two anti-spikes, neuron $\sigma _{l^{(4)}_i}$ can fire by the rule $\bar{a}^2\rightarrow a$ sending a spike to neuron $\sigma _{l_k}$ at certain step. Neuron $\sigma _{l_k}$ will eventually become active to simulate that $M$ reaches instruction $l_k$. The spike in neuron $\sigma _{l^{(5)}_i}$ is annihilated by the anti-spike from neuron $\sigma _{l^{(3)}_i}$. When neuron $\sigma _k$ fires, all the neurons neurons are in the initial configuration, hence system $\Pi '$ continues the simulation and proceeds to a new configuration of the computation.

Therefore, from firing neuron $\sigma _{l_i}$, the system sends one spike to the environment and non-deterministically fires one of neurons $\sigma _{l_j}$ and $\sigma _{l_k}$, which correctly simulates the ADD instruction $l_i:(\mathtt{ADD}(r),l_j,l_k)$.

The FIN module, shown in Fig. 2, simulate the halting instruction $l_h=(\mathtt {HALT})$. Note that if the neuron $\sigma _{l_h}$ is not activated, system $\Pi '$ will never proceed to a halting configuration, because at any moment one of the two neurons $\sigma _{l^{(1)}_h}$ and $\sigma _{l^{(2)}_h}$ in the FIN module will contain one spike and keep fireable. To simulate $M$ proceeding to the halt instruction, neuron $\sigma _{l_h}$ receives one spike and becomes active at some time. By using the rule $a\rightarrow \bar{a}$, neuron $\sigma _{l_h}$ sends an anti-spike to neurons $\sigma _{l^{(1)}_h}$ and $\sigma _{l^{(2)}_h}$. The spike either in neuron $\sigma _{l^{(1)}_h}$ or $\sigma _{l^{(2)}_h}$ will be annihilated by the coming anti-spike. This will halt the computation of $\Pi '$.

Fig. 2

Module FIN of $\Pi '$

From the above description of the modules and their works, it is clear that the 1-output monotonic counter machine $M$ is correctly simulated by the asynchronous ASN P system $\Pi '$. We can check that neurons in system $\Pi '$ have at most two rules. Therefore, it is obtained $N(CM)\subseteq NSpik_{tot}ASNP_m^{asyn}(rule_2)$.

From Lemma 2, we can obtain that

$N(CM)\subseteq NSpik_{tot}ASNP_m^{asyn}(rule_2)\subseteq NSpik_{tot}ASNP_*^{asyn}(rule_*)$.

Combining with Lemma 1, the following theorem can be achieved. $\square$

Theorem 1

$NCM = {NSpik_{tot}}ASNP_m^{asyn}$ $(rule_{*},forg_{*})$.

Therefore, asynchronous ASN P systems can characterize $SLIN$.

From the previous explanation, we can obtain the equivalence between asynchronous ASN P systems without weighted synapses and 1-output monotonic counter machines. Hence, asynchronous ASN P systems hold those closure properties and decision problems that are associated with 1-output monotonic counter machines [7].

• 1. (Union, intersection, complementation) The sets of numbers generated by asynchronous ASN P systems are closed under union and intersection, but not closed under complementation.

• 2. (Membership) For a given asynchronous ASN P system $\Pi$ and a number $n$, it is decidable to determine if $\Pi$ generates $n$.

• 3. (Emptiness) For a given asynchronous ASN P system $\Pi$, it is decidable that if $\Pi$ generates an empty set of numbers.

• 4. (Infiniteness) For a given asynchronous ASN P system $\Pi$, it is decidable that if $\Pi$ generates an infinite set of numbers.

• 5. (Disjointness) For two given asynchronous ASN P systems $\Pi$ and $\Pi '$, it is decidable that if $\Pi$ and $\Pi '$ generate a common number.

• 6. (Containment) For two given asynchronous ASN P systems, it is decidable if the set of numbers generated by one is contained in the set of numbers generated by the other one.

• 7. (Equivalence) For two given asynchronous ASN P systems, it is decidable if they generate the same set of numbers.

4.2 Computing Power of ASN P Systems Using Weighted Synapses

Theorem 2

$NSpik_{tot}ASNP_m^{asyn}(rule_2, wei_3)=\textit{NRE}$.

We only have to prove that $\textit{NRE}\subseteq NSpik_{tot}$ $ASNP_m^{asyn}(rule_2, wei_3)$, since the converse inclusion is straightforward (or we can invoke for it from the Turing-Church thesis). To this aim, we use the characterization of $NRE$ by means of register machines in the generative mode. Let us consider a register machine $M = (m, H, l_0, l_h, I)$. As introduced in Section 2, without any loss of generality, we may assume that in the halting configuration, all registers different from register 1 are empty, and that output register is never decremented during a computation. For each register $r$ of $M$, let $s_r$ be the number of instructions of the form $l_i: (\mathtt{SUB}(r),l_j,l_k)$, i.e., all SUB instructions acting on register $r$. If there is no such SUB instruction, then $s_r=0$, which is the case for the first register $r=1$. In what follows, a specific asynchronous ASN P system $\Pi ''$ will be constructed to simulate the computation of register machine $M$.

The system $\Pi ''$ consists of three types of modules – ADD modules, SUB modules, and a FIN module shown in Figs. 3, 4, 5, respectively. The ADD and SUB modules are used to simulate the ADD and SUB instructions of $M$, and the FIN module is used to output a computation result. These modules will be given in graphical forms indicating neurons, weighted synapses, initial number of spikes and the set of rules present in each neuron. Each weighted synapse is associated with an internal number denoting the number of synapses between each pair of connected neurons, and there is no confliction that synapses with weight 1 were not associated with any numbers. The annihilating rule can be used immediately if it is applicable in any neuron. Here, this rule will not be indicted in the set of rules in graphical neurons for simplification.

Fig. 3

Module ADD of $\Pi ''$ (simulating $l_i: (\mathtt{ADD}(r), l_j, l_k)$)

Fig. 4

Module SUB of $\Pi ''$ (simulating $l_i: (\mathtt{SUB}(r), l_j, l_k)$)

Fig. 5

The FIN module of $\Pi ''$

In general, for each register $r$ of $M$, a neuron $\sigma _{r}$ is associated; the number stored in register $r$ is encoded by the number of spikes in neuron $\sigma _{r}$. Specifically, if register $r$ holds the number $n\ge 0$, then neuron $\sigma _{r}$ contains $2n$ spikes. For each label $l_i$ of an instruction in $M$, a neuron $\sigma _{l_i}$ is associated. In the initial configuration, all neurons are empty, with the exception of neuron $\sigma _{l_0}$ associated with the initial instruction $l_0$ of $M$, which contains one spike.

During a computation, a neuron $\sigma _{l_i}$ having one spike inside will become active and start to simulate an instruction $l_i:(\mathtt{OP}(r),l_j,l_k)$ of $M$: starting with neuron $\sigma _{l_i}$ activated, operating neuron $\sigma _{r}$ as requested by $\mathtt{OP}$, then introducing one spike into neuron $\sigma _{l_j}$ or neuron $\sigma _{l_k}$, which becomes active in this way. When neuron $\sigma _{l_h}$ (associated with the label $l_h$ of the halting instruction of $M$) is activated, a computation in $M$ is completely simulated in $\Pi ''$; the FIN module starts to output the computation result (the number of spikes sent into the environment by the output neuron corresponds to the number stored in register 1 of $M$).

In what follows, the work of modules ADD, SUB and FIN are described (that is, how they simulate the instructions of $M$ and output a computation result).

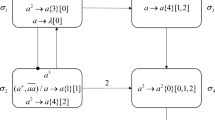
Module ADD (shown in Fig. 3) – simulating an ADD instruction $l_i: (\mathtt{ADD}$ $(r),l_j, l_k)$.

The initial instruction of $M$, the one with label $l_0$, is an ADD instruction. Let us assume that at step $t$, an instruction $l_i : (\mathtt{ADD}(r), l_j , l_k)$ has to be simulated. Having one spike inside, neuron $\sigma _{l_i}$ fires at some time by using the rule $a\rightarrow a$. Since the weight of the synapse between neurons $\sigma _{l_i}$ and $\sigma _r$ is 2, neuron $\sigma _r$ will receive two spikes, which simulates the number in register $r$ is increased by one. Meanwhile, neuron $\sigma _{l_i}$ emits one spike to neuron $\sigma _{l^{(1)}_i}$. With one spike inside, neuron $\sigma _{l^{(1)}_i}$ can fire at some moment sending an anti-spike to neurons $\sigma _{l^{(2)}_i}$ and $\sigma _{l^{(5)}_i}$, respectively. By receiving the anti-spike, neuron $\sigma _{l^{(2)}_i}$ becomes active at any time sending one spike to neurons $\sigma _{l^{(3)}_i}$ and $\sigma _{l^{(4)}_i}$. In neuron $\sigma _{l^{(3)}_i}$, one of the two spiking rules $a\rightarrow a$ and $a\rightarrow \bar{a}$ will be non-deterministically chosen to apply. The non-deterministic choice of the two rules determines the non-deterministic choice of neuron $\sigma _{l_j}$ or $\sigma _{l_k}$ to activate.

In neuron $\sigma _{l^{(3)}_i}$, if the rule $a\rightarrow a$ is applied, then it emits one spike to neurons $\sigma _{l^{(4)}_i}$ and $\sigma _{l^{(5)}_i}$. The anti-spike in neuron $\sigma _{l^{(5)}_i}$ will be annihilated by the spike from neuron $\sigma _{l^{(3)}_i}$, so neuron $\sigma _{l^{(5)}_i}$ contains no spike or anti-spike and keeps inactive. With two spikes inside, neuron $\sigma _{l^{(4)}_i}$ can fire at some time by the rule $a^2\rightarrow a$ sending one spike to neuron $\sigma _{l_j}$, which will become active at some time, starting to simulate the instruction $l_j$ of $M$.

In neuron $\sigma _{l^{(3)}_i}$, if the rule $a\rightarrow \bar{a}$ is applied, then it emits an anti-spike to neurons $\sigma _{l^{(4)}_i}$ and $\sigma _{l^{(5)}_i}$. When the anti-spike arrives in neuron $\sigma _{l^{(4)}_i}$, the spike in the neuron will be annihilated, so neuron $\sigma _{l^{(4)}_i}$ can not fire. Having two anti-spikes, neuron $\sigma _{l^{(5)}_i}$ will fire at some time by the rule $\bar{a}^2\rightarrow a$ sending one spike to neuron $\sigma _{l_k}$. Neuron $\sigma _{l_k}$ will fire at any time, starting to simulate the instruction $l_k$ of $M$.

Therefore, from firing neuron $\sigma _{l_i}$, the system adds two spikes to neuron $\sigma _{r}$ and non-deterministically fires one of the neurons $\sigma _{l_j}$ and $\sigma _{l_k}$, which correctly simulates the ADD instruction $l_i:(\mathtt{ADD}(r),l_j,l_k)$.

Module SUB (shown in Fig. 4) – simulating a SUB instruction $l_i:(\mathtt{SUB}(r),$ $l_j,l_k)$.

A SUB instruction $l_i$ is simulated in $\Pi ''$ in the following way. Initially, neuron $\sigma _{l_i}$ has one spike, and other neurons are empty, except neurons associated with registers. With one spike inside, the rule $a \rightarrow a$ in neuron $\sigma _{l_i}$ is enabled, and neuron $\sigma _{l_i}$ will fire at some step sending one spike to neurons $\sigma _{l^{(1)}_i},\sigma _{l^{(2)}_i}$ and $\sigma _r$. At that moment, neuron $\sigma _{l^{(1)}_i}$ and $\sigma _{l^{(2)}_i}$ contain one spike and keep inactive. For neuron $\sigma _{r}$, there are the following two cases.

Proof

• (1) Neuron $\sigma _{r}$ has $2n$ ($n> 0$) spikes (corresponding to the fact that the number stored in register $r$ is $n$, and $n>0$) before it receives one spike from neuron $\sigma _{l_i}$. In this case, neuron $\sigma _{r}$ contains $2n+1$ spikes after it receives one spike from neuron $\sigma _{l_i}$, and the rule $a(a^2)^+/a^3\rightarrow a$ is enabled. When neurons $\sigma _r$ fires at some step, one spike is sent to neuron $\sigma _{l^{(1)}_i}$, as well as two spikes are sent to neuron $\sigma _{l^{(2)}_i}$. In neuron $\sigma _r$, three spike are consumed, ending with $2n+1-3=2(n-1)$ spikes, which simulates that the number stored in register $r$ is decreased by one. With two spikes inside, neuron $\sigma _{l^{(1)}_i}$ can fire sending one spike to neuron $\sigma _{l^{(3)}_i}$. When neuron $\sigma _{l^{(3)}_i}$ fires, neuron $\sigma _{l^{(2)}_i}$ can receive three anti-spikes. which will immediately annihilate the three spikes in the neuron. By receiving the anti-spike from neuron $\sigma _{l^{(3)}_i}$, neuron $\sigma _{l^{(5)}_i}$ fires at some time sending a spike to neuron $\sigma _{l_j}$, hence neuron $\sigma _{l_j}$ will become active, and the system $\Pi ''$ starts to simulate instruction $l_j$ of $M$.

• (2) Neuron $\sigma _{r}$ has 0 spike (corresponding to the fact that the number stored in register $r$ is $0$) before it receives one spike from neuron $\sigma _{l_i}$. In this case, after neuron $\sigma _r$ receives one spike from neuron $\sigma _{l_i}$, the rule $a\rightarrow \bar{a}$ in neuron $\sigma _r$ is enabled. When neuron $\sigma _r$ fires at some step, an anti-spike is emitted to neuron $\sigma _{l^{(1)}_i}$, as well as two anti-spikes are emitted to neuron $\sigma _{l^{(2)}_i}$. The spike in neuron $\sigma _{l^{(1)}_i}$ can be annihilated by the anti-spike from neuron $\sigma _r$, so the neuron will keep inactive. In neuron $\sigma _r$, one spike is consumed, ending with $0$ spike, which means that the number stored in register $r$ of $M$ is still zero. In neuron $\sigma _{l^{(2)}_i}$, the spike is annihilated by one of the two anti-spikes from neuron $\sigma _r$, so the neuron ends with an anti-spike and the rule $\bar{a}\rightarrow a$ is enabled. Neuron $\sigma _{l^{(2)}_i}$ fires at some time sending one spike to neuron $\sigma _{l_k}$, hence neuron $\sigma _{l_k}$ will become active, and the system $\Pi ''$ starts to simulate instruction $l_k$ of $M$.

The simulation of SUB instruction is correct: system $\Pi ''$ starts from firing neuron $\sigma _{l_i}$ and ends in firing neuron $\sigma _{l_j}$ (if the number stored in register $r$ is great than $0$ and decreased by one), or in firing neuron $\sigma _{l_k}$ (if the number stored in register $r$ is $0$).

Note that there is no interference between the ADD modules and the SUB modules, other than correctly firing the neurons $\sigma _{l_j}$ or $\sigma _{l_k}$, which may label instructions of the other kind. However, it is possible to have interference between two SUB modules. Specifically, there are $s_r$ SUB instructions $l_v$ that act on register $r$, hence neuron $\sigma _{r}$ has synapse connection to all neurons $\sigma _{l_v^{(1)}}$ and $\sigma _{l_v^{(2)}}$. When a SUB instruction $l_i: (\mathtt{SUB}(r), l_j, l_k)$ is simulated, in the SUB module associated with $l_v$ ($l_v\not = l_i$) all neurons receive no spike except for neurons $\sigma _{l_v^{(1)}}$ and $\sigma _{l_v^{(2)}}$.

If neuron $\sigma _r$ fires by the rule $a(aa)^+/a^3\rightarrow a$, then it sends one spike to each of neurons $\sigma _{l_v^{(1)}}$, as well as two spikes to each of neurons $\sigma _{l_v^{(2)}}$. In this case, neuron $\sigma _{l_i^{(3)}}$ will fire at some time sending an anti-spike to each of neurons $\sigma _{l_v^{(1)}}$, and two anti-spikes to each of neurons $\sigma _{l_v^{(2)}}$, with $l_v\not = l_i$. The neurons $\sigma _{l_v^{(1)}}$ and $\sigma _{l_v^{(2)}}$ end with no spike/anti-spike inside. Consequently, the interference among SUB modules will not cause undesired steps in $\Pi ''$ (i.e., steps that do not correspond to correct simulations of instructions of $M$).

If neuron $\sigma _r$ fires by the rule $a\rightarrow \bar{a}$, then it sends anti-spike to each of neurons $\sigma _{l_v^{(1)}}$, as well as two anti-spikes to each of neurons $\sigma _{l_v^{(2)}}$. In this case, neuron $\sigma _{l_i^{(4)}}$ will fire at some time sending one spike to each of neurons $\sigma _{l_v^{(1)}}$, and two spikes to each of neurons $\sigma _{l_v^{(2)}}$ with $l_v\not = l_i$. The neurons $\sigma _{l_v^{(1)}}$ and $\sigma _{l_v^{(2)}}$ end with no spike/anti-spike. The interference among SUB modules will not cause undesired steps in $\Pi ''$.

Module FIN (shown in Fig. 5) – outputting the result of computation.

Assume that the computation in $M$ halts (that is, the halting instruction is reached), which means that neuron $\sigma _{l_h}$ in $\Pi ''$ has one spike. At that moment, neuron $\sigma _{1}$ contains $2n$ spikes, for the number $n\ge 1$ stored in register 1 of $M$. With one spike inside, neuron $\sigma _{l_h}$ will fire at some step sending one spike to neuron $\sigma _{1}$. After neuron $\sigma _{1}$ receives the spike from neuron $\sigma _{l_h}$, the number of spikes in neuron $\sigma _1$ becomes $2n+1$ spikes, and the rule $a(aa)^+/a^2\rightarrow a$ is enabled. When neuron $\sigma _{1}$ fires, it sends one spike into the environment consuming two spikes. Note that the number of spikes in neuron $\sigma _{1}$ is still odd. So, if the number of spikes in neuron $\sigma _{1}$ is not less than three, then neuron $\sigma _{1}$ will fire again at some step sending one spike into the environment. In this way, neuron $\sigma _1$ can fire for $n$ times (i.e., until the number of spikes in neuron $\sigma _{1}$ reaches one). For each time when neuron $\sigma _1$ fires, it sends one spike into the environment. So, in total, neuron $\sigma _1$ sends $n$ spikes into the environment, which is exactly the number stored in register 1 of $M$ at the moment when the computation of $M$ halts. Where neuron $\sigma _1$ contains one spike, no rule is enabled in the neuron, thus system $\Pi ''$ eventually halts.

From the above description of the modules and their works, it is clear that the register machine $M$ is correctly simulated by the system $\Pi ''$, where any neuron contains at most 2 rules, no forgetting rule is used in any neuron, and the most weight of the weighted synapses is 3. Therefore, $N(M)=NSpik_{tot}ASNP_m^{asyn}$ $(rule_2, wei_3)$. This completes the proof. $\square$

5 Final Remarks

We have considered the computing power of asynchronous ASN P systems with and without weighted synapses. In the asynchronous systems, in each time unit, neurons with enabled rules is free to choose to use the rule. In other word, the neurons can remain still and receive spikes or anti-spikes (maybe both) from its neighboring neurons. The asynchronous working manner will decrease the computing power of the ASN P systems. Specifically, ASN P systems working in the asynchronous manner with no weighted synapses can only characterize the $SLIN$. This result is obtained by achieving the equivalence between asynchronous ASN P systems (with no weighted synapses) and 1-output monotonic counter machine. When we use weighted synapses, we prove that the asynchronous ASN P system with weighted synapses (with weight not more than three) can do what Turing machine can do, i.e. achieving the Turing completeness.

There are several open problems and research topics deserving further research. In ASN P systems, spiking rules are of the form $E/b^c\rightarrow b'$, and there are four categories of spiking rules identified by $(b,b')\in \{(a,a),(a,\bar{a}),(\bar{a},a),(\bar{a},\bar{a})\}$. In the proof of Theorem 2, three categories of spiking rules (identified by $(a,a)$, $(a,\bar{a})$ and $(\bar{a},a)$) are used. It is worth to investigate whether the universality can be obtained with using less types of spiking rules.

Artificial Neural networks have been widely applied in optimization (see e.g. [3, 4, 23]) and control systems (see e.g. [5, 22]). It is worthy to investigate the performance of RSSN P systems on these fields. Another interesting problem is when the application of annihilating rules is not obligatorily used in the neurons, how about of the computing power of such systems? Following the “homogenous” idea from [20], can we decrease the number of types of neurons in the universal asynchronous ASN P systems, in sense of having a less number of sets of rules in each neuron. As usual, it is also worth to investigate computing power of asynchronous ASN P systems under different computational modes.