Introduction

In recent years, researchers have identified potential minerals mainly by extraction of weak anomalies in geological, geophysical, and geochemical information (Cheng 2012a, b, 2021). In processing regional geochemical data, complex geological and geographical background conditions have posed difficulties for screening geochemical anomalies: the areas with high element contents may not have minerals, and areas with low element contents, by contrast, may be potential mineral areas. Thus, the detection of weak geochemical anomalies is one of the main challenges in geochemical exploration (Xiong et al. 2018; Zuo et al. 2019; Wang and Zuo 2020).

The processes of element migration and enrichment do not occur for a single element, but follow the affinity characteristics of elements and the matching variations among elements, which lead to the numerical correlation of elements and clustering in space (Cong et al. 2012). Previous studies have shown that the distribution patterns of geochemical anomalies are usually synthetic multi-element anomalies, mainly because some elements tend to show similar geochemical behaviors under specific geological conditions; thus, certain specific symbiotic combinations of elements appear in the final geological products (Wang 2018; Gao 2019). Therefore, the results of multiple geochemical synthesis anomalies are more reliable than those of single-element anomalies. Common information fusion models include logical regression (Mejía-Herrera et al. 2015; Yousefi et al. 2014), random forest (Zhang et al. 2019a, b; Sun et al. 2019; Hong et al. 2021), and deep learning (Moeini and Torab 2017; Zhang et al. 2021), all of which can identify geochemical anomalies against complex geological backgrounds and effectively integrate multivariate information. However, selecting appropriate models plays a crucial role in the regression analysis (Ramezanali et al. 2019). Due to the complexity of the algorithm, the efficiency of data processing is low in random forest and deep learning models (Chen and Wu 2017; Rahimi et al. 2021; Zuo et al. 2021; Zuo et al. 2019). Maximum entropy model is simple to calculate, can quickly and efficiently process data, and has high prediction accuracy, which is suitable for solving classification problems (Phillips et al. 2006; Phillips and Jane 2013). This model has been successfully applied in various fields, such as natural language processing (Dong et al. 2012), economic prediction (Xu et al. 2014), environmental evaluation (Biazar et al. 2020; Biazar and Ferdosi 2020; Aghelpour et al. 2020; Jahangir et al. 2021; Yang et al. 2021; Yang et al. 2020; Azareh et al. 2019), geographical distribution of animal and plant species (Wang et al. 2017), and mineral exploration (Liu et al. 2018; Li et al. 2019, 2021). Liu et al. (2018) applied the maximum entropy model to the potential distribution of orogenic gold deposits based on quantitative critical metallogenic processes in the Tangbale-Hatu belt, western Junggar, China. Li et al. (2019) used the maximum entropy model to predict the metallogenic prospect of the Mila Mountain region in Tibet, and the model considered both positive and negative factors related to mineralization.

In the present study, the copper polymetallic mineralization in the Mila Mountain region, southern Tibet is taken as the research object. The process and results of metallogenic prediction are discussed by using component data factor analysis and the maximum entropy model, to provide a reference for the wide application of machine learning algorithm in mineral resource evaluation and prediction.

Study area and geochemical data

Study area

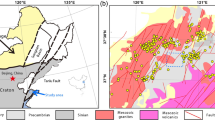
The study area is located in the middle and southern parts of the Gangdese-Nyainqentanglha (terrane) plate in the Tethys structural area of Tibet (29°10′N–29°55′N; 90°45′E–93°00′E), and is one of the most famous copper metallogenic regions in the world (Song et al. 2018; Lin et al. 2017a, b, 2019). The study area is a deeply incised alpine region, with the terrain high in the north and low in the south, high in the east and low in the west. Most of the mining areas are higher than 4500 m above sea level, and some mountaintops are covered with snow year-round, often forming modern glaciers. The climate in the region is a typical plateau continental climate, with a distinct dry season and a rainy season, and rainy season from June to September. The vertical zonation of temperature and vegetation is obvious, with long sunny days, low temperatures, large temperature differences between day and night, short frost-free periods and many snowfall days. The weather is relatively fair from April to September every year, and is suitable for field operations. The streams in the study area are well developed, including mainly the Yarlung-Tsangpo River, the Lhasa River and secondary streams.

Magmatic rocks in the research area widespread, including large deep intrusions and thick volcaniclastic rock layers, mainly distributed north of the Yajiang fault. These igneous rocks are important constituents of the Gangdese volcanic-magmatic arc (Lang et al. 2012). The intrusive rocks from a major component of the magmatic rocks in the Gangdese area, and represent the products of plate subduction-collision events during the evolution of middle-Cenozoic Tethyan tectonics. The general trend of the fault structure in the study area is nearly east-west, which plays an important role in mineralization. The Bouguer gravity anomaly is 350–550 mgL, and has a gradient gradually decreasing from south to north. The anomaly value (ΔT) of the aeromagnetic pole is −300–550 nT. Most of the single positive magnetic anomaly strips are oriented nearly east-west, and the positive and negative magnetic anomalies alternate to form strips (Zhang et al. 2019a, b). The anomalies in geochemical elements such as Cu, Mo, Pb, Zn, Au, and Ag are generally distributed nearly east-west, and the characteristics of element association are regular from south to north (Wang et al. 2010). The study area is very rich in minerals, including ferrous metal minerals, nonferrous metal minerals, precious metal minerals, fuel minerals, building materials, non-metallic minerals, and geothermal resources (Zheng et al. 2016; Yang and Hou 2009). Among them, nonferrous metal (copper, lead-zinc, etc.) building materials and geothermal resources are the dominant assets in the area (Figure 1).

Fig. 1
figure 1

a Tectonic sketch map showing the location of the study area (after Yin and Harrison 2000; Zheng et al. 2021). JS, Jinshajiang suture; LSS, Longmucuo–Shuanghu suture; BNS, Bangonghu–Nujiang suture; IYZS, Indus–Yarlung Zangbo suture; STDS, south Tibetan detachment system; MCT, main central thrust; MBT, main boundary thrust; ALT, Altyn Tagh fault; KF, Kunlun fault; KLF, Karakoram fault; JF, Jiali fault. TH, Tethys Himalaya; HH, Higher Himalaya; LH, Lesser Himalaya. b Generalized geological and deposits distribution map of the study area (Li et al. 2021)

Full size image

Geochemical data

The geochemical dataset utilized in this study was collected as part of the Chinese National Geochemical Mapping project. The actual sampling area of the stream sediment survey was 12,290 km2, and 4141 effective samples were collected (Figure 2) (Xie et al. 1997). The sampling locations were arranged according to specifications, and located at the bottom of modern rivers and riverbeds, or at the bottom of the seasonal flow or in the main channel conducive to gravel deposition and mixed accumulation of various particle sizes. The sampling material was mainly sand, and one sample was combined after multipoint collection within 20–50 m near the sampling point. Samples with particle sizes less than 0.22 mm (60 mesh) were collected using 60-mesh stainless steel sieves and the sample weights were greater than 200 g. All samples were analyzed after drying and sifting. 39 elements such as Cu, Pb, Zn were quantitatively analyzed by the foam adsorption graphite furnace atomic absorption method, AC arc-emission spectroscopy, inductively coupled plasma atomic emission spectroscopy, inductance coupled plasma mass spectrometry, the alkali melting-catalytic electrode method, atomic fluorescence spectroscopy, etc. (Xie et al. 1997, 2008; Wang et al. 2011; Xie 2008). The specific test methods, detection limits and other information for each element are shown in Table 1, and detailed information about the data quality and sampling strategy can be found in these studies (Xie et al. 1997).

Fig. 2
figure 2

Geochemical sampling locations

Full size image
Table 1 Specific test methods and detection limits for each element (Wang et al. 2011)
Full size table

Methods

Log-ratio approach

The commonly used methods of log-ratio transformation include additive log-ratio (alr), central log-ratio (clr), and isometric log-ratio (ilr) (Aitchison 1986; Carranza 2011; Egozcue et al. 2003). The output result of the alr transformation depends mainly on the choice of denominator, so it has strong subjectivity. The clr transformation takes the geometric mean of all variables as the denominator, which can effectively improve upon the alr transformation, and the vectors before and after the transformation correspond one to one; thus, the clr transformation can be used to explain the statistical results based on the clr transformation data using the original variable. However, the clr transformation has the problem of data collinearity, which makes it impossible to use the ordinary least squares regression method (Carranza 2011; Filzmoser et al. 2009b; Zuo et al. 2013). The ilr transformtion solves the problem of data collinearity in clr transformation, and retains all the advantages. The ilr approach transforms the component data in simplex space into real numbers in Euclidean space (Egozcue et al. 2003). The clr transformation is applied to process the regional geochemical data. It involves a transformation from the simplex sample space to D-dimensional real space. A compositional random vector \(X=({x}_{1},{x}_{2},\cdots ,{x}_{D})\) can be defined as follows (Buccianti and Grunsky 2014; Egozcue et al. 2003):

$$clr\left(X\right)=({y}_{1},{y}_{2},\cdots ,{y}_{D})=\left(log\frac{{x}_{1}}{\sqrt[D]{{\prod }_{i=1}^{D}{x}_{i}}},\cdots ,log\frac{{x}_{D}}{\sqrt[D]{{\prod }_{i=1}^{D}{x}_{i}}}\right)$$
(1)

Where, \(\sqrt[D]{{\prod }_{i=1}^{D}{x}_{i}}\) is the geometric mean.

Factor analysis

Factor analysis is one of the most commonly used multivariate statistical methods for dimensionality reduction of datasets. It is an effective method to realize high-dimensional data visualization in low-dimensional space based on variance and covariance matrices, and has been widely used in geochemical data processing (Meigoony et al. 2014; Hoseinpoor and Aryafar 2016; Wu et al. 2020; Yousefi et al. 2014; Zuo et al. 2013; Filzmoser et al. 2009a, b, c). Factor analysis can combine multiple related variables into a single variable, thereby reducing the dimension of a dataset to irrelevant principal components based on the covariance or correlation of the variables (Jolliffe 2002; Reimann et al. 2005; Zuo 2011). In the process of geochemical data processing, each element dataset is divided into several nonobservable factors through factor analysis. These factors extract the main information of the original variables and represent some inherent features of the original dataset, such as complex geologic origin and mineralization process (Johnson and DW 2002; Muller et al. 2008; Zuo 2011).

Maximum entropy model

Maximum entropy theory reflects a basic principle of nature: systems contain both constraints and freedom and always tend toward the maximum degree of freedom under the constraints, that is, maximum entropy (Phillips et al. 2006). Therefore, under known conditions, the system with the largest entropy is most likely to be close to its real state. Specifically, for an event, we often know only part of its situation and know nothing about other aspects of its situation. When building a model for the event, we should attempt to fit the known part to make the model conform to the known situation; for the unknown parts, the uniform distribution is maintained, and the entropy is the largest of the event at this time (Li 2012).

Let \(X=\left\{{x}_{1},{x}_{2},\cdots ,{x}_{n}\right\}\) be a set of discrete random variables, \({p}_{i}=P\left(X={x}_{i}\right)\) be the probability distribution of \({x}_{i}(i=\mathrm{1,2},\cdots ,n)\), and the entropy can be explicity written as:

$$H\left(X\right)=-\sum_{i=1}^{n}{p}_{i}log{p}_{i}$$
(2)

And the entropy satisfies the following condition

$$0\le H\left(X\right)\le logn$$
(3)

Where n is the total number of values available in X, and the right equality holds when X is uniformly distributed.

The maximum entropy principle originates from statistical mechanics (Jaynes 1957), which obtains the maximum entropy model (MaxEnt) when applied to classification problems. We assume that the classification model is a conditional probability distribution \(P\left(Y\left|X\right.\right)\), \(X\in \chi \in {R}^{n}\) is the input data, \(Y\in\) \(y\) \(\in {R}^{n}\) is the output data, \(x\) and \(y\) represent sets of input data and sets of output data, respectively. The model represents the output of Y with a conditional probability P for a given input data X. The maximum entropy model can be defined as follows (Li 2012).

Let \(C\equiv \left\{P\in \mathrm{P}\left|{E}_{P}\left({f}_{i}\right)={E}_{\tilde{P }}\left({f}_{i}\right)\right.,(i=\mathrm{1,2},\cdots ,n)\right\}\) be the set of models that satisfy all constraints, \(H\left(P\right)=-\sum_{x,y}\tilde{P }\left(x\right)P\left(y\left|x\right.\right)lnP\left(y\left|x\right.\right)\) be the conditional entropy defined on the conditional probability distribution \(P\left(Y\left|X\right.\right)\). Then, the model with the largest conditional entropy \(H\left(P\right)\) in the model set \(C\) is called the maximum entropy model.

Where \({E}_{\tilde{P }}\left({f}_{i}\right)={\sum }_{x,y}\tilde{P }\left(x,y\right){f}_{i}(x,y)\) is the expected value of n eigenfunctions \({f}_{i}(x,y)\) about the empirical distribution \(\tilde{P }(x,y)\), and \({E}_{P}\left({f}_{i}\right)={\sum }_{x,y}\tilde{P }\left(x\right)P\left(y\left|x\right.\right){f}_{i}(x,y)\) is the expected value of n eigenfunctions \({f}_{i}(x,y)\) about \(P\left(Y\left|X\right.\right)\) and the empirical distribution \(\tilde{P }\left(X\right)\).

The process of solving the maximum entropy model is a learning process for the model, which can be formalized into a constrained optimization problem (Li 2012).

Let \(T=\left\{({x}_{1},{y}_{1}),({x}_{2},{y}_{2}),\cdots ,({x}_{n},{y}_{n})\right\}\) be the training dataset and \({f}_{i}(x,y),i=\mathrm{1,2},\cdots ,n\) be the eigenfunction. The learning of the maximum entropy model is equivalent to the constrained optimization problem:

$$\underset{P\in C}{max}H\left(P\right)=-\sum_{x,y}\tilde{P }\left(x\right)P\left(y\left|x\right.\right)lnP\left(y\left|x\right.\right)$$
(4)
$$\begin{array}{cc}\mathrm{s}.\mathrm{t}.& {E}_{P}\left({f}_{i}\right)={E}_{\tilde{P }}\left({f}_{i}\right)i=\mathrm{1,2},\cdots ,n\end{array}$$
(5)
$$\sum_{y}P\left(y\left|x\right.\right)=1$$
(6)

According to the optimization problem, the maximum problem is rewritten to the equivalent minimum problem:

$$\underset{P\in C}{min}-H\left(P\right)=\sum_{x,y}\tilde{P }\left(x\right)P\left(y\left|x\right.\right)lnP\left(y\left|x\right.\right)$$
(7)
$$\begin{array}{cc}\mathrm{s}.\mathrm{t}.& {E}_{P}\left({f}_{i}\right)-{E}_{\tilde{P }}\left({f}_{i}\right)=0i=\mathrm{1,2},\cdots ,n\end{array}$$
(8)
$$\sum_{y}P\left(y\left|x\right.\right)=1$$
(9)

The solution derived from the above constrained optimization problem is the solution of maximum entropy model learning. However, the expectation of the empirical distribution is usually not equal to the real situation, but only approximates the real situation. If the solution is strictly based on the above constraint conditions, overfitting of the training data can easily be caused in the learning process. Therefore, the constraint conditions can be appropriately relaxed in the actual solution, and equation \({E}_{P}\left({f}_{i}\right)-{E}_{\tilde{P }}\left({f}_{i}\right)=0i=\mathrm{1,2},\cdots ,n\) can be replaced by \({E}_{P}\left({f}_{i}\right)-{E}_{\tilde{P }}\left({f}_{i}\right)\le {\beta }_{i}\), \({\beta }_{i}\) is a constant, called regularization multiplier (Dudík et al. 2004). The problem of overfitting can be effectively avoided by solving the above constrained optimization problems (Phillips et al. 2004, 2006).

Model evaluation

Model evaluation is an important component of machine learning. In this paper, the MaxEnt model is evaluated by the area under the receiver operating characteristic curve (AUC), Cohen’s maximum kappa coefficient and true skill statistics (TSS). These three metrics are calculated based on the specificity and sensitivity of the prediction model (Li et al. 2019).

Sensitivity (SEN) refers to the percentage of positive samples correctly identified by the classifier, and is used to measure the ability of the classifier to identify positive samples.

$$SEN=\frac{\text{truepositives}}{\begin{array}{ccc}{\text{true}}& {\text{positives}}& +\end{array}\begin{array}{cc}{\text{flase}}& {\text{negatives}}\end{array}}$$
(10)

Specificity (SPE) is the percentage of negative samples correctly identified by the classifier, and is used to measure the ability of the classifier to identify negative samples.

$$SPE=\frac{\text{truenegatives}}{\begin{array}{ccc}{\text{true}}& {\text{negatives}}& +\end{array}\begin{array}{cc}{\text{false}}& {\text{positives}}\end{array}}$$
(11)

The receiver operating characteristic curve (ROC) is plotted with the false positive rate (FPR) as the horizontal axis and the true positive rate (TPR) as the vertical axis.

$$TPR=\frac{\text{truepositives}}{\begin{array}{ccc}{\text{true}}& {\text{positives}}& +\end{array}\begin{array}{cc}{\text{flase}}& {\text{negatives}}\end{array}}$$
(12)
$$FPR=\frac{\text{falsepositives}}{\begin{array}{ccc}{\text{true}}& {\text{negatives}}& +\end{array}\begin{array}{cc}{\text{false}}& {\text{posi}}{\text{tives}}\end{array}}$$
(13)

The AUC is a quantitative evaluation index independent of the threshold, and the greater value indicates a better model classification effect. If the ROC is connected by points with coordinate \(\left\{\left({x}_{1},{y}_{1}\right),\left({x}_{2},{y}_{2}\right),\cdots ,\left({x}_{m},{y}_{m}\right)\right\}\), AUC can be expressed as:

$$AUC=\frac{1}{2}\sum_{i=1}^{m-1}\left({x}_{i+1}-{x}_{i}\right)\left({y}_{i}+{y}_{i+1}\right)$$
(14)

The kappa coefficient refers to the accuracy of prediction relative to random occurrence, and is influenced by the incidence of distribution points and the threshold (Cohen 1960), it can be expressed as:

$${\text{Kappa}}=\frac{\left(TP+TN\right)-{\left(exp{\text{ectedcorrect}}\right)}_{ran}}{{\text{Total}}-{\left(\begin{array}{cc}exp{\text{ected}}& {\text{correct}}\end{array}\right)}_{ran}}$$
(15)

Where, \({\left(exp{\text{ectedcorrect}}\right)}_{ran}=\frac{1}{N}\left[\left(TP+FN\right)\left(TP+FP\right)+\left(TN+FN\right)\left(TN+FP\right)\right]\), TP, TN, FP and FN are true positive, true negative, false positive, and false negative values, respectively.

TSS represents the ability of predictive results to distinguish between “yes” and “no”, independent of the incidence of distribution points, but influenced by thresholds, while TSS = SEN + SPE -1 (Allouche et al. 2006). AUC, TSS, and kappa statistics have different responses to the incidence and threshold of distribution points (Table 2), and can be combined to better evaluate the performance of the model (Swets 1988; Araújo et al. 2005; Coetzee et al. 2009).

Table 2 Measurement standards for AUC, kappa and TSS
Full size table

Results and discussion

Factor analysis for compositional data

In nature, almost all environmental data have the characteristics of component data. Due to the closure effect of component data, traditional multivariate analysis has certain limitations in processing this kind of data (Carranza 2011; Filzmoser et al. 2009a; Zuo et al. 2013; Zuo 2014). Geochemical data are typically compositional data, where the sum of all elements is a fixed value (e.g. 100%) (Aitchison 1986). Aitchison (1986) proposed that the study of component data should focus on the proportional relationships between components rather than the component itself (Aitchison 1986; Filzmoser et al. 2009b; Zuo et al. 2013), thus proposing two classic log ratio transformation methods for “open” component data, namely, the additive log ratio (alr) transformation and central log ratio (clr) transformation, making traditional statistical methods also applicable to the analysis of transformed data (Aitchison 1986; Aitchison et al. 2000; Carranza 2011; Filzmoser and Hron 2009; Chen et al. 2016; Chen et al. 2018).

The clr transformation was carried out on the data for 39 geochemical elements, and the skewness value of the data distribution was then calculated after clr transformation, and compared with the skewness value of the raw data distribution (Figure 3). The skewness value of the data distribution of each element after clr transformation was significantly reduced, indicating that the transformed data distribution was closer to the normal distribution.

Fig. 3
figure 3

Skewness comparison diagram of data distribution

Full size image

Factor analysis was carried out on clr transformed data, and the appropriate factor was determined by eigenvalues greater than 1 and a cumulative variance contribution rate greater than 70%. The element combination reflected by the orthogonal rotation factor load matrix was more reasonable and interpretable than other combinations. Therefore, the maximum variance method was used to classify the element combinations by an orthogonal rotation factor loading matrix. According to Table 3, the 39 variables were attributed to 9 factors, these 9 factors accounted for 73.035% of the total variance of the raw 39 variables. The variance contribution reflects the ability of each factor to explain the total variance of the original variable. A higher value indicates a more important corresponding factor. Then, the factor load after rotation is sorted, and the results obtained are shown in Table 4.

Table 3 Characteristic values and cumulative variance contribution rates
Full size table
Table 4 Orthometric rotating factor loading matrix
Full size table

The combination of elements represented by each factor indicates different geochemical significance. The score distribution map of each factor shows the geological significance represented by each factor (Figure 4). F1 (Zr-La-Th-Nb-Y-Zn-Ti-Cd-Ag) is the element combination of the felsic granite distribution area. The low value area in F2 (SiO2-Al2O3-K2O-Ba-Be-Na2O-Cu) is the main copper mineralization zone in the study area, and there are many ore deposits in the low value area. F3 (CaO-Sr-B-Sn-Li) is the element combination associated with the alkaline magmatic rocks. F4 (Ni-Cr-MgO-Co) mainly reflects the composition characteristics of ultrabasic rocks and ophiolite, which is the Cr-Ni mineralization associated with ultramafic rocks. The low value regions in F5 (Fe2O3-Mn-V-Sb-As) mainly reflect the mineralized zone associated with mineralized fracture structures. F6 (W-Mo-U-Bi) reflects the high-temperature mineralization enrichment zone of ore-forming elements, granite interior and exterior contact zones and zones where intermediate to felsic veins developed. The elements in F7 (P-F) are not indicative of the mineralization process. F8 (Pb-Hg) is closely related to the widespread granite in the area, and F9 (Au) is the stable mineral display of placer gold under the condition of a supergene deposit.

Fig. 4
figure 4

The score distribution map of each factor

Full size image

MaxEnt model parameter analysis

The maximum entropy (MaxEnt) model is a probability distribution prediction model (Ratnaparkhi 2016). The prediction results depend on the sample point data and the environmental variable data affecting the sample point data. The probability of distribution of the sample data in other parts of the study area is determined according to the weight of the environmental variable data, and the point data with quantitative values are converted into data with probability values. In metallogenic prediction, MaxEnt obtains the prediction model by calculating the nonlinear relationship between the geographical coordinates of known deposits and ore-controlling variables in the study area, and then uses this model to simulate the possible distribution of target minerals in the target area. In this study, MaxEnt v3.3.3 software was used to establish metallogenic prediction model.

When using MaxEnt software for modeling, the complexity of the model has a significant impact on the prediction effect of the model. An excessive number of variables will increase the complexity of the model. In addition, when the ore-controlling factors in the model have high collinearity, the model may be overfit. Therefore, the MaxEnt model was constructed with the factor scores in the factor analysis results. Furthermore, when the model parameters are improperly set, overfitting or redundancy of the model may also appear (Kong et al. 2019). Relevant studies show that the over-fitting of the model is mainly controlled by the setting of the regularization multiplier, also known as \(\beta\) (Elith et al. 2011), and the comprehensive performance of the model with a \(\beta\) value between 2 and 4 is the best (Radosavljevic and Anderson 2014; Kong et al. 2019). Therefore, different \(\beta\) values (from 1 to 5 with a step size of 0.5) are tested to find the optimal \(\beta\) value for a particular model (Li et al. 2019; Wang et al. 2017). In the present study, we use the AUC value to evaluate the model, calculate the AUC values corresponding to different \(\beta\) values, and draw ROC curves (Figure 5). Therefore, the model is optimal when \(\beta =2\).

Fig. 5
figure 5

The ROC curve corresponding to the different \(\beta\) values

Full size image

MaxEnt model for geochemical anomaly optimization

The MaxEnt model is constructed with the 9 groups of factor scores as the input parameters. Through a literature review combined with mineralization prediction theory, MaxEnt software randomly selects 75% of the known deposits to establish the training model, and verifies the model accuracy with the remaining 25% of the known deposits. The number of replicates is set to 20 to reduce uncertainties caused by outliers (Li et al. 2019). At the same time, the contribution of each ore-controlling variable to the mine distribution is determined by the Jackknife test brought by MaxEnt version 3. 3.3 software. The MaxEnt parameters are set as follows: the output format is “Logistic”, the output file type is “ASC”, the features are set to “Auto features” after removing “Threshold features”, the regularization multiplier is set to “2”, the replicated run type is “Bootstrap” (Wang et al. 2017; Li et al. 2021), the maximum number of iterations is set to “5000” (Phillips 2005), and the threshold rule is applied to select “10 percent training presence” (Kramer-Schadt et al. 2013). Finally, response curves are created, and the jackknife is drawn to measure variable importance. The resulting data output by MaxEnt software is in ASCII format, and the ArcToolbox toolkit of ArcGIS is used to convert it to a grid, so that the results can be displayed in ArcGIS, and its value is between 0 and 1 (Figure 6).

Fig. 6
figure 6

Copper prospectivity map produced by optimized factor scores using MaxEnt model and the ROC curve

Full size image

The AUC value, kappa coefficient and TSS values of the final prediction results are calculated, the AUC = 0.863, the maximum Kappa = 0.606, and the maximum TSS = 0.657. All the evaluation indexes of the model show that the model has a good ability to identify the favorable/unfavorable areas of copper mineralization. Therefore, we infer that the model is reliable and acceptable, and more accurate than a random model. Figure 6 shows that most of the copper deposits are spatially consistent with the high anomalous probability zone marked in red. The figure illustrates that the model successfully connects the probabilities of multivariate geochemical anomalies with the known copper mineralization.

Table 5 shows the contribution rate of each factor score to the model, and Figure 7 shows the response curve of each factor score in the modeling. Among them, the F2 factor score is the most important ore-controlling variable to explain the occurrence of the copper deposits, reflecting the contribution to the deposit from the perspective of element composition and accounting for 29.3% of the total contribution rate. From the F2 response curve, as the factor score increases, the success rate of predicting copper gradually decreases, which is consistent with the conclusion that copper has a negative load in F2. F5 (25.8%) and F4 (13.5%) are the second and third most important ore controlling factors, respectively.

Table 5 The contributions of ore-controlling variables
Full size table
Fig. 7
figure 7

Response of Cu to factor scores

Full size image

To further eliminate the interaction between ore-controlling variables, the Jackknife analysis built in the MaxEnt model is used to test the importance of the impact of ore-controlling variables on the metallogenic process (Figure 8). The longer the blue bar, the more important the variable is to the distribution of the deposits. F2, F5, and F9 are important variables affecting the distribution of the deposit. The shorter the green bar, the more information the variable has than other variables have, and the variable has a great influence on the distribution of the deposit. F1, F2, and F5 have more unique information for the prediction of favorable metallogenic areas, and they are indispensable. The predictions of the MaxEnt model are consistent with the factor analysis results.

Fig. 8
figure 8

Evaluation of the relative importance of factor scores variables by Jackknife test

Full size image

Regional Cu resource potential

The magmatic activity in the research area was frequent and large-scale, and the collision between the Asian and Indian plates formed a series of complex folds, thrust faults, and transpressional faults. The copper deposits in the study area are generally controlled by deep and large fault structures, nappe-slip structures and strike-slip structures, which are easily mineralized (Hou et al. 2006; Liu et al. 2020). Deep and large faults are usually rock and ore guiding structures, and copper deposits are distributed along main faults or branch faults (Li and Rui 2004; Liu et al. 2020). The mineralization corresponds with the anomaly probability, and their locations are clearly seen on the geochemical maps in Figure 6. In fact, the areas with high anomaly probability are always located at the edges of intermediate-felsic intrusions and the sides of a fault, or in the vicinity of fault intersections, which are favorable metallogenic regions in the study area. These results are consistent with the previous findings in the study area (Zuo et al. 2009; Zuo 2011). In addition, based on the geological background and suitable ore-forming conditions, such as intermediate-felsic intrusions, intersection of faults, and favorable sedimentary rocks, several preliminary prospecting targets are proposed in Figure 9. However, these predicted prospects still need to be further investigated with more information.

Fig. 9
figure 9

The targets area for copper deposits

Full size image

Conclusions

  1. (1)

    Combinations of elements as grouped by factor analysis can reflect the symbiotic and origin relationships of elements. Compared with the original complex element aggregation, the factor analysis results are clearer and simpler. By combining the distribution area and geological characteristics of the corresponding factor combinations, directions for future geological work can be identified.

  2. (2)

    The MaxEnt model used in this study is simple, accurate, and easy to operate, and can fuse multivariate data quickly and effectively. The AUC, kappa, and TSS values illustrate the ability of the model to correctly classify copper deposits.

  3. (3)

    The spatial association of individual ore-controlling variables with occurrences of copper deposits was investigated by response curves, and the relative importance of ore-controlling variables was examined by jackknife analysis in the MaxEnt model, indicating that the second factor score was the most important variable, followed by the fifth factor score.

  4. (4)

    The MaxEnt model can automatically extract and analyze multivariate geochemical anomaly information without relying on expert experience. It is universal and efficient, and can adapt to processing in the big data environment. However, this method also has the problem that the particle size of anomaly extraction is not fine enough. Further narrowing the scope of anomaly extraction to delineate the prospecting target area more accurately is necessary.