Metallic Mineral Resources in the Twenty-First Century: II. Constraints on Future Supply

Abstract

Supplying worldwide demand of metallic raw materials throughout the rest of this century may require 5–10 times the amount of metals contained in known ore deposits. This demand can be met only if mineral deposits containing the required masses of metals, in excess of present day ore reserves, exist in the Earth’s crust. It is, by definition, not known whether or not such mineral deposits exist. On the basis of the statistical distribution of metal tonnages contained in known ore deposits, however, it is possible to place constraints on the size distribution of the deposits that must be discovered in order to meet the expected demand. A nondimensional analysis of the distribution of metal tonnages in deposits of 20 metals shows that most of them follow distributions that, although not strictly lognormal, share important characteristics with a lognormal distribution. Chief among these is the observation that frequency falls off symmetrically and geometrically with deposit size, relative to a median deposit size that is approximately equal to the geometric mean deposit size. An immediate consequence of this behavior is that most of the metal endowment is concentrated in deposits that are several orders of magnitude larger than the median deposit size, and that are much rarer than the most common deposits that cluster around the median deposit size. The analysis reveals remarkable similarities among the statistical distributions of most of the metals included in this study, in particular, the fact that distribution of most metals can be fully described with essentially the same value (about 2–3) of the scale parameter, σ, which is the only parameter needed to describe the behavior of a normalized lognormal variable. This observation makes it possible to derive the following general conclusions, which are applicable to most metals—both scarce and abundant. First, it is unlikely that undiscovered mineral deposits of sizes comparable to those that contain most of the known metal endowment exist in sufficient quantities to supply the expected worldwide demand throughout the rest of this century. Second, if the expected demand is to be met, one must hope that very large deposits, perhaps up to one order of magnitude larger than the largest known deposits, exist in accessible portions of the Earth’s crust, and that these deposits are discovered.

Introduction

Future demand of metallic raw materials is certain to increase relative to historical levels, in response to factors that include increase in world population, industrial and technological development of the world’s less developed regions, and perhaps a generalized increase in affluence. There may be limits to how far each of these processes can go, imposed by the finiteness of nonrenewable natural resources. If for the sake of argument we ignore these limits, and if we assume that past trends in demand of metallic raw material can be extrapolated throughout the twenty-first century, then we can conclude that (Patiño Douce 2015) (i) the known reserves of most metals will be exhausted well before the year 2100, and in some cases as soon as the late 2020s, and (ii) satisfying demand over the rest of this century will require approximately 5–10 times the metal tonnage known to exist in proven ore reserves. Of course, these metal tonnages, and much more, exist in the Earth’s crust, as virtually all rocks contain minute amounts of almost every element in the periodic table. These are “background” concentrations that, when averaged over the entire crust, we call the geochemical abundances of the elements. Extraction of metals from rocks in which the metals have not been significantly enriched relative to their geochemical abundances will forever be in the realm of science-fiction, however, for technological, economic, environmental, and energetic reasons, among others (see, e.g., Nickless et al. 2014). The question before us is whether the vast amounts of metal that society is likely to demand exist in mineral deposits, in which the metals of interest have been enriched by natural processes above their geochemical average abundances, to the extent that extraction may become technologically and economically feasible at some future time. This we do not know.

One can attempt to answer this question at several levels. At the most immediate and applied level, economic geologists will search for mineral deposits of specific types in specific regions of the planet where the geological setting is known to be favorable to their formation. This is a purely geological undertaking, which relies on knowledge of the physicochemical processes responsible for concentrating metals in mineral deposits. This type of work is a crucial part of the answer that we seek, but it is driven by the immediate pursuit of economic profit, rather than by the less immediately tangible concern of whether or when significant economic and social disruptions may be triggered by exhaustion of mineral resources. At a more general level, we can consider work that combines geological understanding of metallogenic processes with statistical analysis of the distribution of known deposits in order to define favorable tracts for mineral exploration, estimate the likelihood of finding undiscovered mineral deposits in such tracts, and perhaps also determine what are the most promising sectors in which to focus exploration within favorable tracts (e.g., Agterberg 1995; Bliss and Menzie 1993; Gerst 2008; Gonçalves 2001; Guj et al. 2011; Harris 1984; Laznicka 1999; Singer 1993, 2006, 2008, 2010, 2013; Wei and Pengda 2002; Singer et al. 2005; Singer and Menzie 2010; Singer and Kouda 2011; Wang et al. 2010, 2011). This work is also of crucial importance in maintaining the supply of metallic raw materials, and in many cases, actual on-the-ground exploration could not proceed without it, or would at least be far less successful. However, estimating the likely absolute limits of the availability of metallic raw materials is not generally a primary concern of this type of studies. Coming up with such estimates (e.g., Skinner 1976) allows one to address the questions of whether, or when, economic growth, and with it population growth, are likely to meet ceilings imposed by lack of natural raw materials.

In this paper, I combine estimates of likely demand for metallic raw materials to the year 2100 (Patiño Douce 2015) with a statistical analysis of size distribution of known mineral deposits in order to describe and quantify the challenges facing metal supply throughout the twenty-first century. Because we do not know how much metal exists in undiscovered mineral resources, it is, by definition, impossible to give precise dates for the exhaustion of particular metals, or even to state that exhaustion will take place this century or within any specific time range in the future. But it is possible to determine the size distribution of the mineral deposits that one must hope exist if one is to have reasonable expectations of meeting the demand to the year 2100. In addition to providing a quantitative description of the challenges of supplying metallic raw materials throughout this century, this contribution may be a useful complement to resource assessment studies (such as Johnson et al. 2014), because it may serve to focus exploration efforts on the types of deposits that can make a real difference to the world’s supply of metals.

This paper is organized as follows. I first derive the rigorous mathematical background that relates the distribution of metal endowment to the distribution of individual deposit sizes. The equations are written as functions of nondimensional tonnage, which simplifies comparisons among multiple metals, as all of the variability among metals can be discussed in terms of a single parameter, which is the scale parameter of a lognormal distribution. In a subsequent section, the distribution of the endowment of 20 metals is analyzed within this mathematical framework. Finally, theory and observations are combined to generate estimates of the size distribution of the deposits that will need to be discovered and developed in order to satisfy expected demand.

Theoretical Background

General Considerations

In order to construct statistical arguments about data, one must begin by determining the probability density function (PDF) that best describes the dataset of interest. Any function P(x) with the following two properties: (i) P(x) ≥ 0 and (ii) ∫P(x)dx = 1 (for −∞ < x < ∞), is a PDF that describes the probabilistic distribution of the values of a random variable x. It has been argued that the lognormal PDF:

$$ P\left( x \right) = \frac{1}{{x\sigma \sqrt {2\pi } }} e^{{\big\lfloor - \frac{{\left( {\ln x - \mu } \right)^{2} }}{{2 \sigma^{2} }}\big\rfloor}} $$

(1)

is widely applicable to describing the distribution of chemical elements in the Earth’s crust, ranging from background concentrations of chemical elements in nonmineralized rocks (e.g., Ahrens 1954a, b) to the distribution of tonnages of mineral deposits (see discussion by Singer 2013). In the lognormal PDF, Eq. (1), μ is known as the location parameter and σ as the scale parameter. The parameters μ and σ are, respectively, the (arithmetic) mean and the standard deviation of the values of ln x, which is, by definition, a normally distributed random variable (see Aitchison and Brown 1957 for the definitive treatment). The lognormal distribution arises when the value of the variable x is the result of a stochastic process in which successive values of a random variable are multiplied with one another to yield the value of x. This is a simple corollary of the central limit theorem (e.g., Sokolnikoff and Redheffer 1966), as the value of ln x is in such a case the result of an additive process of random variables.

The lognormal PDF has been found to offer a reasonably accurate description for the distribution of the values of variables in many biological and physical processes (see review and discussion by Limpert et al. 2001), as well as in economics and sociology (e.g., Aitchison and Brown 1957; Black and Scholes 1973; Allanson 1992). The connection with an underlying multiplicative stochastic process can in many instances be made (e.g., Mitzenmacher 2003; Grönholm and Annila 2007; Loewenstein et al. 2011). In the case of the distribution of chemical elements in nature, the answer may be less clear cut, as whether or not the lognormal distribution applies may depend on how one defines and analyzes the problem. As noted above, Ahrens (1954a, b) argued that background geochemical abundances follow a lognormal distribution. Singer (2013) found that, if mineral deposits are discriminated by metallogenic deposit type, then metal contents in most cases (over 90% of the examples that he studied) follow lognormal distributions. In contrast, if all deposits of a given metal are grouped together, ignoring deposit type, then agreement with a lognormal distribution was found to exist for only one metal (Mo) out of the seventeen metals considered (Singer 2013). In a classic mathematical treatment, Allègre and Lewin (1995) showed that redistribution of chemical elements by natural processes can lead to either lognormal or power-law (also called “fractal” or “Pareto”) distributions of concentrations, depending on the complexity and recurrence of the processes involved. A power-law distribution of grades and tonnages of mineral deposits was proposed by Cargill et al. (1981) and justified on theoretical grounds by Turcotte (1986, 2002) and Agterberg (1995, 2007).

There is a complication, however, when attempting to determine whether grade and tonnage data follow a lognormal or a power-law distribution. This is the fact that, under some circumstances, the two distributions may appear similar to one another on the log–log plots that are customarily used to test for power-law behavior. Taking logarithms on Eq. (1) we find:

$$ \ln P\left( x \right) = - \frac{1}{{2\sigma^{2} }}\left( {\ln x} \right)^{2} - \left( {1 - \frac{\mu }{{\sigma^{2} }}} \right)\ln x - \left[ {\ln \left( {\sigma \sqrt {2\pi } } \right) + \frac{\mu }{{2\sigma^{2} }}} \right]. $$

(2)

If the scale parameter σ is large enough, then the coefficient of the quadratic term may be small enough that a log–log plot of a lognormal distribution will appear as a curve with very gentle negative curvature, which diverges from a power-law line as 1/σ ² (see “Appendix”). If σ is large enough then a power-law fit to the high-end tail of lognormally distributed data (i.e., a straight line in a log–log plot) may yield fit parameters that are statistically significant but that have no physical basis. The argument about whether geochemical concentrations, and grades and tonnages of mineral deposits, follow power-law or lognormal distributions, may arise, to a not insignificant extent, from ignoring this simple mathematical result. Further details, and some of the consequences for estimating future availability of metallic mineral resources, are outlined in the “Appendix”.

It is not my purpose here to justify formally any particular PDF in order to explain the distribution of economically exploitable metal resources. Rather, my goal is to assess the possible limitations on future supply of metallic raw materials. For reasons that I explain in detail below, I will assume that the lognormal PDF is a reasonably good approximation to the distribution of metal contents in mineral deposits even if one ignores metallogenic deposit types (cf. Singer 2013), and I will justify this assumption a posteriori.

The lognormal PDF will be re-cast in terms of nondimensional variables, in order to make general statements about how the metal endowment—i.e., the total amount of metal contained in potentially exploitable mineral deposits—is distributed among deposits of different sizes. One of the advantages of the nondimensional approach is that it greatly facilitates comparing the behavior of metals with hugely different endowments and geochemical abundances. I then evaluate how appropriate the lognormal model is for describing the actual distribution of the known metal endowment of 20 different metals. I find, as Singer (2013) did, that the agreement is not perfect, but I also show that the lognormal PDF captures essential aspects of the distribution of metal endowments. It is this fact that makes it a useful tool for assessing the constraints on the likely supply of metallic raw materials in the future.

Normalized Lognormal Probability Density Function

The arguments in this paper are based exclusively on metal tonnage, which is the mass of metal contained in a mineral deposit. The mass of mineralized rock, also known as ore tonnage, and the grades of the mineral deposits, play no role in these discussions. Metal tonnages in individual mineral deposits vary widely among metals, with characteristic values, for example, of about 10–10² tons for Au, 10⁵–10⁷ tons for Cu, or 10⁸–10¹⁰ tons for Fe. In the accompanying paper (Patiño Douce 2015), I show that converting historical metal extraction figures to nondimensional variables leads to very general conclusions about the likely future demand of metallic raw materials. An equivalent nondimensional formulation of the lognormal PDF will make it possible to discuss the availability of metallic raw materials in general.

Let x be a lognormally distributed random variable, with location parameter μ and scale parameter σ, as described by Eq. (1). Because ln x is normally distributed, the median of ln x has the same value as its (arithmetic) mean, μ. It is easily shown that, if μ ^* is the geometric mean of x, then:

$$ \mu = \ln \mu^{*} $$

(3)

and, given that the logarithm function is monotonic, the median of ln x, μ, represents the same value as the median of x, which we shall label x _m. Thus,:

$$ \ln x_{\text{m}} = \mu $$

(4)

Comparing Eqs. (3) and (4), we see that

$$ \mu^{*} = x_{\text{m}} . $$

(5)

That is, the geometric mean of a lognormally distributed variable is also its median. The geometric mean is therefore a natural estimator of the central value of a lognormally distributed variable, which suggests the following argument. If we normalize the lognormally distributed random variable x to its geometric mean, we obtain a new lognormally distributed random variable z:

$$ z = \frac{x}{{\mu^{*} }} = \frac{x}{{e^{\mu } }} $$

(6)

with geometric mean μ ^* _z  = 1, and location, and scale parameters μ _z  = ln μ ^* _z  = 0 and σ _z  = σ, respectively. The fact that the scale parameter remains unchanged follows from the fact that normalization corresponds to a simple change of origin of the logarithmic variable:

$$ \ln z = \ln x - \mu $$

(7)

The standard deviation of ln z therefore equals the standard deviation of ln x.

The PDF of the original variable, P(x), and that of the normalized, or rescaled, variable, P(z), are related as follows:

$$ P\left( x \right) = \frac{1}{{x\sigma \sqrt {2\pi } }} e^{{\Big\lfloor - \frac{{\left( {\ln x - \mu } \right)^{2} }}{{2 \sigma^{2} }}\Big\rfloor}} = \frac{1}{{z e^{\mu } \sigma \sqrt {2\pi } }} e^{{\Big\lfloor - \frac{{\left( {\ln z} \right)^{2} }}{{2 \sigma^{2} }}\Big\rfloor}} = e^{ - \mu } P\left( z \right) $$

(8)

with

$$ P\left( z \right) = \frac{1}{{z \sigma \sqrt {2\pi } }} e^{{\Big\lfloor - \frac{{\left( {\ln z} \right)^{2} }}{{2 \sigma^{2} }}\Big\rfloor}} . $$

(9)

Suppose now that x represents the metal content of individual mineral deposits taken from a set of deposits of the same metal. One might be interested in the probability of occurrence, or frequency, of deposits with metal contents within a certain interval (x ₁, x ₂). If the total number of deposits is a large number, then this probability, which we shall denote as p[x|(x ₁, x ₂)], will approximate the fraction of the total number of deposits that have metal contents in the interval (x ₁, x ₂). The probability is given by

$$ p \left[ {\left. x \right|\left( {x_{1} ,x_{2} } \right)} \right] = \int_{{x_{1} }}^{{x_{2} }} {P\left( x \right) {\text{d}}x} $$

(10)

and must be equal to the probability that the rescaled metal content, z, is in the interval (z ₁, z ₂), where z ₁ = x ₁ /e ^μ and z ₂ = x ₂ /e ^μ:

$$ p \left[ {\left. x \right|\left( {x_{1} ,x_{2} } \right)} \right] = p \left[ {\left. z \right|\left( {z_{1} ,z_{2} } \right)} \right] = \int_{{z_{1} }}^{{z_{2} }} {P\left( z \right) {\text{d}}z} = \frac{1}{{ \sigma \sqrt {2\pi } }} \int_{{z_{1} }}^{{z_{2} }} {\frac{1}{z}e^{{\Big\lfloor - \frac{{\left( {\ln z} \right)^{2} }}{{2 \sigma^{2} }}\Big\rfloor}} {\text{d}}z .} $$

(11)

We are also interested in the fraction of the total metal endowment (i.e., of the total amount of metal contained in all deposits) that is contained in deposits with metal contents in the interval (x ₁, x ₂). In order to calculate this fraction, we define the following function:

$$ M\left( x \right) = \frac{x P\left( x \right)}{{\mathop \int \nolimits_{0}^{\infty } xP\left( x \right) {\text{d}}x}} = \frac{x P\left( x \right)}{{x_{a} }}, $$

(12)

where x _a is the arithmetic mean of the variable x. We note that M(x) is another PDF (albeit not lognormal), because M(x) ≥ 0 and

$$ \int_{0}^{\infty } {M\left( x \right) {\text{d}}x = 1} $$

(13)

(since it must be x ≥ 0, the integral can be taken from 0 rather than from −∞). The fraction of the total metal endowment contained in deposits with metal contents in the interval (x ₁, x ₂), which we shall denote by m[x|(x ₁, x ₂)], is given by

$$ m \left[ {\left. x \right|\left( {x_{1} ,x_{2} } \right)} \right] = \int_{{x_{1} }}^{{x_{2} }} {M\left( x \right) {\text{d}}x} = \frac{1}{{x_{a} }} \int_{{x_{1} }}^{{x_{2} }} {xP\left( x \right) {\text{d}}x} . $$

(14)

Using Eqs. (6) and (9) to change the variable of integration, we find

$$ \int_{{x_{1} }}^{{x_{2} }} {xP\left( x \right) {\text{d}}x} = e^{\mu } \int_{{z_{1} }}^{{z_{2} }} {zP\left( z \right) {\text{d}}z} $$

(15)

so that

$$ x_{a} = e^{\mu } \int_{0}^{\infty } {zP\left( z \right) {\text{d}}z = e^{\mu } z_{a} } , $$

(16)

where z _a is the arithmetic mean of the rescaled variable z. Substituting Eqs. (15) and (16) in (14):

$$ m \left[ {\left. x \right|\left( {x_{1} ,x_{2} } \right)} \right] = \frac{1}{{z_{a} }} \int_{{z_{1} }}^{{z_{2} }} {zP\left( z \right) {\text{d}}z} = m \left[ {\left. z \right|\left( {z_{1} ,z_{2} } \right)} \right]. $$

(17)

As we should have expected, this shows that the fraction of the metal endowment contained in deposits with metal contents in the interval (x ₁, x ₂) equals the fraction contained within the corresponding interval of the rescaled variable (z ₁, z ₂). Substituting explicit expressions for the arithmetic mean of the variable, z _a

$$ z_{a} = \int_{0}^{\infty } {zP\left( z \right) {\text{d}}z = e^{{\frac{{\sigma^{2} }}{2}}} } $$

(18)

and for P(z), Eq. (9), in (17), we find

$$ m \left[ {\left. z \right|\left( {z_{1} ,z_{2} } \right)} \right] = \frac{{e^{{ - \frac{{\sigma^{2} }}{2}}} }}{{\sigma \sqrt {2\pi } }} \int_{{z_{1} }}^{{z_{2} }} {e^{{\Big\lfloor - \frac{{\left( {\ln z} \right)^{2} }}{{2 \sigma^{2} }}\Big\rfloor}} {\text{d}}z} $$

(19)

and the PDF M(z) is

$$ M\left( z \right) = \frac{z P\left( z \right)}{{z_{a} }} = \frac{{e^{{ - \frac{{\sigma^{2} }}{2}}} }}{{\sigma \sqrt {2\pi } }} e^{{\Big\lfloor - \frac{{\left( {\ln z} \right)^{2} }}{{2 \sigma^{2} }}\Big\rfloor}} . $$

(20)

From Eqs. (11) and (19), we see that, by normalizing to the geometric means, distribution of metal tonnages in deposits of different metals can be compared to one another on the basis of only the scale parameter, σ, for each metal. Under the assumption of lognormal distribution this is simply the standard deviation of the logarithms of the metal contents (but see below). The location parameter, μ, which is a measure of absolute metal contents, does not appear in these equations. Equation (11) describes the frequency of occurrence of deposits within a given size interval, rescaled to the median deposit size (which is the geometric mean deposit size). Equation (19) describes the fraction of the metal endowment that is contained in deposits within a given rescaled size interval. These equations will now be used to study how metal endowment is distributed as a function of deposit size.

Distribution of Metal Endowment

We begin by writing the explicit forms of the antiderivatives of the two PDFs, P(z), Eq. (9), and M(z), Eq. (20):

$$ p\left( z \right) = \int {P\left( z \right) {\text{d}}z} = \frac{1}{2}{\text{erf}}\left( {\frac{\ln z}{\sigma \sqrt 2 }} \right) $$

(21)

$$ m\left( z \right) = \int {M\left( z \right) {\text{d}}z} = \frac{1}{2}{\text{erf}}\left[ {\frac{1}{\sqrt 2 } \left( {\frac{\ln z}{\sigma } - \sigma } \right)} \right] $$

(22)

(these and other explicit algebraic calculations, which are not always easy to do manually, were done with the computer algebra system Maple; the worksheets are available from the author upon request). When evaluated from z = 0 to any arbitrary value z = z _i , the antiderivatives Eqs. (21) and (22) yield the cumulative distribution functions (CDF) corresponding to each of the PDFs. The medians of the distributions, z ^P _m and z ^M _m , are given by the solutions to the equations:

$$ p\left( {z_{m}^{P} } \right) = p\left( \infty \right) - \frac{1}{2} $$

(23)

$$ m\left( {z_{m}^{M} } \right) = m\left( \infty \right) - \frac{1}{2} $$

(24)

Taking the limit z → ∞, we find that p(∞) = m(∞) = ½, so the equations become

$$ \frac{1}{2}{\text{erf}}\left( {\frac{{\ln z_{m}^{P} }}{\sigma \sqrt 2 }} \right) = 0 $$

(25)

and

$$ \frac{1}{2}{\text{erf}}\left[ {\frac{1}{\sqrt 2 } \left( {\frac{{\ln z_{m}^{M} }}{\sigma } - \sigma } \right)} \right] = 0 $$

(26)

The solution to Eq. (25) is

$$ z_{m}^{P} = 1 $$

(27)

which is of course true by construction: the median of the rescaled deposit size is constant and equal to 1, and thus independent of σ. The solution to Eq. (26), which describes the central value of the distribution of metal endowment among deposits of different sizes, is, however, a strong function of the scale parameter σ:

$$ z_{m}^{M} = e^{{\sigma^{2} }} $$

(28)

The significance of the value $e^{{\sigma^{2} }}$ will be discussed further below, but at this point, we note that this result has profound implications for the distribution of the endowment of metallic raw materials, for it means that, if deposit sizes are indeed lognormally distributed, then much of the metal endowment is likely to be concentrated in a relatively small number of large deposits, and that most of the smaller mineral deposits, including those that can be considered to be “typical” because their size is of the order of the median deposit size, contain a rather small proportion of the metal endowment.

In order to quantify this statement, we find the value of the function $p[z |(e^{{\sigma^{2} }},\infty)]$, which yields the frequency of the largest deposits that contain half of the total metal endowment

$$ p \left[ {\left. z \right|\left( {e^{{\sigma^{2} }} ,\infty } \right)} \right] = \int_{{e^{{\sigma^{2} }} }}^{\infty } {P\left( z \right) {\text{d}}z} = p\left( \infty \right) - p\left( {e^{{\sigma^{2} }} } \right) = \frac{1}{2}\left[ {1 - {\text{erf}}\left( {\frac{\sigma }{\sqrt 2 }} \right)} \right]. $$

(29)

As can be seen in Figure 1, $p[z |(e^{{\sigma^{2} }},\infty)]$ is a strong inverse function of the scale parameter. For example, for values of σ about 2–3, which may be appropriate for many metals (see below), 50% of the metal endowment is likely to be contained in the largest 1 to 0.1% of all mineral deposits. In some cases, this may be equivalent to only one or two “giant” or “supergiant” ore deposits. These results are consistent with the findings of Singer (1995) on the distribution of the endowment of copper, lead, zinc, silver and gold. We can expand upon this result by solving for the value of z ^M _q that satisfies the equation:

$$ m\left( {z_{q}^{M} } \right) = m\left( \infty \right) - q $$

(30)

for any desired value of the fraction q of the metal endowment. Expressing q as a percentage of the endowment, we have, for instance, z ^M₅₀  = z ^M _m , i.e., the median of the distribution (compare Eqs. 24 and 30). We also calculate the integral:

$$ p \left[ {\left. z \right|\left( {z_{q}^{M} ,\infty } \right)} \right] = \int_{{z_{q}^{M} }}^{\infty } {P\left( z \right) {\text{d}}z} $$

(31)

which yields the frequency of the largest deposits that contain the fraction q of the metal endowment. Results plotted at constant σ are shown in Figure 2. For values of σ about 2–3, we can expect that 95% of the metal endowment (i.e., virtually all of the metal) may be contained in the largest ~10% of all mineral deposits. This is an important result when considering future availability of metallic raw materials.

Fig. 1

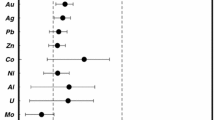
Frequency of the largest deposits (in terms of contained metal tonnage) that contain 50% of the metal endowment, for a range of scale parameters, σ, that span likely values for most metals in this study (see text and Table 2)

Fig. 2

Frequency of the largest deposits (in terms of contained metal tonnage) that contain a given fraction of the metal endowment, q, for several constant values of the scale parameter, σ spanning likely values for most metals in this study (see text and Table 2). Figure 1 is a section of this graph at constant q = 0.5

Another measure of interest is the location of what we may call the “most productive” deposit size interval, defined as follows. Given an interval in rescaled deposit sizes (z _t , ωz _t ), with ω > 1 (an arbitrary constant), we seek the value of z _t that maximizes the total metal tonnage contained in the interval. In particular, given our hypothesis that deposit sizes follow a lognormal distribution, we are interested in the geometric midpoint of the interval, z _max, which is

$$ z_{ \hbox{max} } = \sqrt {\left( {\omega z_{t} } \right) z_{t} } = z_{t} \sqrt {\omega } . $$

(32)

We define the function:

$$ m_{ \hbox{max} } = \int_{{z_{t} }}^{{\omega z_{t} }} {M\left( z \right) {\text{d}}z} = \frac{1}{2}{\text{erf}}\left[ {\frac{1}{\sqrt 2 } \left( {\frac{{\ln \omega z_{t} }}{\sigma } - \sigma } \right)} \right] - \frac{1}{2}{\text{erf}}\left[ {\frac{1}{\sqrt 2 } \left( {\frac{{\ln z_{t} }}{\sigma } - \sigma } \right)} \right] $$

(33)

and find the value of z _t that maximizes this function. This is

$$ z_{t} = \frac{1}{\sqrt \omega }e^{{\sigma^{2} }} $$

(34)

which, substituting in Eq. (32), yields

$$ z_{ \hbox{max} } = e^{{\sigma^{2} }} = z_{m}^{M} = z_{50}^{M} $$

(35)

Thus, the median of M(z), see Eq. (28), which is a strong function of the scale parameter σ, is also the center of the most productive interval, in the sense that, whatever the width ω of this interval is, its contribution to the metal endowment is maximized when the interval is centered at $e^{{\sigma^{2} }}$.

We can now ask that the most productive interval contain a certain fraction, w, of the metal endowment, and solve for the value of ω _w that determines the width of this interval. We make

$$ \int_{{\frac{1}{{\sqrt {\omega_{w} } }}e^{{\sigma^{2} }} }}^{{\sqrt {\omega_{w} } e^{{\sigma^{2} }} }} {M\left( z \right) {\text{d}}z = w} . $$

(36)

The integral simplifies considerably, and the equation becomes

$$ {\text{erf}}\left( {\frac{\sqrt 2 }{4}\frac{{\ln \omega_{w} }}{\sigma }} \right) = w $$

(37)

or

$$ \omega_{w} = e^{{\left[ {\frac{4\sigma }{\sqrt 2 }{\text{erf}}^{ - 1} \left( w \right)} \right]}} . $$

(38)

For constant w, ω _w varies exponentially with the scale parameter σ. It is also of interest to find the frequency with which deposits in this size interval occur, i.e.:

$$ p \left[ {z\left| { \frac{1}{{\sqrt {\omega_{w} } }}e^{{\sigma^{2} }} ,\sqrt {\omega_{w} } e^{{\sigma^{2} }} } \right.} \right] = \int_{{\frac{1}{{\sqrt {\omega_{w} } }}e^{{\sigma^{2} }} }}^{{\sqrt {\omega_{w} } e^{{\sigma^{2} }} }} {P\left( z \right) {\text{d}}z.} $$

(39)

The behavior of the most productive interval is exemplified in Figure 3 for w = 0.5 and 0.95 (i.e., 50 and 95% of the metal endowment, respectively). As the scale parameter σ increases, the probability of occurrence of mineral deposits within the most productive tonnage interval decreases but the interval becomes wider (see Fig. 3). As we saw above, the most productive interval is always centered at $e^{{\sigma^{2} }}$, which, for values of σ about 2–3 (justified below), corresponds to deposits with metal tonnages that are 50–8000 times larger than the median deposit size. Half of the metal endowment is likely to exist in deposits that are within approximately 1 order of magnitude of this size (Fig. 3, right panel), and that make up between 1 and 10% of all mineral deposits (Fig. 3, left panel). Taking 95% of the metal endowment to represent essentially all of the available metal, we see that this amount of metal is likely to be contained in a most productive interval with a width of about 3–4 orders of magnitude (right panel), i.e., covering a large range of deposit sizes on both sides of $e^{{\sigma^{2} }}$, but making up less than half of all deposits, and perhaps as little as 15%, depending on the value of σ (Fig. 3, left panel).

Fig. 3

Geometric width of the most productive interval (right panel), and frequency of deposits with metal tonnages within this interval (left panel), as functions of the scale parameter, σ. Curves are shown for most productive intervals carrying either 50% (w = 0.5) or 95% (w = 0.95) of the metal endowment. The most productive deposit size interval (i.e., the size interval that contains the largest proportion of the metal endowment) is always centered at a normalized metal tonnage equal to $e^{{\sigma^{2} }}$

The conclusions reached in this section can be summarized with the help of Figure 4. The panels show the PDFs, P(ln z) on the left, and M(ln z) on the right. Two curves are shown for each function, for values of σ = 2 and 3. These choices are justified in the next section. The PDF P(ln z) is, by definition, a normal (Gaussian) distribution, which is centered on the origin because, by construction, the mean of the distribution is μ = 0. Using absolute tonnages would simply shift the curve along the horizontal axis, but would change neither its shape nor the following argument. An important point that the graph demonstrates is that the most common deposits (the mode of the distribution) cluster within an interval, some 2 to 3 orders of magnitude wide, centered at the geometric mean size, μ ^* = e ^μ (Eq. 3). The actual width of this interval is determined by the value of σ, a point that I return to below. Deposits that are more than about 2 orders of magnitude larger than the geometric mean are much less common than the “characteristic” deposits of size ~μ ^*, but have a strong influence on the metal endowment. The graph of M(ln z) in Figure 4 makes this clear. The PDF that describes the distribution of metal endowment peaks at $e^{{\sigma^{2} }}$, which is the center of the most productive interval: a large proportion of the endowment is contained in deposits with sizes within a narrow range of $e^{{\sigma^{2} }}$. The most common deposits of size ~μ ^* are too small to make a significant contribution to the metal endowment. Deposits that are much larger than $e^{{\sigma^{2} }}$ could, on the other hand, make a big difference, but they are vanishingly rare. I will return to this point in a later section.

Fig. 4

Comparison of the normalized PDFs for deposit size, P(z), and distribution of metal endowment, M(z), converted to logarithmic values. For a lognormal distribution, metal endowment is concentrated in deposits that are larger than the median (or geometric mean) deposit size. The displacement of the peak of M(z) relative to the peak of P(z) increases with the scale parameter, σ. The same behavior is qualitatively true for any other distribution in which frequency falls off symmetrically and geometrically with distance from the median value

Converting to logarithmic variables as in Figure 4 has the virtue of helping one realize that, although we may be intuitively or educationally predisposed toward arithmetic thinking, many natural variables follow geometric distributions. What this means, if metal tonnages follow a lognormal distribution, is that a difference of a factor of 2 between the sizes of two deposits makes relatively little difference in the metal endowment, whereas a difference of 2 orders of magnitude can make an enormous difference. Or, said in a different way, if we have two deposits with metal tonnages a and b, such that a = 100b, the metal endowment remains virtually unchanged if the size of the smaller deposit is 2b rather than b, but would be strongly affected if the larger deposit did not exist.

The mathematical arguments developed here are rigorously applicable only to random variables that are lognormally distributed. But consider a random variable that, although not lognormal, follows a distribution that resembles the lognormal distribution in some key respects: it is unimodal and symmetric in the logarithms of the variable, and the values of the variable cluster close to its geometric mean. Such a variable will qualitatively behave like a lognormal variable. In particular, the distribution of the cumulative variable that can be derived from it (e.g., cumulative tonnage derived from individual deposit tonnages) will have a peak that is displaced toward larger values of the variable (Fig. 4). We next examine the extent to which this argument is applicable to the distribution of metal tonnages of metallic mineral deposits.

An Appraisal of the Lognormal Hypothesis for Distribution of Metal Tonnages

Metal tonnage data were compiled for mineral deposits of 20 elements (listed in Table 1) from a large number of publicly available data sources (also listed in Table 1; complete data are given in Supplementary Table 1). I only included deposits in which chemical processes were responsible for metal enrichment. Detrital mineral deposits may contain a large fraction of the endowment of some metals, but there can be no expectation that their size distribution follows the same laws as that of deposits of chemical origin. I did, however, include the poorly understood Witwatersrand Au and U deposits, even if it is not entirely clear what their origin is.

Table 1 Metal Tonnage Data Sources

The data vary widely in quality and completeness. Some of the problems that may affect this dataset are:

• (i) Data were collected from both government and industry sources, and the two types of organizations may not be equally forthcoming in providing information. They may also use different criteria to infer metal tonnages from sampling data.

• (ii) The inherent quality of the data is likely to vary significantly, depending on factors such as the quality and density of the sampling used to estimate metal tonnages, as well as on when the data were collected and the tonnage estimates prepared. Dates for the data sources that I used vary from the 1970s to the 2010s, but are likely to include some estimates prepared decades earlier.

• (iii) Although I attempted to only use data that represent total deposit tonnage, it is possible that in a significant number of cases reported tonnages actually refer to remaining metal after significant extraction has taken place. In many cases, it is simply not possible to figure this out from the available sources.

• (iv) Estimates for the amount of metal contained in a mineral deposit vary with the cutoff grade, below which metal recovery is deemed impractical and/or uneconomic. Criteria used to determine cutoff grades vary, and have changed with time.

• (v) The number of available data points varies widely, from several thousand deposits (for Cu, Au, Ag, Zn, and Pb) to less than a hundred for several metals (see Table 1). I thoroughly checked for “double counting.” Whenever two different tonnage estimates were available for the same deposit I used the newer data.

• (vi) Although, for many of the metals included in this study, most or all of the known chemical metallogenic deposit types are included in the compilation, this is not so in some cases. Notably, Li deposits do not include evaporites, which almost certainly contain the largest reserves of this metal, but for which tonnage estimates do not appear to be publicly available.

For each of the elements included in this compilation, I first prepared a sorted list in order of increasing absolute deposit tonnages (Supplementary Table 2), and calculated the geometric mean and the median of the absolute metal tonnages. These results are shown in Table 2. For a lognormal distribution, the geometric mean and the median have the same value. As can be seen in Table 2 and Figure 5, for the 20 metals included in this study, the median and geometric mean of the distribution of individual deposit tonnages have very similar values. With the exception of PGE, the two values are within half an order of magnitude of each other, and in many cases much closer. Equality of the median to the geometric mean is a necessary condition for lognormality, but it is not sufficient. The results summarized in Figure 5 do suggest, however, that the distribution of metal tonnages should be at least qualitatively similar to a lognormal distribution, in the sense described at the end of the previous section, even if data for each metal are grouped without discriminating by metallogenic type (but see Singer 2013, for a formal test).

Table 2 Estimated Statistical Parameters of Metal Tonnage Distribution Functions

Fig. 5

Comparison of the median deposit size versus geometric mean deposit size (in terms of contained metal tonnage) for the 20 metals included in this study (Table 2 and Supplementary Table 2). A necessary, but not sufficient, condition for a lognormal distribution is that the two values be equal

In order to examine this hypothesis further, I began by dividing each deposit tonnage by the value of the geometric mean for the corresponding metal, in order to obtain a sorted list of normalized tonnages, t, for each metal (Supplementary Table 3). Note that the variable t represents observed normalized tonnages. It corresponds to the variable z in the PDFs P(z) and M(z), but whereas z refers to the independent variable in the statistical distribution functions, t represents discrete observations. The difference is important, and I will return to it in subsequent discussions. Histograms were prepared, representing the relative frequencies of the decimal logarithms of the normalized tonnages (Figs. 6–9). Note that all previous and subsequent equations are written in terms of natural logarithms, but the histograms show decimal logarithms. This is because, in my view, it is simpler to understand the range in deposit sizes on the basis of decimal logarithms (i.e., orders of magnitude) than natural logarithms. Moving between both bases is simply a matter of rescaling by a factor of log₁₀ e. For all metals, the bin size for the histograms is 0.2 (corresponding to a width of one fifth of an order of magnitude in metal content), and the frequencies were rescaled to a total of 1. The result of these transformations is that the histograms for the 20 elements are directly comparable to one another, as they all represent scale-free data in both coordinates.

Fig. 6

Deposit size distribution (in terms of contained metal tonnage) for six metals with sizable data bases (indicated by the number of deposits included, n) and reasonably symmetric distributions. Deposit sizes are normalized to the geometric mean deposit size (Supplementary Table 3) and transformed to decimal logarithms, and frequencies are normalized to a total of 1, so that the histograms are directly comparable to one another. Curves show theoretical lognormal PDFs for two different choices of scale parameters, either the standard deviation of the logarithms of the metal tonnages (solid curves) or the square root of the (observed) rescaled tonnage of the deposit located as close as possible to 50% point of the cumulative tonnage distribution (broken curves, see Eq. 35)

The PDF for the logarithms of a lognormally distributed random variable rescaled to a geometric mean μ ^* = 1 is a normal (Gaussian) distribution curve with mean = median = mode = μ = ln μ ^* = 0, i.e., centered at the origin. Also, if a set of random values, t, follows a perfect lognormal distribution, then the standard deviation of the values of ln t, which I will label s _t , equals the standard deviation of the normal PDF that describes the values of ln t, which is also the scale parameter σ of the lognormal PDF that describes the distribution of the values of t. I therefore calculated the standard deviation of the (natural) logarithms of the rescaled tonnages for each metal, which are shown Table 2. The values of s _t were then used to construct normal distribution curves, shown with the solid curves in Figures 6–9, with mean = 0 and standard deviation = s _t· log₁₀ e (this conversion is necessary because the histograms were constructed with values of log₁₀ t.) Note from Table 2 that, with the exceptions of PGE, Sn, and W, the values of s _t cluster in a relatively narrow interval, approximately 2.5–3.5, which suggests that the distribution of the endowment of many different metals follows similar patterns.

Inspection of the histograms suggests that the metals included in this study can be subdivided into three groups, as follows.

The first group, shown in Figures 6 and 7, consists of Cu, Au, Ag, Zn, Pb, Ni, Mo, Co, Mn, and Al. Although the quality of the agreement varies among these metals, probably at least in part because there are significant differences in the number of data points (also shown in the histograms), it appears reasonable to state that in all of these cases the histograms are unimodal, centered on the origin and not significantly skewed. The agreement with the expected normal PDF is mediocre, but there is a consistent observation: with the possible exception of Al, actual deposit size distributions are more strongly peaked than the theoretical PDF (solid curves in the figures). This may suggest that the standard deviation values s _t overestimate the scale parameter σ of the lognormal distribution.

Fig. 7

Same as Figure 6, for four metals that, although with reasonably symmetric distributions, have significantly smaller data bases than those in the previous figure (n < 400)

The second group, shown in Figure 8, consists of Sb, Li, Nb, and REE. The histograms for these four metals display the same general characteristics as those of the previous group and, with the exception of Li, the same relationship to the normal PDF. The number of data points for these four metals is, however, much smaller than those for the first group, which is the reason why they are shown separately. Also, at least for Li it is known that the data do not include the largest deposits (evaporites).

Fig. 8

Same as Figure 6, for four metals with small data bases (n < 100)

The third group, shown in Figure 9, consists of metals for which it is not possible to make a case for an approximately lognormal distribution of deposit sizes. Three of them, PGE, Sn, and W, display clearly bimodal distributions, which are also reflected in their significantly higher standard deviations (Table 2). Another two, Cr and Fe, are noticeably skewed, toward smaller deposits in the case of Cr and larger deposits in the case of Fe. Correspondingly, the standard deviations for these two metals are on the high end of the range of values for all metals other than PGE, Sn, and W (Table 2). Finally, U displays a relatively symmetric histogram centered at the origin, but one that is in very poor agreement with the normal PDF expected from the value of s _t .

Fig. 9

Same as Figure 6, for metals which display poor agreement with a lognormal distribution, either because the observed distribution is bimodal (PGE, Sn, and W), or significantly skewed (Cr, Fe), or insufficiently peaked (U)

The histograms suggest that, with the exceptions noted above, the distributions of deposit sizes for many metals share important characteristics with the lognormal distribution. In particular, the number of deposits falls off geometrically and symmetrically with size relative to a central “characteristic” size, such that deposits that are more than ~3 orders of magnitude larger or smaller than this central size are vanishingly rare. One can then ask whether the lognormal model is a reasonable enough approximation for it to be used to make valid predictions about future availability of metallic mineral resources.

We can expand upon this question by noting that the histograms in Figures 6–9 only convey information about the distribution of deposit sizes. A different question, as I discussed in previous sections, is that of the distribution of metal endowment among deposits of different sizes. In order to address this question, I began by calculating cumulative tonnages going down the sorted rescaled tonnage lists (Supplementary Table 4). Assuming that deposit size distributions are lognormal, the distribution of these cumulative tonnages, once rescaled to a maximum total value of 1, should follow the CDF m(z). I therefore located in the cumulative tonnage lists the deposit size t _q , that is the observed value that corresponds as closely as possible to the point z ^M _q in the function m(z), such that the fraction q of the metal endowment is contained in deposits larger than t _q (corresponding to Eq. 30). Once this point was located I calculated the (observed) frequency of the largest deposits, f _q , that contain the fraction q of the metal endowment. This observed variable corresponds to the calculated frequency p[z|(z ^M _q ,∞)], i.e. Eq. (31). Results for q = 0.5 and 0.95 are summarized in Table 2. Recall that, if metal tonnage distributions are indeed lognormal, then the standard deviation of the log transformed values, s _t (Table 2) corresponds to the scale parameter σ. The values of f _q from Table 2 were thus plotted in Figure 10 against the standard deviations of the logarithms of the metal contents, s _t . Also shown in the figure are the corresponding curves of p[z|(z ^M _q ,∞)] versus σ calculated with Eqs. (30) and (31) (compare Fig. 1). Although scattered, the data follow trends that are similar to those of the calculated curves, but that plot consistently above the curves. This observation restates the previous conclusion that the standard deviation of the log transformed tonnages may overestimate the scale parameter (Figs. 6–9 and associated discussion).

Fig. 10

Observed frequencies of the largest deposits that contain either 50% (circles, top panel) or 95% (triangles, bottom panel) of the endowment of the 20 metals included in Figures. 6–9 (see also Table 2), plotted against the standard deviation of the natural logarithms of the rescaled metal tonnages (also given in Table 2). For comparison, the figure also show curves for the calculated frequency of the largest deposits that contain 50 and 95% of the endowment for a population of deposits that rigorously follows a lognormal distribution, plotted against the scale parameter of the distribution (same as Figure 1)

Because using only the standard deviation of individual deposit tonnages to estimate the scale parameter ignores the distribution of cumulative tonnages, one can ask whether agreement between calculated and observed distributions improves when this additional information is considered. It is possible to estimate an alternate value of σ from Eq. (35). The value of t ₅₀ (Table 2 and Supplementary Table 4) is the rescaled size of the observed deposit that corresponds to the 50% point of the cumulative tonnage distribution, i.e., it approximates the point z ^M₅₀  = z ^M _m , the median of the CDF m(z). I therefore estimated alternate values of σ, which I label σ ^*, from Eq. (35), i.e., σ ^* = $\sqrt {\ln t_{50} }$. The values of σ ^*, also listed in Table 2, are in every case smaller than the values of σ = s _t obtained from the standard deviation of individual deposit sizes. The values of σ ^* were used in Figure 11 to repeat the comparison with the expected distribution of the metal endowment (compare Fig. 10). The agreement with the calculated curves improves significantly, and is particularly good with the 95% cumulative tonnage curve (with the possible exception of PGE, which as we saw above shows a strongly bimodal tonnage distribution). It is important to recapitulate what lies behind the good agreement illustrated in Figure 11: (i) construction of the theoretical probability curves is based on both PDFs, P(z) and M(z); (ii) estimation of σ ^* = $\sqrt {\ln t_{50} }$ relies on the location of the 50% point of the observed cumulative metal endowment distribution; (iii) the values of f _q , which correspond to p[z|(z ^M _q ,∞)], are the frequencies of the largest deposits that contain either 50 or 95% of the observed metal endowment. Because each of these data and calculations are independent of one another, it is unlikely that the agreement shown in Figure 11 is an artifact.

Fig. 11

Same as Figure 10, but in this case, the observed frequencies, which are of the same values as in Figure 10, are plotted against an alternative estimate of the scale parameter, σ ^* (given in Table 2), derived from the observed rescaled tonnage of the deposit located as close as possible to the 50% point of the observed cumulative tonnage distribution (Eq. 35). Agreement with the curves calculated for a theoretical lognormal distribution (same as in Figure 10) improves significantly (compare Fig. 10), and is particularly good for the frequency of largest deposits that contain 95% of the endowment

The values of σ ^* = $\sqrt {\ln t_{50} }$ were also used to plot a second set of normal distribution curves superimposed on the histograms that summarize the distribution of deposit tonnages. These are the dashed curves in Figures 6–9. The agreement of the histograms with the expected curves generally improves. The improvement is especially noticeable for metals for which at least 1000 deposits are included in the dataset (Cu, Au, Ag, Zn, and Pb, Figure 6), but is also seen for metals with much smaller datasets, particularly Al, Sb and REE (Figs. 7 and 8). Note that for most metals σ^* is in the range 2–3, suggesting that it may be possible to draw fairly general inferences about metal distribution by focusing on the behavior of lognormal distributions within this restricted range of scale parameters, as summarized in Figure 4.

We can also compare how the distribution of the observed metal endowment compares to the theoretical frequency of deposits in the most productive interval, centered on z ^M _m  = $e^{{\sigma^{2} }}$, and with the expected width of the interval. This is seen in Figure 12, which shows the same curves as Figure 3, together with the corresponding estimated values for the observed metal tonnages, which were obtained as follows. The normalized size of the deposit at the 50% point of the cumulative metal endowment curves, t ₅₀ was taken from Supplementary Table 4, as before. This point corresponds to the center of the most productive interval, z ^M _m  = $e^{{\sigma^{2} }}$ (Eq. 35). Then another two deposits were identified in the ordered cumulative tonnage table (Supplementary Table 4), corresponding to the lower and upper bounds of the most productive interval. These were defined as the deposits such that either 25 or 47.5% of the cumulative endowment (for the 50 and 95% metal endowment curves, respectively) is contained in deposits smaller and larger than t ₅₀, with ordered sizes ranging between t ₅₀ and the corresponding limiting deposit. These limiting deposit sizes are labeled t ^L₅₀ , t ^U₅₀ , t ^L₉₅ and t ^U₉₅ , and are shown in Table 2 and Supplementary Table 4. The frequency of deposits in these intervals (f ^ω₅₀ or f ^ω₉₅ in Table 2 and Supplementary Table 4) corresponds to the probability of occurrence in the most productive interval (Eq. 39 and left panel in Figure 12), and the ratio between the sizes of the two limiting deposit sizes (t ^U₅₀ /t ^L₅₀ , or t ^U₉₅ /t ^L₉₅ ) corresponds to ω (right panel in Figure 12). The agreement between observed and expected deposit frequencies in the most productive interval is excellent, especially for the wider interval that encompasses 95% of the metal endowment. There is, however, no good agreement with respect to the interval width. In all cases, mineral deposit sizes cluster into narrower tonnage intervals around the value of t ₅₀ than what a lognormal tonnage distribution would predict. A possible interpretation of this observation is that the actual distribution of deposit sizes is even more narrowly peaked than a lognormal PDF with the scale parameter given by σ ^* = $\sqrt {\ln t_{50} }$, shown with the dashed curves in Figures 6–9. But there is an additional important observation, which is that the width of the most productive interval shows relatively little variability among the different metals considered here, and appears to be largely independent of the value of σ. In most cases, the width of the most productive interval that contains 50% of the metal endowment is approximately 1 order of magnitude, and some 2–3 orders of magnitude for 95% of the endowment (Fig. 12).

Fig. 12

Observed frequency of deposits in most productive intervals containing either 50% (circles) or 95% (triangles) of the metal endowment (left panel) and observed width of the most productive interval (right panel), plotted against the alternative estimate of the scale parameter given by σ ^{* =} $\sqrt {\left( {\ln t_{50} } \right)}$—see Eq. (35) and Figure 11. For comparison, the figure also shows the corresponding curves calculated for a lognormal distribution, which are of the same curves shown in Figure 3

Concentration of a large proportion of the metal endowment in deposits of a relatively restricted and approximately constant size range may be the most important departure that the distribution of metals in nature shows relative to a lognormal model. The lack of agreement almost certainly arises from the fact that the simple multiplicative model that underlies the lognormal probability distribution is an oversimplified picture of the processes that are responsible for the concentration of metals in mineral deposits. This is hardly surprising, given the complexity and variability of the chemical and physical pathways responsible for formation of mineral deposits. It also means that, as pointed out by Singer (2013), making predictions about the likelihood of existence of undiscovered mineral deposits in specific mineralized tracts is only possible if one imposes stringent restrictions on metallogenic deposit types, which restrict the variability of mineralization processes. The goal of this paper, however, is distinctly different from making specific predictions aimed at discovering new ore deposits in favorable mineralized tracts.

Distribution of metallic deposit tonnages is not strictly lognormal. However, with a few exceptions, deposit tonnages follow unimodal distributions with approximately geometric scaling centered on the geometric mean size. It is therefore possible to identify a “most common” or “characteristic” deposit size, which corresponds to the median deposit size, which is approximately the same as the geometric mean size. Deposits that are more than a few orders of magnitude larger or smaller than this most common size are vanishingly rare. This behavior is shared with the lognormal distribution, and explains why metal endowment is concentrated in deposits that are considerably larger, and therefore rarer, than the most common deposits (Fig. 4). Singer (1995) found this to be true for deposits of several base and precious metals. The behavior is likely to be quite general, however, as it is observed among deposits of both scarce and abundant metals formed by a wide diversity of metallogenic processes.

Challenges Facing Future Supply of Metallic Raw Materials

In the accompanying paper (Patiño Douce 2015), I show that past demand for metallic raw materials has followed consistent and predictable trends that can be shown to arise from changes in per-capita demand for resources as well as from growth of world population. I also discuss what the implications of extrapolating these trends are, with respect to likely demand of metallic raw material throughout this century. For most metals, the world is likely to need between 5 and 10 times the amount of metal contained in known ore reserves in order to maintain historical patterns of metal consumption until the year 2100. It is possible to place constraints on what types of deposits one must hope exist if one is to have reasonable expectations of meeting the likely demand

Let us begin by examining the “most productive” deposit size interval, that is centered on a normalized deposit size ${\sim}e^{{\sigma^{2} }}$. For values of σ about 2–3, that may be characteristic of many metals, this corresponds to deposits that are 10²–10⁴ times larger than the median deposit size (Fig. 4), and that make up only a small fraction of all mineral deposits (Fig. 3, left panel). For many of the metals examined here, 95% of the known endowment is contained in a “most productive interval” with a width of 2–3 orders of magnitude (Fig. 12), that is in fact narrower than that predicted by a lognormal distribution (Figs. 3, 4). This discrepancy does not affect the following argument, that arises only from the displacement of the peak of the endowment distribution, M(z), toward deposit sizes that are orders of magnitude larger than the median deposit size.

Suppose that future needs will be approximately 5 times the amount of metal contained in known ore reserves (Patiño Douce 2015), and that we expect to rely on deposits with sizes within a “most productive” tonnage interval that contains 95% of the endowment (i.e., virtually all the metal) to supply these needs. Then it would be necessary to find approximately 5 new deposits in this size range for every known deposit of comparable size. If the sampling provided by the known mineral deposits is an accurate representation of the distribution of the entire metal endowment, then this would imply that approximately 5 times the known number of “most common” deposits (Fig. 4) should also exist. It is unlikely that only one out of every five “ordinary” ore deposits is known, especially after more than a century of systematic exploration.

Another possibility is to assume that we have only discovered the smallest deposits, and that truly “supergiant” deposits lurk undiscovered. We can model this possibility as follows. Suppose that we have determined that we will need g times the amount of known reserves in order to supply future needs. The amount of metal known to exist then constitutes a fraction G = 1/(1 + g) < 1 of the total hoped-for resources (which may or may not exist). If all of the known metal is contained in the smallest deposits of this hypothetical endowment, then the normalized size of the largest known deposit, which we can call z _large, is given by the solution to the equation:

$$ \int_{0}^{{z_{\text{large}} }} {M\left( z \right) {\text{d}}z = G} . $$

(40)

We can then determine the size of the (hypothetical) deposit at the center of the (hoped-for) most productive interval, relative to the largest known deposit:

$$ r_{\text{large}} = \frac{{e^{{\sigma^{2} }} }}{{z_{\text{large}} }} $$

(41)

and the probability that deposits larger than the largest known deposit exist is

$$ p \left[ {\left. z \right|\left( {z_{\text{large}} ,\infty } \right)} \right] = \int_{{z_{\text{large}} }}^{\infty } {P\left( z \right) {\text{d}}z.} $$

(42)

Some illustrative results are shown in Figure 13, for values of σ in the range 2–3. Suppose that G is ~0.16, i.e., we will need approximately five times the amount of metal contained in known ore reserves (Patiño Douce 2015). If we expect to rely on “supergiant” deposits to supply future demand of metallic raw materials, then we must hope that the most productive interval is centered on undiscovered deposits containing more than 10 times the amount of metal contained in the largest known deposits (the exact value varies with G and σ, as seen in the top panel of Figure 13). This is the center of the interval, so some of the deposits could be smaller, and some larger. We must also expect that all of these undiscovered deposits make up roughly 1% of all deposits (although there is considerable variability, see bottom panel of Figure 13). One must be careful when attaching a physical meaning to a numerical result such as this one. This number represents not the probability that these very large deposits exist, but rather the frequency with which they must exist if they are to supply future needs. If interpreted as a probability, the number is surprising, as the value is not negligible. A conservative interpretation of this probability would be that, because we have not yet found any of these not-so-rare yet very large deposits, they are unlikely to exist. There is anecdotal evidence that the larger deposits tend to be among the first to be discovered in a previously unexplored favorable geological setting. Although I am not aware of rigorous studies that quantify this statement, if true it would support the conclusion that not-so-rare very large deposits should have already been discovered if they existed. A better theoretical understanding of the physicochemical pathways and processes conducive to the formation of metallic mineral deposits might help to answer the question of whether deposits that large can exist, and thus decide whether their potentially crucial role in supplying future metal needs justifies exploring for them.

Fig. 13

Characteristic size of hypothetical “supergiant” deposits relative to the size of the largest known deposit (top panel), and frequency with which these hypothetical deposits should be expected to occur (bottom panel), plotted as a function of the fraction, G, of the known, proven reserves relative to the hoped-for resources. For example, if the demand will be 5–10 times the amount of metal contained in known ore deposits, then G will be about 0.1–0.2, and the hypothetical “supergiant” deposits needed to supply this demand will have to be approximately 10 times larger than the largest known deposits (top panel). If such deposits exist, then they should make up about 1% of all ore deposits (bottom panel)

We can also contemplate the inverse situation, in which we have discovered all of the largest deposits of the hypothetical endowment, and future demand will have to be met with metal contained in deposits that are smaller than the smallest known deposit. These small deposits may be undiscovered, or may be known but have been ignored because they are perceived to be uneconomic. In this case, we seek the normalized size of the smallest known deposit, z _small, which is given by the solution to the equation:

$$ \int_{{z_{\text{small}} }}^{\infty } {M\left( z \right) {\text{d}}z = G} . $$

(43)

The size of the (hypothetical) deposit at the center of the (hoped-for) most productive interval, relative to the smallest known deposit is

$$ r_{\text{small}} = \frac{{e^{{\sigma^{2} }} }}{{z_{\text{small}} }} $$

(44)

and the probability that deposits smaller than the smallest known deposit exist is

$$ p \left[ {\left. z \right|\left( {0,z_{\text{small}} } \right)} \right] = \int_{0}^{{z_{small} }} {P\left( z \right) {\text{d}}z} . $$

(45)

Results are shown in Figure 14, for the same values of σ as before. For G ~0.16, the most productive interval is in this case centered on undiscovered deposits containing one tenth, or less, of the amount of metal contained in the smallest known deposits. These deposits should be hundreds to thousands of times more common than the known deposits (Fig. 14, bottom). We can safely conclude that most of these deposits do not exist, because we otherwise would have already known about them. Relying on small mineral deposits is therefore not a viable strategy to supply future demand for metallic raw materials.

Fig. 14

Same as Figure 13, but now assuming that we have found all of the largest deposits, and that metal in excess of that contained in known ore reserves will have to be located in deposits smaller than the smallest known deposit. These would be minuscule deposits, less than one tenth the size of the smaller known ore bodies, and thousands of times more abundant than known ore deposits

Conclusions

If past trends in usage of metallic mineral resources continue, then humanity is likely to need several times the known amount of metal contained in proven reserves in order to meet the expected demand to the year 2100. The actual figures vary somewhat among the metals discussed in these papers, but a range of 5–10 times is a conservative estimate for most metals, including abundant and scarce metals (Patiño Douce 2015). These raw materials will have to be extracted from mineral deposits in which the metals of interest have been enriched above their geochemical average concentrations to concentrations that are sufficient to make extraction feasible both technologically and economically. By definition, we do not know whether mineral deposits containing the required amount of metal exist. In this paper, I have used the statistical distribution of metal in known mineral deposits to estimate the sizes of the deposits that will be required to meet expected demand.

The known endowment of all of the metals included in this study is strongly concentrated in a few mineral deposits that are orders of magnitude larger than the “median,” most common, deposits. The reason for this is that deposit sizes follow a roughly symmetric distribution, in which deposit frequency falls off geometrically with size, away from the median size. The distribution is not strictly lognormal, but it is similar enough to it to make the lognormal model a useful predictive tool. Following this line of reasoning, we arrive at the conclusion that, if the metal required to meet future demand exists, it is not to be chiefly found in mineral deposits of comparable size to those already known, nor in deposits that are significantly smaller than those that supply most of the world’s present day demand. Our best hope of meeting future demand is that “supergiant” deposits, perhaps one order of magnitude larger than the largest known deposits, exist. There is no indication that such deposits exist, nor any statistical arguments to expect that they do, nor that they do not. It is not the purpose of this contribution to decide this issue, nor to come up with tonnage estimates of undiscovered mineral resources. The goal is to constrain the sizes of the deposits on which exploration should be focused. This goal is complementary to the estimation of undiscovered resource tonnages. Deposits one order of magnitude larger than the largest known deposits might exist and still lie undiscovered, in which case supply over the rest of this century would not be a problem, albeit at unpredictable environmental and financial costs. But if they do not exist, then we can expect major, perhaps catastrophic, disruptions to the world’s economy sometime before the end of the century, arising from exhaustion of metallic raw material.

Appendix: Lognormal Versus Power-Law Distributions

Consider a rescaled (μ = 0) lognormal PDF, log-transformed as (see Eq. 2):

$$ \ln P\left( z \right) = - \frac{1}{{2\sigma^{2} }}\left( {\ln z} \right)^{2} - \ln z - \ln \left( {\sigma \sqrt {2\pi } } \right) $$

(46)

and a power-law:

$$ \ln Q\left( z \right) = - \beta \ln z - \gamma . $$

(47)

In a log–log plot, the first function is a curve with negative curvature, and the second function is a straight line. For z > $e^{{ - \sigma^{2} }} ,$ it is d ln P(z)/d ln z < 0. Therefore, the high-end tail of a lognormal distribution and a power law with negative exponent may be related as shown in Figure 15. Assume that the two functions are tangent in a log–log plot at a point z _T , as shown in the figure. We wish to know the distance, δ, between the values of the two functions, as a function of the distance from z _T , and the scale parameter σ (see Fig. 15).

Fig. 15

Schematic relationship between the high-end tail of a lognormal PDF, P(z), and a power-law distribution, Q(z). On a log–log plot the power law is a straight line, and the lognormal PDF is a curve with negative curvature. It is always possible to construct a power law that is tangent to P(z) at any arbitrary point, z _T , see text. One can then ask how the distance between the two curves, δ, varies as a function of the scale parameter of P(z) and the distance from z _T

If the curves are tangent at z _T , then

$$ \ln P\left( {z_{T} } \right) = \ln Q\left( {z_{T} } \right) $$

(48)

and

$$ \left. {\frac{d\ln P\left( z \right)}{d\ln z}} \right|_{{z = z_{T} }} = \left. {\frac{d\ln Q\left( z \right)}{d\ln z}} \right|_{{z = z_{T} }} $$

(49)

From the second equation, we get

$$ \beta = 1 + \frac{{\ln z_{T} }}{{\sigma^{2} }} $$

(50)

Solving the first equation for γ, we find

$$ \gamma = \frac{1}{{2\sigma^{2} }}\left( {\ln z_{T} } \right)^{2} + \left( {1 - \beta } \right)\ln z_{T} + \ln \left( {\sigma \sqrt {2\pi } } \right) $$

(51)

and substituting (50), we find

$$ \gamma = \ln \left( {\sigma \sqrt {2\pi } } \right) - \frac{{\left( {\ln z_{T} } \right)^{2} }}{{2\sigma^{2} }} . $$

(52)

Thus, a power law, Eq. (47), with parameters β and γ given by Eqs. (50) and (52), is tangent at z _T to a normalized lognormal PDF with scale parameter σ. We now wish to know how the distance between the functions varies as the value of the variable z moves away from the point, z _T , where the curves are tangent. Call this distance δ (see Fig. 15):

$$ \delta = \ln Q\left( z \right) - \ln P\left( z \right) = \ln \frac{Q\left( z \right)}{P\left( z \right)} $$

(53)

or, explicitly:

$$ \delta = \frac{1}{{2\sigma^{2} }}\left( {\ln z} \right)^{2} + \left( {1 - \beta } \right)\ln z + \ln \left( {\sigma \sqrt {2\pi } } \right) - \gamma . $$

(54)

Substituting Eqs. (50) and (52), we find

$$ \delta = \frac{1}{{2\sigma^{2} }}\left( {\ln z} \right)^{2} - \frac{{\ln z_{T} }}{{\sigma^{2} }}\ln z + \frac{{\left( {\ln z_{T} } \right)^{2} }}{{2\sigma^{2} }} $$

(55)

or:

$$ \delta = \frac{1}{{2\sigma^{2} }}\left( {\ln z - \ln z_{T} } \right)^{2} = \frac{1}{{2\sigma^{2} }}\left( {\ln \frac{z}{{z_{T} }}} \right)^{2} $$

(56)

That is,

$$ \ln \frac{Q\left( z \right)}{P\left( z \right)} = \frac{1}{{2\sigma^{2} }}\left( {\ln \frac{z}{{z_{T} }}} \right)^{2} $$

(57)

The last equation shows an important relationship between the lognormal and power-law distributions: the two functions converge as the scale parameter increases, and they do so quickly, as the convergence goes with the square of the scale parameter. At the limit σ → ∞, the two distributions become indistinguishable. For our purposes, however, it is more relevant to study how the two distributions deviate as a function of the distance from the point of tangency, z _T , for constant values of σ about 2–3 (see text). This is shown in Figure 16.

Fig. 16

The distance between a power law and a lognormal PDF tangent at z _T , given as e ^δ = Q(z)/P(z), as a function of the distance from z _T given as z/z _T . Over a displacement of ~1 order of magnitude from z _T , and for values of σ found here to be characteristic of metallic ore deposits, frequencies predicted by the power law would be less than twice those predicted by a lognormal distribution. The ratio climbs to about 3 to 10 times for a displacement of ~2 orders of magnitude. A power law decays more slowly than an exponential function (such as a lognormal PDF), so it predicts higher frequencies for large deposits. One can interpret this result either as meaning that there are greater chances of finding those large deposits, or as meaning that they do not exist, because, otherwise, we would have already known about them—see text

In this paper, I have modeled the distribution of metal contents in mineral deposits using the lognormal PDF. But suppose that, given the relatively few known mineral deposits in the high-end tail of the distribution, the uncertainty is large enough that power-law behavior cannot be discarded for the largest deposits, i.e., the high-end tail of the distribution can be fitted reasonably well with a straight line in a log–log plot. We saw in the main body of the paper that supplying the world’s metal demand throughout the twenty-first century is likely to require the discovery of deposits 10–100 times larger than the largest known deposits (e.g., assuming that G is ~0.16 in the top panel of Figure 13, see also associated discussion). If deposit size distribution follows a power law, then deposits of this magnitude might be 2–10 times more common than what a lognormal distribution would predict (Fig. 16). Assuming a lognormal distribution, such deposits would make up ~1% of all mineral deposits (bottom panel of Figure 13 with G of ~0.16, and also associated discussion). If, on the other hand, these very large deposits followed a power-law distribution, then we might expect them to be as common as 2–10% of all deposits (Fig. 16). One could use this greater frequency as a source of optimism that the required deposits exist and will be found. Or, following the interpretation that, “if they existed and they were that common we would already have found at least some of them,” one can conclude that assuming a power-law distribution for large deposits should not be a source of greater optimism about meeting future supply of metallic raw materials. The fact remains that statistics cannot answer this question, and that unless and until such giant deposits are discovered we will have no certainty about future supply of metallic raw materials, beyond knowing that smaller deposits will not by themselves be sufficient.