Introduction

Three-part mineral resource assessments provide a framework for making decisions concerning mineral resources under conditions of uncertainty (Singer and Menzie, 2010). The parts include permissive tracts in which general locations of undiscovered deposits are delineated based on a deposit type’s geologic setting; frequency distributions of tonnages and grades of well-explored deposits that serve as models of grades and tonnages of undiscovered deposits; and numbers of undiscovered deposits that are estimated probabilistically by deposit type. Recently improved deposit-density models show how to make probabilistic estimates of numbers of undiscovered deposits and of total tonnages of mineral deposits within permissive tracts.

In estimating the number of mineral deposits within an area, a robust method is based on mineral deposit densities, which are a form of mineral deposit model wherein the numbers of deposits per unit area from the well-explored regions are counted and the resulting frequency distribution enables estimation of the number of undiscovered deposits (Singer, 2008). Deposit densities can be used either directly for estimates or indirectly as guidelines in some other methods. Deposit-density models were designed to be used within the three-part form of assessment, which affects how they should be constructed. In three-part assessments, estimates of the number of undiscovered deposits explicitly represent the probability (or degree of belief) that some fixed but an unknown number of undiscovered deposits that are consistent with the grade-and-tonnage model exist in the delineated tracts. Determining a mineral deposit density requires unambiguous definitions of what is a deposit and what are the delineation rules for that deposit type. These definitions and operational rules, including the spatial rules defining the sampling unit, are necessary for defining deposits to ensure that deposits in grade, tonnage, and deposit-density models correspond to both discovered and estimated undiscovered deposits consistently (Singer and Menzie, 2010). Mineral deposit-density models start with well-explored control tracts where the number of deposits consistent with the grade-and-tonnage model is counted along with the area that is well-explored.

In addition to estimates of number of deposits, estimates of total tonnage of mineral deposits in tracts delineated as permissive for a deposit type are important in assessing undiscovered mineral resources. Density of deposits (number of deposits/area) regression models based on well-explored control areas have power law relationships with areas of permissive tracts and deposit sizes allowing estimation of number of deposits and total deposit tonnages. Empirical evidence also indicates that processes affecting number of deposits and quantity of resources in an area are very general across deposit types. Areas of permissive tracts that geologically could contain the deposits are excellent predictors of numbers of deposits (Singer, 2008; Singer and Kouda, 2008).

Permissive tracts, not rectangular cells, can be considered natural sampling control areas for specific deposit types. Permissive tracts are based on geologic criteria found in descriptive deposit models that are themselves based on studies of known deposits. Use of cells presents problems related to the highly skewed distribution of the physical size of mineral deposits. The physical sizes of deposits by type are highly correlated with the total tonnages of deposits. Because of size distributions, sizes of cells are difficult to define so that a cell can hold either one or no deposit. If cells can hold more than one deposit, then the definition of the probability of a cell containing a deposit becomes questionable. Any fixed cell size makes it difficult or perhaps impossible to relate whatever the associated probability of a deposit in the cell means with respect to the number of deposits.

The relationship between the size of the permissive area and the deposit density has been shown to apply across deposit types (Singer, 2008; Singer and Menzie, 2010). The association of deposit density with deposit size also exists across types. The average aerial extent of mineralization and alteration is not well known for most deposit types so that a surrogate, of known, median deposit tonnage, is used to examine its relationship to deposit density. Tonnages used here are the median tonnages from the control areas. Regression models using these variables provide an easy way to estimate the number of deposits and the total tonnage of mineralized rock within tracts. In this article, we provide a probabilistic method to estimate numbers of deposits and total tract tonnages and compare the estimates made with this system to independent estimates made by experts.

Number of Deposits Estimates

Estimates of numbers of mineral deposits are fundamental to assessing undiscovered mineral resources. Just as the frequencies of grades and tonnages of the well-explored deposits are used to represent grades and tonnages of undiscovered deposits, density of deposits (number of deposits/area) in the well-explored control areas can serve to estimate number of deposits. Empirical evidence indicates that processes affecting the number and quantity of resources in geologic settings are very general across deposit types. Sizes of permissive tracts that geologically could contain the deposits are excellent predictors of the total numbers of deposits.

Regression density models using these variables provide a means to estimate number of deposits and total tonnage of mineralization. Powerful estimators are based on analysis of 10 different deposit types from 109 permissive worldwide control tracts, generalizing across deposit types. Estimates of density of mineral deposits are made by regressing permissive area (a), and mean log-transformed tons in deposits (s), against density of deposits for the 50th percentile estimate. The following equation (R 2 = 0.91) can be used for all deposit types:

$$ { \log }_{ 10} \left( {\text{Density}}_{50} \right) = 4.21- 0.499\,{ \log }_{ 10} \left( a \right) - 0. 2 2 5\,{ \log }_{ 10} \left( s \right) $$
(1)

where Density50 is the 50th percentile estimate in the number of deposits per 100,000 km2 , a is area permissive in square kilometers, and s is mean log size in millions of metric tons.

To estimate 90% confidence limits for lower estimates of density of deposits and 10% confidence limits for upper density estimates, the following equation is used:

$$ { \log }_{ 10} \left( {{\text{Density}}_{ 90} ,{\text{Density}}_{ 10} } \right) = { \log }_{ 10} \left( {{\text{Density}}_{ 50} } \right) \pm 1. 2 90 \cdot 0. 3 4 8 4\cdot \sqrt { 1+ \left( { 1/ 10 9} \right) + \left( { 3. 1 7 3 { } - { \log }_{ 10} \left( a \right)} \right)^{ 2} \cdot \left( { - 0. 3 2 9 2 { } - { \log }_{ 10} \left( t \right)} \right)^{ 2} /\left( { 10 9- 1} \right) \cdot 2. 6 1 5\cdot 1. 1 8 8} $$
(2)

where 1.290 is the Student’s t at the 10% significant level with 106 degrees of freedom, t 10,106df, 0.3484 is the standard deviation of logarithmic values of deposit density given permissive area and deposit size, 109 is the number of control tracts, 3.173 is the mean logarithmic values of control tract area in square kilometers, −0.3292 is mean of logarithmic values of deposit tonnage in millions on metric tons in control tracts, 2.615 is the standard deviation of log-transformed deposit tonnages in control tracts, and 1.188 is standard deviation of logarithmic values of area of control tracts. To convert density estimates to number of deposits estimates at the 90th, 50th, and 10th confidence levels, log density per 100,000 km2 needs to be adjusted for tract size:

$$ N_{{{\text{\%ile}}}} = a/100,000*10^{{{ \log }_{10} \left( {{\text{Density}}_{{{\text{\%ile}}}} } \right)}} $$
(3)

The expected number of deposits can be estimated as 10 to the power of

$$ { \log }_{10} \,E\left( N \right) = { \log }_{10} \left( {N_{50} } \right) + \left( {\left( {\left( {\log_{10} \left( {N_{10} } \right) - \log_{10} \left( {N_{50} } \right)} \right)/t} \right)^{2} } \right)/2 $$
(4)

Estimates made this way are for total number of deposits in tracts. To estimate the number of undiscovered deposits, the known number in a tract must be subtracted from the expected number [Eq. (4)]. In order to estimate the number of undiscovered deposits, the known number of deposits in a tract needs to be subtracted from the estimated total expected number to make a revised expected number of undiscovered deposits estimate. This requires revising the expected number and variance, and estimating a new median and 90th and 10th percentiles. Regression variance is estimated as

$$ {\text{var}}_{N} = \left( {\left( {\log_{10} \left( {N_{10} } \right) - \log_{10} \left( {N_{50} } \right)} \right)/t} \right)^{2} $$
(5)

Revised estimates of median number of deposits adjusted for number of known deposits are 10 to the power of

$$ \log_{10} \left( {N_{50} } \right) = \log_{10} \left( {E\left( N \right) - {\text{known}}\;{\text{number}}} \right)-\text{var}_{N} /2 $$
(6)

log10(N 50) is used in place of R 50 in Equation (2) to make probabilistic estimates of the number of undiscovered deposits while accounting for known deposits.

Tonnage Estimates

The regression coefficients reported here are based on data provided by Singer and Menzie (2010), which are updated from Singer (2008). Estimates of total tonnage of mineral deposits within a tract are made by regressing permissive area (a), and mean (in logs) tons in deposits of the type (s), against total tonnage of deposits in the tract for the 50th percentile estimate. The following regression equation (R 2 = 0.95) can be used for all deposit types:

$$ { \log }_{ 10} \left( {{\text{Tonnage}}_{50} } \right) = - 1.0 9 6+ 0. 70 3 9\,{ \log }_{ 10} \left( a \right) + 0. 6 20 2\,{ \log }_{ 10} \left( s \right) $$
(7)

where a is permissive area in square kilometers, and s is mean log deposit size in millions of metric tons. To estimate a 90% confidence limit for a lower estimate of total tonnage of deposits and a 10% confidence limit for an upper estimate of total tonnage of deposits, we use the following equation:

$$ { \log }_{10} \left( {{\text{Tonnage}}_{90} ,{\text{Tonnage}}_{10} } \right) = { \log }_{10} \left( {{\text{Tonnage}}_{50} } \right) \pm 1.290 \cdot 0.5144 \cdot \sqrt {1 + \left( {1/109} \right) + \left( {3.175 - \log_{10} \left( a \right)} \right)^{2} \cdot \left( { - 0.3292 - \log_{10} \left( t \right)} \right)^{2} /\left( {109 - 1} \right) \cdot 2.615 \cdot 1.191} $$
(8)

where 1.290 is Student’s t at the 10% significance level with 106 degrees of freedom, t 10,106df, 0.5144 is the standard deviation of logarithmic values of tonnage (given permissive area and median deposit size), 109 is the number of control tracts, 3.175 is the mean of logarithmic values of control tract areas in square kilometers, −0.3292 is mean of logarithmic values of deposit sizes in control tracts in millions of metric tons, 2.615 is the standard deviation of logarithmic values of deposit sizes in control tracts in millions of metric tons, and 1.191 is the standard deviation of logarithmic values of area of control tracts. To convert to arithmetic units, Equation (9) can be used.

$$ {\text{Tons}}_{{{\text{\%ile}}}} = 10^{{\log_{10} \left( {{\text{Tonnage}}_{{{\text{\%ile}}}} } \right)}} $$
(9)

The regressions shown above are in log–log space. In arithmetic space, scatter plots are clearly heteroskedastic thereby violating assumptions of tests of significance, and so it is necessary to perform the regressions in log space. Testing suggests that errors about the regressions can be approximated by lognormal distributions. For lognormal distributions, the arithmetic median is estimated by 10u and the arithmetic mean is estimated as 10u+var/2 (Aitchison and Brown 1963). The regression estimate at the 50th percentile is used for the mean estimate in log space.

For example, if the permissive area of a particular deposit type is 1,000 km2 and the median deposit size is 1 Mt, then the 50th percentile estimate would be 10 Mt, the 90th percentile estimate 2 Mt, and the 10th percentile estimate 48 Mt. To estimate undiscovered tonnages where there are known deposits, tonnages of known deposits need to be properly subtracted from the above estimates by counting the total tonnage of the known deposits as an expected tonnage that is subtracted from the total expected tonnage calculated by the regression and then recalculating the percentiles.

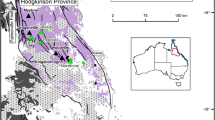
In a more realistic example, the above equations can be used to estimate the number of undiscovered deposits and the tonnage of significant orogenic gold-bearing deposits in the northern Bendigo Zone in Victoria, Australia that is unexplored because it is under cover. As reported by Lisitsin and others (2010), the permissive covered area is 7,600 km2, and the median ore tonnage of the known significant deposits (>0.8 t Au) is 0.3 Mt. Using Equations (1)–(4), the 90th percentile estimate of the number of deposits is 6, the 50th is 18, and the 10th is 51 deposits. The expected number of deposits is 21 (Table 1). Because there are no well-explored deposits known under cover, no adjustment for known deposits is necessary here. Expert estimates of the number of deposits are 15, 25, and 32 at the 90th, 50th, and 10th percentiles, respectively, with an expected number of deposits of 23 (Lisitsin and others, 2010). The expert and regression density estimates are close to each other with the most obvious difference being the lower uncertainty associated with the expert estimates as shown by the smaller difference between the 90th and 10th percentile estimates compared to the regression estimates.

Table 1 Estimates of the Number of Undiscovered Orogenic Gold Deposits in the Northern Bendigo Zone, Victoria, Australia
Full size table

Using Equations (7)–(9) and the tonnage versions of Equations (4)–(6), the 90th percentile estimate is 4 Mt, the 50th is 21 Mt, and the 10th is 95 Mt with an expected number of 28 Mt (Table 2). These estimates can be compared to the total tonnage estimates made by the Monte Carlo simulation of the expert estimates of number of deposits and the tonnages from the grade and tonnage model. The combined estimates are the 90th percentile estimate of 16 Mt or more, the 50th of 54 Mt or more, and the 10th of 110 Mt or more with an expected number of 59 Mt (Lisitsin and others, 2010). Although the expected tonnage from the density regression model is about half of that produced by the method of estimation used by Lisitsin and others (2010), the 10th percentile estimates are similar. At present, there is no way to know which estimate is closer to the correct total undiscovered tonnage in that area.

Table 2 Estimates of Total Tonnage (Mt) of Undiscovered Orogenic Gold Deposits in the Northern Bendigo Zone, Victoria, Australia
Full size table

Conclusions

The regression models of deposit density and tonnage presented above are powerful tools in estimations of number of deposits and of tonnages of these undiscovered mineral deposits. In addition, the universal regression density models presented in this article provide unbiased and reasonable estimates in the most situations. The density models of number of deposits and total tonnages were constructed using control areas with mineral deposits defined by certain consistently applied rules, such as distance to adjacent deposits, grade and tonnage models that follow these rules, and permissive tracts or belts also defined by consistent rules. For most deposit types, the relationships developed here represent robust methods to estimate the numbers of deposits and the total resources in delineated tracts. These tonnage densities and the number of deposit densities (Singer and Menzie, 2010) could be used with the lognormal distributions of contained metals within deposit types (Singer, 2011) to make global resource estimates if permissive tracts were properly delineated. Conditions where regression density estimates of number of deposits and total tonnages are robust are where the deposit type setting can be delineated using geology and the deposits belong to a type based on well-explored deposits with spatial limits and associated grade-tonnage models.

The strength of the relationships (R 2 = 0.95 for tonnage of mineralized rock) argues for the broad use of these predictors of total resources in permissive tracts. Of course where specific density models for a deposit type exist, they are likely to lead to better estimates in that they would have lower variances and should be used rather than the general model presented here. Deposit densities can now be used to provide a guideline for expert judgment or used directly for estimates of number of deposits or of total deposit tonnages of most kinds of mineral deposits. These density models should not be expected to be applicable to situations such as belts of rock that are not permissive or where consistent grade and tonnage models do not exist.

These deposit-density models serve two functions: one, they make explicit the uncertainty related to estimates of number and tonnages of undiscovered mineral deposits, and two, they provide estimates of undiscovered resources that are independent of other methods such as expert judgment.