Uniform solutions to SAT and 3-SAT by spiking neural P systems with pre-computed resources

Abstract

We consider the possibility of using spiking neural P systems for solving computationally hard problems, under the assumption that some (possibly exponentially large) pre-computed resources are given in advance. In particular, we propose two uniform families of spiking neural P systems which can be used to address the NP-complete problems sat and 3-sat, respectively. Each system in the first family is able to solve all the instances of sat which can be built using n Boolean variables and m clauses, in a time which is quadratic in n and linear in m. Similarly, each system of the second family is able to solve all the instances of 3-sat that contain n Boolean variables, in a time which is cubic in n. All the systems here considered are deterministic.

1 Introduction

Spiking neural P systems (SN P systems, for short) have been introduced in (Ionescu et al. 2006b) as a new class of distributed and parallel computing devices, inspired by the neurophysiological behavior of neurons sending electrical impulses (spikes) along axons to other neurons. SN P systems can also be viewed as an evolution of P systems (Păun 1999; Păun 2000; Păun 2002; Păun and Rozenberg 2002; http://ppage.psystems.eu/) corresponding to a shift from cell-like to neural-like architectures. We recall that this biological background has already led to several models in the area of neural computation, e.g., see (Gerstner and Kistler 2002; Maass 2002; Maass and Bishop 1999).

In SN P systems the cells (also called neurons) are placed in the nodes of a directed graph, called the synapse graph. The contents of each neuron consist of a number of copies of a single object type, called the spike. Every cell may also contain a number of firing and forgetting rules. Firing rules allow a neuron to send information to other neurons in the form of electrical impulses (also called spikes) which are accumulated at the target cells. The applicability of each rule is determined by checking the contents of the neuron against a regular set associated with the rule. In each time unit, if a neuron can use some of its rules then one of such rules must be used. The rule to be applied is non-deterministically chosen. Thus, the rules are used in a sequential manner in each neuron, but neurons function in parallel with each other. Observe that, as usually happens in membrane computing, a global clock is assumed, marking the time for the whole system, hence the functioning of the system is synchronized. When a cell sends out spikes it becomes “closed” (inactive) for a specified period of time, that reflects the refractory period of biological neurons. During this period, the neuron does not accept new inputs and cannot “fire” (that is, emit spikes). Another important feature of biological neurons is that the length of the axon may cause a time delay before a spike reaches its target. In SN P systems this delay is modeled by associating a delay parameter to each rule which occurs in the system. If no firing rule can be applied in a neuron, there may be the possibility to apply a forgetting rule, that removes from the neuron a predefined number of spikes.

Formally, a spiking neural membrane system (SN P system, for short) of degree m ≥1, as defined in (Ionescu et al. 2006a) in the computing version (i.e., able to take an input and provide and output), is a construct of the form

$$ \Uppi=(O,\sigma_1,\sigma_2,\ldots,\sigma_m,\,syn,\,in,\,out), $$

where:

• 1. O = {a} is the singleton alphabet (a is called spike);

• 2. $\sigma_1,\sigma_2,\ldots,\sigma_m$ are neurons, of the form ${\sigma_i}= (n_i,R_i),1{\le}i{\le}m,$ where

  • (a) $n_i {\ge}0$ is the initial number of spikes contained in $\sigma_i;$

  • (b) R _i is a finite set of rules of the following two forms:

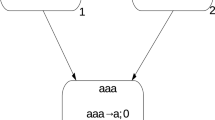
    • (1) firing (also spiking) rules $E/a^c {\to}a;\,d,$where E is a regular expression over a, and $c {\ge}1,\,d {\ge}0$ are integer numbers; if E = a ^c, then it is usually written in the simplified form: $a^c {\to}a;\,d;$ similarly, if d = 0 then it can be omitted when writing the rule;

    • (2) forgetting rules $a^s {\to}\lambda,$ for s ≥1, with the restriction that for each rule $E/a^c\rightarrow a;\,d$ of type (1) from R _i , we have $a^s \not\in L(E)$ (the regular language defined by E);

• 3. $syn \subseteq \{1,2,\ldots,m\} \times \{1,2,\ldots,m\},$ with $(i,i)\not\in syn$ for $1{\leq}i{\leq}m,$ is the directed graph of synapses between neurons;

• 4. $in, out \in \{1,2,\ldots,m\}$ indicate the input and the output neurons of Π, respectively.

A firing rule $E/a^c \to a;\,d \in R_i$ can be applied in neuron σ _i if it contains k ≥c spikes, and $a^k \in L(E).$ The execution of this rule removes c spikes from σ _i (thus leaving k−c spikes), and prepares one spike to be delivered to all the neurons σ _j such that $(i,j) \in syn.$ If d = 0 then the spike is immediately emitted, otherwise it is emitted after d computation steps of the system. As stated above, during these d computation steps the neuron is closed, and it cannot receive new spikes (if a neuron has a synapse to a closed neuron and tries to send a spike along it, then that particular spike is lost), and cannot fire (and even select) rules. A forgetting rule $a^s\to\lambda$ can be applied in neuron σ _i if it contains exactly s spikes; the execution of this rule simply removes all the s spikes from σ _i .

A common generalization of firing rules was introduced in (Chen et al. 2006c; Păun and Păun 2007) under the name of extended rules. These rules are of the form $E/a^c\rightarrow a^p;\,d,$ where $c {\ge}1,p {\ge}1$ and d ≥0 are integer numbers. The semantics of these rules is the same as above, with the difference that now p spikes are delivered (after d time steps) to all neighboring neurons.

The initial configuration of the system is described by the numbers $n_1,n_2,\ldots,n_m$ of spikes present in each neuron, with all neurons being open. During the computation, a configuration is described by both the contents of each neuron and its state, which can be expressed as the number of steps to wait until it becomes open (zero if the neuron is already open). Thus, $\langle r_1/t_1,\ldots,r_m/t_m\rangle$ is the configuration where neuron σ _i contains $r_i{\ge}0$ spikes and it will be open after $t_i\ge 0$ steps, for $i=1,2,\ldots,m;$ with this notation, the initial configuration of the system is $C_0=\langle n_1/0,\ldots,n_m/0\rangle.$

A computation starts in the initial configuration. In order to compute a function $f: {\mathbb{N}} {\to}{\mathbb{N}}$ (functions of the kind $f:{\mathbb{N}}^\alpha \to {\mathbb{N}}^\beta,$ for any fixed pair of integers ${\alpha}{\ge}1$ and ${\beta}{\ge}1,$ can also be computed by using appropriate bijections from ${\mathbb{N}}^\alpha$ and ${\mathbb{N}}^\beta$ to ${\mathbb{N}}),$ a positive integer number is assigned as input to the specified input neuron in. In the original model, as well as in some early variants, the number is encoded as the number of time steps elapsed between the insertion of two spikes into the neuron. To pass from a configuration to another one, for each neuron a rule is chosen among the set of applicable rules, and is executed. Generally, a computation may not halt. However, in any case the output of the system is considered to be the time elapsed between the arrival of two spikes in the designated output cell out. Other possibilities exist to encode input and output numbers, as discussed in (Ionescu et al. 2006a): as the number of spikes contained in neuron in (resp., out) at the beginning (resp., the end) of the computation, as the number of spikes fired in a given interval of time, etc.

A useful extension to the standard model defined above is to consider several input neurons, as already done in (Leporati et al. 2008, 2007a), so that the introduction of the encoding of an instance of the problem to be solved can be done in a faster way, introducing parts of the code in parallel in various input neurons. Formally, we can define an SN P system of degree (m, ℓ), with m ≥1 and $0 \le \ell \le m,$ just like a standard SN P system of degree m, the only difference being that now there are ℓ input neurons denoted by $in_1,\ldots,in_\ell.$ A valid input for an SN P system of degree $(m,\ell)$ is a set of $\ell$ binary sequences, that collectively encode an instance of a problem.

The previous definitions cover many types of systems/behaviors. By neglecting the output neuron we can define accepting SN P systems, in which the natural number (or the vector of natural numbers, in the case of systems having ${\ell} > 1$ input neurons) given in input is accepted if the computation halts. On the other hand, by ignoring the input neuron (and thus starting from a predefined input configuration) we can define generative SN P systems. In (Ionescu et al. 2006b) it was shown that generative SN P systems are universal, that is, can generate any recursively enumerable set of natural numbers. Moreover, a characterization of semilinear sets was obtained by spiking neural P systems with a bounded number of spikes in the neurons. These results can be obtained also for some restricted forms of SN P systems: (Ibarra et al. 2007) shows that one of the following features can be avoided while keeping universality: time delay greater than 0, forgetting rules, outdegree of the synapse graph greater than 2, and regular expressions of complex form. In (García-Arnau et al. 2007) it is shown that universality is kept even if we remove some combinations of two of the above features. These results are true both for the generative and the accepting cases. Finally, in (Păun et al. 2007) the behavior of SN P systems on infinite strings and the generation of infinite sequences of 0 and 1 was investigated, whereas in (Chen et al. 2006a) SN P systems were studied as language generators (over the binary alphabet $\{0,1\}).$

Spiking neural P systems can also be used to solve decision problems, both in a semi-uniform and in a uniform way. When solving a problem Q in the semi–uniform setting, for each specified instance ${\mathcal{I}}$ of Q we build in a polynomial time (with respect to the size of ${\mathcal{I}})$ an SN P system $\Uppi_{Q,{\mathcal{I}}},$ whose structure and initial configuration depend upon ${\mathcal{I}},$ that halts (or emits a specified number of spikes in a given interval of time) if and only if ${\mathcal{I}}$ is a positive instance of Q. On the other hand, a uniform solution of Q consists in a family $\{\Uppi_Q(n)\}_{n \in {\mathbb{N}}}$ of SN P systems such that, when having an instance ${\mathcal{I}}\in Q$ of size n, we introduce a polynomial (in n) number of spikes in a designated (set of) input neuron(s) of $\Uppi_Q(n)$ and the computation halts (or, alternatively, a specified number of spikes is emitted in a given interval of time) if and only if ${\mathcal{I}}$ is a positive instance. The preference for uniform solutions over semi-uniform ones is given by the fact that they are more strictly related to the structure of the problem, rather than to specific instances. Indeed, in the semi-uniform setting we do not even need any input neuron, as the instance of the problem is embedded into the structure (number of spikes, graph of neurons, rules) from the very beginning. If the instances of a problem Q depend upon two parameters (as is the case of sat, the satisfiability of propositional formulas expressed in the conjunctive normal form, where n is the number of variables and m the number of clauses in a given formula), then we will denote the family of SN P systems that solves Q by $\{\Uppi_Q(\langle n,m \rangle)\}_{n,m \in {\mathbb{N}}},$ where $\langle n,m \rangle$ indicates the positive integer number obtained by applying an appropriate bijection (for example, Cantor’s pairing) from ${\mathbb{N}}^2$ to ${\mathbb{N}}.$

The present paper considers SN P systems for solving decision problems, continuing the papers (Leporati et al. 2007a, 2007b, 2008), where one deals with the NP-complete decision problems Subset Sum, sat and 3-sat. For all these problems, constant time and polynomial time solutions were provided by using SN P systems constructed in the semi-uniform setting, working in a non-deterministic way, and also using a series of ingredients added to SN P systems of the standard form: extended rules, the possibility to have a choice between spiking rules and forgetting rules, etc. Here we consider a different situation: we provide uniform constructions for sat and 3-sat (two uniform constructions for solving sat were also presented in (Leporati et al. 2008, 2007b), but the idea of the construction given here is different), assuming that a pre-computed SN P system, possibly having an exponential size with respect to the size of the instances of the problem we want to solve, is given in advance. All the systems we will propose work in a deterministic way.

We will not specify how our pre-computed resources could be built. However, we require that such pre-computed systems have a structure which is as regular as possible, and that they do not contain neither “hidden information” that simplify the solution of specific instances, nor an encoding of all possible solutions (that is, an exponential amount of information that allows to cheat while solving the instances of the problem). These requirements were inspired by open problem Q27 in (Păun 2002). Let us note in passing that the regularity of the structure of the system is related to the concept of uniformity, that in some sense measures the difficulty of constructing the system. For example, when considering families $\{C(n)\}_{n \in {\mathbb{N}}}$ of Boolean circuits, or other computing devices whose number of inputs depends upon an integer parameter n ≥ 1, it is required that for each $n \in {\mathbb{N}}$ a “reasonable” description (see Balcázar et al. 1988–1990) for further discussion on this topic) of C(n), the circuit of the family which has n inputs, can be derived in polynomial time and logarithmic space (with respect to n) by a deterministic Turing machine whose input is 1ⁿ, the unary representation of n. In this paper we will not delve further into the details concerning uniformity; we just rely on reader’s intuition, by stating that it should be possible to build the entire structure of the system using only a polynomial amount of information and a controlled replication mechanism, as it already happens in P systems with cell division.

The rest of the paper is organized as follows. In Sect. 2 we present a uniform family $\{\Uppi_{\rm SAT}(\langle n,m \rangle)\}_{n,m \in {\mathbb{N}}}$ of SN P systems, where for each $n,m \in {\mathbb{N}}$ the system $\Uppi_{\rm SAT}(\langle n,m \rangle)$ solves all the instances of sat which are composed by m clauses, built using n Boolean variables. Section 3 illustrates a uniform family $\{\Uppi_{{3}{\rm SAT}}(n)\}_{n \in {\mathbb{N}}}$ of SN P systems such that every $\Uppi_{{3}{\rm SAT}}(n)$ solves all the instances of 3-sat which can be built using n Boolean variables. Section 4 concludes the paper and gives some directions for future research.

2 Solving SAT

Let us consider the NP-complete decision problem sat (Garey and Johnson 1979, p. 39). The instances of sat depend upon two parameters: the number n of variables, and the number m of clauses. We recall that a clause is a disjunction of literals, occurrences of x _i or $\neg x_i,$ built on a given set $X =\{x_1,x_2,\ldots,x_n\}$ of Boolean variables. Without loss of generality, we can avoid the clauses in which the same literal is repeated or both the literals x _i and $\lnot x_i,$ for any $1 {\leq}i {\leq}n,$ occur. In this way, a clause can be seen as a set of at most n literals. An assignment of the variables $x_1,x_2,\ldots,x_n$ is a mapping $a: X \to \{0,1\}$ that associates to each variable a truth value. The number of all possible assignments to the variables of X is 2ⁿ. We say that an assignment satisfies the clause C if, assigned the truth values to all the variables which occur in C, the evaluation of C (considered as a Boolean formula) gives 1 (true) as a result.

We can now formally state the sat problem as follows.

Problem 1. Name: sat.

• Instance: a set $C =\{C_1, C_2, {\ldots,}C_m\}$ of clauses, built on a finite set $\{x_1,x_2,\ldots,x_n\}$ of Boolean variables.

• Question: is there an assignment of the variables $x_1,x_2,\ldots,x_n$ that satisfies all the clauses in C?

Equivalently, we can say that an instance of sat is a propositional formula $\gamma_n = C_1\wedge C_2\wedge\ldots\wedge C_m,$ expressed in the conjunctive normal form as a conjunction of m clauses, where each clause is a disjunction of literals built using the Boolean variables $x_1,x_2,\ldots,x_n.$ With a little abuse of notation, from now on we will denote by sat(n,m) the set of instances of sat which have n variables and m clauses.

Let us build a uniform family $\{\Uppi_{\rm SAT}(\langle n, m \rangle)\}_{n,m \in {\bf N}}$ of SN P systems such that for all $n,m \in {\mathbb{N}}$ the system $\Uppi_{\rm SAT}(\langle n,m \rangle)$ solves all the instances of sat (n,m) in a number of steps which is quadratic in n and linear in m. All the systems $\Uppi_{\rm SAT}(\langle n,m \rangle)$ will work in a deterministic way.

Because the construction is uniform, we need a way to encode any given instance γ _n of sat(n, m). As stated above, each clause C _i of γ _n can be seen as a disjunction of at most n literals, and thus for each $j\in\{1,2,\ldots,m\}$ either x _j occurs in C _i , or $\lnot x_j$ occurs, or none of them occurs. In order to distinguish these three situations we define the spike variables α _ij , for $1 {\leq}i {\leq}m$ and $1 {\leq}j {\leq}n,$ as variables whose values are amounts of spikes, and we assign to them the following values:

$$ \alpha_{ij}=\left\{\begin{array}{ll} a \quad& \hbox{if }x_j \,\hbox{occurs in }C_i\\ a^{2}\quad&\hbox{if }\lnot x_j \,\hbox{occurs in }C_i\\ \lambda\quad&\hbox{otherwise}. \end{array} \right. $$

(1)

In this way, clause C _i will be represented by the sequence $\alpha_{i1} \alpha_{i2}\ldots\alpha_{in}$ of spike variables; in order to represent the entire formula γ _n we just concatenate the representations of the single clauses, thus obtaining the sequence $\alpha_{11}\alpha_{12}\ldots\alpha_{1n} \alpha_{21}\alpha_{22}\ldots\alpha_{2n}\ldots\alpha_{m1}\alpha_{m2}\ldots \alpha_{mn}.$ As an example, the representation of $\gamma_3 = (x_1 \lor \lnot x_2) \land (x_1 \lor x_3)$ is the sequence $aa^2{\lambda a\lambda}a.$

The (pre-computed) SN P system that solves all the possible instances of sat (n, m) is depicted in a schematic way in Fig. 1. The system is composed by n + 5 layers. The first layer (numbered by 0) is composed by a single input neuron, that we use to insert the representation of the instance $\gamma_n \in$ sat(n, m) to be solved. At each computation step we insert 0, 1 or 2 spikes into the system, according to the value of the spike variable α _ij we are considering in the representation of γ _n . Let us note that in this way we are simulating the insertion of a string whose symbols are taken from a ternary alphabet (where each symbol is used to distinguish one of the three possible situations mentioned in (1)) by using the multiplicity of a single symbol, the spike. However this may be perceived as a betrayal of the original spirit underlying SN P systems, stating that a single symbol should be used; indeed, to the best knowledge of the authors this trick has never been used before in the literature concerning SN P systems. Hence, an alternative approach consists in using two input neurons, as depicted in Fig. 2; in this way, at each step we are able to insert 0,1 or 2 spikes in the system by using two spike trains, each containing 0 or 1 spikes in each position, as usually done in the literature. Going back to Fig. 1, the input is duplicated when going from layer 0 to layer 1. Note that layer 1, as well as the subsequent n−1 layers, is composed by a sequence of n neurons, so that the layer can contain the representation of one clause of the instance. When layer 1 has acquired an entire clause, it starts to duplicate it while sending it to layer 2; after n computation steps the duplication is complete. The computation proceeds towards layer 3, where the clause is further duplicated, and so on, until we obtain 2ⁿ copies of the clause in layer n. Each subsystem contained in this layer is bijectively associated to one possible assignment to variables $x_1,x_2,\ldots,x_n.$ Thus, all possible assignments are tested in parallel against the clause; those assignments that satisfy the clause produce a number of spikes which are elaborated by the corresponding neuron 1 (that occurs in the same row, in layer n + 1), so that a single spike reaches the subsequent neuron 2 and is accumulated in the associated neuron 3, that operates like a counter. When the first clause of γ _n has been processed, the second starts to enter in the subsystems contained in layer n. After n steps the second clause is entirely contained in these subsystems, and all possible assignments are tested. Those which satisfy the clause produce a single spike in the corresponding neuron 2, which is once again accumulated in the associated neuron 3. When all the m clauses of γ _n have been processed, neurons 3 in layer n + 3 contain each the number of clauses which are satisfied by the corresponding assignment. The neurons that contain m spikes fire, sending one spike to neuron out, thus signalling that their corresponding assignment satisfies all the clauses of the instance. Neuron out operates like an or gate: it fires if and only if it contains at least one spike, that is, if and only if at least one of the assignments satisfies all the clauses of γ _n . Hence, the instance given in input is positive if and only if one spike is emitted to the environment after exactly $n^2+nm+4$ steps.

Fig. 1

The structure of the SN P system $\Uppi_{\rm SAT}(\langle n,m \rangle)$ that uniformly solves all the instances of sat(n,m)

Fig. 2

An alternative way to insert the instance of sat $(\langle n,m \rangle)$ into the system

Note the important fact that introducing the input takes nm steps, hence the computation cannot last less than nm steps (and, for the given construction, we cannot separate the introduction of the data from the actual computation). It should also be noted that the number of neurons of the system constructed above is exponential in n.

As we will see, some technicalities are needed to make the system produce exactly one spike in one of the neurons labelled with 2 when the corresponding assignment satisfies the clause. The core of the system is composed by the subsystems that occur in layer n, together with the so called generator (see Fig. 1), that produces the spikes needed to check what assignments satisfy the clause under consideration. To see how this core works, consider the system depicted in Fig. 3, which is a more detailed version of the system illustrated in Fig. 1 for instances built with two Boolean variables. Layer 2 is composed by four subsystems, corresponding to all possible assignments of truth values to the Boolean variables x ₁ and x ₂; each subsystem is composed by n = 2 neurons, one for each Boolean variable.

Fig. 3

Excerpt of the structure of the SN P system $\Uppi_{\rm SAT}(\langle 2,m \rangle).$ All delays equal to 0 in firing rules have been omitted in order to limit the size of the figure

In Fig. 3 only the subsystem that corresponds to the assignment x ₁ = false and x ₂ = true is detailed, together with the details of the corresponding neurons in the subsequent layers, and of the generator. As we can see in the figure, the generator is composed by two neurons, labelled with +  and −, that produce one spike every n steps. This spike is quadruplicated by the neurons labelled by e, that on their turn send their spikes to the neurons that compose the subsystems in layer n. These last neurons are of two types: f and t; the types indicate that the corresponding Boolean variable is assigned with the Boolean value true or false, respectively. The assignment is performed by sending 3 spikes to all the neurons labelled with t, and 4 spikes to all the neurons labelled with f. This means that neurons e in the generator will have three synapses going to neurons t and four synapses towards neurons f. All these spikes arrive every n computation steps, when the spikes indicated by the spike variables α _ij that correspond to a clause of γ _n are contained into the subsystems of layer n. This process is started by putting one spike in neuron s at the beginning of the computation. The delay associated with the rule contained in neuron s allows to send the first spikes from neurons e to neurons t and f exactly when the first clause is contained in layer n.

Recall our encoding of literals in the clauses (1): we have 0 spikes if the variable does not occur in the clause, 1 spike if it occurs non-negated, and 2 spikes if it occurs negated. These spikes are added with those representing the assignments, and the possible results are illustrated in Table 1. From this table we can see that if a neuron labelled with t receives a total number of 4 spikes then the corresponding variable occurs non-negated in the clause and is assigned the truth value true; we can immediately conclude that the clause is satisfied, and thus the neuron sends one spike towards the next layer. Similarly, if a neuron labelled with f receives 6 spikes then the corresponding variable occurs negated in the clause and is assigned the truth value false; also in this case we can immediately conclude that the clause is satisfied, and the neuron signals this event by sending one spike towards the next layer. In all the other cases we cannot conclude anything on the truth value of the clause, and thus no spike is emitted.

Table 1 Number of spikes resulting from the assignment in the neurons of layer n, and its effect on the truth value of the clause

All the spikes which are emitted by neurons t and f are propagated through the neurons that compose layer n, until they reach the corresponding neuron 1. Such a neuron is designed in order to retain only one spike from those received by layer n; indeed, when a second spike arrives, the rule $a^2/a {\to}a;\,0$ sends it to neuron 2, where it is deleted. When the last spike coming from layer n (concerning the clause under consideration) reaches neuron 1, also 3 spikes come from neurons b, thus producing a total of 3, 4 or 5 spikes in neuron 1. If the total number of spikes is 3, then no spike was present in neuron 1 during the last computation step, and no spike arrived from layer n; this means that the 3 spikes come only from the neurons labelled with b, and thus they are removed by applying the forgetting rule $a^3 \to \lambda.$ On the other hand, if one spike was present in neuron 1 during the last computation step and no spike arrives from layer n (or, alternatively, no spike was present and one spike arrives) then the total number of spikes that occur in neuron 1 is 4, and the neuron fires one spike to neuron 2 to signal the fact that the clause is satisfied by the assignment. This firing occurs simultaneously with the emission of one spike from c, so that during the next computation step neuron 2 also fires, confirming to neuron 3 that the clause was satisfied. Finally, if one spike was already present in neuron 1 and a new spike arrives from layer n then the total number of spikes is 5 and neuron 1 fires towards neuron 2, that once again will confirm the satisfiability of the clause by emitting one spike towards neuron 3 during the next computation step. In the meantime, another clause will have reached layer n and a new check with all the possible assignments will have started. As stated above, each time a clause is satisfied by a given assignment a new spike is deposited in the corresponding neuron 3. When one of these neurons contain m spikes, it fires; hence, the number of spikes that will reach neuron out is equal to the number of assignments that satisfy all the clauses of $\gamma_n.$

As a final note on the functioning of the system, we observe that the last neurons that compose the subsystems in layer n are labelled with t ₀ and f ₀, rather than with t and f. The difference between these two kinds of neurons lies in the rule that processes two spikes: in neurons t and f these spikes are simply propagated by the rule $a^2 {\to}a^2;\,0.$ whereas in neurons t ₀ and f ₀ only one spike is propagated (whereas the other one is removed from the system) by the rule $a^2 \to a;\,0,$ so that neuron 1 always receives at most one spike from layer n, during each computation step.

From the description given above we can see that the structure of the system is very regular, and does not contain “hidden information” that would simplify the solution of the problem for some pre-selected instances. Any possible instance $\gamma_n$ of sat(n,m) can be processed; it is completely read by the system in nm computation steps, and the solution (one spike if γ _n is satisfiable, zero spikes otherwise) is produced after $n^2+nm+4$ computation steps.

Someone could find an annoying problem the fact that, after computing the solution of the instance given in input the computation does not halt, since the generator continues to produce its spikes every n-th computation step, that are subsequently removed from the system by neurons 1. Moreover, neuron out fires as many times as the number of assignments that satisfy all the clauses of the instance. However, it is possible to modify the system in such a way that it delivers to the environment at most one spike (if desired, the spike that would eventually be delivered to the environment can be sent to a predefined output neuron instead), and then the computation halts after a polynomial number of steps. The proposed modifications are simple: we just add two intermediate neurons with a rule of type $a{\to}a;0$ in between each neuron 3 and neuron out. In this way we add a total of $2\,{\cdot}\,2^n$ neurons to the system, and neuron out always receives an even number of spikes. The rule of neuron out is changed to $(aa)^+/a \to a;\,0,$ so that it can fire only when an even number of spikes is present. If and when the neuron fires for the first time, the number of spikes it contains becomes odd, thus preventing further spikings. Finally one further neuron, labelled with stop, is added to the system, with a synapse going to the neurons of the generator labelled with +  and −. Neuron stop is initialized with a single spike at the beginning of the computation, and contains a rule of the kind $a {\to}a;\,n^2+nm+4,$ that sends one spike to neurons +  and − when the computation should halt. To these last neurons we add the forgetting rule $a^2 \to \lambda,$ so that when they receive the spike from neuron stop they halt their computations. After a polynomial number of steps the spikes eventually still contained in neurons e and in the neurons that compose layer n reach neurons 1, where they are removed from the system.

We conclude this section by noting that even if the above modifications allow the system to halt its computations after producing the solution, some spikes still remain in the halting configurations; hence, the computations performed by our system cannot be considered strong halting, as defined in (García-Arnau et al. 2007; Ibarra et al. 2007).

3 Solving 3-SAT

In this section we turn our attention to 3-sat, which is defined just like sat (see Problem 1), the only difference being that now each clause contains exactly three literals. In what follows we will sometimes equivalently say that an instance of 3-sat is a Boolean formula γ _n , built on n Boolean variables and expressed in conjunctive normal form, with each clause containing exactly three literals. Similarly to what we did in the previous section, we will denote by 3-sat(n) the set of all instances of 3-sat which can be built using n variables.

Note that the number m of clauses appearing in a sat(n,m) problem may be very large (e.g., exponential) with respect to n: every variable can occur negated or non-negated in a clause, or not occur at all, and hence the number of all possible clauses is 3ⁿ (recall that we look at clauses as sets of at most n literals, in which repetitions of the same literal and the presence of both the negated and the non-negated form of the same variable are forbidden). As shown in (Garey and Johnson 1979, p. 48), every instance γ of sat can be transformed in polynomial time (with respect to n and m) into an instance γ′ of 3-sat, in such a way that γ is satisfiable if and only if γ′ is satisfiable. However this transformation introduces a new set of variables, whose number is polynomial in m (and thus, possibly, exponential in n).

The reason for which we are here interested into 3-sat is that the number of possible 3-clauses which can be built by putting a negated or non-negated variable in each of the three available positions is at most $(2n)^3 =8n^3,$ a polynomial quantity with respect to n. This quantity is obtained by looking at a 3-clause as a triple, and observing that each component of the triple may contain one of the 2n possible literals. If we do not allow the repetition of literals in the clauses, and we also avoid the use of the same variable two or three times in each clause, then the resulting number of possible clauses becomes $2n{\cdot}(2n-2){\cdot}(2n-4),$ which is again $\Uptheta(n^3).$ In what follows we will denote this quantity by Cl(n).

Figure 4 outlines an SN P system which can be used to solve any instance γ _n of 3-sat(n). The input to this system is once again the instance of 3-sat we want to solve, but this time such an instance is given by specifying—among all the possible clauses that can be built using n Boolean variables—which clauses occur in the instance. The selection is performed by putting (in parallel, in the initial configuration of the system) one spike in each of the input neurons $sel_1,sel_2,\ldots,sel_{Cl(n)}$ that correspond to the selected clauses.

Fig. 4

Sketch of a deterministic SN P system that uniformly solves all possible instances of 3-sat(n)

To see how the system works, let us consider the family $\{M^{(n)}\}_{n \in {\mathbb{N}}}$ of Boolean matrices, where M ⁽ⁿ⁾ has 2ⁿ rows—one for each possible assignment to the variables $x_1,x_2,\ldots,x_n$—and one column for each possible 3-clause that can be built using the same variables. As stated above, the number of columns is $Cl(n) \in \Uptheta(n^3),$ a polynomial quantity in n. In order to make the construction of the matrix M ⁽ⁿ⁾ as regular as possible, we could choose to list all the 3-clauses in a predefined order; however, our result is independent of any such particular ordering, and hence we will not bother further with this detail. For every $j \in \{1,2,3,\ldots,2^n\}$ and $i\in \{1,2,\ldots,Cl(n)\},$ the element $M_{ji}^{(n)}$ is equal to 1 if and only if the assignment associated with row j satisfies the clause associated with column i. Table 2 shows an excerpt of matrix M ⁽⁴⁾, where each row has been labelled with the corresponding clause; only the columns that correspond to clauses $x_1 \lor x_2 \lor \lnot x_4$ and $\lnot x_1 \lor \lnot x_2 \lor x_3$ are shown in details.

Table 2 An excerpt of matrix M ⁽⁴⁾. On the left we can see the assignments which are associated to the corresponding rows of the matrix. Only the columns corresponding to the clauses $x_1 \lor x_2 \lor \lnot x_4$ and $\lnot x_1 \lor \lnot x_2 \lor x_3$ are detailed

Let us now consider the algorithm given in pseudocode in Fig. 5. The variable res is a vector of length 2ⁿ, whose components—which are initialized to 1—are bijectively associated with all the possible assignments to $x_1,x_2,\ldots,x_n.$ The components of res are treated as flags: when a component is equal to 1, it indicates that the corresponding assignment satisfies all the clauses which have been examined so far. Initially we assume that all the flags are 1, since we do not have yet examined any clause. The algorithm then considers all the columns of M ⁽ⁿ⁾, one by one. If the column under consideration does not correspond to a selected clause, then it is simply ignored. If, on the other hand, it corresponds to a clause which has been selected as part of the instance, then the components of res are updated, putting to 0 those flags that correspond to the assignments which do not satisfy the clause. At the end of this operation, which can be performed in parallel on all the components, only those assignments that satisfy all the clauses previously examined, as well as the clause currently under consideration, survive the filtering process. After the last column of M ⁽ⁿ⁾ has been processed, we have that the instance γ _n of 3-sat(n) given in input is satisfiable if and only if at least one assignment survives, that is, if and only if the logical or of all the components of res gives 1 as a result.

Fig. 5

Pseudocode of the algorithm used to solve any instance of 3-sat(n)

This algorithm can be easily transformed into a(n exponential size) Boolean circuit, that mimics the operations performed on the matrix M ⁽ⁿ⁾, described by the pseudocode given in Fig. 5. Such a circuit can then be easily simulated using the SN P system that we have outlined in Fig. 4. This system is composed by three layers for each possible 3-clause that can be built using n Boolean variables. Two of these layers are used to store the intermediate values of vector res and the values contained in the columns of M ⁽ⁿ⁾, respectively. The third layer, represented by the boxes marked with Filter in Fig. 4, transforms the current value of res to the value obtained by applying the corresponding iteration of the algorithm given in Fig. 5. This layer is in turn composed by three layers of neurons, as we will see in a moment. The last layer of the system is a simple or gate, which can be easily simulated using one neuron containing the rule $a \to a;\,0.$ Note that this neuron will continue to fire until it consumes all its spikes. An observation on how this system could be modified in order to halt the computation just after determining whether the instance given in input is positive or not is given in the last paragraph of this section.

The system works as follows. During the computation, spikes move from the leftmost to the rightmost layer, and then one spike is (eventually) expelled to the environment. In the initial configuration, every neuron in the first layer (which is bijectively associated with one of the 2ⁿ assignments to the Boolean variables $x_1,x_2,\ldots,x_n)$ contains one spike, whereas neurons $sel_1, sel_2,\ldots,sel_{Cl(n)}$ contain one or zero spikes, depending upon whether or not the corresponding clause is part of the instance γ _n given in input. Stated otherwise, the user must provide one spike—in the initial configuration of the system—to every input neuron sel _i that corresponds to a clause that has to be selected. In order to deliver these spikes at the correct moment to all the filters that correspond to the i-th iteration of the algorithm, every neuron sel _i contains the rule $a {\to}a;4(i-1),$ whose delay is proportional to i. In order to synchronize the execution of the system, also the neurons that correspond to the i-th column of M ⁽ⁿ⁾ deliver their spikes simultaneously with those distributed by neurons sel _i , using the same rules. An alternative possibility is to provide the input to the system in a sequential way, for example as a bit string of length Cl(n), where a 1 (resp., 0) in a given position indicates that the corresponding clause has to be selected (resp., ignored). In this case we should use a sort of delaying subsystem, that delivers— every four time steps—the received spike to all the neurons that correspond to the column of M ⁽ⁿ⁾ currently under consideration. Since the execution time of our algorithm is proportional to the number Cl(n) of all possible clauses containing n Boolean variables, this modification keeps the computation time of the entire system cubic with respect to n.

In the first computation step, all the inputs going into the first layer of filters are ready to be processed. As the name suggests, these filters put to 0 those flags which correspond to the assignments that do not satisfy the first clause (corresponding to the first column of M ⁽ⁿ⁾). This occurs only if the clause has been selected as part of the instance $\gamma_n \in$ 3-sat(n) given in input, otherwise all the flags are kept unchanged, ready to be processed by the next layer of filters. In either case, when the resulting flags have been computed they enter into the second layer of filters together with the values of the second column of M ⁽ⁿ⁾, and the input sel ₂ that indicates whether this column is selected or not as being part of the instance. The computation proceeds in this way until all the columns of M ⁽ⁿ⁾ have been considered, and the resulting flags have been computed. A final or among all these flags reveals whether at least one flag survived all the filtering processes, that is, whether at least one assignment satisfies all the selected clauses.

To conclude the description of the functioning of the system, we just have to describe how the filtering process works. This process is performed in parallel on all the flags: if the clause C _i has been selected then an and is performed between the value $M_{ji}^{(n)}$ (that indicates whether the j-th assignment satisfies C _i ) and the current value of the flag res _j ; as a result, res _j is 1 if and only if the j-th assignment satisfies all the selected clauses which have been encountered up to now. On the other hand, if the clause C _i has not been selected then the old value of res _j is kept unaltered. This filtering process can be summarized by the pseudocode given in Fig. 6, which is equivalent to the following Boolean function:

$$ (\lnot sel_i \land res_j) \lor (sel_i \land res_j \land C_i) $$

Fig. 6

Pseudocode of the Boolean function computed by the blocks marked with Filter in Fig. 4

Such a function can be computed by the Boolean circuit depicted in Fig. 7, that in turn can be simulated by the SN P system illustrated in Fig. 8. Note the system represented in this latter figure is a generic module which is used many times in the whole system outlined in Fig. 4, hence we have not indicated the delays which are needed in neurons sel _i and C _i . Also neuron 1, which is used to negate the value emitted by neuron sel _i , must be activated together with sel _i , that is, after 4(i−1) steps after the beginning of the computation. The spike it contains can be reused in the namesake neuron that occurs in the next layer of filters.

Fig. 7

The Boolean circuit that computes the function Filter whose pseudocode is given in Fig. 6

Fig. 8

An SN P system that computes the function Filter given in Fig. 6, simulating the Boolean circuit of Fig. 7

As we can see, the structure of the system that uniformly solves all the instances of 3-sat(n) is very regular, and does not contain “hidden information”. For the sake of regularity we have also omitted some possible optimizations, that we briefly mention here. The first column of neurons in Fig. 4 corresponds to the initial value of vector res in the pseudocode given in Fig. 5. Since this value is fixed, we can pre-compute part of the result of the first step of computation, and remove the entire column of neurons from the system. In a similar way we can also remove the subsequent columns that correspond to the intermediate values of res, and send these values directly to the next filtering layer. A further optimization concerns the values $M_{ji}^{(n)},$ which are contained in the neurons labelled with C _i . Since these values are given in input to and gates, when they are equal to 1 they can be removed since they do not affect the result; on the other hand, when they are equal to 0 also the result is 0, and thus we can remove the entire and gate.

The total computation time of the system is proportional to the number Cl(n) of columns of M ⁽ⁿ⁾, that is, Θ(n ³). This is the reason why we focused our attention on the 3-sat problem rather than on sat: as stated above, the number m of clauses in a sat(n,m) problem can be exponential with respect to n; this means not only that we should consider a matrix M ^(n,m) which has an exponential number of columns (but whose structure is regular, and thus from this viewpoint we should have no problems), but we should also provide in input an exponentially long bit string to specify what clauses are part of the instance. Last but not the least, also the computation time of the resulting system would be exponential in n.

From the description of the system it is apparent that it spikes to the environment as many times as the number of assignments that satisfy the instance of 3-sat given in input. However, the system can be modified so that it halts after the first spike has been emitted, thus transforming it to an accepting SN P system (if desired, the spike that would eventually be delivered to the environment can be sent to a predefined output neuron instead). It just suffices to duplicate every neuron in the layer preceding neuron out, so that neuron out always receives an even number of spikes. We also modify the rule of the output neuron as $(aa)^+/a {\to}a;0,$ so that it can fire only when an even number of spikes is present. After neuron out has (possibly) fired for the first time, the number of spikes it contains becomes odd and the computation halts.

4 Conclusions and directions for future research

Investigations related to the possibility of using SN P systems for solving computationally hard problems are very recent, and are currently addressed only in a few papers. Besides (Leporati et al. 2007a, 2007b), mentioned above, we also cite (Chen et al. 2006b), where the idea to use a pre-computed SN P system of an arbitrarily large size, but of a rather uniform structure, was introduced, and a way to solve sat in constant time by means of this model was proposed.

The present paper is a contribution to this research direction, with results dealing with pre-computed SN P systems which are used to solve, in a uniform and deterministic way, the NP-complete problems sat and 3-sat. The pre-computed systems we have used solve the problems in a polynomial number of steps, but their size is exponential with respect to the number n of variables of the instances given in input.

It is important to note that, as proved in (Leporati et al. 2007b), an SN P system of polynomial size cannot solve in a deterministic way in a polynomial time an NP-complete problem (unless P = NP) hence, under the assumption that P ≠ NP, efficient solutions to NP-complete problems cannot be obtained without introducing features which enhance the efficiency (pre-computed resources, ways to exponentially grow the workspace during the computation, non-determinism, and so on). A more careful examination of such features—in particular, possible relations with the well known notions of uniformity traditionally studied in the theory of circuit complexity—is a research direction of a clear interest.