Spiking neural P systems with polarizations and astrocytes

Abstract

Spiking neural P systems with polarizations (PSN P systems) use charges $(+,-,0)$ instead of regular expression to obtain excellent computation power and broad application prospect. In this work, astrocyte control mechanism is introduced into PSN P systems, spiking neural P systems with polarizations and astrocytes (PASN P systems) are constructed. Astrocytes are both excitatory and inhibitory influences on synapses, which can effectively reduce the consumption of computing resources (the use of fewer neurons). Because of the effects of astrocytes, PASN P systems are proved to have the computation power equivalent to Turing machines in generation and accepting modes. Furthermore, a small universal PASN P system with 82 neurons is given for computing any Turing computable function, that is, fewer neurons are used to construct the relatively simple and universal PASN P systems.

1 Introduction

Membrane computing, as a current branch of natural computing, aims to abstract computational models (called membrane systems or P systems) from the structure and function of living cells and from the cooperation of cell groups such as tissues and organs [1, 2]. Membrane computing is characterized by the use of distributed parallel computing to make the computation power greater effective and more power [3, 4]. Membrane computing has developed rapidly since it was proposed and has become an emerging research field [5,6,7]. There are three main membrane systems that have been extensively studied: cell-like membrane systems, tissue-like membrane systems and neural-like membrane systems. More detailed information of membrane computing, readers can refer to http://ppage.psystems.eu, the latest research results and developments can be found.

Spiking neural P systems (SN P systems) are a type of neural-like membrane systems in the field of membrane computing, which are abstracted by the way that neurons send spikes to other neurons through synapses to realize information communication [8]. SN P systems can be represented as directed graph, where the vertices of the directed graph represent neurons, and the arcs between the vertices of the directed graph represent synapses along which neurons can send spikes to their associated neurons [9]. Each neuron contains a certain number of spikes, firing rules and forgetting rules. By using the firing rule, the neuron sends information in the form of firing spikes to some other neurons, if the neuron makes use of the forgetting rule, a certain number of spikes will be cleared from the neuron. Typically, there will be an output neuron in the system whose spikes can be sent into the environment [10].

SN P systems have been shown to be computationally universal as a kind of digital generating and accepting devices [11], as language generators [12, 13] and function calculators [14, 15]. Inspired by different biological properties, a quantity of variants of SN P systems have been proposed, such as SN P systems with anti-spikes [16], asynchronous SN P systems [17, 18], local synchronized SN P systems [19], SN P systems with rules on synapses [20], homogenous SN P systems [21, 22], axonal SN P systems [23], SN P systems with scheduled synapses [24], etc. In addition, SN P systems can also solve computationally difficult problems in efficient time (polynomial time or linear time), such as $\texttt{subset}$ $\texttt{sum}$ problems [25], $\texttt{SAT}$ problems [26, 27], $\texttt{PSPACE}$-complete problem [28, 29], and $\texttt{Travelling}$ $\texttt{salesman}$ problem [30]. SN P systems and the variants also have a number of practical applications, such as combinatorial optimization [31], fault diagnosis of power system [32, 33], knowledge expression and fuzzy reasoning [34, 35].

The software implementation of membrane computing is mainly based on the simulation platform developed by $C++$, Java and other programming languages to simulate membrane systems, such as Membrane simulator, SNUPS, $P-Lingua$ and MeCoSim [36,37,38], etc.

Small universal computing devices can use fewer computing resources (time or space) to construct universal computational models, which have always been a hot research direction in the discipline of computer science. A recurrent neural network of 886 neurons can simulate any Turing machine has been demonstrated in [39]. As computing devices, various variants of SN P systems have been proposed, such as universal SN P systems with 84 neurons [2], SN P systems with anti-spikes with 75 neurons [40], SN P systems with homogenous neurons and synapses having 70 neurons [41], SN P systems with astrocytes with 57 neurons and 19 astrocytes [42], all of the variants have been proved to be Turing universal. Most of variants of SN P systems aim to reduce computing resources by reducing the number of neurons, that is, to reduce the use of space resources in computing resources.

In [43], spiking neural P systems with polarizations (PSN P systems) were constructed by introducing membrane potential, where the rules can be triggered only when the polarization condition is satisfied, such systems are more consistent with biological phenomena, moreover, a small universal PSN P system with 164 neurons was given. However, the number of neurons required by PSN P systems are much larger than the traditional SN P systems and some variants of SN P systems, the construction of this kind of universal computing model is also complex. In [44], spiking neural P systems with polarizations and rules on synapses (PSNRS P systems) were proposed, where spiking rules are placed on synapses, a small universal PSNRS P system with 151 neurons were shown to be able to compute any Turing computable functions. Obviously, compared with PSN P systems, PSNRS P systems can simplify the system structure and reduce the computing resources.

It is known (see [45]) that astrocytes can release d-serine, which plays an important role in the production of long-term enhancement of neurons, and release adenosine triphosphate, which produces heterosynaptic inhibition of neuronal activity. In short, astrocytes are both excitatory and inhibitory influences on synapses. Thus, astrocytes can be used to reduce the use of complex parameters to a large extent.

In this work, astrocytes as a control mechanism are introduced into PSN P systems, and make use of the biological characteristics of astrocytes to improve PSN P systems. Meanwhile, in order to solve an open problem raised in [43], we consider using astrocytes to optimize the traditional PSN P systems and reduce computing resources, thus a novel variant of PSN P systems called PSN P system with astrocytes (PASN P systems) is proposed, and the computation power of PASN P systems as generating devices and accepting devices is investigated, respectively. In addition, a small universal PASN P system is constructed, the results show that PASN P systems are equivalent to Turing machines. The main contributions of this work are summarized as follows.

• We introduce the control mechanism of astrocytes into PSN P systems, and propose a novel variant called PASN P systems, where astrocytes connecting different neurons are used to optimize computing resources, that is, the flexibility of PASN P systems is greatly improved, and the structure of such systems is relatively simplified.

• In PASN P systems, astrocytes can control not only the spikes at the synapses of neighboring neurons, but also the charge corresponding to the firing rules. Therefore, utilizing the properties of astrocytes, the computation power of PASN P systems is investigated, we prove that PASN P systems, as number generating devices and number accepting devices, are equivalent to Turing machines.

• Simulating the small universal register machine, we give a small universal PASN P system with 82 neurons. As a computing function, PASN P systems reduce computing resources by 82 neurons compared with PSN P systems.

2 PASN P systems

Before introducing the formal definition of PASN P systems, the reader is assumed to have some knowledge of formal languages and automata. For details, please refer to [46]. The conception of polarizations and astrocytes will also be used, the details of which can be found in [43, 47].

A PASN P system of degree $m \ge 1$ is a tuple

$$\begin{aligned} \Pi =(O,\sigma _1,\sigma _2,\ldots ,\sigma _m,syn,ast_1,\ldots ,ast_l,in,out), \end{aligned}$$

where:

• (1) $O=\{a\}$ is an alphabet and a indicates the spike;

• (2) $\sigma _i$ (${1\leqslant i \leqslant m}$) indicates the neurons, the number of neurons is m, and the form of each neuron is $\sigma _i= (\alpha _i, n_i, R_i)$, where:

  • (1) $\alpha _i \in \{+,0,-\}$ indicates the initial charge of the neuron $\sigma _i$;

  • (2) $n_i$ indicates that there are n spikes in the neuron $\sigma _i$ at the initial moment;

  • (3) $R_i$ is a set of rules for neurons $\sigma _i$, which has the following two forms:

    • a. $\alpha / a^c \rightarrow a; \beta$, where $\alpha , \beta \in \{-,0,+\}$, $c\ge 1$;

    • b. $\alpha / a^s \rightarrow \lambda ; \beta$, where $\alpha ,\beta \in \{-,0,+\}$, $s\ge 1$;

• (3) $syn \in \{ 1,2, \ldots , m\} \times \{ 1,2, \ldots , m\}$ are synapses between neurons, with $(i,j) \in syn$, and i, j are the label of neurons $({1\leqslant i},{j\leqslant m},i\ne j)$;

• (4) $ast_i$ (${1\leqslant i\leqslant l}$) are the label of astrocytes in the form $ast_i\in (syn_{ast_i},t_i)$, $syn_{ast_i}\subseteq syn$ is the set of synapses controlled by astrocytes, and $t_i$ is the threshold in astrocytes;

• (5) $in,out \in \{ 1,2, \ldots , m\}$ represent the labels of the input neuron and the output neuron in the system, respectively.

PSN P systems differ from the traditional SN P systems in the use of rules, the regular expression is replaced by the charge state $(+,-,0)$. Firing rules have the form $\alpha /a^c \longrightarrow a;\beta$, when the neuron $\sigma _i$ is charged with $\alpha$ and the quantity of spikes in the neuron is not less than c spikes, the rule satisfies the running conditions, c spikes are consumed, and a spike and $\beta$ charge are sent to its adjacent neurons. When the rules in the output neuron $\sigma _{out}$ satisfy the excitation condition, the calculation result is sent to the environment, and the charge sent to the environment does not affect the output result. When the input neuron $\sigma _{in}$ receives spikes and a charge from the environment, the initial execution state of the system is related to the charge obtained from the environment. If a neuron $\sigma _{i}$ in the system executes the forgetting rule $\alpha /a^s \longrightarrow \lambda ;\beta$, the neuron $\sigma _{i}$ consumes all the spikes and does not send spikes, and only sends one of charges over $\beta$ to its neighbouring neurons. The use of rules within a neuron is determined by the polarity of the charge carried by the neuron itself, and the change of the charge is as follows.

• Multiple positive charges $(+)$ (resp. $(0),(-))$ are equivalent to a positive charge (resp. a neutral charge, a negative charge), and this charge changes in a way that has the highest priority.

• If a neuron with a positive charge $(+)$ (resp. a negative charge $(-)$) receives a negative charge $(-)$ (resp. a positive charge $(+)$), the polarity of the neuron becomes a neutral charge (0).

• If a neuron with a positive charge $(+)$ or a negative charge $(-)$ receives a neutral charge (0), the polarity of the neuron remains the same.

PASN P systems can effectively reduce the use of forgetting rules and delay rules by astrocytes control the spikes on the protrusions of adjacent neurons, which reduces the use of complex parameters to a large extent. At one point, astrocytes in PASN P systems can control not only the spikes at the synapses of neighboring neurons, but also the charge corresponding to the firing rules. Synapse collection $syn_{ast_i}$ can influence the synapse (i, j) between ordinary neurons, a threshold value $t_i$ can determine the excitatory influence or inhibitory influence of the astrocytes synapse $syn_{ast_i}$ to the synapse (i, j) between neurons. When an astrocyte $ast_i$ senses k spikes of communication at the synapses of adjacent neurons, there are three cases as follow: if $k>t_i$ and $ast_i$ has an inhibitory influence on adjacent synapses, then these k spikes and the charge corresponding to the trigger rule will be removed from the system; if $k<t_i$, $ast_i$ has an excitatory influence to the adjacent synapses, then the k spikes and the charge can be sent to the target neuron; if $k=t_i$, the excitatory influence and inhibitory influence of astrocyte $ast_i$ on adjacent synapses are nondeterministic, and one of the two influences is chosen non-deterministically.

In addition, a synapse (i, j) can be effected by two or more astrocytes, if the astrocytes have excitatory influence to the neuron synapse, the spikes can reach the target neuron along the neuron synapse. If one of them has an inhibitory influence on the neuron synapse, the corresponding spikes are terminated and removed from the system.

PASN P systems work in the generating mode, the time interval between two non-zero values are sent to the environment by the output neuron $\sigma _{out}$, which is encoded as the calculation result, denoted by $N_{2}(\Pi )$. If PASN P systems work in the accepting mode, the output neuron $\sigma _{out}$ is removed, and the input neuron $\sigma _{in}$ is used to read the external spike sequence. It is necessary to recognize that natural numbers are encoded as the time interval between two neighbouring spikes, such as a spike sequence $10^{n-1}1$. When the spike sequence is sent to the input neuron, the system starts to calculate until it stops. If the calculation result of the system reaches a final configuration, it is said that the system has recognized the value n. The set of results recognized by $\Pi$ is denoted by $N_{acc}(\Pi )$ [48].

The family of all sets of numbers generated or accepted by PASN P systems is denoted by $N_{\alpha }PASNP$, where $\alpha \in \{2,acc\}$ indicates that the system is in the generating mode ($\alpha =2$) or the accepting mode ($\alpha =acc$). Furthermore, the system $\Pi$ is used as a computational function and the computing resource consumption is calculated [48].

3 The computation power of PASN P systems

It is well known that a register machine with three registers can precisely generate a recursively enumerable set of natural numbers that can characterize NRE [48]. In this section, the computation power of SN P systems is investigated, we show that PASN P systems can generate all recursively enumerable sets of numbers by simulating the register machine.

A register machine is $M=(m, H, l_0, l_h, I)$, where m indicates the number of registers; H indicates the set of all the instruction labels; $l_0$ indicates the start instruction; $l_h$ indicates the halt instruction, and I indicates the set of all instructions. The specific instruction forms are as follows. ADD instruction $l_i:(ADD(r),l_j,l_k)$ indicates that a register r is incremented by 1, and non-deterministically jumps to the instruction $l_j$ or $l_k$. SUB instruction $l_i:(SUB(r),l_j,l_k)$ indicates that if the register r contains a number greater than 0, the number stored in the register r minus 1 and the instruction $l_j$ is executed in the next step; if the register r is empty, the instruction $l_k$ is executed in the next step. Here register 1 is an output register, which stores the computing results and sends the result to the environment when the calculation halts.

Theorem 1

$N_{2}PASNP=NRE$

Proof

We prove the computation power of PASN P systems $\Pi$ by simulating the register machine M, and only need to confirm the inclusion relation $N_{\alpha }PASNP \supseteq NRE$. The proof process of the system in the generation mode includes an ADD module, a SUB module, and a FIN module. The calculation result of the system are stored in the register 1. During the system format conversion process, there is no corresponding SUB instruction for the register 1 to perform the subtraction operation. When system landscape transfer is stopped, only register 1 is non-empty. In system $\Pi$, each register r has a one-to-one correspondence with a neuron $\sigma _r$ in an ADD or SUB module, and an instruction $l_i$ in H is associated with a neuron $\sigma _{l_i}$ (subscripts denote neurons in the proof process). It must be clear that when the register r stores a number whose size is n, and then the quantitative relationship contained in the corresponding spike reserve in neuron $\sigma _r$ corresponds to 2n. It is worth noting that in each computing module, two auxiliary neurons $\sigma _{r^{(1)}}$ and $\sigma _{r^{(2)}}$ are used to represent the register r.

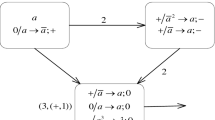
ADD module: simulating an ADD instruction $l_{i}:(\texttt{ADD}(r),l_j,l_k)$.

ADD module as shown in Fig. 1. At step t, suppose neuron $\sigma _{l_i}$ receives a spike and then rule $0/a\longrightarrow a;+$ reaches the firing condition, a spike and a positive charge are sent by neuron $\sigma _{l_i}$ to neuron ${\sigma _{l_{i}^{(1)}}, \sigma _{l_{i}^{(2)}}}$, respectively. It is important to note that the threshold t of the astrocyte $ast_{l_{i}}$ is equal to the k spikes on synapse $(l_{i}, {l_{i}^{(1)}})$, satisfying the condition $k=t$. Since $ast_{l_{i}}$ has an excitatory or inhibitory influence on synapse $(l_{i}, {l_{i}^{(1)}})$, which needs to be considered in two cases.

Case I: At step $t+1$, when $ast_{l_{i}}$ has an excitatory influence on the synapse, then a spike and a positive charge are sent to neurons $\sigma _{l_{i}^{(1)}}$ and $\sigma _{l_{i}^{(2)}}$ along $(l_{i}, {l_{i}^{(1)}})$ and $(l_{i}, {l_{i}^{(2)}})$. At step $t+2$, $ast_{l_{i}}$ senses a total of two spikes transmitted on synapses $({l_{i}^{(1)}}, {l_{i}^{(2)}})$, $({l_{i}^{(2)}}, l_{k})$, and the number of spikes is greater than the threshold in $ast_{l_{i}}$, so the two spikes and charge cannot reach the target neuron and are deleted from the system. At the same time, a spike and a neutral charge are sent to neurons $\sigma _{r^{(1)}}$ and $\sigma _{r^{(2)}}$ along $(l_{i},r^{(1)})$ and $(l_{i},r^{(2)})$, which means that the register r is incremented by 1. And rule $+/a\longrightarrow a;0$ in neuron ${\sigma _{l_{i}^{(1)}}}$ reaches the firing condition, and after application, a spike and a neutral charge are sent to neuron ${\sigma _{l_{j}}}$ along the synapse $({l_{i}^{(1)}},l_j)$. In the next step, the neuron $\sigma _{l_{j}}$ is fired and the system starts to simulate the $l_{j}$ instruction.

Fig. 1

ADD module: simulating $l_{i}:(\texttt{ADD}(r),l_j,l_k)$

Case II: At step $t+1$, a spike and a positive charge are removed when $ast_{l_{i}}$ has an inhibitory influence on synapse $(l_{i}, {l_{i}^{(1)}})$. At step $t+2$, a spike and a natural charge is applied by neuron ${\sigma _{l_{i}^{(2)}}}$ with rule $+/a\longrightarrow a;0$, both of them are sent to neurons $\sigma _{l_k}$, $\sigma _{r^{(1)}}$ and $\sigma _{r^{(2)}}$ through synapses $({l_{i}^{(2)}}, l_{k})$, $({l_{i}^{(2)}}, r^{(1)})$ and $({l_{i}^{(2)}}, r^{(2)})$. In the next step, the neuron $\sigma _{l_{k}}$ is fired and the system starts to simulate the $l_{k}$ instruction.

So far, the simulation of the ADD module is completed, the register r can be incremented by 1, and the $l_{k}$ or $l_{j}$ instruction can be executed non-deterministically. The operation processes of ADD module are shown in Table 1.

Table 1 The numbers of spikes and polarity of neurons in add module (see Fig. 1) during the simulation with neuron $\sigma _{l_j}$ and $\sigma _{l_k}$ finally activated

SUB module: simulating a SUB instruction $l_{i}:(\texttt{SUB}(r),l_j,l_k)$.

Fig. 2

SUB module: simulating $l_{i}:(\texttt{SUB}(r),l_j,l_k)$

SUB module as shown in Fig. 2, it is assumed that at step t, the neuron $\sigma _{l_i}$ is activated after receiving a spike. Since it needs to check the empty or non-empty state of the register r, the astrocytes $ast_{l_{i}}$ check the number of spikes at the adjacent synapses is different, two situations need to be considered.

Case I: When the register r is empty, no spikes are delivered on the synapses $(r^{(1)},r^{(2)})$ and $(r^{(2)},r^{(1)})$. At step $t+1$, rule $0/a\longrightarrow a;+$ in neuron ${\sigma _{l_{i}}}$ reaches the firing condition, a spike and positive charge are sent to neurons ${\sigma _{l_{i}^{(1)}}}$ and ${\sigma _{l_{i}^{(2)}}}$. At step $t+2$, $ast_{l_{i}}$ senses two spikes transmission on adjacent synapses $({l_{i}^{(1)}},l_k)$ and $({l_{i}^{(2)}},{l_{i}^{(3)}})$, the number of spikes is less than the threshold in $ast_{l_{i}}$, and the spikes can reach target neuron. Rule $+/a\longrightarrow a;0$ in neuron ${\sigma _{l_{i}^{(1)}}}$ reaches the firing condition, a spike and a neutral charge are sent to neurons ${\sigma _{l_{i}^{(3)}}}$ and ${\sigma _{l_k}}$. Rule $0/a\longrightarrow \lambda ;-$ in neuron ${\sigma _{l_{i}^{(2)}}}$ reaches the firing condition, a negative charge is sent to neuron ${\sigma _{l_{i}^{(3)}}}$. When neuron ${\sigma _{l_{i}^{(3)}}}$ received a negative charge and a neutral charge, it takes negative charge and stored a spike. At step $t+3$, rule $-/a\longrightarrow \lambda ;0$ in neuron ${\sigma _{l_{i}^{(3)}}}$ reaches the firing condition, a neutral charge is sent to neuron $\sigma _{l_{j}}$, but neuron $\sigma _{l_{j}}$ does not satisfy the excitation condition in the next step. Simultaneously, the neuron $\sigma _{l_{k}}$ is fired and the system starts to simulate the $l_{k}$ instruction.

Case II: When the state of the register r in the SUB module is non-empty, there are two spikes passing on the synapses $(r^{(1)},r^{(2)})$ and $(r^{(2)},r^{(1)})$. Unlike CaseI, at step $t+2$, $ast_{l_{i}}$ senses the adjacent synapses $(r^{(1)},r^{(2)})$, $(r^{(2)},r^{(1)})$, $({l_{i}^{(1)}},l_k)$ and $({l_{i}^{(2)}},{l_{i}^{(3)}})$ each has spike delivery. The number of spikes is greater than the threshold in $ast_{l_{i}}$, causing $ast_{l_{i}}$ to have an inhibitory influence on adjacent synapses, and all spikes involved will be forgotten. Only neuron ${\sigma _{l_{i}^{(3)}}}$ receives a spike and a neutral charge from neuron ${\sigma _{l_{i}^{(1)}}}$. At step $t+3$, rule $0/a\longrightarrow a;0$ in neuron ${\sigma _{l_{i}^{(3)}}}$ reaches the firing condition, a spike and a neutral charge are sent to neuron $l_j$. At this point, the neuron $\sigma _{l_{j}}$ is fired and the system starts to simulate the $l_{j}$ instruction in the next step.

So far, the SUB module can be accurately simulated, if the register r is in a non-empty state, subtract 1 from the register r and jump to the $l_j$ instruction; if the register r is empty, it directly jumps to the $l_k$ instruction. The operation processes of SUB module are shown in Table 2.

Table 2 The numbers of spikes and polarity of neurons in SUB module (see Fig. 2) when the simulation with register $\sigma _{r}$ is empty or not empty

It is worth noting that there is no mutual influence between ADD module and SUB module, and only the corresponding neuron $\sigma _{l_j}$ or $\sigma _{l_k}$ needs to be excited. However, there is mutual influence between the SUB modules. Specifically, if there are multiple SUB instructions $l_i$ acting on register r, then all astrocytes ${ast_{l_{i}}}$ can control synapses $(r^{(1)},r^{(2)})$ and $(r^{(2)},r^{(1)})$. When simulating the SUB instruction $l_{i}:(SUB(r), l_{j}, l_{k})$), astrocyte ${ast_{l_{i}}}$ has a stimulating effect on the synapses $(r^{(1)},r^{(2)})$ and $(r^{(2)},r^{(1)})$, and the spike can reach the target neuron smoothly. When simulating the ADD instruction $l_{i}:(ADD(r), l_{j}, l_{k})$), the interaction between the SUB modules does not cause the wrong calculation process of the system $\Pi$.

FIN module(outputting the result of the computation)

Fig. 3

FIN Module(ending the computation)

FIN module as shown in Fig. 3, which is used to output the result of the computation. Assuming that at step t, neuron $\sigma _{l_h}$ receives a spike. At step $t+1$, neuron $\sigma _{l_h}$ is activated, which uses the rule ${0/a \longrightarrow a;+}$ to reach the firing condition, a spike and a positive charge are sent to neurons ${\sigma _{l_{h}^{(1)}}}$, ${\sigma _{l_{h}^{(2)}}}$, ${\sigma _{l_{h}^{(3)}}}$, respectively. When neurons ${\sigma _{l_{h}^{(2)}}}$ and ${\sigma _{l_{h}^{(3)}}}$ received a positive charge, them take neutral charge and stored a spike. At step $t+2$, $ast_{l_h}^{(1)}$ checks that the number of spikes delivered on synapses $(r^{(1)}, r^{(2)}), (r^{(2)}, r^{(1)})$, $({l_{h}^{(2)}},out)$ and $({l_{h}^{(2)}},{l_{h}^{(4)}})$ are greater than the threshold in $ast_{l_h}^{(1)}$, then these spikes are removed from the system, that is to say, the register r performs a subtraction operation by 1. Simultaneously, rule $+/a\longrightarrow a;0$ in neuron ${\sigma _{l_{h}^{(1)}}}$ reaches the firing condition, a spike and a neutral charge are sent to neuron out. At step $t+3$, a spike is sent to the external environment by the neuron $\sigma _{out}$.

From step $t+2$, neurons ${\sigma _{l_{h}^{(2)}}}$, ${\sigma _{l_{h}^{(3)}}}$ will transmit spikes cyclically, two neurons keep one spike all the time, the median value of register r is decremented by 1 at each step by $ast_{l_h}^{(1)}$. Until step $t+n+2$, the number of spikes in the corresponding neuron of the register is exhausted, and the number of spikes on the adjacent synapses sensed by $ast_{l_h}^{(1)}$ is less than its threshold. Rule $0/a\longrightarrow a;0$ in neuron ${\sigma _{l_{h}^{(2)}}}$ reaches the firing condition that sends a spike and a neutral charge to neurons $\sigma _{out}$ and ${\sigma _{l_{h}^{(4)}}}$, respectively. At step $t+n+3$, rule $0/a\longrightarrow \lambda ;-$ in neuron ${\sigma _{l_{h}^{(4)}}}$ reaches the firing condition that sends a negative charge to neurons $\sigma _{l_{h}^{(2)}}$ and ${\sigma _{l_{h}^{(3)}}}$ to help them return to the initial polarizations, and neurons $\sigma _{l_{h}^{(2)}}$ and $\sigma _{l_{h}^{(3)}}$ stop exchanging spikes. At the same time, the second spike is sent to the outside of the module by neuron $\sigma _{out}$, and the system’s format conversion is stopped. Time interval calculation of the first two spikes: $(t+n+3)-(t+3)=n$, which just corresponds to the calculation result in register 1. The operation processes of FIN module are shown in Table 3.

Table 3 The numbers of spikes and polarity of neurons in fin module (see Fig. 3) during the process of outputting the computational result

According to the above description of each module and its working principle, it is obvious that the system $\Pi$ can simulate the calculation process of the register machine M correctly. Therefore, $N_{2}(\Pi )= N(M)$. The proof is over. $\square$

Theorem 2

$N_{acc}PASNP=NRE$

Proof

In the accepting mode, to prove the computation power of PASN P systems, it is only necessary to prove the inclusion relation $N_{acc}PASNP\supseteq NRE$, which is obtained by the register machine M determined by the simulation of the system $\Pi ^\prime$. System $\Pi ^\prime$ is improved from system $\Pi$ in generation mode. The system $\Pi ^\prime$ proof process in the accepting mode includes an INPUT module, a deterministic ADD module and a SUB module, and the calculation result of the system is stored in the register 1. During the system format conversion process, there is no corresponding SUB instruction for the register 1 to perform the subtraction operation. When system landscape transfer is stopped, only register 1 is non-empty. In the system $\Pi ^\prime$, each register r has a one-to-one correspondence with a neuron $\sigma _r$ in the ADD or SUB module, and an instruction $l_i$ in H is associated with a neuron $\sigma _{l_i}$. It must be clear that when the register r stores a number whose size is n, then the quantitative relationship contained in the corresponding spike reserve in the neuron $\sigma _r$ corresponds to 2n.

The INPUT module of the system is shown in Fig. 4. At step t, the first spike is introduced from outside the system by the input neuron $\sigma _{in}$. At step $t+1$, the spikes on the synapses $(in,in_1)$, $(in,in_2)$ are sensed by $ast_{in}^{(1)}$, the number of spikes is less than the threshold, and rule $0/a\longrightarrow a;+$ in neuron $\sigma _{in}$ reaches the firing condition, a spike and a positive charge are sent to neurons $\sigma _{in_1}$, $\sigma _{in_2}$, $\sigma _{in_3}$ and $\sigma _{in_4}$. From step $t+2$, neurons $\sigma _{in_1}$, $\sigma _{in_2}$ exchange spike information with each other in each subsequent time unit, and neurons $\sigma _{in_2}$ pass through the corresponding synapses $(in_2, 1^{(1)})$ and $(in_2, 1^{(2)})$ send two spikes to register 1.

Fig. 4

INPUT Module of $\Pi ^{\prime }$

Table 4 The numbers of spikes and polarity of neurons in input module (see Fig. 4)

At the end of step $t+n$, the second spike enters the system. At step $t+n+1$, $ast_{in}^{(1)}$ checks that the number of spikes delivered on synapses $(in,in_1)$, $(in,in_2)$, $(in_1,in_2)$, $(in_2,in_1)$ are greater than the threshold in $ast_{in}^{(1)}$, then these spikes are removed from the system. At the same moment, rule $0/a \longrightarrow a;+$ within neuron $\sigma _{in}$ reaches the firing condition and sends a spike and a positive charge to neuron $\sigma _{in_3}$ and neuron $\sigma _{in_4}$. At step $t+n+2$, rule $+/a^2 \longrightarrow \lambda ;-$ in neuron $\sigma _{in_3}$ reaches the firing condition, a negative charge are sent to neuron $\sigma _{in_1}$ and $\sigma _{in_3}$, the neurons are reset to their initial charge state. Rule $+/a^2 \longrightarrow a;0$ in neuron $\sigma _{in_4}$ reaches the firing condition, a spike and neutral charge are sent to neuron $\sigma _{1^{(1)}}$, $\sigma _{1^{(2)}}$, and $\sigma _{l_0}$. At this point, the system will jump to the $l_0$ instruction. The operation processes of INPUT module of $\Pi ^{\prime }$ are shown in Table 4.

As shown in Fig. 5, the deterministic ADD module is mainly used to simulate the ADD instruction $l_i:(ADD(r),l_j)$. The operation process of the ADD module will not be described here.

Fig. 5

ADD Module of $\Pi ^{\prime }$

The SUB module of the system $\Pi ^\prime$ will continue to use the module shown in Fig. 2. Regarding the stop of the system $\Pi ^\prime$, the Fin module is removed from the system, and when the register machine runs to the halting instruction $l_h$ in the accepting mode, there is no rule available in the neuron $\sigma _{l_h}$, that is, the system halts.

According to the above proof, the register machine can be correctly simulated by the system $\Pi ^\prime$ under the accepting mode, and the theorem is proved. $\square$

4 A small universal PASN P system

In this section, a small universal model of PASN P systems $\Pi ^{\prime \prime }$ is constructed as a computational function, which is based on the above research content in this work. The small universal register machine as a calculation function is determined [48], and its structure is shown in Fig. 6.

Fig. 6

The small universal register machine $M_u$

The universal register machine form is $M_u=(8,H,l_0,l_h,I)$, and the register machine contains eight registers and a total of 23 instructions. The ADD instruction of the register machine M in the accepting or recognition mode is determined, and the ADD instruction is written as $l_i: (ADD(r),l_j)$. According to register 0 in PASN P systems constructed in this paper is used to store data. PASNP systems does not allow subtraction operations acting on the register where the computation result is placed, but instruction $l_{19}$ in Fig. 6 obviously does not meet this requirement, and the register machine M needs to be modified. By adding the register 8, the halting instruction is modified as follows:

$$\begin{aligned} l_{22}:(SUB(0),l_{23},l_{h}^\prime ),\qquad l_{23}:(ADD(8),l_{22}),\qquad l_{h}^\prime : HLAT \end{aligned}$$

The content in register is 0 transferred to register 8 through the above instructions. In the calculation process, the value stored in register 8 only increases. Under the condition that the other definition forms are not changed, the modified register machine $M_{u}^{\prime }$ contains 9 registers and 25 instructions, and the result obtained when the system format transfer is terminated will be stored in the register 8.

Theorem 3

There is a universal PASN P system with 65 neurons for computable functions.

Proof

To prove the small universal system $\Pi ^{\prime \prime }$ as a function calculation, it is necessary to make it simulate the register machine $M_u^{\prime }$. The proof process includes INPUT module, deterministic ADD module, SUB module, ADD–ADD module, ADD–SUB module, SUB–ADD module and OUTPUT module. In the system $\Pi ^{\prime \prime }$, the obtained calculation results are stored in the register 8, and finally output to the outside of the system by the OUTPUT module. In the process of system format conversion, the instruction operation on the register 8 will not reduce its content, that is, there is no corresponding SUB instruction on it to perform the SUB operation. In the system $\Pi ^{\prime \prime }$, each register r has a one-to-one correspondence with a neuron $\sigma _r$ in the ADD or SUB module and an instruction $l_i$ in H is associated with a neuron $\sigma _{l_i}$. It must be clear that when the register r stores a number with a size of n, then the quantitative relationship contained in the corresponding spike reserve in the neuron $\sigma _r$ corresponds to 2n.

Fig. 7

INPUT Module of $\Pi ^{\prime \prime }$

The INPUT module of the system $\Pi ^{\prime \prime }$ as shown in Fig. 7. In the INPUT module, the neuron $\sigma _{in}$ identifies the spike train $10^{g(x)-1}10^{y-1}1$, and finally 2g(x), and 2y spikes are stored in the neuron $\sigma _1$, $\sigma _2$ correspondingly. When neuron $\sigma _{in}$ receives the first spike in which rule $0/a\longrightarrow a;+$ reaches the firing condition, a spike and a positive charge are sent to neuron $\sigma _{in_1}$, $\sigma _{in_2}$, $\sigma _{in_3}$, $\sigma _{in_6}$ and $\sigma _{in_7}$. A total of two spikes on the synapses $(in,in_1)$, $(in,in_2)$, are smaller than the threshold in the astrocyte $ast_{in}^{(1)}$ and the spikes can reach the target neuron. At the next moment, rule $0/a\longrightarrow a;0$ in the neuron $\sigma _{in_1}$ and $\sigma _{in_2}$ reaches the firing condition and transmits a spike and a neutral charge to each other. Moreover, sends two spikes and neutral polarity to neuron $\sigma _{1}$ at each step until neuron $\sigma _{in}$ receives the second spike, register 1 contains the value 2g(x).

When the neuron $\sigma _{in}$ receives the second spike, astrocytes $ast_{in}^{(1)}$ senses four spikes in adjacent synapses synapses $(in,in_1)$, $(in,in_2)$, $(in_1,in_2)$, $(in_2,in_1)$, that greater than the threshold of astrocytes $ast_{in}^{(1)}$, the synapse is inhibited. At the same time, neuron $\sigma _{in_3}$ receives the second spike in which rule $+/a^2\longrightarrow a;0$ reaches the firing condition, a spike and a neutral charge are sent to neuron $\sigma _{in_4}$, $\sigma _{in_5}$. A total of two spikes on the synapses $(in_3,in_4)$, $(in_3,in_5)$, are smaller than the threshold in the astrocyte $ast_{in}^{(1)}$ and the spikes can reach the target neuron. At the next moment, rule $0/a\longrightarrow a;0$ in the neuron $\sigma _{in_4}$ and $\sigma _{in_5}$ reaches the firing condition and transmits a spike and a neutral charge to each other. Moreover, sends two spikes and neutral charge to neuron $\sigma _{2}$ at each step. When a third spike enters the system, $ast_{in}^{(1)}$ checks that the number of spikes delivered on synapses $(in,in_1)$, $(in,in_2)$, $(in_4,in_5)$, $(in_5,in_4)$ are greater than the threshold in $ast_{in}^{(1)}$, then these spikes are removed from the system. Neuron $\sigma _{2}$ no longer receives spikes and has a number of 2y spikes stored in it.

Fig. 8

ADD–ADD Module of $\Pi ^{\prime \prime }$

After the third spike enters neuron $\sigma _{in_6}$, rule $+/a^3\longrightarrow \lambda ;-$ in neuron $\sigma _{in_7}$ reaches the firing condition, a negative charge are sent to neurons $\sigma _{in_1}$, $\sigma _{in_2}$, $\sigma _{in_4}$ and $\sigma _{in_5}$, the polarizations of neurons returned to the initial state. Rule $+/a^{3}\longrightarrow a;0$ reaches the firing condition, a spike and a neutral charge are sent to neuron $\sigma _{l_0}$. At this point, the system will jump to the $l_0$ instruction of the register machine $M_u^{\prime }$.

The deterministic ADD module in the system $\Pi ^{\prime \prime }$ is shown in Fig. 5. For the SUB instruction executes the SUB instruction shown in 2. The OUTPUT module is improved on the basis of the module shown in Fig. 3, and the label of neuron $\sigma _{r}$ is modified to a certain label (8, 0), other neurons remain unchanged, and the calculation results are output using the improved module.

According to each module of the small universal system $\Pi ^{\prime \prime }$, the small universal system contains a total of 105 neurons. The introduction of system resources is as follows.

• $9\times 2$ neurons correspond to 18 registers,

• 25 neurons correspond to 25 instruction labels,

• $1\times 10$ auxiliary neurons correspond to 10 ADD instruction modules,

• $3\times 14$ auxiliary neurons correspond to 42 SUB instruction modules,

• 5 neurons in the INPUT module,

• 5 neurons in the OUTPUT module,

In view of the above results, it can still be improved through instruction optimization, and the results as follows. For consecutive ADD instructions: $l_{17}: (ADD(2), l_{21})$ and $l_{21}:(ADD(3),l_{18})$, the model constructed after optimization is recorded as ADD–ADD. In this optimization model, the ADD module corresponding to the $l_{21}$ instruction can be omitted, save 1 neuron. As shown in Fig. 8.

For the continuous ADD and SUB instructions represented as follows, the optimized model is denoted as ADD–SUB, and the form is defined as: $l_i:(ADD(r^\prime ),l_g)$, $l_g:(SUB(r^{\prime \prime }),l_j,l_k )$. After optimization, a total of two neurons are saved. As shown in Fig. 9, the operation process of the improved model will not be described in detail here.

$$\begin{aligned}{} & {} l_5: (ADD(5), l_6 ),\qquad l_6: (SUB(7), l_7, l_8)\\{} & {} \quad l_9: (ADD(6), l_{10}),\qquad l_{10}: (SUB(4), l_0, l_{11}) \end{aligned}$$

Fig. 9

ADD–SUB Module of $\Pi ^{\prime \prime }$

Fig. 10

SUB–ADD Module of $\Pi ^{\prime \prime }$

Regarding continuous SUB and ADD instructions, there are six related instructions, which are usually formally defined as $l_g:(SUB(r^\prime ),l_j,l_k)$, $l_i:(ADD(r^{\prime \prime }),l_g)$, the ADD instructions which can be optimized are $l_1$, $l_5$, $l_7$, $l_9$, $l_{16}$, $l_{22}$, save a total of six neurons. Continuous SUB and ADD instructions, the optimized model is recorded as SUB–ADD, as shown in Fig. 10.

Subtraction instructions can be divided into three categories:

• (1) $l_0: (SUB(1), l_1,l_2 ),\qquad l_3: (SUB(5), l_2,l_4 ),\qquad l_4: (SUB(6), l_5,l_3 )$ $l_6: (SUB(7), l_7,l_8 ),\qquad l_8: (SUB(6), l_9,l_{10} ),\qquad l_{11}:(SUB(5), l_{12},l_{13} )$ $l_{12}: (SUB(5), l_{14},l_{15} ),\qquad l_{14}: (SUB(5), l_{16},l_{17} ),\qquad l_{h}: (SUB(0), l_{22},l_h^\prime )$

• (2) $l_{10}: (SUB(4), l_{0},l_{11} ),\qquad l_{18}: (SUB(4), l_{0},l_{h}),\qquad l_{19}: (SUB(0), l_{0},l_{18} )$

• (3) $l_{13}: (SUB(2), l_{18},l_{19} ),\qquad l_{15}: (SUB(3),l_{18},l_{20})$

For the first set of SUB instructions, an auxiliary neuron can be shared between different SUB instructions, as shown in Fig. 11. For the second and third groups of subtraction SUB, two auxiliary neurons can be shared between different SUB instructions, as shown in Fig. 12. By grouping subtraction instructions. Save a total of 14 neurons.

Fig. 11

SUB–SUB Module of $\Pi ^{\prime \prime }$ share one neurons

Fig. 12

SUB–SUB Module of $\Pi ^{\prime \prime }$ share two neurons

The proof process of the module will not be repeated, but it should be pointed out that the two modules SUB–ADD and ADD–SUB are both optimization models based on the SUB module. Therefore, by using ADD–ADD, ADD–SUB, SUB–ADD, and SUB–SUB optimization instructions, a total of 23 neurons are saved. Reduced computing resource consumption of small universal systems from 105 to 82. $\square$

5 Conclusion and discussion

In this work, the control mechanism of astrocytes is added to PSN P systems to construct PASN P systems. As number generating devices and number accepting devices, PASN P systems are proved to be equivalent to Turing machines. In addition, a small universal PASN P system is constructed as a computing function, which is used to simulate the modified small universal register machine $M_u^\prime$, we demonstrate that the small universal system uses 82 neurons, a reduction of 82 neurons compared to the small universal SN P system with polarization proposed in [43] and a reduction of 69 neurons compared to the small universal SN P system with polarization and rules on synapses proposed in [44]. Therefore, it is of great significance to put forward PASN P systems and prove its Turing universality.

PASN P systems inherit the advantages of ASN P systems and PSN P systems. In applications, the advantage of PASN P systems can also be used to characterize NRE in both synchronous mode and asynchronous mode, or to build basic logic gates and Boolean circuits [42]. PAS P systems have great advantages to solve the real-life problems, such as recognition of handwritten digit letters recognition of handwritten numerals [49], autonomous robot control [50], and information processing and learning [51], that is worth investigating.

Based on PASN P systems, some topics and open problems are suggested. For instance, whether the number of neurons can be reduced by using extended rules or increasing the use of astrocytes. It would also be interesting to design regular expressions that express polarization behavior, or try to incorporate learning strategies into PASN P systems to solving practical engineering problems.