Experiments on the reliability of stochastic spiking neural P systems

Abstract

In the area of membrane computing, time-freeness has been defined as the ability for a timed membrane system to produce always the same result, independently of the execution times associated to the rules. In this paper, we use a similar idea in the framework of spiking neural P systems, a model inspired by the structure and the functioning of neural cells. In particular, we introduce stochastic spiking neural P systems where the time of firing for an enabled spiking rule is probabilistically chosen and we investigate when, and how, these probabilities can influence the ability of the systems to simulate, in a reliable way, universal machines, such as register machines.

1 Introduction and motivations

Membrane computing (known also as P systems) is a model of computation inspired by the structure and the functioning of living cells (a monograph dedicated to the area is Păun 2002, an updated bibliography can be found at the web-page http://ppage.psystems.eu). Essentially, a P system is a synchronous parallel computing device based on multiset rewriting in compartments where a global clock is assumed and each rule of the system is executed in one time step.

Starting from the idea that different reactions may take different times to be executed (or to be started, when enabled) a timed model of P system was introduced in Cavaliere and Sburlan (2005), where to each rule of the system is associated a time of execution. The goal was to understand how time could be used to influence the result produced by the P system (see, e.g., Cavaliere and Zandron 2006) and, possibly, how to design computational powerful time-free systems where the output produced is independent of the timings associated to the rules, e.g., Cavaliere and Deufemia (2006).

In this paper we use a similar idea in the framework of spiking neural P systems, (in short, SN P systems), which have been introduced in Ionescu et al. (2006) as computing devices inspired by the structure and functioning of neural cells (a friendly introduction to the area is Păun 2007). We investigate how the timing of the spiking rules can influence the output produced by the systems and in particular can influence the ability of the systems to simulate universal computing devices.

The main idea of an SN P system is to have several one-membrane cells (called neurons) which can hold any number of spikes; each neuron fires (we also say, spikes) in specified conditions (after accumulating a specified number of spikes). In the standard definition of SN P systems, the functioning of the system is synchronous: a global clock is assumed and, in each time unit, each neuron that can use a rule does it. The system is synchronized but the work of the system is sequential: only (at most) one rule is used in each neuron. One of the neurons is considered to be the output neuron and its spikes are also sent to the environment. The moments of time when (at least) one spike is emitted by the output neuron are marked with 1, the other moments are marked with 0. The binary sequence obtained in this manner is called the spike train of the system—it is infinite if the computation does not stop.

To a spike train one can associate various numbers, which can be considered as computed (we also say generated) by an SN P system. For instance, in Ionescu et al. (2006) only the distance between the first two spikes of a spike train was considered, then in Păun et al. (2006) several extensions were examined: the distance between the first k spikes of a spike train, or the distances between all consecutive spikes, taking into account all intervals or only intervals that alternate, all computations or only halting computations, etc.

In Ionescu et al. (2006) it is proved that synchronized SN P systems, with spiking rules in the standard form (i.e., they produce only one spike) are universal – they can characterize NRE, the family of Turing computable sets of natural numbers; normal forms of universal SN P systems were presented in Ibarra et al. (2007).

In the proof of these results, the synchronization plays an important role and, in general, the synchronization is a very powerful feature, useful in controlling the work of a computing device. However implementing synchronization is not always easy or possible and is (not always) biologically justified, as, for instance, in case of network of spiking neurons (see, e.g., Gerstner 2000). For these reasons in (Cavaliere et al. 2007a, b) an asynchronous version of SN P systems, where at each step of the computation a spiking rule can be applied or skipped, has been considered. There has been shown that removing the synchronization, in some cases, can lead to a decrease of the computational power of the systems. In the same papers, it is also conjectured that asynchronous spiking neural P systems using standard rules are not universal.

However, the border between synchronous and asynchronous systems seems to be not so drastic in natural systems, and in many other artificial systems, e.g., networks of computers. In many cases we encounter networks of computational units that do not work in a synchronous way, i.e., they do not use same global clock, but still they do their operations in an “enough” synchronous way, in such way that the functioning of the entire system follows the specified goals.

We try to capture such intuition in the framework of SN P systems by considering stochastic SN P systems (in short, SSN P systems) where to each rule, when enabled, is associated a probability to fire in a certain time interval. This means that, during the computation of an SSN P system, an enabled rule may not spike immediately but can remain silent for a certain (probabilistic) time interval and then spikes. During such interval the neuron where the rule is present could receive other spikes from the neighboring neurons or maybe other rules can fire in the same neuron. The computation would then continue in the new circumstances (maybe different rules are enabled now—the contents of the neuron has changed). If there is competition between enabled rules for using the spikes present in the same neuron, the fastest (probabilistically determined) rule spikes.

The choice of the probability distributions for the firing of the rules clearly influences the synchrony of the entire system. Because of the results in Cavaliere et al. (2007b), we can expect that the probability distributions for the firing of the rules influence the ability for the systems to simulate, in a reliable way, computational universal machines. In this paper we do not want to provide a formal proof for this statement but rather we want to present ways to investigate such “influence”.

We first show that an SSN P system can simulate universal machines when the probability distributions can be chosen in an arbitrary manner. When such distributions cannot be arbitrarily chosen but they are given, then, the reliability of an SSN P system (i.e., the ability for the system to work correctly) depends on the given distributions, and, in some cases, on the variance associated to the distributions. In general, one has to use statistical analysis to investigate the reliability of the systems, when, for instance, varying the variance associated to the distributions. In this paper, we provide such an analysis for a specific example of SSN P system and considering a specific register machine program. We also show how, using such method of analysis, it is possible to identify the (maximal) value for the variance that guarantees that the system has a certain chosen reliability.

The functioning of the SSN P system is somehow similar to the one of stochastic Petri nets, Marsan (1989) where a time of delay for each transition is used. However, motivations and questions of the two paradigms are clearly different (modeling network of spiking neurons for computability study in our case, modeling concurrent processes in case of stochastic Petri nets). This is more evident when considering the control associated to the single computational unit: regular expressions associated to each neuron in an SSN P system, presence of tokens in the places in stochastic Petri nets.

Probabilities have been also used in the more general framework of P systems. In particular, in Obtulowicz and Păun (2003) and Madhu (2003) probabilities have been associated with the localization of single objects and with rules and universality has been shown when such probabilities are chosen in a very specific way. However, no explicit analysis of the reliability of the systems has been presented. A different approach is used in Muskulus et al. (2007) and Pescini et al. (2005) where sequential membrane systems have been investigate using Markov chains theory. In these papers however probability distributions are not directly associated to the timing of the rules, but are rather obtained by starting from chemical reactions and molecular dynamics; the goal of the authors is, in fact, to provide algorithms to investigate dynamics of molecular systems.

We conclude by mentioning a similar work presented in Maass (1996) in the framework of network of spiking neurons where each neuron has associated a given threshold that specifies when a neuron fires. In Maass (1996) the author shows how a network of spiking neurons, with noisy neurons (i.e., the time of firing is not deterministic) can simulate, in a reliable way, boolean circuits and finite state automata. In our case, we use more general and abstract type of neurons and, for this reason, we can investigate more “complex” and general encodings such as the one of register machines.

The rest of this paper is organized as follows. We recall in Sect. 2 some basic concepts used throughout the paper, and we formally define in Sect. 3 the class of SSN P systems. Section 4 is devoted to the characterization of the computational power of SSN P systems, for which we prove, under precise conditions, universality. We report in Sect. 5 the results of a simulation study aiming at evaluating the reliability of SSN P systems computations under more general conditions than those defined in Sect. 4. Section 6 provides conclusions and directions for future research.

2 Preliminaries

We introduce in this section a limited amount of concepts and technical notation, assuming the reader has some familiarity with (basic elements of) language and automata theory, random variables and register machines. Additional information can be found in standard books, for instance Salomaa (1973) for languages and automata theory, Trivedi (2001) for random variables, Minsky (1967) for register machines.

2.1 Languages and regular expressions

For an alphabet V, $V^{\ast}$ is the free monoid generated by V with respect to the concatenation operation and the identity λ (the empty string); the set of all nonempty strings over V, that is, $V^{\ast}$−{λ}, is denoted by V ⁺. When V = {a} is a singleton, then we simply write $a^{\ast}$ and a ⁺ instead of $\{V\}^{\ast}$, {a}⁺. The length of a string $x\in V^{\ast}$ is denoted by |x|.

A regular expression over an alphabet V is constructed starting from λ and the symbols from V and using the operation of union, concatenation and Kleene +, using parentheses when necessary for specifying the order of operations. Specifically, (i) λ and each $a \in V$ are regular expressions, (ii) if E ₁ and E ₂ are regular expressions over V, then $(E_1) \cup (E_2), (E_1)(E_2)$ and (E ₁)⁺ are regular expressions over V, and (iii) nothing else is a regular expression over V. Non-necessary parentheses are omitted when writing a regular expression and $(E)^+ \cup \{\lambda\}$ is written in the form $(E)^{\ast}.$

To each regular expression E we associate a language L(E) defined in the following way: (i) L(λ) = {λ} and L(a) = {a}, for all $a \in V,$ $(ii) L((E_1) \cup (E_2)) = L(E_1) \cup L(E_2), L((E_1)(E_2)) = L(E_1)L(E_2),$ and $L((E_1)^+) = L(E_1)^+$ for all regular expressions E ₁, E ₂ over V.

2.2 Random variables

A random variable is an abstraction for the concept of chance, whose specification requires the definition of a probability measure over the set of possible values (the domain). Depending on their domain, random variables can be classified as discrete ones, when the possible values form a finite or countable set, or continuous ones, when the set of possible values is uncountable. For the purposes of this paper, we shall restrict ourselves to considering random variables whose domain is a subset of R ⁺, the set of nonnegative real numbers. An example of a discrete random variable is the number obtained rolling a die, which only has 6 possible values. Examples of continuous random variable are the lifetime of an electric lamp and the air temperature in a room at a given time/day, for which the domain is a subset of real numbers.

The function that assigns probabilities to the elements of the domain is called the probability distribution function of the random variable. Being a probability measure, this function is always non-negative and the sum of its values over the whole domain is equal to 1. More precisely, we distinguish between two forms of the probability distribution function:

• the probability density function (pdf, hereafter) is the function f(x) that returns, for each value x of the domain, the probability that the variable takes value x;

• the cumulative density function (cdf, hereafter) is the function F(x) that returns, for each value x of the domain, the probability that the variable is less or equal than x.

For instance, if X is the discrete random variable that represents the result obtained when rolling a die, its domain, which we denote by Dom(X), is the set {1,2, … ,6}, its pdf is the function $f_{X}(x)=1/6, x\in Dom(X).$ The cdf of X is F _X (x) defined as $F_{X}(x)=x/6, x\in Dom(X).$ The discrete random variable Y whose domain contains only one possible value $\tilde{y}$ is a special case of random variable, called the deterministic random variable. Its pdf assigns a value 1 to $\tilde{y}$ and 0 to any other value. Its cdf is conveniently denoted by the shifted Heaviside function $H(y-\tilde{y}),$ where the Heaviside function is defined as H(y) = 0 if y < 0 and H(y) = 1 if y ≥ 0.

The continuous random variable Z representing the lifetime of an electric lamp is satisfactorily modeled by a negative exponential distribution, whose pdf is defined as $f_{Z}(z)=\lambda e^{-\lambda z},$ z ≥ 0, and its cdf at z ≥ 0 is the integral of the pdf over [0,z], given by $F_{Z}(t)=1-e^{-\lambda z},$ for z ≥ 0.

The expected value (also called the average value or mean value) of a random variable X, usually denoted as E[X], is defined as $E[X]=\sum_{x\in Dom(X)}xf_{X}(x)$ if X is discrete, and as $E[X]=\int_{x\in Dom(X)}xf_{X}(x)dx$ if X is continuous. For instance, the expected value of the discrete random variable X representing the value obtained by rolling a die is E[X] = 3.5 (notice it does not belong to Dom(X)), and the expected value of the continuous random variable Y representing the lifetime of an electric lamp is E[Y] = λ⁻¹.

The variance of a random variable X, usually denoted as Var[X], is a non-negative number defined as $Var[X]=\sum_{x\in Dom(X)}(x-E[X])^2f_{X}(x)$ if X is discrete, and as $Var[X]=\int_{x\in Dom(X)}(x-E[X])^2f_{X}(x)dx$ if X is continuous. Intuitively, the variance of a distribution is a measure of the spread of the distribution around the expected value. Thus, the variance of a deterministic random variable is 0, whereas the variance of a negative exponential distribution as the one modeling the lifetime of an electric lamp is λ⁻².

An interesting and commonly used random variable is the normal (also called Gaussian) distribution. Its pdf is defined in terms of two parameters, μ and σ² ≥ 0, which are indeed the expected value and the variance of the distribution itself. For instance, the air temperature in a room at a given time/day can be thought to follow a normal distribution whose value μ is the historical average and σ² is a measure of the variation around the expected value. A normal distribution of parameters μ and σ² is denoted by N(μ,σ²). The pdf of a normal random variable U distributed as N(μ,σ²) is $U(u)=(\sigma \sqrt{2\pi})^{-1}e^{-(u-\mu)^2/2\sigma^2}.$ The cdf of a normal random variable does not have an analytical form; rather its tabulations are provided in statistical books for the case N(0,1) (called the standard normal distribution). It is interesting to notice that a variable distributed as $N(\tilde{x},0)$ corresponds to a deterministic random variable whose only possible value is $\tilde{x}.$

2.3 Register machines

A (non-deterministic) register machine is a construct M = (m,H, l ₀, l _h ,I) where m is the number of registers, H is the set of instruction labels, l ₀ is the start label (labeling an ${\tt ADD}$ instruction), l _h is the halt label (assigned to an ${\tt HALT}$ instruction) and I is the set of instructions; each label from H labels only one instruction from I, thus precisely identifying it. The instructions are of the following general forms:

• $l_i: ({\tt ADD}(r),l_j,l_k),$ adds 1 to register r and then goes non-deterministically to one of the instructions with labels l _j ,l _k ;

• $l_i:({\tt SUB}(r),l_j,l_k),$ if register r is non-empty, then subtracts 1 from it and goes the instruction with label l _j , else goes to the instruction with label l _k ;

• $l_h:({\tt HALT}),$ is the halt instruction.

A computation of a register machine M is defined in the following way. The machine starts with all empty registers (i.e., storing the number zero). Initially, the instruction with label l ₀ is executed. The computation proceeds by applying the instructions as indicated by the labels (and made possible by the contents of the registers); if the halt instruction is reached, the computation halts and the number n stored at that time in the first register (output register) is the output of the computation. Because of the non-determinism present in the ${\tt ADD}$ instruction, a machine M may have multiple halting computations. Without loss of generality, we can assume that, for any instruction as above, l _j and l _k are different from l _i .

We denote by ${\mathcal{C}}_{M}$ the set of halting computations of M, and by Out(c), the output produced by a computation $c\in{\mathcal{C}}_{M}.$ Then $N(M) = \{Out(c), c\in {\mathcal{C}}_{M}\}$ is the set of all natural numbers computed by machine M. We denote by RM _NDET the class of non-deterministic register machines. It is known (see, e.g., Minsky 1967) that RM _NDET computes all sets of numbers which can be computed by a Turing machine, hence characterizes NRE.

3 Stochastic spiking neural P systems

We introduce here a class of SN P system, called stochastic spiking neural P systems (in short, SSN P systems). SSN P systems are obtained from SN P systems by associating to each spiking rule a firing time that indicates how long an enabled rule waits before it is executed. Such firing times are random variables whose probability distribution functions have domain contained in R ⁺.

Informally, an SSN P system is an asynchronous SN P system (Cavaliere et al. 2007b) where the firing of the rules (hence, the asynchrony present in the system) is stochastically regulated. Formally, an SSN P system is a quadruple

$$ \Uppi = (O,\Upsigma,syn,i_o) $$

where:

• 1. O = {a} is the singleton alphabet (a is called spike);

• 2. Σ = {σ₁,σ₂, … ,σ _m } are neurons, of the form

  $$ \sigma_i = (n_i,R_i), 1\leq i \leq m, $$

  where:

  • n _i  ≥ 0 is the initial number of spikes contained by the neuron;

  • R _i is a finite set of rules, of the following two forms:

    • (a) $E/a^r\rightarrow a;F^{\prime}$ where E is a regular expression over O, r ≥ 1, and F′ is a probability distribution function with domain in R ⁺;

    • (b) $a^s\rightarrow \lambda;F^{\prime\prime}$ for some s ≥ 1, with the restriction that $a^s \not \in L(E)$ for any rule of type (a) in R _i , and F′′ is a probability distribution with domain in R ⁺;

• 3. $syn \subseteq \{1,2,\ldots,m\}\times \{1,2,\ldots,m\}$ with $(i,i) \not \in syn$ for 1 ≤ i ≤ m is a set of synapses among the neurons;

• 4. i _o ∈Σ is the output neuron.

A rule of type $E/a^r\rightarrow a;F^{\prime}$ present in neuron i, for $i \in \{1,2,\ldots,m\},$ is a firing (also called spiking) rule: provided that the contents of neuron i (i.e., the number of spikes present in it) is described by the regular expression E, then the rule is enabled and can fire (spike). When the rule fires, r spikes are consumed in neuron i and exactly 1 spike is sent to all the neurons to which neuron i is linked through the synapses. A rule of type $a^s \rightarrow \lambda;F^{\prime\prime}$ is a forgetting rule, and it functions in a similar way. The only difference with respect to the firing rule is that, when the forgetting rule fires, s spikes are consumed in neuron i and no spike is sent out.

From the moment in which a rule is enabled up to the moment when the rule fires, a random amount of time elapses, whose probability distribution is specified by the function F associated to the rule (different rules may have associated different distributions).

Therefore, if a rule is enabled in neuron i and before the rule fires the neuron receives new spikes or another rule in neuron i fires, it may happen that the rule is not enabled anymore because the contents of neuron i has changed.

We suppose, that once the rule fires, the update of the number of spikes in the neuron, the emission of spikes and the update of spikes in the receiving neurons are all simultaneous and instantaneous events. Multiple rules may be simultaneously enabled in the same neuron. Whenever multiple enabled rules in a neuron draw the same random firing time, the order with which those rule fire is randomly chosen, with a uniform probability distribution across the set of possible firing orders.

A configuration of an SSN P system Π is composed by the neurons with their associated contents. Using the rules in the way described above, in each neuron, the system Π passes from a configuration to another configuration: such a step is called transition. Notice that, because of the way the firing of the rules has been defined, in general there is no upper bound on how many rules fire for each transition.

A sequence of transitions, starting in the initial configuration, is called computation. A halting computation is a computation that reaches a halting configuration, i.e., one in which no rule is enabled. We denote by ${\mathcal{C}}_{\Uppi}$ the set of all halting computations of an SSN P system Π. For an halting computation $c \in {\mathcal{C}}_{\Uppi},$ Out(c), the output produced by c, is defined as the contents of the output neuron in the halting configuration and $N(\Uppi) = \{Out(c), c\in {\mathcal{C}}_{\Uppi}\}$ is the set of natural numbers generated by Π.

In what follows, we will use the usual convention to simplify spiking systems rule syntax, writing $a^r\rightarrow a;F$ when the regular expression of the rule is a ^r.

4 Computational Power of SSN P Systems

In this section we discuss the computational power of SSN P systems, by relating their capabilities to those of register machines. In particular, we construct specific SSN P systems modules that can simulate the instructions of a register machine. We show that an SSN P system can “simulate” an (synchronous) SN P system, hence a register machine, provided that the distributions associated to the spiking rules are appropriately chosen. However, notice that “standard” SN P systems (i.e, non stochastic), as usually considered in literature, cannot be directly seen as a special case of SSN P systems (in fact, SSN P systems do not include a closed state of neurons). In the proof of the following theorem, we combine normals forms of SN P systems presented in Ibarra et al. (2007) and Ionescu et al. (2006).

Theorem 1

For every $M \in RM_{NDET}$ there exists an SSN P system Π such that N(M) = N(Π).

Proof

Let r ₁,r ₂, … ,r _m be the registers of M, with r ₁ being the output register, and H = {l ₀, l ₁, … ,l _n , l _h } the set of labels for the instructions I of M. Without any loss of generality, we may assume that in the halting configuration, all registers of M different from r ₁ are empty, and that the output register is never decremented during the computation, we only add to its contents. □

We construct the SSN P system $\Uppi = (O = \{a\},\Upsigma, syn, i_o)$ that simulates the register machine M. In particular, we only present separate types of modules that can be used to compose the SSN P system Π. Each module simulates an instruction of the register machine M (we distinguish between a deterministic and non-deterministic version of the ${\tt ADD}$).

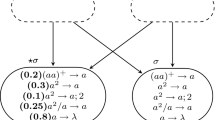
• 1. A deterministic add instruction $l_i:({\tt ADD}(r_p),l_j,l_j),$ for some $p \in \{2,\ldots,m\}$ and $i,j\in \{0,1,\ldots,n\}\cup\{h\},$ is simulated by the module presented in Fig. 1.

• 2. A deterministic add instruction to register $r_1, l_i:({\tt ADD}(r_1),l_j,l_j),$ for some $i,j\in \{0,1,\ldots,n\}\cup\{h\}$ is simulated by a module as the one shown in Fig. 1, where neuron l ¹ _i is removed and neuron nr ₁ has no rules.

• 3. A non-deterministic add instruction, $l_i:({\tt ADD}(r_p),l_j,l_k),$ for some $p \in \{2,\ldots,m\}$ and $i,j,k\in \{0,1,\ldots,n\}\cup\{h\}$ is simulated by the module shown in Fig. 2; Again, as in the deterministic case, $l_i:({\tt ADD}(r_1),l_j,l_k)$ (i.e., a non-deterministic add instruction to register 1) is simulated by a module as the one in Fig. 2, but in which neuron l ¹ _i is removed and neuron nr ₁ has no rules inside.

• 4. A sub instruction, $l_i:({\tt SUB}(r_p),l_v,l_w),$ for some $p \in \{2,\ldots,m\}$ and $i,j,k\in \{0,1,\ldots,n\}\cup\{h\}$ is simulated by the module shown in Fig. 3.

Fig. 1

Module for the deterministic ${\tt ADD}$ instruction

Fig. 2

Module for the non-deterministic ${\tt ADD}$ instruction

Fig. 3

Module for the ${\tt SUB}$ instruction

Neuron nr _j , for each $j \in \{1,\ldots,m\},$ corresponds to the register r _j of M. Neuron nl _j , for each $j \in \{0,1,\ldots,n\}\cup\{h\},$ corresponds to the (starting point of) instruction l _j in the set I. In the initial configuration of Π all neurons are empty, except the neuron nl ₀ corresponding to the initial instruction of M that has 1 spike. The output neuron of Π is defined to be nr ₁ corresponding to register r ₁ of M (we recall that such register is only subject to add instructions).

Finally, to complete the specification of the modules, we select the probability distribution functions associated to the rules as follows:

• F ₁(x) is defined as the Gaussian normal distribution with average μ₁ and variance σ², which we shortly denote as N(μ,σ²), where we set μ₁ = 1 and σ² = 0 so that F ₁(x) = H(x−1);

• F ₂(x) is defined to be N(μ₂,σ²), with μ₂ = 2 and σ² = 0;

• F ₃(x) is defined to be 0.5H(x−1) + 0.5H(x−2), i.e., F ₃(x) is the discrete uniform distribution in {1,2});

• F ₄(x) is defined to be N(μ₄,σ²), with μ₄ = 0.5 and σ² = 0.

We now show how, because of the selected distributions of firing rules, each instruction of the register machine can be correctly simulated by the corresponding presented module.

Let us suppose that, at an arbitrary time t, the register machine M is in a given configuration, in which it is to execute the instruction at label l _i with a given state of r ₁, r ₂, … ,r _m registers, and suppose that the SSN P system Π is in a configuration that corresponds to that of M, that means:

• neuron nr _i contains a number of spikes that is twice the contents of register r _i , for i = 2,3, … ,m;

• neuron nr ₁ contains a number of spikes equal to the contents of register r ₁;

• all other neurons are empty except neuron nl _i that contains exactly 1 spike.

Notice that, by construction, the initial configuration of Π corresponds to the initial one of M. Consider now the various possible cases for the instruction l _i that M starts executing at time t.

• $l_i:({\tt ADD}(r_p),l_j,l_j)$ (deterministic add)—module shown in Fig. 1. Suppose first that p≠1. Then, the execution of instruction l _i is simulated in Π in the following way. At time t + 1 neuron nl _i fires (with probability 1, because of the chosen distributions), one spike is introduced (at time t + 1, hence instantaneously) in neurons l ¹ _i and l ² _i . At time t + 2 neurons l ¹ _i and l ² _i fire with probability 1 and two spikes are added to neuron nr _p . Also, at time t + 2, one spike is added to neuron nl _j . Except the ones mentioned, no other rule can fire in neurons l ¹ _i ,l ² _i and nr _p . Then, Π reaches, starting from the supposed configuration, and with probability 1, a configuration that corresponds to the state of M after the execution of instruction l _i . If p = 1, the execution of instruction l _i is simulated in a similar way, the only difference being that only 1 spike is deposited in neuron nr ₁ at time t + 2. Thus, again Π reaches with probability 1 a configuration that corresponds to the state of M after the execution of instruction l _i .

• $l_i:({\tt ADD}(r_p),l_j,l_k)$ (non-deterministic add)—module shown in Fig. 2. In this case, the execution of the instruction l _i is simulated in Π as follows. We only describe the case when p≠1, the non-deterministic add to register r ₁ is similar. At time t + 1, neuron nl _i fires with probability 1, and at the same time one spike is introduced in neuron l ¹ _i and l ² _i . At time t + 2, neurons l ¹ _i and l ² _i fire with probability 1, two spikes are then added to the neuron nr _p and one spike is added to neurons l ³ _i , l ⁴ _i and l ⁵ _i . Neurons l ⁴ _i and l ⁵ _i fire, with probability 1, at time t + 3 and t + 4, respectively, emitting one spike to neuron l ⁶ _i and l ⁷ _i . In neuron l ³ _i , the rule $a \rightarrow a; F_3(x)$ fires at a time that is either t + 3 or t + 4, with equal probability 2⁻¹, and l ³ _i emits one spike to neurons l ⁶ _i and l ⁷ _i : this probabilistic choice of the firing time in l ³ _i simulates the non-deterministic choice of the ${\tt ADD}$ instruction.

  In fact, if neuron l ³ _i fires at time t + 3, then one spike is sent to both neurons l ⁶ _i and l ⁷ _i . The rule $a^2 \rightarrow a; F_1(x)$ fires with probability 1 in neuron l ⁶ _i at time t + 4, sending one spike to neuron nl _j . The forgetting rule in neuron l ⁷ _i fires with probability 1 at time t + 3.5. At time t + 4, the spike emitted by neuron l ⁵ _i also reaches neuron l ⁷ _i , the forgetting rule is enabled and it fires, with probability 1, at time t + 4.5.

  If neuron l ³ _i fires at time at time t + 4, the spike that was deposited in neuron l ⁶ _i by the firing of l ⁴ _i at time t + 3 gets consumed, with probability 1, by using the forgetting rule at time t + 3.5. Then, the spike deposited at time t + 4 in l ⁶ _i by the firing of neuron l ³ _i enables again the forgetting rule of neuron l ⁶ _i , and the spike present in l ⁶ _i is consumed, with probability 1, at time t + 4.5. Also, at time t + 4, 2 spikes are deposited in neuron l ⁷ _i (coming from neurons l ⁵ _i and l ³ _i ). This allows the rule $a^2 \rightarrow a; F_1(x)$ in neuron l ⁷ _i to fire at time t + 5 with probability 1 and to send 1 spike in neuron nl _k . In both considered cases, when 1 spike reaches either neuron nl _j or nl _k , no rule can fire anymore in neurons l ¹ _i , l ² _i , … , l ⁷ _i and nr _p .

  The system Π can only execute, when starts from the supposed configuration, with probability 1, the above described transitions. Therefore, Π reaches, with probability 1, the configuration that corresponds to the state of M after the instruction l _i has been executed.

• $l_i:({\tt SUB}(r_p),l_j,l_k)$ (non-deterministic sub)—module shown in Fig. 3. The execution of instruction l _i is simulated in Π in the following way. At time t + 1, neuron nl _i fires with probability 1 and one spike is added to neuron nr _p and one spike is added to both neurons l ¹ _i and l ² _i . Neuron l ¹ _i fires at time t + 2 with probability 1 and deposits one spike in neuron l ³ _i . Also, neuron l ² _i fires, with probability 1, at time t + 2 and deposits one spike in neuron l ⁴ _i . Which rules fires in neuron nr _p and at which time depends on the contents of the neuron at time t. There are the two possible cases.

  • (i) The number of spikes in neuron nr _p at time t is 0. Then, the forgetting rule $a \rightarrow \lambda; F_1(x)$ consumes the single spike present in the neuron, at time t + 2, with probability 1.

  • (ii) The number of spikes in neuron nr _p at time t is 2k with k > 0. Then, the rule $a(aa)^+ \rightarrow a; F_1(x)$ fires at time t + 2 with probability 1, depositing one spike in neuron l ³ _i .

  Notice that both rules present in neuron nr _p consume an odd number of spikes and then, once a rule is applied, no other rule in such neuron is enabled anymore.

  In the case (i) only one spike reaches neuron l ³ _i at time t + 2, and this spike is consumed, with probability 1, by using the forgetting rules, at time t + 3. Also, only one spike is deposited in neuron l ⁵ _i at time t + 3, which fires, with probability 1, at time t + 4 depositing one spike in neuron nl _k .

  In the case (ii), two spikes are deposited in neuron l ³ _i at time t + 2, which enable the rule $a^2\rightarrow a;F_1(x).$ Neuron l ³ _i then fires, with probability 1, at time t + 3, depositing one spike in neuron nl _j and one spike in neuron l ⁵ _i . Neuron l ⁵ _i has two spikes at time t + 3 which are consumed, with probability 1, by the forgetting rule $a^2 \rightarrow \lambda;F_1(x)$ at time t + 4.

  Starting from the supposed configuration Π can only execute, with probability 1, the above described transitions. Therefore, Π reaches, with probability 1, the configuration that corresponds to the state of M after the instruction l _i has been executed.

The execution of an instruction (${\tt ADD}$ or ${\tt SUB}$) in M followed by the ${\tt HALT}$ instruction is simulated in Π by simulating the corresponding instruction (${\tt ADD}$ or ${\tt SUB}$) as described above and then sending 1 spike to the neuron nl _h . By construction, neuron nl _h does not have any outgoing synapse to other neurons. Hence, the firing of its rule $a \rightarrow a;F_1(x)$ consumes the spike without sending any. Thus, also in this case Π halts in a configuration that correspond to the situation of M when the register machine halts.

From the above description, it is clear that Π can be composed using the presented modules in such a way that can simulate each computation of M and each computation in Π can be simulated in M. Therefore, the Theorem follows.

A remark concerns the dashed neurons shown in Figs. 1–3. They represent the neurons shared among the modules. In particular, this is true for the neurons corresponding to the registers of M. Each neuron nr _p , with $p \in \{2,3,\ldots,m\}$ subject of a ${\tt SUB}$ instruction sends a spike to several, possibly to all, neurons l ³ _i , i = 0,1, … ,n, but only one of these also receives at same time a spike from the corresponding neuron l ¹ _i . In all other cases, the other neurons forget the unique received spike.

A last comment closes the proof—it concerns the probabilities of the computations in Π. Each numbers $x \in N(\Uppi)$ is obtained with a probability p(x) greater than zero. However not all the numbers in N(Π) are obtained in Π with the same probability. Indeed, for every computation c in M such that Out(c) = x, there is a probability $2^{-u_{c}}$ that Π simulates exactly such computation where u _c is the number of non-deterministic ${\tt ADD}$ instructions executed in c. Therefore, the overall probability p _x is given by $\sum_{c\in M \vert Out(c)=x}2^{-u_{c}}.$

5 Experiments on the reliability of SSN P systems

The SSN P system Π constructed in the proof of Theorem 1 works correctly because of the appropriate choice of the probability distributions for the firing times associated to the rules in the neurons. In fact, the chosen distributions constrain the possible computations of Π in a way that the register machine M is able to simulate all the computations of Π and vice versa.

It was crucial in Theorem 1 that some of the chosen probability distributions had zero variance. It is interesting to understand what happens to the correctness of the computation when this is not true anymore. In other words, what happens if we use the modules defined in Theorem 1 but we select, for all of them, a value of σ² > 0? In informal words, this corresponds to increase the degree of non-synchronization in the constructed SSN P system: more variance is admitted for the distributions, more non-synchronous is the obtained system. As mentioned in the Introduction, in some cases asynchronous spiking neural P systems are not universal (Cavaliere et al. 2007b), so we conjecture that having distributions with non-zero variance makes more difficult (if not impossible) to simulate a register machine, with good “reliability”.

Therefore, from a computational point of view it is interesting to understand how the asynchrony present in the system influences its ability to correctly simulate a register machine. Moreover, considering distributions with non-zero variance is interesting also from a biological point of view: spiking in neurons is the result of biochemical reactions, which are inherently stochastic processes, hence they generally have a non-zero variance associated to their distributions.

As it has been shown in Theorem 1, by using σ² = 0, each of the considered SSN P modules simulates the corresponding register machine instruction. When σ² > 0 such an equivalence may not exists anymore, since the synchronization of the neurons in the modules is crucial. For example, consider the following transitions of the module corresponding to the deterministic ${\tt ADD}$ instruction, as shown in Fig. 1. Neurons l ¹ _i and l ² _i simultaneously receive 1 spike, but it may happen that the rule in l ¹ _i neuron fires at time t and the one in neuron l ² _i fires at time t + δ, where δ depends on σ² and may be large enough to make the two spikes in neuron nr _p to be consumed, one after the other, without actually increasing the number of spikes in neuron nr _p as it should be done for a proper simulation of the ${\tt ADD}$ instruction.

For an SSN P systems Π constructed as described in Theorem 1 we define the notion of correct simulation of a single instruction of the register machine M. We say that Π simulates correctly the instruction with label l _i of M (suppose that l _i is followed by the instruction with label l _j ) when the following thing is true. If Π starts from the configuration that corresponds to the configuration of M when instruction l _i is started, then Π executes a sequence of transitions that leads to the configuration of Π that corresponds to that of M after the instruction l _i has been executed and, during these transitions, the contents of all the neurons of Π, except nl _i and nl _j , have not been modified.

Let p _ADD , p _ADD–ND and p _SUB be the probability that Π simulates correctly a deterministic ${\tt ADD}$ instruction, a non-deterministic ${\tt ADD}$ instruction and the ${\tt SUB}$ instruction of M, respectively. Theorem 1 shows that, when σ² = 0 is used, we have that p _ADD , p _ADD–ND and p _SUB are all equal to 1. When σ² > 0, this is not true anymore. To quantitatively evaluate the effect of the variance σ² we have developed a simulator of SSN P systems, based on the Möbius modeling framework (Clark et al. 2001).

We report the outcome of simulation experiments conducted to evaluate probabilities p _ADD , p _ADD–ND and p _SUB when varying the variance σ² > 0. We present in Fig. 4 the obtained results for p _ADD , p _ADD–ND and p _SUB when σ² is varied in the range [0.01,0.1]. These probabilities have been computed with 10000 simulation batches for every value of σ², with confidence level of 95%. The width of the confidence intervals for the simulation results is in each case below 0.1%, too narrow to be shown in Fig. 4.

Fig. 4

Probabilities p _ADD , p _ADD–ND and p _SUB for values of σ² in [0.01,0.1]

To give a quantitative feeling to the reader, we underline this well-known fact: the probability that a random sample of a random variable distributed as N(μ,σ²) is far from μ more than σ is about 0.3, more than 2σ is about 0.05 and more than 3σ is about 0.003. For instance, when σ² = 0.1, a random sample drawn from distribution F ₁(x) will have probability 0.3 of being outside interval [0.7,1.3] and probability 0.05 of being outside interval [0.4,1.6]. Such variability brings asynchrony in the considered instruction modules and this makes possible many transitions, which would not occur if σ² = 0. Therefore, it is not surprising that probabilities p _ADD , p _ADD–ND and p _SUB decrease as σ² increases (as Fig. 4 shows).

From Fig. 4 it is also possible to observe that probabilities p _ADD , p _ADD–ND and p _SUB are close to 1 (i.e., the corresponding instructions are simulated correctly) when σ² takes values in the lower part of the considered range of variation. This result supports the idea that Π is able to simulate correctly, with high probability, long computations of the register machine M even for values of σ² > 0.

To understand more precisely how Π can simulate M in a reliable way, when a non-negative variance σ² is considered, we define a probability metric called the reliability of Π, which we use to characterize the ability of Π to compute correctly a number in Out(M).

The reliability of a system is defined as a function R(t), t ≥ 0, which expresses the probability that in the interval of time [0,t] the system has been working correctly, supposing that the system was working correctly at time t = 0 (this follows the standard definition of reliability. See, e.g., Laprie 1995). The definition of the correct behavior of the system has to be given with reference to a specification of the system, or alternatively can be given with respect to another system, which is assumed to be always correct. We choose the second approach: In what follows, we shall evaluate the reliability of the SSN P system Π (when varying σ²) by comparing the sequences of transitions performed by Π against the ones that are performed by a register machine M.

Precisely, we define the reliability R ^M_Π (n) as the probability that Π simulates correctly a sequence of n instructions executed by M, when M starts from the initial configuration and Π starts from the corresponding one.

In what follows we experiment on a particular SSN P system (and on a particular computed set of numbers) how the variance of firing rules distribution times systems affects the reliability. For this purpose we consider the set of natural numbers $Pow2= \{n \vert n = 2^m, m \geq 0 \}$ that is the set of natural numbers that are power of 2 (actually, Pow2 is also a non-semilinear set of natural numbers). The set Pow2 can be computed, for instance, by the register machine $M^{\prime}=(2, \{l_0, l_1, \ldots, l_8, l_h\},l_0, l_h, I),$ which moves the contents of register 1 to register 2 and back, and, in this latter steps, doubles the contents; ${\tt ADD}$ with label l ₁ is a “dummy” instruction, used only for the non-deterministic choice between continuation of the computation or halting: the object added is, in fact, subtracted again in the ${\tt SUB},$ at l ₂ or l ₈.Instructions I are the following ones:

• l ₀: $({\tt ADD}(r_1),l_1,l_1)$

• l ₂: $({\tt SUB}(r_1),l_3,l_3)$

• l ₄: $({\tt ADD}(r_2),l_3,l_3)$

• l ₅: $({\tt SUB}(r_2),l_6,l_1)$

• l ₆: $({\tt ADD}(r_1),l_7,l_7)$

• l ₇: $({\tt ADD}(r_1),l_5,l_5)$

• l ₈: $({\tt SUB}(r_1),l_h,l_h)$

• l _h : $({\tt HALT})$

Let Π be the SSN P system that corresponds to M, built as described in Theorem 1, using the modules presented in Figs. 1–3 and having σ² > 0.

We evaluate the function $R^{M^{\prime}}_{\Uppi}(n)$ by using simulations for values of σ² close to 0.01. We show in Fig. 5 the simulation results, which were computed with 100000 batches of simulation for each considered value of σ², with a confidence level of 95%. The width of confidence intervals is within 5% of the estimated values (they are not shown in Fig. 5 for the sake of clarity).

Fig. 5

Reliability function $R^{M^{\prime}}_{\Uppi}(n)$ for different values of σ²

The reliability functions plotted in Fig. 5 show that, as σ² increases, Π has higher and higher probability of performing incorrect simulations. However, for σ² = 0.01, the probability that Π is able to simulate correctly computations of M′ composed by 15.000 instructions is still quite high, 0.9. For such value of σ², the value of the reliability function at n = 1000 is of about 0.996. This means that, if we restrict our attention to the computations of M′ that are composed by less than 1000 instructions and consider σ² = 0.01, then we observe that Π can simulate correctly these computations with probability 0.996.

We can also use the above described procedure to design systems with arbitrary reliability. In fact, constructing an opportune Fig. 5, one can identify, for an arbitrary register machine M, the maximal value of σ² for which is possible to construct, using the approach given in Theorem 1, an SSN P system Π with a reliability R ^M _Π(n) that is at least k, with k an arbitrarily chosen constant 0 ≤ k ≤ 1.

Finally, it is important to mention that, for a given register machine M, several equivalent SSN P systems can be constructed, using different constructions (Theorem 1 shows only one of them). These SSN P systems, even equivalent from a computational point of view, can have very different reliability. A way to get different SSN P systems, with different reliability, is, for instance, to construct different modules to simulate the register machine instructions.

For instance, consider the module shown in Fig. 6, for which we define F ₁(x) = N(1,σ²). It is easy to check that, when σ² = 0, the module shown in Fig. 6 (we call it ADD2) is equivalent to the module shown in Fig. 1 (we call it ADD). In fact, both of them, for σ² = 0, simulate correctly the (deterministic) ${\tt ADD}$ instruction of the register machine.

Fig. 6

An alternative SSN P module $l_i:({\tt ADD}(r_p),l_j,l_j)$

However, having an intermediate neuron makes the module in Fig. 6 more reliable than the module in Fig. 1. We can check that by calculating, using the above described procedure, p _ADD2. This is clear from the comparison between p _ADD and p _ADD2 presented in Fig. 7.

Fig. 7

Probabilities p _ADD and p _ADD2 for values of σ² in [0.01,0.1]

6 Perspectives

Constructing reliable and powerful computational devices by combining several simple (bio-inpired) units has been studied intensively in computer science, starting from classical cellular automata. Recently, several researchers are investigating the possibility of constructing fault-tolerant systems, especially computer architectures and software by using ideas coming from nanotechnology and from biological processes (see, e.g., Heath et al. 1998).

In our case, we have investigated, in the framework of SN P systems, a kind of fault-tolerance that concerns the possibility to obtain powerful (universal) computing devices, when using computational units that are simple and non-synchronized. We have defined a stochastic version of SN P systems (SSN P system) where to each rule is associated a stochastic “waiting” time and we have presented a preliminary study that shows how the degree of asynchrony (expressed as variance) among the neurons can influence the ability of an SSN P systems to simulate/execute in a reliable way the program of a register machine.

The topic is very general and several lines of research can be followed. The most interesting one concerns the possibility to implement powerful computing devices (possibly, universal) using SSN P systems having a high degree of asynchrony, i.e., with distributions associated to the firing times with an high variance. When is this possible? What is the price to pay for that? An important question that we have not answered in the paper is the following one. Can the topology of the network influence the reliability of the constructed system? (in this case one may find motivations and inspirations from the topology of the real networks of neurons). Another relevant question: Can the redundancy (i.e., number of neurons and connections) help in obtaining more reliable systems? This appears to be true, at least in view of the better reliability (Fig. 7) of the module presented in Fig. 6 compared to that of the module shown in Fig. 1. How much redundancy can help and what is the best way to use redundancy? In this respect we expect to find classes of SSN P systems, with large asynchrony, where it is possible to encode arbitrarily long computations, with arbitrarily small error, by using an unbounded number of neurons (for instance, by following the approaches proposed in Soloveichik et al. (2008), Zavattaro and Cardelli (2008) where reliable computations have been encoded using chemistry).

Another line of research concerns the study of class of SSN P system where reliability can be analytically investigated. For instance, in case of exponential distributions, one should be able to construct an equivalent Markov chain and then studying in an analytical manner the reliability of the system. Are there other cases where this is possible? In general, as seen in Sect. 5, there is a link between the type of transitions executed and the reliability of the system (not all transitions are equally relevant/dangerous for the reliability of an SSN P system). Is there a possibility to limit the number of certain type of transitions? (this is, of course, very much linked to the number of minimal instructions of a certain type that one has to use in a register machine program—hence one may find links between reliability and Kolmogorov complexity).