The weighted Moore–Penrose generalized inverse and the force analysis of overconstrained parallel mechanisms

Abstract

This paper reveals the relationship between the weighted Moore–Penrose generalized inverse and the force analysis of overconstrained parallel mechanisms (PMs), including redundantly actuated PMs and passive overconstrained PMs. The solution for the optimal distribution of the driving forces/torques of redundantly actuated PMs is derived in the form of a weighted Moore–Penrose inverse. Therefore, different force distributions can be achieved simply by changing the value of the weighted factor matrix in terms of different optimization goals, and this approach greatly improves computational efficiency in solving such problems. In addition, the explicit expression is deduced between the weighted Moore–Penrose generalized inverse and the constraint wrenches solution of general passive overconstrained PMs (in which each supporting limb may supply single or multiple constraint wrenches). In this expression, the weighted factor matrix is composed of the stiffness matrices of each limb’s constraint wrenches. As numerical examples, the driving forces/torques or the constraint forces/couples for two kinds of overconstrained PMs are solved directly by the weighted Moore–Penrose generalized inverse. The verification results show the correctness of the relationship obtained in this paper between the weighted Moore–Penrose generalized inverse and the force analysis of overconstrained PMs. Using the Moore–Penrose generalized inverse to solve the driving forces/torques or constraint forces/couples of overconstrained PMs provides solutions of a unified, simple form and improves computational efficiency.

1 Introduction

The overconstrained parallel mechanism (PM) is a special kind of PM that can be divided into two categories, based on the characteristics of its constraints. One category is the redundantly actuated PM, which has more driving joints than its degrees of freedom (DOFs). This type of PM has the advantages of avoiding kinematic singularities [1, 2], increasing load capability [3] and improving dynamic characteristics [4]. The other category is the passive overconstrained PM, which contains common constraints or redundant constraints [5–7]. This kind of PM has the advantages of simple structure, high rigidity, high accuracy, and high load-carrying capacity [8]. The overconstrained PMs have recently been investigated and applied ever more extensively.

With actuation redundancy, the optimal distribution of all driving forces/torques for a redundantly actuated PM is difficult to identify. Most studies on this problem have obtained the optimal force distribution by establishing a specific optimization goal and then combining this goal with a force/torque equilibrium equation. For example, Zheng et al. [9] discussed the optimal load distribution algorithms for two coordinating industrial robots that were handling a single object, and these researchers selected the least energy consumption and the minimum exerted force on the object as their optimization goals. Gardner et al. [10] introduced the partitioned actuator set control method, which offers superior traction performance for the system. They used this method to solve the force distribution of redundantly actuated robotic systems with closed kinematic chains. Nahon et al. [11] regarded mechanical hands as redundantly actuated kinematic chains (when they are grasping an object). These authors used a quadratic-programming approach to solve the dynamic forces of the mechanical hands with the minimum internal force as their optimization goal. Gao et al. [12] proposed a generalized stiffness matrix method that included all of the major system compliances to solve the force distribution of walking machines or multi-fingered grippers, and their results satisfied the material deformation laws. Huang et al. [13] and Zhao et al. [14] proposed the weighted coefficient method to solve the optimal distribution of the over-determinate inputs for walking machines. In addition, based on a decomposition of the task, constraint and posture space, Sapio et al. [15] presented a novel approach to effectively address the motion control of holonomically constrained multibody systems, which allows for the simultaneous specification of desired constraint forces. To sum up, none of the above studies have investigated the explicit relationship between the weighted Moore–Penrose inverse [16] and the driving forces/torques solution of redundantly actuated PMs obtained on the basis of differing optimization goals. Although the weighted generalized inverse has been applied in kinematics and statics of robots [17, 18], its direct application in the dynamics of redundantly actuated PMs has not yet been reported.

In this paper, we derive the explicit relationship between the weighted Moore–Penrose generalized inverse and the driving forces/torques solution of redundantly actuated PMs on the basis of the [13, 14]. With this relationship, we can directly apply the weighted Moore–Penrose generalized inverse to solve the force distribution of redundantly actuated PMs.

Some investigations have carried out force analyses of passive overconstrained PMs. Force analysis of a PM with US- and UPS-type limbs (U, P and S represent the universal, prismatic and spherical joints, respectively) was carried out by Vertechy et al. [19]. Wojtyra [20] used three different techniques of Jacobian matrix analysis to detect constraints and joints for which reactions can be uniquely determined despite the existence of redundant constraints. Afterwards, Wojtyra et al. [21] discussed which parts of the overconstrained mechanism should be modeled as flexible bodies to obtain a unique set of all-joint reactions. Huang et al. [22] analyzed the kinetostatics of the 4-R(CRR) overconstrained PM (with R and C representing the revolute joint and the cylindrical joint, respectively) on the basis of reciprocal screw theory. Bi et al. [23] established a complete and solvable dynamic model of an overconstrained PM by combining the Newton–Euler formation with the compliance conditions. Gallardo et al. [24] performed the dynamic analysis of a 2-DOF parallel spherical mechanism on the basis of screw theory and the principle of virtual work. Yao et al. [25] solved the force distribution problem of a statically indeterminate 6-axis force sensor. Wang et al. [26] solved the force analysis of a fully pre-stressed 6-axis force/torque sensor with dual layers. Kerr et al. [27] solved the problem of grasping a rigid object with a hand that has redundant grasping contacts by taking into account the compliance at each contact point. Besides, Neto et al. [28] discussed several different methodologies to handle the constraint violation correction or their stabilization and the existence of redundant constraints during the solution of the dynamic and kinematic analysis of multibody systems. Among these methods, the Moore–Penrose generalized inverse can be used to handle the existence of redundant constraints. However, the above-mentioned studies did not involve the weighted Moore–Penrose generalized inverse in the process of force analysis of general passive overconstrained PMs, except for [26, 27], both of which studied special overconstrained PMs. In these special PMs, each supporting limb supplies only an axial constraint force to the moving platform, and the analysis of such PMs is relatively easy.

Therefore, in this paper we investigate the application of the weighted Moore–Penrose generalized inverse in the force analysis of general passive overconstrained PMs, in which the supporting limbs may supply multiple constraint forces/couples, and not only an axial constraint force.

The remainder of this paper is organized as follows. The relationship between the weighted Moore–Penrose generalized inverse and the optimal force distribution of redundantly actuated PMs is explored in Sect. 2. A numerical example is given to verify the correctness of using the weighted Moore–Penrose generalized inverse in redundantly actuated PMs. In Sect. 3, we demonstrate the application of the weighted Moore–Penrose generalized inverse in the force analysis of general passive overconstrained PMs. In Sect. 4, we discuss the commonalities and differences between applications of the weighted Moore–Penrose generalized inverse in the force analysis of redundantly actuated PMs and in the analysis of passive overconstrained PMs. Finally, some concluding remarks are summarized in Sect. 5.

2 Relationship between the weighted Moore–Penrose generalized inverse and the force analysis of redundantly actuated PMs

In this section, the explicit relationship between the weighted Moore–Penrose generalized inverse and the optimal driving force/torque distribution of redundantly actuated PMs is revealed on the basis of [13, 14].

2.1 Derivation of the solution for the force distribution of redundantly actuated PMs in the form of the weighted Moore–Penrose generalized inverse

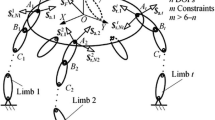
A 6-legged walking machine [13], as shown in Fig. 1, whose main body is supported by at least three legs while moving, can be regarded as a PM composed of three or more supporting limbs (legs), a moving platform (the main body) and a base (the ground). Each leg consists of three links connected to each other and to the main body by revolute joints. The contacting relation between each foot and the ground can be regarded as a spherical joint. Then, the joints of each leg from the ground to the main body are denoted as joints 1, 2, 3, and 4, respectively. The main body has six DOFs, and each leg contains three actuated revolute joints (joints 2, 3 and 4). Therefore, the total number of actuated joints is greater than the DOFs of the machine’s body. For this 6-legged walking machine, the PM (which is composed of the supporting legs, the main body and the ground) is redundantly actuated.

Fig. 1

Schematic diagram of a 6-legged walking machine

The dynamic equilibrium equation of a redundantly actuated 6-legged walking machine with $n$ ($3 \le n \le 6$) legs contacting the ground at any one moment is as follows [13, 14]:

$$ \bigl[ \boldsymbol{G}_{q}^{p} \bigr]^{\mathrm{T}} \{ \boldsymbol{F}_{p} \} + \sum_{r = 1}^{n} \Biggl( \bigl[ \boldsymbol{g}_{q}^{\phi} \bigr]^{\mathrm{T}(r)} \{ \boldsymbol{T}_{\phi} \}^{(r)} + \sum _{m = 3}^{5} \bigl[ \boldsymbol{G}_{q}^{m} \bigr]^{\mathrm{T} ( r )} \{ \boldsymbol{F}_{m} \}^{ ( r )} \Biggr) = \{ \boldsymbol{0} \} $$

(1)

where $\{ \boldsymbol{T}_{\phi} \}^{(r)}$ is a 6-dimensional column vector composed of the input torques (i.e., driving torques) of the $r$th leg, with the first three components being zero since they denote the input torques of the inactive spherical joint, and with the last three components representing the input torques of the actuated joints 2, 3, 4 within the same leg in sequence. $[ \boldsymbol{G}_{q}^{m} ]^{ ( r )}$ and $[ \boldsymbol{G}_{q}^{p} ]$ are the Jacobian matrices of generalized joint coordinates to the coordinate frames which are fixed with the $r$th supporting leg’s $m$th link and are fixed with the body, respectively. $[ \boldsymbol{g}_{q}^{\phi} ]^{ ( r )}$ is defined as the Jacobian matrix for four joints of the $r$th leg with respect to the six generalized joint coordinates. $\{ \boldsymbol{F}_{p} \}$ and $\{ \boldsymbol{F}_{m} \}^{ ( r )}$ are the 6-component force vectors composed of external loads, weight and inertia forces, which act on the main body and on the $m$th link of the $r$th leg, respectively.

It is assumed that there are no mutual effects among the actuated joints, i.e., they are considered to be independent of each other. Then, to obtain the optimal distribution of input torques for a redundantly actuated walking machine, the objective function of optimization (as selected by the authors of [13, 14]) is as follows:

$$ \boldsymbol{f}_{\mathrm{obj}} = \sum_{h = 1}^{6} T_{Qh}^{2} A_{Qh} + \sum _{j = 1}^{k} T_{sj}^{2} A_{sj} $$

(2)

where $T_{Qh}$ ($h = 1,2, \ldots, 6$) represents the $h$th generalized input torque, i.e., the $h$th non-redundant driving torque, $T_{sj}$ ($j = 1,2, \ldots ,k$) represents the $j$th non-generalized input torque, i.e., the $j$th redundant driving torque, and $A_{Qh}$ and $A_{sj}$ are positive weighted coefficients which can be given different values in terms of different objective functions. For example, if $A_{Qh} = 1$ and $A_{sj} = 1$, the objective function (2) means the minimization of the driving torques of the motors, and if $A_{Qh} = \dot{q}_{h}^{2}$ and $A_{sj} = \dot{q}_{j}^{2}$, the objective function (2) means the minimization of the energy of the motors, in which $\dot{q}_{h}$ and $\dot{q}_{j}$ represent the driving velocities of the $h$th non-redundantly actuated joint and the $j$th redundantly actuated joint, respectively.

Rearranging Eq. (2) in matrix form yields

$$ \boldsymbol{f}_{\mathrm{obj}} = \{ \boldsymbol{T}_{Q} \}^{\mathrm{T}} [ \boldsymbol{A}_{Q} ] \{ \boldsymbol{T}_{Q} \} + \{ \boldsymbol{T}_{s} \}^{\mathrm{T}} [ \boldsymbol{A}_{s} ] \{ \boldsymbol{T}_{s} \} $$

(3)

where

$$\begin{aligned} & \{ \boldsymbol{T}_{Q} \} = \begin{pmatrix} T_{Q1} & T_{Q2} & \cdots & T_{Q6} \end{pmatrix} ^{\mathrm{T}}, \qquad \{ \boldsymbol{T}_{s} \} = \begin{pmatrix} T_{s1} & T_{s2} & \cdots & T_{sk} \end{pmatrix} ^{\mathrm{T}}, \\ & [ \boldsymbol{A}_{Q} ] = \begin{pmatrix} A_{Q1} & 0 & 0 & 0 \\ 0 & A_{Q2} & 0 & 0 \\ 0 & 0 & \ddots & 0 \\ 0 & 0 & 0 & A_{Q6} \end{pmatrix}, \qquad [ \boldsymbol{A}_{s} ] = \begin{pmatrix} A_{s1} & 0 & 0 & 0 \\ 0 & A_{s2} & 0 & 0 \\ 0 & 0 & \ddots & 0 \\ 0 & 0 & 0 & A_{sk} \end{pmatrix}, \end{aligned}$$

and both $[ \boldsymbol{A}_{Q} ]$ and $[ \boldsymbol{A}_{s} ]$ are positive definite matrices that are recognized as the weighted factor matrices.

For this situation, the general expression of the weighted optimization distribution of $\{ \boldsymbol{T}_{s} \}$ was derived under the constraint condition in Eq. (1) as follows [13, 14]:

$$ \{ \boldsymbol{T}_{s} \} = - \bigl( [ \boldsymbol{A}_{s} ] + \bigl[ \boldsymbol{g}_{q}^{\phi} \bigr] [ \boldsymbol{A}_{Q} ] \bigl[ \boldsymbol{g}_{q}^{\phi} \bigr]^{\mathrm{T}} \bigr)^{ - 1} \bigl[ \boldsymbol{g}_{q}^{\phi} \bigr] [ \boldsymbol{A}_{Q} ] \Biggl( \sum _{r = 1}^{n} \sum_{m = 3}^{5} \bigl[ \boldsymbol{G}_{q}^{m} \bigr]^{\mathrm{T} ( r )} \{ \boldsymbol{F}_{m} \}^{ ( r )} + \bigl[ \boldsymbol{G}_{q}^{p} \bigr]^{\mathrm{T}} \{ \boldsymbol{F}_{p} \} \Biggr). $$

(4)

In addition, the relationship between $\{ \boldsymbol{T}_{Q} \}$ and $\{ \boldsymbol{T}_{s} \}$, for which the details are explained in [13, 14], is derived from Eq. (1) as

$$ \{ \boldsymbol{T}_{Q} \} = - \Biggl( \sum _{r = 1}^{n} \sum_{m = 3}^{5} \bigl[ \boldsymbol{G}_{q}^{m} \bigr]^{\mathrm{T} ( r )} \{ \boldsymbol{F}_{m} \}^{ ( r )} + \bigl[ \boldsymbol{G}_{q}^{p} \bigr]^{\mathrm{T}} \{ \boldsymbol{F}_{p} \} + \bigl[ \boldsymbol{g}_{q}^{\phi} \bigr]^{\mathrm{T}} \{ \boldsymbol{T}_{s} \} \Biggr). $$

(5)

The above equation can be rearranged as

$$ \sum_{r = 1}^{n} \sum _{m = 3}^{5} \bigl[ \boldsymbol{G}_{q}^{m} \bigr]^{\mathrm{T} ( r )} \{ \boldsymbol{F}_{m} \}^{ ( r )} + \bigl[ \boldsymbol{G}_{q}^{p} \bigr]^{\mathrm{T}} \{ \boldsymbol{F}_{p} \} = - \bigl( \{ \boldsymbol{T}_{Q} \} + \bigl[ \boldsymbol{g}_{q}^{\phi} \bigr]^{\mathrm{T}} \{ \boldsymbol{T}_{s} \} \bigr) $$

(6)

which can be further rewritten as

$$ \boldsymbol{F} = - \begin{pmatrix} \boldsymbol{I} & [ \boldsymbol{g}_{q}^{\phi} ]^{\mathrm{T}} \end{pmatrix} \begin{pmatrix} \{ \boldsymbol{T}_{Q} \} \\ \{ \boldsymbol{T}_{s} \} \end{pmatrix} = - \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}}\boldsymbol{f} $$

(7)

where $\boldsymbol{F} = \sum_{r = 1}^{n} \sum_{m = 3}^{5} [ \boldsymbol{G}_{q}^{m} ]^{\mathrm{T} ( r )} \{ \boldsymbol{F}_{m} \}^{ ( r )} + [ \boldsymbol{G}_{q}^{p} ]^{\mathrm{T}} \{ \boldsymbol{F}_{p} \}$, $\boldsymbol{f} = ( \{ \boldsymbol{T}_{Q} \} \ \{ \boldsymbol{T}_{s} \} )^{\mathrm{T}}$, and $\boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} = ( \boldsymbol{I} \ [ \boldsymbol{g}_{q}^{\phi} ]^{\mathrm{T}} )$ with full row-rank.

Substituting Eq. (4) into Eq. (5) yields

$$ \{ \boldsymbol{T}_{Q} \} = - \bigl( \boldsymbol{I} - \bigl[ \boldsymbol{g}_{q}^{\phi} \bigr]^{\mathrm{T}} \bigl( [ \boldsymbol{A}_{s} ] + \bigl[ \boldsymbol{g}_{q}^{\phi} \bigr] [ \boldsymbol{A}_{Q} ] \bigl[ \boldsymbol{g}_{q}^{\phi} \bigr]^{\mathrm{T}} \bigr)^{ - 1} \bigl[ \boldsymbol{g}_{q}^{\phi} \bigr] [ \boldsymbol{A}_{Q} ] \bigr)\boldsymbol{F}. $$

(8)

Rearranging Eq. (4) and Eq. (8), we can get

$$ \boldsymbol{f} = - \begin{pmatrix} \boldsymbol{I} - [ \boldsymbol{g}_{q}^{\phi} ]^{\mathrm{T}} ( [ \boldsymbol{A}_{s} ] + [ \boldsymbol{g}_{q}^{\phi} ] [ \boldsymbol{A}_{Q} ] [ \boldsymbol{g}_{q}^{\phi} ]^{\mathrm{T}} )^{ - 1} [ \boldsymbol{g}_{q}^{\phi} ] [ \boldsymbol{A}_{Q} ] \\ ( [ \boldsymbol{A}_{s} ] + [ \boldsymbol{g}_{q}^{\phi} ] [ \boldsymbol{A}_{Q} ] [ \boldsymbol{g}_{q}^{\phi} ]^{\mathrm{T}} )^{ - 1} [ \boldsymbol{g}_{q}^{\phi} ] [ \boldsymbol{A}_{Q} ] \end{pmatrix} \boldsymbol{F} = - \boldsymbol{W}' \boldsymbol{F} $$

(9)

where

$$\boldsymbol{W}' = \begin{pmatrix} \boldsymbol{I} - [ \boldsymbol{g}_{q}^{\phi} ]^{\mathrm{T}} ( [ \boldsymbol{A}_{s} ] + [ \boldsymbol{g}_{q}^{\phi} ] [ \boldsymbol{A}_{Q} ] [ \boldsymbol{g}_{q}^{\phi} ]^{\mathrm{T}} )^{ - 1} [ \boldsymbol{g}_{q}^{\phi} ] [ \boldsymbol{A}_{Q} ] \\ ( [ \boldsymbol{A}_{s} ] + [ \boldsymbol{g}_{q}^{\phi} ] [ \boldsymbol{A}_{Q} ] [ \boldsymbol{g}_{q}^{\phi} ]^{\mathrm{T}} )^{ - 1} [ \boldsymbol{g}_{q}^{\phi} ] [ \boldsymbol{A}_{Q} ] \end{pmatrix}. $$

To reveal the relationship between the weighted Moore–Penrose generalized inverse and the force analysis of the redundantly actuated PMs, we introduce the following definition and theorem.

Definition

[16, 29, 30]

Let $\boldsymbol{A} \in \mathbb{C}^{m \times n}$ be of rank $r$, $\boldsymbol{M}$ and $\boldsymbol{N}$ be positive definite Hermite matrices of orders $m$ and $n$, respectively. Then, the unique matrix $\boldsymbol{X} \in \mathbb{C}^{n \times m}$ that satisfies the following four conditions

$$ \begin{aligned}[c] &(\mbox{a})\quad \boldsymbol{AXA} = \boldsymbol{A}, \qquad (\mbox{b})\quad \boldsymbol{XAX} = \boldsymbol{X}, \qquad (\mbox{c})\quad ( \boldsymbol{MAX} )^{*} = \boldsymbol{MAX}, \\ &(\mbox{d})\quad ( \boldsymbol{NXA} )^{*} = \boldsymbol{NXA} \end{aligned} $$

(10)

is called the weighted Moore–Penrose generalized inverse of the matrix $A$, and is denoted by $\boldsymbol{X} = \boldsymbol{A}_{\boldsymbol{MN}}^{ +}$.

The $\boldsymbol{A}_{\boldsymbol{MN}}^{ +}$ is unique and can be calculated by [29, 31]

$$ \boldsymbol{A}_{\boldsymbol{MN}}^{ +} = \boldsymbol{N}^{ - \frac{1}{2}} \bigl( \boldsymbol{M}^{\frac{1}{2}}\boldsymbol{AN}^{ - \frac{1}{2}} \bigr)^{ +} \boldsymbol{M}^{\frac{1}{2}} $$

(11)

where the superscripts “$\frac{1}{2}$” and “$- \frac{1}{2}$” denote the square root and the inverse square root of a given matrix, respectively. A simple method to calculate the square root and the inverse square root of a positive definite matrix is provided in the Appendix.

Besides, the $\boldsymbol{A}_{\boldsymbol{MN}}^{ +}$ can also be obtained by [18, 30]

$$ \boldsymbol{A}_{\boldsymbol{MN}}^{ +} = \boldsymbol{N}^{ - 1} \boldsymbol{C}^{ *} \bigl( \boldsymbol{CN}^{ - 1} \boldsymbol{C}^{ *} \bigr)^{ - 1} \bigl( \boldsymbol{B}^{ *} \boldsymbol{MB} \bigr)^{ - 1}\boldsymbol{B}^{ *} \boldsymbol{M} $$

(12)

where $\boldsymbol{A} = \boldsymbol{BC}$ is a full-rank factorization of $\boldsymbol{A}$, in which $\boldsymbol{B} \in \mathbb{C}^{m \times r}$ has full column-rank, $\boldsymbol{C} \in \mathbb{C}^{m \times r}$ has full row-rank.

Theorem

[16]

Let $\boldsymbol{A} \in \mathbb{C}^{m \times ( r + p )}$, $\boldsymbol{A} = [ \boldsymbol{U}\ \boldsymbol{V} ]$, where $\boldsymbol{U} \in \mathbb{C}^{m \times r}$ and $\boldsymbol{V} \in \mathbb{C}^{m \times p}$ consist of the first r columns and the last $p$ columns of $\boldsymbol{A}$, respectively. Assume that $\boldsymbol{N}$ is an $( r + p ) \times ( r + p )$ positive definite matrix. If $\boldsymbol{N}$ is partitioned as $\boldsymbol{N} = \bigl( {\scriptsize\begin{matrix}{} \boldsymbol{N}_{r} & \boldsymbol{L} \cr \boldsymbol{L}^{*} & \boldsymbol{N}_{p} \end{matrix}} \bigr)$, then the weighted Moore–Penrose generalized inverse of the partitioned matrix $\boldsymbol{A}$ is

$$ \boldsymbol{A}_{\boldsymbol{M},\boldsymbol{N}}^{ +} = \begin{pmatrix} \boldsymbol{U}_{\boldsymbol{M},\boldsymbol{N}r}^{ +} ( \boldsymbol{I} - \boldsymbol{VH} ) - ( \boldsymbol{I} - \boldsymbol{U}_{\boldsymbol{M},\boldsymbol{N}r}^{ +} \boldsymbol{U} )\boldsymbol{N}_{r}^{ - 1}\boldsymbol{LH} \\ \boldsymbol{H} \end{pmatrix} $$

(13)

where

$$\begin{aligned} \boldsymbol{H} &= \boldsymbol{C}_{\boldsymbol{M},\boldsymbol{K}1}^{ +} + \bigl( \boldsymbol{I} - \boldsymbol{C}_{\boldsymbol{M},\boldsymbol{N}r}^{ +} \boldsymbol{C} \bigr)\boldsymbol{K}_{1}^{ - 1} \bigl( \boldsymbol{D}^{*} \boldsymbol{N}_{r} - \boldsymbol{L}^{*} \bigr) \boldsymbol{U}_{\boldsymbol{M},\boldsymbol{N}r}^{ +}, \\ \boldsymbol{C}& = \bigl( \boldsymbol{I} - \boldsymbol{UU}_{\boldsymbol{M},\boldsymbol{N}r}^{ +} \bigr)\boldsymbol{V}, \\ \boldsymbol{D} &= \boldsymbol{U}_{\boldsymbol{M},\boldsymbol{N}r}^{ +} \boldsymbol{V}, \\ \boldsymbol{K}_{1} &= \boldsymbol{N}_{p} + \boldsymbol{D}^{*}\boldsymbol{N}_{r}\boldsymbol{D} - \bigl( \boldsymbol{D}^{*}\boldsymbol{L} + \boldsymbol{L}^{*} \boldsymbol{D} \bigr) - \boldsymbol{L}^{*} \bigl( \boldsymbol{I} - \boldsymbol{U}_{\boldsymbol{M},\boldsymbol{N}r}^{ +} \boldsymbol{U} \bigr) \boldsymbol{N}_{r}^{ - 1}\boldsymbol{L}, \end{aligned}$$

and $\boldsymbol{M}$ is a $m \times m$ positive definite matrix.

In view of the expression of $\boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}}$ as shown in Eq. (7), let $\boldsymbol{U} = \boldsymbol{I}$, $\boldsymbol{V} = [ \boldsymbol{g}_{q}^{\phi} ]^{\mathrm{T}}$ and select $\boldsymbol{N} = \boldsymbol{W} = \bigl( {\scriptsize\begin{matrix}{} [ \boldsymbol{A}_{Q} ] & \boldsymbol{0} \cr \boldsymbol{0} & [ \boldsymbol{A}_{s} ] \end{matrix}} \bigr)$. Thus, $\boldsymbol{N}_{r} = [ \boldsymbol{A}_{Q} ]$, $\boldsymbol{N}_{p} = [ \boldsymbol{A}_{s} ]$ and $\boldsymbol{L} = \boldsymbol{0}$. In addition, for the redundantly actuated walking machine, Eq. (7) is a compatible equation, so we let $\boldsymbol{M} = \boldsymbol{I}$. Then, substituting these matrices into the above theorem, it can be found that the matrix $\boldsymbol{W}'$ is just the $\boldsymbol{W}$-weighted Moore–Penrose generalized inverse of the partitioned force Jacobian matrix $\boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}}$.

Therefore, the optimal distribution of all driving torques of a 6-legged walking machine can be solved directly using the $\boldsymbol{W}$-weighted Moore–Penrose generalized inverse of the partitioned force Jacobian matrix $\boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}}$, with $\boldsymbol{W} = \bigl( {\scriptsize\begin{matrix}{} [ \boldsymbol{A}_{Q} ] & \boldsymbol{0} \cr \boldsymbol{0} & [ \boldsymbol{A}_{s} ]\end{matrix}} \bigr)$ as the weighted factor matrix.

Considering that $\boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}}$ is a full row-rank matrix, its $\boldsymbol{W}$-weighted Moore–Penrose generalized inverse has the following general expression, regardless of whether $\boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}}$ is partitioned:

$$\begin{aligned} \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \bigr)_{\boldsymbol{W}}^{ +} &= \boldsymbol{W}^{ - \frac{1}{2}} \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \boldsymbol{W}^{ - \frac{1}{2}} \bigr)^{ +} = \boldsymbol{W}^{ - \frac{1}{2}} \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}}\boldsymbol{W}^{ - \frac{1}{2}} \bigr)^{\mathrm{T}} \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \boldsymbol{W}^{ - \frac{1}{2}} \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \boldsymbol{W}^{ - \frac{1}{2}} \bigr)^{\mathrm{T}} \bigr)^{ -} \\ &= \boldsymbol{W}^{ -} \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \bigr)^{\mathrm{T}} \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \boldsymbol{W}^{ -} \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \bigr)^{\mathrm{T}} \bigr)^{ -}. \end{aligned}$$

(14)

Therefore, the general expression of the optimal distribution for all input torques of a walking machine, as shown in Eq. (9), can be rewritten in the following form:

$$ \boldsymbol{f} = - \boldsymbol{W}'\boldsymbol{F} = - \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \bigr)_{\boldsymbol{W}}^{ +} \boldsymbol{F} = - \boldsymbol{W}^{ -} \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \bigr)^{\mathrm{T}} \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \boldsymbol{W}^{ -} \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \bigr)^{\mathrm{T}} \bigr)^{ -} \boldsymbol{F}. $$

(15)

When taking the elastic deformations of input joints into consideration, we should select the total elastic potential energy of the walking machine as the objective function of optimization [26, 27] as follows:

$$ \boldsymbol{f}_{\mathrm{obj}} = \frac{1}{2} \Biggl( \sum _{h = 1}^{6} k_{Qh}\delta_{Qh}^{2} + \sum_{j = 1}^{k} k_{sj} \delta_{sj}^{2} \Biggr) $$

(16)

where $k_{Qh}$ ($h = 1,2, \ldots ,6$) and $k_{sj}$ ($j = 1,2, \ldots, k$) represent the actuated stiffness of the generalized joints and the non-generalized joints, respectively; $\delta_{Qh}$ and $\delta_{sj}$ represent the elastic deformation of the generalized joints and the non-generalized joints, respectively. Therefore, $k_{Qh}$ and $\delta_{Qh}$, $k_{sj}$ and $\delta_{sj}$ satisfy the following equations:

$$ \delta_{Qh} = T_{Qh}/k_{Qh}\quad \mbox{and}\quad \delta_{sj} = T_{sj}/k_{sj}. $$

(17)

Substituting Eq. (17) into Eq. (16), we obtain

$$ \boldsymbol{f}_{\mathrm{obj}} = \frac{1}{2} \Biggl( \sum _{h = 1}^{6} T_{Qh}^{2} k_{Qh}^{ - 1} + \sum_{j = 1}^{k} T_{sj}^{2} k_{sj}^{ - 1} \Biggr). $$

(18)

Comparing Eq. (18) and Eq. (2), we find that the only difference between these two equations is that $A_{Qh}$ and $A_{sj}$ in Eq. (2) are replaced by $k_{Qh}^{ - 1}$ and $k_{sj}^{ - 1}$ in Eq. (18), and thus the optimal distribution of all actuated torques can be obtained with the minimum elastic potential energy of the whole machine by Eq. (15), where

$$ \begin{aligned}[c] &\boldsymbol{W} = \begin{pmatrix} [ \boldsymbol{A}_{Q} ] & \boldsymbol{0} \\ \boldsymbol{0} & [ \boldsymbol{A}_{s} ] \end{pmatrix}, \qquad [ \boldsymbol{A}_{Q} ] = \begin{pmatrix} k_{Q1}^{ - 1} & 0 & 0 & 0 \\ 0 & k_{Q2}^{ - 1} & 0 & 0 \\ 0 & 0 & \ddots & 0 \\ 0 & 0 & 0 & k_{Q6}^{ - 1} \end{pmatrix} \quad \mbox{and}\quad\\ & [ \boldsymbol{A}_{s} ] = \begin{pmatrix} k_{s}^{ - 1} & 0 & 0 & 0 \\ 0 & k_{s2}^{ - 1} & 0 & 0 \\ 0 & 0 & \ddots & 0 \\ 0 & 0 & 0 & k_{sk}^{ - 1} \end{pmatrix}. \end{aligned} $$

(19)

In general, for a redundantly actuated PM with an actuation redundancy $r$ satisfying $r=m-n$, in which $m$ denotes the number of actuations and $n$ represents the number of the DOFs of the PM, its dynamic equilibrium equation can always be arranged in the following form [11, 32]:

$$ \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \bigr)_{n \times m} \boldsymbol{f}_{m \times 1} = ( \not{\boldsymbol{S}}_{\boldsymbol{F}} )_{n \times 1} $$

(20)

where $\boldsymbol{f}$ is a column vector composed of $m$ driving forces/torques, $\boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}}$ is the $n \times m$ force Jacobian matrix, and $\not{\boldsymbol{S}}_{\boldsymbol{F}}$ is the $n$-dimensional generalized external force vector, which is composed of the supporting links’ and the moving platform’s inertial forces/torques, gravity and external forces/torques.

To find an optimal solution to the force analysis of the redundantly actuated PMs given by Eq. (20), the objective function shown as Eq. (2) can still be selected. Thus, the optimal distribution of driving forces/torques of a general redundantly actuated PM can also be solved directly using the $\boldsymbol{W}$-weighted Moore–Penrose generalized inverse, that is,

$$ \boldsymbol{f} = \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \bigr)_{\boldsymbol{W}}^{ +} \not{\boldsymbol{S}}_{\boldsymbol{F}}. $$

(21)

Then, the following conclusions can be drawn:

• 1. If $\boldsymbol{W} = \operatorname {diag}( \dot{q}_{1}^{2} \ \dot{q}_{2}^{2} \ \cdots \ \dot{q}_{n}^{2} )$, where $\dot{q}_{i}$ denotes the angular/linear velocity of the $i$th actuated joint, the objective function of optimization transforms into $\boldsymbol{f}_{\mathrm{obj}} = \sum_{i = 1}^{n} f_{i}^{2} \dot{q}_{i}^{2}$. Then, using Eq. (21), $\boldsymbol{f}$ can be obtained with the minimum input energy of the motors.

• 2. If $\boldsymbol{W} = \boldsymbol{I}$, then Eq. (21) can be further simplified as follows:

  $$ \boldsymbol{f} = \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \bigr)^{\mathrm{T}} \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \bigr)^{\mathrm{T}} \bigr)^{ - 1}\not{\boldsymbol{S}}_{\boldsymbol{F}} = \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \bigr)^{ +} \not{\boldsymbol{S}}_{\boldsymbol{F}} $$

  (22)

  where $( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} )^{ +}$ is just the pseudo-inverse of the force Jacobian matrix $\boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}}$. Then, the objective function of optimization transforms into $\boldsymbol{f}_{\mathrm{obj}} = \sum_{i = 1}^{n} f_{i}^{2}$, and $\boldsymbol{f}$ can be obtained in terms of the minimum driving forces/torques [9, 13, 33].

• 3. If $\boldsymbol{W} = \operatorname {diag}( k_{1}^{ - 1} \ k_{2}^{ - 1} \ \cdots \ k_{n}^{ - 1} )$, where $k_{i}$ denotes stiffness of the $i$th actuated joint, then based on the above analyses, the objective function of optimization is $\boldsymbol{f}_{\mathrm{obj}} = \frac{1}{2}\sum_{i = 1}^{n} k_{i}\delta_{i}^{2} = \frac{1}{2}\sum_{i = 1}^{n} f_{i}^{2} k_{i}^{ - 1}$. Then, using Eq. (21), $\boldsymbol{f}$ can be obtained with minimum elastic potential energy of the whole mechanism [34].

By using Eq. (21) to solve the driving forces/torques for a general redundantly actuated PM, we can choose different values of the positive definite weighted factor matrix $\boldsymbol{W}$, so that different optimization goals can be achieved. More importantly, this method has the advantages of unified and simple expression and high computational efficiency.

2.2 Solving the optimal input distribution of the redundantly actuated PM using the weighted Moore–Penrose generalized inverse

Based on the above analyses, the detailed steps for solving the optimal input distribution of redundantly actuated PMs can be summarized as follows:

• 1. Establish the force/torque equilibrium equation for the generalized external forces and all driving forces/torques to get the force Jacobian matrix $\boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}}$, as in Eq. (7).

• 2. Determine the value of the positive definite weighted factor matrix $\boldsymbol{W}$ by selecting an optimization goal.

• 3. Solve the optimal distribution of all driving forces/torques by resorting to the $\boldsymbol{W}$-weighted Moore–Penrose inverse of the matrix $\boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}}$, using Eq. (21).

In what follows, the 6-legged walking machine is taken as a numerical example to verify the correctness of using the weighted Moore–Penrose generalized inverse to solve the optimal force distribution of the redundantly actuated PMs.

The set of parameters of the 6-legged walking machine is given as follows. The size of the main body is $380 \times 190 \times 20\ \mbox{mm}^{3}$. The lengths of each leg’s links from the ground to the main body are $l_{1} = 160~\mbox{mm}$, $l_{2} = 120~\mbox{mm}$, and $l_{3} = 80~\mbox{mm}$, respectively. The weight of the main body is 100 N. When the machine is walking, the length of each step is 180 mm. The span of the feet located on both sides of the main body is 590 mm, and the height of the main body’s center is 150 mm. The masses of each leg are neglected, and the minimum driving torques are selected as the optimization goal.

At a moment when the main body is supported by legs 1, 3 and 5, we choose joint 2 of leg 1, joints 3 and 4 of leg 3, and joints 2, 3 and 4 of leg 5 as the generalized actuated joints, with the rest of the joints being non-generalized actuated joints. Then, the input torques of the non-generalized actuated joints and those of the generalized actuated joints can be solved by Eqs. (4) and (5) (as derived by Huang et al. [13]), respectively. Otherwise, all of the input torques can be solved directly using the $\boldsymbol{W}$-weighted Moore–Penrose generalized inverse, i.e., Eq. (21) derived in this paper. The resulting two sets of values are shown in Table 1.

Table 1 Input torques solved by the expressions derived by Huang et al. [13] and by the $\boldsymbol{W}$-weighted Moore–Penrose generalized inverse

Table 1 shows that the non-generalized input torques of the walking machine (as solved by Eq. (4)) and the generalized input torques (as solved by Eq. (5)) are exactly equal to those obtained directly by Eq. (21). Therefore, the force analysis of a redundantly actuated PM can be solved directly by resorting to the weighted Moore–Penrose inverse.

In addition, the results obtained by other optimal methods for the force distribution of the redundantly actuated PMs are consistent with those obtained by directly using the weighted Moore–Penrose generalized inverse. For example, the optimal force solution of a planar redundantly actuated hand as solved by Nahon et al. [11] is exactly equal to that solved by Eq. (21) with the same weighted factor matrix. The force optimization of a planar redundantly actuated 2-DOF PM as obtained by Wu et al. [32] (with the minimum deformations of key components as the optimization goal) is consistent with that obtained by Eq. (21) (with the weighted factor matrix composed of the deformations of each component under the effects of unit force/torque).

3 Relationship between the weighted Moore–Penrose generalized inverse and the force analysis of passive overconstrained PMs

In this section, the relationship between the weighted Moore–Penrose generalized inverse and the force analysis of passive overconstrained PMs is discussed on the basis of the results obtained previously by the authors of [26, 27, 35].

3.1 Passive overconstrained PMs in which each limb supplies only one constraint force/couple

For a passive overconstrained PM in which each supporting limb supplies only one constraint force along the axial direction of the limb to its moving platform (such as the 7-SS 6-axis force sensor PM [26] or the redundant grasping problem [27]), its force analyses were carried out by Wang et al. [26] and Kerr et al. [27]. These researchers found that the solution of each limb’s axial force or each grasping force is just the stiffness-weighted Moore–Penrose generalized inverse solution, as shown below:

$$ \boldsymbol{f} = \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \bigr)_{\boldsymbol{W}}^{ +} \not{\boldsymbol{S}}_{\boldsymbol{F}} = \boldsymbol{W}^{ -} \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \bigr)^{\mathrm{T}} \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \boldsymbol{W}^{ -} \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \bigr)^{\mathrm{T}} \bigr)^{ - 1}\not{\boldsymbol{S}}_{\boldsymbol{F}} $$

(23)

where $\boldsymbol{f}$ is the vector composed of all limbs’ axial forces or all grasping forces, $\not{\boldsymbol{S}}_{\boldsymbol{F}}$ denotes the 6-dimensional external force, $\boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}}$ is the matrix mapping $\boldsymbol{f}$ into $\not{\boldsymbol{S}}_{\boldsymbol{F}}$, $\boldsymbol{W}$ is the stiffness-weighted factor matrix that is given by $\boldsymbol{W} = \operatorname {diag}^{ - 1} ( k_{1}\ k_{2} \ \cdots \ k_{n} )$, and $k_{i}$ denotes each limb’s axial stiffness or contact stiffness.

If the axial stiffness or contact stiffness of all limbs is completely equal, then Eq. (23) can be simplified into

$$ \boldsymbol{f} = \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \bigr)^{ +} \not{\boldsymbol{S}}_{\boldsymbol{F}}. $$

(24)

From Eq. (23), we can conclude that by using the weighted Moore–Penrose generalized inverse, the constraint forces/couples of the passive overconstrained PMs (in which each limb supplies only one constraint force/couple to the moving platform) can be solved directly.

3.2 Passive overconstrained PMs in which each limb supplies multiple constraint forces/couples

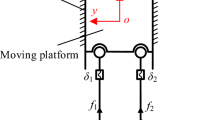
As mentioned in Sect. 3.1, for the special kind of passive overconstrained PMs in which each supporting limb supplies only one constraint force/couple to the moving platform, the weighted Moore–Penrose generalized inverse can be directly used to solve the constraint forces/couples. However, for the general passive overconstrained PMs in which each limb supplies more than one forces/couples to the moving platform, it is not clear that whether the weighted Moore–Penrose generalized inverse can be directly used to solve the constraint forces/couples. For example, the 3-PRRR orthogonal 3-DOF translational overconstrained PM [35], each supporting limb of which supplies an actuated force and two constraint couples to the moving platform. In the following, we will investigate whether the weighted Moore–Penrose generalized inverse can be directly used to the force analysis of the general passive overconstrained PMs.

The schematic diagram of a general passive overconstrained PM that consists of a moving platform, a fixed base and $t$ supporting limbs is shown in Fig. 2. Assume that the $i$th limb supplies $N_{i}$ ($i = 1,2, \ldots,t$) constraint wrenches (including the actuation wrenches, which are not reciprocal to the twist of the driving joint, but are reciprocal to all the twists of the other joints within the $i$th limb [36]) to the moving platform, as denoted by $\not{\boldsymbol{S}}_{j}^{i}$ ($j = 1,2, \ldots,N_{i}$), respectively. For a general passive overconstrained PM, the inequality $N_{1} + N_{2} + \cdots + N_{t} > 6$ is always satisfied.

Fig. 2

Schematic diagram of a general passive overconstrained PM

For convenience of analysis, a reference coordinate system $O$-$\mathit{XYZ}$ is attached at a central point $O$ on the moving platform. In the absence of gravity and friction, the force/torque equilibrium equation of the moving platform can be expressed as

$${\mathit{S̸}}_{\mathit{F}}=f_1^1{\widehat{\mathit{S̸}}}_1^1+f_2^1{\widehat{\mathit{S̸}}}_2^1+\cdots f_{N1}^1{\widehat{\mathit{S̸}}}_{N1}^1+\cdots +f_1^t{\widehat{\mathit{S̸}}}_1^t+f_2^t{\widehat{\mathit{S̸}}}_2^t+\cdots f_{Nt}^t{\widehat{\mathit{S̸}}}_{Nt}^t={\mathit{G}}_{\mathit{f}}^{\mathit{F}}\mathit{f}$$

(25)

where $\not{\boldsymbol{S}}_{\boldsymbol{F}}$ stands for the 6-dimensional external wrench imposed on the moving platform, $\boldsymbol{f} = ( f_{1}^{1} \ f_{2}^{1} \ \cdots \ f_{N1}^{1} \ \cdots \ f_{1}^{t} \ f_{2}^{t} \ \cdots \ f_{Nt}^{t} )^{\mathrm{T}}$ in which $f_{j}^{i}$ $( i = 1,2, \ldots,t,j = 1,2, \ldots,N_{i} )$ is the magnitude of $\not{\boldsymbol{S}}_{j}^{i}$, and $\boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}}$ is the $6 \times ( N_{1} + N_{2} + \cdots + N_{t} )$ matrix mapping $\boldsymbol{f}$ into $\not{\boldsymbol{S}}_{\boldsymbol{F}}$, which is given by

$${\mathit{G}}_{\mathit{f}}^{\mathit{F}}=\left(\begin{array}{ccccccccc}{\widehat{\mathit{S̸}}}_1^1& {\widehat{\mathit{S̸}}}_2^1& \cdots & {\widehat{\mathit{S̸}}}_{N1}^1& \cdots & {\widehat{\mathit{S̸}}}_1^t& {\widehat{\mathit{S̸}}}_2^t& \cdots & {\widehat{\mathit{S̸}}}_{Nt}^t\end{array}\right)$$

(26)

in which ${\widehat{\mathit{S̸}}}_j^i$ represents the unit screw of $\not{\boldsymbol{S}}_{j}^{i}$, expressed in the coordinate system $O$-$\mathit{XYZ}$.

The general expression of the magnitudes of the $N_{i}$ constraint wrenches supplied by the $i$th supporting limb was derived by Xu et al. [35] as

$$ \boldsymbol{f}^{i} = \boldsymbol{K}_{i} \boldsymbol{J}_{i}^{\mathrm{T}}\boldsymbol{K}^{ - 1} \not{\boldsymbol{S}}_{\boldsymbol{F}},\quad i = 1,2, \ldots, t $$

(27)

where $\boldsymbol{f}^{i} = ( f_{1}^{i} \ f_{2}^{i} \ \cdots \ f_{N_{i}}^{i} )^{\mathrm{T}}$, ${\mathit{J}}_i=({\widehat{\mathit{S̸}}}_1^i{\widehat{\mathit{S̸}}}_2^i\cdots {\widehat{\mathit{S̸}}}_{N_i}^i)$, $\boldsymbol{K}_{i}$ is the $N_{i} \times N_{i}$ stiffness matrix of the $i$th limb’s constraint wrenches (including the actuation wrenches), which is the mapping matrix between the magnitudes of the limb’s constraint wrenches and the elastic deformations of the limb’s end in the axes of constraint wrenches under the action of those wrenches [35], and $\boldsymbol{K}$ is the stiffness matrix of the whole mechanism, which can be obtained by

$$ \boldsymbol{K} = \boldsymbol{J}_{1}\boldsymbol{K}_{1} \boldsymbol{J}_{1}^{\mathrm{T}} + \boldsymbol{J}_{2} \boldsymbol{K}_{2}\boldsymbol{J}_{2}^{\mathrm{T}} + \cdots + \boldsymbol{J}_{t}\boldsymbol{K}_{t}\boldsymbol{J}_{t}^{\mathrm{T}}. $$

(28)

It should be noted that for a general passive overconstrained PM, one constraint wrench may produce coupling deformation in the axis of another constraint wrench within the same limb. Thus, the stiffness matrix $\boldsymbol{K}_{i}$ of the $i$th limb’s constraint wrenches is a symmetric matrix, but not a diagonal matrix, and this matrix has the following form:

$$ \boldsymbol{K}_{i} = \begin{pmatrix} c_{11}^{i} & c_{12}^{i} & \cdots & c_{1N_{i}}^{i} \\ c_{21}^{i} & c_{22}^{i} & \cdots & c_{2N_{i}}^{i} \\ \vdots & \vdots & \vdots & \vdots \\ c_{N_{i}1}^{i} & c_{N_{i}2}^{i} & \cdots & c_{N_{i}N_{i}}^{i} \end{pmatrix} ^{ - 1} $$

(29)

where $c_{jk}^{i} = c_{kj}^{i}$ ($j,k = 1,2, \ldots,N_{i}$), and $c_{jk}^{i}$ denotes the elastic deformation of the $i$th limb’s end in the axis of constraint wrench $\not{\boldsymbol{S}}_{j}^{i}$ under the action of unit wrench $\not{\boldsymbol{S}}_{k}^{i}$. Thus, if the deformations generated by $\not{\boldsymbol{S}}_{j}^{i}$ and $\not{\boldsymbol{S}}_{k}^{i}$ are independent of each other, then $c_{jk}^{i} = 0$ ($j \ne k$), or on the contrary, $c_{jk}^{i} \ne 0$.

Let $\boldsymbol{W} = \operatorname {diag}^{ -} ( \boldsymbol{K}_{1} \ \boldsymbol{K}_{2} \ \cdots \ \boldsymbol{K}_{t} )$, then Eq. (28) can be rearranged as

$$ \boldsymbol{K} = \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \boldsymbol{W}^{ -} \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \bigr)^{\mathrm{T}}. $$

(30)

Combining the matrices $\boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}}$ and $\boldsymbol{W}$, Eq. (27) can be rewritten as

$$ \boldsymbol{f} = \boldsymbol{W}^{ -} \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \bigr)^{\mathrm{T}}\boldsymbol{K}^{ - 1}\not{\boldsymbol{S}}_{\boldsymbol{F}}. $$

(31)

Substituting Eq. (30) into Eq. (31) yields

$$ \boldsymbol{f} = \boldsymbol{W}^{ -} \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \bigr)^{\mathrm{T}} \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \boldsymbol{W}^{ -} \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \bigr)^{\mathrm{T}} \bigr)^{ - 1}\not{\boldsymbol{S}}_{\boldsymbol{F}} = \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \bigr)_{\boldsymbol{W}}^{ +} \not{\boldsymbol{S}}_{\boldsymbol{F}} $$

(32)

where

$$\boldsymbol{W} = \begin{pmatrix} \boldsymbol{K}_{1} & 0 & 0 & 0 \\ 0 & \boldsymbol{K}_{2} & 0 & 0 \\ 0 & 0 & \ddots & 0 \\ 0 & 0 & 0 & \boldsymbol{K}_{t} \end{pmatrix} ^{ - 1} $$

is the $( N_{1} + N_{2} + \cdots + N_{t} ) \times ( N_{1} + N_{2} + \cdots + N_{t} )$ weighted factor matrix.

From Eq. (32), it can be seen that the weighted Moore–Penrose generalized inverse can also be applied to the force analysis of the general passive overconstrained PMs in which each supporting limb supplies more than one force/couple. The weighted factor matrix $\boldsymbol{W}$ is a symmetric matrix, as it is composed of the non-diagonal stiffness matrices $\boldsymbol{K}_{i}$ of all limbs’ constraint wrenches. For redundantly actuated PMs, however, the weighted factor matrix $\boldsymbol{W}$ is a diagonal matrix, as it is assumed that there are no mutual effects among the actuated joints, i.e., a condition of $c_{jk}^{i} = 0$ ($j \ne k$) always exists.

3.3 Solving the constraint wrenches of the passive overconstrained PM using the weighted Moore–Penrose inverse

On the basis of the analyses in Sects. 3.1 and 3.2, the detailed steps for the force analysis of a general passive overconstrained PM by using the weighted Moore–Penrose generalized inverse can be summarized as follows:

• 1. Establish the force/torque equilibrium equation of the moving platform to get the mapping matrix $\boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}}$, as shown in Eq. (25).

• 2. Solve the stiffness matrix $\boldsymbol{K}_{i}$ of each supporting limb’s constraint wrenches (including the actuation wrenches), the details of which are available in [35]. For the overconstrained PMs in which each limb contains only one force/couple, the stiffness matrix $\boldsymbol{K}_{i}$ is equal to $k_{i}$. Although each limb contains more than one force/couple, $\boldsymbol{K}_{i}$ is a positive definite symmetric matrix.

• 3. Construct the positive definite weighted factor matrix $\boldsymbol{W}$ as $\boldsymbol{W} = \operatorname {diag}^{ -} ( \boldsymbol{K}_{1} \ \boldsymbol{K}_{2} \ \cdots \ \boldsymbol{K}_{t} )$.

• 4. Then, the force analysis of the passive overconstrained PM can be solved directly by Eq. (32).

For passive overconstrained PMs, the $\boldsymbol{W}$-weighted Moore–Penrose generalized inverse has the physical meaning of minimizing the elastic potential energy of the mechanism because the weighted factor matrix $\boldsymbol{W}$ consists of the stiffness matrices of each supporting limb’s constraint wrenches.

In what follows, numerical examples are given to verify the correctness of using the weighted Moore–Penrose generalized inverse to solve the constraint wrenches of general passive overconstrained PMs. Concerning the passive overconstrained PMs in which each limb supplies only a constraint force, Kerr et al. [27] and Wang et al. [26] have validated that the constraint forces solution is equal to the $\boldsymbol{W}$-weighted Moore–Penrose generalized inverse solution, so that no more numerical examples for these cases are given. As for the passive overconstrained PMs in which each limb supplies multiple constraint forces/couples, we take the $2\mbox{-}\mathrm{RPU}{+}\mathrm{SPR}$ passive overconstrained PM [37] as a numerical example.

The schematic diagram of the $2\mathrm{RPU} {+} \mathrm{SPR}$ passive overconstrained PM is shown in Fig. 3. This PM consists of a moving platform, a fixed base and three supporting limbs. The first two limbs are of identical kinematic structure, and they connect the fixed base to the moving platform by a passive R joint, an actuated P joint and a passive U joint, in sequence. The third limb connects the fixed base to the moving platform by a passive S joint, an actuated P joint and a passive R joint, in sequence. In addition, for the RPU limb, the axis of the R joint is parallel to the axis of the U joint close to the base, and is perpendicular to the axis of the P joint within the same limb. The axes of the two R joints within the two RPU limbs are parallel to each other, and the axes of the two U joints close to the moving platform are collinear. For the SPR limb, the axis of the R joint is parallel to the axis of the U joint close to the moving platform of the RPU limb.

Fig. 3

Schematic diagram of the $2\mathrm{RPU}{+}\mathrm{SPR}$ passive overconstrained PM

For the purpose of analysis, a reference coordinate system $O$-$\mathit{XYZ}$ is attached at the midpoint $O$ of the side $R_{1} R_{2}$ on the base, as shown in Fig. 3, with the $X$-axis parallel to the axis of the R joint within the RPU limb, and the $Z$-axis perpendicular to the base. For the RPU limb, reciprocal screw theory indicates that three wrenches are imposed on the moving platform. These wrenches include a driving force along the axial direction of the limb, a constraint force parallel to the $X$-axis and passing through the center of the U joint within the corresponding limb, and a constraint couple perpendicular to the two axes of the U joint. These wrenches are denoted by $\not{\boldsymbol{S}}_{j}^{i}$ ($i = 1,2,j = 1,2,3$), respectively. The SPR limb exerts two wrenches to the moving platform, namely, a driving force along the axial direction of the limb and a constraint force passing through the center of the S joint and parallel to the axis of the R joint within this limb. These two wrenches are denoted by $\not{\boldsymbol{S}}_{j}^{3}$ ($j = 1,2$), respectively.

To solve the constraint forces/couples (including the driving forces) of the $2\mathrm{RPU}{+}\mathrm{SPR}$ mechanism using the weighted Moore–Penrose generalized inverse, the mapping matrix $\boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}}$ (which maps the constraint forces/couples $\boldsymbol{f}$ into the external wrench $\not{\boldsymbol{S}}_{\boldsymbol{F}}$) should be built first.

The force/torque equilibrium equation of the moving platform for the $2\mathrm{RPU}+\mathrm{SPR}$ mechanism can be expressed as

$${\mathit{S̸}}_{\mathit{F}}=f_1^1{\widehat{\mathit{S̸}}}_1^1+f_2^1{\widehat{\mathit{S̸}}}_2^1+f_3^1{\widehat{\mathit{S̸}}}_3^1+f_1^2{\widehat{\mathit{S̸}}}_1^2+f_2^2{\widehat{\mathit{S̸}}}_2^2+f_3^2{\widehat{\mathit{S̸}}}_3^2+f_1^3{\widehat{\mathit{S̸}}}_1^3+f_2^3{\widehat{\mathit{S̸}}}_2^3={\mathit{G}}_{\mathit{f}}^{\mathit{F}}\mathit{f}$$

(33)

where ${\mathit{G}}_{\mathit{f}}^{\mathit{F}}=({\widehat{\mathit{S̸}}}_1^1{\widehat{\mathit{S̸}}}_2^1{\widehat{\mathit{S̸}}}_3^1{\widehat{\mathit{S̸}}}_1^2{\widehat{\mathit{S̸}}}_2^2{\widehat{\mathit{S̸}}}_3^2{\widehat{\mathit{S̸}}}_1^3{\widehat{\mathit{S̸}}}_2^3)$ is a $6 \times 8$ mapping matrix.

Second, the weighted factor matrix $\boldsymbol{W}$ should be derived.

The stiffness matrix $\boldsymbol{K}_{1}$ of the $R_{1} P_{1} U_{1}$ limb’s constraint wrenches can be obtained by the following steps [35].

For the purpose of analysis, a local coordinate system $o_{1}$-$x_{1}y_{1}z_{1}$ is attached at the end of the $\mathrm{R}_{1} P_{1} U_{1}$ limb, as shown in Fig. 3, with the $y_{1}$-axis parallel to the axis of the $R$ joint within the $R_{1} P_{1} U_{1}$ limb, and the $z_{1}$-axis pointing along the axis of the limb. Thus, the unit screws of the actuation wrench $\not{\boldsymbol{S}}_{1}^{1}$ and the constraint wrenches $\not{\boldsymbol{S}}_{2}^{1}$ and $\not{\boldsymbol{S}}_{3}^{1}$ can be expressed in the coordinate frame $o_{1}$-$x_{1}y_{1}z_{1}$ as

$$\{\begin{array}{c}{}^{o1}\widehat{\mathit{S̸}}_1^1={(001000)}^{\mathrm{T}}\hfill \\ {}^{o1}\widehat{\mathit{S̸}}_2^1={(010000)}^{\mathrm{T}}\hfill \\ {}^{o1}\widehat{\mathit{S̸}}_3^1={(000sin{\theta }_{1}0cos{\theta }_1)}^{\mathrm{T}}\hfill \end{array}$$

(34)

where $\theta_{1}$ is the angle between $\not{\boldsymbol{S}}_{1}^{1}$ and $\not{\boldsymbol{S}}_{3}^{1}$.

Based on the analysis method proposed by Dai et al. [38, 39], the compliance matrix of the $R_{1} P_{1} U_{1}$ limb can be expressed in the coordinate frame $o_{1}$-$x_{1}y_{1}z_{1}$ as

$$ {}^{o1}\boldsymbol{C}_{1} = \begin{pmatrix} \frac{l_{1}^{3}}{3EI_{1}} & 0 & 0 & 0 & \frac{l_{1}^{2}}{2EI_{1}''} & 0 \\ 0 & \frac{l_{1}^{3}}{3EI_{1}} & 0 & - \frac{l_{1}^{2}}{2EI_{1}''} & 0 & 0 \\ 0 & 0 & \frac{l_{1}}{EA_{1}} & 0 & 0 & 0 \\ 0 & - \frac{l_{1}^{2}}{2EI_{1}''} & 0 & \frac{l_{1}}{EI_{1}'} & 0 & 0 \\ \frac{l_{1}^{2}}{2EI_{1}''} & 0 & 0 & 0 & \frac{l_{1}}{EI_{1}'} & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{l_{1}}{GI_{p1}} \end{pmatrix} $$

(35)

where $l_{1} = l_{11} + l_{12}$, $I_{1} = \frac{I_{11}I_{12}l_{1}^{3}}{l_{12}^{3}I_{11} + ( l_{11}^{3} + 3l_{11}^{2}l_{12} + 3l_{12}^{2}l_{11} )I_{12}}$, $I_{1}' = \frac{I_{11}I_{12}l_{1}}{l_{11}I_{12} + l_{12}I_{11}},I_{1}^{''} = \frac{I_{11}I_{12}l_{1}^{2}}{l_{12}^{2}I_{11} + ( l_{11}^{2} + 2l_{11}l_{12} )I_{12}}$, $A_{1} = \frac{A_{11}A_{12}l_{1}}{l_{11}A_{12} + l_{12}A_{11}}$, $I_{p1} = \frac{I_{p11}I_{p12}l_{1}}{l_{11}I_{p12} + l_{12}I_{p11}}$, $l_{1 1}$ and $l_{12}$ denote the length of links $R_{1} P_{1}$ and $P_{1} U_{1}$, $A_{1 1}$ and $A_{12}$ are the cross-sectional areas of links $R_{1} P_{1}$ and $P_{1} U_{1}$, $E$ and $G$ are the elastic modulus and shear modulus of links $R_{1} P_{1}$ and $P_{1} U_{1}$, and $I_{1 1}$, $I_{p11}$, $I_{12}$ and $I_{p12}$ denote the inertia parameters of the cross-section of links $R_{1} P_{1}$ and $P_{1} U_{1}$, respectively.

Then, under the effect of the $R_{1} P_{1} U_{1}$ limb’s constraint wrenches $\not{\boldsymbol{S}}_{1}^{1}$, $\not{\boldsymbol{S}}_{2}^{1}$ and $\not{\boldsymbol{S}}_{3}^{1}$, the deflection twist generated at the end of the $R_{1} P_{1} U_{1}$ limb is

$$\left(\begin{array}{c}{\delta }_{1x}\\ {\delta }_{1y}\\ {\delta }_{1z}\\ {\psi }_{1x}\\ {\psi }_{1y}\\ {\psi }_{1z}\end{array}\right)={}^{o1}{\mathit{C}}_1(f_1^1{}^{o1}{\widehat{\mathit{S̸}}}_1^1+f_2^1{}^{o1}{\widehat{\mathit{S̸}}}_2^1+f_3^1{}^{o1}{\widehat{\mathit{S̸}}}_3^1)=\left(\begin{array}{c}0\\ f_2^1\frac{l_1^3}{3E{I}_1}-f_3^{1}sin{\theta }_1\frac{l_1^2}{2E{I}_1^{{}^{″}}}\\ f_1^1\frac{l_1}{E{A}_1}\\ -f_2^1\frac{l_1^2}{2E{I}_1^{{}^{″}}}+f_3^{1}sin{\theta }_1\frac{l_1}{E{I}_1^{\prime }}\\ 0\\ f_3^{1}cos{\theta }_1\frac{l_1}{G{I}_{p1}}\end{array}\right).$$

(36)

Thus, the overall deflection of the $R_{1} P_{1} U_{1}$ limb’s end in the axes of the constraint wrenches $\not{\boldsymbol{S}}_{1}^{1}$, $\not{\boldsymbol{S}}_{2}^{1}$ and $\not{\boldsymbol{S}}_{3}^{1}$ in the local coordinate frame $o_{1}$-$x_{1}y_{1}z_{1}$ can be obtained as

$$\begin{array}{rl}\left(\begin{array}{c}{\delta }_1^1\\ {\delta }_2^1\\ {\psi }_3^1\end{array}\right)& ={\left(\begin{array}{ccc}{}^{o1}\widehat{\mathit{S̸}}_1^1& {}^{o1}\widehat{\mathit{S̸}}_2^1& {}^{o1}\widehat{\mathit{S̸}}_3^1\end{array}\right)}^{\mathrm{T}}\left(\begin{array}{c}{\delta }_{1x}\\ {\delta }_{1y}\\ {\delta }_{1z}\\ {\psi }_{1x}\\ {\psi }_{1y}\\ {\psi }_{1z}\end{array}\right)\\ & =\left(\begin{array}{c}{f}_1^1\frac{l_1}{E{A}_1}\\ f_2^1\frac{l_1^3}{3E{I}_1}-f_3^{1}sin{\theta }_1\frac{l_1^2}{2E{I}_1^{{}^{″}}}\\ sin{\theta }_1(-f_2^1\frac{l_1^2}{2E{I}_1^{{}^{″}}}+f_3^{1}sin{\theta }_1\frac{l_1}{E{I}_1^{\prime }})+f_3^1{cos}^2{\theta }_1\frac{l_1}{G{I}_{p1}}\end{array}\right)={\mathit{C}}_1\left(\begin{array}{c}{f}_1^1\\ f_2^1\\ f_3^1\end{array}\right)\end{array}$$

(37)

where

$$\boldsymbol{C}_{1} = \begin{pmatrix} \frac{l_{1}}{EA_{1}} & 0 & 0 \\ 0 & \frac{l_{1}^{3}}{3EI_{1}} & - \frac{l_{1}^{2}\sin \theta_{1}}{2EI_{1}''} \\ 0 & - \frac{l_{1}^{2}\sin \theta_{1}}{2EI_{1}^{''}} & \frac{l_{1}\sin^{2}\theta_{1}}{EI_{1}'} + \frac{l_{1}\cos^{2}\theta_{1}}{GI_{p1}} \end{pmatrix} , $$

and $\boldsymbol{K}_{1} = \boldsymbol{C}_{1}^{ - 1}$ is just the stiffness matrix of the $R_{1} P_{1} U_{1}$ limb’s constraint wrenches.

Similar to the above solution process, the stiffness matrices of the $R_{2} P_{2} U_{2}$ and the SPR limbs’ constraint wrenches can be obtained in the corresponding local coordinate frames as

$$ \boldsymbol{K}_{2} = \boldsymbol{C}_{2}^{ - 1} = \begin{pmatrix} \frac{l_{2}}{EA_{2}} & 0 & 0 \\ 0 & \frac{l_{2}^{3}}{3EI_{2}} & - \frac{l_{2}^{2}\sin \theta_{2}}{2EI_{2}^{''}} \\ 0 & - \frac{l_{2}^{2}\sin \theta_{2}}{2EI_{2}^{''}} & \frac{l_{2}\sin^{2}\theta_{2}}{EI_{2}'} + \frac{l_{2}\cos^{2}\theta_{2}}{GI_{p2}} \end{pmatrix} ^{ - 1}\quad \mbox{and}\quad \boldsymbol{K}_{3} = \boldsymbol{C}_{3}^{ - 1} = \begin{pmatrix} \frac{l_{3}}{EA_{3}} & 0 \\ 0 & \frac{l_{3}^{3}}{3EI_{3}} \end{pmatrix} $$

(38)

where

$$\begin{aligned} l_{i} &= l_{i1} + l_{i2} \quad ( i = 2,3 ),\qquad A_{i} = \frac{A_{i1}A_{i2}l_{i}}{l_{i1}A_{i2} + l_{i2}A_{i1}} \quad ( i = 2,3 ),\\ I_{2} &= \frac{I_{21}I_{22}l_{2}^{3}}{l_{22}^{3}I_{21} + ( l_{21}^{3} + 3l_{21}^{2}l_{22} + 3l_{22}^{2}l_{21} )I_{22}},\qquad I_{p2} = \frac{I_{p21}I_{p22}l_{2}}{l_{21}I_{p22} + l_{22}I_{p21}},\\ I_{2}' &= \frac{I_{21}I_{22}l_{2}}{l_{21}I_{22} + l_{22}I_{21}},\qquad I_{2}'' = \frac{I_{21}I_{22}l_{2}^{2}}{l_{22}^{2}I_{21} + ( l_{21}^{2} + 2l_{21}l_{22} )I_{22}},\quad \mbox{and}\quad\\ I_{3} &= \frac{I_{31}I_{32}l_{3}^{3}}{l_{32}^{3}I_{31} + ( l_{31}^{3} + 3l_{31}^{2}l_{32} + 3l_{32}^{2}l_{31} )I_{32} + 3l_{31}l_{32}l_{3} ( I_{31} - I_{32} )}. \end{aligned}$$

Thus, the weighted factor matrix $\boldsymbol{W}$ of the $2\mathrm{RPU}{+}\mathrm{SPR}$ mechanism can be obtained as

$$ \boldsymbol{W} = \begin{pmatrix} \boldsymbol{K}_{1} & \boldsymbol{0} & \boldsymbol{0} \\ \boldsymbol{0} & \boldsymbol{K}_{2} & \boldsymbol{0} \\ \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{K}_{3} \end{pmatrix} ^{ - 1}. $$

(39)

Finally, if the external wrench $\not{\boldsymbol{S}}_{F}$ is given, then the constraint forces/couples of the $2\mathit{RPU}{+}\mathit{SPR}$ mechanism can be obtained directly by substituting the mapping matrix $\boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}}$, the weighted factor matrix $\boldsymbol{W}$ and the external wrench $\not{\boldsymbol{S}}_{F}$ into Eq. (32).

A set of structural parameters of the $2\mathrm{RPU}{+}\mathrm{SPR}$ overconstrained PM are given as $E = 2.07 \times 10^{11}\ \mbox{Pa}$, $\mu = 0.29$, $G = E/ ( 2(1 + \mu ) )$, $l_{11} = l_{21} = l_{31} = 140~\mbox{mm}$, $d_{11} = d_{21} = d_{31} = 20~\mbox{mm}$, and $d_{1 2} = d_{2 2} = d_{3 2} = 16~\mbox{mm}$, where $d_{i1} ( i = 1,2,3 )$ denotes the cross-sectional diameter of cylindrical links $R_{1} P_{1}$, $R_{2} P_{2}$ and $SP_{3}$, and $d_{i2} ( i = 1,2,3 )$ denotes the cross-sectional diameter of cylindrical links $P_{1} U_{1}$, $P_{2} U_{2}$ and $P_{3} R_{3}$. Then, the parameters of the cross-section of links $R_{1} P_{1}$, $R_{2} P_{2}$ and $SP_{3}$ can be obtained by $A_{i1} = \pi d_{i1}^{2}/4$, $I_{i1} = \pi d_{i1}^{4}/64$, $I_{pi1} = \pi d_{i1}^{4}/32$, and the parameters of links $P_{1} U_{1}$, $P_{2} U_{2}$ and $P_{3} R_{3}$ can be obtained by $A_{i2} = \pi d_{i2}^{2}/4$, $I_{i2} = \pi d_{i2}^{4}/64$ and $I_{pi2} = \pi d_{i2}^{4}/32$. In the initial configuration, the moving platform is parallel to the base, $l_{12} = l_{22} = 200~\mbox{mm}$, $l_{32} = 205.5~\mbox{mm}$, and $\theta_{1} = \theta_{2} = 10.16^{ \circ}$. The external wrench imposed on the moving platform expressed in the reference coordinate frame $O$-$\mathit{XYZ}$ is $\not{\boldsymbol{S}}_{F} = ( 10\ \mathrm{N} \quad 10\ \mathrm{N}\quad - 10\ \mathrm{N} \quad 10\ \mathrm{N} {\cdot}\mathrm{m} \quad 10\ \mathrm{N} {\cdot}\mathrm{m} \quad 10\ \mathrm{N} {\cdot}\mathrm{m} )^{\mathrm{T}}$. By resorting to the Adams simulation software, the force simulation model of the $2\mathrm{RPU}{+}\mathrm{SPR}$ mechanism is built up, as shown in Fig. 4, in which all links within each limb are built as flexible bodies, and the moving platform, base and all kinematic joints are considered as rigid bodies.

Fig. 4

Force simulation model of the $2\mathrm{RPU}{+}\mathrm{SPR}$ mechanism

Then, both the theoretical values of all constraint forces/couples (including the driving forces) of the $2\mathrm{RPU}{+}\mathrm{SPR}$ mechanism solved by Eq. (32) and the corresponding simulation values measured by the simulation model are listed in Table 2.

Table 2 Comparison between the theoretical values of the constraint wrenches and the simulation values

It can be seen from Table 2 that the maximum error between the theoretical values and the simulation values is less than 0.5 %, which effectively shows that the force analysis results obtained using the weighted Moore–Penrose generalized inverse for the $2\mathrm{RPU}{+}\mathrm{SPR}$ passive overconstrained PM are correct.

For the 3-PRRR orthogonal 3-DOF translational overconstrained PM, if a set of structure parameters are given as the same as those used in [35], then the theoretical results obtained by Eq. (32) in this paper are also identical with those obtained by Xu et al. [35].

4 Discussion of the application of the weighted Moore–Penrose generalized inverse in the force analysis of overconstrained PMs

From the previous two sections, we can conclude that the weighted Moore–Penrose generalized inverse can be applied to force analyses of both redundantly actuated PMs and passive overconstrained PMs, and that their solutions have the following common form:

$$ \boldsymbol{f} = \bigl( \boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}} \bigr)_{\boldsymbol{W}}^{ +} \not{\boldsymbol{S}}_{\boldsymbol{F}} $$

(40)

in which $\boldsymbol{f}$ is a vector composed of driving forces/torques or constraint forces/couples, $\not{\boldsymbol{S}}_{\boldsymbol{F}}$ denotes the generalized external force, $\boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}}$ is the matrix mapping $\boldsymbol{f}$ to $\not{\boldsymbol{S}}_{\boldsymbol{F}}$ (which can be obtained by establishing the force/torque equilibrium equation of the whole mechanism or of the moving platform), and $\boldsymbol{W}$ is the weighted factor matrix.

In other words, the weighted Moore–Penrose generalized inverse can be applied to solve not only the forces/torques distribution problems for redundantly actuated PMs, but also the forces/couples of general passive overconstrained PMs in which each limb supplies multiple constraint forces/couples to the moving platform.

One difference between these two applications of the weighted Moore–Penrose generalized inverse is that for the redundantly actuated PMs, the value of the weighted factor matrix $\boldsymbol{W}$ can be given arbitrarily according to different optimization goals, so that there are an infinite number of solutions for the driving forces/torques distribution problem. For the passive overconstrained PMs, however, the weighted factor matrix $\boldsymbol{W}$ has a unique value, because the elastic deformation compatibility relationship of the PMs must be taken into account. In other words, the optimization goal of the minimum elastic potential energy for this kind of PM is always achieved passively. Therefore, from this point of view, the solution for the force analysis of the passive overconstrained PMs can simply be regarded as a special solution for the redundantly actuated PMs, for cases in which the minimum elastic potential energy of the whole mechanism is selected as the optimization goal.

The other difference between these two applications concerns the elements of the weighted factor matrix $\boldsymbol{W}$. For the redundantly actuated PMs, the weighted factor matrix $\boldsymbol{W}$ is a diagonal matrix composed of the weighted factors of each actuated joint, and each factor represents only the weight of the corresponding actuated joint, as it is assumed that there are no mutual effects among the actuated joints, i.e., they are considered to be independent of each other. For the passive overconstrained PMs, however, the weighted factor matrix $\boldsymbol{W}$ is composed of the stiffness matrices of each limb’s constraint wrenches (including the actuation wrenches), and the stiffness matrix of a limb’s constraint wrenches is a symmetric matrix, not a diagonal matrix, as the elastic deformations of the limb’s end produced by the constraint wrenches within the same limb are coupled, so the weighted factor matrix $\boldsymbol{W}$ of this kind of PM is a symmetrical matrix rather than a diagonal matrix.

5 Conclusions

This paper discusses the relationship between the weighted Moore–Penrose generalized inverse and the force analyses of both redundantly actuated PMs and passive overconstrained PMs. The main conclusions reached are as follows:

• 1. Based on the principles of linear algebra, the optimal force distribution solution of a redundantly actuated walking machine (obtained by the weighted coefficient method [13]) is just the weighted Moore–Penrose generalized inverse solution of the force Jacobian matrix $\boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}}$. Therefore, the driving forces/torques of the redundantly actuated PMs can be solved directly by the weighted Moore–Penrose generalized inverse, and various optimization goals can be achieved by choosing different values of the positive definite weighted factor matrix. In other words, the weighted Moore–Penrose generalized inverse can be used in the dynamics of the redundantly actuated PMs.

• 2. By further deriving the general analytical expression for the solution of each supporting limb’s constraint wrenches in the general passive overconstrained PMs (as obtained by Xu et al. [35]), it is found that the solution is just the weighted Moore–Penrose generalized inverse solution of the force mapping matrix $\boldsymbol{G}_{\boldsymbol{f}}^{\boldsymbol{F}}$, in which the weighted factor matrix consists of the stiffness matrices of each limb’s constraint wrenches. Therefore, the constraint forces/couples of the general passive overconstrained PMs (in which each limb may supply single or multiple constraint forces/couples) can be solved directly by means of the weighted Moore–Penrose generalized inverse.

The relationship between the weighted Moore–Penrose generalized inverse and the force analysis of overconstrained PMs (including both general redundantly actuated PMs and passive overconstrained PMs) is that the driving forces/torques or constraint forces/couples can be solved directly by the weighted Moore–Penrose generalized inverse, which supplies a simple and highly efficient method for the force analysis of this kind of PM.

Appendix:  A method to calculate the square root and the inverse square root of a positive definite matrix

Let $\boldsymbol{A}$, $\boldsymbol{B} \in \mathbb{C}^{n \times n}$, if $\boldsymbol{B}^{2} = \boldsymbol{A}$, then $\boldsymbol{B}$ is a square root of $\boldsymbol{A}$, denoted by $\boldsymbol{B} = \boldsymbol{A}^{\frac{1}{2}}$. If $\boldsymbol{B}$ is a solution of the matrix equation $\boldsymbol{AB}^{2} = \boldsymbol{I}$, then $\boldsymbol{B}$ is an inverse square root of $\boldsymbol{A}$, denoted by $\boldsymbol{B} = \boldsymbol{A}^{ - \frac{1}{2}}$. There is a vast amount of literature focusing on the square root or the inverse square root of a matrix [40–45]. If $\boldsymbol{A}$ is a nonsingular matrix, its square root and inverse square root always exist.

Particularly, if $\boldsymbol{A}$ is a positive definite symmetric square matrix, then there exists a unique positive definite symmetric square root $\boldsymbol{B}$. Several different methods have been proposed for finding the square root of a positive definite symmetric square matrix [40, 42]. Here, we provide a basic method.

Let $\boldsymbol{A}$, $\boldsymbol{B} \in \mathbb{C}^{n \times n}$, if there is an invertible matrix $\boldsymbol{P}$ such that $\boldsymbol{P}^{ - 1}\boldsymbol{AP} = \boldsymbol{B}$, then $\boldsymbol{A}$ is similar to $\boldsymbol{B}$, denoted by $\boldsymbol{A} \sim \boldsymbol{B}$. If $\boldsymbol{A} \sim \boldsymbol{B}$, then they have the same eigenvalues but different eigenvectors. In addition, if $\boldsymbol{A}$ is similar to a diagonal matrix $\boldsymbol{B}$, then $\boldsymbol{A}$ is diagonalizable.

If $\boldsymbol{A}$ is an $n$ by $n$ positive definite symmetric Hermitian matrix, it can be diagonalized by using its eigenvectors properly, i.e.,

$$ \boldsymbol{P}^{ - 1}\boldsymbol{AP} = \boldsymbol{P}^{\mathrm{T}} \boldsymbol{AP} = \boldsymbol{\varLambda} $$

(41)

where $\boldsymbol{P}$ is a unitary matrix whose columns consists of $n$ linearly independent and orthogonal eigenvectors of $\boldsymbol{A}$, and $\boldsymbol{\varLambda} = \operatorname {diag}( \lambda_{1},\lambda_{2}, \ldots,\lambda_{n} )$, in which $\lambda_{i}$ is the $i$th eigenvalue of $\boldsymbol{A}$.

From Eq. (41) we can get

$$ \boldsymbol{A} = \boldsymbol{P\varLambda P}^{ - 1}. $$

(42)

Since $\boldsymbol{A}$ is a positive definite symmetric Hermitian matrix, all eigenvalues of $\boldsymbol{A}$ are real and positive, i.e., $\lambda_{i}\ (i = 1,2, \ldots,n ) > 0$. Thus, the square root of the diagonal matrix $\boldsymbol{\varLambda}$ can be obtained as $\boldsymbol{\varLambda}^{\frac{1}{2}} = \operatorname {diag}( \lambda_{1}^{\frac{1}{2}},\lambda_{2}^{\frac{1}{2}}, \ldots,\lambda_{n}^{\frac{1}{2}} )$. Let $\boldsymbol{B} = \boldsymbol{P\varLambda}^{\frac{1}{2}}\boldsymbol{P}^{ - 1}$, then

$$\begin{aligned} \boldsymbol{B}^{2} &= \boldsymbol{BB} = \bigl( \boldsymbol{P \varLambda}^{\frac{1}{2}}\boldsymbol{P}^{ - 1} \bigr) \bigl( \boldsymbol{P \varLambda}^{\frac{1}{2}}\boldsymbol{P}^{ - 1} \bigr) = \boldsymbol{P \varLambda}^{\frac{1}{2}}\boldsymbol{P}^{ - 1}\boldsymbol{P \varLambda}^{\frac{1}{2}}\boldsymbol{P}^{ - 1} = \boldsymbol{P \varLambda}^{\frac{1}{2}}\boldsymbol{\varLambda}^{\frac{1}{2}}\boldsymbol{P}^{ - 1} \\ & = \boldsymbol{P\varLambda P}^{ - 1} = \boldsymbol{A}. \end{aligned}$$

(43)

Then by the definition of the square root of a given matrix, it follows from Eq. (43) that $\boldsymbol{B} = \boldsymbol{P\varLambda}^{\frac{1}{2}}\boldsymbol{P}^{ - 1}$ is the unique square root of $\boldsymbol{A}$, i.e.,

$$ \boldsymbol{A}^{\frac{1}{2}} = \boldsymbol{P\varLambda}^{\frac{1}{2}} \boldsymbol{P}^{ - 1}. $$

(44)

Similarly, the inverse square root of $\boldsymbol{A}$ can be derived by

$$ \boldsymbol{A}^{ - \frac{1}{2}} = \boldsymbol{P\varLambda}^{ - \frac{1}{2}} \boldsymbol{P}^{ - 1}. $$

(45)

The weighted factor matrices $\boldsymbol{M}$ and $\boldsymbol{N}$ in Eq. (11) are positive definite symmetric Hermitian matrices. Therefore, the $\boldsymbol{M}^{\frac{1}{2}}$, $\boldsymbol{N}^{\frac{1}{2}}$, $\boldsymbol{M}^{ - \frac{1}{2}}$ and $\boldsymbol{N}^{ - \frac{1}{2}}$ can be calculated by Eqs. (44) and (45).