Keywords

1 Introduction

The redundantly actuated parallel mechanisms (PMs) have received widespread attention for the merits of eliminating kinematic singularities [1, 2], enhancing carrying capacity [3] and improving motion accuracy [4]. The redundant constraints rise in this kind of PMs since the number of the driving joints is larger than the degrees of freedom (DOFs) of the mechanisms. In view that all driving forces/torques of this kind of PMs can be given actively on the basis of the optimal goals, the redundantly actuated PMs can also be called as the active overconstrained PMs. There exist another kind of overconstrained PMs relative to the active overconstrained PMs, i.e., the passive overconstrained PMs, in which the constraints imposed on the moving platform by the supporting limbs are linear dependent [5, 6]. For this kind of overconstrained PMs, the constraint forces/moments can not be given actively. The passive overconstrained PMs have been widely applied in the occasions of high load bearing [7] for the characteristics of simple structure, high rigidity and high precision [8].

Due to the existence of the redundant constraints, the force analysis of both the redundantly actuated PMs and the passive overconstrained PMs belong to the statically indeterminate problem. Therefore, a certain number of supplementary equations are required to solve the driving forces/torques and constraint forces/moments. For the redundantly actuated PMs, there are theoretically an infinite number of solutions for their driving forces/torques distribution problem. Nevertheless, the uncoordinated driving force distribution will lead to the generation of larger internal forces or even destroy the mechanism in practical application. Therefore, the driving forces/torques of this kind of PMs can be distributed according to different optimization goals. A new method for solving the inverse dynamics and internal force of the redundantly actuated PM was proposed under the condition of considering the elastic deformation of limbs [9]. Harada et al. [10] studied a strategy of driving force distribution in order to achieve the goal of force balance of each limb. Nokleby et al. [11] proposed a method to determine the driving force of the non-redundantly and redundantly actuated parallel robots by using scaling factor. Wojtyra et al. [12–14] solved the constraint reaction forces in joints of the redundant constraint mechanism. Besides, the driving forces/torques of the redundantly actuated mechanism is optimized in [15–18]. For the passive overconstrained PMs, the force analysis of this kind of mechanisms has also received extensive attention from the domestic and foreign scholars, since it contributes to the design, manufacture and control of the mechanisms. The statically indeterminate force problem of the passive overconstrained PMs has unique solution, which can not be arbitrarily distributed. A general method for force analysis of the passive overconstrained PMs was proposed in [19]. By applying the reciprocal-screw theory, the kinetostatics of the 4-R (CRR) Parallel Manipulator with overconstraints is presented in [20]. Bonnemains et al. [21] analyzed the dynamics of an overconstrained PKM with compliances: the Tripteor X7. Sapio et al. [22] studied the method for motion control and computation of the constraint forces. Vertechy et al. [23] analyzed the static and stiffness of the PM with the US and UPS limbs. Based on the Newton-Euler method, the inverse dynamic model of the overconstrained mechanism is constructed in [24]. Li et al. [25] explored deformation compatibility conditions and twist/wrench mapping models of the two-DOF overconstrained PM considering gravitational effects.

All of the above mentioned literatures focused on the methods for force analysis of the redundantly actuated mechanisms and the passive overconstrained mechanisms, but no research has been carried out about the essential difference of the statically indeterminate force problem between the two kinds of overconstrained mechanisms. Therefore, this paper mainly studies the differences in the force analysis of the two kinds of overconstrained PMs. Taking the typical 2RPR+P redundantly actuated mechanism as an example, the mechanism on the driving forces/torques distribution is analyzed, in the condition of considering and without considering the system stiffness. Besides, the future works are put forward.

2 Coordination Conditions of Both the Overconstrained PMs

It is assumed that the stiffness of the moving platform of both the redundantly actuated PMs and the passive overconstrained PMs is much larger than that of all supporting limbs, as a result, the moving platform can be regarded as a rigid body. In order to ensure that each limb and the moving platform are always connected, the displacements of all limbs should meet a certain coordination relationship. For the redundantly actuated PMs, the displacement coordination condition contains the input displacements of the actuators and the elastic deformations of the system. While for the passive overconstrained PMs, the displacement coordination condition just refers to the elastic deformations of the system.

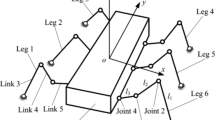
Taking the 2RPR+P redundantly actuated PM shown in Fig. 1 as an example, in which the axes of the two RPR supporting limbs and the P limb are parallel. The displacement coordination condition of this mechanism is that the displacements of the two limbs are completely equal during the moving process of the mechanism. Here, the displacement includes two parts. One part is the input displacement of the ith (i = 1, 2) actuator, and the other part is the tension and compression elastic deformation of the corresponding limb. The displacement coordination condition of the 2RPR+P mechanism can be expressed as

$$ d_{1} + \delta_{1} = d_{2} + \delta_{2} . $$
(1)

where, \( d_{i} \) and \( \delta_{i} \) represent the magnitudes of the input displacement and the tension and compression elastic deformation of the ith limb, respectively.

Fig. 1
figure 1

Schematic diagram of the 2RPR+P redundantly actuated PM

Full size image

When the actuation joints of the 2RPR+P mechanism are locked, it becomes a passive overconstrained mechanism. For this 2RR+P passive overconstrained PM, the displacement coordination condition reduces to \( \delta_{1} = \delta_{2} \). Let k i denote the stiffness of the ith limb, then the magnitude F i of the constraint force supplied by the ith limb can be formulated by \( F_{i} = k_{i} \delta_{i} \). Sequentially, combining the force/moment equilibrium equation of the moving platform, i.e., \( F = F_{1} + F_{2} \), the unique solutions of the constraint forces imposed on the moving platform by the two limbs can be solved, where F denotes the magnitude of the external force exerted on the moving platform along the axial direction of the three limbs. Therefore, from the perspective of the displacement coordination, it can be said to some extent that the passive overconstrained mechanism is a special case of the active overconstrained mechanisms (i.e., the redundantly actuated mechanisms).

3 Driving Forces/Torques Distribution of the Redundantly Actuated PMs

3.1 Driving Forces/Torques Distribution Without Considering the Stiffness of the System

Generally speaking, the control mode of actuators can be categorized into three types: position, speed and torque control mode. The influences of the position and torque control modes on the driving forces/torques distribution of the redundantly actuated mechanisms are only discussed in this paper.

When the stiffness of the system is not considered, the displacement coordination condition of the redundantly actuated mechanisms only contains the input displacements of the actuators. For the 2RPR+P redundantly actuated mechanism, the displacement coordination condition can be formulated as: \( d_{1} = d_{2} \).

In the position control mode of the actuators, the input displacements are given directly. The displacement coordination condition (i.e., \( d_{1} = d_{2} \)) of the 2RPR+P mechanism is always met.

  1. 1.

    Assuming that the driving force F i is not determined by the input displacement of the ith actuator, the driving forces of the two limbs can be arbitrarily distributed as long as the force equilibrium equation (i.e., \( F = F_{1} + F_{2} \)) of the moving platform is satisfied.

  2. 2.

    Assuming that the driving force F i of the ith actuator is determined by its input displacement, the relationship might as well be denoted by

    $$ F_{i} = A_{i} d_{i} , $$
    (2)

    where A i is a coefficient.

Substituting Eq. (2) into the force equilibrium equation of the moving platform of the 2RPR+P mechanism yields

$$ A_{1} d_{1} + A_{2} d_{2} = F. $$
(3)

Combining Eq. (3) and the displacement coordination equation of the mechanism leads to

$$ d_{1} = d_{2} = \frac{F}{{A_{1} + A_{2} }}. $$
(4)

Thus, the driving force F i of the ith actuator can be derived by substituting Eq. (4) into Eq. (2), as following:

$$ F_{i} = \frac{{A_{i} F}}{{A_{1} + A_{2} }}. $$
(5)

which shows that the driving forces of the two limbs can be uniquely solved in this case. In other words, if the driving force of the ith actuator is determined by its input displacement, the driving forces of the 2RPR+P mechanism can not be distributed arbitrarily, which is inconsistent with the general phenomena that the driving forces/torques of the redundantly actuated PMs can be distributed arbitrarily according to different optimization goals.

  1. 3.

    Assuming that the driving force of the actuator within the non-redundant limb (the first RPR limb) is determined by its input displacement, while that within the redundant limb (the second RPR limb) has nothing with the input displacement, the following equations can be obtained:

    $$ \left\{ {\begin{array}{*{20}l} {F_{1} = A_{1} d_{1} } \hfill \\ {F_{2} = F - A_{1} d_{1} } \hfill \\ \end{array} } \right., $$
    (6)

    which indicate the driving forces can be distributed arbitrarily through changing the input displacement of the actuator within the non-redundant limb.

In the torque control mode of the actuators, the driving forces are given directly.

  1. 1.

    Assuming that the input displacement d i of the ith actuator is followed, in other words, it is not determined by the driving force, the displacement coordination condition \( (d_{1} = d_{2} ) \) of the 2RPR+P mechanism is always met. Therefore, in this case, the driving forces of the two limbs can also be arbitrarily distributed.

  2. 2.

    Assuming that the input displacements of the actuators are determined by the driving forces, i.e., \( d_{i} = F_{i} /A_{i} \), the two driving forces are uniquely solved by combining the displacement coordination equation and the force equilibrium equation of the mechanism, as shown in Eq. (5).

  3. 3.

    Assuming that the input displacement d 1 of the actuator within the first RPR limb is determined by its driving force f 1, while the input displacement d 2 within the second RPR limb is followed, the displacement coordination condition \( (d_{1} = d_{2} ) \) can always be satisfied. Therefore, in this assumption, the driving forces of the 2RPR+P redundantly actuated PM can also be arbitrarily distributed on the condition that the force equilibrium equation of the mechanism is met.

3.2 Driving Forces/Torques Distribution Considering the Stiffness of the System

When the stiffness of the system is taken into consideration, the displacement coordination condition of the redundantly actuated mechanisms is shown in Eq. (1).

  1. 1.

    Under the first assumption described in the position control mode of the actuators in Sect. 3.1, the displacement coordination condition shown in Eq. (1) can be rearranged as

    $$ \frac{{F_{1} }}{{k_{1} }} - \frac{{F_{2} }}{{k_{2} }} = d_{2} - d_{1} . $$
    (7)

    On the basis of the force equilibrium equation of the mechanism, the two driving forces of the 2RPR+P mechanism can be arbitrarily distributed, since Eq. (7) is always satisfied.

  2. 2.

    Under the second assumption described in the position control mode of the actuators in Sect. 3.1, as shown in Eq. (2), the following equations can be gotten

    $$ \left\{ {\begin{array}{*{20}l} {A_{1} d_{1} + A_{2} d_{2} = F} \hfill \\ {d_{1} + \frac{{A_{1} d_{1} }}{{k_{1} }} = d_{2} + \frac{{A_{2} d_{2} }}{{k_{2} }}} \hfill \\ \end{array} } \right.. $$
    (8)

    from which we can get

    $$ \left\{ {\begin{array}{*{20}c} {F_{1} = \frac{{k_{1} A_{1} \left( {k_{2} + A_{2} } \right)}}{{k_{1} A_{1} \left( {k_{2} + A_{2} } \right) + k_{2} A_{2} \left( {k_{1} + A_{1} } \right)}}F} \\ {F_{2} = \frac{{k_{2} A_{2} \left( {k_{1} + A_{1} } \right)}}{{k_{1} A_{1} \left( {k_{2} + A_{2} } \right) + k_{2} A_{2} \left( {k_{1} + A_{1} } \right)}}F} \\ \end{array} .} \right. $$
    (9)

    It can be seen from Eq. (9) that the two driving forces can not be distributed arbitrarily in this assumption.

  3. 3.

    Under the third assumption described in the position control mode in Sect. 3.1, Eq. (1) can be rearranged as

    $$ \frac{{A_{1} d_{1} }}{{k_{1} }} + d_{1} = \frac{{F_{2} }}{{k_{2} }} + d_{2} . $$
    (10)

    If the two driving forces are distributed arbitrarily under the condition that \( F_{1} + F_{2} = F \), Eq. (10) is always met. Consequently, in this case, the driving forces can be distributed arbitrarily through changing the input displacement of the actuator within the non-redundant limb.

In the torque control mode of the actuators, once the driving force is given, the elastic deformation of the corresponding limb can be computed by \( \delta_{i} = F_{i} /k_{i} \).

  1. 1.

    Under the first assumption described in the torque control mode of the actuators in Sect. 3.1, the displacement coordination condition shown in Eq. (1) can always be satisfied. Thus, the driving forces have an infinite number of solutions.

  2. 2.

    Under the second assumption described in the torque control mode in Sect. 3.1, Eq. (1) turns to

    $$ \frac{{F_{1} }}{{A_{1} }} + \frac{{F_{1} }}{{k_{1} }} = \frac{{F_{2} }}{{A_{2} }} + \frac{{F_{2} }}{{k_{2} }}. $$
    (11)

Combining Eq. (11) and the force equilibrium equation of the mechanism Eq. (9) can be obtained, so the solutions of the driving forces are unique in this situation.

  1. 3.

    Under the third assumption described in the torque control mode in Sect. 3.1, Eq. (1) can be rearranged as

    $$ \frac{{F_{1} }}{{A_{1} }} + \frac{{F_{1} }}{{k_{1} }} = d_{2} + \frac{{F_{2} }}{{k_{2} }}. $$
    (12)

If the two driving forces are distributed arbitrarily satisfying the force equilibrium equation of the mechanism, Eq. (12) is always met since the input displacement d 2 is followed. Therefore, there are also an infinite number of solutions for the driving force distribution.

4 Conclusions

This paper analyzes the differences between the statically indeterminate force problem of the redundantly actuated PMs and that of the passive overconstrained PMs. The main conclusions reached are as follows:

  1. 1.

    The coordination conditions of both the overconstrained PMs are different. The redundantly actuated PMs satisfy the displacement coordination including the input displacements of the actuators and the elastic deformation of the system, while the passive overconstrained PMs need to meet the elastic deformation coordination.

  2. 2.

    Under the conditions of considering and without considering the system stiffness, the relationship between the driving force and the input displacement of an actuator in the position and torque control modes is discussed.

Based on the discussions demonstrated in this paper, future works are suggested: the experiment system of the 2RPR+P redundantly actuated mechanism need to be established, then, the magnitudes of the driving forces of the mechanism are respectively measured through switching the position and torque control modes of the actuators. On the basis of the experimental data the relationship between the input displacement and the driving force of an actuator under different control modes can be derived, which will greatly contribute to the control of the redundantly actuated mechanisms.