1 Introduction

Multibody systems are often modeled as constrained systems. The mathematical models associated with this type of systems can be derived by various approaches [1]. The widely used models are typically formulated in terms of index-3 differential algebraic equations (DAEs), composed of a set of differential equations and a set of algebraic constraint equations expressing additional relations among the generalized coordinates of the model. To solve these DAEs, many numerical solution approaches have been proposed in the literature [1–7]. However, mathematical studies underline the numerical difficulties associated with the solution of these DAEs, mostly related to the stability of the available integration schemes. If governing equations are not turned into minimal form and dynamic simulation is based on the mathematical model expressed via redundant coordinates [8], progressive drifts of the computed solution from the position, velocity or acceleration constraint manifolds are likely to occur during the simulation. Two kinds of popular techniques to solve this “drift” problem are the constraint violation stabilization (CVS) techniques and the constraint violation elimination (CVE) techniques [2].

The constraint violation stabilization techniques attempt to minimize or eliminate the drift by introducing some correction terms consisting of constraint equations into the equations of motion. One of the most popular methods in engineering practice is Baumgarte’s constraint stabilization method [9]. But Baumgarte’s method involves selecting parameters which are problem-dependent, and no general procedure exists for their determination [10]. Park et al. [11, 12] derived the staggered stabilization technique based on penalty formulation which is robust but conditionally stable. Bayo et al. [13] proposed the augmented Lagrangian formulation which is another constraint violation stabilization technique. The idea behind this formulation is to choose large penalty factors so as to drive the constraints to zero. This formulation can also work with redundant constraints and singular configurations [14]. In practical applications, the augmented Lagrangian formulation solves the equations of motion through an iterative process, and a finite value of the penalty factor must be selected to avoid numerical ill conditioning. Braun and Goldfarb [15] proposed another constraint violation stabilization technique in which the violated position and velocity constraints are used as correction terms in the modified constraint equations at velocity and acceleration levels. The method does not require the Lagrange multipliers to be computed or any iteration. The equation of motion is based on the pseudo-inverse of a constraint matrix such that it can be used under redundant constraints and kinematic singularities. Blajer [16] developed the method by Braun and Goldfarb and then compared it with other constraint violation suppression methods. The developed method assumes a full-rank constraint matrix which can lead to a more effective formulation using the block matrix inversion scheme. The results indicate that none of the compared methods for constraint violation suppression considerably improves accuracy based on a simple case study.

In contrast to the constraint violation stabilization techniques, the constraint violation elimination techniques are post-stabilization methods without any modification in the motion equations and result in satisfaction of the constraints within machine accuracy. The corrected solution is a projection of the approximate solution onto the constraint manifold, and it is also called a projection method. A projection based on Lagrange multipliers was first proposed by Lubich [17] to modify the approximation position and velocity of a constrained multibody system after each time step, which is solved by the modified Newton iteration. Eich [18] proposed a constrained least-squares-based method which is similar to the method by Lubich when the mass matrix is used as a weight [5, 6, 19]. Yoon et al. [20] developed a geometric elimination method of constraint violations using a gradient-based procedure where generalized coordinates were corrected by the geometric constraint equations and the generalized velocities were corrected by the energy constraint. Instead of calculating the energy of the system, Yu and Chen [21] used the velocity constraint equations directly to correct the values of the generalized velocity, and the method was developed based on the theorem of the generalized inverse of matrices with independent constraints. Based on the pseudo-inverse of the constraint matrix, the geometric elimination method was also used by Aghili and Piedbœuf [22] in their “constraint inertia matrix” formulation which can deal with the presence of redundant constraints or a singular configuration. Blajer [23] developed a unified geometric formulation based on the geometric interpretation of constrained dynamics and pointed out that neglecting the inertial attributes may occasionally lead to physical inconsistency in mathematical formulation. The mass matrix used as a weight indicates an energy norm in the velocity level for the projection methods [5, 6, 17, 19]. An improved scheme for one-step elimination of the energy constraint violation was proposed as well by Blajer [24]. The geometrical projection method was also utilized by Nikravesh [25] to correct the initial conditions prior to performing kinematic or forward dynamic analysis of multibody systems. Terze et al. [8, 26, 27] formulated a constraint elimination method within the framework of the null space formulation, which can correct the constraint violation regardless of the actual magnitude of violation. The projective criterion, defined in [23] and then optimized in [8, 27], was used in the generalized coordinates (positions or velocities) partitioning to identify a set of independent variables. Displacement and velocity constraint violations were then iteratively eliminated by successively adjusting the sole dependent variables to satisfy the constraint equations, where the independent displacements and velocities were kept unchanged. Bayo and Ledesman [28] formulated a “mass-orthogonal” projection method to improve the situation where the augmented Lagrangian formulation [13, 14] satisfies the weighted constraint to machine accuracy but doesn’t satisfy to the same level of accuracy for individual constraints at position, velocity and acceleration levels. Cuadrado et al. [29] developed a more efficient implementation of the mass-orthogonal projection which requires only successive forward reductions and back-substitutions, and then Blajer [30] gave a correcting formulation which doesn’t need to update the Lagrange multipliers. The energy consideration with velocity projection was studied by Orden et al. [31, 32], providing an alternative interpretation of its effect on the stability and a practical criterion for the mass-orthogonal projection matrix selection. Blajer [30] also gave a geometrical interpretation to the augmented Lagrangian formulation which is capable of treating systems with changing topologies, redundant constraints, singular positions and some singularity of the mass matrix where the mass-orthogonal projection method can still be applied but the geometric elimination method cannot [20, 21, 23, 24]. Although the mass-orthogonal method had shown good performance in constraint violation correction, the use of a penalty method requires very large penalty values that adversely affect the numerical conditioning of the algebraic linear system to be solved. It also shows less physical meaning than the geometrical projection method when the mass matrix is utilized as the weight, as the position and velocity constraints are introduced approximately based on the augmented Lagrangian formulation by a large penalty factor.

However, as Blajer [30] pointed out, the implementation of the physically consistent projection requires the mass matrix be invertible which is not always satisfied. For example, in the spatial multibody dynamics, the mass matrix could be singular when more than six coordinates are used to define the position and the attitude of the rigid body [33–35]. This is always the case when Euler parameters or natural coordinates are used, which can avoid the drawback that the minimal set of orientation coordinates including three independent parameters (e.g., Euler angles, Bryan angles, Rodriguez parameters, etc.) have a singular position in those locations where these parameters are not defined unequivocally [3–5, 33–37]. In other occasions, it is possible to assign a null mass and inertia tensor to a body simply because its inertia is very small, e.g., when some massless link members are present [30, 33, 34]. Vlasenko and Kasper [36] proposed a successive coordinate projection strategy to eliminate the constraint violations of spatial multibody systems described in absolute coordinates with Euler parameters. The Euler parameters’ normality constraints violations are corrected in the first step by the geometric orthogonal projection method, which has been proved not to change the order of the mistake of joint constraints during the first step. Then the joint constraints’ violations are corrected in the second step by the geometric or physical (energy norm) orthogonal projection method, which also does not influence the Euler parameters’ normality constraints corrected in the first step. In the second step, the first time derivatives of Euler parameters were translated to angular velocities by a translation matrix [4, 37], which is also used to translate the equation of constraints, and this translation is also applied in [26] to avoid the singularity of the mass matrix. To reduce the computational cost for the translation, rebuilding of the equation of constraints for joints on the velocity level is needed [36]. It should be mentioned that although the obtained result is correct, the mass matrix singularity seems to be unnoticed in the energy projection method in Eqs. (2.18) and (2.19) in [36]. It had been interpreted by Blajer that the mass-orthogonal projection method can deal with some singularity of the mass matrix [28–32], and it is also capable of treating systems with changing topologies, redundant constraints and singular positions which are not considered in this paper. Although we have concluded that large penalty values adversely affect the numerical conditioning of the algebraic linear system and the mass-orthogonal method shows less physical meaning than the geometrical projection method with a mass weight matrix, it had been shown that the leading matrix applied in the mass-orthogonal projection method, which is derived from the augmented Lagrangian formulation [13, 14], is always positive definite, i.e., invertible, even in singular positions and/or with linearly dependent constraints and some singularity of the mass matrix. The present paper proposes a modified physically consistent projection method with this characteristic, and moreover, the penalty factor can be eliminated by an analytic derivation.

As it is indicated in the comparative study [38], for solving index one multibody DAE systems of moderate size, optimal performances have been recorded for the methods based on the least-squares block solution, which could be explained observing that: (i) many linear algebra operations are applied to small-order matrices; (ii) a reduced number of matrix operations are involved. However, for large matrices with a high percentage of zero-valued elements, the use of sparse matrix algorithms is recommended which can speed up the processing and avoid numerical problems and accuracy losses for badly conditioned matrices [8]. Based on the geometrical interpretation provided in [8, 23, 24, 26], the manifold orthogonal directions in the physically consistent (energy norm) orthogonal projection method are actually found along the ‘near-orthogonal’ direction by using the state vector approximate numerical values, and this direction is not determined exactly. Also, the projection method is based on adding additional terms to system’s dynamic equations, which may turn the correction procedure into more complex and numerically extensive [8]. Nevertheless, the recent comparative study with a relatively simple case for Baumgarte’s method, the physical orthogonal projection method and the upgraded constraint violation stabilization method (see [15] and [16]) indicated that none of the three methods for constraint stabilization/elimination considerably improves the accuracy of the constraint consistent solutions. The geometric orthogonal projection method also provides a simple procedure to correct the initial values of the dependent state variables [16, 25]. The geometric orthogonal projection method has shown the stability for complex mechanical systems in [36], where the Yamaha YZF-R1 Motorcycle engine was modeled. Considering the computational efficiency and accuracy, the block matrix inversion scheme based geometric projection method is developed in this paper for moderate size problems. The explicit block matrix inversion method is extended to the mass matrix singular problem which appears in the physically consistent projection method for the constraint violations elimination of the spatial multibody dynamics with Euler parameters as the orientation coordinates. The proposed formulation allows the Euler parameters’ normality constraint violations and joint constraint violations to be eliminated at the same time. Furthermore, the constraints in the position level and the velocity level could reach machine precision during numerical integration. The elimination of position constraints’ violation may require few iterations, then, having the system position revised, the velocity correction can be done in one step.

The structure of the rest of the paper is as follows. In Sect. 2, the general form of the equations of motion in spatial multibody dynamics is presented. In Sect. 3, the constrained and weighted least-squares method combined with the block matrix inversion based constraint violations’ elimination projection method is derived. The physical orthogonal projection method is modified to solve the mass matrix singularity in Sect. 4. In Sect. 5, two benchmark examples of spatial multibody dynamics systems are given to verify the performance of the proposed formulation. Section 6 provides the conclusions.

2 Spatial multibody dynamics equations with quaternions

2.1 Attitude with quaternions and constraint equations

Absolute coordinates are widely used in general purpose multibody simulation software for the motion description of mechanical systems. In this case, the configuration of a rigid body is defined by the global position vector of the origin of the body coordinate system and by a set of orientation coordinates describing the orientation of the body coordinate system with respect to the global coordinate system.

As pointed out in the introduction, a three-parametric description of rotations may lead to singularities [3–5, 33–37] in the equations of motion. Therefore, a description in terms of four parameters, so-called quaternions for Euler parameters, is used. Let n be the number of bodies of the system, and \(\boldsymbol{r}^{i} = ( r_{1}^{i}, r_{2}^{i}, r_{3}^{i} )^{\mathrm{T}}\) be the vector of position coordinates of body i and \(\boldsymbol{\varLambda}^{i} = ( \varLambda_{0}^{i}, \varLambda_{1}^{i}, \varLambda_{2}^{i}, \varLambda_{3}^{i} )^{\mathrm {T}}\) be the vector of orientation coordinates of body i. Then the vector of absolute coordinates of the ith body q i can be written as

$$ \boldsymbol{q}^{i} = \bigl( \boldsymbol{r}^{i\mathrm{T}}, \boldsymbol{\varLambda}^{i\mathrm{T}} \bigr)^{\mathrm{T}}. $$
(1)

Let q=(q 1T,…,q nT)T denote the vector of absolute coordinates of a multibody system. The equation of additional constraints for the simulated system is assumed bilateral, holonomic and scleronomic. The position-level constraint equations are

$$ \boldsymbol{C} ( \boldsymbol{q} ) = 0. $$
(2)

The constraint equations can be expressed as

$$ \boldsymbol{C} ( \boldsymbol{q} ) = \bigl( \boldsymbol{C}_{\mathrm{E}} ( \boldsymbol{q} ), \boldsymbol{C}_{\mathrm{J}} ( \boldsymbol{q} ) \bigr)^{\mathrm{T}} $$
(3)

where C E(q) is the constraint equations for Euler parameters, and C J(q) denotes the other equations such as the joint constraint equations.

The Euler parameter generalized coordinates of each body must satisfy the normalization constraint equations. For Euler parameters, we have

$$ \boldsymbol{C}_{\mathrm{E}} ( \boldsymbol{q} ) = \bigl( C_{\mathrm{E}}^{1} \bigl( \boldsymbol{q}^{1} \bigr),\ldots, C_{\mathrm{E}}^{n} \bigl( \boldsymbol{q}^{n} \bigr) \bigr)^{\mathrm{T}} $$
(4)

where \(C_{\mathrm{E}}^{i} ( \boldsymbol{q}^{i} ) = \boldsymbol{\varLambda}^{i\mathrm{T}}\boldsymbol{\varLambda}^{i} - 1\).

The use of non-minimal coordinate sets implies also the dependencies of the first time derivative of coordinates, i.e., the constraint equations at the velocity level are

$$ \dot{\boldsymbol{C}} ( \boldsymbol{q} ) = \boldsymbol{C}_{\boldsymbol{q}} ( \boldsymbol{q} )\dot{\boldsymbol{q}} = 0 $$
(5)

where \((\,\dot{}\,) = \mathrm{d} (\ ) / \mathrm{d}t\), and constraint matrix C q (q)=∂ C(q)/∂ q.

Clearly, for the Euler parameters’ example we have

$$ \boldsymbol{C}_{\mathrm{E}\boldsymbol{q}} ( \boldsymbol{q} ) = \operatorname{diag} \bigl( \boldsymbol{C}_{\mathrm{E}\boldsymbol{q}}^{1},\ldots, \boldsymbol{C}_{\mathrm{E}\boldsymbol{q}}^{n} \bigr) $$
(6)

where \(\boldsymbol{C}_{\mathrm{E}\boldsymbol{q}}^{i} = ( 0, 0, 0, 2\varLambda_{0}^{i}, 2\varLambda_{1}^{i}, 2\varLambda_{2}^{i}, 2\varLambda_{3}^{i} )\).

The second differential of the position level’s constraint equations with respect to time, i.e., the constraint equations at the acceleration level are

$$ \ddot{\boldsymbol{C}} ( \boldsymbol{q} ) = \boldsymbol{C}_{\boldsymbol{q}} ( \boldsymbol{q} )\ddot{\boldsymbol{q}} - \boldsymbol{\gamma} = 0 $$
(7)

where

$$ \boldsymbol{\gamma} = - \frac{\partial( \boldsymbol{C}_{\boldsymbol{q}}\dot{\boldsymbol{q}} )}{\partial \boldsymbol{q}}\dot{\boldsymbol{q}}. $$
(8)

For Euler parameters we have

$$ \boldsymbol{\gamma}_{\mathrm{E}} = \bigl( \gamma_{\mathrm{E}}^{1},\ldots, \gamma_{\mathrm{E}}^{n} \bigr)^{\mathrm{T}} $$
(9)

where \(\gamma_{\mathrm{E}}^{i} = - 2\dot{\boldsymbol{\varLambda}}^{i\mathrm{T}}\dot{\boldsymbol{\varLambda}}^{i}\).

2.2 Spatial multibody dynamics equations

Using Cartesian dependent coordinates, the Lagrange equations of the first kind take the form:

$$ \boldsymbol{M}\ddot{\boldsymbol{q}} + \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}}\boldsymbol{\lambda} = \boldsymbol{Q} $$
(10)

where M is the mass matrix, and λ is the vector of Lagrange multipliers. The vector of generalized force Q accounts for the applied force and additional terms (gyroscopic, etc.) that may appear due to the particular type of generalized coordinates.

The mass matrix for a spatial multibody with quaternions can be expressed as

$$\begin{aligned} \boldsymbol{M} =& \operatorname{diag} \bigl( \boldsymbol{M}^{1},\ldots, \boldsymbol{M}^{n} \bigr), \end{aligned}$$
(11)
$$\begin{aligned} \boldsymbol{M}^{i} =& \left [ \begin{array}{c@{\quad}c} \boldsymbol{m}^{i} & 0 \\ 0 & 4\boldsymbol{L}^{i\mathrm{T}}\boldsymbol{J}^{i}\boldsymbol{L}^{i} \end{array} \right ], \end{aligned}$$
(12)
$$\begin{aligned} \boldsymbol{L}^{i} =& \left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} - \varLambda_{1}^{i} & \varLambda_{0}^{i} & \varLambda_{3}^{i} & - \varLambda_{2}^{i} \\ - \varLambda_{2}^{i} & - \varLambda_{3}^{i} & \varLambda_{0}^{i} & \varLambda_{1}^{i} \\ - \varLambda_{3}^{i} & \varLambda_{2}^{i} & - \varLambda_{1}^{i} & \varLambda_{0}^{i} \end{array} \right ] \end{aligned}$$
(13)

where m i and J i are the 3×3 matrices of the translation mass and the rotational inertia, respectively. We can see that Eq. (12) is a 7×7 singular matrix of rank 6 where the attitude of the multibody is described by the quaternion, making the mass matrix of Eq. (11) also singular. Singular inertia matrices may appear when more than six coordinates are used to define the position of a rigid body in a three-dimensional space. When Euler parameters or natural coordinates are used, this is always the case [34]. The redundant coordinates can be determined in accordance with the quaternion constraint Eqs. (2)–(4).

The position, velocity, and acceleration vector in Eq. (10) must satisfy the corresponding constraint equations of Eqs. (2), (5), and (7). Then a system of index-3 DAEs is constituted with Eq. (10). If only Eqs. (10) and (7) are considered, the following index-1 DAE system which is equivalent to an ordinary differential equation (ODE) system is obtained:

$$ \left [ \begin{array}{c@{\quad}c} \boldsymbol{M} & \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \\ \boldsymbol{C}_{\boldsymbol{q}} & 0 \end{array} \right ]\left [ \begin{array}{c} \ddot{\boldsymbol{q}} \\ \boldsymbol{\lambda} \end{array} \right ] = \left [ \begin{array}{c} \boldsymbol{Q} \\ \boldsymbol{\gamma} \end{array} \right ]. $$
(14)

To illustrate the conditions for the existence and uniqueness of solutions, the subsystem where the joint’s constraints are not at first enforced gives

$$ \left [ \begin{array}{c@{\quad}c} \boldsymbol{M} & \boldsymbol{C}_{\mathrm{E}\boldsymbol{q}}^{\mathrm{T}} \\ \boldsymbol{C}_{\mathrm{E}\boldsymbol{q}} & 0 \end{array} \right ]\left [ \begin{array}{c} \ddot{\boldsymbol{q}} \\ \boldsymbol{\lambda}_{\mathrm{E}} \end{array} \right ] = \left [ \begin{array}{c} \boldsymbol{Q} \\ \boldsymbol{\gamma}_{\mathrm{E}} \end{array} \right ]. $$
(15)

Based on the necessary and sufficient condition proposed in [34], the solution exists and is unique if any possible movement (i.e., which satisfies the constraint equations) involves positive kinetic energy,

$$\begin{aligned} \bar{T} =& \frac{1}{2}\dot{\boldsymbol{q}}^{\mathrm{T}}\boldsymbol{M} \dot{\boldsymbol{q}} = \sum_{i = 1}^{n} \frac{1}{2} \dot{\boldsymbol{r}}^{i\mathrm{T}}\boldsymbol{m}^{i}\dot{\boldsymbol{r}}^{i} + \sum_{i = 1}^{n} 2 \dot{\boldsymbol{\varLambda}}^{i\mathrm{T}}\boldsymbol{L}^{i\mathrm {T}} \boldsymbol{J}^{i}\boldsymbol{L}^{i}\dot{\boldsymbol{\varLambda}}^{i} \\ =& \sum_{i = 1}^{n} \frac{1}{2}\dot{\boldsymbol{r}}^{i\mathrm{T}}\boldsymbol{m}^{i} \dot{\boldsymbol{r}}^{i} + \sum_{i = 1}^{n} \frac{1}{2}\boldsymbol{\omega}^{i\mathrm{T}}\boldsymbol{J}^{i} \boldsymbol{\omega}^{i} \end{aligned}$$
(16)

with

$$ \bar{T} > 0 \quad\forall\dot{\boldsymbol{r}}^{i} \ne0 \mbox{ or } \forall \boldsymbol{\omega}^{i} \ne0 $$
(17)

where \(\boldsymbol{\omega}^{i} = 2\boldsymbol{L}^{i}\dot{\boldsymbol{\varLambda}}^{i}\) is the angular velocity of body i in the coordinate systems corresponding to J i.

As m i and J i for each body are positive definite, Eq. (17) always holds, which is equivalent with the following condition [33, 34]:

$$ \operatorname{rank} \left [ \begin{array}{c} \boldsymbol{M} \\ \boldsymbol{C}_{\mathrm{E}\boldsymbol{q}} \end{array} \right ] = 7n, $$
(18)

or

$$ \left [ \begin{array}{c} \boldsymbol{M} \\ \boldsymbol{C}_{\mathrm{E}\boldsymbol{q}} \end{array} \right ]\boldsymbol{\xi} = 0\quad \mbox{if and only if}\quad \boldsymbol{\xi} = 0. $$
(19)

It should be mentioned that the second row of Eq. (19), C Eq ξ=0, is not considered in [3, 39] which gives a sufficient but not a necessary condition that the mass matrix M be positive definite [34]. However, the positive definite mass matrix condition is too restrictive [34], and it is not always satisfied as shown in Eqs. (11)–(13).

As is indicated in [34], the condition of Eq. (19) gives that the accelerations and constraint forces are determined, but the Lagrange multipliers’ vector λ E is not if matrix C Eq does not have full rank, which means that the coefficient matrix on the left of Eq. (15) is singular. It can be seen from Eq. (6) that the full rank condition for C Eq is always satisfied, and then the coefficient matrix on the left of Eq. (15) is always nonsingular.

The necessary and sufficient condition for the existence and uniqueness of the solution to Eq. (14) remains (see [34])

$$ \operatorname{rank} \left [ \begin{array}{c} \boldsymbol{M} \\ \boldsymbol{C}_{\boldsymbol{q}} \end{array} \right ] = 7n. $$
(20)

It can be seen that Eq. (20) is always satisfied as Eq. (18) is always satisfied, which means the accelerations and constraint forces are determined. The assumption that redundant constraints are not considered, i.e., C q is of full rank, will lead to the Lagrange multipliers’ vector λ being also determined, and then the coefficient matrix on the left of Eq. (14) is nonsingular.

The Lagrange multipliers involved in Eq. (14) can be eliminated by several approaches [1, 16], such as Maggi’s formulation, the null space formulation [26], the Udwadia–Kalaba formulations [40], the Udwadia–Phohomsiri formulation [33], the least-squares block solution where the Moore–Penrose pseudo-inverse method is used for the singular mass matrix problem [38, 41], and so on. Based on a comparative study in [38], optimal performances have been recorded for the methods based on the least-squares block solution for a moderate size problem which is also considered here. As Lagrange multipliers can be eliminated, the ODEs are obtained, but they still may not be in the minimal form [1, 16, 23, 24, 26]. These non-minimal form governing equations can be solved by standard ODE integration schemes (e.g., Runge–Kutta or a multistep method), but they suffer from a constraint stabilization problem [1–7]. As the constraint equations are not imposed completely, the positions and/or velocities provided by the integrator suffer from the “drift” phenomenon. One of the most popular solutions to this problem is the geometrical projection method with physically consistent meaning of position and velocity vectors [16, 23–25, 36].

3 Geometrical projection method

The geometrical projection method presented here is based on the standard constrained optimization procedures [5, 6, 25, 36, 42], which can also be obtained consistently by the gradient-based procedure [20], the generalized inverse method [21], the orthogonal projection scheme [23, 24], and so on. This method adjusts all of the estimates of the coordinates and velocities through a process in such a way that their corresponding sums-of-squares of the corrections are minimal.

3.1 Constrained and weighted least squares method

A constrained and weighted least squares problem is defined as [5, 6, 25, 36, 42]

$$ \Vert \boldsymbol{x} - \tilde{\boldsymbol{x}} \Vert _{\boldsymbol{A}}^{2} \to\min_{\boldsymbol{x}}\quad\mbox{with } \boldsymbol{Gx} - \bar{\boldsymbol{b}} = \mathbf{0} $$
(21)

where \(\tilde{\boldsymbol{x}}\) and x are the known and to be calculated values, respectively. G is the constraint matrix, and \(\bar{\boldsymbol{b}}\) is the constant term. The norm \(\Vert \cdot \Vert _{\boldsymbol{A}}^{2}\) is given by a weight matrix A,

$$ \Vert \boldsymbol{x} - \tilde{\boldsymbol{x}} \Vert _{\boldsymbol{A}}^{2} = ( \boldsymbol{x} - \tilde{\boldsymbol{x}} )^{\mathrm{T}}\boldsymbol{A} ( \boldsymbol{x} - \tilde{\boldsymbol{x}} ). $$
(22)

If A is positive definite and G is of full rank, a solution of Eq. (21) exists and is unique [5, 6, 42]. In fact, these conditions are sufficient but not necessary, and they are too restrictive. The solution is also well defined for a semi-definite matrix A as long as the second order sufficiency condition and the constraint qualification hold [6, 34, 42].

Equation (21) is equivalent to

$$ \Vert \Delta\boldsymbol{x} \Vert _{\boldsymbol{A}}^{2} \to\min _{\Delta\boldsymbol{x}}\quad\mbox{with } \boldsymbol{G}\Delta\boldsymbol{x} - \boldsymbol{b} = \mathbf{0} $$
(23)

where \(\Delta\boldsymbol{x} = \boldsymbol{x} - \tilde{\boldsymbol{x}}\), \(\boldsymbol{b} = \bar{\boldsymbol{b}} - \boldsymbol{G}\tilde{\boldsymbol{x}}\).

If we couple the target function and the constraints by introducing Lagrange multipliers μ, then the problem is equivalent to determining the minimum norm solution to a linear system of equations:

$$\begin{aligned} \boldsymbol{A}\Delta\boldsymbol{x} + \boldsymbol{G}^{\mathrm {T}}\boldsymbol{\mu} =& \mathbf{0}, \end{aligned}$$
(24)
$$\begin{aligned} \boldsymbol{G}\Delta\boldsymbol{x} - \boldsymbol{b} =& \mathbf{0}, \end{aligned}$$
(25)

or in matrix notation

$$ \left [ \begin{array}{c@{\quad}c} \boldsymbol{A} & \boldsymbol{G}^{\mathrm{T}} \\ \boldsymbol{G} & 0 \end{array} \right ]\left \{ \begin{array}{c} \Delta\boldsymbol{x} \\ \boldsymbol{\mu} \end{array} \right \} = \left \{ \begin{array}{c} 0 \\ \boldsymbol{b} \end{array} \right \}. $$
(26)

We assume that the matrix A is positive definite, i.e., A is invertible. Using the block matrix inversion scheme [23, 42, 43],

$$ \left [ \begin{array}{c@{\quad}c} \boldsymbol{R} & \boldsymbol{S} \\ \boldsymbol{T} & \boldsymbol{U} \end{array} \right ]^{ - 1} = \left [ \begin{array}{c@{\quad}c} \boldsymbol{R}^{ - 1} + \boldsymbol{Y}_{1}\boldsymbol{X}_{1}^{ - 1}\boldsymbol{Z}_{1} & - \boldsymbol{Y}_{1}\boldsymbol{X}_{1}^{ - 1} \\ - \boldsymbol{X}_{1}^{ - 1}\boldsymbol{Z}_{1} & \boldsymbol{X}_{1}^{ - 1} \end{array} \right ] $$
(27)

where X 1=U−TR −1 S, Y 1=R −1 S, Z 1=TR −1, and this means that the matrix R is nonsingular.

Applying the scheme Eq. (27) to Eq. (26), one obtains

$$\begin{aligned} \Delta\boldsymbol{x} =& \boldsymbol{A}^{ - 1}\boldsymbol{G}^{\mathrm{T}} \bigl( \boldsymbol{GA}^{ - 1}\boldsymbol{G}^{\mathrm{T}} \bigr)^{ - 1}\boldsymbol{b}, \end{aligned}$$
(28)
$$\begin{aligned} \boldsymbol{\mu} =& - \bigl( \boldsymbol{GA}^{ - 1}\boldsymbol{G}^{\mathrm{T}} \bigr)^{ - 1}\boldsymbol{b}. \end{aligned}$$
(29)

For a nonlinear system, the constraint can be expressed as

$$ \boldsymbol{g} ( \boldsymbol{x} ) = \mathbf{0}. $$
(30)

Then it can be linearized as

$$ \boldsymbol{g} ( \boldsymbol{x} ) \approx\boldsymbol{g} ( \tilde{\boldsymbol{x}} ) + \boldsymbol{G} ( \tilde{\boldsymbol{x}} )\Delta\boldsymbol{x} = 0 $$
(31)

where

$$ \boldsymbol{G} ( \boldsymbol{x} ) = \partial\boldsymbol{g} ( \boldsymbol{x} )/ \partial\boldsymbol{x}. $$
(32)

Then the linearized constrained and weighted least squares problem is obtained from Eqs. (23) and (30), and the minimum norm solution to the linearized system defined by Eqs. (24) and (31) can be found iteratively by Eqs. (28) and (29).

For the multibody dynamics systems, after solving Eq. (14) or the form with Lagrange multipliers eliminated from the acceleration \(\ddot{\boldsymbol{q}}\), the values of the coordinates \(\tilde{\boldsymbol{q}}\) and the velocities \(\tilde{\dot{\boldsymbol{q}}}\) on the new time step are calculated. The problem at hand is to translate the violations into appropriate position and velocity corrections which are given by:

$$\begin{aligned} \Delta\boldsymbol{q} =& \bar{\boldsymbol{q}} - \tilde{\boldsymbol{q}}, \end{aligned}$$
(33)
$$\begin{aligned} \Delta\dot{\boldsymbol{q}} =& \bar{\dot{\boldsymbol{q}}} - \tilde{\dot{\boldsymbol{q}}} \end{aligned}$$
(34)

where \(\bar{\boldsymbol{q}}\) and \(\bar{\dot{\boldsymbol{q}}}\) are corrected constraint consistent position and velocity of the system, respectively, and they are required to satisfy the constraints:

$$\begin{aligned} \boldsymbol{C} ( \bar{\boldsymbol{q}} ) =& 0, \end{aligned}$$
(35)
$$\begin{aligned} \dot{\boldsymbol{C}} ( \bar{\boldsymbol{q}},\bar{\dot{\boldsymbol{q}}} ) =& 0. \end{aligned}$$
(36)

This problem can be solved iteratively by the projection method based on the constrained and weighted least squares method as shown above, and two popular solutions [5, 6, 17–21, 23–25] will be given in the following subsections.

3.2 Geometrical orthogonal projection method (GOPM)

This method is also known as the coordinate projection method that was first proposed by Eich [18] based on the constrained least squares method. It was also derived by Yoon et al. [20] who used a gradient-based procedure, and developed by Yu and Chen [21] based on the theorem of the generalized inverse. In the geometrical orthogonal projection method (GOPM), the weight matrix A is chosen as

$$ \boldsymbol{A} = \boldsymbol{I} $$
(37)

where I is the identity matrix. It corresponds to performing the projection orthogonally in the usual Euclidean metric.

The constrained least squares problem for position constraint equation can be expressed as

$$ \left [ \begin{array}{c@{\quad}c} \boldsymbol{I} & \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \\ \boldsymbol{C}_{\boldsymbol{q}} & 0 \end{array} \right ]\left \{ \begin{array}{c} \Delta\boldsymbol{q} \\ \boldsymbol{\mu} \end{array} \right \} = \left \{ \begin{array}{c} 0 \\ - \tilde{\boldsymbol{C}} \end{array} \right \} $$
(38)

where \(\tilde{\boldsymbol{C}} = \boldsymbol{C} ( \tilde{\boldsymbol{q}})\).

Then, a much more useful formula for the elimination of violation of position equations is obtained based on Eq. (28):

$$ \Delta\boldsymbol{q} = - \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigl( \boldsymbol{C}_{\boldsymbol{q}}\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigr)^{ - 1}\tilde{\boldsymbol{C}}. $$
(39)

After the position constraint violations are corrected, the elimination of violation of velocity constraint equations can be done by using a formula similar to that for the position. It has the form

$$ \left [ \begin{array}{c@{\quad}c} \boldsymbol{I} & \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \\ \boldsymbol{C}_{\boldsymbol{q}} & 0 \end{array} \right ]\left \{ \begin{array}{c} \Delta\dot{\boldsymbol{q}} \\ \boldsymbol{\mu} \end{array} \right \} = \left \{ \begin{array}{c} 0 \\ - \tilde{\dot{\boldsymbol{C}}} \end{array} \right \}, $$
(40)

or in a resolved form

$$ \Delta\dot{\boldsymbol{q}} = - \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigl( \boldsymbol{C}_{\boldsymbol{q}}\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigr)^{ - 1}\tilde{\dot{\boldsymbol{C}}} $$
(41)

where \(\tilde{\dot{\boldsymbol{C}}} = \dot{\boldsymbol{C}} ( \bar{\boldsymbol{q}}, \tilde{\dot{\boldsymbol{q}}} )\).

Due to the nonlinearity of the constrained equation, the correction based on GOPM can be solved iteratively by Eqs. (39) and (41).

3.3 Physical orthogonal projection method

This method was proposed by Blajer [23], and he pointed out that GOPM is somewhat physically inconsistent. As q may in general be translational or rotational coordinates, the entries of constraint gradients (rows of C q ) may have different units. Consequently, the entries of the matrix \(\boldsymbol{C}_{\boldsymbol{q}}\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}}\) may be calculated by summing up terms of different units. In the physical orthogonal projection method, the weight matrix A is chosen as

$$ \boldsymbol{A} = \boldsymbol{M}. $$
(42)

This weight matrix has also appeared in Lubich [17]. The constrained least squares problem for position constraint equation can be expressed as

$$ \left [ \begin{array}{c@{\quad}c} \boldsymbol{M} & \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \\ \boldsymbol{C}_{\boldsymbol{q}} & 0 \end{array} \right ]\left \{ \begin{array}{c} \Delta\boldsymbol{q} \\ \boldsymbol{\mu} \end{array} \right \} = \left \{ \begin{array}{c} 0 \\ - \tilde{\boldsymbol{C}} \end{array} \right \}, $$
(43)

or in a resolved form

$$ \Delta\boldsymbol{q} = - \boldsymbol{M}^{ - 1}\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigl( \boldsymbol{C}_{\boldsymbol{q}}\boldsymbol{M}^{ - 1} \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigr)^{ - 1}\tilde{\boldsymbol{C}}. $$
(44)

The same procedure is adopted as before, and the formula for the elimination of violation of velocity has the form

$$ \Delta\dot{\boldsymbol{q}} = - \boldsymbol{M}^{ - 1} \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigl( \boldsymbol{C}_{\boldsymbol{q}} \boldsymbol{M}^{ - 1}\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigr)^{ - 1}\tilde{\dot{\boldsymbol{C}}}. $$
(45)

The mass matrix used as a weight indicates an energy norm at the velocity level. Due to the nonlinearity of the constrained equation, the correction based on the physical orthogonal projection method can be found iteratively by Eqs. (44) and (45).

It can be found from

$$ \dot{\boldsymbol{C}} = \boldsymbol{C}_{\boldsymbol{q}}\bar{\dot{\boldsymbol{q}}} = \boldsymbol{C}_{\boldsymbol{q}} ( \tilde{\dot{\boldsymbol{q}}} + \Delta \dot{\boldsymbol{q}} ) = \boldsymbol{C}_{\boldsymbol{q}}\tilde{\dot{\boldsymbol{q}}} - \boldsymbol{C}_{\boldsymbol{q}}\boldsymbol{A}^{ - 1}\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigl( \boldsymbol{C}_{\boldsymbol{q}}\boldsymbol{A}^{ - 1} \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigr)^{ - 1}\tilde{\dot{\boldsymbol{C}}} = \tilde{\dot{\boldsymbol{C}}} - \tilde{\dot{\boldsymbol{C}}} = \mathbf{0}. $$
(46)

As Blajer [23] pointed out, usually two or at most three iterations are needed to achieve \(\boldsymbol{C} ( \bar{\boldsymbol{q}} ) = 0\) with reasonable numerical accuracy. Then, having the system position revised, the velocity correction can be done in one step as shown in Eq. (46). It can be observed that an invertible mass matrix A=M must be taken in Eqs. (44) and (45). However, as Eqs. (11)–(13) show, for the spatial multibody system where attitude is described by the quaternion, the mass matrix is singular. This means that the physical orthogonal projection method, Eqs. (44) and (45), cannot be used directly for a spatial multibody system with the dynamic control equations like Eqs. (10)–(13), which is also indicated in [30] arguing that the physical orthogonal projection method cannot applied for singular mass matrix problems. As the mass matrix does not appear in GOPM, GOPM can still be used for a spatial multibody system. However, the potential drawback of GOPM is the necessity of keeping constraint violation small during integration [8], moreover, the physical inconsistencies still exist. In order to develop a physical orthogonal projection type method for a spatial multibody system, the mass matrix singularity problem must be solved in advance.

4 Modified physical orthogonal projection method

4.1 Modified mass-orthogonal projection method (MMOPM)

As Blajer [23] concluded, the matrix \(\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}}\boldsymbol{C}_{\boldsymbol{q}}\) introduced in the zero-eigenvalue theorem [44] may also be formed by summing terms, although they have different units. In fact, the matrix \(\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}}\boldsymbol{C}_{\boldsymbol{q}}\) had appeared as a penalty term in the mass-orthogonal projection method proposed by Bayo and Ledesman based on the augmented Lagrangian formulation [28]. Then Cuadrado et al. [29] and Blajer [30] developed a more efficient implementation of the mass-orthogonal projection which doesn’t need to update the Lagrange multipliers. The mass-orthogonal projection method correcting the position constraint violation is also used by solving the constrained minimization problem with the mass matrix as the weight matrix

$$ \Vert \Delta\boldsymbol{q} \Vert _{\boldsymbol{M}}^{2} \to\min _{\Delta\boldsymbol{q}}\quad\mbox{with } \boldsymbol{C} = \mathbf{0}. $$
(47)

In order to solve the problem posed by Eq. (47), the mass-orthogonal projection method uses the augmented Lagrangian formulation [13, 14] based method which chooses large penalty factors so as to drive the constraints to zero and minimize the following function:

$$ V = \frac{1}{2}\Delta\boldsymbol{q}^{\mathrm{T}}\boldsymbol{M}\Delta \boldsymbol{q} + \frac{1}{2}\boldsymbol{C}^{\mathrm{T}}\boldsymbol{\alpha C} + \boldsymbol{C}^{\mathrm{T}}\boldsymbol{\sigma}^{\boldsymbol{q}} $$
(48)

where a non-negative matrix α is the penalty factor, usually assumed identical for all the constraints (although the constraints may be scaled so that each one has a different penalty value), i.e., α=α I and σ q is the auxiliary vector of Lagrange multipliers for the position correction.

Differentiating Eq. (48) with respect to q and equating to zero yields

$$ \frac{\partial V}{\partial\boldsymbol{q}} = \boldsymbol{M}\Delta \boldsymbol{q} + \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \boldsymbol{\alpha C} + \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}}\boldsymbol{\sigma}^{\boldsymbol{q}} = 0. $$
(49)

To solve the nonlinear algebraic Eq. (49), the constraint can be linearized as

$$ \boldsymbol{C} \approx\tilde{\boldsymbol{C}} + \boldsymbol{C}_{\boldsymbol{q}} \Delta\boldsymbol{q}. $$
(50)

Substituting Eq. (50) into Eq. (49), the following iteration formulation is given:

$$ \boldsymbol{M}\Delta\boldsymbol{q} + \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \boldsymbol{\alpha C}_{\boldsymbol{q}}\Delta\boldsymbol{q} + \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \boldsymbol{\alpha}\tilde{\boldsymbol{C}} + \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \boldsymbol{\sigma}^{\boldsymbol{q}} = 0 $$
(51)

where the linearization of C q is omitted as the terms involving C qq are smaller than \(\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}}\boldsymbol{\alpha C}_{\boldsymbol{q}}\) [28]. As an iterative procedure for the Lagrange multipliers σ q is needed, a more efficient implementation of the projection eliminating the Lagrange multipliers’ updating in the iteration is proposed by Cuadrado et al. [29] and explicitly given by Blajer [30] as follows:

$$ \Delta\boldsymbol{q} = - \boldsymbol{A}_{\alpha}^{ - 1} \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}}\boldsymbol{\alpha}\tilde{\boldsymbol{C}} $$
(52)

where

$$ \boldsymbol{A}_{\alpha} = \boldsymbol{M} + \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \boldsymbol{\alpha C}_{\boldsymbol{q}}. $$
(53)

Based on the same concept, i.e., the constrained minimization problem with the augmented Lagrangian formulation, the mass-orthogonal projection method corrects the velocity constraint violation by minimizing the following function:

$$ V = \frac{1}{2}\Delta\dot{\boldsymbol{q}}^{\mathrm{T}}\boldsymbol{M} \Delta\dot{\boldsymbol{q}} + \frac{1}{2}\dot{\boldsymbol{C}}^{\mathrm{T}} \boldsymbol{\alpha}\dot{\boldsymbol{C}} + \dot{\boldsymbol{C}}^{\mathrm {T}}\boldsymbol{\sigma}^{\dot{\boldsymbol{q}}} $$
(54)

where \(\boldsymbol{\sigma}^{\dot{\boldsymbol{q}}}\) is the auxiliary vector of Lagrange multipliers.

With the same procedure adopted as before, an efficient formula for the elimination of violation of velocity has the following explicit form [29, 30]:

$$ \Delta\dot{\boldsymbol{q}} = - \boldsymbol{A}_{\alpha}^{ - 1} \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}}\boldsymbol{\alpha}\tilde{\dot{\boldsymbol{C}}}. $$
(55)

As Blajer [30] concluded, the leading matrix A α shown in Eqs. (52) and (55) remains positive definite even in the presence of changing topologies (varying number of constraints), redundant constraints, singular positions, and possibly singular M. As we know, the condition number of the leading matrix of A α increases as α becomes larger, with singularity occurring in the limit, and the ill-conditioning displays itself. As mentioned in [28], a good choice for α when working in double precision arithmetic is 107.

Although the mass-orthogonal projection formulation contains a mass matrix, it remains less physically consistent than the physical orthogonal method, as the position and velocity constraints are introduced approximately based on the augmented Lagrangian formulation in Eqs. (48) and (54) by a large penalty factor with mathematical but without apparent physical meaning. Moreover, the violated velocity correction Eq. (55) needs an iterative process because it can’t lead to a correction like Eq. (46).

As it can be seen, the leading matrix A α can deal with some singularity of M, and we can choose the leading matrix as the weight matrix,

$$ \boldsymbol{A} = \boldsymbol{A}_{\alpha}. $$
(56)

Then constrained least squares problem with the weight matrix in Eq. (56) for the position constraint equations can be expressed as

$$ \Vert \Delta\boldsymbol{q} \Vert _{\boldsymbol{A}_{\alpha}}^{2} = \Delta \boldsymbol{q}^{\mathrm{T}}\boldsymbol{A}_{\alpha} \Delta\boldsymbol{q} = \Delta\boldsymbol{q}^{\mathrm{T}}\boldsymbol{M}\Delta\boldsymbol{q} + \Delta \boldsymbol{q}^{\mathrm{T}}\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm {T}} \boldsymbol{\alpha C}_{\boldsymbol{q}}\Delta\boldsymbol{q} $$
(57)

with

$$ \boldsymbol{C} \approx\tilde{\boldsymbol{C}} + \boldsymbol{C}_{\boldsymbol{q}} \Delta\boldsymbol{q} = 0, $$
(58)

or

$$ \left [ \begin{array}{c@{\quad}c} \boldsymbol{A}_{\alpha} & \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \\ \boldsymbol{C}_{\boldsymbol{q}} & 0 \end{array} \right ]\left \{ \begin{array}{c} \Delta\boldsymbol{q} \\ \boldsymbol{\mu} \end{array} \right \} = \left \{ \begin{array}{c} 0 \\ - \tilde{\boldsymbol{C}} \end{array} \right \}. $$
(59)

As leading matrix A α is positive definite, the resolved form can still be obtained by using the block matrix inversion scheme and Eq. (28) as

$$ \Delta\boldsymbol{q} = - \boldsymbol{A}_{\alpha}^{ -1} \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigl( \boldsymbol{C}_{\boldsymbol{q}} \boldsymbol{A}_{\alpha}^{ - 1}\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigr)^{ - 1}\tilde{\boldsymbol{C}}. $$
(60)

Due to the nonlinearity of the constrained equation, the correction based on Eq. (60) must be found iteratively.

With the same procedures mentioned as before, the formula for the elimination of velocity violation has the form

$$ \Delta\dot{\boldsymbol{q}} = - \boldsymbol{A}_{\alpha}^{ - 1} \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigl( \boldsymbol{C}_{\boldsymbol{q}} \boldsymbol{A}_{\alpha}^{ - 1}\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigr)^{ - 1}\tilde{\dot{\boldsymbol{C}}}. $$
(61)

This is the so-called Modified Mass-Orthogonal Projection Method (MMOPM). As can be seen, the obtained Eqs. (60) and (61) are similar to Eqs. (44) and (45), although the physical consistency had been weakened by inconsistent units between the mass matrix M and the penalty term \(\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}}\boldsymbol{\alpha C}_{\boldsymbol{q}}\). Substituting the mass matrix M in the physical orthogonal projection method with the leading matrix A α will not increase the complexity in the correction procedure. On the other hand, the modified correction formulation, Eqs. (60) and (61), is better than Eqs. (52) and (55) of the mass-orthogonal projection method from the viewpoint of physical consistency. At the same time, the violated velocity can be corrected by only one step based on Eq. (46). However, one should be aware that the formulation depends on \(\det( \boldsymbol{C}_{\boldsymbol{q}}\boldsymbol{A}_{\alpha}^{ - 1}\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} ) \ne0\), or that C q is of full rank. This means that the correction formulation cannot deal with the cases of changing topologies (varying number of constraints), redundant constraints and singular positions which are not considered here.

4.2 Generalized physical orthogonal projection method (GPOPM)

As we can see, all the previous correction formulae and the projection schemes for the constraint violation problem are based on Eq. (28). If we go further, we will find that they are based on the block matrix inversion scheme Eq. (27) where the weight matrix A must be positive definite, i.e., A is invertible. However, for the constrained and weighted least squares problem, the solution remains well defined for a semi-definite A as long as the second order sufficiency condition and the constraint qualification hold [6, 34, 42]. When the weight matrix A is taken as the singular mass matrix M, the Moore–Penrose pseudo-inverse of the coefficients matrix in Eq. (43) can be expressed in the following form [38, 41]:

$$ \left [ \begin{array}{c@{\quad}c} \boldsymbol{M} & \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \\ \boldsymbol{C}_{\boldsymbol{q}} & 0 \end{array} \right ]^{ +} = \left [ \begin{array}{c@{\quad}c} 0 & \boldsymbol{C}_{\boldsymbol{q}}^{ +} \\ ( \boldsymbol{C}_{\boldsymbol{q}}^{ +} )^{\mathrm{T}} & - ( \boldsymbol{C}_{\boldsymbol{q}}^{ +} )^{\mathrm{T}}\boldsymbol{R} \end{array} \right ] + \left [ \begin{array}{c} \boldsymbol{I} \\ - \boldsymbol{R}^{\mathrm{T}} \end{array} \right ]\boldsymbol{P}\left [ \begin{array}{c@{\quad}c} \boldsymbol{I} & - \boldsymbol{R} \end{array} \right ] $$
(62)

where P=D +, D=EME, \(\boldsymbol{E} = \boldsymbol{I} - \boldsymbol{C}_{\boldsymbol{q}}^{ +} \boldsymbol{C}_{\boldsymbol{q}}\), \(\boldsymbol{R} = \boldsymbol{MC}_{\boldsymbol{q}}^{ +}\). D + and \(\boldsymbol{C}_{\boldsymbol{q}}^{ +}\) imply that the left pseudo-inverse of D and the right pseudo-inverse of C q , respectively, are given by

$$\begin{aligned} \boldsymbol{D}^{ +} =& \bigl( \boldsymbol{D}^{\mathrm{T}} \boldsymbol{D} \bigr)^{ - 1}\boldsymbol{D}^{\mathrm{T}}\quad\mbox{for }\boldsymbol{D}^{ +} \boldsymbol{D} = \boldsymbol{I}, \end{aligned}$$
(63)
$$\begin{aligned} \boldsymbol{C}_{\boldsymbol{q}}^{ +} =& \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigl( \boldsymbol{C}_{\boldsymbol{q}}\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigr)^{ - 1}\quad\mbox{for } \boldsymbol{C}_{\boldsymbol{q}} \boldsymbol{C}_{\boldsymbol{q}}^{ +} = \boldsymbol{I}. \end{aligned}$$
(64)

Equation (62) maintains its validity also in the case of a rank-deficient constraint matrix, i.e., in the cases of changing topologies and redundant constraints. Moreover, as illustrated before, the coefficients matrix of Eq. (14) is invertible, then the inverse of the coefficients’ matrix is identical to the right hand side of Eq. (62). Hence, the constrained and weighted least squares problem for position constraint correction can be expressed as

$$ \Delta\boldsymbol{q} = - \bigl( \boldsymbol{C}_{\boldsymbol{q}}^{ +} - \boldsymbol{PMC}_{\boldsymbol{q}}^{ +} \bigr)\tilde{\boldsymbol{C}}. $$
(65)

With the same procedure applied as before, the formula for the elimination of velocity violation has the form

$$ \Delta\dot{\boldsymbol{q}} = - \bigl( \boldsymbol{C}_{\boldsymbol{q}}^{ +} - \boldsymbol{PMC}_{\boldsymbol{q}}^{ +} \bigr)\tilde{\dot{\boldsymbol{C}}}. $$
(66)

Substituting the pseudo-inverses of Eqs. (63) and (64) into Eqs. (65) and (66), an explicit expression can be obtained. Although in the least-squares block solution based scheme the block matrix is found by using the concept of a Moore–Penrose generalized inverse, it shows that the solution is effective as implied in [38], leading to a more complex expression. If the constraint matrix is not of full rank, i.e., the coefficients’ matrix is singular, then the Moore–Penrose inverse scheme may be appropriate. As the coefficients matrix of Eq. (14) or Eq. (43) is invertible, a more effective block inversion method is utilized in the following.

Choi and Cheong [45] proposed a block inversion method for the invertible matrix with all singular diagonal entries of the block matrix. And the matrices of coefficients in Eq. (14) satisfy the Type I model in [45]. The Type I matrix is described as a 2×2 block matrix, where R and U on the diagonal are singular while S and T off the diagonal have full ranks. Then the block matrix inverse for this case can be obtained in the following form:

$$ \left [ \begin{array}{c@{\quad}c} \boldsymbol{R} & \boldsymbol{S} \\ \boldsymbol{T} & \boldsymbol{U} \end{array} \right ]^{ - 1} = \left [ \begin{array}{c@{\quad}c} \boldsymbol{X}_{2}^{ - 1} - ( \boldsymbol{X}_{2}^{ - 1}\boldsymbol{S} + \boldsymbol{T}_{\boldsymbol{X}_{2}}^{ +} \boldsymbol{Z}_{2}^{ - 1}\boldsymbol{U} )\boldsymbol{S}_{\boldsymbol{X}_{2}}^{ +} & \boldsymbol{T}_{\boldsymbol{X}_{2}}^{ +} \boldsymbol{Z}_{2}^{ - 1} \\ ( \boldsymbol{I} - ( \boldsymbol{I} - \boldsymbol{Y}_{2}^{ - 1} )\boldsymbol{Z}_{2}^{ - 1}\boldsymbol{U} )\boldsymbol{S}_{\boldsymbol{X}_{2}}^{ +} & ( \boldsymbol{I} - \boldsymbol{Y}_{2}^{ - 1} )\boldsymbol{Z}_{2}^{ - 1} \end{array} \right ] $$
(67)

where X 2=R+ST, \(\boldsymbol{Y}_{2} = \boldsymbol{TX}_{2}^{ - 1}\boldsymbol{S}\), \(\boldsymbol{Z}_{2} = \boldsymbol{I} + \boldsymbol{U} ( \boldsymbol{I} - \boldsymbol{Y}_{2}^{ - 1} )\), X 2, Y 2 and Z 2 are invertible. In other words, |X 2|≠0, |Y 2|≠0 and |Z 2|≠0 need to hold for the existence of the block matrix inverse. \(\boldsymbol{S}_{\boldsymbol{X}_{2}}^{ +}\) and \(\boldsymbol{T}_{\boldsymbol{X}_{2}}^{ +}\) denote the left weighted pseudo-inverse of S and the right weighted pseudo-inverse of T, respectively, and they are given by

$$\begin{aligned} \boldsymbol{S}_{\boldsymbol{X}_{2}}^{ +} =& \boldsymbol{Y}_{2}^{ - 1} \boldsymbol{TX}_{2}^{ - 1}\quad\mbox{for } \boldsymbol{S}_{\boldsymbol{X}_{2}}^{ +} \boldsymbol{S} = \boldsymbol{I}, \end{aligned}$$
(68)
$$\begin{aligned} \boldsymbol{T}_{\boldsymbol{X}_{2}}^{ +} =& \boldsymbol{X}_{2}^{ - 1} \boldsymbol{SY}_{2}^{ - 1}\quad\mbox{for } \boldsymbol{TT}_{\boldsymbol{X}_{2}}^{ +} = \boldsymbol{I}. \end{aligned}$$
(69)

Applying the scheme Eq. (67) to Eq. (43), we have the inverse of the coefficient matrix of Eq. (43),

$$ \left [ \begin{array}{c@{\quad}c} \boldsymbol{M} & \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \\ \boldsymbol{C}_{\boldsymbol{q}} & \mathbf{0} \end{array} \right ]^{ - 1} = \left [ \begin{array}{c@{\quad}c} \boldsymbol{F}_{11} & \boldsymbol{F}_{12} \\ \boldsymbol{F}_{21} & \boldsymbol{F}_{22} \end{array} \right ] $$
(70)

where

$$ \boldsymbol{F}_{12} = \boldsymbol{A}_{1}^{ - 1} \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigl( \boldsymbol{C}_{\boldsymbol{q}} \boldsymbol{A}_{1}^{ - 1}\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigr)^{ - 1} $$
(71)

with

$$ \boldsymbol{A}_{1} = \boldsymbol{M} + \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \boldsymbol{C}_{\boldsymbol{q}}. $$
(72)

The constrained and weighted least squares problem for the position constraint equation based on Eq. (43) can be expressed as

$$ \Delta\boldsymbol{q} = - \boldsymbol{F}_{12}\tilde{\boldsymbol{C}} = - \boldsymbol{A}_{1}^{ - 1}\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm {T}} \bigl( \boldsymbol{C}_{\boldsymbol{q}}\boldsymbol{A}_{1}^{ - 1} \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigr)^{ - 1}\tilde{\boldsymbol{C}}. $$
(73)

With the same procedure applied as before, the formula for the elimination of the velocity violation has a similar form, namely

$$ \Delta\dot{\boldsymbol{q}} = - \boldsymbol{A}_{1}^{ - 1} \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigl( \boldsymbol{C}_{\boldsymbol{q}} \boldsymbol{A}_{1}^{ - 1}\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigr)^{ - 1}\tilde{\dot{\boldsymbol{C}}}. $$
(74)

This is the so-called Generalized Physical Orthogonal Projection Method (GPOPM). Comparing Eq. (73) and Eq. (74) with Eq. (44) and Eq. (45), it can be found that the modified mass matrix A 1 takes the place of the mass matrix M, which will not increase the complexity in the correction procedure. It is noted that the modified mass matrix A 1 in Eq. (73) and Eq. (74) is as same as the leading matrix A α in Eq. (60) and Eq. (61) when α=I. \(\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}}\boldsymbol{\alpha C}_{\boldsymbol{q}}\) is simply added to the mass matrix without any physical basis to eliminate the singularity of the mass matrix in Eq. (53), while A 1 in Eq. (73) and Eq. (74) is derived from Eq. (43) directly to meet the request of minimal energy error norm, and the penalty factor is not needed, so GPOPM is physically consistent.

4.3 Discussion of modified physical orthogonal project method

It can be found that the Type I block matrix inversion method [45] can also be utilized to the diagonal entries of the block matrix with one invertible sub-block matrix. Combining Eq. (27) and Eq. (67), when M is positive definite, it can be found that

$$ \boldsymbol{M}^{ - 1}\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigl( \boldsymbol{C}_{\boldsymbol{q}}\boldsymbol{M}^{ - 1}\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigr)^{ - 1} = \boldsymbol{A}_{1}^{ - 1} \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm {T}} \bigl( \boldsymbol{C}_{\boldsymbol{q}} \boldsymbol{A}_{1}^{ - 1}\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigr)^{ - 1}. $$
(75)

This means that the correction formulae, Eqs. (44) and (45), for the invertible M can be unified by the formulae Eqs. (73) and (74) for the singular M.

When M is positive semi-definite, as A α is invertible when α≠0, it can be found that

$$ \boldsymbol{A}_{\alpha}^{ - 1}\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigl( \boldsymbol{C}_{\boldsymbol{q}}\boldsymbol{A}_{\alpha}^{ - 1} \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigr)^{ - 1} = \boldsymbol{A}_{\alpha+ 1}^{ - 1}\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigl( \boldsymbol{C}_{\boldsymbol{q}}\boldsymbol{A}_{\alpha+ 1}^{ - 1} \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigr)^{ - 1} $$
(76)

with

$$ \boldsymbol{A}_{\alpha+ 1} = \boldsymbol{M} + \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} ( \boldsymbol{\alpha} + \boldsymbol{I} )\boldsymbol{C}_{\boldsymbol{q}}. $$
(77)

Taking α=I,2I,…,k I, we can obtain

$$ \boldsymbol{A}_{1}^{ - 1}\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm {T}} \bigl( \boldsymbol{C}_{\boldsymbol{q}}\boldsymbol{A}_{1}^{ - 1} \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigr)^{ - 1} = \boldsymbol{A}_{k}^{ - 1}\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm {T}} \bigl( \boldsymbol{C}_{\boldsymbol{q}}\boldsymbol{A}_{k}^{ - 1} \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigr)^{ - 1} $$
(78)

with

$$ \boldsymbol{A}_{k} = \boldsymbol{M} + k\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \boldsymbol{C}_{\boldsymbol{q}}. $$
(79)

This means that a large penalty factor of α introduced by Bayo [28] with 107 is consistent with α=I by Eq. (78), although a relatively large factor leading to a proper condition is shown in the mass-orthogonal projection method. And for the singular M by the quaternion used in spatial multibody system, the penalty factor of α can be very small, such as α=I, then from the mathematic point of view, the correction formulae Eqs. (60) and (61) are consistent with Eqs. (73) and (74), but the penalty factors are eliminated and the physical consistency is better. However, the position and velocity correction formulae consistent relations with different α may not be satisfied for the other variants, such as the auxiliary vector Lagrange multipliers μ which need not be calculated in the projection methods shown above.

It can also be found that the correction formulae could be used not only for the spatial system but also for the planar system by Eq. (75). The attitude of the planar system can be expressed as an angular parameter and a positive definite M can be taken. Similar to Eq. (46), after the revision of the system’s position, the velocity correction can be done in one step. In practical operation, the position and velocity corrections can be applied after each step of integration or after a sequence of steps when the constraint violations surpass accepted values [23].

Based on the block matrix inversion scheme Eq. (67), an explicit form of ODEs which eliminates the Lagrange multipliers in Eq. (14) with a singular mass matrix can also be given as follows:

$$ \ddot{\boldsymbol{q}} = \bigl[ \boldsymbol{A}_{1}^{ - 1} - \boldsymbol{A}_{1}^{ - 1}\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm {T}} \bigl( \boldsymbol{C}_{\boldsymbol{q}}\boldsymbol{A}_{1}^{ - 1} \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigr)^{ - 1} \boldsymbol{C}_{\boldsymbol{q}}\boldsymbol{A}_{1}^{ - 1} \bigr] \boldsymbol{Q} + \boldsymbol{A}_{1}^{ - 1}\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigl( \boldsymbol{C}_{\boldsymbol{q}}\boldsymbol{A}_{1}^{ - 1} \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigr)^{ - 1}\boldsymbol{\gamma} $$
(80)

and

$$ \boldsymbol{\lambda} = \bigl( \boldsymbol{C}_{\boldsymbol{q}}\boldsymbol{A}_{1}^{ - 1} \boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigr)^{ - 1} \boldsymbol{C}_{\boldsymbol{q}}\boldsymbol{A}_{1}^{ - 1} \boldsymbol{Q} + \bigl[ \boldsymbol{I} - \bigl( \boldsymbol{C}_{\boldsymbol{q}} \boldsymbol{A}_{1}^{ - 1}\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}} \bigr)^{ - 1} \bigr]\boldsymbol{\gamma}. $$
(81)

A generalized Udwadia–Kalaba type formulation [38, 40, 41] may also be obtained by a transformation of Eq. (80) as the mass matrix singularity is avoided.

It should be mentioned that from the numerical point of view [41], the matrices \(\boldsymbol{C}_{\boldsymbol{q}}\boldsymbol{A}^{ - 1}\boldsymbol{C}_{\boldsymbol{q}}^{\mathrm{T}}\) in the previous correction formulations and ODEs Eqs. (80) and (81) could be ill conditioned and their direct inversion is then prone to round-off errors. The evaluation of this term related inverse through matrix decomposition, such as Gram–Schmidt orthogonalization, singular value decomposition, Householder QR factorization, and so on, is considered numerically more robust [41].

5 Numerical examples

To verify the feasibility and accuracy of the developed constraint violation suppressing formulation, two benchmark problems are presented in this section, a five-bar pendulum system [4, 28, 31] and a spatial slider–crank mechanism [3, 46, 47]. The degrees of freedom are described by means of seven generalized coordinates for each body (three for describing the position of the center of mass and four Euler parameters for describing the attitude), which leads to a singular mass matrix. Of course, since the four Euler parameters are constrained by the relationship that the sum of their squared values has to be equal to one, each body has six degrees of freedom. The magnitude of gravity is g=9.8 m/s2. The equation of motion is integrated using the Runge–Kutta method [6].

In order to control the constraint violations during the time integration process, various projection methods are used here to perform numerical simulation, such as GOPM, MMOPM and GPOPM, where each time step requires several iterations with a tolerance in the position of Δq T MΔq=10−12, and only one step of iteration in the velocity. The Baumgarte’s constraint stabilization method is also performed for comparison. As highlighted in [9, 10], a suitable choice of the two parameters involved in this method is found by numerical experiments.

5.1 Five-bar pendulum

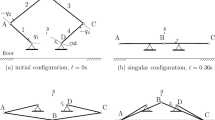
This system is composed of five prismatic bars having unit length, cross-section 0.1×0.1 m2 and unit masses, linked by revolute joints, one of them being fixed. The system is released from rest under the action of gravity from the configuration shown in Fig. 1.

Fig. 1
figure 1

Initial configuration of a five-bar pendulum

Full size image

The spatial multibody system has a total of 35 dependent coordinates with seven for each bar. These coordinates are related by a set of 30 constraint equations, where five equations correspond to the quaternion constraints with one for each bar. There are 25 more equations related to the five revolute joints, with five constraints for each joint. Based on these considerations, the system has a total number of five degrees of freedom. The motion is integrated for 10 s with a time step Δt=0.01 s.

The position and the velocity results of the tip are displayed in Figs. 2 and 3, and the violation is eliminated by the proposed GPOPM. The details of the tip motion show that a dramatic change happened during 5–6 s, after that stable motion was obtained, thus indicating good convergence characteristics of the method even under very strong motions.

Fig. 2
figure 2

Time history of the tip position of a five-bar pendulum based on GPOPM

Full size image
Fig. 3
figure 3

Time history of the tip velocity of a five-bar pendulum based on GPOPM

Full size image

The corresponding violation suppressing results for the position and the velocity are shown in Figs. 4 and 5, respectively. The two related parameters of the Baumgarte’ method are selected to be 25 based on the numerical experiments involving a trial-and-error procedure, which gives relatively small constraint errors. It is apparent that the violation is serious and may be unlimited when applying the direct integration method without violation control. Baumgarte’s method is better, but it can’t control the violation within the given error tolerance and parameters’ selection is needed here.

Fig. 4
figure 4

Position constraint errors of a five-bar pendulum

Full size image
Fig. 5
figure 5

Velocity constraint errors of a five-bar pendulum

Full size image

It can also be seen that, when various constraint projection methods are utilized, constraint satisfaction within machine precision can be obtained. In this example, for the position constraints’ violation elimination, the MMOPM with a penalty factor α=107, the GPOPM with a positive semi-definite mass matrix and the GOPM with the identity matrix show almost the same performances. Meanwhile, for the velocity constraints’ violation elimination, MMOPM shows a higher error as the large penalty factor introduces a numerical error into the constraint correction process, whereas GOPM and GPOPM perform better. Although the same error control characteristic can be reached by the GOPM and the GPOPM, Blajer [23] had pointed out that GOPM may occasionally lead to inconsistencies in the mathematical modeling. From this example, we can find that the present GPOPM not only has good physical consistency but also shows excellent performances in position and velocity constraints’ violation elimination.

5.2 Spatial slider–crank mechanism

In this example, the dynamic response of the spatial slider–crank mechanism shown in Fig. 6 is simulated. The mechanism consists of a crank of length 0.08 m, a connecting rod of length 0.3 m, and a sliding block. The crank is connected to the ground at A by a revolute joint. A spherical joint at B connects the crank to the connecting rod, which in turn is connected to the sliding body by a universal joint at C. The block is constrained to the ground by a prismatic joint D with the sliding displacement s. The masses of the crank, connecting rod and sliding block are respectively m c=0.12 kg, m r=0.5 kg, and m s=2.0 kg. The mass moments of inertia for the three bodies are:

$$\begin{aligned} \boldsymbol{J}_{\mathrm{c}} =& \left [ \begin{array}{c@{\quad}c@{\quad}c} 0.0001 & 0 & 0 \\ 0 & 0.00001 & 0 \\ 0 & 0 & 0.0001 \end{array} \right ]~\mbox{kg}\,\mbox{m}^{2},\qquad \boldsymbol{J}_{\mathrm{r}} = \left [ \begin{array}{c@{\quad}c@{\quad}c} 0.004 & 0 & 0 \\ 0 & 0.0004 & 0 \\ 0 & 0 & 0.004 \end{array} \right ] ~\mbox{kg}\,\mbox{m}^{2},\\ \boldsymbol{J}_{\mathrm{s}} =& \left [ \begin{array}{c@{\quad}c@{\quad}c} 0.0001 & 0 & 0 \\ 0 & 0.0001 & 0 \\ 0 & 0 & 0.0001 \end{array} \right ]~\mbox{kg}\,\mbox{m}^{2}. \end{aligned}$$
Fig. 6
figure 6

Spatial slider–crank mechanism [3, 46]

Full size image

Gravity is acting in the negative Z-direction. The forward dynamic response of the multibody system is studied, given that the crank is driven from the initial position θ=0 rad with initial angular speed of 6 rad/s.

The mechanism is described by 21 generalized coordinates, constrained by three Euler parameter normalization constraints and 17 joint constraints. Based on these considerations, the system has only one degree of freedom. The numerical experiment is performed with a time step Δt=0.01 s for 10 s.

The computed position and velocity of the slider are plotted versus time in Figs. 7 and 8, respectively, where the violation is eliminated by the proposed GPOPM. Since the system is conservative, plots are periodic, and they are in good agreement with the results shown in Haug [3].

Fig. 7
figure 7

Time history of the slider position based on GPOPM

Full size image
Fig. 8
figure 8

Time history of the slider velocity based on GPOPM

Full size image

The corresponding violation suppressing results for the position and the velocity are shown in Figs. 9 and 10, respectively. The two related parameters of the Baumgarte’ method are also selected to be 25 as in the previous example based on the numerical experiments, which gives relatively small constraint errors. It is also apparent that the violation is serious and may be unlimited when applying the direct integration method without violation control. Baumgarte’s method is better, but it can’t control the violation within the given error tolerance and parameters’ selection is needed. It can also be seen that, when various constraint projection methods are utilized, constraint satisfaction within machine precision and almost the same performances as in the first example of the GOPM, MMOPM and GPOPM can be obtained. The MMOPM shows more obvious and periodic errors than the other two methods for the velocity correction, due to the introduction of a large penalty factor. From this example, we can still find that the presented GPOPM not only has good physical consistency but also shows excellent performances in position and velocity constraints’ violation elimination for a periodic multibody dynamical system.

Fig. 9
figure 9

Position constraint errors of a spatial slider–crank mechanism

Full size image
Fig. 10
figure 10

Velocity constraint errors of a spatial slider–crank mechanism

Full size image

6 Conclusions

In this paper, we proposed a physically consistent (energy norm) constraint violation suppressing formulation for solving the spatial multibody systems dynamics governed by DAEs with a singular mass matrix. The constraint violation suppressing formulation is one of the geometrical projection methods which project the constraint violated solution back onto the acceptable constraint manifolds. The projection method is implemented based on the constrained least squares optimization procedures, where the sum-of-squares of the corrections are minimal for a given weight matrix. The physical orthogonal projection method is recommended, as the mass matrix weight implies the minimal energy errors norm, which gives the consistent inertial attributes for translational and rotational coordinates, i.e., is physically consistent. For solving moderate size multibody systems, optimal performances have been recorded by the block solution based scheme [38] as: (i) many linear algebra operations are applied to small-order matrices; (ii) a reduced number of matrix operations are involved. The block matrix inversion scheme is utilized to obtain the correction formulation. However, the positive definite weighted matrix block inversion scheme based physical orthogonal projection formulation cannot handle the mass matrix singular problem well, which occurs in spatial multibody systems dynamics when the body attitude is described by the quaternion (or Euler parameters) with the normalization constraint equation. The present paper developed the block inversion solution based physical projection method and proposed two explicit modified physical orthogonal projection formulations, MMOPM and GPOPM.

MMOPM modifies the mass matrix directly by adding a penalty factor matrix, which appears in the mass-orthogonal projection method based on the augmented Lagrangian formulation and leads to a positive definite weight matrix satisfying the block matrix inversion scheme condition. Comparing with the existing mass-orthogonal projection method where the constraints are introduced approximately by a large penalty factor with mathematical meaning, MMOPM is more physically consistent, while a penalty factor is still involved. GPOPM is a generalization of the physical orthogonal projection method, where the constrained least squares method is implemented based on the positive semi-definite mass matrix which is the necessary condition for the projection method. The correction formulation is obtained by using a more general expression of the block matrix inversion method for the invertible matrix with all singular diagonal entries of the block matrix. The block matrix inversion can also be implemented by the concept of Moore–Penrose generalized inverse, but this leads to a more complex expression than for GPOPM as the coefficients matrix, where the full constraint matrix is considered here, is invertible. It has been shown that MMOPM and GPOPM are consistent with each other in the mathematical meaning, while the penalty factor disappears in GPOPM.

Benchmark numerical examples of spatial multibody systems with a singular mass matrix have verified the feasibility and accuracy of the proposed approaches. The constraints in the position and the velocity could reach machine precision during the numerical integration. The elimination of violation of the position constraints may require few iterations, while the violation of the velocity constraints is removed in one step. Numerical results also show that MMOPM is less accurate in the velocity correction than GPOPM, which may be caused by the numerical ill-conditioning problem resulting from the large penalty factor. GOPM can also obtain almost the same precision as GPOPM based on the numerical examples, but GOPM neglects the inertial attributes and may occasionally lead to physical inconsistencies in mathematical modeling.

We can conclude that GPOPM not only has good physical consistency but also shows excellent performances in position and velocity constraints’ violation elimination for a spatial multibody dynamic system. The normalization constraint for Euler parameters can be corrected with the joint constraints at the same time. Furthermore, the requirement of coordinate partition has also been avoided during the numerical integration. Additionally, the proposed methods can be treated as a generalization to the original projection method, and they can also be applied to the constraint violation suppression of the planar multibody dynamics. The modified projection method can also be extended directly for solving mass matrix singularity problems caused by massless members which satisfy the condition discussed by Blajer [30]. As for large matrices with a high percentage of zero-valued elements, the use of sparse matrix algorithms can speed up the processing and avoid the numerical problems and accuracy losses. The proposed correction formulation based on the block matrix inversion scheme is recommended for solving multibody systems of moderate size as indicated in [38]. For complex mechanical systems, the geometric projection method based correction formulation retains the stability as shown in [36], where the Yamaha YZF-R1 Motorcycle engine is modeled. Future work may concentrate on the applications of the presented violation correction formulation in complex systems.