1 Introduction

In the field of aerospace and aeronautical industry, many engineering structures are typically flexible and are subjected to large overall motions. Numerical models used to represent these structures must allow for large displacements and rotations of arbitrary magnitude. Geometrically exact beam that has been well developed over the decades is the most suitable model that can describe large motions accurately. The concept of geometrically exact [1, 2] stems from the identification of the analytical models which states that, once the kinetic assumptions have been made, the ensuing developments are strictly kept within the framework of these assumptions and no further kinematic assumptions are introduced. In general, the assumption of small strain is used, but the strain–displacement relationship is exactly described.

Beginning with the work of Reissner [3], the exact intrinsic equations for beam static equilibrium are derived under the limitation of unrestrained warping. Following with the work of Simo and Vu-Quoc [4, 5], the research of geometrically exact beam theories and numerical implementations has yielded significant advances. For example, Bauchau and Hong [6] developed a naturally curved and twisted beam model, in which the strain level remains low under arbitrarily large deflections and rotations. The governing equations of motion were discretized in the time domain and the incremental formula was assembled to fit the energy decay and energy saving integration schemes [7], improving the stability and efficiency of the simulation. However, both the Wiener–Milenković and Rodrigues parameters were used to vectorize the total and incremental rotation tensors, respectively, which increased the complexity of rotation vectorization. It is also inconvenient for finite element modeling to define the cross-sectional mass and stiffness properties as user inputs. Hodges and his co-workers [8, 9] developed a geometrically exact intrinsic dynamics model of beams that can be initially curved and twisted. The beam constitutive law is based on a separate finite element analysis and is valid for anisotropic beams with nonhomogeneous cross-sections. Currently, an Euler–Bernoulli beam [10] has been developed, and the large deformation is taken into account. Four Euler parameters, not a minimal set representation of rotation, are used to describe the rotation which increases the size of the discretized system. Jelenić [11] pointed out that establishing the relationships between the large rotations and strains appears to be the biggest problem in which the interpolation of rotation becomes a key issue. Many refinements [12, 13] as to the interpolation of finite rotation have been made, and the interpolation algorithms were carefully designed.

Even though the geometrically exact beam model has been well developed, there still exist difficulties that hinder wide application of this model in the industry. First, the identification of cross-sectional stiffness properties becomes difficult, especially when the beam-like structures are made of inhomogeneous materials with complex cross-sectional configurations. Second, the finite rotations do not form a linear space, an application of the linear interpolation technique to a finite rotation directly will lose objectivity, which increases the complexity of rotation interpolation. Third, the general one-dimensional beam theory cannot predict the warping of cross-section due to the rigid plane assumption of the cross-section. But the details of the cross-sectional strain field are necessary inputs for the fatigue analysis during the post process.

This paper aims to develop a new type of a beam dynamic model, solving the modeling difficulties mentioned above. The dimension reduction approach based on variational asymptotic method has been combined with the one-dimensional dynamic model. Current approach can predict the cross-sectional stiffness properties automatically and use them as inputs for one-dimensional beam analysis. Only the Wiener–Milenković parameters, a minimal set of representation, are used to vectorize a finite rotation. The total translation and the incremental conformal rotation vector become the unknowns, leading to the total and incremental variables mixed formula of governing equations of motion. The rotation tensor is determined through the composition of initial and incremental rotations to avoid the singularity of conformal rotation vector. Algorithm 1 developed by Jelenić and his co-worker [11] has been applied in this paper to interpolate rotations without loss of objectivity. Finally, the three-dimensional strain field can be recovered once the time histories of one-dimensional strains are integrated from the one-dimensional beam problem.

The outline of the paper is as follows. Section 2 describes the related details of the nonlinear beam theory, especially the strain–displacement relations and the theory of dimension reduction. Then special attention is paid to the vectorization and interpolation of finite rotation. Section 3 presents three numerical examples to validate the new geometrically exact beam element developed in this paper.

2 Nonlinear beam theory

2.1 Kinematics of deformation

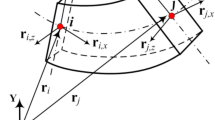
A beam with a cross-section of arbitrary shape is depicted in Fig. 1, in which the beam length is L and the area of cross-section is Ω. The plane of cross-section is defined by the base vectors \(\bar{b}_{2}\), \(\bar{b}_{3}\) of orthogonal basis \(\mathcal{B}_{0}(\bar{b}_{1},\bar{b}_{2},\bar{b}_{3})\) and \(\bar {B}_{2}\), \(\bar{B}_{3}\) of basis \(\mathcal{B}(\bar{B}_{1},\bar{B}_{2},\bar{B}_{3})\) in the undeformed and deformed configurations, respectively. The corresponding rotation tensors that bring inertial basis \(\mathcal{I}(\bar{i}_{1},\bar{i}_{2},\bar {i}_{3})\) to \(\mathcal{B}_{0}\) and \(\mathcal{B}_{0}\) to \(\mathcal{B}\) are denoted as R 0 and R. Note that \(\bar{i}_{i}\) for i=1,2,3 are orthogonal unit vectors. For the undeformed state, the position vector of a material point on the beam is written as

$$ \underline{x}(\alpha_{1},\alpha_{2}, \alpha_{3}) = \underline {u}_{0}(\alpha_{1}) + \alpha _{2}\bar{b}_{2}(\alpha_{1})+ \alpha_{3}\bar{b}_{3}(\alpha_{1}) $$
(1)

where \(\underline{u}_{0}(\alpha_{1})\) is the position vector of a point on the reference line, α 1 is the arc length along the reference line, α 2 and α 3 are the cross-section coordinates. The special formulas of covariant base vectors, \(\underline{g}_{i} = {\partial\underline{x} }/{\partial\alpha_{i}}\), are derived from Eq. (1) as

$$ \underline{g}_{1} = \bar{b}_{1} + \alpha_{2}\tilde{\kappa }_{0}\bar{b}_{2} + \alpha_{3}\tilde{\kappa} _{0}\bar{b}_{3},\qquad \underline{g}_{2} = \bar{b}_{2},\qquad \underline{g}_{3} = \bar{b}_{3} $$
(2)

where \(\bar{b}_{1}\) is defined as \(\bar{b}_{1} = {\partial\underline {u}_{0}}/{\partial\alpha_{1}}\), \(\underline{\kappa}_{0}\) is the initial curvature vector of the beam, \(\tilde{\kappa}_{0} = R_{0}^{\prime}R_{0}^{T}\), and usually the components of \(\underline {\kappa}_{0}\) are resolved in the body-attached frame \(\mathcal{B}_{0}\) as \(\lfloor \kappa _{0}^{1},\kappa_{0}^{2},\kappa_{0}^{3}\rfloor^{T} = R_{0}^{T}\underline{\kappa} _{0}\). The notation (⋅)′ represents the spatial derivatives respect to α 1, i.e., (⋅)′=∂(⋅)/∂α 1. Correspondingly, the contravariant base vectors [14] satisfy

$$ \underline{g}^{1} = \frac{\bar{b}_{1}}{\sqrt{g}},\qquad \underline{g}^{2} = \bar{b}_{2} + \alpha_{3} \kappa_{0}^{1}\frac{\bar{b}_{1}}{\sqrt{g}},\qquad \underline{g}^{3} = \bar{b}_{3} - \alpha_{2}\kappa_{0}^{1} \frac {\bar{b}_{1}}{\sqrt{g}} $$
(3)

where \(\sqrt{g} = 1 - \alpha_{2}\kappa_{0}^{3} + \alpha_{3}\kappa_{0}^{2} > 0\) and is near unit. In the deformed state, the position vector of the material point becomes

$$ \underline{X}(\alpha_{1},\alpha_{2}, \alpha_{3}) = \underline {u}_{0}(\alpha_{1}) + \underline{u} (\alpha_{1}) + \alpha_{2}\bar{B}_{2}( \alpha_{1})+\alpha_{3}\bar{B}_{3}(\alpha _{1}) + \underline{w} (\alpha_{1},\alpha_{2}, \alpha_{3}) $$
(4)

where \(\underline{u}(\alpha_{1})\) is the displacement of the reference line point, \(\underline{w}(\alpha_{1},\alpha_{2},\alpha_{3})\) is the warping displacement of the beam material point,

$$\underline{w}(\alpha_{1},\alpha_{2},\alpha_{3}) = \sum_{i=1}^{3}w_{i}(\alpha _{1},\alpha_{2},\alpha_{3})\bar{B}_{i}( \alpha_{1}). $$

Similarly, the deformed covariant base vectors, \(\underline{G}_{i} = {\partial\underline{X} }/{\partial\alpha_{i}}\), can be derived from this position’s representations

$$ \begin{aligned} \underline{G}_{1} &= \bar{b}_{1} + \underline{u}^{\prime} + \alpha _{2}\tilde{\kappa}_{1}\bar{B}_{2} + \alpha_{3}\tilde{\kappa}_{1}\bar{B}_{3} + w_{i}^{\prime}\bar {B}_{i} + w_{i}\tilde{\kappa} _{1} \bar{B}_{i},\\ \underline{G}_{2} &= \bar{B}_{2} + w_{i,2}\bar{B}_{i},\qquad \underline {G}_{3} = \bar{B}_{3} + w_{i,3}\bar{B}_{i} \end{aligned} $$
(5)

where \(\underline{\kappa}_{1}\) is the curvature vector defined as \(\tilde{\kappa}_{1} = (RR_{0})^{\prime}(RR_{0})^{T}\), and notation (⋅),i indicates a derivative with respect to the material coordinate α i for i=2,3. Typically, the components of \(\underline{\kappa}_{1}\) are known in the body-attached frame \(\mathcal{B}\) as \(\underline{\kappa }_{1}^{*}=\lfloor\kappa_{1}^{1}, \kappa_{1}^{2}, \kappa_{1}^{3}\rfloor^{T} = R_{0}^{T}R^{T}\underline {\kappa}_{1}\).

Fig. 1
figure 1

Curved beam configurations

Full size image

The deformation is most concisely described in terms of the deformation gradient tensor,

$$ F = \underline{G}_{1}\underline{g}^{1T} + \underline {G}_{2}\underline{g}^{2T} + \underline{G}_{3} \underline{g}^{3T} = \underline{G}_{i}\underline{g}^{iT}. $$
(6)

The polar decomposition theorem in continuum mechanics states that the deformation gradient tensor can always be decomposed into two parts, one corresponding to a pure rotation and the other to a pure deformation, which is a useful theorem that implies the decoupling of rigid rotation and deformation. In this paper, the deformation gradient tensor is defined in the body-attached frame directly as

$$ F^{*} = \underline{G}_{1}^{*} \underline{g}^{*1T} + \underline {G}_{2}^{*} \underline{g}^{*2T} + \underline{G}_{3}^{*} \underline{g}^{*3T} $$
(7)

where the deformed covariant base vectors \(\underline{G}_{i}\) and undeformed contravariant base vectors \(\underline{g}^{i}\) have been projected into the body-attached frames \(\mathcal{B}\) and \(\mathcal{B}_{0}\), respectively, such that \(\underline{G} _{i}^{*} = R_{0}^{T}R^{T}\underline{G}_{i}\), and \(\underline{g}^{*i} = R_{0}^{T}\underline{g}^{i}\), for i=1,2,3. The alternative formulation of F ∗ can be written as

$$ F^{*} = R_{0}^{T}R^{T} \underline{G}_{i}\underline{g}^{iT}R_{0}. $$
(8)

Because \(\underline{G}_{i}^{*}\) and \(\underline{g}^{*i}\) are both measured in the body-attached frame, even though the frame can translate and rotate arbitrarily in the spatial domain with the time varying, the following physical properties always hold: the deformation gradient tensor F ∗ only describes pure deformation and the rigid rotation has been automatically filtered out. For this definition, the small strain and small local rotation assumptions must be applied. Following the geometric relationship between the rotation tensor and base vectors of the body-attached frame,

$$ RR_{0} = [\bar{B}_{1},\bar{B}_{2}, \bar{B}_{3} ],\qquad R_{0} = [\bar{b}_{1}, \bar{b}_{2},\bar{b}_{3} ], $$
(9)

it is not difficult to find the deformation gradient tensor in details as

$$ F^{*} = \left [ \begin{array}{c@{\quad}c@{\quad}c} \bar{B}_{1}^{T}\underline{G}_{i}\underline{g}^{iT}\bar{b}_{1},& \bar{B}_{1}^{T}\underline{G}_{i}\underline{g}^{iT}\bar{b} _{2},&\bar{B}_{1}^{T}\underline{G}_{i}\underline{g}^{iT}\bar {b}_{3}\\ \bar{B}_{2}^{T}\underline{G}_{i}\underline{g}^{iT}\bar{b}_{1},& \bar{B}_{2}^{T}\underline{G}_{i}\underline{g}^{iT}\bar{b} _{2},&\bar{B}_{2}^{T}\underline{G}_{i}\underline{g}^{iT}\bar {b}_{3}\\ \bar{B}_{3}^{T}\underline{G}_{i}\underline{g}^{iT}\bar{b}_{1},& \bar{B}_{3}^{T}\underline{G}_{i}\underline{g}^{iT}\bar{b} _{2},&\bar{B}_{3}^{T}\underline{G}_{i}\underline{g}^{iT}\bar{b}_{3} \end{array} \right ], $$
(10)

and the components of F ∗ can be written as

$$ F_{ij}^{*} = \bar{B}_{i}^{T} \underline{G}_{k}\underline{g}^{kT}\bar{b}_{j}, $$
(11)

which is identical to the mixed formulation of Hodges [8].

2.2 Strain–displacement relations

For the majority of engineering beam problems that are treatable with a beam theory at all, the theory of small local deformation and local rotation is adequate. Based on this theory, the Lagrangian strain tensor [14] is simplified to

$$ \varepsilon_{ij} = \frac{1}{2} \bigl(F_{ij}^{*}+F_{ji}^{*}\bigr) - \delta_{ij}, $$
(12)

and the associated strain field is given as follows:

$$\begin{aligned} \sqrt{g}\varepsilon_{11} =& \gamma_{11} + \alpha_{3}\bigl(\kappa _{1}^{2}- \kappa_{0}^{2}\bigr) - \alpha_{2}\bigl( \kappa_{1}^{3}-\kappa _{0}^{3}\bigr) + w_{1}^{\prime} + \kappa_{0}^{1}( \alpha_{3}w_{1,2}-\alpha _{2}w_{1,3}) + \kappa_{1}^{2}w_{3} - \kappa_{1}^{3}w_{2}, \\ \sqrt{g}2\varepsilon_{12} =& 2\gamma_{12} - \alpha_{3}\bigl(\kappa _{1}^{1}- \kappa_{0}^{1}\bigr) + w_{2}^{\prime} + \sqrt{g}w_{1,2} + \kappa _{0}^{1}( \alpha_{3}w_{2,2}-\alpha_{2}w_{2,3}) + \kappa_{1}^{3}w_{1} - \kappa_{1}^{1}w_{3}, \\ \sqrt{g}2\varepsilon_{13} =& 2\gamma_{13} + \alpha_{2}\bigl(\kappa _{1}^{1}- \kappa_{0}^{1}\bigr) + w_{3}^{\prime} + \sqrt{g}w_{1,3} + \kappa _{0}^{1}( \alpha_{3}w_{3,2}-\alpha_{2}w_{3,3}) + \kappa_{1}^{1}w_{2} - \kappa_{1}^{2}w_{1}, \\ \varepsilon_{22} =& w_{2,2}, \\ 2\varepsilon_{23} =& w_{2,3}+w_{3,2}, \\ \varepsilon_{33} =& w_{3,3}, \\ \varepsilon_{21} =& \varepsilon_{12},\qquad \varepsilon_{31} = \varepsilon _{13},\qquad \varepsilon_{32} = \varepsilon_{23}, \end{aligned}$$
(13)

where γ 11, 2γ 12 and 2γ 13 are the components of the force strain vector \(\underline{e}_{1}^{*}\), and are conveniently expressed in terms of one-dimensional variables as

$$ \underline{e}_{1}^{*} = \lfloor \gamma_{11},2\gamma_{12},2\gamma _{13} \rfloor^T = R_{0}^{T}R^{T}\bigl( \underline{u}_{0}^{\prime} + \underline{u}^{\prime}\bigr) - \bar{i}_{1}. $$
(14)

For the Lagrangian strain formulation, both quantities \(\underline{e}_{1}^{*}\) and \(\underline{\kappa}_{1}^{*}\) are measured in the body-attached frame \(\mathcal{B}\), which will be used as generalized strain measurements for further dynamic analysis. Usually, the initial curvature \(\underline{\kappa }_{0}\) is not zero, and the covariant base vector \(\underline{g}_{1}\) will never be a unit vector, so the initial curvature has contributions to the Lagrangian strain formulation. In order to obtain a more simplified representation of the strain field, the definition of the Lagrangian strain further modifies to

$$ \varepsilon_{ij} = \frac{1}{2} \bigl(F_{ij}^{*}+F_{ji}^{*}\bigr) - \frac {1}{2}\bigl(\underline{g} ^{iT}\bar{b}_{j}+ \underline{g}^{jT}\bar{b}_{i}\bigr). $$
(15)

For the prismatic beam, the modified formulation will recover Eq. (12). The matrix form of the strain field is obtained from the modified stain definition as

$$ \underline{\varepsilon}^{*} = \varGamma_{h} \underline{w}+ \varGamma _{\epsilon} \underline{\epsilon}^{*} + \varGamma_{R} \underline{w}+ \varGamma_{\ell}\underline {w}^{\prime} $$
(16)

with the following notations

$$ \begin{aligned} \underline{\varepsilon}^{*} &= \left \vert \begin{array}{c} \varepsilon_{11}\\ 2\varepsilon_{12}\\ 2\varepsilon_{13}\\ \varepsilon_{22}\\ 2\varepsilon_{23}\\ \varepsilon_{33} \end{array} \right \vert ,\qquad \varGamma_{h} = \left [ \begin{array}{c@{\quad}c@{\quad}c} 0 & 0 & 0\\ \frac{\partial}{\partial\alpha_{2}} & 0 & 0\\ \frac{\partial}{\partial\alpha_{3}} & 0 & 0\\ 0 & \frac{\partial}{\partial\alpha_{2}} & 0\\ 0 & \frac{\partial}{\partial\alpha_{3}} & \frac{\partial}{\partial\alpha_{2}}\\ 0 & 0 & \frac{\partial}{\partial\alpha_{3}} \end{array} \right ],\\ \varGamma_{\epsilon} &= \frac{1}{\sqrt{g}}\left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 1 &0 &0 &0 &\alpha_{3} &-\alpha_{2}\\ 0 &1 &0 &-\alpha_{3}&0 &0\\ 0 &0 &1 &\alpha_{2} &0 &0\\ 0 &0 &0 &0 &0 &0\\ 0 &0 &0 &0 &0 &0\\ 0 &0 &0 &0 &0 &0 \end{array} \right ], \end{aligned} $$
(17)

and

$$ \underline{\epsilon}^{*} = \left \vert \begin{array}{c} \underline{e}_{1}^{*}\\ \underline{\kappa}_{1}^{*} \end{array} \right \vert ,\qquad \varGamma_{R} = \frac{1}{\sqrt{g}}\left [ \begin{array}{c} \tilde{\kappa}_{1} + \kappa_{0}^{1}(\alpha_{3}\frac{\partial }{\partial\alpha_{2}} - \alpha _{2}\frac{\partial}{\partial\alpha_{3}})I_{3}\\ O_{3} \end{array} \right ],\qquad \varGamma_{\ell} = \frac{1}{\sqrt{g}}\left [ \begin{array}{c} I_{3}\\ O_{3} \end{array} \right ] $$
(18)

where I 3 is the 3×3 identity matrix, O 3 the 3×3 zero matrix. If the shear strains 2γ 12 and 2γ 13 are neglected, the strain field, Eq. (16), is exactly the same as Eq. (14) of Yu et al. [9], even though the one-dimensional strain vector \(\underline{e} _{1}^{*}\) and curvature \(\underline{\kappa}_{1}^{*}\) have slightly different physical significance.

2.3 Dimension reduction

The strain energy of the beam cross-section is defined as

$$ U = \frac{1}{2}\int_{\varOmega} \underline{ \varepsilon }^{*T}\mathcal{D}\underline{\varepsilon}^{*}\sqrt {g}\,d\alpha_{2}\,d\alpha_{3} $$
(19)

where \(\mathcal{D}\) is the 6×6 symmetric material matrix in the cross-sectional basis. It is well-known that a beam has one dimension that is much larger than the other two, so the beam is always treated as a one-dimensional problem. Hodges and his coworkers [9, 14, 15] have developed a dimension reduction approach to construct a one-dimensional beam theory from three-dimensional elasticity. Based on variational asymptotic method [16], a minimization problem needs to be solved to represent the three-dimensional strain energy, Eq. (19), by finding the strain energy which could be stored in an imaginary one-dimensional body. In doing so, the warping must be defined as a linear function of one-dimensional strain measures and its derivatives, \(\underline{w}= \underline{w}(\underline {\epsilon}^{*},\underline{\epsilon}^{*\prime})\), then it disappears from the problem and affects only the elastic constants of the beam. Finally, the three-dimensional strain energy of the beam cross-section can be reproduced in terms of one-dimensional quantities

$$ U = \frac{1}{2} \underline{\epsilon}^{*T} \mathcal{C}^{*} \underline {\epsilon}^{*} $$
(20)

where \(\mathcal{C}^{*}\) is an approximation of the stiffness matrix of the beam cross-section. The finite element based approach for the computation of \(\mathcal{C}^{*}\) can be found in [17]. Referring Yu’s algorithm [17], the paper develops a linear two-dimensional finite element code for cross-section analysis which is combined with a one-dimensional beam procedure to solve the three-dimensional beam problem. In details, the two-dimensional finite element based approach will calculate the stiffness matrix \(\mathcal{C}^{*}\) used for further one-dimensional analysis, and then the warping field \(\underline{w}\) will be recovered once the force strain of the reference line is evaluated by the one-dimensional procedure.

2.4 Semi-discretized governing equations of motion

The paper has paid special attention to the slender, closed-section beams. Based on the assumption of small local deformation, the contribution of sectional warping to beam kinematic energy is neglected. The governing equations of motion of the beam are derived from Hamilton’s principle. Note that the velocity of a material point can be obtained by taking a time derivative of position, Eq. (4), and resolved in basis \(\mathcal {B}\) to find

$$ \dot{\underline{u}}^{*} = R_{0}^{T}R^{T} \dot{\underline{u}} + \tilde{s}^{*T}\underline{\omega}^{*} $$
(21)

where \(\dot{(\cdot)}\) indicates a derivative with respect to time, \(\underline{\omega}^{*}\) are the components of the angular velocity vector measured in basis \(\mathcal{B}\) and \(\tilde{\omega}^{*} = R_{0}^{T}R^{T}\dot{R}R_{0}\), \(\underline{s}^{*}\) is the in-plane vector also measured in basis \(\mathcal{B}\), \(\underline{s}^{*} =\alpha_{2}\bar{i}_{2}+\alpha_{3}\bar{i}_{3}\). The variation of the kinetic energy

$$ \delta K = \int_{L} \int _{\varOmega} \rho\delta\dot{\underline {u}}^{*T}\dot{ \underline{u} }^{*}\,d\varOmega \,d\alpha_{1} $$
(22)

is recast as

$$ \delta K = \int_{L}\delta \underline{v}^{*T}M^{*}\underline {v}^{*}\,d \alpha_{1} $$
(23)

where the following notations

$$ \underline{v}^{*} = \left \vert \begin{array}{c} R_{0}^{T}R^{T}\dot{\underline{u}}\\ \underline{\omega}^{*} \end{array} \right \vert ,\qquad M^{*} = \left [ \begin{array}{c@{\quad}c} m I_3 & \tilde{\eta}^{*T}\\ \tilde{\eta}^{*} & \iota^{*}\\ \end{array} \right ] $$
(24)

and the sectional mass constants

$$ m = \int_{\varOmega}\rho \,d\varOmega,\qquad \tilde{\eta}^{*} = \int_{\varOmega}\rho\tilde{s}^{*} \,d\varOmega,\qquad \iota^{*} = \int_{\varOmega}\rho \tilde{s}^{*}\tilde{s}^{*T} \,d\varOmega $$
(25)

are defined, and ρ is the density of the beam material. Meanwhile, the variation in sectional velocity is found to be

$$ \delta\underline{v}^{*} = \left \vert \begin{array}{c} R_{0}^{T}R^{T}(\delta\dot{\underline{u}} + \tilde{\dot{u}}\underline{\delta \psi})\\ R_{0}^{T}R^{T}\underline{\delta{\dot{\psi}}} \end{array} \right \vert $$
(26)

where \(\underline{\delta\psi}\) is the virtual rotation vector defined in inertial frame, \(\widetilde{\delta\psi} = \delta(RR_{0})R_{0}^{T}R^{T}\).

The variation of the strain energy in the beam, δU, is modified to

$$ \delta U = \int_{L}\delta\underline{ \epsilon}^{*T}\mathcal{C}^{*} \underline{\epsilon}^{*}\,d \alpha_{1} = \int_{L}\delta\underline{e}_{1}^{*T} \underline{N}_{1}^{*}\,d\alpha _{1} + \int _{L} \delta \underline{\kappa}_{1}^{*T} \underline{M}_{1}^{*} \,d\alpha_{1} $$
(27)

using the definition of beam’s sectional loads

$$ \left \vert \begin{array}{c} \underline{N}_{1}^{*}\\ \underline{M}_{1}^{*} \end{array} \right \vert = \mathcal{C}^{*}\left \vert \begin{array}{c} \underline{\epsilon}^{*}\\ \underline{\kappa}^{*} \end{array} \right \vert . $$
(28)

It is not difficult to find the variations in strain components from Eq. (14) as

$$ \delta\underline{e}_{1}^{*} = R_{0}^{T}R^{T}\bigl(\delta\underline {u}^{\prime} + \widetilde{\underline{u}_{0}^{\prime}+ \underline{u}^{\prime}}\underline {\delta\psi}\bigr),\qquad\delta \underline{ \kappa}_{1}^{*} = R_{0}^{T}R^{T} \underline{\delta\psi }^{\prime}. $$
(29)

Virtual work done by the externally applied force is

$$ \delta W = \int_{L}\delta \underline{u}^{T}\underline{F}\,d\alpha_{1} + \int _{L} \underline {\delta\psi}^{T} \underline{T}\,d \alpha_{1} $$
(30)

where \(\underline{F}\) and \(\underline{T}\) are applied loads per unit span, measured in the inertial frame. Substituting Eqs. (23), (27) and (30) into Hamilton’s principle and integrating by parts yields the governing equations of motion as follows:

$$\begin{aligned} \begin{aligned} \dot{\underline{h}} - \underline{N}^{\prime}_{1} &= \underline {F}, \\ \tilde{\dot{u}}\underline{h}+ \dot{\underline{g}} - \bigl( \widetilde{\underline{u}_{0}^{\prime}+\underline{u} ^{\prime}}\bigr)\underline{N}_{1} - \underline{M}_{1}^{\prime} &= \underline{T} \end{aligned} \end{aligned}$$
(31)

where \(\underline{h}\) and \(\underline{g}\) are the components of the sectional linear and angular momenta measured in the inertial frame, respectively. Meanwhile, the beam’s sectional forces and moments are transferred, \(\underline{N} _{1} = RR_{0}\underline{N}_{1}^{*}\) and \(\underline{M}_{1} = RR_{0}\underline{M}_{1}^{*}\).

For semi-discretization of beam modeling, the Galerkin approximation states that

$$ \int_{L} \underline{w}_{6\times1}^{T} \left ( \begin{array}{c} \dot{\underline{h}} - \underline{N}^{\prime}_{1} - \underline{F}\\ \tilde{\dot{u}}\underline{h}+ \dot{\underline{g}} - (\widetilde{\underline{u}_{0}^{\prime}+\underline{u} ^{\prime}})\underline{N}_{1} - \underline{M}_{1}^{\prime} - \underline{T} \end{array} \right ) \,d\alpha_{1} = 0 $$
(32)

where \(\underline{w}_{6\times1}\) is a test function. The classical choice of a test function utilizes the shape functions, \(\underline{w}= \mathcal {H}\underline {\delta x}\), where \(\mathcal{H}\) is the interpolation matrix containing the components of shape functions, h i , at all n nodes of a beam element, \(\underline{\delta x}\) is the variation of the nodal displacements and rotations. The interpolation matrix \(\mathcal{H}\) and variations \(\underline{\delta x}\) are given as

$$ \mathcal{H}^{T} = \left [ \begin{array}{c@{\quad}c} h_{1}I & 0\\ 0 & h_{1}I\\ h_{2}I & 0\\ 0 & h_{2}I\\ \vdots& \vdots\\ h_{n}I & 0\\ 0 & h_{n}I \end{array} \right ]_{6n\times6},\qquad \underline{\delta x} = \left \vert \begin{array}{c} \delta\underline{u}_{1}\\ \underline{\delta\psi}_{1}\\ \delta\underline{u}_{2}\\ \underline{\delta\psi}_{2}\\ \vdots\\ \delta\underline{u}_{n}\\ \underline{\delta\psi}_{n} \end{array} \right \vert _{6n\times1}. $$
(33)

Integrating the Galerkin weak form, Eq. (32), by parts will yield a set of semi-discretized governing equations of motion. In general, implicit integrators are applied to solve these equations. However, the finite rotation forms a set of second-order orthogonal tensor including three independent variables with six constraints, so that the rotation vectorization must be applied before the integration. The paper utilizes the Wiener–Milenković parameters [18], or equivalently the conformal rotation vector, to vectorize the rotations. The conformal rotation vector, \(\underline{c}= 4\tan(\phi/4)\bar{n}\), describes the finite rotation of magnitude ϕ about an appropriate axis \(\bar{n}\). This vector, \(\underline{c}^{T} = \lfloor c_{1}, c_{2}, c_{3}\rfloor\), is a minimal set representation of rotation, but the singularity can first occur when ϕ=ϕ±2π. The current implementation selects the total translation \(\underline{u}\) and incremental conformal rotation vector, \(\Delta\underline{c}= 4\tan(\Delta\phi/4)\bar{n}\), as unknowns to avoid the singularity. Only a small time step is used to achieve convergence and guarantee the accuracy of the solution when advancing the integration from initial time t i to final time t f . As depicted in Fig. 1, the incremental rotation ΔR becomes small and Δϕ<2π. Furthermore, the interpolation approach proposed by Jelenić and Crisfield [11] has been applied in this paper to guarantee the compatibility and objectivity of rotation interpolation. Figure 1 also shows the configuration of the beam at the beginning time t i of a typical time step. If the dynamic simulation successfully proceeds up to time t i , both the corresponding translation and rotation tensors are determined. Further observations show that the angular velocity, \(\underline{\omega}\), can be computed from

$$ \tilde{\omega}= \Delta\dot{R}\Delta R^{T},\qquad \underline{\omega}= H(\Delta\underline{c})\Delta \dot{\underline{c}} $$
(34)

where \(H(\Delta\underline{c})\) is the conformal rotation vector related matrix [18]. The discrete formula of governing equations of motion in the state space is derived from the Galerkin weak form as

$$ \left [ \begin{array}{c@{\quad}c} \Delta\mathcal{H}& 0\\ 0 & \mathcal{M} \end{array} \right ] \left \vert \begin{array}{c} \dot{\hat{\underline{u}}}_{n}\\ \dot{\hat{\underline{v}}}_{n} \end{array} \right \vert = \left \vert \begin{array}{c} \hat{\underline{v}}_{n}\\ \hat{\underline{f}}_{n} \end{array} \right \vert $$
(35)

where the following notations are introduced:

$$\begin{aligned} \begin{aligned} \hat{\underline{u}}_{n} &= \left \vert \begin{array}{c} \underline{u}_{1}\\ \Delta\underline{c}_{1}\\ \underline{u}_{2}\\ \Delta\underline{c}_{2}\\ \vdots\\ \underline{u}_{n}\\ \Delta\underline{c}_{n} \end{array} \right \vert ,\qquad \hat{\underline{v}}_{n} = \left \vert \begin{array}{c} \underline{v}_{1}\\ \underline{\omega}_{1}\\ \underline{v}_{2}\\ \underline{\omega}_{2}\\ \vdots\\ \underline{v}_{n}\\ \underline{\omega}_{n} \end{array} \right \vert ,\\ \Delta\mathcal{H}&= \left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} I & & & & & & \\ & H(\Delta\underline{c}_{1}) & & & & & \\ & & I & & & &\\ & & & H(\Delta\underline{c}_{2}) & & &\\ & & & & \ddots& &\\ & & & & & I & \\ & & & & & & H(\Delta\underline{c}_{n}) \end{array} \right ], \end{aligned} \end{aligned}$$
(36)

together with the discretized mass matrix

$$ \mathcal{M}_{6n \times6n} = \int_{L} \mathcal{H}^{T}\left [ \begin{array}{c@{\quad}c} mI & \tilde{\eta}^{T} \\ \tilde{\eta}& \iota\\ \end{array} \right ] \mathcal{H}\,d\alpha_{1} $$
(37)

and right-hand side vector

$$ \hat{\underline{f}}_{6n\times1} = \int_{L} \mathcal{H}^{T}\left \vert \begin{array}{c} -\tilde{\omega}\tilde{\eta}^{T}\underline{\omega}+ \underline{N}_{1}^{\prime} + \underline{F}\\ -\tilde{\omega} \iota \underline{\omega}+ (\widetilde{\underline{u}_{0}^{\prime}+\underline{u}^{\prime }})\underline{N}_{1} + \underline{M}_{1}^{\prime} + \underline{T} \end{array} \right \vert \,d \alpha_{1} . $$
(38)

The mass constants have been transformed into inertial frame, \(\underline{\eta}= RR_{0} \underline{\eta} ^{*}\) and \(\iota= RR_{0}\iota ^{*} R_{0}^{T}R^{T}\).

3 Numerical examples

3.1 Cantilevered beam

A rectangular cantilevered beam of 508 mm in length, 25.4 mm in width and 50.8 mm in height is depicted in Fig. 2. The cross-section is divided into four layers made of two different isotropic materials along the α 3 direction. The Young’s modulus E for the top and bottom layers is 2.6×107 psi, and for the middle two it is 2.6×106 psi; the Poisson’s ratio is μ=0.3. Five cubic one-dimensional beam elements discretize the beam along a reference line. The beam cross-section discretizes into 192 two-dimensional quadrilateral elements, each containing 8 nodes. The stiffness of the cross-section has been calculated based on the variational asymptotic method, and the predictions of current approach are the same as those of [17]. The beam suffers transverse loads of magnitude 89.0 kN at the tip, and the deformed configuration can be found in Fig. 2. The same problem has been solved by LS-DYNA version 9.7.1, where the beam had been discretized into 5000 three-dimensional solid elements, as shown in Fig. 3. Concentrated forces with the amplitude of 706.35 N have been directly applied to each node on the surface of the beam tip cross-section in the transverse direction, which is equivalent to a load of magnitude 706.35×126=89.0 kN applied at the centroid of the tip cross-section, where 126 is the total number of nodes on the surface of the cross-section. The deformed configuration is also presented in Fig. 3. The dynamic response of the beam was integrated by 2-stage Radau IIA algorithm [19] in this paper. The time histories of displacement and velocity in the transverse direction of the centroid of the beam tip cross-section are described in Fig. 4. The results of the current model are compared with those of the three-dimensional LS-DYNA model. The relative error

$$ \epsilon_{r} = \frac{1}{N}\sum _{i=1}^{N}\frac{|u^{f}_{3i}-u^{d}_{3i}|}{|u^{d}_{3i}|} $$
(39)

is used to measure the displacement difference, where N is the total number of sampling points, \(u^{f}_{3i}\) and \(u^{d}_{3i}\) are the sampling points of transverse displacement, u 3, predicted by the proposed approach and LS-DYNA, respectively. This quantity is computed as ϵ r =0.224 %, and a perfect curve fit is observed. For general one-dimensional beam theory, the deformation of an arbitrary point on the beam cross-section cannot be predicted due to the rigid plane assumption of the cross-section. The current warping beam model can predict the three-dimensional strain tensor of an arbitrary point. The time history of the strain component ε 22 of a point, (254.0,−1.5875,−11.1125) mm, is depicted in Fig. 5. The result has been compared with that of LS-DYNA, and the relative error is calculated as ϵ r =1.3669 %.

Fig. 2
figure 2

Rectangular cantilevered beam

Full size image
Fig. 3
figure 3

LS-DYNA model of rectangular cantilevered beam

Full size image
Fig. 4
figure 4

Transverse response of rectangular cantilevered beam: solid line (⋄), the result of the current approach; dashed line (+), the result of LS-DYNA

Full size image
Fig. 5
figure 5

Time history of strain ε 22 of rectangular cantilevered beam: solid line (⋄), the result of the current approach; solid line (∘), the result of LS-DYNA

Full size image

3.2 Buckling of circular arch

The second example deals with the buckling of a circular arch, as depicted in Fig. 6. The arch frame is clamped at one end and hinged at another, which is subjected to a vertical compressive load applied at its middle. The radius of the arch is R=100, and the swept angle of the arch is θ=215∘. The Young’s modulus is selected as E=3.0×106 for isotropic material, and the Poisson’s ratio is μ=0. The rectangular cross-section has the size of 1×4, then the bending stiffnesses are determined directly as EI yy =1.6×107 and EI zz =1.0×106. The two-dimensional finite element code discretizes the cross-section into 400 elements, each element contains 4 nodes. The calculated bending stiffnesses, EI yy and EI zz , are the same as from analytical results, the calculated torsional stiffness is J=1.68757×107, and the calculated shearing stiffnesses are K 22=5.04168×106 and K 33=5.0026×106, respectively.

Fig. 6
figure 6

Circular arch configurations: solid line (∘), undeformed configuration; solid line (□), the first buckling mode; solid line (⋄), the second buckling mode

Full size image

This buckling problem has been solved for Euler–Bernoulli kinematics in [20], and the analytical solution for the first critical load is determined as P ana=897.0. The numerical solution of Ibrahimbegović [21] for the same problem is P num=897.3. The current approach simulates the whole buckling process dynamically. The arch is discretized into 20 cubic beam elements along a reference line, and the inertial load has been neglected by using a tiny material density, ρ=1.0×10−9. The simulation results show that if the compressive load reaches 897.0, the buckling happens. The buckling mode is described in Fig. 6. When the compressive load continuously increases to 907.4, the snap-through happens, and the buckling mode, eight-loop like shape, is observed. The warping of the arch middle cross-section is depicted in Fig. 7, in which the snapshots of warping fields at these two buckling modes are captured. The middle cross-section rotates 202.7∘ when the eight-loop buckling happens. Obviously, the warping is small even though a large arch deformation has happened.

Fig. 7
figure 7

Circular arch local warping fields: dashed line, undeformed cross-section; dashed–dotted line, deformed cross-section of the first buckling mode; solid line, deformed cross-section of the second buckling mode

Full size image

3.3 Jeffcott rotor with flexible anisotropic bearings

The last example deals with the Jeffcott rotor which is composed of a flexible anisotropic shaft of length L=1 m and of a mid-span rigid disk of mass M=5 kg and radius R=0.18 m, as depicted in Fig. 8. The shaft, modeled by six equally spaced cubic beam elements developed in this paper, is connected to the end flexible couplings, represented by concentrated springs. The finite stiffness end bearings consist of revolute joints connected to the ground by concentrated springs. The relative rotation of the left-hand side revolute joint was prescribed to have a constant angular speed Ω=24 rad/s. The sectional properties of the shaft and the stiffness properties of the elastic coupling can be found in [22]. The rigid disk suffers an external perturbation along the \(\bar{i}_{3}\) axis, f 3=100sin(20πt) N for t∈[0,0.05] s. The 3-stage Radau IIA algorithm [19] is applied to predict the forced response of Jeffcott rotor. The simulation runs for a total of 1 s with a time step Δt=0.1 ms. Figure 9 presents the time histories of translation components, u 2 and u 3, and rotation component, c 1, of the midpoint of shaft, respectively. The same problem has been solved by using DYMORE [7], after modeling the flexible shaft by the beam element of Bauchau and Hong [6]. The simulation results can also be found in Fig. 9. Once again, the relative error of u 3, Eq. (39), is calculated as ϵ=2.698×10−8. Apparently, it can be concluded that the dynamic responses of the beam model implemented in the paper can perfectly match those of the beam model developed by Bauchau and Hong.

Fig. 8
figure 8

Jeffcott rotor with flexible anisotropic bearings

Full size image
Fig. 9
figure 9

Displacement components u 2, u 3 and rotation component c 1 of Jeffcott rotor with isotropic bearing. (Top figure) u 2 by Radau IIA, solid line (∘); u 3 by Radau IIA, solid line (⋄); u 2 by DYMORE, dashed line (△); u 3 by DYMORE, dashed line (▽). (Bottom figure) c 1 by Radau IIA, solid line (∘); c 1 by DYMORE, dashed line (△)

Full size image

4 Conclusion

A new type of geometrically exact beam element with small warping is developed in this paper, which features large displacements and rotations together with small strains. The dimension reduction approach based on variational asymptotic method has been explored. A linear two-dimensional finite element procedure is developed to predict the cross-sectional stiffness and recover the cross-sectional strain fields. The mixed formula of governing equations of motion for one-dimensional beam is presented, in which the rotation was vectorized by Wiener–Milenković parameters and the singularity of finite rotation was avoided. The implicit Radau IIA algorithms are applied to solve the dynamic problem of the new beam element. The paper presents three numerical examples to validate the developed beam model. The first one focuses on the warping prediction of the new element. The simulation results have been compared to those of the three-dimensional solid model created by commercial software, LS-DYNA. The second example simulates the buckling process of a circular arch by using the new beam element. The calculation results prove the capability of the new beam to accurately describe a large deformation. The last one, a Jeffcott rotor, validates the new element by comparing it with the beam developed by Bauchau and Hong. It can be concluded that the current beam modeling approach features high accuracy, and the new beam element with warping is robust enough to predict large deformations.