Introduction

The investigation of the nonlinear coupling phenomenon in nonlinear dynamics is of great significance for a broad range of applications, including aerospace, robot and vehicle engineering. Due to the larger elastic deformation of flexible components, the high accuracy analysis is difficult to achieve using either the traditional multi-rigid-body system dynamics or flexible multi-body dynamics with small deformation. Therefore, the flexible multi-body dynamics model with large displacements and rotations is widely used in nonlinear dynamics for its high calculation accuracy and efficiency [1,2,3,4]. Two commonly used methods are the absolute nodal coordinate formulation (ANCF) and the geometrically exact formulation (GEF).

Shabana [5] first proposed the ANCF method and further established a one-dimensional beam element model, which was called as the milestone in the development of flexible multi-body system dynamics [6, 7]. Such method was first applied to study the dynamics of flexible systems with large deformation by Escalona et al. [8]. Based on the ANCF method, a three-dimensional beam element [9, 10] and a planar beam element of gradient-deficient ANCF [11] were proposed, respectively. Gerstmayr et al. [12] extended the planar beam element of gradient-deficient ANCF to the spatial beam element of gradient-deficient ANCF. Subsequently, Schwarze et al. [13] proposed a reduced integration solid shell finite element. To investigate the thermoelastic effect on the deployment of space structure, Wu et al. [14] proposed a new approach based on flexible multibody system. Sopanen and Mikkola [15] presented an accurately elastic force model to avoid the Poisson locking. Omar et al. [16] established a simplified model of leaf spring with the ANCF method. Liu et al. [17,18,19] proposed a new hybrid-coordinate formulation which was suitable for dealing with the flexible multibody systems with large deformation. Tian et al. [20,21,22] studied the dynamic modeling and analyzed the planar flexible multi-body systems with clearance and lubricated revolute joints. To model composite laminated plates accurately, Liu et al. [23] proposed a new type of composite laminated plate element of ANCF and derived the efficient formulations to evaluate both the elastic force and the Jacobian.

The other commonly used method was GEF theory, which was first proposed by Reissner [24]. Simo and Vu-Quoc [25] further improved the GEF theory by developing the implicit time stepping algorithm, the exact linearization of the algorithm and associated configuration update. In the field of study for limitation of invariance to rigid-body rotations, Crisfield et al. [26] proposed a new method for the two-node element by obtaining the relative rotation matrix and interpolating the rotation vector. Huang et al. [27] demonstrated that the obtained approximation is invariant under the superposed rigid body motions, and the objectivity of the continuum model is preserved.

From the above researches, it can be found that both the ANCF method and the GEF theory developed rapidly and widely used. To analyze the difference between the two theories, Romero [28] studied and compared the two methods in statics, they proposed that the ANCF theory should be considered for the codes that do not work with rotation variables, and when the concentrated moments and imposed rotations are needed to be sustained by the structural models, the GEF theory is suitable because these features cannot be achieved by the ANCF element. Subsequently, Bauchau et al. [29] performed a comparative analysis of both the computational accuracy and efficiency of the two methods on the two-dimensional plane. However, only some static response in two-dimensional plane are concerned, the systematic study on statics and dynamics which is much closer to the practical engineering have not been studied yet, especially the responses of the three-dimensional model.

Motivated by the aim mentioned above, the governing equations are established based on the ANCF fully parameterized beam element, the ANCF gradient-deficient beam element and the GEF beam element. Both the static and dynamic responses of the three-dimensional flexible multibody system with large deformation are simulated in detail, the characteristics of each element type for analyzing the nonlinear dynamics of flexible multibody systems are provided. Based on the results, the appropriate choice of formulation for high calculation accuracy and efficiency in different applications is also given.

Theoretical Model of the Beam Element and Computational Strategy

ANCF Fully Parameterized Beam Element

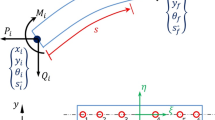
The schematic of the three-dimensional fully parameterized beam element with two nodes is shown in Fig. 1, which is described by the absolute node coordinates.

Fig. 1
figure 1

The three-dimensional fully parameterized beam element

Full size image

The position vector of any point on the element can be expressed as [5, 6]

$${r} = \overline{e}\overline{S}\left( {\xi ,\eta ,\zeta } \right)$$
(1)

where ξ = x/l, η = y/l, ζ = z/l, x, y, z are the local coordinates of the element, respectively, l is the length of the element. Generalized coordinates of the element can be expressed as

$$\overline{e} = \left[ {\begin{array}{*{20}c} {r_{i} } & {r_{i,x} } & {r_{i,y} } & {r_{i,z} } & {r_{j} } & {r_{j,x} } & {r_{j,y} } & {r_{j,z} } \\ \end{array} } \right]$$
(2)

where ri,x, ri,y, ri,z represent the partial derivative vector of the position vector r along ξ, η, ζ direction, respectively, that is, ri,x = əri/əx, ri,y = əri/əy, ri,z = əri/əz. It can be found from Eq. (2) that there is one position vector and three slope vectors are defined on one node. The shape function of the beam element can be expressed as

$$\overline{S} = \left[ {\begin{array}{*{20}c} {S_{1} } & {S_{2} } & {S_{3} } & {S_{4} } & {S_{5} } & {S_{6} } & {S_{7} } & {S_{8} } \\ \end{array} } \right]^{T}$$
(3)

where S1 = 1 − 3ξ2 + 2ξ3, S2 = l (ξ − 2ξ2 + ξ3), S3 = l (η − ξ η), S4 = l (ζ − ξ ζ), S5 = 3ξ2 − 2ξ3, S6 = l (− ξ 2 + ξ3), S7 = l ξ η, S8 = l ξ ζ.

In addition, it can be obtained by reference [5, 9] for more details on the ANCF fully parameterized beam element.

ANCF Gradient-Deficient Beam Element

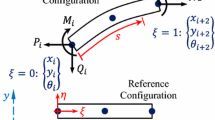
The schematic of the ANCF gradient-deficient beam element described by absolute node coordinates is shown in Fig. 2.

Fig. 2
figure 2

The gradient-deficient beam element

Full size image

Generalized coordinates of the element can be expressed as [30]

$$\overline{e} = \left[ {\begin{array}{*{20}c} {r_{i} } & {r_{i,x} } & {r_{j} } & {r_{j,x} } \\ \end{array} } \right]$$
(4)

Both nodes include one position vector r and its partial derivative vector along ξ direction. The position vector of any point on the centerline can be expressed as

$$r\left( \xi \right) = \overline{e}\overline{S}\left( \xi \right)$$
(5)

The shape function of beam elements is expressed as

$$\overline{S} = \left[ {\begin{array}{*{20}c} {S_{1} } & {S_{2} } & {S_{3} } & {S_{4} } \\ \end{array} } \right]^{T}$$
(6)

where S1 = 1 − 3ξ2 + 2ξ3, S2 = l (ξ − 2ξ2 + ξ3), S3 = 3ξ2 − 2ξ3, and S4 = l (− ξ2 + ξ3).

In addition, it can be obtained by reference [30] for more details on the ANCF gradient-deficient beam element.

Three-Dimensional GEF Beam Element

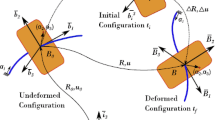
Figure 3 shows the configurations of the three-dimensional beam element, which are described by three reference basis vectors denoted by k1, k2, k3 and three body basis vectors denoted by λ1, λ2, λ3.

Fig. 3
figure 3

Configurations of three-dimensional beam element

Full size image

The position vectors of the point before and after deformation are assumed as x0 = (x0, y0, z0)T and x = (x, y, z)T, respectively. From the geometric relationship, the position vector can be derived as [8]

$$\left\{ {\begin{array}{*{20}c} {x_{0} = \left( {x_{0} ,y_{0} ,z_{0} } \right)^{T} = r_{0} + y_{0} \lambda_{1}^{0} + z_{0} \lambda_{2}^{0} } \\ {x = \left( {x,y,z} \right)^{T} = r + y_{0} \lambda_{1} + z_{0} \lambda_{2} } \\ \end{array} } \right.$$
(7)

where r0 and r are functions of x0, respectively. The expression of the deformation gradient tensor can be written as [31]

$$F = \frac{{{\text{dx}}}}{{{\text{dx}}_{0} }} = \left[ {\begin{array}{*{20}c} {r^{\prime} + y_{0} \lambda_{1}^{\prime } + z_{0} \lambda_{2}^{\prime } } & {\lambda_{1} } & {\lambda_{2} } \\ \end{array} } \right]$$
(8)

where represents the derivative along x direction.

To obtain the six objective strain metrics of the spatial GEF beam element, the translational strain vector γ and rotational strain vector κ are introduced as the following [32].

$$\gamma = \left\{ {\begin{array}{*{20}c} \varepsilon \\ {\gamma_{1} } \\ {\gamma_{2} } \\ \end{array} } \right\} = R^{T} r^{\prime} - \gamma_{0} ,\kappa = \left[ {\begin{array}{*{20}c} 0 & { - \kappa_{3} } & {\kappa_{2} } \\ {\kappa_{3} } & 0 & { - \kappa_{1} } \\ { - \kappa_{2} } & {\kappa_{1} } & 0 \\ \end{array} } \right] = R^{T} R - \kappa_{0}$$
(9)

where R is the functions of x0, ε is the axial strain, γ1 and γ2 are shear strains of the beam element at the current reference frame (λ1, λ2, λ3). κ1 is the torsional strains, κ2 and κ3 are the bending strains of the beam element at the current reference frame (λ1, λ2, λ3). κ0 and γ0 denote the curvature and the strain vector of the beam element at the initial configuration, respectively.

In addition, it can be obtained by reference [24, 25] for more details on the three-dimensional GEF beam element.

Computational Strategy

The assembly of both ANCF fully parameterized beam element and geometrically exact beam element can be carried out is similar to the traditional finite element method. The nodal coordinate on the finite element can be easily transformed into the generalized coordinate on the flexible multibody system. Then the final dynamic equations of the constrained rigid-flexible multibody system [33, 34] can be expressed as:

$$\left\{ {\begin{array}{*{20}c} {M\ddot{q} + F(q) + \Phi_{q}^{T} \lambda = Q(q,\dot{q})} \\ {\Phi (q,t) = 0} \\ \end{array} } \right.$$
(10)

where M, q, F, Q, Φ, Φq, and λ denote the total mass matrix, the generalized coordinate vectors, the elastic force, the generalized external force vector, the system constraint equation, Jacobi matrix for generalized coordinates and the Lagrange multiplier vector, respectively.

Since the step limitation can be induced by the conditional convergence characteristics of the explicit integration algorithm and the implicit integral algorithm is always used to analyze such dynamic equations of the system, the transformation of the dynamic equations is required. The generalized-a implicit integral algorithm proposed by Arnold and Brüls [35] is applied here, during which the equations are discretized into algebraic equations by the finite difference method. The iterative equations can be expressed as

$$\left\{ \begin{aligned} M\ddot{q}_{n + 1} + F\left( {q_{n + 1} } \right) + \Phi_{q}^{T} \lambda_{n + 1} - Q\left( {q_{n + 1} ,\dot{q}_{n + 1} } \right) & = 0 \\ \Phi \left( {q_{n + 1} ,t_{n + 1} } \right) & = 0 \\ \end{aligned} \right.$$
(11)

where the subscript n + 1 represents the value of the variable at n + 1 step during the iteration. Tian et al. [36] and Liu et al. [37] reported that the superiority of the generalized-a implicit integral algorithm was exhibited in dealing with the dynamics of the flexible multibody system with clearance joints.

Results and Discussion

Static Response of the Beam Element

To investigate the accuracy and efficiency of the ANCF fully parameterized beam element, the ANCF gradient-deficient beam element and the GEF beam element, A representative numerical example of three-dimensional cantilever beam is adopted. The theoretical model is shown in Fig. 4. Because the cross-sectional deformation of beam is not involved in the ANCF gradient-deficient beam element, only the displacement response of point A is studied, which is the geometric center of the free end section. In addition, the static responses calculated by the ABAQUS finite element software are regarded as the exact solutions, and the cantilever beam is divided into ten B32 elements. The geometric and material parameters of the cantilever beam are listed in Table 1.

Fig. 4
figure 4

Theoretical model of the cantilever beam

Full size image
Table 1 Geometric and material parameters of the cantilever beam
Full size table

For the axial deformation of the cantilever beam including axial tension and compression, a concentrated load F is applied on the point A along x direction. The displacements of point A calculated by different elements are listed in Table 2, in which Poisson’s ratio λ = 0.3 and concentrated force of 1 kN, 10 kN, − 1 kN and – 10 kN are adopted. It can be found from Table 2 that the result calculated by GEF beam element has a good agreement with the exact solution no matter the beam is in tension or compression state, while the results based on both ANCF fully parameterized beam element and ANCF gradient-deficient beam element are smaller than the exact solution.

Table 2 Displacements of point A when the cantilever beam is in axial deformation state
Full size table

Due to the three-dimensional constitutive relation applied in ANCF fully parameterized beam element, the plane cross-section assumption is not applicable in the three-dimensional model and part of the energy provided by the external force is transformed into the deformation of the cross section, which leads to the smaller results of the ANCF fully parameterized beam element. The large-strain assumption is the factor that induces the smaller value of ANCF gradient-deficient beam element. The computational efficiency of the ANCF fully parameterized beam element is lower than that of the GEF beam element due to the longer time of calculating elastic force by the triple integral. Besides, the computational efficiency of the ANCF fully parameterized beam element is also lower than that of the ANCF gradient-deficient beam element due to the less degree of freedom of the ANCF gradient-deficient beam element. As a result, both the high calculation accuracy and efficiency can be achieved by the GEF beam element in the axial deformation of the cantilever beam.

For the plane bending deformation of the cantilever beam, the concentrated load along z direction is applied on the point A. The results are listed in Table 3, in which the cases with two values of λ are included to study the effect of Poisson’s ratio. The displacements of point A along x and z direction are denoted by u and w, respectively. Table 3 shows that the result calculated by ANCF fully parameterized beam element becomes more accurate when the effect of Poisson’s blocking is removed by reducing λ from 0.3 to 0. Because the cross-sectional deformation of beam can be calculated by the precise geometric nonlinear relation in GEF beam element and that is not involved in the ANCF gradient-deficient beam element, the results based on the ANCF gradient-deficient beam element and the GEF beam element are not affected by the Poisson’s ratio. In comparison, the results obtained by both ANCF gradient-deficient beam element and GEF beam element are closer to the exact results than that of ANCF fully parameterized beam element.

Table 3 Displacements of point A when the cantilever beam is in plane bending state
Full size table

For the bending deformation in three-dimension case, two concentrated loads of − 50 N are applied simultaneously along y direction and z direction on point A. The results are provided in Table 4, in which the cases with two values of λ are adopted. Apparently, the results based on both the ANCF gradient-deficient beam element and the GEF beam element are in good agreement with the exact solutions in three directions, but the results based on the ANCF fully parameterized beam element are relatively poor, especially when λ is 0.3.

Table 4 Displacements of point A when the cantilever beam is in three-dimensional bending state
Full size table

The pure bending deformation of the cantilever beam is also studied by applying the moment M on point A around the z-axis. The angle of rotation α of the free end in this case can be expressed as [38]

$$\alpha = \frac{ML}{{{\text{EI}}}}$$
(12)

where M, EI, L denote the applied moment, flexural rigidity and beam length. Equation (12) shows that the angle of rotation increases with the increasing moment, it can be found that 360° angle of rotation can be obtained when M is 2πEI/L, which is the typical nonlinear large deformation and can be regarded as the exact solution in the case of bending deformation of the cantilever beam.

To compare the high calculation accuracy and convergence rate, the beam is divided into 10, 20 and 30 elements, the results based on the above three elements are shown in Table 5. Table 5 shows that the number of convergence element of both ANCF gradient-deficient beam element and GEF beam element are 20. The results of both the ANCF gradient-deficient beam element and the GEF beam element are closer to the exact result of 360º than that of ANCF fully parameterized beam element. While for the ANCF fully parameterized beam element with different Poisson’s ratio, the element number larger than 30 is required to achieve convergence. As a result, the GEF beam element has the high calculation accuracy and efficiency. The diagram of nonlinear large deflection curves calculated by the GEF beam element is shown in Fig. 5, from which the configuration of the beam caused by different various moment can be found intuitively.

Table 5 Angles of rotation of the free end when the cantilever beam is in pure bending state
Full size table
Fig. 5
figure 5

Diagram of nonlinear large deflection curves with different external moment

Full size image

For the torsion deformation of the cantilever beam, the torque T is applied to the free end around x-axis. Due to the neglect of the cross section, the ANCF gradient-deficient beam element is not considered to solve the response in this case. The beam has also been divided into 10, 20 and 30 elements, the results based on other two types of elements are given in Table 6 under the conditions of T = − 10 Nm and T = − 100 Nm. Table 6 shows that there are good agreements between the results of the GEF beam element and ABAQUS, and the results converge faster when the beam is only discretized into ten elements for GEF beam element. In comparison, the results of the ANCF fully parameterized beam element are quite different from the exact solutions whether Poisson’s ratio exists or not.

Table 6 Angles of rotation of the free end when the cantilever beam is in torsion state
Full size table

According to the above analyses, the suitable element can be selected to solve the static response of the flexible multibody system with large deformation. The GEF beam element has the highest accuracy among the three beam elements when the beam is in axial tension, axial compression and torsion states. Both the ANCF gradient-deficient beam and the GEF beam element have the higher accuracy and efficiency than that of the ANCF fully parameterized beam element when the beam is bent. It is necessary to note that the GEF beam element is the best choice as the cross-sectional deformation of beam needs to be considered.

Dynamic Response of the Beam Element

To study the accuracy of beam element in dynamics, both the three-dimensional simple and double pendulum models are investigated. Due to the ignorance of the cross-sectional deformation, the ANCF gradient-deficient beam element cannot be adopted to solve the three-dimensional dynamic response. In addition, since commercial software cannot directly simulate the dynamics of the flexible multi-body system with large deformation, the simulation of commercial software is not be adopted in the model. Therefore, only the results of the ANCF fully parameterized beam element and the GEF beam element are analyzed in this section, and the dynamic responses simulated by the GEF beam element with time step of 10–4 s are used as reference values.

The Simple Pendulum Model

The dynamic response of the simple pendulum is discussed first. The simple pendulum has a dimension of 1 m × 0.01 m × 0.01 m as shown in Fig. 6, in which an ideal spherical hinge is used to constrain the fixed end. The density, Poisson’s ratio and Young’s modulus are 2700 kg/m3, 0.3 and 3 × 107 Pa, respectively, and the flexible body is divided into ten elements in calculation. Applying the initial condition of θ = 90° and releasing it, the dynamic behaviors of the simple pendulum are induced by gravity.

Fig. 6
figure 6

The schematic of the simple pendulum

Full size image

The displacements of point B which is the geometric center of the free end section along x, y and z direction are shown in Fig. 7a. The results based on the ANCF fully parameterized beam element with time step of 10–2 s and 10–4 s are denoted by the red solid line and blue long dotted line, respectively. The results obtained by the GEF beam element with time step of 10–2 s and 10–4 s are represented by the blue short dotted line and the red dotted line, respectively. Figure 7a1 shows that there is a small difference between the displacement along x direction of the ANCF fully parameterized beam element and the GEF beam element, while the varying tendency has a good consistency. In Fig. 7a2, the displacements along y direction of both elements are zero, which means that the dynamic behavior occurs only in x–z plane. In Fig. 7a3, two apparent features can be found, one is that four curves have good consistency at the initial stage and the difference occurs after about 1.5 s, the peaks of the GEF beam element are higher than that of the ANCF fully parameterized beam element at the later stage. It is the effect of the deviation accumulates with time that leads to the gradual increase in the difference. The other feature is that the different time step has an effect on the calculation accuracy. The smaller time step allows a higher iteration accuracy and calculation accuracy during computation, but the simulation time will be longer.

Fig. 7
figure 7

Displacements of point B along x, y, z direction. The Young’s moduli are (a1–a3) 3 × 107 Pa and (b1–b3) 7 × 1011 Pa, respectively

Full size image

Subsequently, the Young’s modulus of the simple pendulum is transformed into 7 × 1011 Pa from 3 × 107 Pa to enhance the stiffness of simple pendulum and other calculation conditions remain unchanged. The displacements are shown in Fig. 7b, in which the line types of the curve are the same meaning with the above description. We can find that there is a good agreement among the four curves along x, y, z direction, even though the time steps are different, because the influence of nonlinear factor is weakened by the enhanced stiffness.

The Double Pendulum Model

To further study the accuracy of the ANCF fully parameterized beam element and the GEF beam element used in three-dimensional model, the displacement responses of the double pendulum are analyzed, the corresponding schematic diagram is shown in Fig. 8, in which two flexible rods are connected by a ball joint. At the initial moment, both rods are kept in the horizontal plane, i.e., x–y plane and released, the dynamic behaviors are caused by gravity. Two kinds of Young's modulus are used for calculation and both flexible rods are divided into ten elements, respectively, the time step of 10–4 s is adopted, other material and geometric parameters of the rod are the same as those of the accuracy simple pendulum.

Fig. 8
figure 8

Schematic diagram of the double pendulum

Full size image

The displacements of point C which is the geometric center of the section along x, y, z direction based on the two beam elements are shown in Fig. 9, in which the Young’s modulus of 2 × 108 Pa and 7.2 × 1010 Pa for both rods are applied, respectively. The simulation results of the ANCF fully parameterized beam element and the GEF beam element are denoted by the red solid line and blue dotted line, respectively. Figure 9a shows that the two curves are different at the later stage when Young’s modulus is small, while the consistency becomes better with the increase of Young’s modulus as shown in Fig. 9b. Such phenomenon is similar with the situation of the simple pendulum, which is also caused by decreasing elastic deformation of the flexible body and the weakened the nonlinear factor.

Fig. 9
figure 9

Displacements of point C along x, y, z direction. The Young’s moduli of both rods are (a1–a3) 2 × 108 Pa and (b1–b3) 7.2 × 1010 Pa, respectively

Full size image

As a result, it can be concluded that the ANCF fully parameterized beam element and the GEF beam element have higher accuracy for solving dynamic system with large stiffness, while the GEF beam element is the best choice when the stiffness is small.

Conclusions

To achieve the required high accuracy and efficiency in different projects of flexible multibody system with nonlinear large deformation, the characteristics and applicable conditions of the commonly used beam elements which are ANCF fully parameterized beam element, ANCF gradient-deficient beam element and GEF beam element are provided by analyzing both static and dynamic models.

In the statics of the flexible multibody system with nonlinear deformation, the displacement responses of the cantilever beam under axial deformation, torsion and bending are analyzed in detail. The GEF beam element is recommended first when the discretized element is subjected to axial tension, axial compression and torsion. When the element is bent, both ANCF gradient-deficient beam and GEF beam element have the high accuracy and efficiency. In addition, the GEF beam element is the unique choice when the deformation of element section is considered.

For dynamics, the cases of both the simple and double pendulums are analyzed. It can be found that the Young’s modulus and time step in calculation have a great effect on the displacement response due to the factor of nonlinear deformation. The results of the ANCF fully parameterized beam element and the GEF beam element have good consistency when the Young’s modulus is large. While the GEF beam element is the best choice for the small Young’s modulus. All the results are helpful for the selection of beam elements to achieve high accuracy and efficiency of multibody system with nonlinear large deformation.