Heat transfer analysis of Walters’-B fluid with Newtonian heating through an oscillating vertical plate by using fractional Caputo–Fabrizio derivatives

Abstract

This paper presents a study of Walters’-B fluid with Caputo–Fabrizio fractional derivatives through an infinitely long oscillating vertical plate by Newtonian heating under the action of transverse magnetic field. The fractional calculus approach is employed to obtain a system of fractional partial differential equations. The governing equations of momentum and energy are converted first into dimensionless form and then solved by employing Laplace transformation. The Laplace inverse transform has been evaluated both analytically and numerically. The graphical illustrations represent the behavior of material parameters on the solutions. A comparison between exact and numerical solutions is presented in tabular and graphical form. The variation in Nusselt number with the change in fractional and physical parameters is also presented. The velocity and temperature of the fluid decreases with the enhancement in the fractional parameter for small values of time, and it has the opposite behavior for greater values of time.

1 Introduction

During the past several years, heat transfer and fluid motion over enlarged surfaces has attained much attention from scientists and engineers because of their applications in industries like metal spinning, wire drawing, piping and casting systems, cooling of metallic sheets, etc. The behavior of Walters’-B fluid model descries the several polymeric liquids encountered in chemical engineering and biotechnology.

Ariel (1994) and Andersson (1992) have studied the analytical results for nonlinear differential equations of the fourth order. Roy and Chaudhury (1980) evaluated heat and mass transfer analysis of Walters’-B fluid through a plane wall using a perturbation method. Raptis and Takhar (1989) studied Walters’-B fluid with thermal convection flow by a numerical technique. Chang et al. (2011) discussed the heat generated flow of a viscoelastic fluid in a porous medium over a vertical plate. Wang (2003) investigated the influence of the Walters’-B fluid through a plane wall. Mass and heat transfer of a viscoelastic fluid under the action of transverse magnetic field in a free convection flow was discussed by Khan et al. (2016).

The instability of non-Newtonian fluid in a porous channel was examined by Sharma et al. (2002). Chaudhary and Jain (2006) discussed the heat effects on a hydromagnetic mass flow of a viscoelastic fluid through a flat plate. The numerical or approximate results of transient and steady flows of Walters’-B fluid were evaluated for a diverse range of geometries in Kumar and Srivastava (2005), Ghasemi et al. (2011), Nandeppanavar et al. (2010), Prakash et al. (2010), Pal and Mondal (2011), Ali et al. (2016, 2017) and Bhattacharyya et al. (2011).

The hydrodynamic stability of a rotated Walters’-B fluid in the presence of nanoparticles and thermal conduction was evaluated by Sharma and Rana (2001). The Walters’-B fluid (Walters 1962) model was originated to move viscous fluids having elastic behaviors. Soundalgekar and Puri (1969) studied the mathematical aspects of a viscoelastic fluid having a two-dimensional flow through a porous vertical plane wall.

The two-dimensional viscoelastic flow over a smooth surface was investigated by Mahapatra et al. (2007). Nadeem and Akbar (2010) applied numerical integration to find solutions of peristaltic flow of a viscoelastic fluid in a smooth angles tube. Khan et al. (2014) discussed mass transfer in Walters’-B fluid and investigated the effect of Walters’-B parameter on velocity. Rath and Bastia (1978) applied a perturbation technique to discuss the heat transfer and steady flow of Walters’-B fluid within two adjoining smooth porous plates along a common axis. Nanousis (1993) studied the MHD flow of a rotating incompressible Walters’-B fluid.

The viscoelastic flow with a slip condition because of a two-dimensional smooth surface was investigated by Wang (2002). The axisymmetric, uniform, turbulent movement of a Newtonian fluid along an extended sheet having a slip condition was evaluated by Ariel (2007). Wang (2009) reinvestigated the viscous flow through an inextensible sheet under a suction and slip condition. Ariel et al. (2006) reinvestigated the influence of a partial slip condition on the flows of several rate type fluids through an extended plane.

Fractional calculus is used to discuss the viscoelastic properties of materials, such as memory effects. For generalizations of different physical concepts, fractional calculus is a suitable frame-work and an efficient tool. Gemant (1938) was the first to use the fractional derivatives for visco-elasticity. The generalization of several classical dynamics problems was done by many researchers. A relative discussion of Caputo–Fabrizio and Atangana–Baleanu non-integer derivatives to study the flow of a generalized Casson fluid was presented by Sheikh et al. (2017). Exact results of time fractional free convectional flow of a Jeffrey fluid was given in Saqib et al. (2017). The Caputo time fractional derivative has been developed to be more accurate by taking the Laplace transform. In Friedrich (1991) fractional methods were used to study the rheological characteristics of materials. Khan et al. (2017) employed Caputo–Fabrizio derivatives and studied heat transfer aspects in Maxwell fluid model. Vieru et al. (2017) found analytical results for convective flow of an electrically conducting rate type fluid with thermal diffusion through a porous medium by using Caputo fractional derivatives. Vieru et al. (2015) presented the analytical results for fractional free convective flow with constant mass diffusion and Newtonian heating. Shah and Khan (2016) used fractional derivatives for the heat transfer of differential type fluid and attained exact results. Imran et al. (2017) used Caputo time fractional derivatives and found the analytical results for differential type fluid with Newtonian heating. Some latest articles related to the application of Caputo–Fabrizio fractional derivatives are given in Imran et al. (2018), Shah et al. (2017), Butt et al. (2017) and Ahmad et al. (2017).

The purpose of this article is to determine the effect of non-integer time fractional derivatives on heat transfer in Walters’-B fluid over an oscillating vertical plate. Newtonian heating is considered at the boundary of the smooth surface. A contemporary definition of fractional derivatives, named as Caputo–Fabrizio fractional derivatives, has been employed in this article. The analytical solutions of temperature and velocity field have been procured by using the Laplace transform. A comparison between exact and numerical solutions is presented in both graphical and tabular form. For the validation of results, we used two Laplace inverse numerical processes named as Tzou’s and Stehfest’s algorithm. A comparison of obtained results is presented in Table 1. In Table 2, the influence of the physical parameter on heat transfer rate is established. The impact of fractional parameter on dimensionless temperature and velocity field is presented in Tables 3 and 4. Finally, some graphs are plotted to see the impact of the material parameters.

Table 1 Comparison between numerical and analytical results

Table 2 Physical parameters’ effect on Nusselt number

Table 3 Fractional effect on the velocity field

Table 4 Fractional effect on the temperature distribution

2 Formulation of the problem and governing equations

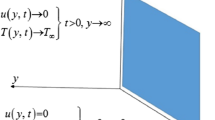
Let us consider a uniform free convectional flow of Walters’-B fluid along an oscillating vertical flat plate with Newtonian heating. Due to the buoyancy strength, the change in temperature extends upward over the plate. The plate is set cognate to the $x$-axis in rising direction and perpendicular to the $y$-axis. The movement is along a magnetic field of strength $B _{0}$ acting perpendicular to the plate. Further, we considered that the induced magnetic field is at very small scale and the magnetic Reynolds number is nugatory. Since the electric field is absent, the electric field caused by charges is neglected. At the beginning for $t \leq 0$, the fluid and plate are at rest and at monotonous temperature $T _{\infty }$. After time $t > 0$, the difference between the temperature is lowered or raised to $T _{w}$. The geometry of the flow is shown in Fig. 1.

Fig. 1

Schematic diagram and physical geometry of the problem

The momentum and energy equations for an unsteady Walter’-B fluid (Khan et al. 2016) are:

$$\begin{gathered} \frac{\partial u(y,t)}{\partial t} = \biggl( \upsilon - \frac{k_{0}}{ \rho } \frac{\partial }{\partial t} \biggr) \frac{\partial ^{2}u(y,t)}{ \partial y^{2}} - \frac{\sigma B_{0}^{2}}{\rho } u(y,t) + (T - T_{ \infty } )g \gamma _{T}, \end{gathered}$$

(1)

$$\begin{gathered} k\frac{\partial ^{2}T(y,t)}{\partial y^{2}} = \rho c_{p}\frac{\partial T(y,t)}{\partial t}. \end{gathered}$$

(2)

The incorporated conditions are:

$$\begin{gathered} T(y,0) = T_{\infty },\qquad u(y,0) = 0,\quad y \ge 0, \end{gathered}$$

(3)

$$\begin{gathered} \frac{\partial T(y,t)}{\partial y} \bigg| _{y = 0} = - \frac{h}{k} \bigl[ T(0,t) \bigr] ,\qquad u(0,t) = 0,\quad t > 0, \end{gathered}$$

(4)

$$\begin{gathered} T(\infty ,t) = \infty ,\qquad u(\infty ,t) = 0. \end{gathered}$$

(5)

Take the following dimensionless variables:

$$ v = \frac{\upsilon h^{2}u}{gk^{2}},\qquad y = \frac{hy}{k},\qquad \tau = \frac{ \upsilon h^{2}t}{k^{2}},\qquad \theta ^{ *} = \frac{T - T_{\infty }}{T_{ \infty }}. $$

(6)

Introducing the above variables into (1)–(5), we obtain

$$\begin{gathered} \frac{\partial v(y,\tau )}{\partial \tau } = \biggl( 1 - \beta \frac{ \partial }{\partial \tau } \biggr) \frac{\partial ^{2}v(y,\tau )}{ \partial y^{2}} - Mv(y,\tau ) + \mathit{Gr}\theta (y,\tau ), \end{gathered}$$

(7)

$$\begin{gathered} \mathit{Pr} \frac{\partial \theta (y,\tau )}{\partial y} = \frac{\partial ^{2} \theta (y,\tau )}{\partial y^{2}}. \end{gathered}$$

(8)

Also the dimensionless conditions are

$$\begin{gathered} v ( y,0 ) = 0,\qquad \theta ( y,0 ) = 0,\quad y \ge 0. \end{gathered}$$

(9)

$$\begin{gathered} \frac{\partial \theta ( 0,\tau ) }{\partial y} \bigg|_{y = 0} = - \bigl[ 1 + \theta ( 0,\tau ) \bigr] ,\qquad v ( 0,\tau ) = 0,\quad \tau > 0, \end{gathered}$$

(10)

$$\begin{gathered} \theta ( y,\tau ) \to 0,\qquad v ( y,\tau ) \to 0,\quad \text{as}\ y \to \infty ,\ \tau \ge 0. \end{gathered}$$

(11)

Here $\mathit{Gr} = \gamma _{T}T_{\infty }$ is the thermal Grashof number, $\mathit{Pr} = \frac{\mu c_{p}}{k}$ is the Prandtl number, $M = \frac{k^{2} \sigma B_{0}^{2}v}{h^{2}\mu }$ is the magnetic parameter, and $\beta = \frac{k_{0}h^{2}}{\rho k^{2}}$ is Walter’ B fluid index.

The time fractional model of the problem is obtained by replacing the ordinary derivative with $D_{t}^{\alpha } (\cdot)$ in (7)–(8):

$$\begin{gathered} D_{\tau }^{\alpha } v(y,\tau ) = \bigl( 1 - \beta D_{\tau }^{\alpha } \bigr) \frac{\partial ^{2}v(y,\tau )}{\partial y^{2}} - Mv(y,\tau ) + \mathit{Gr}\theta (y,\tau ), \end{gathered}$$

(12)

$$\begin{gathered} \mathit{Pr} D_{t}^{\alpha } \theta (y,\tau ) = \frac{\partial ^{2}\theta (y, \tau )}{\partial y^{2}}. \end{gathered}$$

(13)

Here $D_{t}^{\alpha } (\cdot)$ is the Caputo–Fabrizio operator, which is defined as

$$ D_{t}^{\alpha } v(y,t) = \frac{1}{1 - \alpha } \int _{0}^{t} \exp \biggl( \frac{ - \alpha (t - \tau )}{1 - \alpha } \biggr) u'(\tau )\,d \tau ,\quad 0 < \alpha < 1. $$

(14)

3 Solution of the fractional model

The fractional differential equations (12)–(13) with the conditions (9)–(11) will be solved in this section.

3.1 Solution of temperature distribution

By employing the Laplace transform to (10), (11) and (13), we obtain

$$\begin{gathered} \frac{\partial ^{2}\bar{\theta } (y,q)}{\partial y^{2}} - \biggl[ \frac{q \mathit{Pr} }{(1 - \alpha )q + \alpha } \biggr] \bar{\theta } (y,q) = 0, \end{gathered}$$

(15)

$$\begin{gathered} \frac{\partial \bar{\theta} ( y,q ) }{\partial y} \bigg|_{y = 0} = - \biggl[ \bar{\theta} ( 0,q ) + \frac{1}{q} \biggr] ,\quad\text{and}\quad \bar{\theta} ( y,q ) \to 0, \quad \text{as}\ y \to \infty . \end{gathered}$$

(16)

Here $q$ is the Laplace parameter. Equation (15) can be written as

$$ \biggl[ \frac{qb_{0}\mathit{Pr} }{q + b_{0}\alpha } \biggr] \bar{\theta } (y,q) - \frac{\partial ^{2}\bar{\theta } (y,q)}{\partial y^{2}} = 0, $$

where $b_{0} = \frac{1}{1 - \alpha }$.

The solution of the above differential equation by taking conditions (16) is

$$ \bar{\theta } (y,q) = \frac{1}{ \sqrt{\frac{b_{0}q\mathit{Pr} }{q + b_{0}\alpha }} - 1 }\cdot\frac{1}{q}\exp \biggl( - y\sqrt{ \frac{b _{0}q\mathit{Pr} }{q + b_{0}\alpha }} \biggr) . $$

(17)

or

$$ \bar{\theta } (y,q) = \frac{1}{ \sqrt{\frac{aq}{q + b}} - 1 }\cdot\frac{1}{q}\exp \biggl( - y\sqrt{ \frac{aq}{q + b}}\, \biggr) . $$

(18)

where $a = b_{0}\mathit{Pr}$, $b = b_{0}\alpha$ and $m = a - 1$.

The Laplace inverse of (18) is procured by means of the following inverse formulas:

$$\begin{gathered} L^{ - 1} \biggl\{ \frac{1}{q}\exp \biggl( - y\sqrt{ \frac{mq}{q + n}} \,\biggr) \biggr\} = 1 - \frac{2m}{\pi } \int _{0}^{\infty } \frac{ \operatorname{Sin} (yx)}{(m + x^{2})x}\exp \biggl( - \frac{nx^{2}t}{m + x^{2}} \biggr)\, dx, \\ L^{ - 1} \biggl\{ \frac{1}{\sqrt{q^{2} - d^{2}}} \biggr\} = I_{0}(dt),\qquad L^{ - 1} \biggl\{ \frac{1}{q - a} \biggr\} = e^{at}. \end{gathered}$$

By the convolution theorem, we get

$$ \theta (y,t) = \theta _{1}(t) * \theta _{2}(y,t) = \int _{0}^{t} \theta _{1}(t - \tau )\theta _{2}(y,\tau )\,d\tau , $$

where

$$ \theta _{1}(t) = \biggl( \frac{a}{m}\delta '(t) + \frac{abm + ab}{m^{3}}e ^{\frac{b}{m}t} \biggr) \cdot\frac{1}{\sqrt{a}} I_{0} \biggl( \frac{b}{2}t \biggr) e^{\frac{ - b}{2}t} - \frac{1}{m}\delta (t) - \frac{b(c + 1)}{m ^{2}}e^{\frac{b}{m}t}, $$

(19)

and

$$ \theta _{2}(y,t) = 1 - \frac{2a}{\pi } \int _{0}^{\infty } \frac{\sin (yx)}{x(a + x^{2})}\exp \biggl( - \frac{bx^{2}t}{x^{2} + a} \biggr)\, dx. $$

(20)

Equation (18) represents the solution of the temperature field in the transformed domain. The inverse Laplace transform of (18) is also found numerically for validation and presented in Sect. 4.

3.2 Solution of the velocity field

Taking Laplace transformation of (10), (11) and (12), we obtain

$$\begin{gathered} \biggl[ \frac{qb_{0}}{q + b_{0}\alpha } \biggr] \bar{v}(y,q) = \biggl[ \frac{1}{q} - \frac{\beta qb_{0}}{q + b_{0}\alpha } \biggr] \frac{ \partial ^{2}\bar{v}(y,q)}{\partial y^{2}} - M\bar{v}(y,q) + \mathit{Gr}\bar{\theta} (y,q), \end{gathered}$$

(21)

$$\begin{gathered} \bar{u} ( 0,q ) = 0\quad \mbox{and}\quad \bar{u} ( y,q ) \to 0,\quad \mbox{as}\ y \to \infty . \end{gathered}$$

(22)

Here $b_{0} = \frac{1}{1 - \alpha }$.

By using (17) into (21) and rearranging, we have

$$\begin{aligned} &\frac{\partial ^{2}\bar{v}(y,q)}{\partial y^{2}} - \biggl[ \frac{(M + b_{0})q + qb_{0}}{ (1 - \beta b_{0})q + b_{0}\alpha } \biggr] \bar{v}(y,q) \\ &\quad = \frac{ - (q + b_{0}\alpha )\mathit{Gr}}{ (1 - \beta b_{0})q + b_{0}\alpha }\cdot\frac{1}{ \sqrt{\frac{qb _{0}\mathit{Pr} }{q + b_{0}\alpha }} - 1 }\cdot\frac{1}{q}\exp \biggl( - y\sqrt{ \frac{qb _{0}\mathit{Pr} }{q + b_{0}\alpha }} \biggr) . \end{aligned}$$

(23)

Solving (23) by using condition (22), we get

$$\begin{aligned} \bar{v}(y,q) &= \frac{ - \mathit{Gr}(q + b_{0}\alpha )}{ (1 - \beta b_{0})q + b_{0}\alpha }\cdot\frac{1}{ \sqrt{\frac{qb_{0} \mathit{Pr} }{q + b_{0}\alpha }} - 1 } \\ &\quad{}\times\biggl[ \frac{1}{q}\exp \biggl( - y\sqrt{\frac{(M + b_{0})q + qb_{0}}{ (1 - \beta b_{0})q + b _{0}\alpha }} \biggr) - \frac{1}{q}\exp \biggl( - y \sqrt{\frac{qb _{0}\mathit{Pr} }{q + b_{0}\alpha }} \biggr) \biggr] . \end{aligned}$$

(24)

Equation (24) in suitable form is written as

$$ \bar{v}(y,q) = \bar{v}_{1}(y,q)\cdot \bigl( \bar{v}_{2}(y,q) - \bar{v}_{3}(y,q) \bigr) . $$

(25)

The inverse Laplace of the above expression is obtained by means of the following inverse formulas:

$$\begin{gathered} L^{ - 1} \biggl\{ \frac{1}{\sqrt{q^{2} - d^{2}}} \biggr\} = I_{0}(dt), \qquad L^{ - 1} \biggl\{ \frac{1}{q - a} \biggr\} = e^{at}, \\ \begin{aligned} &L^{ - 1} \biggl\{ \frac{1}{q}\exp \biggl( - y\sqrt{ \frac{cq + f}{dq + 1}} \biggr) \biggr\} \\ &\quad = \frac{c}{d}e^{\frac{ - t}{d}} \int _{0}^{\infty } \operatorname{erfc} \biggl( \frac{y}{2 \sqrt{z}} \biggr) e^{\frac{ - cz}{d}}I_{0} \biggl( \frac{z}{d}\sqrt{(c - df)zt} \biggr)\, dz \\ &\qquad{} + \frac{f}{d} \int _{0}^{\infty } \int _{0}^{t} \operatorname{erfc} \biggl( \frac{y}{2\sqrt{z}} \biggr) e^{ - \frac{cz + x}{d}}I_{0} \biggl( \frac{z}{d}\sqrt{(c - df)zt} \biggr)\, dx\,dz, \end{aligned} \\ L^{ - 1} \biggl\{ \frac{1}{q}\exp \biggl( - y\sqrt{ \frac{mq}{q + n}} \,\biggr) \biggr\} = 1 - \frac{2m}{\pi } \int _{0}^{\infty } \frac{ \operatorname{Sin} (yx)}{(m + x^{2})x}\exp \biggl( - \frac{nx^{2}t}{m + x^{2}} \biggr)\, dx. \end{gathered}$$

By using the above inverse Laplace formulas in (25), we get

$$\begin{gathered} v_{1}(y,\tau ) = \frac{\mathit{Gr}}{\sqrt{a} ( 1 - \beta b_{0} ) } \biggl\{ \delta '(t) + \frac{b(1 - 2\beta b_{0})}{1 - \beta b_{0}}\delta (t) + \frac{ \alpha ^{2}\beta ^{2}b_{0}^{4}}{(1 - \beta b_{0})^{2}}e^{ - \frac{b}{1 - \beta b_{0}}t} \biggr\} * e^{ - \frac{b}{2}t}I_{0} \biggl( \frac{b}{2}t \biggr) . \end{gathered}$$

(26)

$$\begin{gathered} \begin{aligned}[b] v_{2}(y,\tau ) &= \frac{c}{d}e^{\frac{ - t}{d}} \int _{0}^{\infty } \operatorname{erfc} \biggl( \frac{y}{2\sqrt{z}} \biggr) e^{\frac{ - cz}{d}}I_{0} \biggl( \frac{z}{d}\sqrt{(c - df)zt} \biggr)\, dz \\ &\quad{}+ \frac{f}{d} \int _{0}^{ \infty } \int _{0}^{t} \operatorname{erfc} \biggl( \frac{y}{2\sqrt{z}} \biggr) e^{ - \frac{cz + x}{d}}I_{0} \biggl( \frac{z}{d}\sqrt{(c - df)zt} \biggr)\, dx\,dz \end{aligned} \end{gathered}$$

(27)

$$\begin{gathered} v_{3}(y,t) = 1 - \frac{2a}{\pi } \int _{0}^{\infty } \frac{\sin (yx)}{x(a + x^{2})}\exp \biggl( - \frac{bx^{2}t}{x^{2} + a} \biggr)\, dx, \end{gathered}$$

(28)

where $a = b_{0}\mathit{Pr}$, $b = b_{0}\alpha$, $c = \frac{M + b_{0}}{b}$, and $d = \frac{1 - \beta }{b}$.

Equation (24) represents the solution of the velocity field in the Laplace transform domain. Recently, many researchers have used numerical algorithms for the inverse Laplace transform in a productive way to evaluate such models (Abdullah et al. 2017; Raza et al. 2017; Sheng et al. 2011; Tong et al. 2009; Jiang et al. 2017). Therefore, in this manuscript, we have employed numerical algorithms for validation of our obtained solutions. The Stehfest’s algorithm (Stehfest 1970) is written as

$$\begin{aligned} v(y,\tau )=\frac{\ln (2)}{\tau } \sum_{k = 1}^{2p} M_{k} \bar{v} \biggl( y, k\frac{\ln (2)}{\tau } \biggr) , \end{aligned}$$

(29)

where $p$ is a natural number and

$$\begin{aligned} M_{k} = ( - 1)^{k + p}\sum_{i = [ \frac{k + 1}{2} ] } ^{\min (k,p)} \frac{i^{p}(2n)!}{(p - i)!i!(i - 1)!(k - i)!(2i - k)!}. \end{aligned}$$

(30)

The Tzou’s algorithm (Tzou 1997) is written as

$$ v(y,\tau ) = \frac{e^{4.7}}{\tau } \Biggl[ \frac{1}{2}\bar{v} \biggl( y, \frac{4.7}{ \tau } \biggr) + \operatorname{Re} \Biggl\{ \sum _{m = 1}^{N_{1}} ( - 1)^{m} \bar{v} \biggl( y, \frac{4.7 + m\pi i}{\tau } \biggr) \Biggr\} \Biggr] . $$

(31)

3.3 Rate of heat transfer

The rate of heat transfer from the plate to the fluid is known as Nusselt number. The mathematical form is

$$ \mathit{Nu} = - \biggl| \frac{\partial \theta }{\partial y} \biggr| _{y = 0}. $$

(32)

From (19), we get the expression of Nusselt number in the transformed domain as

$$ \mathit{Nu} = \frac{1}{ \sqrt{\frac{b_{0}q\mathit{Pr} }{q + b{}_{0}\alpha }} - 1 }\cdot\frac{1}{q} \biggl( \sqrt{ \frac{b_{0}q\mathit{Pr} }{q + b_{0} \alpha }} \biggr) . $$

(33)

The results for Nusselt number have been tabulated in Sect. 4.

4 Numerical solutions and physical discussion

Numerical solutions are depicted graphically in this section to show the influence of different physical parameters.

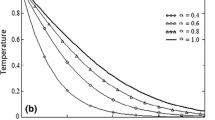
Figure 2 depicts the impact of the time fractional parameter $\alpha$ on the dimensionless temperature distribution. All of the graphs are plotted versus spatial variable $y$. By enhancing the impact of the fractional parameter, the temperature distribution decreases for small values of time but has the opposite behavior for large time values. Physically, it happens due to the memory effect of the viscoelastic behavior of the fluid. Figure 3 represents the domination of Prandtl number on dimensionless temperature distribution. It is found that the temperature field decreases for larger values of $\mathit{Pr}$. Physically, we can say that the viscosity of the material decreases, and the thickness of the thermal boundary layer also decreases.

Fig. 2

Fractional effect on temperature

Fig. 3

Prandtl number effect on temperature

Figure 4 shows the effect of the fractional parameter $\alpha$ on the velocity field. The velocity field is a decreasing function of the fractional parameter $\alpha$ for lower values of time but has the opposite behavior for large time values. Figure 5 illustrates the effect of thermal Grashof number $\mathit{Gr}$ on the velocity field. It is found that the dimensionless velocity field increases for larger values of thermal Grashof number $\mathit{Gr}$. Physically, we can say that the cooling of the plate produced a stronger velocity field. The convection currents in the plates are produced due to a change in the temperature gradient.

Fig. 4

Fractional effect on velocity

Fig. 5

Grashof number effect on velocity

The effect of Prandtl number on the velocity field is plotted in Fig. 6. The velocity field is also an increasing function of Prandtl number $\mathit{Pr}$ and for greater values of time it shows similar behavior. Figure 7 illustrates the influence of the transverse magnetic field on velocity. It is found that the dimensionless velocity field increases for larger values of $M$ and it is also seen that greater values of the magnetic parameter produced weaker velocity field. It is discovered that the magnetic field produces a drag force that resists the fluid flow, which causes a decrease in the velocity field. Physically, it represents the fact that the Lorentz force behaves as a frictional force to the flow, which causes a decrease in the motion of the fluid.

Fig. 6

Prandtl number effect on velocity

Fig. 7

Magnetic parameter effect on velocity

Figure 8 shows the effect of Walter’s-B fluid parameter on velocity. The velocity field decreases for larger values of the parameter $\beta$. A comparison between numerical and exact solutions is plotted in Fig. 9. From these plots, we find good agreement between the exact and numerical solutions.

Fig. 8

Walter’s-B parameter effect on velocity

Fig. 9

Comparison of exact and numerical solutions

To compare our exact solution, we employed two numerical methods, Tzou’s and Stehfest’s algorithms. The exact and numerical results are presented in Table 1. From this table, we found an equivalence relation between them. Table 2 allows one to check the impact of the physical and fractional variables on Nusselt number. The heat transfer rate is directly proportional to the fractional parameter $\alpha$ and $\mathit{Pr}$. Tables 3 and 4 are presented to show the influence of the fractional parameter on the dimensionless velocity field and temperature distribution. It is noted that with greater values of the fractional parameter, velocity and temperature decrease.

5 Conclusions

In this paper, the unsteady flow of a fractional Walter’s-B fluid with Newtonian heating under the influence of uniform magnetic field has been calculated. The thermal boundary condition is taken along the flat oscillating vertical plate. The solution of the mathematical model is found by employing Laplace transformation. The results have been found both analytically and numerically. These are some of the main results of the study:

• 1. The solutions for the velocity field and temperature distribution are obtained both numerically and analytically. The solutions satisfy both initial and boundary conditions.

• 2. Table 1 shows the good agreement between numerical and exact solutions.

• 3. The fractional parameter $\alpha$ is directly proportional to the velocity and temperature field for lower values of time.

• 4. The thickness of the boundary layer increases near the plate in time.

• 5. The temperature distribution decreases by increasing $\mathit{Pr}$.

• 6. The velocity field is directly proportional to $\mathit{Gr}$.

• 7. The influence of the magnetic parameter is opposite to the velocity field. Weaker velocity fields are produced by increasing magnetic field strength.

• 8. The rate of heat transfer is enhanced with time but decreased with increasing values of $\mathit{Pr}$ and $\alpha$.