Peristaltic flow of Walter’s B fluid in a uniform inclined tube

Abstract

In this investigation, peristaltic flow of Walter’s B fluid in a uniform inclined tube is discussed. The formulation of the problem is made in a cylindrical coordinate system. The analytical solutions have been calculated by using a regular perturbation method by taking δ as the perturbation parameter. The expressions for pressure rise and friction forces were calculated using numerical integration. The graphical results are presented to discuss the various physical quantities of the Walter’s B fluid parameter α, amplitude ratio φ, angle of inclination β and wave length δ.

Introduction

The analysis of peristaltic flow in a circular tube has numerous applications in various branches of science. The word peristaltic means clasping and compressing. Peristaltic transport is a physical mechanism that occurs because of the action of a progressive wave that propagates along the length of a distensible tube containing fluid. The peristaltic mechanism is a natural method of moving contents within hollow structures by successive contractions of the muscular fibers. This mechanism is responsible for transport of biological fluids such as urine in the ureter, chyme in gastro-intestinal tract, semen in the vas deferens and ovum in the female fallopian tube. Considerable analysis has been carried out on this mechanism, primarily for a Newtonian fluid with a periodic train of sinusoidal peristaltic waves. Several theoretical and experimental investigations [1–4] have been made to study the peristaltic flow. Hakeem et al. [5, 6] discussed the peristaltic flow of generalized Newtonian fluid and Carreau fluid in a uniform tube. Peristaltic transport of a third order fluid in a circular cylindrical tube have been discussed by Hayat et al. [7]. Muthu et al. [8] studied the peristaltic motion of micropolar fluid in circular cylindrical tubes. Peristaltic flow of a Herschel-Bulkley fluid in a non-uniform tube was presented by Nadeem and Akbar [9]. Peristaltic transport of a third order fluid under the effect of a magnetic field was investigated by Hayat et al. [10]. Another development dealing with peristaltic flow problems in a tube is mentioned in Refs. [11–14].

Many of the biofluids have been observed to behave as suspensions of deformable or rigid particles in a Newtonian fluid. For example, blood is a suspension of various cells in plasma, cervical mucus is a suspension of macromolecules in a water-like liquid, chyme is a suspension of semi-digested food, etc. In view of this, some researchers have tried to account for the suspension behaviour of biofluids by considering non-Newtonian fluids [15–18].

To examine the importance of peristaltic flow of non-Newtonian fluid, we present the peristaltic flow of Walter’s B fluid in a uniform tube. To the best of our knowledge, no attempt has been made to solve the peristaltic flow problem considering the Walter’s B fluid model. The governing equations of Walter’s B fluid in cylindrical coordinates have been modeled. The analytical solutions were calculated using a regular perturbation method. The expressions for pressure rise and friction forces have been calculated using numerical integration. The behaviors of pressure gradient, pressure rise and frictional forces for different physical parameters are presented graphically.

Mathematical model

For an incompressible fluid, the balances of mass and momentum are given by

$$ {\text{div}}{\mathbf{V}}{ = 0,} $$

(1)

$$ \rho {\frac{{\text{d}}{\mathbf{V}}}{{{\text{d}}t}}} = {\text{div}}{\mathbf{S}} + \rho {\mathbf{f}}, $$

(2)

where $\rho$ is the density, V is the velocity vector, S is the Cauchy stress tensor, f represents the specific body force, and d/dt represents the material time derivative. The constitutive equation for Walter’s B’ fluid is given by [18]

$$ {\mathbf{S}} = - p{\mathbf{I}} + {{\uptau}}, $$

(3)

$$ \tau = 2\eta_{0} {\mathbf{e}} - 2k_{0} {\frac{\delta {\mathbf{e}}}{\delta t}}, $$

(4)

$$ {\mathbf{e}} = \nabla {\mathbf{V}}{\mathbf{ + }}\left( {\nabla {\mathbf{V}}} \right)^{T} , $$

(5)

$$ {\frac{\delta {\mathbf{e}}}{\delta t}} = {\frac{\partial {\mathbf{e}}}{\partial t}} + {\mathbf{V}}.\nabla {\mathbf{e}} - {\mathbf{e}}\nabla {\mathbf{V}} - \left( {\nabla {\mathbf{V}}} \right)^{T} {\mathbf{e}}, $$

(6)

in which −p I is the spherical part of the stress due to constraint of incompressibility, τ is the extra stress tensor, η ₀ is the coefficient of viscosity, e is the rate of strain tensor, T denotes the transpose, and $\delta /\delta t$ denotes the convected differentiation of a tensor quantity in relation to the material motion.

Problem formulation

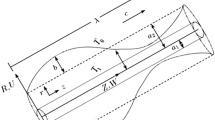
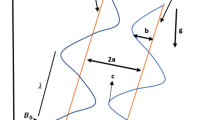
We considered an incompressible Walter’s B’ fluid in a uniform tube. The flow is produced due to a sinusoidal wave train propagating with constant speed c along the walls of the tube, and the geometry of the wall surface is defined as

$$ \bar{{\mathbf{h}}} = {\mathbf{a}} + {\mathbf{b}}\sin {\frac{2\pi }{\lambda }}\left( {\bar{Z} - c\bar{t}} \right),\, $$

(7)

where a is the radius of the tube at the inlet, b is the wave amplitude, λ is the wavelength, c is the propagation velocity, and $\bar{t}$ is the time. We considered the cylindrical coordinate system $(\bar{R},\,\bar{Z})$, in which $\bar{Z} - {\text{axis}}$ lies along the centerline of the tube and $\bar{R}$ is transverse to it. The governing equations in the fixed frame for an incompressible flow are given as

$$ {\frac{{\partial \bar{U}}}{{\partial \bar{R}}}} + {\frac{{\bar{U}}}{{\bar{R}}}} + {\frac{{\partial \bar{W}}}{{\partial \bar{Z}}}} = 0, $$

(8)

$$ \rho \left( {{\frac{\partial }{{\partial \bar{t}}}} + \bar{U}{\frac{\partial }{{\partial \bar{R}}}} + \bar{W}{\frac{\partial }{{\partial \bar{Z}}}}} \right)\bar{U} = - {\frac{{\partial \bar{P}}}{{\partial \bar{R}}}} + {\frac{1}{{\bar{R}}}}{\frac{\partial }{{\partial \bar{R}}}}\left( {\bar{R}\bar{\tau }_{{\bar{R}\bar{R}}} } \right) + {\frac{\partial }{{\partial \bar{Z}}}}\left( {\bar{\tau }_{{\bar{R}\bar{Z}}} } \right) - {\frac{{\bar{\tau }_{{\bar{\theta }\bar{\theta }}} }}{{\bar{R}}}} + \rho g\sin \beta, $$

(9)

$$ \rho \left( {{\frac{\partial }{{\partial \bar{t}}}} + \bar{U}{\frac{\partial }{{\partial \bar{R}}}} + \bar{W}{\frac{\partial }{{\partial \bar{Z}}}}} \right)\bar{W} = - {\frac{{\partial \bar{P}}}{{\partial \bar{Z}}}} + {\frac{1}{{\bar{R}}}}{\frac{\partial }{{\partial \bar{R}}}}\left( {\bar{R}\bar{\tau }_{{\bar{R}\bar{Z}}} } \right) + {\frac{\partial }{{\partial \bar{Z}}}}\left( {\bar{\tau }_{{\bar{Z}\bar{Z}}} } \right) + \rho g\cos \beta, $$

(10)

where $\bar{P}$ is the pressure and $\bar{U}$, $\bar{W}$ are the respective velocity components in the radial and axial directions in the fixed frame, respectively.

In the fixed coordinates $\left( {\bar{R},\,\bar{Z}} \right),$ the flow is unsteady; it becomes steady in a wave frame $\left( {\bar{r},\,\bar{z}} \right)$ moving with the same speed as the wave moves in the $\bar{Z}$ direction. The transformations between the two frames are

$$ \bar{r} = \bar{R}, \quad \bar{z} = \bar{Z} - c\bar{t}, $$

(11)

$$ \bar{u} = \bar{U}, \quad \bar{w} = \bar{W} - c, $$

(12)

where $\bar{u}$ and $\bar{w}$ are the velocities in the wave frame.

The corresponding boundary conditions are

$$ {\frac{{\partial \bar{w}}}{{\partial \bar{r}}}} = 0, \quad \bar{u} = 0\;{\text{at}}\;\bar{r} = 0, $$

(13a)

$$ \bar{w} = - c,\quad\bar{u} = - c{\frac{{{\text{d}}\bar{h}}}{{{\text{d}}\bar{z}}}}\;{\text{at}}\;\bar{r} = \bar{h} = a + b\sin {\frac{2\pi }{\lambda }}\left( {\bar{z}} \right). $$

(13b)

We introduce the non-dimensional variables as follows

$$ \begin{aligned} R = & {\frac{{\bar{R}}}{a}}, \quad r = {\frac{{\bar{r}}}{a}},\quad Z = {\frac{{\bar{Z}}}{\lambda }}, \quad z = {\frac{{\bar{z}}}{\lambda }}, \quad W = {\frac{{\bar{W}}}{c}}, \quad w = {\frac{{\bar{w}}}{c}}, \quad \tau = {\frac{{a\bar{\tau }}}{{c\eta_{0} }}} \\ U = & {\frac{{\lambda \bar{U}}}{ac}}, \quad u = {\frac{{\lambda \bar{u}}}{ac}}, \quad P = {\frac{{a^{2} \bar{P}}}{{c\lambda \eta_{0} }}}, \quad t = {\frac{{c\bar{t}}}{\lambda }}, \quad \delta = {\frac{a}{\lambda }}, \quad Re = {\frac{\rho ca}{{\eta_{0} }}}, \\ h = & {\frac{{\bar{h}}}{a}} = 1 + \varphi \sin 2\pi z, \quad \alpha = {\frac{{k_{0} c}}{{\eta_{0} a}}}, \quad E = {\frac{{\eta_{0} c}}{{\rho ga^{2} }}}. \\ \end{aligned} $$

(14)

Making use of (12) and (14), (8) to (10) along with boundary conditions (13a, 13b) take the form

$$ {\frac{\partial u}{\partial r}} + \frac{u}{r} + {\frac{\partial w}{\partial z}} = 0,\, $$

(15)

$$ Re\delta^{3} \left( {u{\frac{\partial }{\partial r}} + w{\frac{\partial }{\partial z}}} \right)u = - {\frac{\partial P}{\partial r}} - {\frac{\delta }{r}}{\frac{\partial }{\partial r}}\left( {r\tau_{rr} } \right) - \delta^{2} {\frac{\partial }{\partial z}}\left( {\tau_{rz} } \right) - {\frac{{\delta \tau_{\theta \theta } }}{r}} + {\frac{\sin \beta }{E}}, $$

(16)

$$ Re\delta \left( {u{\frac{\partial }{\partial r}} + w{\frac{\partial }{\partial z}}} \right)\,w = - {\frac{\partial P}{\partial z}} - \frac{1}{r}{\frac{\partial }{\partial r}}\left( {r\tau_{rz} } \right) - \delta {\frac{\partial }{\partial z}}\left( {\tau_{zz} } \right) + \delta {\frac{\cos \beta }{E}},\, $$

(17)

$$ {\frac{\partial w}{\partial r}} = 0, \quad u = 0{\text{ at }}r = 0, $$

(17a)

$$ w = - 1, \quad u = - {\frac{{{\text{d}}h}}{{{\text{d}}z}}}, \;{\text{at}}\; r = h = 1 + \varphi \sin 2\pi z, $$

(17b)

Where

$$ \tau_{rr} = 2\delta {\frac{\partial u}{\partial r}} - 2\alpha \left[ {\delta^{2} u{\frac{{\partial^{2} u}}{{\partial r^{2} }}} + \delta^{2} w{\frac{{\partial^{2} u}}{\partial r\partial z}} - 2\delta^{2} \left( {{\frac{\partial u}{\partial r}}} \right)^{2} - {\frac{\partial w}{\partial r}}\left( {{\frac{\partial u}{\partial z}}\delta^{2} + {\frac{\partial w}{\partial r}}} \right)} \right], $$

$$ \begin{gathered} \tau_{rz} = \left( {{\frac{\partial u}{\partial z}}\delta^{2} + {\frac{\partial w}{\partial r}}} \right) - \alpha \left[ {\delta^{3} u{\frac{{\partial^{2} u}}{{\partial r^{2} }}} + \delta u{\frac{{\partial^{2} w}}{{\partial r^{2} }}} + w\delta {\frac{{\partial^{2} w}}{\partial r\partial z}} + w{\frac{{\partial^{2} u}}{{\partial z^{2} }}}\delta^{3} - } \right. \hfill \\ \left. {2{\frac{\partial u}{\partial r}}{\frac{\partial u}{\partial z}}\delta^{3} - \delta \left( {{\frac{\partial u}{\partial z}}\delta^{2} + {\frac{\partial w}{\partial r}}} \right)\left( {{\frac{\partial u}{\partial r}} + {\frac{\partial w}{\partial z}}} \right) - {\frac{\partial w}{\partial r}}{\frac{\partial w}{\partial z}}\delta } \right], \hfill \\ \end{gathered} $$

$$ \tau_{zz} = 2\delta {\frac{\partial w}{\partial z}} - 2\alpha \left[ {\delta^{2} u{\frac{{\partial^{2} w}}{\partial r\partial z}} + \delta^{2} w{\frac{{\partial^{2} w}}{{\partial z^{2} }}} - {\frac{\partial u}{\partial z}}\delta^{2} \left( {{\frac{\partial u}{\partial z}}\delta^{2} + {\frac{\partial w}{\partial r}}} \right) + 2\delta^{2} \left( {{\frac{\partial w}{\partial z}}} \right)^{2} } \right], $$

$$ \tau_{\theta \theta } = 2\frac{u}{r}\delta - 2\alpha \delta^{2} \left[ {u{\frac{\partial u}{\partial z}} - {\frac{{3u^{2} }}{{r^{2} }}}} \right]. $$

In the above equations δ, Re and α represent the wave number, Reynolds number and Walter’s B fluid parameter, respectively. Elimination of the pressure gradient from (16) and (17) gives

$$ {\frac{\partial }{\partial r}}\left[ { - Re\delta \left( {u{\frac{\partial }{\partial r}} + w{\frac{\partial }{\partial z}}} \right)w + \frac{1}{r}{\frac{\partial }{\partial r}}\left( {r\tau_{rz} } \right) + \delta {\frac{\partial }{\partial z}}\left( {\tau_{zz} } \right)} \right] = {\frac{\partial }{\partial z}}\left[ { - Re\delta^{3} \left( {u{\frac{\partial }{\partial r}} + w{\frac{\partial }{\partial z}}} \right)u + {\frac{\delta }{r}}{\frac{\partial }{\partial r}}\left( {r\tau_{rr} } \right) + \delta^{2} {\frac{\partial }{\partial z}}\left( {\tau_{rz} } \right) - \delta {\frac{{\tau_{\theta \theta } }}{\tau }} + {\frac{\sin \beta }{E}}} \right] $$

(18)

Corresponding boundary conditions in dimensionless form are

$$ u = 0, \quad {\frac{\partial w}{\partial r}} = 0, \;{\text{a}}\; r = r_{1} , $$

(19)

$$ u = - {\frac{{{\text{d}}h}}{{{\text{d}}z}}}, \quad w = - 1,{\text{ at}}\;r = h = 1 + \varphi \sin 2\pi z. $$

(20)

Solution to the problem

Since (18) is a highly non-linear equation, its exact solution may not be possible. For the perturbation solution, we expand u, w, F, $\tau$ and P by taking $\delta$ as the perturbation parameter

$$ w = w_{0} + \delta w_{1} + O(\delta^{2} ), $$

(21a)

$$ u = u_{0} + \delta u_{1} + O(\delta^{2} ), $$

(21b)

$$ F = F_{0} + \delta F_{1} + O(\delta^{2} ), $$

(21c)

$$ \tau = \tau_{ij}^{\left( 0 \right)} + \delta \tau_{ij}^{\left( 1 \right)} + O(\delta^{2} ), $$

(21d)

$$ P = P_{0} + \delta P_{1} + O(\delta^{2} ) $$

(21e)

Substituting (21a) to (21e) in (16) to (20) and then finding the solutions for all systems, we arrive at the final solutions, which are defined as follows:

$$ \begin{aligned} w\left( {r,z} \right) = & - 1 + \left( {{\frac{{r^{2} - h^{2} }}{4}}} \right)\left( {{\frac{\partial P}{\partial z}} - {\frac{\sin \beta }{E}}} \right) + \delta \left( {a_{18} \left( {r^{6} - h^{6} } \right)} \right. + \\ & \left. {a_{19} \left( {r^{4} - h^{4} } \right) + a_{20} \left( {r^{2} - h^{2} } \right)} \right), \\ \end{aligned} $$

(22)

$$ u\left( {r,z} \right) = a_{5} r + \delta \left( {a_{21} r^{7} + a_{22} r^{5} + a_{23} r^{4} + a_{24} r^{3} + a_{25} r} \right), $$

(23)

$$ {\frac{{{\text{d}}P}}{{{\text{d}}z}}} = {\frac{{ - 8E\left( {2F + h^{2} } \right) + h^{4} \sin \alpha }}{{Eh^{4} }}} + \delta \left( {{\frac{{a_{21} }}{{h^{4} }}}} \right). $$

(24)

The corresponding stream function can be calculated as

$$ u = - \frac{1}{r}{\frac{\partial \Uppsi }{\partial z}}{\text{ and }}w = \frac{1}{r}{\frac{\partial \Uppsi }{\partial r}}. $$

(25)

The pressure rise ΔP and friction force F are defined as follows

$$ \Updelta P = \mathop \int \limits_{0}^{1} {\frac{{{\text{d}}P}}{{{\text{d}}z}}}{\text{d}}z, $$

(26)

$$ F = \mathop \int \limits_{0}^{1} h^{2} \left( { - {\frac{{{\text{d}}P}}{{{\text{d}}z}}}} \right){\text{d}}z, $$

(27)

where ${\frac{{{\text{d}}P}}{{{\text{d}}z}}}$ is defined in (24). The constants appearing in the above differential equations are defined as follows

$$ \begin{aligned} a_{1} & = \frac{1}{2}\left( {{\frac{{\partial P_{0} }}{\partial z}} - {\frac{\sin \beta }{E}}} \right),\quad a_{2} = a_{1}^{2} \lambda_{1} ,\quad a_{3} = - a_{1} hh^{\prime} - {\frac{{a_{1}^{2} h^{3} h^{\prime}}}{2}} + {\frac{{b_{1} h^{2} }}{4}} + {\frac{{b_{1} a_{1} h^{4} }}{4}}, \\ a_{4} & ={\frac{{a_{1}^{2} hh^{\prime}}}{4}} - {\frac{{b_{1} }}{4}} - b_{1} a_{1} h^{2} ,\quad b_{1} = \left( {{\frac{{\rm d}P_{0}}{{\rm d}z}}} \right)^{\prime } ,\quad b_{2} = {\frac{{b_{1} a_{1} h^{4} }}{2}},\quad b_{3} = \left( {{\frac{{{\text{d}}P_{1} }}{{\text{d}}z}}} \right)^{\prime } , \\ a_{5} & = - {\frac{{a_{1} hh^{\prime}}}{2}},\quad a_{6} = a_{5} a_{1} ,\quad a_{7} = {Re} b_{2} ,\quad a_{8} = {\frac{{3a_{2}^{\prime } }}{2}} + {Re} a_{6} + {Re} a_{4} ,\quad a_{9} = {Re} a_{3} , \\ a_{10} & = \alpha a_{5} a_{1} ,\quad a_{11} = {\frac{{\alpha a_{1} a_{1}^{\prime } }}{2}},\quad a_{12} = - {\frac{{\alpha a_{1} a_{1}^{\prime } h^{2} }}{2}},\quad a_{13} = {\frac{{\alpha a_{1} a_{1}^{\prime } }}{2}}, \\ a_{14} & = - {\frac{{\alpha a_{1} a_{1}^{\prime } h^{2} }}{2}} + \alpha a_{5} a_{1} - \alpha a_{1}^{2} hh^{\prime},\quad a_{15} = {\frac{{\alpha a_{1} hh^{\prime}}}{2}}\left( {{\frac{{\partial P_{0} }}{\partial z}} - {\frac{\sin \beta }{E}}} \right), \\ a_{16} & = {\frac{{a_{8} }}{4}} + a_{11} - a_{13} ,\quad a_{17} = {\frac{{a_{9} }}{2}} + a_{10} + a_{12} - a_{14} - a_{15} ,\quad a_{18} = {\frac{{a_{7} }}{36}}, \\ a_{19} & = {\frac{{a_{16} }}{4}},\quad a_{20} = {\frac{{a_{17} }}{2}},\quad a_{21} = a_{18} \left( { - 6h^{8} } \right) + a_{19} \left( {{\frac{{ - 16h^{6} }}{3}}} \right) + a_{20} \left( { - 4h^{4} } \right) \\ \end{aligned} $$

The non-dimensional expressions for the five considered wave forms are given [9] by the following equations:

• 1. Sinusoidal wave:

  $$ h\left( z \right) = 1 + \varphi \sin \left( {2\pi z} \right) $$

• 2. Triangular wave:

  $$ h\left( z \right) = 1 + \varphi \left\{ {{\frac{8}{{\pi^{3} }}}\mathop \sum \limits_{n = 1}^{\infty } {\frac{{\left( { - 1} \right)^{n + 1} }}{{\left( {2n - 1} \right)}}}\sin \left( {2\pi \left( {2n - 1} \right)z} \right)} \right\} $$

• 3. Square wave:

  $$ h\left( z \right) = 1 + \varphi \left\{ {{\frac{4}{\pi }}\mathop \sum \limits_{n = 1}^{\infty } {\frac{{\left( { - 1} \right)^{n + 1} }}{{\left( {2n - 1} \right)}}}\cos \left( {2\pi \left( {2n - 1} \right)z} \right)} \right\} $$

• 4. Trapezoidal wave:

  $$ h\left( z \right) = 1 + \varphi \left\{ {{\frac{32}{{\pi^{2} }}}\mathop \sum \limits_{n = 1}^{\infty } {\frac{{\sin {\tfrac{\pi }{8}}\left( {2n - 1} \right)}}{{\left( {2n - 1} \right)^{2} }}}\sin \left( {2\pi \left( {2n - 1} \right)z} \right)} \right\} $$

• 5. Multi-sinusoidal wave:

  $$ h\left( z \right) = 1 + \varphi \sin \left( {2m\pi z} \right) $$

Graphical discussion

In this section the pressure rise, frictional forces, axial pressure gradient and stream lines are discussed carefully and shown graphically (see Figs. 1–13). The pressure rise is calculated numerically by using Mathematica. Figures 1–4 show the pressure rise ΔP against volume flow rate Θ for different values of angle of inclination β, amplitude ratio φ, wave length δ and Walter’s B fluid parameter α. These figures indicate that the relation between pressure rise and volume flow rate are inversely proportional to each other. Figure 1 shows that with the increase in β the pressure rise increases. Peristaltic pumping occurs in the region −1 ≤ Θ ≤ 0.5 for various values of φ and α (see Figs. 2 and 4), and −1 ≤ Θ ≤ −0.4 for Fig. 3; otherwise augmented pumping occurs. Further, the pressure rise increases with an increase in φ and δ, but decreases with an increase in α. Figures 5–8 describe the variation of frictional forces. It is seen that frictional forces have the opposite behavior compared to the pressure rise. Figures 9–13 are prepared to show the behavior of the pressure gradient for different wave shapes. It is observed that for $z\varepsilon \left[ {0,0.5} \right]$ and [1.1, 1.5], the pressure gradient is small, while the pressure gradient is large in the interval $z\varepsilon \left[ {0.51,\,1} \right]$. Moreover, it is seen that the pressure gradient increases with an increase in φ. The effects of different parameters on streamlines for the trapping phenomenon for five different waveforms can be seen in Fig. 14a–e. It was observed that the size of the trapping bolus in triangular waves is smaller compared to the trapezoidal and sinusoidal waves.

Fig. 1

Pressure rise versus flow rate for α = 0.05, φ = 0.01, δ = 0.4, Re = 6, E = 0.1

Fig. 2

Pressure rise versus flow rate for α = 0.05, β = 0.4, δ = 0.1, Re = 8, E = 0.1

Fig. 3

Pressure rise versus flow rate for β = 0.05, α = 0.4, φ = 0.1, Re = 5, E = 0.1

Fig. 4

Pressure rise versus flow rate for β = 0.05, δ = 0.4, φ = 0.1, Re = 6, E = 0.1

Fig. 5

Frictional forces versus flow rate for α = 0.05, φ = 0.01, δ = 0.4, Re = 6, E = 0.1

Fig. 6

Frictional forces versus flow rate for α = 0.05, β = 0.4, δ = 0.1, Re = 8, E = 0.1

Fig. 7

Frictional forces versus flow rate for β = 0.05, α = 0.4, φ = 0.1, Re = 5, E = 0.1

Fig. 8

Frictional forces versus flow rate for β = 0.05, δ = 0.4, φ = 0.1, Re = 6, E = 0.1

Fig. 9

Pressure gradient versus (sinusoidal waves) z for β = 0.1, α = 0.4, Re = 8, δ = 0.2, E = 0.1, Q = −1

Fig. 10

Pressure gradient versus z (square waves) for β = 0.1, α = 0.4, Re = 8, δ = 0.2, E = 0.1, Q = −1

Fig. 11

Pressure gradient versus z (trapezoidal waves) for β = 0.1, α = 0.4, Re = 8, δ = 0.2, E = 0.1, Q = −1

Fig. 12

Pressure gradient versus z (triangular waves) for β = 0.1, α = 0.4, Re = 8, δ = 0.2, E = 0.1, Q = −1

Fig. 13

Pressure gradient versus z (multi-sinusoidal wave) for β = 0.1, α = 0.4, Re = 8, δ = 0.2, E = 0.1, Q = −1

Fig. 14

Streamlines for (a) sinusoidal wave, (b) trapezoidal wave, (c) triangular wave and (d) square wave. (e) Multi-sinusoidal wave for α = 0.05, φ = 0.4, Re = 7, E = 0.1, Θ = 1.5, δ = 0.1, β = 0.3