Multi-layer color image encryption using random matrix affine cipher, RP2DFrHT and 2D Arnold map

Abstract

Confidentiality, integrity, authenticity, non-repudiation and storing and transmitting images over the unsecured channel has become a challenging task nowadays. In this scenario, a robust image encryption technique over open network has grasped a great deal of attention. In this paper to meet this challenge, we have established a new multi-layer robust color image encryption using random matrix affine cipher (RMAC), reality preserving two dimensional discrete fractional Hartley transform (RP2DFrHT) and two dimensional Arnold map. The first stage of encryption is designed through RMAC. RMAC provides security in co-ordinate domain as well as in geometrical domain. So if a hacker has knowledge about all the pixels of an image, but has no information about the mechanism of co-ordinate domain he/she cannot steal any information. The second stage of encryption is obtained incorporating the concept of RP2DFrHT. The reality preserving transform eliminates the complex-valued coefficients and provides the real-valued coefficients of encrypted image. The real-valuedness of data provides convenient platform for display, storage and transmission in digital domain. The third stage of encryption is done using 2D Arnold map, which not only enhances the security but also enlarges key space. Therefore, the proposed technique provides security in geometrical, co-ordinate, frequency and time domains simultaneously. The security of our proposed technique depends upon the secret keys as well as their correct arrangements. Simulation analysis provides the complete visual results of all stages of encrypted and decrypted images. Sensitivity analysis validates that our proposed technique is highly sensitive towards its secret keys and their arrangements. Statistical analysis such as histogram analysis, MSE, PSNR, correlation coefficient, entropy analysis and resistivity of classical attacks validates the effectiveness and feasibility of our proposed work. Moreover, comparison analysis testifies that our proposed technique functions significantly well as compared to existing similar techniques.

1 Introduction

Internet is a valuable resource for us. In today’s world, we rely too much on the Internet. It is very useful tool for work, education, shopping, personal entertainment, etc. Network and communication technologies are the important modes of transferring images over the Internet. Images are used in various fields such as engineering services, scientific experiments, medical imaging, advertising, art exhibition and online education, etc. With the increasing use of digital technologies for transmitting and storing images, secure transmission of images is a major concern. Image data is highly sensitive and prone to abrupt by intruders. Also image has high redundancy and strong correlation between the pixels. To protect sensitive data from an unauthorized access is a prime agenda nowadays. Therefore, secure communication is required for transmission of images over the Internet. In respond to this demand, cryptography and steganography are the two important security systems which offered a convenient platform for secure data transmission. Steganography is an efficient technique of hiding the fact that communication is taking place by hiding information in other information. It is profitable in various applications like government services, business communications, military services and medical services, etc. Abdulla [1] has contributed a significant work on the basis of steganography. In his work, he has developed secure and efficient image-based steganography approaches that enhance embedding efficient and improve message un-detectability. Whereas, cryptography enables us to transmit images over a public domain from a sender to a receiver in such a way that the opponent cannot guess what is being transmitted. The public channel could be telephone line, computer network, etc. The information that the sender wants to send to the receiver is called plaintext. The plaintext could be images, English text, numerical data, or anything. The plaintext is encrypted using a predetermined key and the resulting ciphertext is sent over the public channel. The opponent cannot guess the plaintext from the ciphertext. The receiver decrypts the ciphertext using the encryption key and reconstructs the plaintext. Image encryption plays an important role in the field of information hiding. While dealing with image encryption techniques, intrinsic properties of images such as high redundancy, bulk data capacity and strong correlation between the pixels must be considered. Due to intrinsic properties of images, techniques based on classical cryptography are less efficient for digital images. To overcome this issue, several methods have been proposed for secure transmission of images over the unsecured channel. Refregier and Javidi [29] was the first one who proposed optical image encryption using double random phase encoding (DRPE). This concept highlighted the encryption technique. DRPE was further extended from Fourier domain to the fractional Fourier domain [5, 12, 25, 26], Fresnel domain [13, 15, 32], gyrator domain [6, 21], Hartley transform [3, 4, 20], fractional wavelet transform [7, 9, 23], fractional Mellin transform [36, 43, 44], fractional Hartley transform [14, 27, 30, 31, 40, 42]. The aforementioned image encryption techniques on the basis of fractional transform have provided better performance and higher security. However the major drawback with these techniques is the complex-valued coefficients of encrypted images. The complex-valued coefficients of encrypted images not only make them inconvenient for display, but also increases the storage, computational and communication complexities in digital domain. To overcome these shortcomings, Venturini and Duhamel [37] proposed reality preserving fractional transform. The reality preserving fractional transform eliminates the burden of complex-valued coefficients and provides the real-valued coefficients of encrypted image. The real-valued nature of data is convenient for display and decreases the storage, computational and communication complexities of the encrypted image in digital environment. On the basis of this method, Guleria et al. [10] proposed a novel approach for security of multiple color images using asymmetric RSA cryptosystem, reality preserving fractional discrete cosine transform and Arnold transform.

Our contribution

The concepts of RMAC, RP2DFrHT and 2D Arnold map are merged to design a new multi-layer robust color image encryption. The major contributions of our proposed encryption technique are as listed below.

• 1. Affine cipher is a well known and most commonly used encryption scheme. Earlier developed techniques [30, 46] using affine cipher are secured in geometrical domain only. However, in this paper the security system designed in the first stage of encryption through RMAC possesses security in co-ordinate domain as well as in geometrical domain. So if a hacker has knowledge about all the pixels of an image, but has no information about the mechanism of co-ordinate domain he/she cannot steal any information. The main reason is that in co-ordinate domain only the positions of the pixels are modified whereas the values of the pixels remain constant. In addition, arrangement of RMAC is very sensitive.

• 2. To provide next layer of security RP2DFrHT is implemented. Its inherent characteristic over other fractional transforms is the effective potential of real-valuedness which offers the convenient medium for display, storage and transmission over the unsecured public environment.

• 3. To provide extra layer of security in third stage of encryption Arnold map is used. The existing techniques [2, 11, 22] have used periodic property of Arnold map in decryption process, whereas in our proposed technique decryption process is done using inverse Arnold map. Moreover, we have used the generalized Arnold map which is faster. The encryption and decryption process require secret keys which enlarges our key space and enhances the security system significantly.

  To summarize this, our proposed encryption technique provides multi-layer security in geometrical, co-ordinate, frequency and time domains. It provides convenient medium for storage, display as well as transmission in digital domain. The security of the proposed technique depends not only upon the secret keys, but their arrangements also play a vital role. The secret keys and their arrangements are highly sensitive for robustness.

Paper organization

We have organized the remaining sections of the paper as follows: Mathematical formulation of RMAC, RP2DFrHT and 2D Arnold map are explained in Section 2. The whole procedure of implementation of presented technique are covered in Section 3. In Section 4, simulation is provided. (i) Security analysis and (ii) Statistical analysis can be viewed through Sections 5 and 6 respectively. In Section 7, comparison analysis is provided. Lastly, the proposed technique is concluded in Section 8.

2 Preliminaries

In this section, we give a brief introduction of RMAC, RP2DFrHT and 2D Arnold map which are used in our proposed encryption technique.

2.1 Random matrix affine cipher (RMAC) [18]

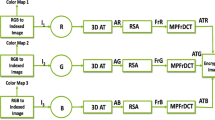
Affine cipher is a well recognized mono-alphabetic substitution cipher mostly used for encryption of textual data. In our proposed technique RMAC [18] is used which performed better as compared to affine cipher. The proposed technique provides security in co-ordinate domain as well as in geometrical domain. The algorithm of RMAC is demonstrated in Fig. 1. The pixel intensity of m × n RGB image is given in matrix Y. The pixels of the image are categorized in even and odd numbered rows and columns. Even and odd numbered rows of the matrix Y are multiplied by the multiplicative parameters χ and η respectively. The co-ordinates of even and odd numbered rows are shifted by the shift parameters α and β respectively. The multiplicative parameters χ and η are coprime to n i.e $\gcd (\chi ,n)=1$ and $\gcd (\eta ,n)=1$ and 0 < α≠β < n. Similar mechanism is adopted for even and odd numbered columns. Even and odd numbered columns of the matrix Y are multiplied by the multiplicative parameters λ and ω respectively. The co-ordinates of even and odd numbered columns are shifted by the shift parameters γ and δ respectively. The multiplicative parameters λ and ω are coprime to m i.e $\gcd (\lambda ,m)=1$ and $\gcd (\omega ,m)=1$ and 0 < γ ≠ δ < m. The mathematical expression of RMAC on RGB image matrix Y is given as follows.

$$ \begin{array}{@{}rcl@{}} Y^{\prime}_{\text{even row},~p}&\equiv&\chi Y_{\text{even row},~i+\alpha (\text{mod} {n})},\\ Y^{\prime}_{\text{odd row},~q}&\equiv &\eta Y_{\text{odd row},~i+\beta (\text{mod} {n})},\\ Y^{\prime}_{~k,~\text{even column}}&\equiv& \lambda Y_{j+\gamma(\text{mod} {m}),~\text{even column}},\\ Y^{\prime}_{l,~\text{odd column}}&\equiv &\omega Y_{j+\delta(\text{mod} {m}),~\text{odd column}}. \end{array} $$

(1)

Fig. 1

Framework of RMAC for an RGB image of size m × n

The inverse random matrix affine cipher (IRMAC) for decoding an RGB image $Y^{\prime }$ is provided below.

$$ \begin{array}{@{}rcl@{}} Y_{\text{even row},~i}&\equiv& \mu Y^{\prime}_{\text{even row},~p+n-\alpha(\text{mod} {n})},\\ Y_{\text{odd row},~i}&\equiv& \kappa Y^{\prime}_{\text{odd row},~q+n-\beta(\text{mod} {n})},\\ Y_{j,~\text{even column}}&\equiv& \nu Y^{\prime}_{k+m-\gamma(\text{mod} {m}),~\text{even column}},\\ Y_{j,~\text{odd column}}&\equiv& \sigma Y^{\prime}_{l+m-\delta(\text{mod} {m}),~\text{odd column}}, \end{array} $$

(2)

where μχ ≡ 1(modn), κη ≡ 1(modn), νλ ≡ 1(modm) and σω ≡ 1(modm). The matrix Y is an original RGB image whereas the matrix $Y^{\prime }$ is the matrix after using RMAC. Shift parameters and multiplier parameters are used as secret keys.

2.2 Reality preserving two dimensional discrete fractional Hartley transform (RP2DFrHT) [17, 45]

The elements of the N × N discrete Hartley transform (DHT) matrix H are as follows.

$$ H_{ab}=\frac{1}{\sqrt{N}}\left [\cos\left( \frac{2 \pi ab}{N}\right)+\sin\left( \frac{2 \pi ab}{N}\right)\right], $$

(3)

where 0 ≤ a, b ≤ N − 1.

Tridiagonal matrix S is given below.

$$ S= \left[\begin{array}{cccccc} 2 & 1 & 0&{\dots}&0&1\\ 1 & 2\cos\left( \frac{2\pi}{N}\right) & 1&{\dots}&0&0\\ 0&1&2\cos\left( \frac{4\pi}{N}\right)&{\dots}&0&0\\ {\vdots}&{\vdots}&{\vdots}&{\ddots}&{\vdots}&{\vdots}\\ 0&0&0&{\dots}&2\cos\left[\frac{2(N-2)\pi}{N}\right]&1\\ 1&0&0&{\dots}&1&2\cos\left[\frac{2(N-1)\pi}{N}\right] \end{array}\right]. $$

(4)

The eigen-decomposition of the N × N DHT matrix H [27] is given below.

$$ H=UDU^{\prime}, $$

(5)

where U is a matrix obtained from the eigenvector of the tridiagonal matrix S given in (4), D is a diagonal matrix which consists of the eigenvalues of DHT matrix as its diagonal entries and $U^{\prime }$ is the transpose of the matrix U.

The discrete fractional Hartley transform H^c is obtained by taking the c th power of the matrix H as given below.

$$ H^{c}=UD^{c} U^{\prime}, $$

(6)

where c is the fractional order.

The two dimensional discrete fractional Hartley transform (2DFrHT) for the N × N matrix X is

$$ Z=H^{c}X(H^{c})'. $$

(7)

The encrypted image obtained using 2DFrHT is a complex-valued image, whereas the original image is a real-valued image. To achieve real-valued encrypted image, reality preserving two dimensional discrete fractional Hartley transform (RP2DFrHT) [17, 45] is used.

The RP2DFrHT kernel matrix is given as

$$ {R^{c}_{H}} = \left[\begin{array}{cc} \text{Re}(H^{c}) & -\text{Im}(H^{c}) \\ \text{Im}(H^{c}) &\text{Re}(H^{c}) \end{array}\right]. $$

(8)

The RP2DFrHT for the N × N matrix X is given as

$$ E={R^{c}_{H}}X{R^{d}_{H}}, $$

(9)

where c and d are the fractional orders.

The IRP2DFrHT for decoding the N × N matrix E is given as

$$ X=R^{-c}_{H}ER^{-d}_{H}. $$

(10)

2.3 2D Arnold map [33]

The two dimensional (2D) Arnold map is enormously utilized in image encryption algorithms. It is used to dislocate the position of the pixels in an RGB image. The 2D Arnold map is shown below.

$$ \begin{bmatrix} x^{\prime}\\ y^{\prime} \end{bmatrix}=\begin{bmatrix} 1& v\\ u& uv+1 \end{bmatrix}\begin{bmatrix} x\\ y \end{bmatrix}(\text{mod} {n}), $$

(11)

The inverse Arnold map is given below.

$$ \begin{bmatrix} x\\ y \end{bmatrix}=\begin{bmatrix} uv+1& -v\\ -u& 1 \end{bmatrix}\begin{bmatrix} x^{\prime}\\ y^{\prime} \end{bmatrix}(\text{mod} {n}), $$

(12)

where u and v are the Arnold keys, (x, y) are the original pixels, ($x^{\prime }$, $y^{\prime }$) are the pixels after using 2D Arnold map and u, v∈ $\mathbb {Z}^{+}$, $\mathbb {Z}^{+}$ is the set of positive integers.

3 Proposed method

We design a new multi-layer encryption technique for color image security. In the proposed technique, the concepts of RMAC, RP2DFrHT and Arnold map are merged. The proposed technique is discussed in two phases. First phase is an encryption process and second phase is a decryption process.

Phase 1: Encryption process

Encryption is the phenomenon of converting plain image (original) into an unintelligible format of image called encrypted image. The whole encryption process is diagrammatically represented in the form of flowchart in Fig. 2. Firstly, three color components as red (R), green (G) and blue (B) are obtained by splitting the RGB image. Secondly, each component of RGB image is processed separately. A detailed description is given as below.

Fig. 2

Flowchart of Encryption process

Stage-I (RMAC):-

This stage involves the generation of the first stage encrypted image. The RMAC is implemented on each component of the original RGB color image. Two types of parameters are required in this stage. One is shift parameters and another is multiplier parameters. The shift parameters and multiplier parameters are as given below.

• 1. For red component (R): The shift parameters are α_R, β_R, γ_R, δ_R and the multiplier parameters are χ_R, η_R, λ_R, ω_R.

• 2. For green component (G): The shift parameters are α_G, β_G, γ_G, δ_G and the multiplier parameters are χ_G, η_G, λ_G, ω_G.

• 3. For blue component (B): The shift parameters are α_B, β_B, γ_B, δ_B and the multiplier parameters are χ_B, η_B, λ_B, ω_B.

At the end of this stage, red, green and blue components of the first stage encrypted image are obtained for red, green and blue components of the original RGB image.

Stage-II (RP2DFrHT):-

The second stage encrypted image is obtained by using RP2DFrHT. The RP2DFrHT is implemented on each component of the first stage encrypted image. The implementation is done using the fractional orders. The fractional orders for each component are as given below.

• 1. For red component (R): The fractional orders are c_R and d_R.

• 2. For green component (G): The fractional orders are c_G and d_G.

• 3. For blue component (B): The fractional orders are c_B and d_B.

At the end of this stage, red, green and blue components of the second stage encrypted image are obtained for red, green and blue components of the first stage encrypted image.

Stage-III (Arnold map):-

The complete encrypted image is obtained by scrambling the pixels of each component of the second stage encrypted image. The scrambling is done using Arnold map. In this stage the Arnold keys are given as follows.

• 1. For red component (R): The Arnold keys are u_R and v_R.

• 2. For green component (G): The Arnold keys are u_G and v_G.

• 3. For blue component (B): The Arnold keys are u_B and v_B.

At the end of this stage, red, green and blue components of the third stage encrypted image are obtained for red, green and blue components of the second stage encrypted image. By combining red, green and blue components of the third stage encrypted image, we obtain the complete encrypted image.

Phase 2: Decryption process

The process of converting an encrypted image into a plain image (original) is called decryption. It is basically a reverse process of the encryption. The whole decryption process is diagrammatically represented in the form of flowchart in Fig. 3. The whole procedure is processed using correct secret keys as well as their correct arrangements. A detailed description is given as below.

Fig. 3

Flowchart of Decryption process

Stage-I (Reverse of Arnold map):-

The complete encrypted image firstly segregated into red, green and blue components. The inverse Arnold map is applied on each component R, G, B of the encrypted image. At the end of this stage, scrambled pixels are converted into unscrambled pixels. The red, green and blue components of the first stage decrypted image are obtained for red, green and blue components of the complete encrypted image.

Stage-II (Reverse of RP2DFrHT):-

In this stage IRP2DFrHT is applied to decrypt the image obtained in the first stage. The inverse fractional orders for each component are as given below.

• 1. For red component (R): The inverse fractional orders are $c^{-1}_{R}$ and $d^{-1}_{R}$.

• 2. For green component (G): The inverse fractional orders are $c^{-1}_{G}$ and $d^{-1}_{G}$.

• 3. For blue component (B): The inverse fractional orders are $c^{-1}_{B}$ and $d^{-1}_{B}$.

At the end of this stage, red, green and blue components of the second stage decrypted image are obtained for red, green and blue components of the first stage decrypted image.

Stage-III (Reverse of RMAC):-

Lastly inverse RMAC is applied to decrypt the image obtained in the second stage. The decryption keys involve in this process are as follows.

• 1. For red component (R): The inverse shift parameters are $\alpha _{R}^{-1}$, $\beta _{R}^{-1}$, $\gamma _{R}^{-1}$, $\delta _{R}^{-1}$ and the inverse multiplier parameters are μ_R, κ_R, ν_R, σ_R.

• 2. For green component (G): The inverse shift parameters are $\alpha _{G}^{-1}$, $\beta _{G}^{-1}$, $\gamma _{G}^{-1}$, $\delta _{G}^{-1}$ and the inverse multiplier parameters are μ_G, κ_G, ν_G, σ_G.

• 3. For blue component (B): The inverse shift parameters are $\alpha _{B}^{-1}$, $\beta _{B}^{-1}$, $\gamma _{B}^{-1}$, $\delta _{B}^{-1}$ and the inverse multiplier parameters are μ_B, κ_B, ν_B, σ_B.

As μ_Rχ_R ≡ 1(modN), κ_Rη_R ≡ 1(modN), ν_Rλ_R ≡ 1(modN), σ_Rω_R ≡ 1(modN), μ_Gχ_G ≡ 1(modN), κ_Gη_G ≡ 1(modN), ν_Gλ_G ≡ 1(modN), σ_Gω_G ≡ 1(modN), μ_Bχ_B ≡ 1(modN), κ_Bη_B ≡ 1(modN), ν_Bλ_B ≡ 1(modN), σ_Bω_B ≡ 1(modN). At the end of this stage, red, green and blue components of the third stage decrypted image are obtained. By combining red, green and blue components of the third stage decrypted image, we obtain the complete decrypted image.

4 Simulation

In this section, simulation is done to examine the authenticity and feasibility of the proposed encryption technique. For simulation, Lena color image of size 512 × 512 × 3 is taken as shown in Fig. 4a. The first stage encrypted image obtained using RMAC is given in Fig. 4b. The shift parameters and multiplier parameters used in this stage are as follows.

• 1. For red component (R): The shift parameters are α_R = 450, β_R = 170, γ_R = 145, δ_R = 371 and the multiplier parameters are χ_R = 233, η_R = 147, λ_R = 313, ω_R = 291.

• 2. For green component (G): The shift parameters are α_G = 151, β_G = 71, γ_G = 250, δ_G = 300 and the multiplier parameters are χ_G = 119, η_G = 417, λ_G = 505, ω_G = 215.

• 3. For blue component (B): The shift parameters are α_B = 399, β_B = 501, γ_B = 192, δ_B = 497 and the multiplier parameters are χ_B = 451, η_B = 273, λ_B = 337, ω_B = 119.

Figure 4c represents the second stage encrypted image by incorporating RP2DFrHT. The fractional orders used in this stage are as follows.

• 1. For red component (R): The fractional orders are c_R = 0.7, d_R = 0.3.

• 2. For green component (G): The fractional orders are c_G = 0.4, d_G = 0.5.

• 3. For blue component (B): The fractional orders are c_B = 0.9, d_B = 0.6.

Figure 4d represents the complete encrypted image obtained after using Arnold map. The Arnold keys used in this stage are as follows.

• 1. For red component (R): The Arnold keys are u_R = 130, v_R = 160.

• 2. For green component (G): The Arnold keys are u_G = 97, v_G = 100.

• 3. For blue component (B): The Arnold keys are u_B = 99, v_B = 110.

The Fig. 5 represents the correct demonstration of decrypted image for each stage employing correct secret keys and their correct arrangements. The complete encrypted image is given in Fig. 5a. The first stage decrypted image is obtained using inverse Arnold map as shown in Fig. 5b. The second stage decrypted image is obtained using IRP2DFrHT as shown in Fig. 5c. Lastly, Fig. 5d gives the complete decrypted image. This stage is obtained using inverse RMAC. The inverse shift parameters and inverse multiplier parameters are as given below.

• 1. For red component (R): The inverse shift parameters are $\alpha _{R}^{-1}$ = 62, $\beta _{R}^{-1}$ = 342, $\gamma _{R}^{-1}$ = 367, $\delta _{R}^{-1}$ = 141 and the inverse multiplier parameters are μ_R = 345, κ_R = 411, ν_R = 265, σ_R = 139.

• 2. For green component (G): The inverse shift parameters are $\alpha _{G}^{-1}$ = 361, $\beta _{G}^{-1}$ = 441, $\gamma _{G}^{-1}$ = 262, $\delta _{G}^{-1}$ = 212 and the inverse multiplier parameters are μ_G = 327, κ_G = 97, ν_G = 73, σ_G = 231.

• 3. For blue component (B): The inverse shift parameters are $\alpha _{B}^{-1}$ = 113, $\beta _{B}^{-1}$ = 11, $\gamma _{B}^{-1}$ = 320, $\delta _{B}^{-1}$ = 15 and the inverse multiplier parameters are μ_B = 235, κ_B = 497, ν_B = 433, σ_B = 327.

Fig. 4

Encryption results for Lena color image a The original Lena color image b The first stage Lena encrypted image c The second stage Lena encrypted image and d The complete Lena encrypted image

Fig. 5

Decryption results for Lena color image a The complete Lena encrypted image b The first stage decrypted image c The second stage decrypted image and d The complete decrypted image

5 Security analysis

The sensitivity analysis is done to validate the role of secret keys and their arrangements. The proposed technique is highly sensitive towards its secret keys and their arrangements. In other words, some simple modification in the secret keys or in the arrangements would provide a distorted version of the original image. The sensitivity analysis is done in five phases as given below.

Sensitivity analysis-I

The sensitivity analysis-I is shown in Fig. 6. This stage is performed with incorrect Arnold keys while all other secret keys and their arrangements are kept same. The incorrect Arnold keys for each color component are taken as follows.

• 1. For red component (R): The Arnold keys are u_R = 131 and v_R = 160.

• 2. For green component (G): The Arnold keys are u_G = 97 and v_G = 101.

• 3. For blue component (B): The Arnold keys are u_B = 100 and v_B = 111.

The complete encrypted image is displayed in Fig. 6a. The outcome of the first stage decrypted image with incorrect Arnold keys of inverse Arnold map is given in Fig. 6b. The second stage decrypted image with correct decryption keys of IRP2DFrHT is given in Fig. 6c. The complete decrypted image with correct parameters and arrangements of IRMAC is shown in Fig. 6d. It is clear from Fig. 6 that the complete decrypted image is totally different from the original color image. Hence, Arnold keys are very sensitive for the proposed technique.

Fig. 6

Results of Sensitivity analysis-I for incorrect Arnold keys a The complete Lena encrypted image b The first stage decrypted image c The second stage decrypted image d The complete decrypted image

Sensitivity analysis-II

This stage of sensitivity analysis is performed with approximate fractional orders of RP2DFrHT. However, Arnold keys and parameters of IRMAC are kept correct. The complete procedure is illustrated in Fig. 7. The approximate fractional orders for each color component are as follows.

• 1. For red component (R): The fractional orders are c_R = 0.7 and d_R = 0.2.

• 2. For green component (G): The fractional orders are c_G = 0.3 and d_G = 0.5.

• 3. For blue component (B): The fractional orders are c_B = 0.8 and d_G = 0.5.

The complete encrypted is represented in Fig. 7a. The outcome of the first stage decrypted image using accurate Arnold keys is shown in Fig. 7b. The outcome of the second stage decrypted image with approximate keys of IRP2DFrHT is shown in Fig. 7c. The complete decrypted image with correct parameters and the arrangements of IRMAC is shown in Fig. 7d. It is clear from Fig. 7 that the complete decrypted image is entirely different from the original color image. This stage shows that the fractional orders are highly sensitive.

Fig. 7

Results of Sensitivity analysis-II for approximate fractional orders a The complete Lena encrypted image b The first stage decrypted image c The second stage decrypted image d The complete decrypted image

Sensitivity analysis-III

This stage of sensitivity analysis is shown in Fig. 8. In this stage the sensitivity analysis is done using incorrect inverse shift parameters while remaining secret keys are kept same. The incorrect inverse shift parameters for each component are as follows.

• 1. For red component (R): The inverse shift parameters are $\alpha _{R}^{-1}$ = 65, $\beta _{R}^{-1}$ = 341, $\gamma _{R}^{-1}$ = 360, $\delta _{R}^{-1}$ = 100.

• 2. For green component (G): The inverse shift parameters are $\alpha _{G}^{-1}$ = 364, $\beta _{G}^{-1}$ = 442, $\gamma _{G}^{-1}$ = 265, $\delta _{G}^{-1}$ = 211.

• 3. For blue component (B): The inverse shift parameters are $\alpha _{B}^{-1}$ = 110, $\beta _{B}^{-1}$ = 16, $\gamma _{B}^{-1}$ = 322, $\delta _{B}^{-1}$ = 18.

The complete encrypted image is shown in Fig. 8a. The outcome of the first stage decrypted image using accurate Arnold keys is given in Fig. 8b. The outcome of the second stage decrypted image with correct IRP2DFrHT keys is given in Fig. 8c. The complete decrypted image is obtained using incorrect inverse shift parameters whereas inverse multiplier parameters and arrangements of IRMAC are kept same. This stage is displayed in Fig. 8d. It is clear from Fig. 8 that the complete decrypted image is completely different from the original color image. The sensitivity analysis-III interferences that the shift parameters are highly sensitive.

Fig. 8

Results of Sensitivity analysis-III for incorrect inverse shift parameters a The complete Lena encrypted image b The first stage decrypted image c The second stage decrypted image d The complete decrypted image

Sensitivity analysis-IV

Sensitivity analysis-IV is done using approximate inverse multiplier parameters whereas inverse shift parameters, fractional orders and Arnold keys are not disturbed. The approximate inverse multiplier parameters for each color component are as follows.

• 1. For red component (R): The inverse multiplier parameters are μ_R = 347, κ_R = 151, ν_R = 239, σ_R = 459.

• 2. For green component (G): The inverse multiplier parameters are μ_G = 239, κ_G = 7, ν_G = 211, σ_G = 381.

• 3. For blue component (B): The inverse multiplier parameters are μ_B = 431, κ_B = 507, ν_B = 143, σ_B = 91.

The complete encrypted image is shown in Fig. 9a. The first stage decrypted image is displayed in Fig. 9b which is attained using accurate Arnold keys. The second stage decrypted image is displayed in Fig. 9c with correct IRP2DFrHT keys. The complete decrypted image is shown in Fig. 9d obtained using approximate inverse multiplier parameters whereas inverse shift parameters and arrangements of IRMAC are kept correct. The complete decrypted image is entirely different from the original image as shown in Fig. 9. Therefore, in this stage we conclude that the multiplier parameters are very sensitive.

Fig. 9

Results of Sensitivity analysis-IV for approximate inverse multiplier parameters a The complete Lena encrypted image b The first stage decrypted image c The second stage decrypted image d The complete decrypted image

Sensitivity analysis-V

Sensitivity analysis-V is done using incorrect arrangements of IRMAC while other secret keys and their arrangements are kept correct. Incorrect arrangements for each color component are taken as follows.

• 1. For red component (R): The inverse shift parameters are $\alpha _{R}^{-1}$ = 367, $\beta _{R}^{-1}$ = 342, $\gamma _{R}^{-1}$ = 141, $\delta _{R}^{-1}$ = 62 and the inverse multiplier parameters are μ_R = 345, κ_R = 139, ν_R = 411, σ_R = 265.

• 2. For green component (G): The inverse shift parameters are $\alpha _{G}^{-1}$ = 441, $\beta _{G}^{-1}$ = 262, $\gamma _{G}^{-1}$ = 361, $\delta _{G}^{-1}$ = 212 and the inverse multiplier parameters are μ_G = 97, κ_G = 327, ν_G = 231, σ_G = 73.

• 3. For blue component (B): The inverse shift parameters are $\alpha _{B}^{-1}$ = 320, $\beta _{B}^{-1}$ = 113, $\gamma _{B}^{-1}$ = 15, $\delta _{B}^{-1}$ = 11 and the inverse multiplier parameters are μ_B = 497, κ_B = 327, ν_B = 235, σ_B = 433.

The complete encrypted image is shown in Fig. 10a. The first stage decrypted image using correct Arnold keys is represented in Fig. 10b. The outcome of the second stage decrypted image using correct IRP2DFrHT keys is displayed in Fig. 10c. The complete decrypted image is obtained using incorrect arrangements of IRMAC whereas all other parameters are kept same. This stage is displayed in Fig. 10d. The complete decrypted image is entirely different from the original color image as displayed in Fig. 10. Hence, sensitivity analysis-V ensures that not only the magnitude of parameters but their arrangements are also very sensitive.

Fig. 10

Results of Sensitivity analysis-V for incorrect arrangements of IRMAC a The complete Lena encrypted image b The first stage decrypted image c The second stage decrypted image d The complete decrypted image

6 Statistical analysis

Visual differentiation between original and encoded/ decoded image is not possible. It would be possible in statistical analysis. An ideal encryption technique should resist all types of statistical attacks. To validate the effectiveness and feasibility of our presented encryption technique, we have done a statistical analysis in this section.

6.1 Histogram analysis

The statistical behaviour of input and output images are analyzed in histogram analysis. The histogram analysis is a graphical representation of the number of pixels against different intensity values found in an image. Figure 11a,b,c and d represent the histogram of the original Lena color image, the first stage Lena encrypted image, the second stage Lena encrypted image and the complete Lena encrypted image as given in Fig. 4a,b,c and d respectively. After analyzing all encrypted images, we have found that not only the histogram of the complete encrypted image, but also the histograms of different stages of the encrypted images are different from the original image. This ensures that the information about the original image cannot be leaked at any stage of the encrypted image. This also provides the robustness against potential attack. The histogram of the decrypted image is also obtained. Figure 12a,b,c and d represent the histogram of the complete Lena encrypted image, the first stage decrypted image, the second stage decrypted image and the complete decrypted image as shown in Fig. 5a,b,c and d respectively. The similarity between the histogram of the complete decrypted image and the histogram of the original image demonstrates the effectiveness of our proposed technique.

Fig. 11

Histogram results for encryption process a histogram of the original Lena color image b histogram of the first stage Lena encrypted image c histogram of the second stage Lena encrypted image d histogram of the complete Lena encrypted image

Fig. 12

Histogram results for decryption process a histogram of the complete Lena encrypted image b histogram of the first stage decrypted image c histogram of the second stage decrypted image d histogram of the complete decrypted image

6.2 Mean squared error (MSE)

The mean squared error between input RGB image and output RGB image for each red, green and blue component are mathematically calculated as.

$$ MSE=\frac{1}{{N \times M}}\sum\limits_{n=1}^{N}\sum\limits_{m=1}^{M}|f(n,m)-\hat f(n,m)|^{2}, $$

(13)

where N and M are pixels of an RGB image, f(n,m) is the input image and $\hat f(n,m)$ is the output image. Tables 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 and 11 represent the values of MSE between original image and output image for each RGB component. The MSE values between complete encrypted image shown in Fig. 4d and original image shown in Fig. 4a are given in Table 3. This table shows that the MSE values for each component of the RGB color image are very high. Higher values of MSE indicate that the original image is totally changed. The MSE values between complete decrypted image shown in Fig. 5d and original image are given in Table 6. This table shows that the MSE values for each component of RGB image is zero which guarantee that the original image and the complete decrypted image are both identical.

Table 1 MSE_(R,G,B), PSNR_(R,G,B) and Correlation_(R,G,B) of Fig. 4b and a

Table 2 MSE_(R,G,B), PSNR_(R,G,B) and Correlation_(R,G,B) of Fig. 4c and a

Table 3 MSE_(R,G,B), PSNR_(R,G,B) and Correlation_(R,G,B) of Fig. 4d and a

Table 4 MSE_(R,G,B), PSNR_(R,G,B) and Correlation_(R,G,B) of Figs. 5b and 4a

Table 5 MSE_(R,G,B), PSNR_(R,G,B) and Correlation_(R,G,B) of Figs. 5c and 4a

Table 6 MSE_(R,G,B), PSNR_(R,G,B) and Correlation_(R,G,B) of Figs. 5d and 4a

Table 7 MSE_(R,G,B), PSNR_(R,G,B) and Correlation_(R,G,B) of Figs. 6d and 4a

Table 8 MSE_(R,G,B), PSNR_(R,G,B) and Correlation_(R,G,B) of Figs. 7d and 4a

Table 9 MSE_(R,G,B), PSNR_(R,G,B) and Correlation_(R,G,B) of Figs. 8d and Fig. 4a

Table 10 MSE_(R,G,B), PSNR_(R,G,B) and Correlation_(R,G,B) of Figs. 9d and 4a

Table 11 MSE_(R,G,B), PSNR_(R,G,B) and Correlation_(R,G,B) of Figs. 10d and 4a

6.3 Peak signal-to-noise ratio (PSNR)

The peak signal-to-noise ratio between input RGB image and output RGB image for each RGB component are mathematically calculated as.

$$ PSNR=10~.~\log_{10}\frac{(255)^{2}}{MSE}. $$

(14)

Tables 1–11 represent the values of PSNR between original image and output image for each RGB component. The PSNR values between complete encrypted image shown in Fig. 4d and original image shown in Fig. 4a are given in Table 3. This table shows that the PSNR values for each component of the RGB color image are low. Lower values of PSNR indicate that the original image is completely changed. The PSNR values between complete decrypted image shown in Fig. 5d and original image are given in Table 6. This table shows that the PSNR values for each component of RGB image is infinity which guarantee that the original image and the complete decrypted image are both identical.

6.4 Correlation coefficient

To measure linear relationship between the pixels of two images, correlation coefficient (C) is considered. The limiting value of C lies between -1 and + 1 i.e. -1 ≤ C ≤ + 1. If C is + 1 it means the strong positive correlation. If C is -1 it means the negative relationship between two images. If C is 0 it means no relationship between two images. For the original image, the value of C is close to + 1, whereas for the encrypted image, the value of C is close to 0.

Tables 1–11 represent the values of correlation coefficient between original image and output image for each RGB component. The values of C between complete encrypted image shown in Fig. 4d and original image shown in Fig. 4a are given in Table 3. This table shows that the values of C for each component of the RGB color image are tending to zero which indicate that the original image is totally changed. The values of C between complete decrypted image shown in Fig. 5d and original image are given in Table 6. This table shows that the values of C for each component of RGB image are + 1 which guarantee that the original image and the complete decrypted image are both identical.

The results of the aforementioned statistical tools interference that without knowing correct secret keys and their correct arrangements, unauthorized person cannot obtain any information from the encrypted image. The ideal value of each statistical tool validates that using correct secret keys and their correct arrangements the complete correct original image has recovered. Tables 7–11 signify the sensitivity of secret keys and their arrangements mathematically. We have also obtained correlation coefficients in horizontal, vertical and diagonal directions which are given in Table 12.

Table 12 Correlation coefficients in horizontal, vertical and diagonal directions

6.5 Entropy analysis

To quantify the impulsiveness of the information, entropy analysis is done. The mathematical expression of entropy is given as follows.

$$ H(s)=-\sum\limits_{j=1}^{M}p(s_{j})\log_{2}p(s_{j}), $$

(15)

where H(s) denotes the entropy of data s, p(s_j) is the probability occurrence of the case s_j and M is the total number of all possible occurrences. The ideal value of H(s) should be 8 bits. The entropy estimation should be near to ideal value to provide invulnerability from entropy attacks. The values of entropy estimation of red, green and blue components of the original image, the first stage encrypted image, the second stage encrypted image, the complete encrypted image and the complete decrypted image are listed in Table 13. It is justified that our proposed encryption technique is more secure against entropy based attacks.

Table 13 Entropy values for red, green and blue components of Lena color image

6.6 Resisting classical attacks

While dealing with cryptanalysis, classical attacks are classified into four categories: chosen-plaintext attack (CPA), known-plaintext attack (KPA), chosen-ciphertext attack (CCA) and ciphertext-only attack (COA). In CPA, the cryptanalyst has tentative access to the encryption system and he tries to find a ciphertext corresponding to the randomly chosen plaintext. In KPA, the cryptanalyst has availability of both plaintext and ciphertext. The cryptanalyst randomly receives these samples instead of selecting. In CCA, the cryptanalyst has temporary access to decryption system to find comparative plaintext corresponding to the arbitrarily picked ciphertext. In COA, the cryptanalyst has access to a certain number of ciphertexts and have no information about the plaintext. Among them, chosen-plaintext is the most remarkable attack. If encryption algorithm restricts chosen-plaintext attack then it opposes other three attacks too. In this paper, our encryption technique is designed in such a way that the security of the system depends not only upon the secret keys, but also upon the correct arrangements of all secret keys. As the proposed technique has exceptionally huge key size. Therefore, it is difficult for hackers to analyze accurate secret keys and appropriate arrangements of all hidden keys. In Section 5, we have demonstrated the sensitivity analysis of our encryption technique. Therefore, owing to all these properties the proposed technique is unaffected by above all four typical attacks.

7 Comparison analysis

In this section, we have compared our proposed encryption technique with the existing similar techniques [7, 8, 11, 16, 18, 19, 22, 24, 28, 34, 35, 38, 39, 41, 42, 46].

Table 14

• 1. Chen and Zhao [7] proposed an encryption scheme in optical domain using fractional wavelet transform (FWT). Two series of keys are used in their scheme. The security of their scheme depends upon keys only.

• 2. Tao et al. [35] presented a cryptographic technique using multi orders of fractional Fourier transform (FRFT). The security of their technique depends only upon the keys. The nature of encrypted image is complex-valued. The security of their technique is given in the frequency domain.

• 3. Lang [19] developed a technique using the concept of reality preserving multiple-parameter fractional Fourier transform (RPMPFRFT). The security of his scheme depends upon the parameters of RPMPFRFT.

• 4. Liu et al. [22] introduced a scheme for color image in which Arnold transform and color-blend operation in discrete cosine transform domain play a vital role. The random angle data in color blend operation and parameters of Arnold transform are taken as a key. The security of their scheme depends in co-ordinate domain as well as in frequency domain.

• 5. Wu et al. [39] presented an encryption scheme using multiple-order discrete fractional cosine transform (MODFrCT). The security of their scheme depends upon fractional orders only. Their scheme provides security in frequency domain only.

• 6. Prasad et al. [28] introduced an encryption scheme using FRFT and wavelet transform. Final encoded image obtained in their scheme is complex-valued. Their scheme provides security in frequency domain only.

• 7. Zhu et al. [46] presented an algorithm for image security based on Arnold transform and affine cipher. Their scheme is secure in co-ordinate domain as well as in geometrical domain. The security depends upon secret keys only.

• 8. Kumar et al. [18] introduced their first encryption algorithm for RGB image using discrete wavelet transform and random matrix affine cipher. Their scheme provides two layers of security.

• 9. Zhao et al. [42] designed a scheme based on optical domain using two dimensional fractional Hartley transform (FRHT). The random phase codes and fractional orders are taken as keys. The final encrypted image is a complex-valued in their scheme.

• 10. Tao et al. [34] introduced double random amplitude encoding method using multiple-parameter discrete fractional Hadamard transform (MPDFrHaT). The ciphertext obtained in their scheme after encryption is complex-valued data.

• 11. Wu et al. [38] proposed a lossless cryptographic technique for color image utilizing two dimensional discrete wavelet transform and six dimensional hyperchaotic system. The system is secure in frequency domain as well as in spatial domain.

• 12. Mishra and Sharma [24] proposed an image encryption scheme utilizing random matrix shift cipher (RMSC) and discrete fractional Fourier transform (DFrFT). The secret keys as well as their arrangements are established for the immunity of the system. The nature of encrypted image is complex-valued.

• 13. Chen and Zhao [8] proposed an optical image encryption in accordance with wavelength multiplexing and lensless Fresnel transform holograms. The parameter of Fresnel transform and random phase masks are taken as a key.

• 14. Joshi et al. [16] designed a technique for color image data based on FRFT. The fractional order and random phase masks are taken as a key for the enhancement of security of the system.

• 15. Zhang and Xiao [41] proposed an image encryption scheme based on optical domain using discrete Chirikov standard map and chaos-based fractional random transform. The encrypted image obtained in their scheme has complex coefficients.

• 16. Guo et al. [11] introduced a technique for color image data using discrete fractional random transform (DFRNT) and Arnold transform (AT) in the intensity-hue-saturation (IHS) color space. The encrypted image obtained in their technique has complex coefficients.

8 Conclusions

In this paper, we have proposed a robust multi-layer color image encryption by merging the concepts of RMAC, RP2DFrHT and 2D Arnold map. The encryption has been done in three phases. Firstly, RGB image has been divided into its three components R, G, B. In the first phase, RMAC has been employed to transform the pixels in co-ordinate domain as well as in geometrical domain. In the second phase, RP2DFrHT has been used to transform the pixels in frequency domain. RP2DFrHT provides real-valued encrypted image. The real-valuedness property of RP2DFrHT decreases the storage, computational and communication complexities of the encrypted image in digital environment. In the final phase, an additional layer of security has been provided using Arnold map. Arnold map provides chaotic behaviour in our proposed encryption technique. For correct image encryption, we have adopted the reverse steps of the encryption process. Moreover presented technique has provided security in geometrical domain, co-ordinate domain, frequency domain and time domain. Sensitivity analysis has been done to demonstrate the sensitivity of the secret keys and their arrangements. Statistical analysis has been done to prove the resistance against all types of statistical attacks.