Multiple colour image encryption using multiple parameter FrDCT, 3D Arnold transform and RSA

Abstract

We introduce a novel image encryption and decryption algorithm for multiple images incorporating multiple parameter fractional discrete cosine transform (MPFrDCT), 3D Arnold transform and RSA cryptosystem. Before encryption, the images are changed into their indexed formats by removing their color maps. The indexed formats of the images are taken as the red, green and blue channel of an $\textsf{RGB}$ image. Firstly, the $\textsf{RGB}$ image is taken as the input of 3D Arnold transform. The 3D Arnold transform not only dislocates the pixel positions, but also changes the pixel values. Mathematically, the 3D map performs both permutation as well as substitution. The distorted image is now encrypted using RSA cryptosystem which is a public key cryptosystem. The RSA cryptosystem makes the image secure in public domain as the hard problem is the factorization of large primes which is unbreakable. Lastly, the domain of the encrypted image is changed to frequency domain using MPFrDCT. If the secret keys are known to an unauthorized person, the encryption algorithm is still secure as the security of the presented cryptosystem depends upon the secret keys and the arrangements of the secret keys. The proposed image encryption algorithm is storage efficient. The statistical and simulation analysis are conducted to evaluate the robustness of the presented encryption and decryption processes.

1 Introduction

Due to vast development of network and communication technologies, exchange of digital images over the public channel has increased. The major issues in transmitting images over the public channel are storage and security of the images.

The security of the images can be achieved by developing image encryption algorithm. Several color image encryption algorithms are introduced in this research field [18, 22, 40, 44] using Mellin transform, random phase encoding and Arnold transform etc. Optical image encryption algorithm [28] has been introduced in fourier transform domain. Researchers have also developed image encryption algorithms [10, 11, 19, 21, 41] in fractional Fourier transform domain which is the generalization of Fourier transform. Image encryption algorithms based on choatic mapping combined with Hartley transform domain [8, 23], Gyrator transform [1,2,3,4,5, 31] and wavelet transform [6, 9, 26] have been proposed.

Multiple images are taken together to make the image encryption algorithms storage efficient. This concept was introduced by Situ and Zhang [32] incorporating wavelet multiplexing. Later, multiple image encryption algorithms [14, 17, 20, 30, 37, 39] are developed in fractional Fourier transform domain, Arnold transform, Gyrator transform and Fresnel domain. At the same time, double image encryption algorithm [29, 43] using multi-parameter fractional Fourier transform are proposed. The addition of chaotic map, dual pixel scrambling random phase encoding etc. adds an extra layer of security to the image encryption algorithms due to their scrambling behavior. Nonlinear amplitude and phase truncation based multiple image encryption algorithm [34, 35] in Fourier transform domain are also presented by different researchers. Nowadays, many researchers [12, 13, 16, 24, 25, 36, 42] are working in this field.

Our contribution

We propose a novel technique to encrypt multiple images together in a multi-parameter frequency domain. Initially, three indexed images are extracted from three $\textsf{RGB}$ images. The three indexed images are treated as red, green and blue plane of an $\textsf{RGB}$ image. The 3D Arnold transform is applied on the constructed $\textsf{RGB}$ image. This transform permutes as well as changes the pixel values of the image. After this step, each pixel value is encrypted using RSA cryptosystem. This improves the security of the image as the hard problem in RSA cryptosystem is factoring of large primes. Lastly, MPFrDCT is applied on each encrypted pixel value. The encrypted image is a single image which makes the image encryption algorithm storage efficient as it is convenient to transform single image as compared to multiple images. The decryption process is the reverse of the encryption process. After decryption, three images are recovered from the single encrypted image. Comparison, statistical and security analyzes are done to testify the proposed encryption algorithm.

Novelity

The presented image encryption algorithm is multi-layered secure in comparison to existing similar image encryption algorithms which are only single layered secure. The security in time, frequency and co-ordinate domain is developed using RSA cryptosystem, Arnold 3D cat map and multi-parameter FrDCT. The secret parameters in the scheme are the large primes in RSA, multiple parameters of MPFrDCT, secret keys and the arrangements of secret keys. If an unauthorized person has access to secret keys still he is unable to get the original image as he does not know about the arrangements of secret keys. The presented image encryption algorithm is efficient in comparison to existing similar techniques in terms of time complexity, storage complexity and communication complexity. Therefore, the presented scheme is novel.

In Section 2, we have described the building blocks briefly. These are 3D Arnold transform, MPFrDCT, RSA cryptosystem and Chirikov standard map. The encryption and decryption algorithm is presented in Section 3. Simulation is conducted in Section 4. In Section 5, we briefly compare our proposed algorithm with the similar techniques. Finally, the conclusion is done in Section 6.

2 Preliminaries

The fundamental building blocks RSA cryptosystem, MPFrDCT, discrete Chirikov standard map and 3D Arnold transform are briefly explained in this Section.

2.1 3D Arnold transform

The 2D Arnold transform permutes the position of the pixel in an image of size $M\times M$ [30, 33] using the following map.

$$\begin{aligned} \left( \begin{array}{c} r'_{1} \\ r'_{2} \\ \end{array} \right)= & {} \left( \begin{array}{cc} 1 &{} 1 \\ 1 &{} 2 \\ \end{array} \right) \left( \begin{array}{c} r_1\\ r_2\\ \end{array} \right) (\text {mod}~ M), \end{aligned}$$

(2.1)

where $(r'_{1}, r'_{2})$ is the new pixel position after permutation and $(r_1, r_2)$ is the old pixel position before permutation. The Arnold transfer only shifts the pixel positions from one position to another position. The intensity values of the pixels remain unchanged.

The 3D Arnold transform permutes and substitutes the image pixels using the following map.

$$\begin{aligned} \left( \begin{array}{c} r'_{1} \\ r'_{2} \\ r'_{3} \end{array} \right)= & {} \left( \begin{array}{ccc} 1 &{} 1 &{} 0\\ 1 &{} 2 &{} 0\\ z_1 &{} z_2 &{} 1 \end{array} \right) \left( \begin{array}{c} r_1\\ r_2\\ r_3\\ \end{array} \right) , \end{aligned}$$

(2.2)

where the $(\text {mod}~ M)$ is applied in the calculation of first two rows and $(\text {mod}~ 256)$ is applied in the calculation of last row. The 3D Arnold transform first permutes the pixel position and then the substitution operation is done to change the pixel values. The third parameter

$$r'_{3} = z_1 \times r_1 + z_2 \times r_2 + r_3 (\text {mod}~ 256),$$

where $r'_{3}$ is the pixel intensity after mapping and $r_{3}$ is the pixel intensity before mapping. The inverse 3D Arnold map is given as below.

$$\begin{aligned} \left( \begin{array}{c} r_{1} \\ r_{2} \\ r_{3} \end{array} \right)= & {} \left( \begin{array}{ccc} 2 &{} -1 &{} 0\\ -1 &{} 2 &{} 0\\ -z_1 &{} -z_2 &{} 1 \end{array} \right) \left( \begin{array}{c} r'_{1}\\ r'_{2}\\ r'_{3}\\ \end{array} \right) , \end{aligned}$$

(2.3)

If the 3D Arnold transform is applied on the image t times, then the same image can be obtained using inverse 3D Arnold transform t times. The parameter t is kept secret.

2.2 Assymetric key cryptosystem: RSA cryptosystem

An asymmetric key cryptosystem is a public key cryptosystem in which two different keys are used for image encryption and decryption process. One key is called public key and another is secret key. The secret key is kept hidden with the decrypter and the public key is made available for everyone. There is mathematical relation between the two keys. The RSA cryptosystem involves following steps.

• 1. Firstly, two large different primes p and q are selected at random.

• 2. Generate the integer n by computing $n=p*q$. Compute

  $$\begin{aligned} \phi (n)=(p-1)(q-1), ~\text {where} \end{aligned}$$
  $$\begin{aligned} \phi (n)=\{x\in \mathbb {N}: (x, n)=1 ~\text {and}~ x<n\} \end{aligned}$$

  is the number of positive integers less than n and relatively prime to n.

• 3. The encryption key e is the integer less than and relatively prime to $\phi (n)$, where, $(e, \phi (n))=1$ and $1<e <\phi (n)$. The encryption key is made available for everyone and is known as public key.

• 4. The decryption key d is the inverse of encryption key e modulo $\phi (n)$, i.e, $d=e^{-1}(\text {mod}~\phi (n))$. The decryption key is kept secret and is known as secret key.

• 5. The plaintext message $y \in \mathbb {Z}_{n}$ is encrypted by computing $y^{e}(\text {mod}~ n) =c$, where $\mathbb {Z}_{n} = \{0, 1, 2, ..., n-1\}$, c is called ciphertext.

• 6. The ciphertext c is decrypted by computing $c^{d}(\text {mod}~ n)\equiv y^{ed}(\text {mod}~ n)\equiv y(\text {mod}~ n)$, as $ed\equiv 1(\text {mod}~ \phi (n))$.

The RSA cryptosystem is secure as long as the attacker does not know about the factorization of n. So, the hard problem in RSA cryptosystem is factoring of large primes. This hard problem is also known as factoring problem. It states that it is computationally infeasible to factorize $n=p*q$, where p and q are large primes. RSA cryptosystem withstands frequency analysis attack indirectly by its encryption algorithm. In frequency analysis attack, the frequency distribution of ciphertext is analyzed to guess the corresponding plaintext. This attack is more effective where messages are replaced by a fixed pattern like in substitution cipher. The frequency of the ciphertext reveals the original plaintext whereas in RSA cryptosystem the ciphertext is obtained by taking the large power of the plaintext. The resulting ciphertext is a complex mathematical transformation rather than a simple substitution or transposition of the plaintext. The ciphertext looks like a random string of numbers and reveals nothing about the plaintext. Moreover, the key size in RSA is nearly 2048 bits or more which makes it computationally infeasible to factorize the modulus and break the encryption algorithm using brute force or other known attacks.

In the proposed encryption algorithm, an $\textsf{RGB}$ image with size $M\times N \times 3$ is encrypted using RSA cryptosystem. Each channel is a two dimensional matrix, say X, of size $M\times N$, where $X = [X_{i, j}], i = 1, 2, \ldots , M, j=1, 2, \ldots , N$. Each matrix has $M*N$ elements which are called pixels. Each pixel $X_{i, j}$ is encrypted using the encryption key e as

$$\begin{aligned} C_{i, j} = X_{i,j}^{e}(\text {mod}~ n). \end{aligned}$$

Decrypt $C_{i, j}$ using decryption key d as follows.

$$\begin{aligned} C_{i, j}^{d}(\text {mod}~ n)=X_{i,j}. \end{aligned}$$

2.3 Chirikov standard map

This invertible map is useful in generating $\{\eta (j)\}_{j=1, 2, ...}$ and $\{\delta (j)\}_{j=1, 2,...}$ which are random sequences using initial guesses $\{\eta _0\}, \{\delta _0\} \in [0, 2\pi )$. The two sequences are mathematically generated as follows.

$$\begin{aligned} \eta _{j+1}= & {} (\eta _j+\delta _j)(\text {mod}~ 2\pi ) \end{aligned}$$

(2.4)

$$\begin{aligned} \delta _{j+1}= & {} (\eta _j+\rho \sin (\eta _j+\delta _j))(\text {mod}~ 2\pi ), \end{aligned}$$

(2.5)

where $\rho >0$ is a control parameter and $\eta _j, \delta _j \in [0, 2\pi ), \forall i$.

2.4 Multi-parameter fractional discrete cosine transform (MPFrDCT)

The DCT is an operator $\mathcal {C}: \mathbb {R}^{N} \rightarrow \mathbb {R}^{N}$. The input and output of this map are both real vector of size N. The kernel matrix $\textbf{C}$ for $\mathcal {C}$ is given as below.

$$\begin{aligned} \textbf{C}= & {} \bigg \Vert \frac{1}{\sqrt{M}}\varepsilon _{k}\cos (2\pi \frac{l(2n+1)}{4M})\bigg \Vert . \end{aligned}$$

(2.6)

where $n, l=0,1, ...,M-1, \varepsilon _{0}=1, \varepsilon _{k}=\sqrt{2}, l\ge 1$.

The properties of the matrix $\mathcal {C}$ are as follows.

• 1. $\textbf{C}$ is a unitary matrix.

• 2. $\textbf{C}$ has M orthonormal eigenvectors $x_l$ with the property $x_{m}^{*}x_l=\delta _{ml}$, where

  $$\begin{aligned} \delta _{ml}= \left\{ \begin{array}{ll} 1, &{} \hbox {if m=l} \\ 0 , &{} \hbox {otherwise.} \end{array} \right. \end{aligned}$$

  (2.7)

• 3. The eigenvalue $\lambda _l$ corresponds to eigenvector $x_l$ where $\lambda _l = e^{j\varphi _l},~ 0<\varphi _l<\pi \in \mathbb {R}$ and it lies on the unit circle.

• 4. $\textbf{C}$ is diagonalized as follows.

  $$\begin{aligned} \textbf{C}=X\Lambda X^{*} = \sum _{l}X_{n}e^{j\varphi _l}, \end{aligned}$$

  (2.8)

  where $\Lambda$ is a diagonal matrix with diagonal entries as $\lambda _l$, $X_l=x_lx_{l}^{*}$ is unitary and $X_mX_l=\delta _{ml}X_m$ and $\sum _{l}X_{l}=I$

The map $\mathcal {C}_{a}: \mathbb {R}^{N} \rightarrow \mathbb {R}^{N}$ is an extension of the operator $\mathcal {C}$ and it is called fractional discrete cosine transform (FrDCT) [7], where “fraction” $a \in \mathbb {R}$. The operator $\mathcal {C}_{a}$ possess the following properties.

• 1. $\mathcal {C}_{a+b}=\mathcal {C}_{a}\mathcal {C}_{b}$, this property is called additive property.

• 2. $\mathcal {C}_{1}=\mathcal {C}$, i.e, for $a=1$, $\mathcal {C}_{a}=\mathcal {C}$.

The kernel matrix $\textbf{C}_{a}$ for FrDCT is given below.

$$\begin{aligned} \textbf{C}_{a}=X\Lambda ^{a} X^{*}. \end{aligned}$$

(2.9)

Alternatively,

$$\begin{aligned} \textbf{C}_{a}=2\text {Re}\bigg [\displaystyle \sum _{l=1}^{K} X_l\lambda _{l}^{a}\bigg ] +Y_{1}(1)^{a}+Y_{-1}(-1)^{a}, \end{aligned}$$

(2.10)

where $X_l=x_lx_{l}^{*}, K=\nicefrac {(M-\varrho _{1}-\varrho _{-1})}{2}$, 1 and -1 are the eigenvalues with the algebraic multiplicities $\varrho _{1}$ and $\varrho _{-1}$, $Y_1$ is the total number of $\varrho _{1}$ matrices $X_l$ for eigenvalue 1, and $Y_{-1}$ is the total number of $\varrho _{-1}$ matrices $X_l$ for eigenvalue -1.

For instance, take $M=4M_0$, $M_0 \in \mathbb {Z}$, (2.10) becomes

$$\begin{aligned} \textbf{C}_{a}=2\text {Re}\bigg [\displaystyle \sum _{l=1}^{\nicefrac {M}{2}} X_l\lambda _{l}^{a}\bigg ] =2\text {Re}\bigg [\displaystyle \sum _{l=1}^{\nicefrac {M}{2}} X_le^{j\omega _la}\bigg ]=\displaystyle \sum _{l=1}^{\nicefrac {M}{2}}\bigg (A_{l}\cos (\omega _la)+B_{l}\sin (\omega _la)\bigg ), \end{aligned}$$

(2.11)

where $\omega _l=\varphi _l+2\pi q_l, ~l=1, 2, ..., \frac{M}{2}, 0<\varphi _l<\pi$, $A_l = 2\text {Re}[X_l], B_l=2\text {Im}[X_l]$, $q_l$ is the random sequence generated as explained in Section 2.3. For FrDCT, $\mathbf {q_l} = (q_1, q_2, ..., q_{\nicefrac {M}{2}})$, is the random sequence . Both $\mathbf {q_l}$ and a are secret.

Multi-parameter fractional discrete cosine transform (MPFrDCT) of fractional order a, b for an image $I_{M, N}$ of size $M \times N$ is defined as follows:

$$\begin{aligned} I'_{M, N} = C_aI_{M, N}C_{b}^{T}, \end{aligned}$$

where, $C_{b}^{T}$ is the notation for the transpose of $C_{b}$. The inverse MPFrDCT is computed a follows:

$$\begin{aligned} I_{M, N} = C_{-a}I'_{M, N}C_{-b}^{T}. \end{aligned}$$

3 Description of the proposed algorithm

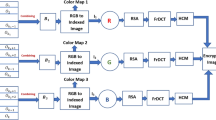
In the design of an image encryption algorithm, a security system is developed by incorporating 3D Arnold transform, RSA cryptosystem and MPFrDCT. Firstly three $\textsf{RGB}$ images are taken and converted into their indexed formats after removing the colour maps. The obtained three indexed images are named as $\mathsf{I_1}$, $\mathsf{I_2}$ and $\mathsf{I_3}$ and are treated as red, green and blue channel of an $\textsf{RGB}$ image. The image encryption and decryption processes are pictorially displayed in Figs. 1 and 2 respectively.

Fig. 1

Encryption Process

Fig. 2

Decryption Process

• Step 1 (Arnold 3D Transform): Firstly, Arnold 3D map is applied on each channel of an $\textsf{RGB}$ image. The input matrices are $\mathsf{I_1}$, $\mathsf{I_2}$ and $\mathsf{I_3}$. The mechanism involved in this step is given below.

  • 1. The Arnold 3D map is applied $t_1, t_2$ and $t_3$ times on $\mathsf{I_1}$, $\mathsf{I_2}$ and $\mathsf{I_3}$. The three matrices $\textsf{AR}$, $\textsf{AG}$ and $\textsf{AB}$ are obtained as output.

  • 2. The matrices $\textsf{AR}$, $\textsf{AG}$ and $\textsf{AB}$ are treated as red, green and blue channel of an $\textsf{RGB}$ image image.

• Step 2 (RSA Cryptosystem): Secondly, each pixel intensity of each channel of the $\textsf{RGB}$ image is encrypted as discused in Section 2.2 using RSA Cryptosystem. The public key and secret key for each component are given as below.

  • 1. For red channel input matrix is $\textsf{AR}$, the public and secret keys are $p_r, q_r, n_r=p_r*q_r$, $\phi (n_r)=(p_r-1)(q_r-1), e_r, d_r=e_{r}^{-1}(\text {mod}~ n_r)$, where $(e_r, \phi (n_r))=1$ and $1<e_r<\phi (n_r)$.

  • 2. For green channel input matrix is $\textsf{AG}$, the public and secret keys are $p_g, q_g, n_g=p_g*q_g$, $\phi (n_g)=(p_g-1)(q_g-1), e_g, d_g=e_{g}^{-1}(\text {mod}~ n_g)$, where $(e_g, \phi (n_g))=1$ and $1<e_g<\phi (n_g)$.

  • 3. For blue channel input matrix is $\textsf{AB}$, the public and secret keys are $p_b, q_b, n_b=p_b*q_b$, $\phi (n_b)=(p_b-1)(q_b-1), e_b, d_b=e_{b}^{-1}(\text {mod}~ n_b)$, where $(e_b, \phi (n_b))=1$ and $1<e_b<\phi (n_b)$.

  The output matrices of this stage are $\textsf{FrR}$, $\textsf{FrG}$ and $\textsf{FrB}$.

• Step 3 (Multi-Parameter Fractional Discrete Cosine Transform (MPFrDCT)): The MPFrDCT is applied on the output matrices $\textsf{FrR}$, $\textsf{FrG}$ and $\textsf{FrB}$ as explained in Section 2.4. The initial control parameters are generated according to the conditions explained in Section 2.3.

  • 1. The initial parameters $x_0$, $y_0$ and $\rho$ are taken randomly.

  • 2. The two random sequences $\textbf{s}$ and $\textbf{t}$ are generated following the () and (2.42.5) $(1000+\nicefrac {M}{2})$ times. Each random sequence is of length $\nicefrac {M}{2}$. The sequences $\textbf{s}$ and $\textbf{t}$ are divided by $\pi$ to generate sequences $\mathbf {s'}$ and $\mathbf {t'}$. Both the sequences lie in the range [0, 2).

  • 3. Generate the sequences $\mathbf {q_1}$ and $\mathbf {q_2}$ as follows.

    $$\begin{aligned} q_{1}(j)= \left\{ \begin{array}{ll} 0, &{} \text {if}\,\,0\le \mathbf {s'(j)}\le 1 \\ 1 , &{} {1}< \mathbf {s'(j)}\le 2 \end{array} \right. \end{aligned}$$

    (3.1)
    $$\begin{aligned} q_{2}(j)= \left\{ \begin{array}{ll} 0, &{} \text {if}\,\,0\le \mathbf {t'(j)}\le 1 \\ 1 , &{} 1< \mathbf {t'(j)}\le 2 \end{array} \right. \end{aligned}$$

    (3.2)

    where $j=1, 2, ..., \nicefrac {M}{2}$.

  • 4. Apply MPFrDCT with parameters a and b.

  The output of this step are $\textsf{ATR}$, $\textsf{ATG}$ and $\textsf{ATB}$. The encryption algorithm encrypts three images together and produces a single encrypted image. The single encrypted image saves storage and communication cost. The decryption algorithm is just the reverse of the encryption algorithm. In decryption, firstly inverse MPFrDCT is applied on the encrypted image with parameters $-a$ and $-b$. Now the partially encrypted image is decrypted using RSA cryptosystem. The secret keys used in the step are $d_r$, $d_g$, and $d_b$ such that $e_rd_r\equiv 1 (\text {mod}~ \phi (n_r))$, $e_gd_g\equiv 1 (\text {mod}~ \phi (n_g))$ and $e_bd_b\equiv 1 (\text {mod}~ \phi (n_b))$. Lastly, the inverse Arnold 3D map is applied $t_1$, $t_2$ and $t_3$ times on each channel of the partially encrypted image. The inverse secret keys for RSA cyptosystem are $d_r, d_g$ and $d_b$. Finally, colour maps are added to each channel of the decrypted images to get back the original $\textsf{RGB}$ color images.

4 Simulation results

Simulation analysis is done to prove that the real world tests are conducted using the proposed encryption scheme. The three experimental images for simulation are Baboon, Lena and Peppers from top to bottom given in Fig. 3(a). Each image is an $\textsf{RGB}$ image of size $512 \times 512 \times 3$. Firstly, the colour maps are extracted from these three images to produce three indexed images $\mathsf{I_1}$, $\mathsf{I_2}$ and $\mathsf{I_3}$. Three indexed images $\mathsf{I_1}$, $\mathsf{I_2}$ and $\mathsf{I_3}$ are combined together to produce an $\textsf{RGB}$ image of size $512 \times 512 \times 3$. The public and secret keys for red channel are $p_r=59, q_r=61, n_r=3599$, $\phi (n_r)=3480, e_r=17, d_r=1433$. The public and secret keys for green channel are $p_g=73, q_g=79, n_g=5767$, $\phi (n_g)=5616, e_g=19, d_g=3547$. The public and secret keys for blue channel are $p_b=83, q_b=89, n_b=7387$, $\phi (n_b)=7216, e_b=23, d_b=1255$. Control parameters and initial guesses are set as $x_0 = 0.5489$, $y_0=0.4517$ and $\rho =0.3587$ to generate random sequences $\textbf{q}_1$ and $\textbf{q}_2$. The MPFrDCT parameters are $a=0.5762$ and $b=0.3982$. The parameters for Arnold 3D transform are set as $t_1=23$, $t_2=50$ and $t_3=87$ for red, green and blue channel respectively. These parameters are kept secret. The single encrypted image of three color images is Fig. 3(b). The parameters for decryption process are taken as follows. The inverse Arnold 3D parameters are $t_1=23$, $t_2=50$ and $t_3=87$. The inverse parameters for MPFrDCT are $-a$ and $-b$. The correctly decrypted images are displayed in Fig. 3(c).

Fig. 3

Encryption/Decryption Results

4.1 Security analysis

Security analysis is a tool to check the robustness of the encryption technique. The secret keys for the decryption of the encrypted image are $d_r=1433, d_g=3547, d_b=1255$, $t_1=23$, $t_2=50$, $t_3=87$, $x_0= 0.5489, y_0=0.4517$, $\rho =0.3587$, $a=0.5762$ and $b= 0.3982$. The images will be recovered correctly if the decrypter uses these secret keys in correct order. The encryption technique is very sensitive to secret keys. By sensitivity, we mean if we do small changes in the secret keys, the decrypter would not be able to get the original images. The sensitivity parameters are $d_r, d_g, d_b$, , $x_0, y_0$, $\rho$, $t_1$, $t_2$, $t_3$, a, and b. The sensitivity analyzes are done briefly in this Section to prove our claim.

4.1.1 Key space analysis

To check the robustness of the algorithm, key space analysis plays a vital role. There is a direct relationship between the robustness and the key space size. The secret keys involved in the proposed encryption algorithm are (i) the iteration numbers of Arnold 3D map $t_1, t_2$ and $t_3$, (ii) initial parameters $x_0$ and $y_0$, (iii) control parameter $\rho$, (iv) decryption keys $d_r, d_g, d_b$ in RSA cryptosystem and (v) fractions a and b. The hard problem in RSA cryptosystem is factoring algorithm, i.e., the factorization of $n_r, n_g$ and $n_b$. If $n_r, n_g$ and $n_b$, all are 1024 bits long, the factorization is completely infeasible. The control parameter $\rho$ and initial guesses $x_0, y_0$ are very small parameters. If we take the precision $10^{-14}$, the key would be approximately of size $10^{70}$. Also, the iteration numbers are integers and very large to withstand the exhaustive attack.

4.1.2 Key sensitivity analysis

This test is conducted to demonstrate that the secret parameters are very sensitive. The term sensitivity means the small changes in the secret parameters would not allow decrypter to decrypt images correctly. Figure 3(a) shows the three input colour images. The single encrypted image is given in Fig. 3(b). Correctly decrypted images using correct secret keys with their correct arrangements are displayed in Fig. 3(c).

Sensitivity analysis-I

This sensitivity analysis is executed using incorrect keys $d_r$, $d_g$ and $d_b$. The incorrect keys are $d_r=3547, d_g=1255, d_b=1433$. The three decrypted images using these secret keys are given in Fig. 4a(i)-(iii).

Fig. 4

a(i)-a(iii) is Sensitivity Analysis-I using wrong $d_r=3547, d_g=1255$ and $d_b=1433$, b(i)-b(iii) is Sensitivity Analysis-II using wrong iteration numbers $t_1=50, t_2=87$ and $t_3=23$ , c(i)-c(iii) is Sensitivity Analysis-III using wrong fractions $a=0.3982$ and $b=0.5762$

Sensitivity analysis-II

This sensitivity analysis is executed with incorrect iteration numbers of 3D Arnold map. The iteration parameters are $t_1=50, t_2=87$ and $t_3=23$. The three decrypted images using these secret keys are shown in Fig. 4b(i)-(iii).

Sensitivity analysis-III

This sensitivity analysis is executed with random parameters of MPFrDCT. The random parameters are $a=0.3982$ and $b=0.5762$. The other secret parameters are not changed. The three decrypted images using these secret keys are shown in Fig. 4c(i)-(iii).

Sensitivity analysis-IV

This sensitivity analysis is executed with incorrect initial parameters $x_0=0.4517$ and $y_0=0.6489$. The three decrypted images using these parameters are displayed in Fig. 5(a). The incorrect decrypted images with incorrect control parameter $\rho =0.8375$ are shown in Fig. 5(b).

Fig. 5

Sensitivity Analysis-IV using (a) wrong initial guesses $x_0=0.4517$ and $y_0=0.6489$ and (b) wrong control parameter $\rho =0.8375$

4.1.3 Robustness against CPA and CCA

The proposed encryption algorithm should resist chosen-plaintext attack (CPA) and chosen-ciphertext attack (CCA). In CPA, the attacker has access to plaintexts of his choice. He received ciphertexts for the selected plaintexts. In CCA, the attacker has access to ciphertexts of his choice. He also received the corresponding plaintexts. The attacker tries to develop a relationship between the ciphertexts and plaintexts. If he succeed in developing relationship, he would be able to guess the secret keys. The security of this cryptosystem depends upon the secret parameters as well as their arrangements. Due to vast key space, it is practically impossible to develop a relation between the plaintexts and ciphertexts. Hence the proposed encryption scheme is CPA as well as CCA secure.

4.2 Statistical analysis

The statistical analysis is conducted to effectively present the results of the proposed encryption algorithm. Entropy analysis, peak signal to noise ratio (PSNR), mean square error (MSE), correlation coefficients and histogram analysis are conducted in this Section. These tests are briefly explained as given below.

4.2.1 Entropy analysis

The randomness is measured by entropy. For an input y, the entropy H(y) is given by the following equation.

$$\begin{aligned} H(y)= & {} -\displaystyle \sum _{x=0}^{2^{n}-1}p(y_x)\log _{b}p(y_x), \end{aligned}$$

(4.1)

where logarithm of the probability $p(y_x)$ of the event $y_x$ to the base b is taken. The base b is 2 or 10. We have computed the entropy values of original Baboon, Lena , Peppers color images Fig. 3(a), encrypted image Fig. 3(b), decrypted Baboon, Lena, Peppers color images Fig. 3(c) and are given in Table 1. If the entropy of the encrypted images is the same as the entropy of the original image, then we can say that the algorithm decrypts the images correctly. It is clear from the Table 1 that the entropy of decrypted images matches with the entropy of original images. So original images are successfully recovered after encryption. If the randomness in encrypted images is less than 8, it shows the proposed algorithm can withstand any type of attack. As the randomness in encrypted images is less than 8, the proposed algorithm is secure against any type of attack.

Table 1 Entropy Analysis

4.2.2 PSNR, MSE and correlation analysis

The PSNR is the ratio of the maximum power of the signal to the power of corrupting noise. Mathematically it is expressed as a logarithmic quantity in decibel scale. It is computed between the input and output image using the following mathematical equation.

$$\begin{aligned} \text {PSNR}= & {} 10. \log _{10}\bigg (\frac{MAX_{I}^{2}}{MSE}\bigg ) = 20.\log _{10}\bigg (\frac{MAX_{I}^{2}}{\sqrt{MSE}}\bigg )\end{aligned}$$

(4.2)

$$\begin{aligned}= & {} 20. \log _{10}\bigg (MAX_{I}\bigg ) -10.\log _{10}\bigg (MSE\bigg ), \end{aligned}$$

(4.3)

where $MAX_{I}$ represents the maximum pixel intensity of the image. The higher the PSNR, the better the quality of the decrypted image.

The mean squared error (MSE) is calculated between input and output image using the following equation. It tells us how how close a regression line is to a set of points.

$$\begin{aligned} \text {MSE}= \frac{1}{M\times N}\displaystyle \sum _{m=1}^{M}\displaystyle \sum _{n=1}^{N}\bigg [\bigg |\phi (m\Delta \alpha ,n\Delta \beta )-\phi _{0}(m\Delta \alpha ,n\Delta \beta )\bigg |^{2}\bigg ], \end{aligned}$$

(4.4)

where $M \times N$ is the size of an RGB image, $\phi _0$ and $\phi$ are input and output image, $\Delta \alpha$ and $\Delta \beta$ are the sizes of pixels. The zero MSE indicates that the error is minimum in correctly decrypted images.

The correlation coefficient (CC) is also computed between input and output image. Practically, the value of this coefficient is between $-1$ and 1. The value 1 indicates the strong correlation between the two images whereas -1 represents the weak correlation. Weak correlation is also known as negatively correlated. If the value is 0, it shows no relationship between the input and output image.

The PSNR, MSE and CC of the three input images, encrypted image, decrypted images, incorrect decrypted images using wrong iteration numbers $t_1=50, t_2=87$ and $t_3=23$, wrong decrypted images using incorrect RSA secret keys $d_r=3547, d_g=1255$ and $d_b=1433$, wrong decrypted images using wrong fractions $a=0.3982$ and $b=0.5762$, wrong decrypted images using wrong initial guesses $x_0=0.4517$ and $y_0=0.6489$ and wrong decrypted images using wrong control parameter $\rho =0.8375$ are given in Tables 3–8. From the Table 2, we see that PSNR is INf, MSE is 0 and CC is 1. These values prove that the decrypted image is of good quality and is same as the original image as the error is zero. Lower PSNR, Higher MSE and zero CC values in Table 3 indicates that nothing can be retrieved from the encrypted image. The values of PSNR, MSE and CC in Tables 4, 5, 6, 7, 8 prove that the decrypted image is not of good quality.

Table 2 PSNR, MSE and CC of decrypted images

Table 3 PSNR, MSE and CC of single encrypted image

Table 4 PSNR, MSE and CC of incorrectly decrypted images with wrong iteration numbers $t_1=50, t_2=87$ and $t_3=23$

Table 5 PSNR, MSE and CC of incorrectly decrypted images with wrong RSA secret keys $d_r=3547$, $d_g=1255$ and $d_b=1433$

Table 6 PSNR, MSE and CC of incorrectly decrypted images with wrong fractions $a=0.3982$ and $b=0.5762$

Table 7 PSNR, MSE and CC of incorrectly decrypted images with wrong initial guesses $x_0=0.4517$ and $y_0=0.6489$

Table 8 PSNR, MSE and CC of incorrectly decrypted images with wrongm control parameter $\rho =0.8375$

4.2.3 Correlation analysis

The correlation coefficient gives an idea about the relationship betweens the adjacent pixels. The correlation coefficients are computed for each channel of an $\textsf{RGB}$ image following the (4.5). Table 9 represents the correlation coefficient of red, green and blue channel of three experimental images Baboon, Lena and Peppers. The Table 9 clearly shows that the pixel values are linearly correlated. The correlation coefficients of the single encrypted image are also computed and given in Table 10. The values are approximately zero. This means pixel values do not share any relation. Lastly, correlation coefficients of decrypted images are given in Table 11. The pixel values are close to 1.

$$\begin{aligned} \text {C}=\frac{\displaystyle \sum _{m=1}^{M}\displaystyle \sum _{n=1}^{N}(\nu (m,n)-\overline{\nu })(\mu (m,n)-\overline{\mu })}{\sqrt{\bigg (\displaystyle \sum _{m=1}^{M}\displaystyle \sum _{n=1}^{N}(\nu (m,n)-\overline{\nu })^{2}\bigg )\bigg (\displaystyle \sum _{m=1}^{M}\displaystyle \sum _{n=1}^{N}(\mu (m,n)-\overline{\mu })^{2}\bigg )}}, \end{aligned}$$

(4.5)

where $\nu$ and $\mu$ are the input and output image, $\overline{\nu }$ and $\overline{\mu }$ are the mean values of input and output image respectively.

Table 9 Correlation Coefficients of original images

Table 10 Correlation Coefficients of encrypted image

Table 11 Correlation Coefficients of decrypted images

4.2.4 Histogram analysis

This statistical analysis represents the number of pixels in an image at different intensity values. The histogram of each component of an $\textsf{RGB}$ image is computed. The histogram of the input Baboon colour image is given in Fig. 6(a). Figure 6(b) and (c) represent the histogram of Lena color image and Peppers color image respectively. The histogram of the single encrypted image is displayed Fig. 6(d). The histogram of the encrypted image is different from the histogram of input images Baboon, Lena and Peppers. This confirms that the proposed encryption algorithm is free from statistical attacks.

Fig. 6

Histogram analysis of (a) Baboon, (b) Lena, (c) Peppers and (d) encrypted image

4.2.5 Occlusion attack

The robustness of the technique is tested by conducting the Occlusion attack by cropping encrypted image $25\%$ and $50\%$ from all the four sides, i.e, left, right, top and bottom. The $25\%$ cropped images from all the four sides are shown in Fig. 7(a), (b), (c) and (d). The three decrypted images after $25\%$ cropping are displayed in Figs. 7(e), 8(f), (g) and 9(h). The $50\%$ cropped images from lall the four sides are given in Fig. 10(a), (b), (c) and (d). The decrypted images are given in Figs. 10(e), 11(f), (g) and 12(h), respectively. It is visually clear that the proposed encryption algorithm has successfully defended the cropping attack.

Fig. 7

(a), (b), (c) and (d) 25% Cropped Images from all the four sides (e) fully decrypted image corresponding to Fig. 7(a)

Fig. 8

(f) fully decrypted image corresponding to Fig. 7(b); (g) fully decrypted image corresponding to Fig. 7(c)

Fig. 9

(h) fully decrypted image corresponding to Fig. 7(d)

Fig. 10

(a), (b), (c) and (d) 50% Cropped Images from all the four sides (e) fully decrypted image corresponding to Fig. 10(a)

Fig. 11

(f) fully decrypted image corresponding to Fig. 10(b); (g) fully decrypted image corresponding to Fig. 10(c)

Fig. 12

(h) fully decrypted image corresponding to Fig. 10(d)

5 Comparison

We have done the comparison of our proposed encryption scheme with the existing similar schemes. Several researchers have given their contribution in the field of multiple image encryption algorithm. Some key differences are illustrated in Table 12.

Table 12 Comparison analysis

• 1. Joshi et al. [14], Wang and Zhao [34] and Liu et al. [20] have developed image encryption algorithm for multiple images. The building blocks used are double random phase and fractional Fourier transform.

• 2. Yong et al. [39] introduced a novel scheme using rotation multiplexing method. Wang and Zhao [35] proposed multiple image encryption technique in Fourier domain.

• 3. Later discrete fractional Fourier transform and Fourier transform became the epicenter of research. The image encryption algorithms in these domains are given in [29, 43]. These schemes have used chaotic maps, pixel scrambling techniques, fractional orders, and the random phase masks.

• 4. The multiple image encryption techniques are also given in Gyrator transform domain. Shi et al. [30] proposed the scheme in geometric and frequency domain. The secret key parameters are Arnold and wavelet transform.

• 5. Wu et al. introduced the concept of encryption of four images together using discrete fractional Fourier transform. The fractional orders are taken as the secret keys. Zhang and Xiao [42] presented his contribution using Chirikov standard map, discrete fractional random transform and chaotic logistic maps. The security is based on pixel scrambling operation, fractional orders and random phase masks.

• 6. Wu et al. [36] introduced triple color image encryption scheme. The building blocks incorporated are FrDCT, Arnold transform and cyclic shift. The secret keys are iteration numbers and control parameter.

• 7. Wu et al. [38] proposed an image encryption algorithm incorporating random fractional discrete cosine transform with the dependent scrambling and diffusion. The proposed algorithm can withstand common classical attacks.

• 8. Qiu et al. [27] proposed double-image encryption algorithm using discrete fractional angular transform with fractional Fourier transform. The algorithm is applied on two grey scale images.

6 Conclusions

We have introduced multi-layer secure image encryption technique using MPFrDCT, Arnold 3D transform and RSA cryptosystem. Three images are encrypted jointly to produce a single encrypted image. The single encrypted image is easy to transfer over the public channel. It saves communication and storage complexity. In the scheme, firstly three indexed images are generated by removing the color maps. The three indexed formats are taken as the three channel, i.e., $\textsf{R, G}$ and $\textsf{B}$ of an $\textsf{RGB}$ image. Firstly, Arnold 3D map is registered on the $\textsf{RGB}$ image. Later RSA cryptosystem is enforced to encrypt each pixel of the $\textsf{RGB}$ image. It is a public key cryptosystem. Lastly, MPFrDCT is incorporated on the $\textsf{RGB}$ image. The decryption is just revere of these steps. The security of the scheme depend upon secret keys as well as their proper arrangements. The robustness of the scheme is tested by simulation analysis. A detailed comparison is also done with the existing similar schemes.