1 Introduction

The recent advancements in digital imaging technology have made it possible to acquire high-quality images using a variety of capturing devices. However, the images captured in low-light environments generally exhibit degraded quality because of the limited dynamic ranges. These low-quality images degrade the performance of subsequent image processing and computer vision applications such as surveillance, object detection and tracking, and autonomous driving. Therefore, the development of effective visibility or contrast enhancement algorithms for low-light images is essential, driving a significant amount researches into improving the quality of low-light images [5, 6, 13,14,15, 18, 23, 25, 32, 36].

Contrast enhancement techniques attempt to increase the visibility of the input image by deriving a transformation function that maps input pixel values to output pixel values [10, 11, 38]. Contrast enhancement techniques can be broadly classified into two groups according to how their transformation functions are derived: global and local approaches [11]. A global approach maps all pixels in an entire input image using a single transformation function. On the contrary, a local approach derives the transformation function for each pixel adaptively using the information in its local neighborhood. However, because a local approach demands higher computational resources and its level of enhancement is more difficult to control, global techniques are more widely used in practice [11].

The most commonly used global contrast enhancement technique is histogram equalization (HE) [11] due to its simplicity and effectiveness. HE makes the output histogram approximate a uniform distribution by spreading intensity values. However, HE techniques may cause over-enhancement of the intensities frequently occurring in an image. To overcome the limitations of conventional HE and further improve its performance, many techniques have been proposed [2, 7, 17, 21, 22, 33]. However, these algorithms provide inferior enhancement performance for low-light images, since they do not consider their characteristics.

Another widely used global contrast enhancement technique is gamma correction, which derives its transformation function as a simple power function [11]. While gamma correction is simple and effective, finding an optimal parameter for a specific image or specific region of an image is important but challenging, as they have different characteristics, and thus, have different optimal parameters. To address this challenge, recent gamma correction-based contrast enhancement techniques have attempted to adaptively find optimal gamma parameters that maximize the quality of output images [9, 15, 16, 29, 36]. For example, in [15], Huang et al. determined the gamma parameter as a function of the probability distribution of pixel values in an image. Rahman et al. [29] classified images into several classes based on their statistical properties, and then, determined the gamma parameter for each class according to the characteristics of the image. In [36], Yang et al. formulated optimization problems using the median of pixel values in an image. However, as the median is a nonlinear function, the optimal parameter is obtained iteratively, leading to computational inefficiency for being employed in practical applications.

Recently, inspired by the success of convolutional neural networks (CNNs) in various image processing and computer vision tasks, many CNN-based low-light image enhancement techniques have been developed [4, 8, 12, 28, 31, 34, 37]. Furthermore, it has been shown that learning-based approaches that use CNNs provide higher enhancement performance than conventional model-based approaches. However, the main disadvantage of the learning-based approaches is that their performance is highly dependent on the training datasets. In addition, learning-based approaches generally demand higher computational and memory complexities than model-based approaches, making it difficult to employ them in applications with limited computational and memory resources.

In this work, we propose an efficient low-light image enhancement algorithm based on an optimization-based gamma correction parameter estimation. First, we divide the dynamic range of the image into dark and bright ranges. Second, inspired by the recent success of applying convex optimization to image enhancement [19,20,21,22], which shows the theoretical completeness and computational efficiency via closed-form solutions, we formulate the gamma parameter estimation for each range as a convex optimization problem that maximizes the image contrast subject to the constraint on the gamma value. By efficiently solving the optimization problems, we obtain the optimal gamma parameter for each range. Finally, we obtain an enhanced image by merging the independently enhanced dark and bright regions. Experimental results on real-world images demonstrate that the proposed algorithm provides higher-quality images than state-of-the-art algorithms, while demanding significantly lower computational complexities.

The remainder of this paper is organized as follows: Section 2 describes the proposed low-light image enhancement algorithm, and Section 3 discusses experimental results. Finally, Section 4 concludes this work.

2 Proposed algorithm

Figure 1 shows an overview of the proposed algorithm. The input RGB image is first converted into the YCbCr color space to separate the luminance and chrominance information, and then the luminance channel is normalized. Then, the input image is segmented into dark and bright regions. Next, the contrast of the dark and bright regions in the image are enhanced independently using the optimal gamma correction parameter for each region. Finally, we obtain an enhanced image by merging the enhanced dark and bright regions.

Fig. 1
figure 1

Overview of the proposed algorithm. First, we normalize the luminance map of an input image, and then, separate the luminance map into dark and bright regions. Next, we enhance the contrast of the luminance map for dark and bright regions independently based on the optimal gamma correction parameter estimation. Finally, we obtain the output image by fusing the enhanced dark and bright regions

Full size image

2.1 Luminance normalization

The perceptual contrast in a color image is mainly determined by the luminance channel [30]. Thus, we enhance the contrast of the luminance channel while maintaining the consistency of color information. To this end, in this work, we first obtain luminance information by transforming the color space. Specifically, we convert the color input image in the RGB color space into the YCbCr color space, which is a the most frequently used color space in digital imaging systems. Y is the luminance component, while Cb and Cr are the blue-difference and red-difference chrominance components, respectively [30]. The luminance component Yi is given by

$$ Y_{i}(x,y) = 0.299 {{I}_{i}^{R}}(x,y)+0.587 {{I}_{i}^{G}}(x,y)+0.114 {{I}_{i}^{B}}(x,y), $$
(1)

where \({{I}_{i}^{R}}\), \({{I}_{i}^{G}}\), and \({{I}_{i}^{R}}\) denote the intensities of the red, green, and blue channels, respectively, of the input image. Then, we normalize the luminance values to the range [0,1] using the logarithmic function as

$$ Y_{L}(x,y) =\log_{M}(Y_{i}(x,y) + \varepsilon), $$
(2)

where \(M = \max \limits (Y_{i}(x,y))\), and ε is set to 1 to enforce YL to be positive.

2.2 Optimal gamma correction parameter estimation

Gamma correction obtains the output pixel value y given the input pixel value x using the power function with parameter γ as

$$ \begin{array}{@{}rcl@{}} & y = x^{\gamma}, \end{array} $$
(3)

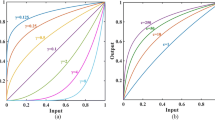
where x and y are normalized to the range [0,1]. Note that, while gamma correction in (3) is simple and effective, finding an optimal parameter for a specific image is challenging, as they have different optimal parameters due to different characteristics. We also observe that, when γ < 1, gamma correction in (3) improves the brightness and contrast of dark regions in the image, while pixel value clipping may occur in bright regions. On the contrary, when γ > 1, it can recover the details of bright regions, but excessively darkens dark regions.

In this work, to address the aforementioned limitation of gamma correction, we develop an algorithm that selects two different gamma values for the dark and bright regions of the image. Thus, we first divide the histogram of the input image into two parts: dark and bright regions, with a threshold of 0.5. In particular, the bright region contains the pixels with YL(x,y) > 0.5, whereas those with YL(x,y) ≤ 0.5 belong to the dark region.

Then, we estimate the optimal parameters for the bright and dark regions independently by considering the statistical properties of the input images inspired by the recent work in [36]. Specifically, the optimal gamma parameter is determined to equalize the average and standard deviation of the luminance intensities in each range. In [36], the median value of the pixel luminance intensities is shown to be effective in enhancing the contrast and recovering the details in the dark and bright regions, respectively. However, computation of the median is nonlinear; thus, their algorithm finds the optimal gamma parameters iteratively in a set of predetermined parameter candidates, demanding higher computational resources. Instead, we use the average, which leads to convex optimization, to estimate the optimal gamma values more efficiently, as we will describe in detail.

As mentioned earlier, we obtain the optimal gamma parameter by equalizing the average and the standard deviation of the luminance intensities in each region. Because the optimal parameter estimation procedures in the two regions are almost identical, we describe only the dark region, i.e., 0 < γd ≤ 1. Specifically, let \(\mathbf {s}_{d} = [s_{d,1}, s_{d,2}, \ldots , s_{d,N_{d}}]^{T}\) denote the vector of original pixel values in the dark range. Then, each pixel value in sd is transformed by gamma correction in (3) with parameter γd. Therefore, the gamma-corrected pixel values in the output image can be compactly written as \(\phi ^{\gamma _{d}}(\textbf {s}_{d}) = \left [{s}_{d,1}^{\gamma _{d}}, {s}_{d,2}^{\gamma _{d}}, \ldots , {s}_{d,N_{d}}^{\gamma _{d}}\right ]^{T}\). We attempt to improve the brightness and contrast by equalizing the average intensity value of the output image with the standard deviation of intensities in the input image. In addition, the optimal parameter γd should satisfy the constraint 0 < γd ≤ 1 to increase the brightness. Thus, we can formulate a constrained optimization problem, i.e.,

$$ \begin{array}{ll} \underset{\gamma_{d}}{\text{minimize}} & \displaystyle \left( \frac{1}{N_{d}}\mathbf{1}^{T}\phi^{\gamma_{d}}(\textbf{s}_{d}) - \sigma_{d} \right)^{\!2} \\ \text{subject to} & 0 < \gamma_{d} \leq 1, \end{array} $$
(4)

where 1 denotes a column vector, all elements of which are one. In addition, σd and Nd are the standard deviation of pixel values and the number of pixels in the dark range, respectively. Note that the cost function in (4) is convex, since it is an exponential function, and the feasible constraint set is convex. Thus, the optimization in (4) is a convex optimization problem, which ensures that a solution, if it can be found, is a global solution, and it can be solved efficiently by employing convex optimization theories.

To solve the optimization, we first define the Lagrangian \({\mathscr{L}}: \mathbb {R}\times \mathbb {R}\times \mathbb {R} \rightarrow \mathbb {R}\) associated with the problem in (4) as

$$ \mathcal{L}(\gamma_{d}, \mu, \lambda) = \left( \frac{1}{N_{d}}\mathbf{1}^{T}\phi^{\gamma_{d}}(\textbf{s}_{d}) - \sigma_{d} \right)^{\!2} -\mu\gamma_{d} + \lambda(\gamma_{d}-1), $$
(5)

where μ and λ are the Lagrange multipliers for the constraints. Then, we can write the Karush-Kuhn-Tucker (KKT) conditions [3] for (5) as

$$ \begin{array}{@{}rcl@{}} \phantom{\frac{2}{N_{d}}\!\left( \frac{1}{N_{d}}\mathbf{1}^{T}\phi^{\gamma_{d}}(\textbf{s}_{d}) - \sigma_{d}\right) \!\sum\limits_{i=1}^{N_{d}} {s}_{d, i}^{\gamma_{d}}}0 < \gamma_{d} &\leq 1, \end{array} $$
(6)
$$ \begin{array}{@{}rcl@{}} \mu, \lambda &\geq 0, \end{array} $$
(7)
$$ \begin{array}{@{}rcl@{}} \mu\gamma_{d} &= 0, \end{array} $$
(8)
$$ \begin{array}{@{}rcl@{}} \lambda(\gamma_{d}-1) &= 0, \end{array} $$
(9)
$$ \begin{array}{@{}rcl@{}} \frac{2}{N_{d}}\!\left( \frac{1}{N_{d}}\mathbf{1}^{T}\phi^{\gamma_{d}}(\textbf{s}_{d}) - \sigma_{d}\right) \!\sum\limits_{i=1}^{N_{d}} {s}_{d, i}^{\gamma_{d}} \ln{s_{d, i}} - \mu + \lambda &= 0. \end{array} $$
(10)

From the primal feasibility in (6) and the complementary slackness in (8), μ = 0. Thus, we can rewrite the KKT conditions in (6)–(10) as

$$ \begin{array}{@{}rcl@{}} 0 < \gamma_{d} &\leq 1, \end{array} $$
(11)
$$ \begin{array}{@{}rcl@{}} \lambda &\geq 0, \end{array} $$
(12)
$$ \begin{array}{@{}rcl@{}} \lambda(\gamma_{d}-1) &= 0, \end{array} $$
(13)
$$ \begin{array}{@{}rcl@{}} \frac{2}{N_{d}}\!\left( \frac{1}{N_{d}}\mathbf{1}^{T}\phi^{\gamma_{d}}(\textbf{s}_{d}) - \sigma_{d}\right) \!\sum\limits_{i=1}^{N_{d}} {s}_{d, i}^{\gamma_{d}} \ln{s_{d, i}} + \lambda &= 0. \end{array} $$
(14)

Since we now have a single complementary slackness condition in (13), we consider two cases:

  • Case 1: γd = 1.

  • Case 2: λ = 0.

In Case 1, since 0 < sd,i ≤ 0.5, \({\sum }_{i=1}^{N_{d}} s_{d, i}\ln {s_{d, i}} < 0\). Thus, in (14), the term \(\frac {1}{N_{d}}\mathbf {1}^{T}\phi ^{1}(\textbf {s}_{d}) - \sigma _{d} = \frac {1}{N_{d}}{\sum }_{i=1}^{N_{d}} s_{d, i}-\sigma _{d}\) must be non-negative. However, both values, \(\frac {1}{N_{d}}{\sum }_{i=1}^{N_{d}} s_{d, i}\) and σd, depend on the pixel value distributions of the input image; thus, it may become negative, which violates the stationarity condition in (14). In Case 2, the stationarity condition in (14) becomes

$$ \frac{2}{N_{d}}\!\left( \frac{1}{N_{d}}\mathbf{1}^{T}\phi^{\gamma_{d}}(\textbf{s}_{d}) - \sigma_{d}\right) \! {\sum}_{i=1}^{N_{d}} {s}_{d, i}^{\gamma_{d}}\ln{s_{d, i}} = 0. $$
(15)

Thus, we obtain the optimal γd that satisfies (15). Let us recall that sd,i denotes a pixel value in the dark region, i.e., 0 < sd,i ≤ 0.5. Therefore, \({\sum }_{i=1}^{N_{d}} s_{d, i}^{\gamma _{d}}\ln {s_{d, i}} < 0\) always holds true, and we can rewrite (15) as

$$ \frac{1}{N_{d}}\mathbf{1}^{T}\phi^{\gamma_{d}}(\textbf{s}_{d}) - \sigma_{d} = \frac{1}{N_{d}}\sum\limits_{i=1}^{N_{d}} {s}_{d, i}^{\gamma_{d}}-\sigma_{d} = 0, $$
(16)

and find the solution to (16).

In this work, since (16) is differentiable, we employ Newton’s method [27] to find the optimal solution iteratively. Specifically, let \({\gamma }_{d}^{(n)}\) denote the value of γd at the n th iteration. Then, starting from \({\gamma }_{d}^{(1)} = 1\), we update γd by

$$ {\gamma}_{d}^{(n)} = {\gamma}_{d}^{(n-1)} - \frac{{\sum}_{i=1}^{N_{d}} {s}_{d, i}^{\gamma^{(n-1)}_{d}}-\sigma_{d}}{{\sum}_{i=1}^{N_{d}} {s}_{d, i}^{\gamma^{(n-1)}_{d}}\ln{s_{d, i}}}, \quad n=2,3,{\ldots} $$
(17)

until convergence. More specifically, we define the convergence rate at the n th iteration as \(\xi ^{(n)} = |{\gamma }_{d}^{(n)} - {\gamma }_{d}^{(n-1)}|\) and run the iteration until ξ(n) < 10− 7.

Next, we obtain the optimal gamma value γb for the bright range in a similar manner. However, the optimal gamma value should satisfy the constraint 1 < γb ≤ 10 in the optimization in (4). In addition, the standard deviation of pixel values in the bright region is set to σb = 1 − σd, assuming that the dark pixels are dominant in low-light images.

2.3 Fusion of corrected images

The two optimal gamma values γd and γb are then used independently to enhance the luminance intensities Yd and Yb in the dark and bright regions, respectively, via (3). Next, we apply an image fusion technique, which is the process of combining relevant information from multiple images into a single image [30], to obtain the output luminance map. Specifically, we obtain the enhanced luminance map Yo by the weighted sum of the two gamma corrected images adaptively as

$$ Y_{o}(x,y) = w(x,y) {Y}_{d}^{\gamma_{d}}+(1-w(x,y)) {Y}_{b}^{\gamma_{b}}(x,y), $$
(18)

where w(x,y) is a spatially varying weight to control the relative contribution of each region to the enhanced luminance, given by

$$ w(x,y) = \exp\!\left( -\frac{Y_{b}(x,y)^{2}}{2{{\sigma}_{w}^{2}}} \right)\!. $$
(19)

The parameter σw, which determines the sensitivity of the weight to the luminance value in the dark range, is fixed to 0.5 to provide the best subjective quality.

2.4 Adaptive color restoration

The proposed algorithm enhances the contrast of the image in the luminance domain in (18). Thus, we should obtain the color channels of the enhanced image from the luminance channel. Therefore, in this work, based on the observation that higher saturation values in the bright regions in images cause dazzling, we attenuate the saturation of pixel colors with bright intensity. More specifically, we use the following mapping

$$ {I}_{o}^{c}(x,y) = Y_{o}(x,y)\!\left( \frac{{{I}_{i}^{c}}(x,y)}{Y_{i}(x,y)} \right)^{\!s(x,y)}, $$
(20)

where Yi and Yo are the luminance values of the input and output images, respectively. \({I}_{i}^{c}\) and \({I}_{o}^{c}\) are the input and output color components, respectively, where c ∈{R,G,B}. The exponent s, which is less than 1, is a saturation parameter and represents the correlation between the input and output color components. In this work, we set \(s(x,y) = 1-\tanh (Y_{b}(x,y))\) to make it luminance-adaptive.

3 Experimental results

We evaluate the performance of the proposed low-light enhancement algorithm on the test images in the Exclusively Dark (ExDark) dataset [24] both qualitatively and quantitatively. The dataset contains 7,363 images captured under low-light conditions. We report the results on five images: Bicycle, Bus, Table, Station, and Street in the dataset as shown in Figs. 2, 3, 4, 5 and 6. We compare the performance of the proposed algorithm with those of five conventional low-light image enhancement algorithms: Huang et al.’s algorithm [15], Lim et al.’s algorithm [23], Guo et al.’s algorithm [13], Yang et al.’s algorithm [36], and Loh and Chan’s algorithm [25]. The proposed algorithm is implemented in two ways for formulating the cost function in (4): using the median value (Median) and using the average value (Average) of the pixel luminance intensities. All parameter settings in the conventional algorithms were determined to provide the best overall subjective quality. For reproducibility, we also provide our MATLAB implementation on our project website.Footnote 1

Fig. 2
figure 2

Low-light image enhancement results for the Bicycle image. The input image in a is enhanced by b Huang et al.’s algorithm [15], c Lim et al.’s algorithm [23], d Guo et al.’s algorithm [13], e Yang et al.’s algorithm [36], f Loh and Chan’s algorithm [25], the proposed algorithms using g the median and h the average

Full size image
Fig. 3
figure 3

Low-light image enhancement results for the Table image. The input image in a is enhanced by b Huang et al.’s algorithm [15], c Lim et al.’s algorithm [23], d Guo et al.’s algorithm [13], e Yang et al.’s algorithm [36], f Loh and Chan’s algorithm [25], the proposed algorithms using g the median and h the average

Full size image
Fig. 4
figure 4

Low-light image enhancement results for the Bus image. The input image in a is enhanced by b Huang et al.’s algorithm [15], c Lim et al.’s algorithm [23], d Guo et al.’s algorithm [13], e Yang et al.’s algorithm [36], f Loh and Chan’s algorithm [25], the proposed algorithms using g the median and h the average

Full size image
Fig. 5
figure 5

Low-light image enhancement results for the Station image. The input image in a is enhanced by b Huang et al.’s algorithm [15], c Lim et al.’s algorithm [23], d Guo et al.’s algorithm [13], e Yang et al.’s algorithm [36], f Loh and Chan’s algorithm [25], the proposed algorithms using g the median and h the average

Full size image
Fig. 6
figure 6

Low-light image enhancement results for the Street image. The input image in a is enhanced by b Huang et al.’s algorithm [15], c Lim et al.’s algorithm [23], d Guo et al.’s algorithm [13], e Yang et al.’s algorithm [36], f Loh and Chan’s algorithm [25], the proposed algorithms using g the median and h the average

Full size image

Figures 2–6 compare the enhancement results for the test images. Huang et al.’s algorithm tends to under-enhance dark regions in input images, providing dark results, e.g., the front of the bus in Fig. 4b and the road in Fig. 6b. While Lim et al.’s algorithm performs well in contrast enhancement, it provides blurred results with detail losses due to its excessive denoising, especially on the surface of the road in Fig. 2c and the mountain in Fig. 5c. Guo et al.’s algorithm produces overall good enhancement results, but tends to yield over-exposure artifacts, e.g., the legs in Fig. 3d. Yang et al.’s algorithm and the proposed algorithm using the median tend to lose color saturation, because the median is less effective in measuring the contrast of the image. Moreover, Yang et al.’s algorithm results in the intensity reversal, e.g., the bright window in Fig. 3e. In contrast, Loh and Chan’s algorithm and the proposed algorithm provide comparable and better enhancement results with less visible artifacts. However, as will be discussed later, the proposed algorithm requires significantly less computational resources than Loh and Chan’s algorithm.

Next, we compare the results of the proposed algorithm with those of the conventional algorithms using four objective quality metrics: natural image quality evaluator (NIQE) [26], measure of enhancement (EME) [1], patch-based contrast quality index (PCQI) [35], and quality-aware relative contrast measure (QRCM) [6]. In all metrics, a higher score implies better performance.

  • NIQE: The NIQE metric [26] quantifies the naturalness of an image using statistical features, which are derived from a set of natural undistorted images, related to a natural scene statistics model.

  • EME: EME [1] approximates the average contrast in an image by computing scores based on the minimum and maximum intensities in the non-overlapping blocks and then averaging them.

  • PCQI: PCQI [35] predicts the human perception of contrast variations between an image pair based on adaptive representations of local patch structures, i.e., mean intensity, signal strength, and signal structure.

  • QRCM: The QRCM metric [6] quantifies the relative change in contrast and distortion on the output image relative to the input image by measuring the gradient magnitude difference between the input and output images.

Table 1 shows the quantitative comparisons of the low-light image enhancement results on the test images. For each metric, the best and the second best results are boldfaced and underlined, respectively. First, since the proposed algorithm enhances the contrast via the optimal parameter, the proposed algorithm shows the highest NIQE scores, providing the most natural results. Second, the proposed algorithm also provides the best overall performance in terms of EME and PCQI, since the proposed algorithm effectively maintains local details. Third, Yang et al.’s algorithm [36] and the proposed algorithm provide comparable performance in terms of QRCM. Finally, the median-based formulation in the proposed algorithm provides comparable or even better performance than Yang et al.’s algorithm. By using the average-based formulation, the proposed algorithm further improves the enhancement performance by significant margins. To summarize, since the proposed algorithm provides higher-quality images, it yields the overall highest scores in terms of these metrics.

Table 1 Quantitative comparison of the image enhancement results using four quality metrics: NIQE [26], EME [1], PCQI [35], and QRCM [6]. For each metric, the best and the second best results are boldfaced and underlined, respectively
Full size table

Finally, we evaluate the computational complexity of the proposed algorithm with those of conventional algorithms. Table 2 compares the execution times required to process all test images shown in Figs. 2–6. We used a PC with a 2.2 GHz CPU and 8 GB RAM in this test. All algorithms were straightforwardly implemented in MATLAB without code optimization. Lim et al.’s algorithm [23] requires the longest computation time, since it employs an iterative image decomposition scheme. Loh and Chan’s algorithm [25] also requires significant computation time due to its patch-based processing. Huang et al.’s [15], Guo et al.’s [13], and Yang et al.’s algorithms [36] shorten the time significantly. The proposed algorithm using the average value drastically reduces the time further by efficiently solving the convex optimization problem, which is iteratively solved in [36] due to its nonconvex formulation. The advantage of the proposed average-based formulation is confirmed by the fact that the computation times of Yang et al.’s algorithm and the proposed algorithm using the median value are comparable. Note that we iteratively apply the formula in (17) to find an optimal solution, but the average number of iterations for all test images is only 3.42. These results indicate that the proposed algorithm performs better than conventional algorithms while demanding significantly less computational resources. Therefore, the proposed algorithm is efficient enough to be employed in a wide range of practical applications, even in devices with limited computational resources, which is infeasible with conventional algorithms [13, 15, 23, 25, 36].

Table 2 Average computation times in seconds of Huang et al.’s algorithm [15], Lim et al.’s algorithm [23], Guo et al.’s algorithm [13], Yang et al.’s algorithm [36], Loh and Chan’s algorithm [25], and the proposed algorithms for the test images
Full size table

4 Conclusions

We proposed an efficient gamma correction-based low-light image enhancement algorithm by developing an optimization-based parameter estimation scheme. We first separated an input image into the luminance and chrominance channels, and then normalized the luminance image. Next, we divided the luminance image into dark and bright regions, and then formulated a convex optimization problem for each region to maximize the image contrast subject to the constraint on the gamma value. By efficiently solving the optimization problems using convex optimization theories, we obtained the optimal gamma correction parameter for each region. Finally, we obtained an enhanced image by merging the enhanced dark and bright regions obtained using the optimal parameters. Experimental results on real-world images demonstrated that the proposed algorithm outperforms state-of-the-art algorithms in terms of both subjective and objective qualities, while requiring significantly lower computational complexities.