1 Introduction

With the development of information technology, a lot of information is being generated all the time. Senders and receivers of information do not want information to be accessed by unauthorized others. Thus, they encrypt information in ciphertext forms that are difficult for third parties to understand. Among all forms of information, image information is widely used because of its intuitive, visual and information-rich characteristics. It is regrettable that the traditional encryption methods, such as Advanced Encryption Standard (AES) and Rivest-Shamir-Adleman (RSA), are not suitable for image encryption. Such methods are characterized by poor encryption effect, slow speed, and poor practicability when used for encrypting information with a large amount of data or strong correlation between adjacent pixels, such as images or videos. Fields such as medicine [28], aerospace, education, the military, and others all need to encrypt images. Therefore, an encryption algorithm suitable for images is needed to achieve good encryption effect, high efficiency, effectively reduce the correlation of adjacent pixels, and have the ability to resist various attacks. And numerous encryption algorithms have been proposed, including the DNA code [5, 23, 29, 33], cellular automata encryption [11, 20, 24, 32], wavelet transform encryption [4, 37], chaos encryption [2, 25] and True Random Number Generator (TRNG) [30]. Among these schemes, the chaos encryption algorithm has been widely used for encryption owing to its advantages of satisfactory randomness, high sensitivity to initial values, high complexity, ergodicity, and the encryption time is shorter than others which used DNA or cellular automata, etc.

In terms of an encryption algorithm based on a digital chaotic map, its security not only depends on the performance of the chaotic map and superiority of the encryption algorithm but also on calculation accuracy. Theoretically, chaos map has the characteristics of aperiodic, unpredictability, aperiodic and pseudo-random. It is regrettable that owing to the influence of truncation and round-off errors, the trajectory of chaotic map will eventually fall into a period when running on finite-precision equipment. Numerous studies have shown that when map enters a cycle, the dynamic characteristics of digital chaotic map will degrade, and the security of the encryption algorithm based on chaotic map will be reduced and become vulnerable to attacks. To solve this problem, various methods have been proposed, which can be divided into the following. 1) Expand the precision [9, 34]. In the methods, chaotic map will fall into a period owing to the limitation of the precision. Expanding precision can prolong the time of chaotic map entering a period. However, this effect is limited, as precision cannot be magnified indefinitely. Thus, chaotic map will eventually fall into a period. 2) A different method involves combining multiple maps [7, 17, 21, 40]. There are two types of combination: cascading and switching. Cascading and switching both ignore the possible interactions of multiple maps, which would not be reflected in a small number of experiments. Moreover, the problem of each map itself cannot be solved, and the effect of its combination depends on the superiority of the strategy. 3) Another method is perturbing map [14,15,16, 18], including perturbing parameters and perturbing states, in which constants, variables, functions, or a chaotic map can be selected as the perturbation source. An appropriate disturbance object and source are selected according to cost and effect. The main difficulty lies in how to select the appropriate disturbance source and disturbance object, whether it will cause excessive extra cost. 4) The feedback control method [10, 12, 38]. Utilizing the state function to control the state variables of digital chaotic map, thereby destroying the original state space. However, digital chaotic map performance cannot be improved significantly using only this method, working better when combined with other methods. Based on the above methods, we propose a new method based on perturbation and feedback control. We choose the parameter and the state variable of the map itself as the disturbance source, resulting in no additional cost. The parameter and the state variable of the current map perturb with each other, update the parameter according to the current state variable, update the current state variable with the updated parameters, and finally use a nonlinear function to carry out feedback control on the state variables, thus destroying the state space and increasing the randomness and complexity of the generated chaotic sequence.

Among the various chaotic maps, the 1D logistic map is a classical type that is widely used owing to its simple structure, small number of parameters, easy implementation, and low cost. However, because it has few parameters and a simple structure, this chaotic map has low security and can be cracked easily; moreover, its period is short under low computing precision. Hence, in this study, we propose a method based on double perturbation and feedback control to improve the 1D logistic map to suppress dynamic degradation. The state variable and system parameter perturb each other and introduce a nonlinear function as a feedback function to destroy the state space. The experimental results show that the improved logistic map can achieve better statistical and cryptographic properties, including ergodicity, ideal autocorrelation, high approximate entropy (ApEn) and permutation entropy (PE), and satisfactory randomness, compared with the original logistic map. Furthermore, we design a new image encryption algorithm as a simple application based on the improved map. The simulation results show that the encryption algorithm based on the improved map demonstrates high security and can resist different types of attacks.

Overall, the significant advantages of the improved method include the following. 1) The method uses the parameter and the state variable of the map itself as the perturbation source, does not introduce an external system or a high-dimensional analog chaotic system as a perturbation source, thereby reducing implementation costs. 2) This novel hybrid method can considerably reduce the dynamical degradation of a digital Logistic map. (3) This method is universal to all digital chaotic maps.

The rest of the paper is organized as follows. In Section 2, we take Logistic map and Baker map as examples to prove the model we proposed is universal, and the effect is good. A simple image encryption algorithm based the improved Logistic map is proposed in Section 3. The security analysis results are presented in Section 4, and Section 5 concludes the paper.

2 Improved model

2.1 Models of original and improved logistic maps

The 1D Logistic map is one of the most widely used chaotic maps in chaos-based encryption algorithm. The mathematical model of Logistic map can be described as

$$ {x}_{i+1}=a{x}_i\left(1-{x}_i\right) $$
(1)

Where a is the system parameter and a ∈ (3.56,4], xi is the state variable of the i-th iteration. Theoretically, the 1D Logistic map has pseudorandom trajectories and satisfactory ergodicity in the phase space [0, 1]. However, if the map is simulated on a computer or other finite precision devices, dynamical degradation emerges. The output trajectory will fall into a cycle, and the phase space will not traverse the entire space.

To reduce the dynamical degradation in the digital logistic map, we propose a perturbation and feedback hybrid control method. Utilizing the current state variable to update parameters, and then using the updated parameters to perturb the current state variable. By perturbing the state variable and the parameter of the current map with each other and using the state feedback function to destroy the state space, the original chaos map can be improved and the dynamic degradation of the original chaos map can be suppressed.

First, system parameter a is perturbed by current state variable xi as

$$ p(i)=\left\{\begin{array}{c}a+\left(4-a\right)x(i)\kern4em i=1\\ {}a+\left(4-a\right)\frac{\left(x(i)+x\left(i-1\right)\right)}{2}\kern2.25em i>1\end{array}\right. $$
(2)

where p(i) is the perturbed parameter, x(i − 1) and x(i) are the state variables. The value 4 of the equation represents the maximum value within the value range of system parameters. In the parameter perturbation, p(i) is always changed with the current and the last state variables, which demonstrate satisfactory randomness.

And then the current state variable x(i) is perturbed by the updated parameter p(i):

$$ h(i)={10}^3\times p(i)\times x(i)\ \mathit{\operatorname{mod}}\ 1 $$
(3)

where p(i) is the previously perturbed parameter, and h(i) is the perturbed state variable. mod 1 means to produce a value between the range [0, 1). The following mod 1 is the same, no more tautology.

Finally, an improved Logistic map is constructed by the perturbed parameter, the perturbed state variable and a nonlinear function. Here, we select the sine function as the feedback function owing to its simple structure and low cost. The mathematical model of the improved Logistic map can be described as follows:

$$ x\left(i+1\right)=p(i)\ast h(i)\ast \left(1-h(i)\right)+\sin \left(\pi \ast h(i)\right)\mathit{\operatorname{mod}}\ 1 $$
(4)

Where p(i) is determined by Eq. (2), h(i) is determined by Eq. (3). Not only can sine function be used as feedback function, but any nonlinear function can be used as well. There is no obvious difference in improvement effect. If use the cosine function as a feedback function, the equation can be described as

$$ x\left(i+1\right)=p(i)\ast h(i)\ast \left(1-h(i)\right)+\cos \left(\pi \ast h(i)\right)\mathit{\operatorname{mod}}\ 1 $$
(5)

And under the same parameters, the trajectory of the chaotic sequence generated by this equation does not enter a loop after more than 4000 iterations, the point distribution in the phase diagram is random and dense, the graph of the autocorrelation function is close to δ function. This indicates that the correlation of values at different times in the sequence is very low. The original 1D Logistic map will enter into a period even after the accuracy reaches 230. The improved method using cosine function as feedback function cannot detect the period after the accuracy reaches 222, while the improved method using sine function as feedback function cannot detect the period after the accuracy reaches 220. And after stabilization, the ApEn and the PE are 1 and 2.1, respectively, with little difference from the improved method with sine function as feedback function. Therefore, the nonlinear function here can be selected according to the situation. Just for security reasons, we can choose a more complex nonlinear function, such as more complex exponential functions, etc. The nonlinear function is selected according to the user’s needs, here only take sine and cosine as examples.

The idea of this perturbation method is universal to all digital chaotic maps, and the general model can be described as follows:

$$ x\left(i+1\right)=F\left(p(i),h\left(p(i),x(i)\right),\kern0.5em m\left(h\left(p(i),x(i)\right)\right)\right) $$
(6)

Where function F represents an any chaotic map, p(i) is the parameter perturbed by the state variable, h(p(i), x(i)) is the new state variable combining the perturbed parameter and the current state variable. m(h(p(i), x(i))) is the non-linear feedback function which uses the new state variable h as the input parameter.

2.2 Models of original and improved baker maps

For example, 2D Baker map is improved using the method we proposed. The original 2D Baker map can be described as:

$$ \left(x\left(i+1\right),y\left(i+1\right)\right)=\left\{\begin{array}{c}\left(\frac{x(i)}{a}, ay(i)\right)\kern4.75em 0<x(i)\le a\\ {}\left(\frac{\left(x(i)-a\right)}{\left(1-a\right)},\left(1-a\right)y(i)+a\right)\kern1.75em a<x(i)\le 1\end{array}\right. $$
(7)

Where a ∈ (0, 1) is the chaotic control parameter. The perturbed parameter is:

$$ p(i)=\left\{\begin{array}{c}a+\left(1-a\right)x(i)\kern4em i=1\\ {}a+\left(1-a\right)\frac{\left(x(i)+x\left(i-1\right)\right)}{2}\kern2.25em i>1\end{array}\right. $$
(8)

And then update the state variable x(i) and y(i) by the perturbed parameter to obtain h1(i) and h2(i):

$$ h1(i)={10}^3\times p(i)\times x(i)\ \mathit{\operatorname{mod}}\ 1 $$
(9)
$$ h2(i)={10}^3\times p(i)\times y(i)\ \mathit{\operatorname{mod}}\ 1 $$
(10)

Finally, the improved 2D Baker map can be described as:

$$ \left(x\left(i+1\right),y\left(i+1\right)\right)=\left\{\begin{array}{c}\left(\frac{h1(i)}{p(i)}+\sin \left(\pi \ast h1(i)\right)\mathit{\operatorname{mod}}\ 1,p(i)h2(i)\right)\ 0<x(i)\le p(i)\\ {}\left(\frac{\left(h1(i)-p(i)\right)}{\left(1-p(i)\right)},\left(1-p(i)\right)h2(i)+p(i)\right)\kern1.25em p(i)<x(i)\le 1\end{array}\right. $$
(11)

The performance before and after the improvement is shown in Section 2.4. It is proved that our method is universal to all digital chaotic maps.

2.3 Performance analysis of the improved logistic map

Several properties of the improved and original Logistic map are analyzed to evaluate the improved version, including the trajectory and phase space, autocorrelation function, sensitivity to initial value, ApEn, PE and the step size before entering into the period.

2.3.1 Trajectory and phase diagram

An ideal chaotic map should have a random-like trajectory and satisfactory ergodicity in the phase space. Precision is set to p = 12, control parameter and initial value are set to a = 3.99, x0 = 0.3215, respectively. Figure 1a and b show the trajectories of the original and improved Logistic maps, respectively. From the figure, the original logistic map iterates less than 200 times before entering a cycle. However, though the improved map iterates more than 4000 times, it does not enter a cycle. Figure 2a and b present the phase diagrams of the original and improved logistic maps with a precision of 2−16, respectively. The phase diagram of the original map is a fixed shape similar to a U shape, and its density is also relatively low. However, the phase diagram of the improved map has a discrete distribution with no fixed shape, and its density is higher than that of the original map. The improved map destroys the original state space through the interaction perturbation of parameters and states, thereby resulting in increased security.

Fig. 1
figure 1

Trajectory diagrams of the (a) original Logistic map and (b) improved Logistic map

Full size image
Fig. 2
figure 2

Phase diagrams of (a) original Logistic map and (b) improved Logistic map

Full size image

2.3.2 Autocorrelation analysis

Auto-correlation functions describe the correlation between two values in a sequence. In an ideal chaotic map, autocorrelation will quickly decay along with the interval in one sequence. Thus, the autocorrelation function will be similar to the δ-function. By generating two sequences from the original and the improved Logistic map with a precision of 2−18, we plot autocorrelation functions in Fig. 3a and b. Figure 3a shows that the autocorrelation coefficient will decrease with increased or reduced interval and increase suddenly in particular intervals. Figure 3b demonstrates that the autocorrelation of the improved map is similar to the δ function, which will rapidly decrease to 0, except that the interval is 0. This indicates that the autocorrelation of the sequence generated by the improved map quickly decay along with the interval. That is to say, the correlation of any two values in the sequence is very low.

Fig. 3
figure 3

Autocorrelation function diagrams of (a) original Logistic map and (b) improved Logistic map

Full size image

2.3.3 Period analysis

A digital chaotic map would enter a cycle finally at finite compute precision. The step length before the map enters a cycle is a key measure for investigating dynamical degradation. Three group initial values of the original and improved logistic maps are selected, and their step length before entering the cycle is calculated. The results are shown in Table 1, where the original map is vulnerable to computing precision, and the improved map is more stable. Furthermore, the step length of the improved map is longer than that of the original map, which is more suitable for encryption.

Table 1 The step length before enter the cycle
Full size table

2.3.4 Sensitivity to initial conditions

Sensitivity to initial conditions can be described as follows. If the control parameters are fixed, then the generated sequences will differ completely by two initial conditions with subtle differences. An ideal chaotic map should have satisfactory sensitivity to initial conditions. In other words, the sequences generated by the ideal chaotic map will change dramatically when the initial values are only slightly changed. In this test, we set the fixed parameter to a = 3.99, precision p is 12, and the initial values are x0 = 0.3215. We change the parameters a = 3.99 + 2−12 and x0 = 0.3215 + 2−12, respectively. The generated sequences are compared in Fig. 4, which shows that though we change the size by one bit, the two generated sequences are completely different, which proves that the improved map demonstrates satisfactory sensitivity to initial values.

Fig. 4
figure 4

Sensitivity analysis of initial condition

Full size image

2.3.5 Complexity analysis

ApEn and PE

In general, ApEn and PE are used to evaluate the complexity of chaotic maps. ApEn measures the probability of the new pattern generated in the sequences with the growing embedding dimension [26]. The larger the probability, the more complex the sequence. PE is a complexity measure, which was introduced in [3]. PE compares the size of several consecutive values in the sequence and sums up different order types. Then Shannon’s entropy is used to measure the uncertainty of these ordering. This measure can be implemented easily and is computationally faster than other comparable methods, such as Lyapunov exponents, while also being robust to noise. The PE of an ideal random sequence should be close to 1. Set a = 3.99 and x0 = 0.3125 and calculate the ApEn and PE of the sequences generated by the original and improved Logistic map with different compute precisions. The results are shown in Figs. 5 and 6. The figures indicate that for ApEn and PE, the entropy values of the improved sequence are higher than those of the original. The PE of the improved map is very close to 1, which is the ideal value. The sequences generated by the improved map are complex.

Fig. 5
figure 5

ApEn analysis with different precisions

Full size image
Fig. 6
figure 6

PE analysis with different precisions

Full size image

Lyapunov exponent and information entropy

Lyapunov exponent [22] λ can characterize the motion of the system, it is also used to attest the chaotic dynamics of the system. A chaotic map with positive LE will have completely diverged trajectories after a certain number of iterations, while a larger LE value is an indicator of higher unpredictability and sensitivity. That is to say, for chaotic systems, there must be a positive Lyapunov exponent, and the bigger the exponent, the better the chaotic performance. From the Figs. 7 and 8, it’s obvious that the improved map has wider parameter range, higher Lyapunov exponent and better chaotic performance, which indicates that our method effectively improves the performance of the original map and suppress the dynamical degradation.

Fig. 7
figure 7

Lyapunov exponent diagram of the 1D Logistic map

Full size image
Fig. 8
figure 8

Lyapunov exponent diagram of the improved Logistic map

Full size image

The concept of information entropy was first proposed by Shannon, who used information entropy to describe the uncertainty of information source. The higher the entropy is, the more uncertain the information is. When a = 3.8 and x0 = 0.3125, the information entropy of the sequence generated by the improved map is 2.5, and the improved one is 3.2730.

NIST randomness test based on the chaotic sequence

Randomness testing of a sequence determines whether the test sequence is truly random or the difference between the test sequence and true randomness. Hypothesis testing is the basis of randomness testing techniques. The most common sequence randomness test is the NIST test [31]. We performed NIST tests on the chaotic sequence {x} generated by the 1D improved Logistic map. In this experiment, 1,000,000 bits of sequence were selected for NIST test, and the results are shown in Table 2.

Table 2 The NIST test results of {x}
Full size table

In the NIST random test, p < 0.01 means that the random sequence fails the test item, and the sequence is not random. Table 1 shows that the p values of the 15 test items are greater than the significance level (0.01). The p values of 11 items (block-frequency, Cumulative Sums, Runs, Longest Run of Ones, Non Periodic Template, Overlapping Template, Approximate Entropy, Random Excursions, Random Excursions Variant, Linear Complexity, and Serial) are more than 0.5. These results show that the sequence generated by the improved map is random, and the security of the algorithm is guaranteed.

2.3.6 Bifurcation analysis

The control parameter of chaotic maps dictates their chaotic behavior. Some maps, such as 1D Logistic map have a small range of chaotic parameter values that result in chaotic behavior, whereas the remaining values lead to non-chaos. And the size of parameter directly affects the size of key space. Therefore, a wider range of chaotic parameters is particularly desirable for chaotic cryptographic algorithms. Figures 9 and 10 show the bifurcation diagrams of the original and the improved 1D Logistic map. According to the two figures, it’s clear that the improved map has chaotic behavior in a wider range of the chaotic parameters.

Fig. 9
figure 9

bifurcation diagram of the 1D Logistic map

Full size image
Fig. 10
figure 10

bifurcation diagram of the improved Logistic map

Full size image

2.3.7 State-mapping network

The state-mapping network(SMN) of a digital map in a small-precision digital domain can work as an efficient tool for classifying its structure and coarsely verify its randomness [13]. The state-mapping network, like the scale index [6], is an evaluation criterion for the randomness of chaotic maps. In an SMN, every possible value in the digital domain is considered as a node and the mapping relationship between any pair of nodes is a directed edge, differing from the traditional approaches treating a digital chaotic map as a black box with different explanations according to the test results of the output. And Figs. 11 and 12 show the SMN of the original and the improved map under the computing precision of 5, respectively. From the figures, it’s clear that the average length of the orbit of the improved map is larger than that of original, which proves the effectiveness of the improved method.

Fig. 11
figure 11

SMN of the original Logistic map

Full size image
Fig. 12
figure 12

SMN of the improved Logistic map

Full size image

2.4 Performance analysis of the improved baker map

Precision is set to p = 12, control parameter and initial value are set to a = 0.59, x0 = 0.3215, y0 = 0.4215, respectively. From the trajectory diagrams, we can find that the improvement method is effective and extend of the time before entering a cycle. The phase diagram of the improved Baker map is more random and denser, which indicates that the improvement method is effective. And the auto-correlation analysis shows that the shape of the improved map is similar to δ function. That is to say, the correlation of any two values in the sequence is very low, the sequence is random. Under the precision, the periods of the original and the improved map are 11 and 260, the step lengths before entering the period are 80 and 2009, respectively. These two groups of numbers show the effectiveness of the method proposed, which can restrain the dynamic degradation of chaotic maps and effectively extend the period of chaos maps. The complexity of the sequence generated by the improved map is better than the original one, too.

3 Simple cryptosystem based on the improved model

This section mainly introduces a simple image encryption based on the improved Logistic map. And the algorithm is suitable to color and grayscale image. Bring two different initial values, x and y, to the improved 1D Logistic map and then obtained two chaotic sequences, {X} and {Y}. After row and column substitution, use sequence {X} to scramble the pixel position of the substituted image to enhance the scrambling effect. Then, sequence {Y} is used to diffuse the image matrix. Finally, a fixed value L is obtained by calculating the pixel sum of the plaintext image itself, which is used to fold the diffused image to obtain the final cipher text image.

3.1 Secret key structure

As shown in Fig. 13, the secret key of the proposed cryptosystem comprises five parts, including system parameter a ∈ (3.56,4), initial values x, y ∈ (0, 1), flip substitution length L ∈ [1,256), and the average pixel value of the image, b ∈ (0, 1). Where the formulas for calculating L and b are stated in Section 3.2. If the image is RGB color image, the image is divided into R, G and B channels, then three b values and three L values will emerge, that is, br, bg, bb, Lr, Lg and Lb, representing the b value and L value of each channel, as shown in Fig. 14.

Fig. 13
figure 13

Secret key structure of gray image

Full size image
Fig. 14
figure 14

Secret key structure of colored image

Full size image

3.2 Image encryption algorithm and decryption algorithm

To prove the effectiveness and applicability of our method, we design a simple colored image encryption algorithm based on the improved logistic map. The encryption algorithm is easy. Thus, its security is based mainly on the improved logistic map, which implies that the improved logistic map demonstrates high cryptographic security and can be used in cryptography.

If the plaintext image is in grayscale, it is used directly for encryption. And if the plaintext image is a colored image, the image only needs to be divided into three channels, R, G and B, and then each channel is respectively encrypted. Finally, merge the three encrypted results together to obtain the cipher text image. We take the encryption of a gray image as an example to introduce the encryption algorithm.

  1. Step 1.

    Assume P is the plain image with the size of M × N. Convert the plain image P into image A with a size of 256 × 256. Set the secret keys, a, x, y.

  2. Step 2.

    Update initial values x and y using the average pixel of the image A, b value. This operation relates the initial value of the chaotic map to the plaintext image. The function mean(·) represents the average value.

$$ b= mean(A)- floor\left( mean(A)\right) $$
(12)
$$ {x}^{\prime }=x+b\ \mathit{\operatorname{mod}}\ 1 $$
(13)
$$ {y}^{\prime }=y+b\ \mathit{\operatorname{mod}}\ 1 $$
(14)
  1. Step 3.

    Compute the fixed length L, which is used to fold image, taking it as a component of the secret key.

$$ L= mean(A)\ \mathit{\operatorname{mod}}\ 255+1 $$
(15)
  1. Step 4.

    Set the row index to i = 1, and the column index to j = 1.

  2. Step 5.

    In the image A, swap the i-th row with the p-th row and the j-th column with the q-th column. The generation of p and q is shown below.

$$ p= round\left( mean\left(A\left(i,:\right)\right)+b\right)\ \mathit{\operatorname{mod}}\ 256+1 $$
(16)
$$ q= round\left( mean\left(A\left(:,j\right)\right)+b\right)\ \mathit{\operatorname{mod}}\ 256+1 $$
(17)

where A(i,:) represents the i-th row of the image A, A(: j) represents the j-th column. The function round(·) is a quantization function, rounding off to an integer.

  1. Step 6.

    Repeat steps 4 and 5 for i = 1 ~ 256, thereby obtaining substituted image B. Scan permutated image B from top to bottom and left to right to generate sequence {B}.

  2. Step 7.

    Bring the updated initial value, x′ and y′, into the improved Logistic map to generate two sequences, that is, {X} and {Y}. Sequence {B} is shuffled using the sort index of sequence {X}, obtaining the permutated sequence {C}.

$$ \left\{{X}_{s1},{X}_{s2},{X}_{s3},{X}_{s4},\dots \right\}= sort\left(\left\{X\right\}\right) $$
(18)
$$ \left\{C\right\}=\left\{{B}_{s1},{B}_{s2},{B}_{s3},{B}_{s4},\dots \right\} $$
(19)

where sort(·) is the sort function, which takes the sequence value from small to large.

  1. Step 8.

    Transform sequences {C} and {Y} from 1D sequences to 2D matrices C and Y, whose sizes are 256 × 256. The two matrices are XORed to obtain cipher text matrix E′.

$$ {E}^{\prime }=C\oplus Y $$
(20)
  1. Step 9.

    Using the previously calculated L value, flip the cipher text image as shown in Fig. 15. Next, obtain the final encrypted image E.

Fig. 15
figure 15

Encrypted image E′

Full size image

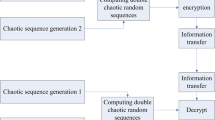
The decryption process is the reverse of the encryption process. The values of b and L are passed to the recipient as part of the secret keys. The flow charts of the entire encryption process, decryption process, and process for the colored image are shown in the Figs. 16, 17 and 18, respectively.

Fig. 16
figure 16

Flowchart of the encryption process for grayscale image

Full size image
Fig. 17
figure 17

Flowchart of decryption process for the grayscale image

Full size image
Fig. 18
figure 18

Flowchart of encryption/decryption process for the colored image

Full size image

3.3 Simulation results

The colored Lena image, the grayscale cameraman image, the black image and the white image are taken as examples. The computing precision is set to n = 2−16 and a = 3.99, x0 = 0.8215, y0 = 0.532. Let the computing precision be 2−16 in the subsequent numerical experiments unless an additional description exists. Figures 19, 20, 21 and 22 show the simulation results of the color image, grayscale image, black image and white image, respectively. The encrypted image no longer provides information on the plain image, and the decrypted image is the same as the plain image, thereby indicating that the algorithm is effective.

Fig. 19
figure 19

Colored Lena image; a plain image; b encrypted image; and (c) decrypted image

Full size image
Fig. 20
figure 20

Grayscale cameraman image; a plain image; b encrypted image; and (c) decrypted image

Full size image
Fig. 21
figure 21

Black image; a plain image; b encrypted image; and (c) decrypted image

Full size image
Fig. 22
figure 22

White image; a plain image; b encrypted image; and (c) decrypted image

Full size image

4 Performance analysis and comparison

4.1 Key space

The key space of a secure encryption algorithm should be larger than 2128 [7]. As shown in Section 3.1, for the gray image, when the computing precision is 10−16, the key space is 0.44 × 1016 × 1 ∗ 1016 × 1 × 1016 × 1 × 1016 × 255 × 1016 = 1.112 × 1082 ≈ 2259 ≫ 2128, which is larger than ones in Ref. [1] (2156) and Ref. [39] (2256). For the colored image, 0.44 × 1016 × 1 ∗ 1016 × 1 × 1016 × (1 × 1016)3 × (255 × 1016)3 = 0.44 × 2553 × 10144 ≫ 2128, which is larger than ones in Ref. [2] (1070) and Ref. [36] (1088). Therefore, we can conclude that whether the image is grayscale or colored, the key space is sufficiently large to resist different types of brute-force attacks.

4.2 Histogram analysis

The histogram shows the distribution of the pixel intensity values for the images. Figure 23 shows the pixel intensity distribution of the plain and encrypted images of the colored Lena image and the grayscale cameraman image. The figures show that the distribution of the original image is not uniform, but the cipher image is nearly uniform. Figures 23c and 24c illustrate that the decrypted image completely preserves the information of the plain image. And the Fig. 25a and b shows the histogram diagrams of the encrypted black and the white image, respectively. Therefore, the algorithm has high resistance to statistical analysis attacks.

Fig. 23
figure 23

Histogram results of colored Lena image; a plain image; b encrypted image; and (c) decrypted image

Full size image
Fig. 24
figure 24

Histogram results of grayscale cameraman image; a plain image; b encrypted image; and (c) decrypted image

Full size image
Fig. 25
figure 25

Histogram results of encrypted (a) the black image; b the white image

Full size image

4.3 Correlation analysis

Pixel correlation is a common method for evaluating the performance of the image encryption algorithm. In the image, the reduction of the correlation of adjacent pixels is a requirement for a secure encryption algorithm. The correlation of two adjacent pixels is measured as follows:

$$ {\rho}_{xy}=\frac{\sum_{i=1}^N\left({x}_i-E(x)\right)\left({y}_i-E(y)\right)}{\sqrt{\sum_{i=1}^N{\left({x}_i-E(x)\right)}^2{\sum}_{i=1}^N{\left({y}_i-\mathrm{E}(y)\right)}^2}} $$
(21)

where x and y are two adjacent pixels, and N is the sample counts, and \( E(x)=\frac{1}{N}{\sum}_{i=1}^N{x}_i \), \( E(y)=\frac{1}{N}{\sum}_{i=1}^N{y}_i \). The distribution of adjacent pixels in different directions is shown in Fig. 26. In Figs. 26a-c, the Lena image has a strong correlation between adjacent pixels in the horizontal, vertical and diagonal directions. Figure 26d-f show that the points of the encrypted image are full of space and distribute randomly, with no obvious distribution characteristics. Furthermore, Table 3 presents the value of ρxy for the different algorithms. For both algorithms, the values between two adjacent pixels are substantially reduced, but our method is relatively satisfactory.

Fig. 26
figure 26

Distribution of adjacent pixels; a horizontal direction of plain image; b vertical direction of plain image; c diagonal direction of plain image; d horizontal direction of encrypted image; e vertical direction of encrypted image; f diagonal direction of encrypted image

Full size image
Table 3 Correlation coefficients of different algorithm
Full size table

4.4 Key sensitivity

Key sensitivity is the degree of result changes when the key is only slightly changed during the encryption process and the decryption process. A satisfactory image encryption algorithm should demonstrate outstanding key sensitivity. Figure 27 shows that during the encryption process, the encrypted images differ considerably if one secret key is changed only by 2−16. The proposed cryptosystem remains extremely sensitive to minimum step size 2−16 in the encryption and decryption processes and thus reliable in practical applications.

Fig. 27
figure 27

Key sensitivity tests results; a plain image; b encrypted image; c encrypted image with a + 2−16; d subtraction of (b) and (c); e encrypted image with x + 2−16; f subtraction of (b) and (e); g encrypted image with y + 2−16; h subtraction of (b) and (g); i decrypted image; j decrypted image with a + 2−16; k decrypted image with x + 2−16; and (j) decrypted image with y + 2−16

Full size image

In addition to the direct experiments mentioned above, a numerical experiment is conducted to detect key sensitivity by calculating the mean square error (MSE) to evaluate the sensitivity.

$$ MSE=\frac{1}{M}{\sum}_{i=1}^M{\left({y}_i-{x}_i\right)}^2 $$
(22)

where yi represents the pixel of the changed image, and xi represents the pixel of the original image. The initial values and parameters of the encryption system are changed in a small range to calculate their MSE values and compare them. The results are showed in Fig. 28. From the figure, it’s obvious that regardless of the parameter, their MSE values are large and 0 only when the change is 0. That is to say, only the correct key can be successfully decrypted or encrypted. Minor changes in the key will lead to large errors during the encryption process or decryption process.

Fig. 28
figure 28

MSE tests results; the encryption process: a MSE of x; b MSE of y; and (c) MSE of a; the decryption process: d MSE of x; e MSE of y; and (f) MSE of a

Full size image

4.5 Information entropy analysis

Information entropy is used to evaluate the randomness of images, and the entropy of an information source is

$$ H(m)={\sum}_{i=1}^Mp\left({m}_i\right)\mathit{\log}\frac{1}{p\left({m}_i\right)} $$
(23)

where m represents a message source, M is the total number of symbols, and p(mi) is the probability of symbol mi [8]. For a 256 × 256 grayscale image, the maximum information entropy is 8. The results of the different algorithms are listed in Table 4. As we use a colored image as the sample, three channels exist. Thus, we list information entropy values at three different channels. Table 3 shows that regardless of the channel, the information entropy is close to the ideal value of 8. Therefore, obtaining visual information from an encrypted image is nearly impossible, even with relatively low precision.

Table 4 Information entropy of different algorithms
Full size table

4.6 Analysis of resistance to differential attacks

A differential attack is an effective method and the most common mode of attack. Thus, resistance to differential attacks is important. The number of pixel changing rate (NPCR) and unified average changed intensity (UACI) are two common methods for measuring ability to resist differential attacks. Our cryptosystem is evaluated by the mathematical model established in [35]. The NPCR and UACI are as follows:

$$ NPCR\left(C1,C2\right)={\sum}_{i=1}^M{\sum}_{j=1}^N\frac{\left|\mathit{\operatorname{sign}}\left(C1\left(i,j\right)-C2\right(i,j\left)\right)\right|}{MN} $$
(24)
$$ UACI\left(C1,C2\right)={\sum}_{i=1}^M{\sum}_{j=1}^N\frac{\left|C1\left(i,j\right)-C2\Big(i,j\Big)\right|}{MNF} $$
(25)

where M × N is the size of the plain image, C1 and C2 represent two different images of the same size, F is the largest allowed pixel value in the images, and sign(·) is the symbol function. If C1(i, j) = C2(i, j), then |sign(·)| =0, otherwise, |sign(·)| =1. M = N = 256, and F = 255 are set. The ideal value of the NPCR is 0.9961, and the ideal value of the UACI is 0.3346. Table 5 shows the NPCR and the UACI of the different algorithms for the colored Lena image. The values of our method are close to ideal values and competitive with those of other algorithms.

Table 5 NPCR and UACI of different algorithms
Full size table

4.7 Robustness analysis against noise and occlusion attacks

To further analyze the security of the proposed algorithm based on the improved Logistic map, robustness to noise and occlusion attacks is detected. In a satisfactory image encryption algorithm, the pixel changes of the encrypted image should have less impact on the decryption process. The tests results are shown in Figs. 29 and 30. Figure 29 indicates that though three different noises are added to the ciphertext image, it can still decrypt the correct original image. To prove the ability of the algorithm to resist data loss attacks, we process the ciphertext images and obtain images with loss ratios of 0.1, 0.2, and 0.3 with different directions. The images are decrypted separately, and the result is shown in Fig. 30 The two figures illustrate that the proposed method based on the improved logistic map exhibits strong robustness to noise and occlusion attacks.

Fig. 29
figure 29

Robustness against noise attack; encrypted image with (a) 0.2 salt and pepper noise; b 0.02 speckle noise; and (c) 0.02 gaussian noise; decrypted image with (d) 0.2 salt and pepper noise; e 0.02 speckle noise; and (f) 0.02 gaussian noise

Full size image
Fig. 30
figure 30

Robustness against occlusion attack; encrypted image with (a) 0.3 data loss; b 0.1 data loss; and (c) 0.2 data loss; decrypted image with (d) 0.3 data loss; e 0.1 data loss; and (f) 0.2 data loss

Full size image

5 Conclusion

In this study, a new and improved method is proposed to improve the original 1D Logistic map to suppress the dynamical degradation of the digital chaotic map. The method includes the interaction perturbation of system parameters and state variables as well as a nonlinear feedback function. We use the original Logistic map as the sample. This improved method is also applicable to other maps. We evaluate the performance of the improved Logistic map, and the results show that the map has a wide distribution, high complexity and randomness, and a sufficiently large length before entering a cycle under low computing precision. Thus, the improved logistic map demonstrates satisfactory dynamic performance and a wide application prospect. To prove practicability and applicability, we design a new, simple colored image encryption algorithm based on the improved map. We utilize the colored Lena image as the sample image. When the computing precision is 2−16, the simulation results demonstrate that the performance of this encryption algorithm is excellent in all aspects and highly resistant to different attacks. Therefore, the proposed algorithm is applicable to devices with finite computing precision. In the future, we will propose a better encryption algorithm based on this improved method. Reduce costs as much as possible while ensuring safe performance. Achievements notwithstanding, more properties and applications of various chaotic maps and encryption algorithm call for further exploration in the near future.